Beyond Importance Scores: Interpreting Tabular ML by Visualizing Feature Semantics
Abstract
:1. Introduction
1.1. Our Contribution
1.2. Related Literature
2. Materials and Methods
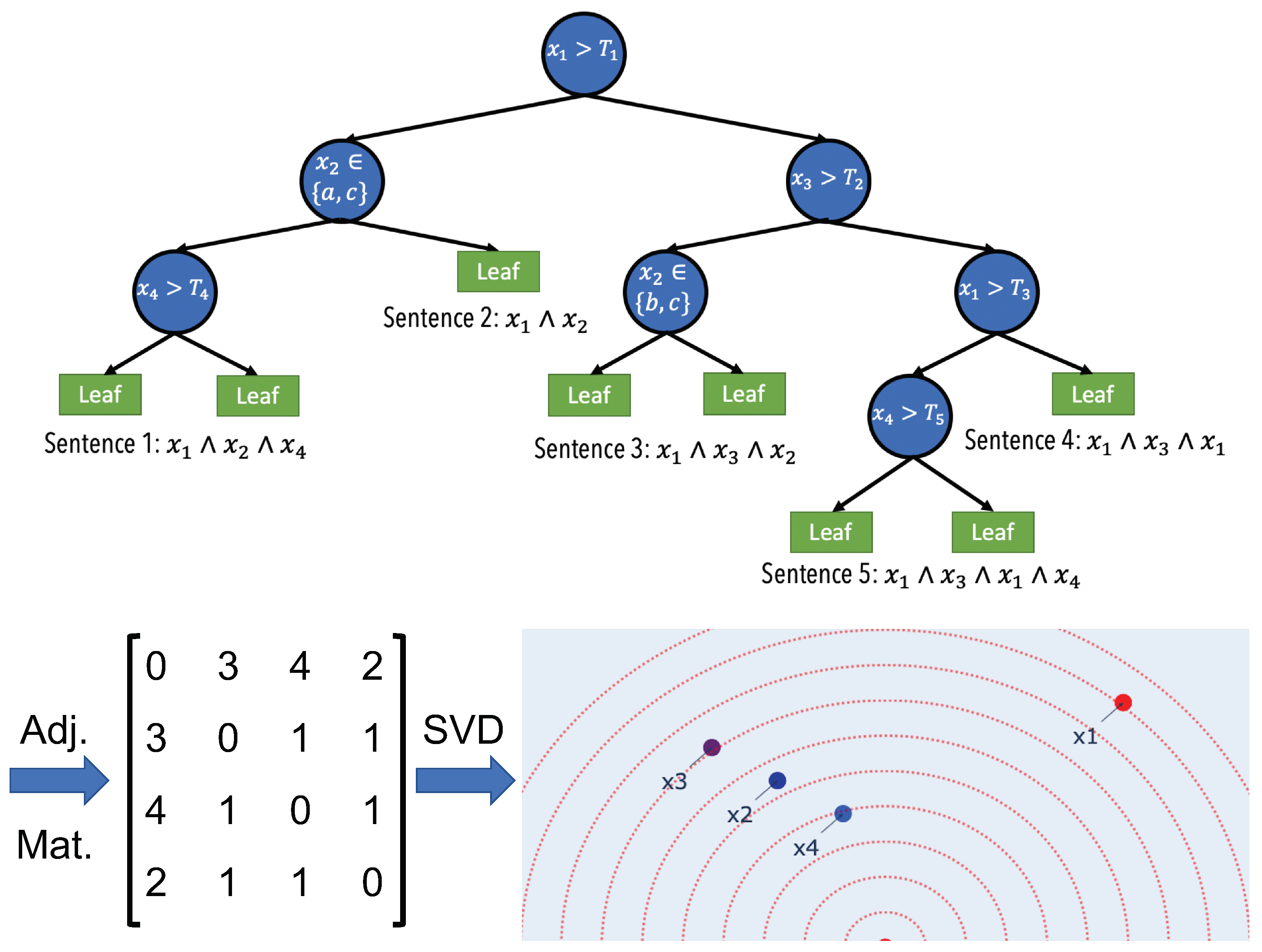
2.1. Semantic Embedding
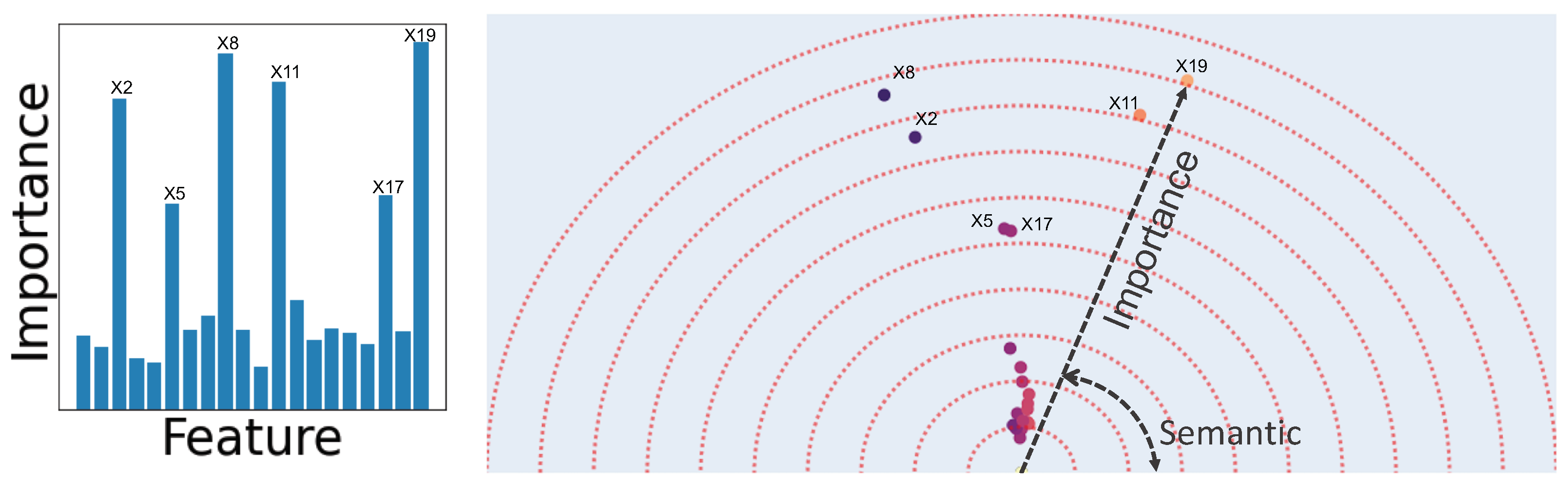
2.2. Feature Importance
2.3. Human-Understandable Visualization
2.4. Feature Vectors Algorithm
| Algorithm 1 Feature Vectors |
|
2.5. Comparison with Existing Methods
3. Experiments and Results
3.1. Easy to Implement
| 1 | from featurevec import FeatureVec |
| 2 | from sklearn.ensemble import RandomForestClassifier |
| 3 | X, y, feature_names = data_loader () |
| 4 | predictor = RandomForestClassifier ().fit (X, y) |
| 5 | fv = FeatureVec ( |
| 6 | mode = ’classify ’, |
| 7 | feature_names = feature_names, |
| 8 | tree_generator = predictor |
| 9 | ) |
| 10 | fv.fit (X, y) |
| 11 | fv.plot () |
3.2. Case Studies on Real-World Datasets
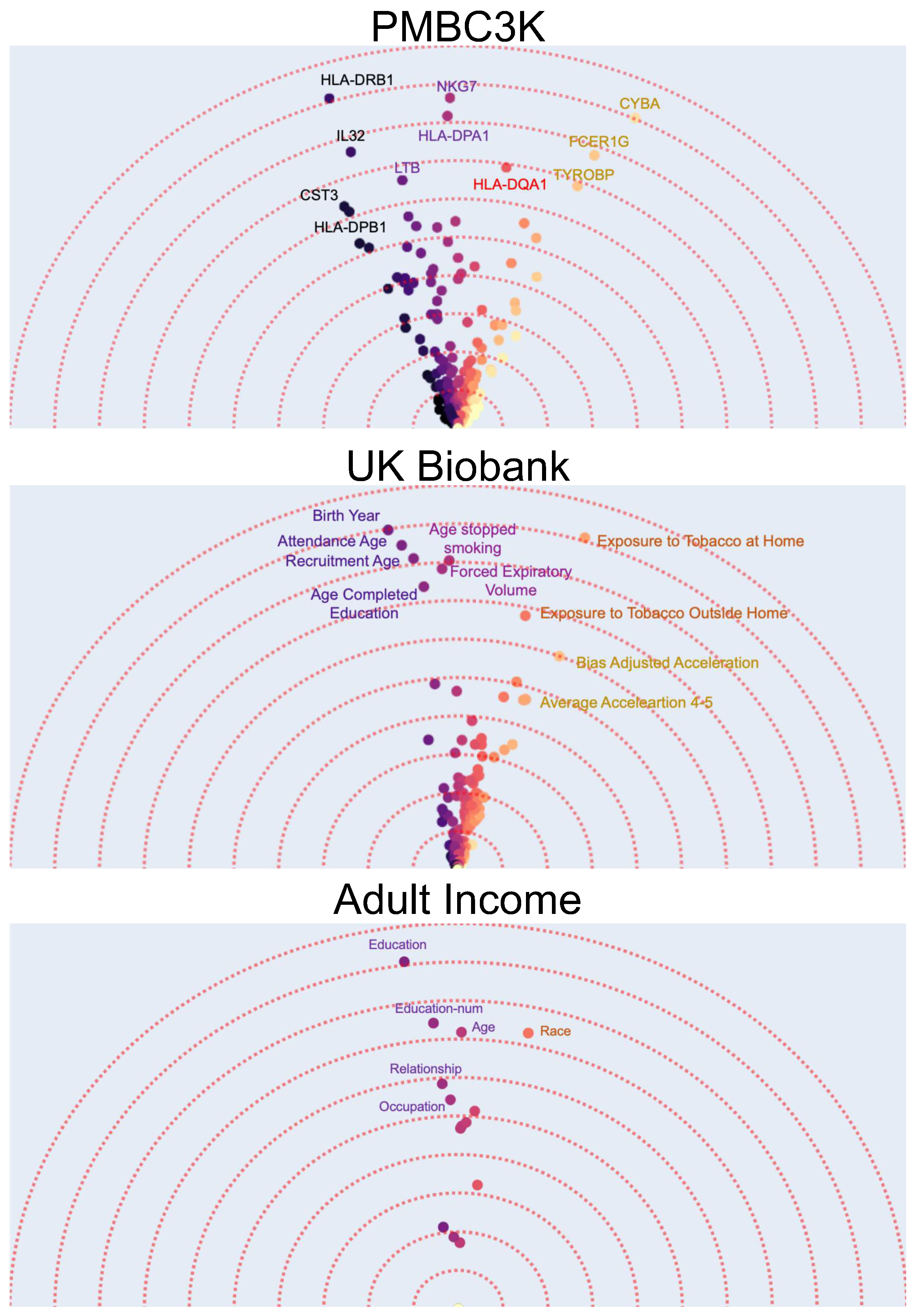
- The first dataset contains gene expression of around 1800 genes for 3000 peripheral blood mononuclear cells (PBMCs) from a healthy donor [55] i.e., each data point is a single cell and has 1800 numerical features. Using K-means algorithm, the data points are clustered into eight different groups. The task is a binary prediction with a goal to predict whether a given cell is normal (i.e., belongs to the largest cluster) or not. Using interpretability methods after training a binary classifier model on this dataset can allow us to find the important (e.g., top-10) features (i.e., gene expressions). These could potentially be used as “marker genes” that determine if a cell is normal or not. Using Feature Vectors, however, in addition to finding the marker genes by their importance, we have a more detailed interpretation of how the different marker genes interact in determining if a cell is normal (Figure 3a). A gene can be characterized as important not just by the magnitude of it’s contribution but also by it’s uniqueness. In this case, it can be observed that the effects of marker genes can be clustered into four major groups with similar genes. Furthermore, although the HLA-DQA1 gene is not among the top-5 genes with the highest feature-importance, it is an important marker as it is unique and does not have any other similar genes to it.
- As our second dataset we use the UK Biobank dataset [56]. The UK Biobank dataset has comprehensive phenotype and genotype information of 500,000 individuals in the UK. This information includes among others gender, age, medical history, diet, etc. Using the original dataset and specifically the medical history data, we create a new dataset by selecting the subset of individuals (data points) that are later diagnosed with lung cancer and randomly selecting another equally large subset of individuals that do not get lung cancer. The result is a new binary classification dataset where the task is to predict whether a person will be diagnosed with lung cancer. We use the 341 phenotypic features that have the least number of missing values in the dataset. It is known that a number of phenotypic factors can be used to predict lung cancer but it might not be clear whether they all carry similar information. Therefore, after applying the Feature Vectors algorithm to this dataset, we can investigate the high importance features and how they cluster together. Figure 3 shows that there are three main groups of phenotypic features. A group of features that are related to age and how much time has passed since the person stopped smoking, a group of features that show the overall exposure to tobacco, and a group of features that describe the activity level.
- As out last dataset, we choose the classic and frequently used adult income prediction dataset from the UCI repository of machine learning datasets [57,58]. This dataset is extracted from census data and contains demographical information (marital status, education, etc.) of around 50 thousand individuals. The task is to predict whether their income is above 50 thousand dollars. After applying the Feature Vectors algorithm to this dataset, we can see that education (including education-num), age, and race are the best predictors. An interesting observation is that education as a categorical feature and education-num as a numerical feature are semantically similar while education is a better predictor. This is expected as the number of years of education is an approximate indicator of education level.
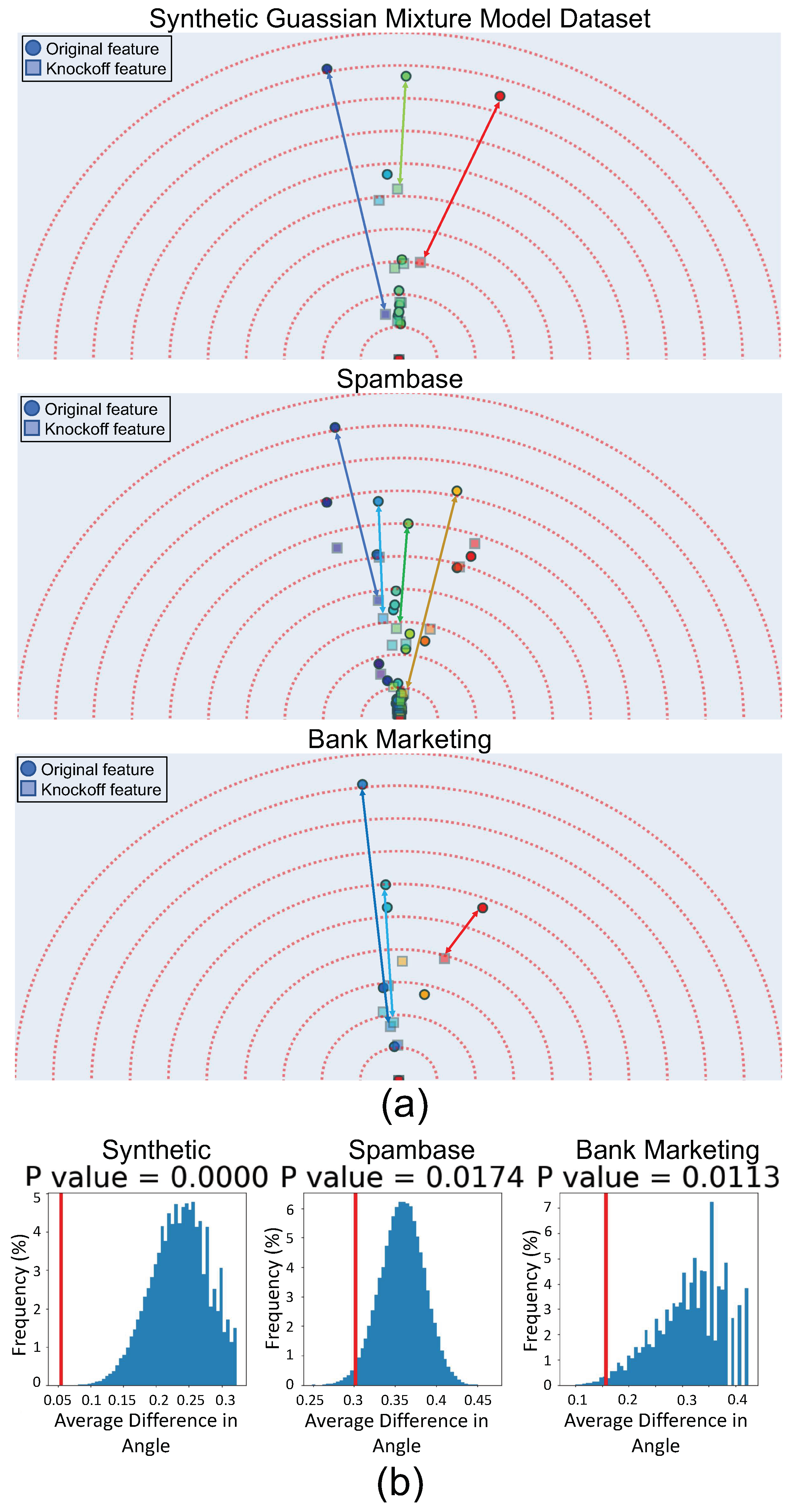
3.3. Validating Feature Vector Angles Using Knockoffs
- Conditional independence from outcome:
- Exchangeability
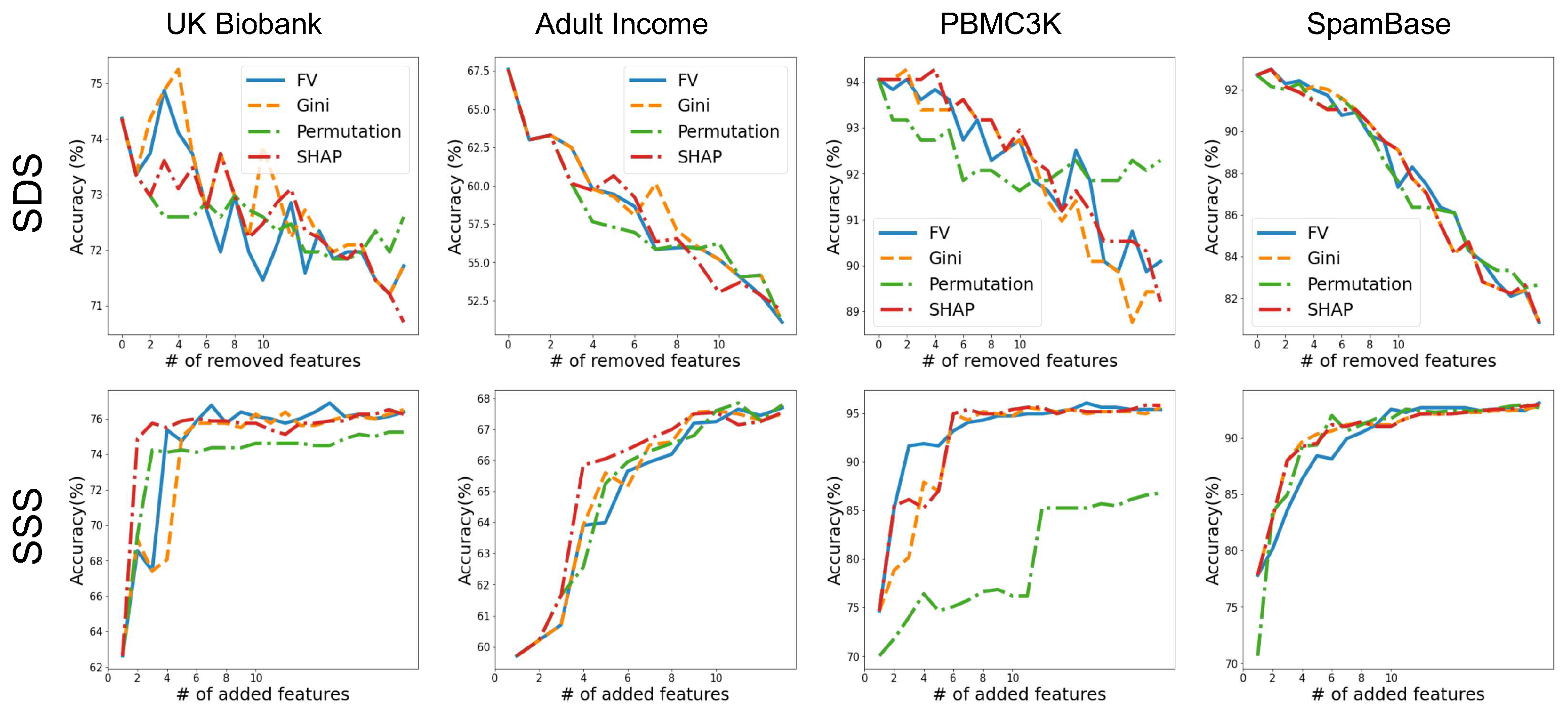
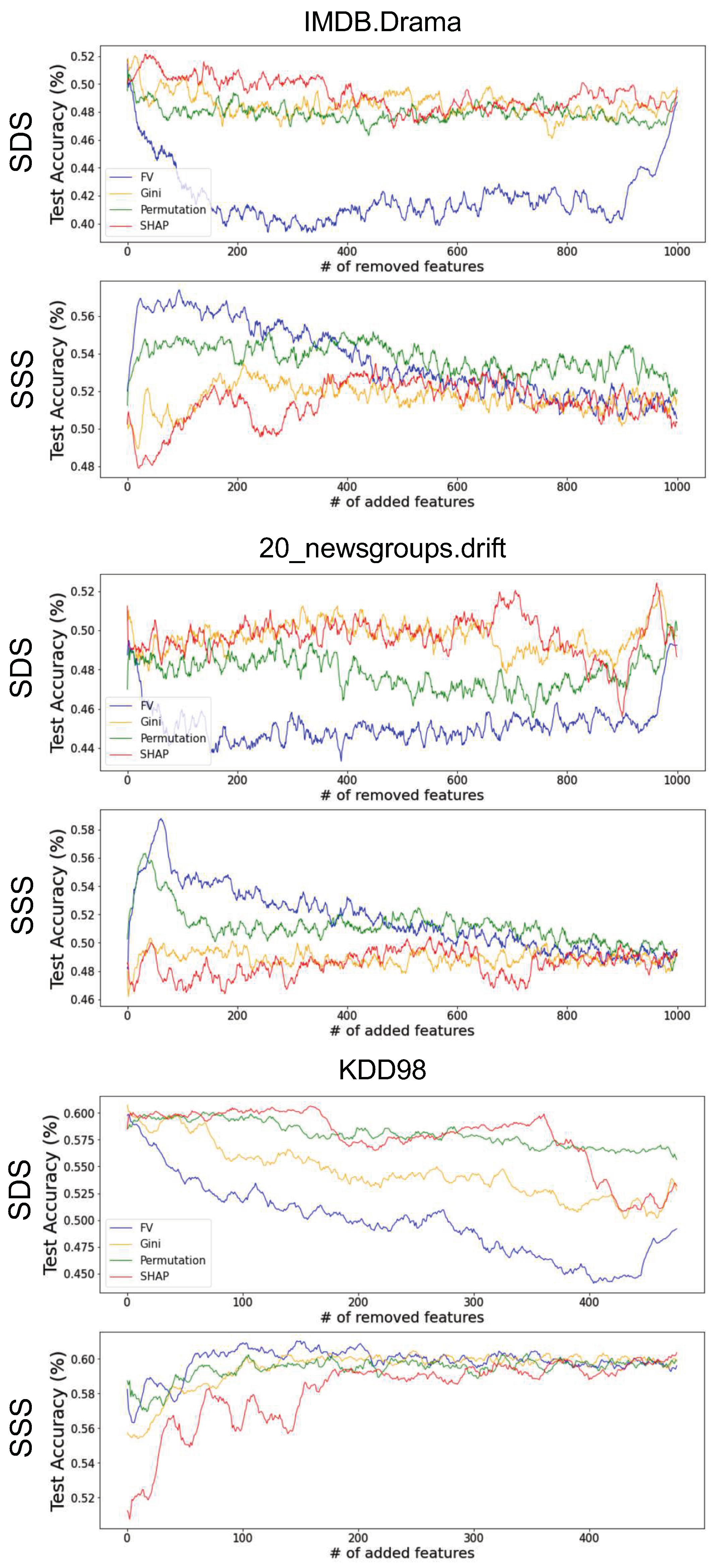
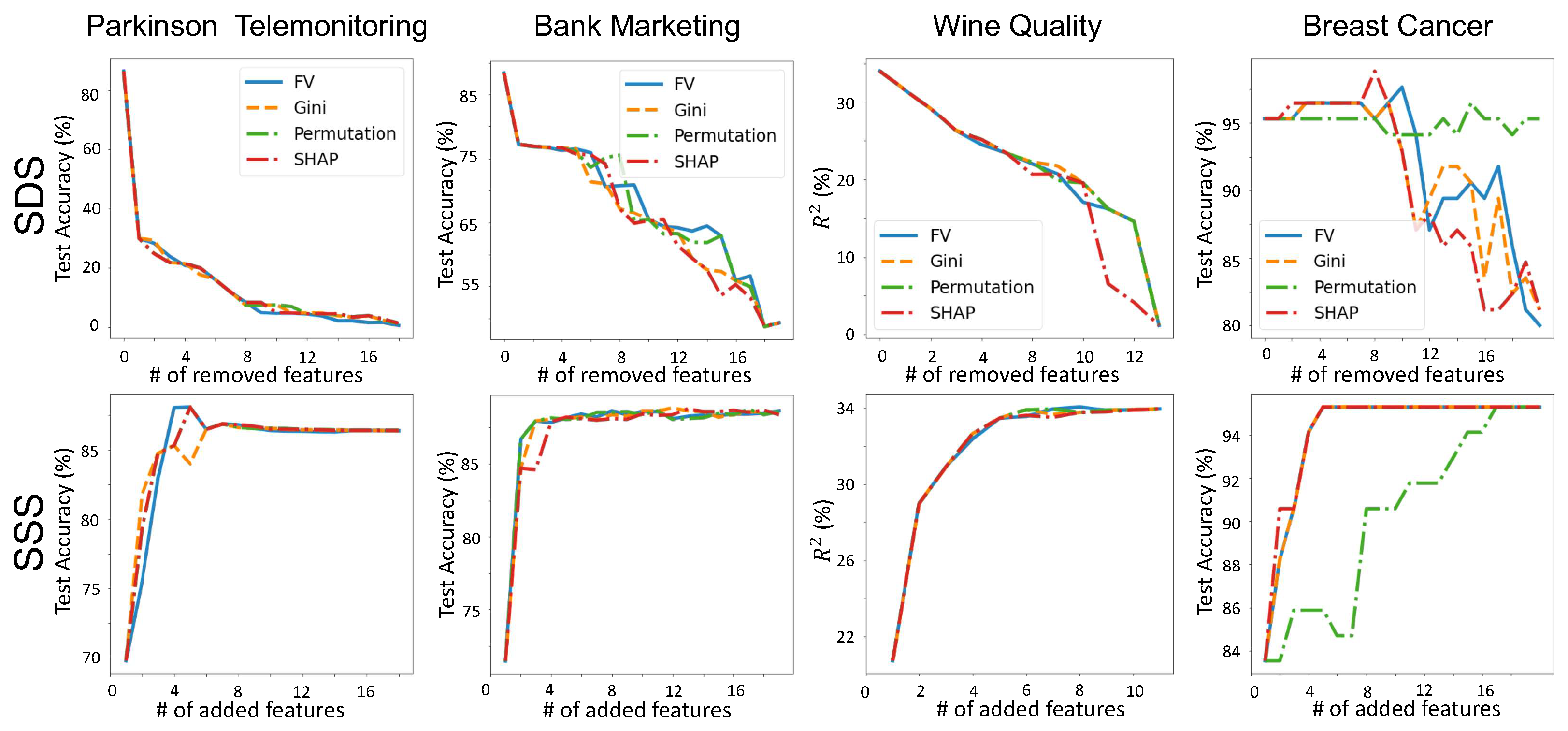
3.4. Validating Feature-Importance Scores
- Smallest Destroying Subset (SDS)—Smallest subset of features that by removing them an accurate model cannot be trained.
- Smallest Sufficient Subset (SSS)—Smallest subset of features that are sufficient for training an accurate model.
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Two Dimensional Embeddings Are Sufficient
| Dataset | Explained Variance (%) |
|---|---|
| UK Biobank Lung Cancer Prediction | 81 |
| PBMC3k | 85 |
| Adult Income | 92 |
| Spambase | 86 |
| Bank Marketing | 98 |
| Parkinson Telemonitoring | 99 |
| Wine Quality | 98 |
| Breast Cancer | 87 |
Appendix B. Comparing Feature-Importance Methods
Appendix C. Comparing Feature-Importance Methods in High-Dimensional Setting
References
- Ouyang, D.; He, B.; Ghorbani, A.; Yuan, N.; Ebinger, J.; Langlotz, C.P.; Heidenreich, P.A.; Harrington, R.A.; Liang, D.H.; Ashley, E.A.; et al. Video-based AI for beat-to-beat assessment of cardiac function. Nature 2020, 580, 252–256. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, A.; Ouyang, D.; Abid, A.; He, B.; Chen, J.H.; Harrington, R.A.; Liang, D.H.; Ashley, E.A.; Zou, J.Y. Deep learning interpretation of echocardiograms. NPJ Digit. Med. 2020, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Dixon, M.F.; Halperin, I.; Bilokon, P. Machine Learning in Finance; Springer: Berlin, Germany, 2020. [Google Scholar]
- Heaton, J.B.; Polson, N.G.; Witte, J.H. Deep learning for finance: Deep portfolios. Appl. Stoch. Model. Bus. Ind. 2017, 33, 3–12. [Google Scholar] [CrossRef]
- Goodman, B.; Flaxman, S. European Union regulations on algorithmic decision-making and a “right to explanation”. AI Mag. 2017, 38, 50–57. [Google Scholar] [CrossRef] [Green Version]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, New York, NY, USA, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Arik, S.O.; Pfister, T. Tabnet: Attentive interpretable tabular learning. arXiv 2019, arXiv:1908.07442. [Google Scholar]
- Yang, Y.; Morillo, I.G.; Hospedales, T.M. Deep neural decision trees. arXiv 2018, arXiv:1806.06988. [Google Scholar]
- Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.; Li, M.; Smola, A. Autogluon-tabular: Robust and accurate automl for structured data. arXiv 2020, arXiv:2003.06505. [Google Scholar]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine learning interpretability: A survey on methods and metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Model-agnostic interpretability of machine learning. arXiv 2016, arXiv:1606.05386. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Poursabzi-Sangdeh, F.; Goldstein, D.G.; Hofman, J.M.; Wortman Vaughan, J.W.; Wallach, H. Manipulating and measuring model interpretability. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; pp. 1–52. [Google Scholar]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F.; et al. Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav). In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2668–2677. [Google Scholar]
- Zhou, B.; Sun, Y.; Bau, D.; Torralba, A. Interpretable basis decomposition for visual explanation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 119–134. [Google Scholar]
- Bouchacourt, D.; Denoyer, L. Educe: Explaining model decisions through unsupervised concepts extraction. arXiv 2019, arXiv:1905.11852. [Google Scholar]
- Ghorbani, A.; Wexler, J.; Zou, J.Y.; Kim, B. Towards Automatic Concept-based Explanations. Adv. Neural Inf. Process. Syst. 2019, 32, 9277–9286. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics New York; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Sandri, M.; Zuccolotto, P. A bias correction algorithm for the Gini variable importance measure in classification trees. J. Comput. Graph. Stat. 2008, 17, 611–628. [Google Scholar] [CrossRef]
- Auret, L.; Aldrich, C. Empirical comparison of tree ensemble variable importance measures. Chemom. Intell. Lab. Syst. 2011, 105, 157–170. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Fransisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Chen, J.; Song, L.; Wainwright, M.; Jordan, M. Learning to explain: An information-theoretic perspective on model interpretation. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 883–892. [Google Scholar]
- Ancona, M.; Ceolini, E.; Öztireli, C.; Gross, M. Towards better understanding of gradient-based attribution methods for Deep Neural Networks. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April– 3 May 2018. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Tsang, M.; Rambhatla, S.; Liu, Y. How does this interaction affect me? Interpretable attribution for feature interactions. arXiv 2020, arXiv:2006.10965. [Google Scholar]
- Sundararajan, M.; Dhamdhere, K.; Agarwal, A. The Shapley Taylor Interaction Index. In Proceedings of the International Conference on Machine Learning, PMLR, Vienna, Austria, 12–18 July 2020; pp. 9259–9268. [Google Scholar]
- Janizek, J.D.; Sturmfels, P.; Lee, S.I. Explaining explanations: Axiomatic feature interactions for deep networks. J. Mach. Learn. Res. 2021, 22, 1–54. [Google Scholar]
- Friedman, J.H.; Popescu, B.E.; et al. Predictive learning via rule ensembles. Ann. Appl. Stat. 2008, 2, 916–954. [Google Scholar] [CrossRef]
- Hooker, G. Discovering additive structure in black box functions. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 575–580. [Google Scholar]
- Greenwell, B.M.; Boehmke, B.C.; McCarthy, A.J. A simple and effective model-based variable importance measure. arXiv 2018, arXiv:1805.04755. [Google Scholar]
- Basu, S.; Kumbier, K.; Brown, J.B.; Yu, B. Iterative random forests to discover predictive and stable high-order interactions. Proc. Natl. Acad. Sci. USA 2018, 115, 1943–1948. [Google Scholar] [CrossRef] [Green Version]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Zhao, Q.; Hastie, T. Causal interpretations of black-box models. J. Bus. Econ. Stat. 2021, 39, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Janvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Levy, O.; Goldberg, Y.; Dagan, I. Improving distributional similarity with lessons learned from word embeddings. Trans. Assoc. Comput. Linguist. 2015, 3, 211–225. [Google Scholar] [CrossRef]
- Wilson, B.J.; Schakel, A.M. Controlled experiments for word embeddings. arXiv 2015, arXiv:1510.02675. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Candes, E.; Fan, Y.; Janson, L.; Lv, J. Panning for gold:‘model-X’knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2018, 80, 551–577. [Google Scholar] [CrossRef] [Green Version]
- 10x Genomics. 3k PBMCs from a Healthy Donor. 2016. Available online: https://www.10xgenomics.com/resources/datasets/3-k-pbm-cs-from-a-healthy-donor-1-standard-1-1-0 (accessed on 18 October 2021).
- Sudlow, C.; Gallacher, J.; Allen, N.; Beral, V.; Burton, P.; Danesh, J.; Downey, P.; Elliott, P.; Green, J.; Landray, M.; et al. UK biobank: An open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015, 12, e1001779. [Google Scholar] [CrossRef] [Green Version]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 18 October 2021).
- Kohavi, R. Scaling up the accuracy of naive-bayes classifiers: A decision-tree hybrid. Kdd 1996, 96, 202–207. [Google Scholar]
- Gimenez, J.R.; Ghorbani, A.; Zou, J. Knockoffs for the mass: New feature importance statistics with false discovery guarantees. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, PMLR, Naha, Okinawa, Japan, 16–18 April 2019; 2125–2133. [Google Scholar]
- Dabkowski, P.; Gal, Y. Real time image saliency for black box classifiers. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; 6970–6979. [Google Scholar]
- Vanschoren, J.; van Rijn, J.N.; Bischl, B.; Torgo, L. OpenML: Networked Science in Machine Learning. SIGKDD Explor. 2013, 15, 49–60. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorbani, A.; Berenbaum, D.; Ivgi, M.; Dafna, Y.; Zou, J.Y. Beyond Importance Scores: Interpreting Tabular ML by Visualizing Feature Semantics. Information 2022, 13, 15. https://doi.org/10.3390/info13010015
Ghorbani A, Berenbaum D, Ivgi M, Dafna Y, Zou JY. Beyond Importance Scores: Interpreting Tabular ML by Visualizing Feature Semantics. Information. 2022; 13(1):15. https://doi.org/10.3390/info13010015
Chicago/Turabian StyleGhorbani, Amirata, Dina Berenbaum, Maor Ivgi, Yuval Dafna, and James Y. Zou. 2022. "Beyond Importance Scores: Interpreting Tabular ML by Visualizing Feature Semantics" Information 13, no. 1: 15. https://doi.org/10.3390/info13010015
APA StyleGhorbani, A., Berenbaum, D., Ivgi, M., Dafna, Y., & Zou, J. Y. (2022). Beyond Importance Scores: Interpreting Tabular ML by Visualizing Feature Semantics. Information, 13(1), 15. https://doi.org/10.3390/info13010015






