Understanding Collections of Related Datasets Using Dependent MMD Coresets
Abstract
:1. Introduction
2. Background and Related Work
2.1. Coresets and Measure-Coresets
2.2. MMD-Coresets
2.3. Coresets for Understanding Datasets and Models
2.4. Criticising MMD Coresets
2.5. Dependent and Correlated Random Measures
3. Understanding Multiple Datasets Using Coresets
3.1. Understanding Multiple Datasets Using MMD-Coresets
3.2. Dependent MMD Coresets
3.3. Model Understanding and Extrapolation
3.4. A Greedy Algorithm for Finding Dependent Coresets
| Algorithm 1.dmmd: Selecting dependent MMD coresets |
Require: Datasets ; candidate set U; kernel ; threshold ; for all ; ; while do for all do for all do Calculate using Equation (7) end for for all do end for end for for all do for all do end for end for end while |
3.5. Limitations
4. Experimental Evaluation
4.1. Evaluation of Dependent MMD Coreset Algorithm
| Algorithm 2. A dependent protodash algorithm |
Require: Datasets , candidate set U, kernel , threshold , for all , , for all do end for while do for all do end for for all do end for end while |
4.2. Interpretable Data Summarizations
4.2.1. A Shared Support Allows for Easier Comparison of Datasets
4.2.2. Dependent Coresets Allow Us to Visualize Data Drift in Collections of Images
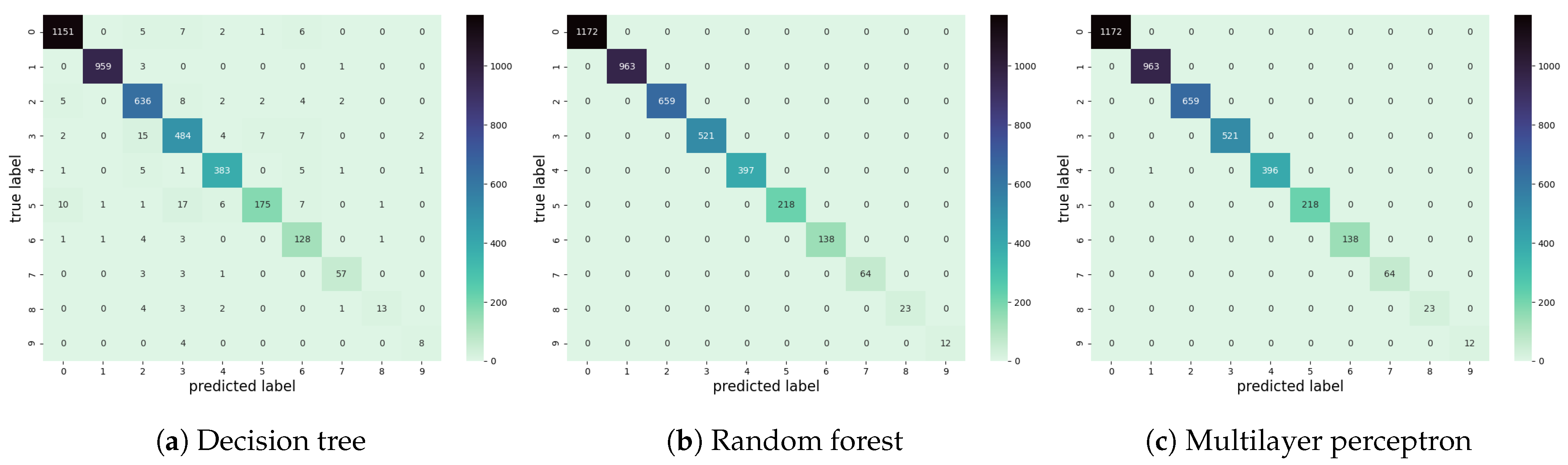
4.3. Dependent Coresets Allow Us to Understand Model Generalization
4.4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Larrazabal, A.J.; Nieto, N.; Peterson, V.; Milone, D.H.; Ferrante, E. Gender imbalance in medical imaging datasets produces biased classifiers for computer-aided diagnosis. Proc. Natl. Acad. Sci. USA 2020, 117, 12592–12594. [Google Scholar] [CrossRef] [PubMed]
- Chen, I.Y.; Johansson, F.D.; Sontag, D. Why is my classifier discriminatory? In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 3543–3554. [Google Scholar]
- Buolamwini, J.; Gebru, T. Gender shades: Intersectional accuracy disparities in commercial gender classification. In Proceedings of the 1st Conference on Fairness, Accountability and Transparency, New York, NY, USA, 23–24 February 2018; pp. 77–91. [Google Scholar]
- Shankar, S.; Halpern, Y.; Breck, E.; Atwood, J.; Wilson, J.; Sculley, D. No classification without representation: Assessing geodiversity issues in open data sets for the developing world. arXiv 2017, arXiv:1711.08536. [Google Scholar]
- Alexander, R.G.; Schmidt, J.; Zelinsky, G.J. Are summary statistics enough? Evidence for the importance of shape in guiding visual search. Vis. Cogn. 2014, 22, 595–609. [Google Scholar] [CrossRef]
- Lauer, T.; Cornelissen, T.H.; Draschkow, D.; Willenbockel, V.; Võ, M.L.H. The role of scene summary statistics in object recognition. Sci. Rep. 2018, 8, 14666. [Google Scholar] [CrossRef] [Green Version]
- Kaufmann, L.; Rousseeuw, P. Clustering by means of medoids. In Statistical Data Analysis Based on the L1-Norm and Related Methods; Springer: Berlin/Heidelberg, Germany, 1987; pp. 405–416. [Google Scholar]
- Bien, J.; Tibshirani, R. Prototype selection for interpretable classification. Ann. Appl. Stat. 2011, 5, 2403–2424. [Google Scholar] [CrossRef] [Green Version]
- Mak, S.; Joseph, V.R. Projected support points: A new method for high-dimensional data reduction. arXiv 2017, arXiv:1708.06897. [Google Scholar]
- Mak, S.; Joseph, V.R. Support points. Ann. Stat. 2018, 46, 2562–2592. [Google Scholar] [CrossRef]
- Kim, B.; Khanna, R.; Koyejo, O.O. Examples are not enough, learn to criticize! Criticism for interpretability. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2280–2288. [Google Scholar]
- Wilson, D.R.; Martinez, T.R. Reduction techniques for instance-based learning algorithms. Mach. Learn. 2000, 38, 257–286. [Google Scholar] [CrossRef]
- Gurumoorthy, K.S.; Dhurandhar, A.; Cecchi, G.; Aggarwal, C. Efficient data representation by selecting prototypes with importance weights. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 260–269. [Google Scholar]
- Chen, Y.; Welling, M.; Smola, A. Super-samples from kernel herding. In Proceedings of the 26th Conference on Uncertainty in Artificial Intelligence Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, 8–11 July 2010; pp. 109–116. [Google Scholar]
- Phillips, J.M.; Tai, W.M. Near-optimal coresets of kernel density estimates. Discret. Comput. Geom. 2020, 63, 867–887. [Google Scholar] [CrossRef] [Green Version]
- Karnin, Z.; Liberty, E. Discrepancy, coresets, and sketches in machine learning. In Proceedings of the 32nd Conference on Learning Theory Conference on Learning Theory, Phoenix, AZ, USA, 25–28 June 2019; pp. 1975–1993. [Google Scholar]
- Tai, W.M. Optimal Coreset for Gaussian Kernel Density Estimation. arXiv 2021, arXiv:2007.08031. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Pratt, K.B.; Tschapek, G. Visualizing concept drift. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 735–740. [Google Scholar]
- Hohman, F.; Wongsuphasawat, K.; Kery, M.B.; Patel, K. Understanding and visualizing data iteration in machine learning. In Proceedings of the CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; pp. 1–13. [Google Scholar]
- Agarwal, P.K.; Har-Peled, S.; Varadarajan, K.R. Approximating extent measures of points. J. ACM 2004, 51, 606–635. [Google Scholar] [CrossRef]
- Claici, S.; Solomon, J. Wasserstein coresets for Lipschitz costs. Stat 2018, 1050, 18. [Google Scholar]
- Müller, A. Integral probability metrics and their generating classes of functions. Adv. Appl. Probab. 1997, 29, 429–443. [Google Scholar] [CrossRef]
- Bach, F.; Lacoste-Julien, S.; Obozinski, G. On the equivalence between herding and conditional gradient algorithms. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- Lacoste-Julien, S.; Lindsten, F.; Bach, F. Sequential kernel herding: Frank-Wolfe optimization for particle filtering. In Proceedings of the 18th International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 9–12 May 2015; pp. 544–552. [Google Scholar]
- Phillips, J.M. ε-samples for kernels. In Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 6–8 January 2013; pp. 1622–1632. [Google Scholar]
- Lopez-Paz, D.; Muandet, K.; Schölkopf, B.; Tolstikhin, I. Towards a learning theory of cause-effect inference. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1452–1461. [Google Scholar]
- Feldman, D. Introduction to core-sets: An updated survey. arXiv 2020, arXiv:2011.09384. [Google Scholar]
- Potter, M.C.; Wyble, B.; Hagmann, C.E.; McCourt, E.S. Detecting meaning in RSVP at 13 ms per picture. Atten. Percept. Psychophys. 2014, 76, 270–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Y.; Ou, Y.; Lex, A.; Phillips, J.M. Visualization of big spatial data using coresets for kernel density estimates. In Proceedings of the IEEE Visualization in Data Science (VDS), Phoenix, AZ, USA, 1 October 2017; pp. 23–30. [Google Scholar]
- Kim, B.; Rudin, C.; Shah, J.A. The Bayesian case model: A generative approach for case-based reasoning and prototype classification. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1952–1960. [Google Scholar]
- Aamodt, A.; Plaza, E. Case-based reasoning: Foundational issues, methodological variations, and system approaches. AI Commun. 1994, 7, 39–59. [Google Scholar] [CrossRef]
- Murdock, J.W.; Aha, D.W.; Breslow, L.A. Assessing elaborated hypotheses: An interpretive case-based reasoning approach. In Case-Based Reasoning Research and Development, Proceedings of the 5th International Conference on Case-Based Reasoning, Trondheim, Norway, 23–26 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 332–346. [Google Scholar]
- MacEachern, S.N. Dependent nonparametric processes. In ASA Proceedings of the Section on Bayesian Statistical Science; American Statistical Association: Alexandria, VA, USA, 1999; Volume 1, pp. 50–55. [Google Scholar]
- Quintana, F.A.; Mueller, P.; Jara, A.; MacEachern, S.N. The dependent Dirichlet process and related models. arXiv 2020, arXiv:2007.06129. [Google Scholar]
- De Iorio, M.; Müller, P.; Rosner, G.L.; MacEachern, S.N. An ANOVA model for dependent random measures. J. Am. Stat. Assoc. 2004, 99, 205–215. [Google Scholar] [CrossRef]
- Dubey, A.; Hefny, A.; Williamson, S.; Xing, E.P. A nonparametric mixture model for topic modeling over time. In Proceedings of the 13th SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 530–538. [Google Scholar]
- Garreau, D.; Jitkrittum, W.; Kanagawa, M. Large sample analysis of the median heuristic. arXiv 2017, arXiv:1707.07269. [Google Scholar]
- Kiela, D.; Bottou, L. Learning image embeddings using convolutional neural networks for improved multi-modal semantics. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 36–45. [Google Scholar]
- Chen, M.; Radford, A.; Child, R.; Wu, J.; Jun, H.; Luan, D.; Sutskever, I. Generative pretraining from pixels. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; pp. 1691–1703. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 29th IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Athalye, A.; Engstrom, L.; Ilyas, A.; Kwok, K. Synthesizing robust adversarial examples. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 284–293. [Google Scholar]
- Steed, R.; Caliskan, A. Image representations learned with unsupervised pre-training contain human-like biases. In Proceedings of the 4th Conference on Fairness, Accountability, and Transparency, Online, 3–10 March 2021; pp. 701–713. [Google Scholar]
- Ginosar, S.; Rakelly, K.; Sachs, S.; Yin, B.; Efros, A.A. A century of portraits: A visual historical record of American high school yearbooks. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 7–13 December 2015; pp. 1–7. [Google Scholar]
- Marcel, S.; Rodriguez, Y. Torchvision the machine-vision package of torch. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 1485–1488. [Google Scholar]
- Gebru, T.; Morgenstern, J.; Vecchione, B.; Vaughan, J.W.; Wallach, H.; Daumé, H., III; Crawford, K. Datasheets for datasets. In Proceedings of the 5th Workshop on Fairness, Accountability, and Transparency in Machine Learning, Stockholm, Sweden, 13–15 July 2018. [Google Scholar]
- Chmielinski, K.S.; Newman, S.; Taylor, M.; Joseph, J.; Thomas, K.; Yurkofsky, J.; Qiu, Y.C. The Dataset Nutrition Label (2nd Gen): Leveraging Context to Mitigate Harms in Artificial Intelligence. In Proceedings of the NeurIPS 2020 Workshop on Dataset Curation and Security, Online, 11 December 2020. [Google Scholar]
- Hull, J.J. A database for handwritten text recognition research. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 550–554. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]








 ; the average weight for the 2000s is shown in red
; the average weight for the 2000s is shown in red  .
.
 ; the average weight for the 2000s is shown in red
; the average weight for the 2000s is shown in red  .
.




 and shown in red
and shown in red  ; images along axis show corresponding exemplars.
; images along axis show corresponding exemplars.
 and shown in red
and shown in red  ; images along axis show corresponding exemplars.
; images along axis show corresponding exemplars.
 and weights for are shown in red
and weights for are shown in red  .
.
 and weights for are shown in red
and weights for are shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
 ; where the highest probability class differs from the true class, the highest probability class is shown in red
; where the highest probability class differs from the true class, the highest probability class is shown in red  .
.
| set that indexes datasets and associated measures | |
| a dataset indexed by | |
| true distribution at , | |
| set of candidate locations | |
| Dirac measure (i.e., point mass) at u. | |
| a probability measure used to approximate , that takes the form , where |
| Distance | |
|---|---|
| 1-Wasserstein distance | |
| Maximum mean discrepancy | for some RKHS |
| Total variation |
| 1900s | 1910s | 1920s | 1930s | 1940s | 1950s | 1960s | 1970s | 1980s | 1990s | 2000s | 2010s |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 35 | 98 | 308 | 1682 | 2650 | 2093 | 2319 | 2806 | 2826 | 2621 | 2208 | 602 |
| Model | Accuracy on | Accuracy on |
|---|---|---|
| MLP | 0.9998 | 0.8531 |
| Random Forest | 1.0 | 0.7129 |
| Decision Tree | 0.9585 | 0.5880 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williamson, S.A.; Henderson, J. Understanding Collections of Related Datasets Using Dependent MMD Coresets. Information 2021, 12, 392. https://doi.org/10.3390/info12100392
Williamson SA, Henderson J. Understanding Collections of Related Datasets Using Dependent MMD Coresets. Information. 2021; 12(10):392. https://doi.org/10.3390/info12100392
Chicago/Turabian StyleWilliamson, Sinead A., and Jette Henderson. 2021. "Understanding Collections of Related Datasets Using Dependent MMD Coresets" Information 12, no. 10: 392. https://doi.org/10.3390/info12100392
APA StyleWilliamson, S. A., & Henderson, J. (2021). Understanding Collections of Related Datasets Using Dependent MMD Coresets. Information, 12(10), 392. https://doi.org/10.3390/info12100392






