A Novel Joint TDOA/FDOA Passive Localization Scheme Using Interval Intersection Algorithm
Abstract
:1. Introduction
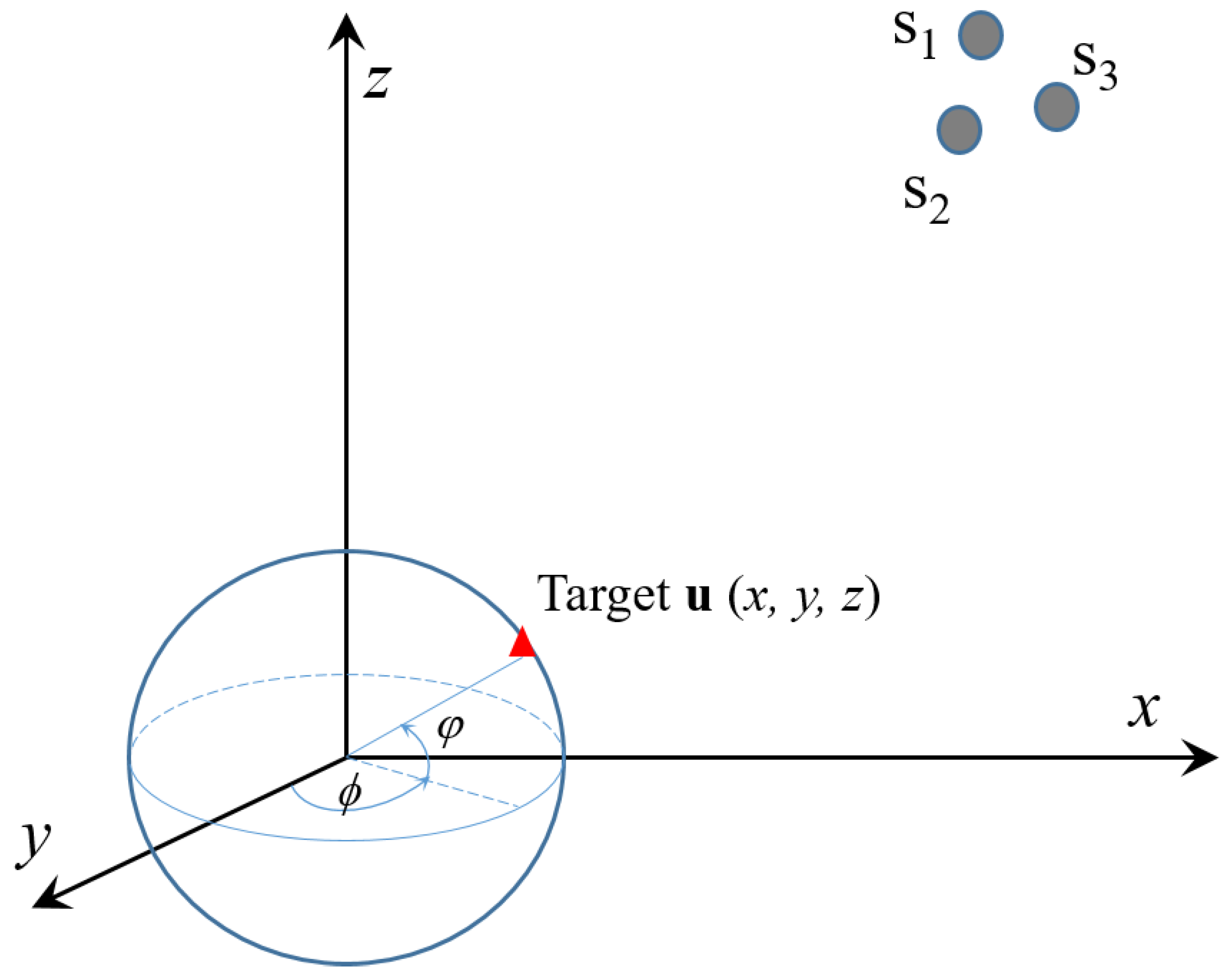
2. Background and Methods
3. Performance Evaluation
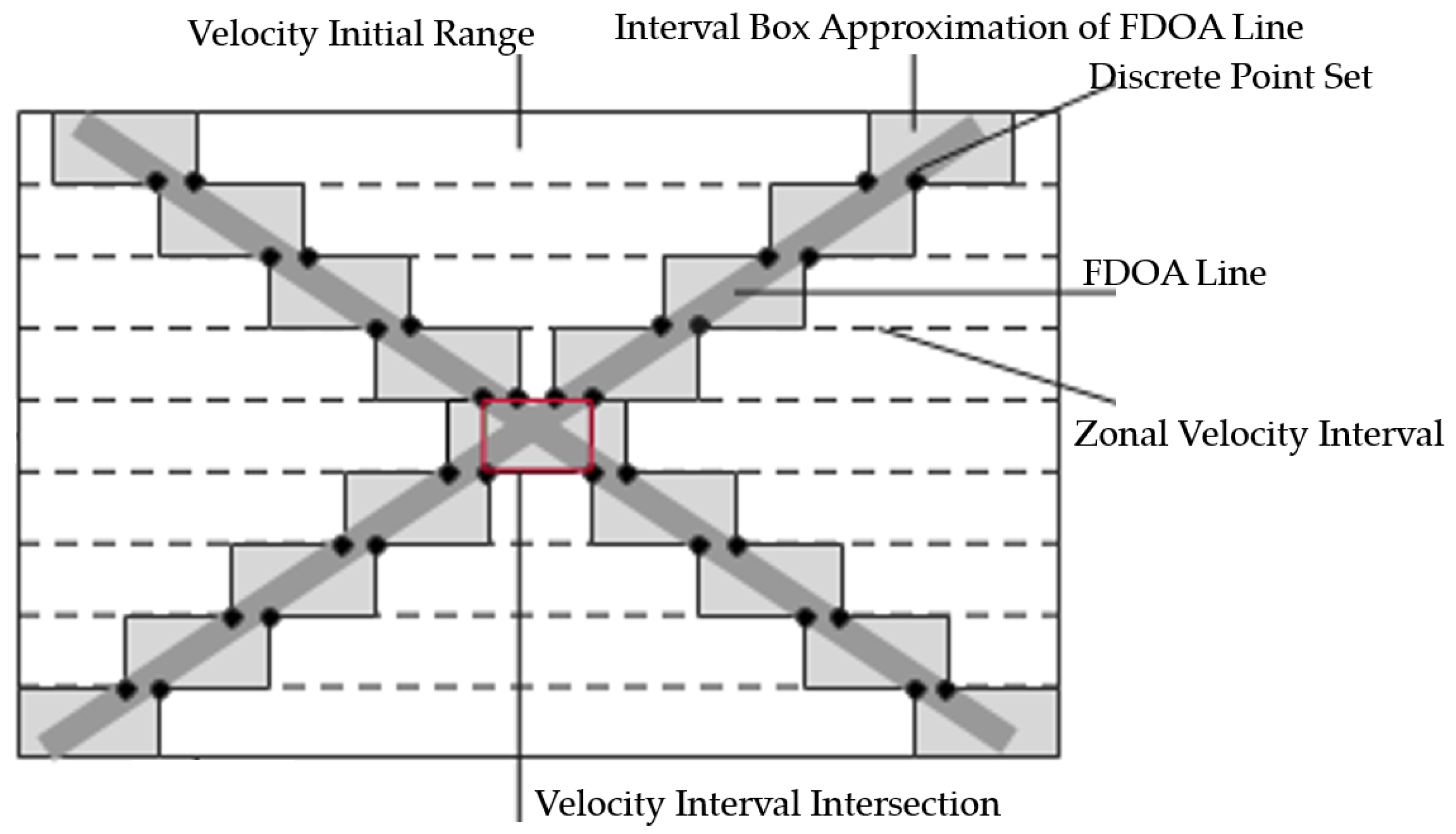
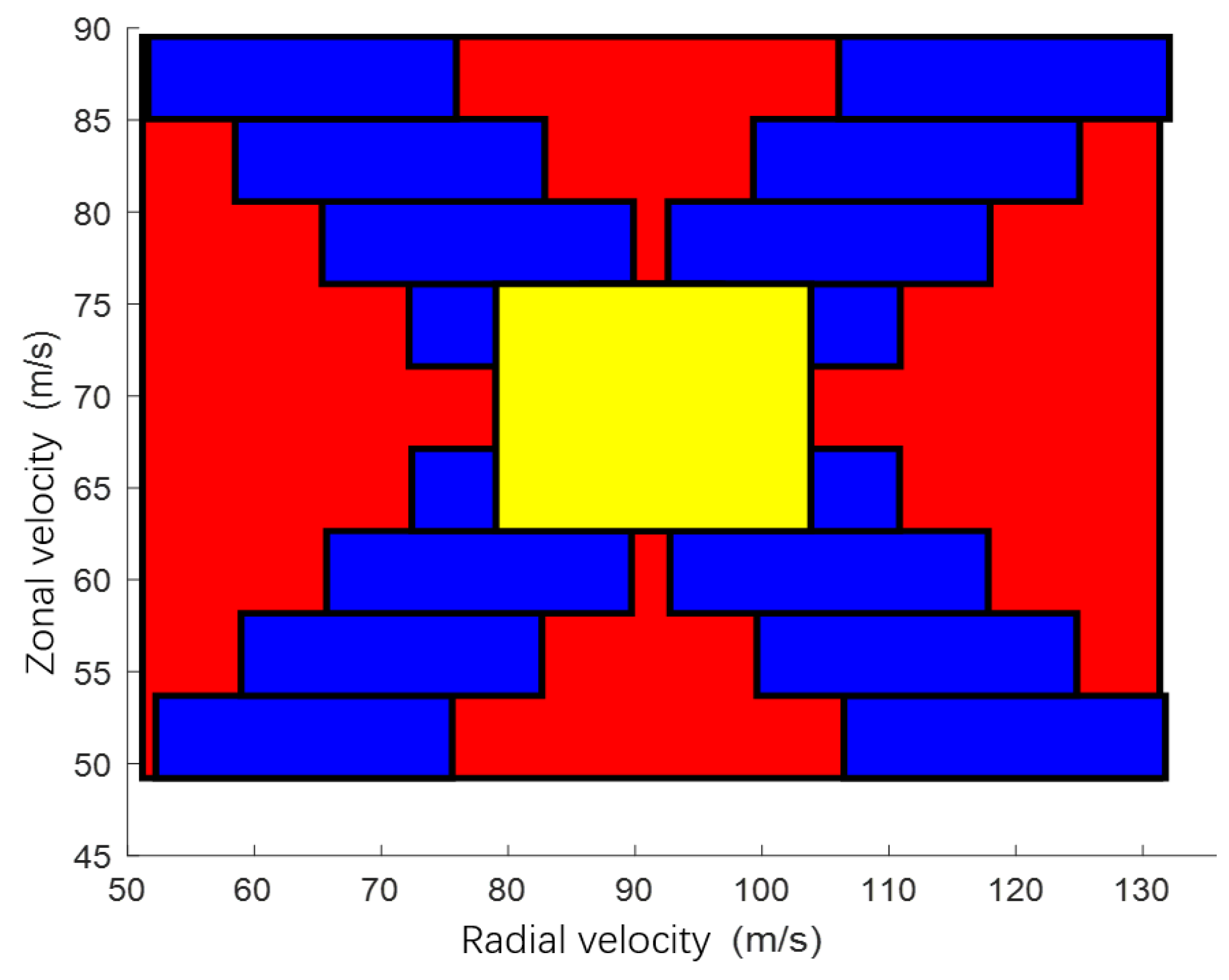
3.1. The Illustration of Interval Computation for TDOA/FDOA-Based Localization
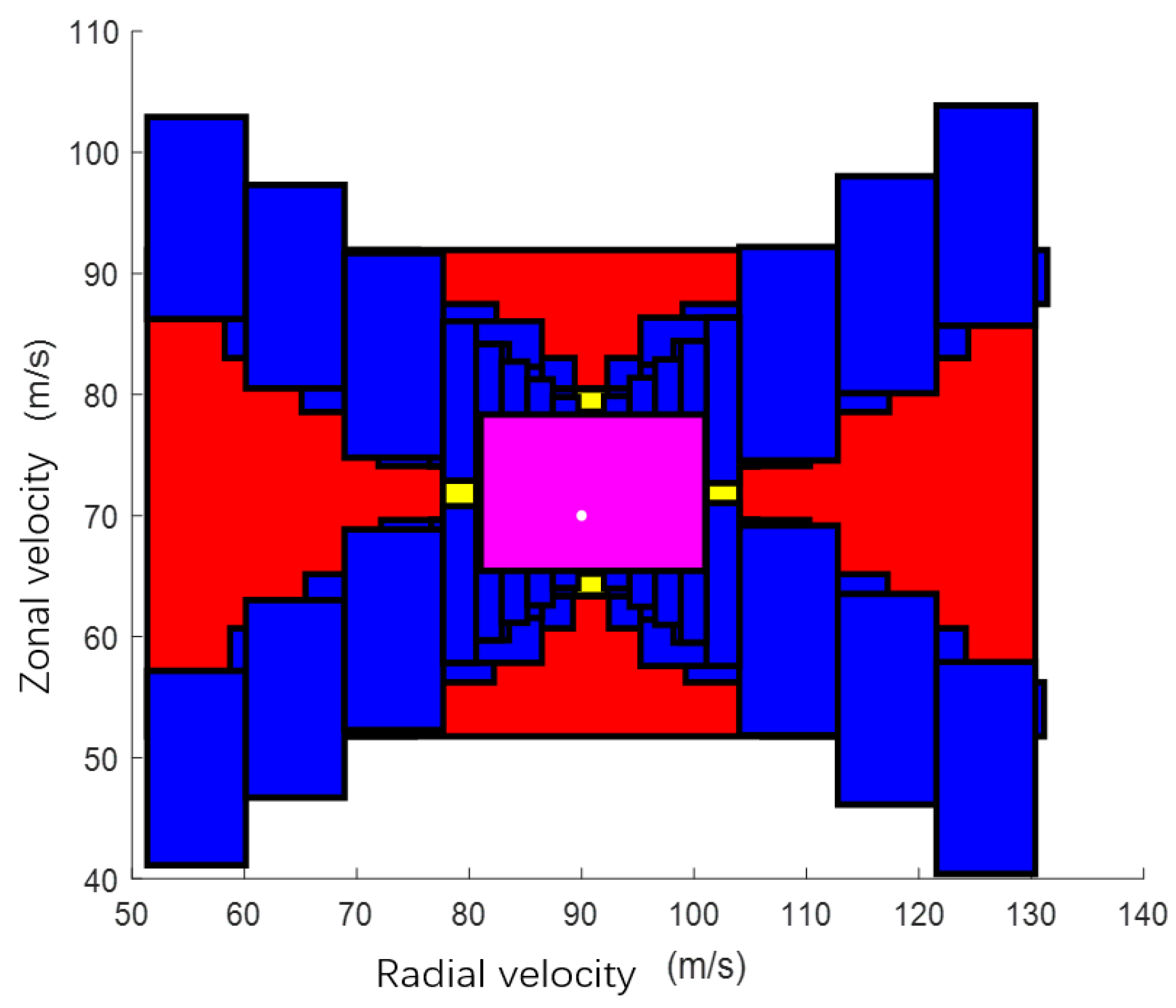
3.2. The Performance Evaluation under the Measurement Error
3.3. The Performance Evaluation under the Ephemeris Error
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, K.; Oh, J.; You, K. TDOA-/FDOA-Based Adaptive Active Target Localization Using Iterated Dual-EKF Algorithm. IEEE Commun. Lett. 2019, 23, 752–755. [Google Scholar] [CrossRef]
- Zhou, B.; Ahn, D.; Lee, J.; Sun, C.; Ahmed, S.; Kim, Y. A Passive Tracking System Based on Geometric Constraints in Adaptive Wireless Sensor Networks. Sensors 2018, 18, 3276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.; Cai, S.; Li, Y.; Ansari, N. A Bias-Reduced Nonlinear WLS Method for TDOA/FDOA-Based Source Localization. IEEE Trans. Veh. Technol. 2015, 65, 8603–8615. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, R.; Zhao, Y. A Bias Compensation Method for Distributed Moving Source Localization Using TDOA and FDOA with Sensor Location Errors. Sensors 2018, 18, 3747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Congfeng, L.; Jinwei, Y.; Juan, S. Direct solution for fixed source location using well-posed TDOA and FDOA measurements. J. Syst. Eng. Electron. 2020, 31, 666–673. [Google Scholar] [CrossRef]
- Ho, K.C.; Xu, W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements. IEEE Trans. Signal Process. 2004, 52, 2453–2463. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Ansari, N. A Semidefinite Relaxation Method for Source Localization Using TDOA and FDOA Measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y. An Efficient Semidefinite Relaxation Algorithm for Moving Source Localization Using TDOA and FDOA Measurements. IEEE Commun. Lett. 2017, 21, 80–83. [Google Scholar] [CrossRef]
- Qu, X.; Xie, L.; Tan, W. Iterative Constrained Weighted Least Squares Source Localization Using TDOA and FDOA Measurements. IEEE Trans. Signal Process. 2017, 65, 3990–4003. [Google Scholar] [CrossRef]
- Andrew, A.M. Applied Interval Analysis, with Examples in Parameter and State Estimation, Robust Control and Robotics; Springer: London, UK, 2001. [Google Scholar]
- Qin, N.; Wang, C.; Shan, C.; Yang, L. Interval analysis-based Bi-iterative algorithm for robust TDOA-FDOA moving source localisation. Int. J. Distrib. Sens. Netw. 2021, 17, 1–9. [Google Scholar] [CrossRef]
- Liu, S.; Han, C.; Di, R. Removal of attitude errors based on multi-target multi-sensor environment in earth-centered earth-fixed coordinates. In Proceedings of the 2010 International Conference on Information, Networking and Automation (ICINA), Kunming, China, 18–19 October 2010; pp. V2-10–V2-14. [Google Scholar]

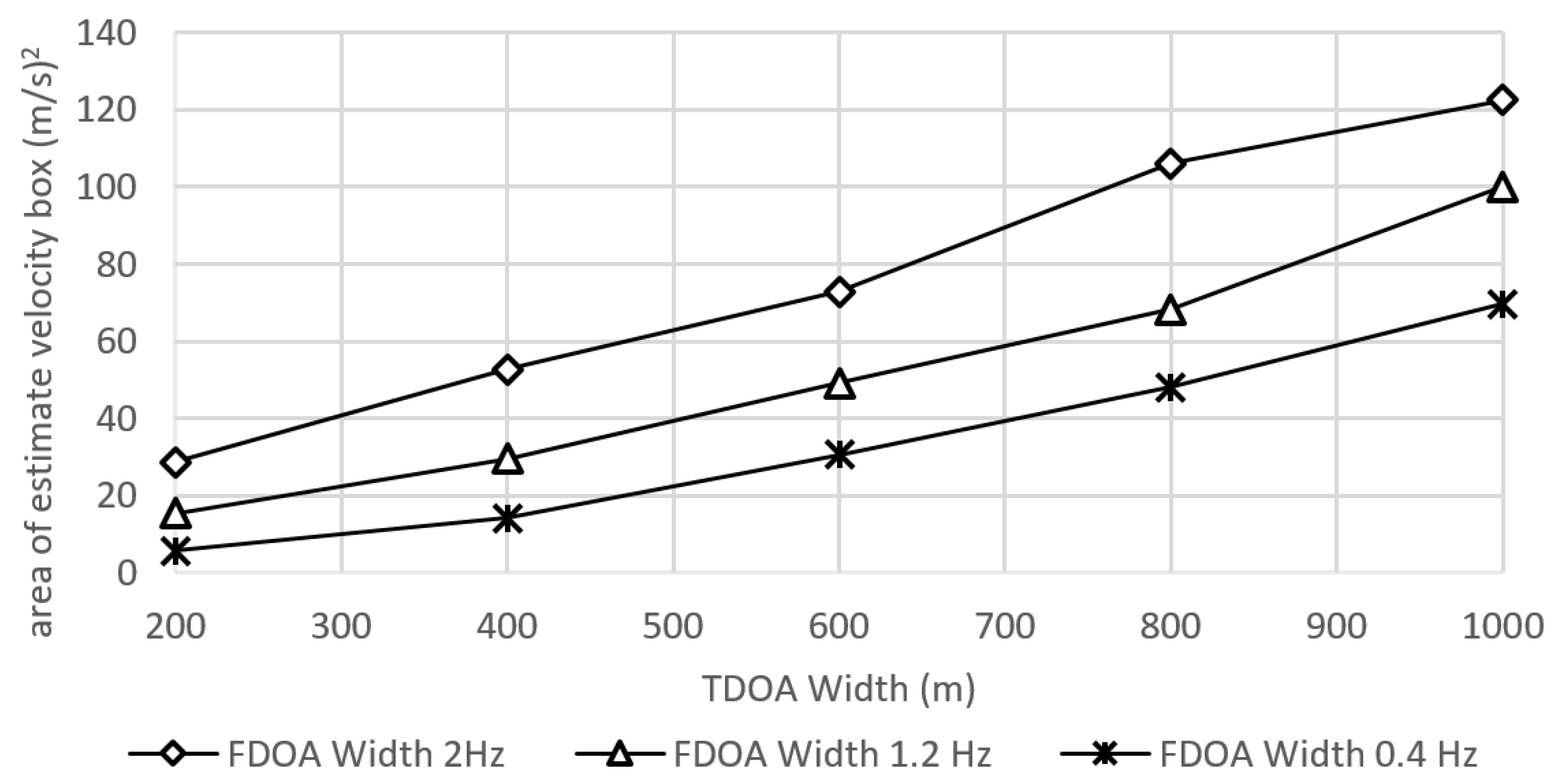
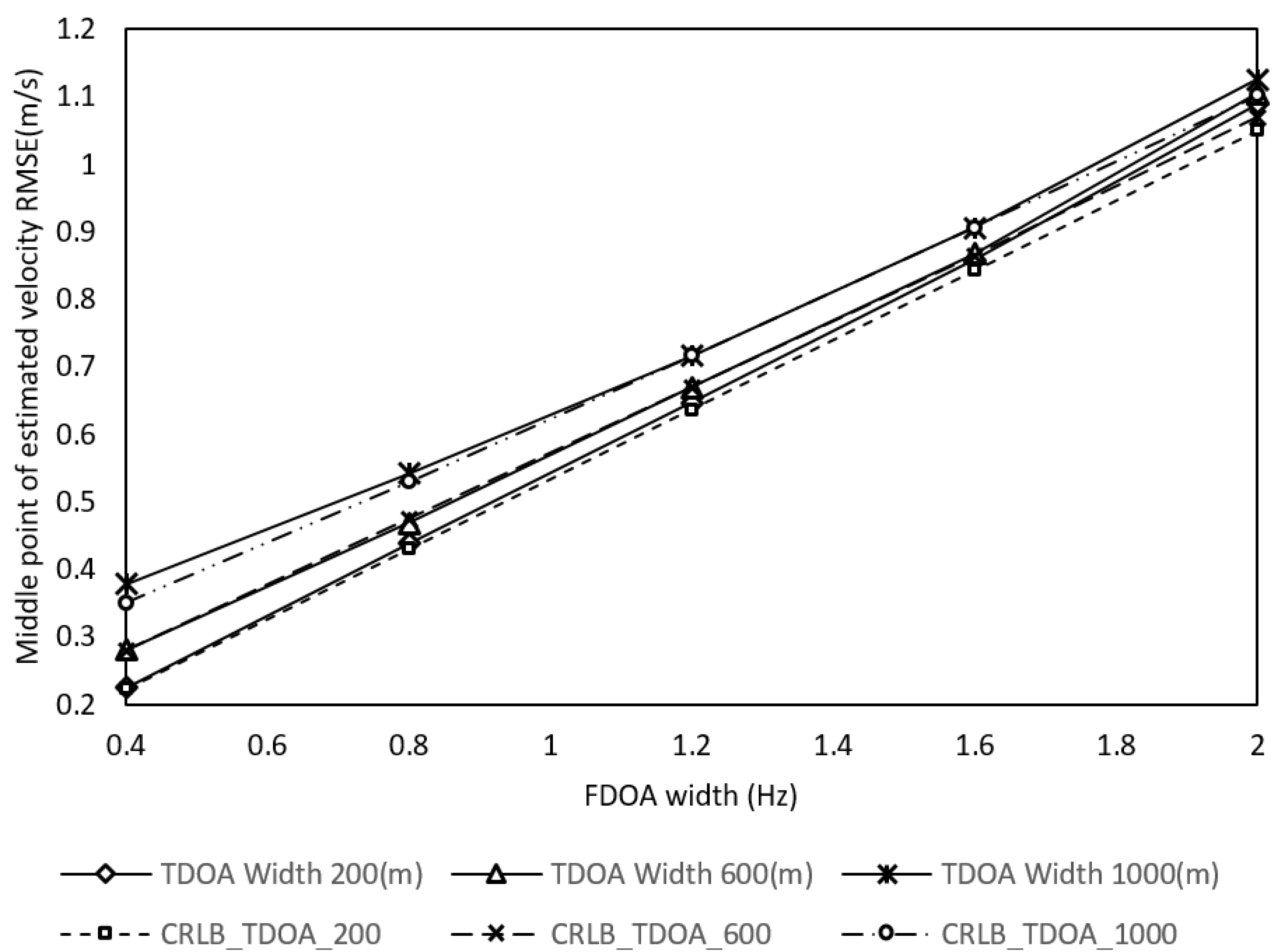
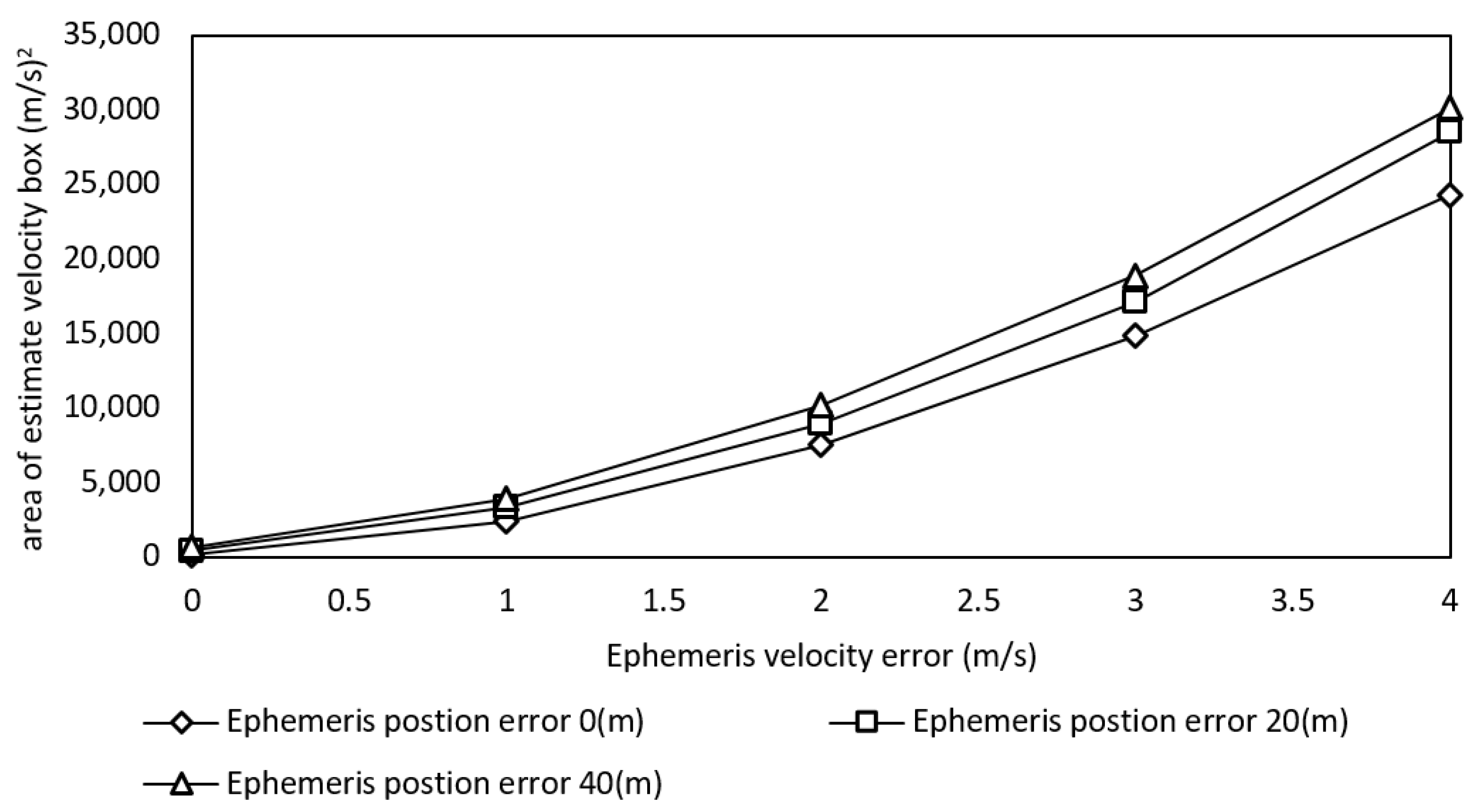

| Area of the Velocity Estimation (m/s)2 | Inclusion Rate (%) | Computational Cost per Run (s) | RMSE (m/s) |
|---|---|---|---|
| 218.2461 | 100 | 7.2 | 1.2774 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, L.; Pang, M.; Shan, C.; Sun, C.; Kim, Y.; Zhou, B. A Novel Joint TDOA/FDOA Passive Localization Scheme Using Interval Intersection Algorithm. Information 2021, 12, 371. https://doi.org/10.3390/info12090371
Ai L, Pang M, Shan C, Sun C, Kim Y, Zhou B. A Novel Joint TDOA/FDOA Passive Localization Scheme Using Interval Intersection Algorithm. Information. 2021; 12(9):371. https://doi.org/10.3390/info12090371
Chicago/Turabian StyleAi, Lingyu, Min Pang, Changxu Shan, Chao Sun, Youngok Kim, and Biao Zhou. 2021. "A Novel Joint TDOA/FDOA Passive Localization Scheme Using Interval Intersection Algorithm" Information 12, no. 9: 371. https://doi.org/10.3390/info12090371
APA StyleAi, L., Pang, M., Shan, C., Sun, C., Kim, Y., & Zhou, B. (2021). A Novel Joint TDOA/FDOA Passive Localization Scheme Using Interval Intersection Algorithm. Information, 12(9), 371. https://doi.org/10.3390/info12090371






