Distributed Hypothesis Testing over Noisy Broadcast Channels

Abstract

This paper studies binary hypothesis testing with a single sensor that communicates with two decision centers over a memoryless broadcast channel. The main focus lies on the tradeoff between the two type-II error exponents achievable at the two decision centers. In our proposed scheme, we can partially mitigate this tradeoff when the transmitter has a probability larger than $1/2$ to distinguish the alternate hypotheses at the decision centers, i.e., the hypotheses under which the decision centers wish to maximize their error exponents. In the cases where these hypotheses cannot be distinguished at the transmitter (because both decision centers have the same alternative hypothesis or because the transmitter’s observations have the same marginal distribution under both hypotheses), our scheme shows an important tradeoff between the two exponents. The results in this paper thus reinforce the previous conclusions drawn for a setup where communication is over a common noiseless link. Compared to such a noiseless scenario, here, however, we observe that even when the transmitter can distinguish the two hypotheses, a small exponent tradeoff can persist, simply because the noise in the channel prevents the transmitter to perfectly describe its guess of the hypothesis to the two decision centers.

1. Introduction

In Internet of Things (IoT) networks, data are collected at sensors and transmitted over a wireless channel to remote decision centers, which decide on one or multiple hypotheses based on the collected information. In this paper, we study simple binary hypothesis testing with a single sensor but two decision centers. The results can be combined with previous studies focusing on multiple sensors and a single decision center to tackle the practically relevant case of multiple sensors and multiple decision centers. We consider a single sensor for simplicity and because our main focus is on studying the tradeoff between the performances at the two decision centers that can arise because the single sensor has to send information over the channel that can be used by both decision centers. A simple, but highly suboptimal, approach would be to time-share communication and serve each of the two decision centers only during a part of the transmission. As we will see, better schemes are possible, and, in some cases, it is even possible to serve each of the two decision centers as if the other center was not present in the system.

In this paper, we follow the information-theoretic framework introduced in [1,2]. That means each terminal observes a memoryless sequence, and depending on the underlying hypothesis $\mathcal{H}\in \{0,1\}$, all sequences follow one of two possible joint distributions, which are known to all involved terminals. A priori, the transmitter, however, ignores the correct hypothesis and has to compute its transmit signal as a function of the observed source symbols only. Decision centers observe outputs of the channel, and, combined with their local observations, they have to make a decision on whether $\mathcal{H}=0$ or $\mathcal{H}=1$. The performance of the decision center is measured by its type-II error exponent, i.e., the expontial decay in the length of the observations of the probability of deciding on $\mathcal{H}=0$ when the true hypothesis is $\mathcal{H}=1$. As a constraint on the decision center, we impose that the type-I error probability, i.e., the probability of deciding $\mathcal{H}=1$ when the true hypothesis is $\mathcal{H}=0$, vanishes (at any desired speed) with increasing observation lengths. The motivation for studying such asymmetric requirements on the two error probabilities stems, for example, from alert systems, where the miss-detection event is much more harmful than the false-alarm event, and, as a consequence, in our systems we require the miss-detection probability to decay much faster than the false-alarm probability.

This problem setting has first been considered for the setup with a single sensor and a single decision center when communication is over a noiseless link of given capacity [1,2]. For this canonical problem, the optimal error exponent has been identified in the special cases of testing against independence [1] and testing against conditional independence [3,4].

The scheme proposed by Shimokawa–Han–Amari in [3,4] yields an achievable error exponent for all distributed hypothesis testing problems (not only testing against conditional independence) [3,4], but it might not be optimal in general [5]. The Shimokawa–Han–Amari (SHA) scheme has been extended to various more involved setups such as noiseless networks with multiple sensors and a single decision center [2,6,7]; networks where the sensor and the decision center can communicate interactively [8,9]; multi-hop networks [10]; networks with multiple decision centers [10,11,12,13].

The works most closely related to the current paper are [10,12,13,14,15,16]. Specifically, Refs [10,12,13,14] consider a single-sensor multi-detector system where communication is over a common noiseless link from the sensor to all decision centers. Focusing on two decision centers, two scenarios can be encountered here: (1) the two decision centers have the same null and alternate hypotheses, and as a consequence, both aim at maximizing the error exponent under the same hypothesis $\mathcal{H}$; or (2) the two decision centers have opposite null and alternate hypotheses and thus one decision center wishes to maximize the error exponent under hypothesis $\mathcal{H}=0$ and the other under hypothesis $\mathcal{H}=1$. The second scenario is motivated by applications where the decision centers have different goals. Hypothesis testing for scenario 1) was studied in [10,12,13,14], and the results showed a tradeoff between the exponents achieved at the two decision centers. Intuitively, the tradeoff comes from the fact that communication from the sensor is serving both decision centers at the same time. Scenario 2) was considered in [12,13]. In this case, a tradeoff only occurs when the sensor’s observation alone provides no advantage in guessing the hypothesis. Otherwise, a tradeoff-free exponent region can be achieved by the following simple scheme: the sensor takes a tentative guess on the hypothesis based only on its local observations. It communicates this tentative guess to both decision centers using a single bit and then dedicates the rest of the communication using a dedicated SHA scheme only to the decision center that wishes to maximize the error exponent under the hypothesis that does not correspond to its guess. The other decision center simply keeps the transmitter’s tentative guess and ignores the rest of the communication.

In this paper, we extend these previous works to memoryless broadcast channels (BC). Hypothesis testing over BCs was already considered in [10], however, only for above scenario 1 where both decision centers have the same null and alternate hypothesis and in the special case of testing against conditional independence, in which case the derived error exponents were proved to be optimal. Interestingly, when testing against conditional independence over noisy channels, only the capacity of the channel matters but not the properties, see [15,16]. General hypothesis testing over noisy channels is much more challenging and requires additional tools, such as joint source-channel coding and unequal error protection (UEP) coding [17]. The latter can, in particular, be used to specially protect the communication of the sensor’s tentative guess, which allows one to avoid a degradation of the performance of classical hypothesis testing schemes.

We present general distributed hypothesis testing schemes over memoryless BCs, and we analyze the performances of these schemes with a special focus on the tradeoff in exponents they achieve for the two decision centers. We propose two different schemes, depending on whether the sensor can distinguish with error probability $\ne 1/2$ the two null hypotheses at the two decision centers. If a distinction is possible (because the decision centers have different null hypothesis and the sensor’s observations follow different marginal distributions under the two hypotheses), then we employ a similar scheme as proposed in [12,13] over a common noiseless link, but where the SHA scheme is replaced by the UEP-based scheme for DMCs in [15]. That means, the sensor makes a tentative guess about the hypothesis and conveys this guess to both decision centers using an UEP mechanism. Moreover, the joint source-channel coding scheme in [15] with dedicated codebooks is used to communicate to the decision center that aims to maximize the error exponent under the hypothesis that does not correspond to the sensor’s tentative guess. This scheme shows no tradeoff between the exponents achieved at the two decision centers in various interesting cases. Sometimes, however, a tradeoff arises because even under UEP the specially protected messages can be in error and because the decision centers can confuse the codewords of the two different sets of codebooks. For the case where the sensor cannot reasonably distinguish the alternate hypotheses at the two decision centers (because both decision centers have the same alternate hypotheses or the sensor’s observations have the same marginal observations under both hypotheses), we present a scheme similar to [10] but again including UEP. In this scheme, a tradeoff between the exponents achieved at the two decision centers naturally arises and mostly stems from the inherent tradeoff in distributed lossy compression systems with multiple decoders having different side informations.

Notation

We mostly follow the notation in [18]. Random variables are denoted by capital letters, e.g., $X$, $Y$, and their realizations by lower-case letters, e.g., $x$, y. Script symbols such as $\mathcal{X}$ and $\mathcal{Y}$ stand for alphabets of random variables, and ${\mathcal{X}}^n$ and ${\mathcal{Y}}^n$ for the corresponding n-fold Cartesian products. Sequences of random variables $(X_i,\dots ,X_j)$ and realizations $(x_i,\dots ,x_j)$ are abbreviated by $X_i^j$ and $x_i^j$. When $i=1$, then we also use $X^j$ and $x^j$ instead of $X_1^j$ and $x_1^j$.

We write the probability mass function (pmf) of a discrete random variable X as $P_X$; to indicate the pmf under hypothesis $\mathcal{H}=1$, we also use $Q_X$. The conditional pmf of X given Y is written as $P_{X|Y}$, or as $Q_{X|Y}$ when $\mathcal{H}=1$. The term $D(P\parallel Q)$ stands for the Kullback–Leibler (KL) divergence between two pmfs P and Q over the same alphabet. We use $tp(a^n,b^n)$ to denote the joint type of the pair of sequences $(a^n,b^n)$, and cond_tp$\left(a^n\right|b^n)$ for the conditional type of $a^n$ given $b^n$. For a joint type ${\pi }_{ABC}$ over alphabet $\mathcal{A}\times \mathcal{B}\times \mathcal{C}$, we denote by $I_{{\pi }_{ABC}}(A;B|C)$ the conditional ßmutual information assuming that the random triple $(A,B,C)$ has pmf ${\pi }_{ABC}$; similarly for the entropy $H_{{\pi }_{ABC}}\left(A\right)$ and the conditional entropy $H_{{\pi }_{ABC}}\left(A\right|B)$. Sometimes we abbreviate ${\pi }_{ABC}$ by $\pi$. In addition, when ${\pi }_{ABC}$ has been defined and is clear from the context, we write ${\pi }_A$ or ${\pi }_{AB}$ for the corresponding subtypes. When the type ${\pi }_{ABC}$ coincides with the actual pmf of a triple $(A,B,C)$, we omit the subscript and simply write $H\left(A\right)$, $H\left(A\right|B)$, and $I(A;B|C)$.

For a given $P_X$ and a constant $\mu >0$, let ${\mathcal{T}}_{\mu }^n\left(P_X\right)$ be the set of μ-typical sequences in ${\mathcal{X}}^n$ as defined in [8] (Section 2.4). Similarly, ${\mathcal{T}}_{\mu }^n\left(P_{XY}\right)$ stands for the set of jointly μ-typical sequences. The expectation operator is written as $\mathbb{E}[·]$. We abbreviate independent and identically distributed by i.i.d. The log function is taken with base 2. Finally, in our justifications, we use (DP) and (CR) for “data processing inequality” and “chain rule”.

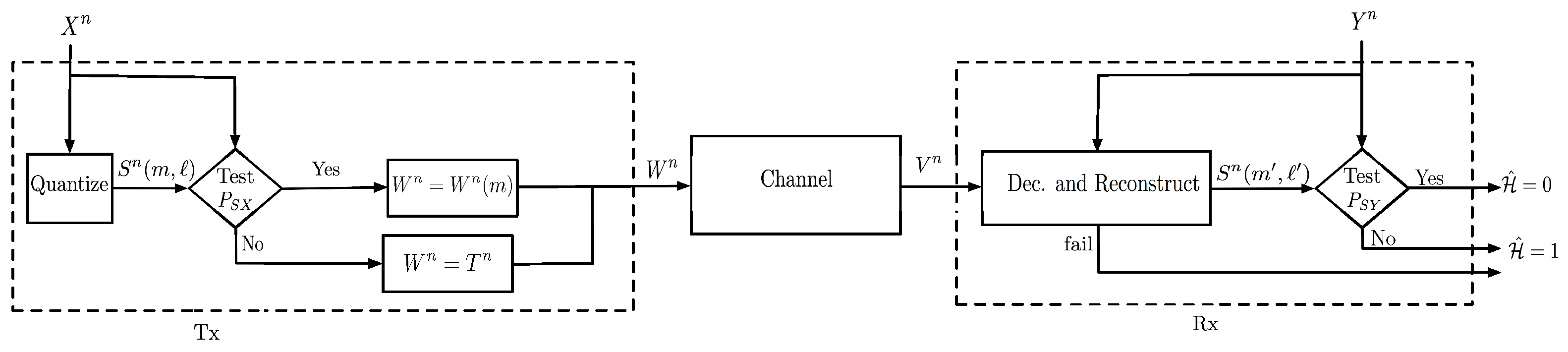
2. System Model

Consider the distributed hypothesis testing problem in Figure 1, where a transmitter observes sequence $X^n$, Receiver 1 sequence $Y_1^n$, and Receiver 2 sequence $Y_2^n$. Under the null hypothesis:

$$\begin{array}{c}\hfill \mathcal{H}=0:(X^n,Y_1^n,Y_2^n)\mathrm{i}.\mathrm{i}.\mathrm{d}.\sim P_{X{Y}_1{Y}_2},\end{array}$$

(1)

and under the alternative hypothesis:

$$\begin{array}{c}\hfill \mathcal{H}=1:(X^n,Y_1^n,Y_2^n)\mathrm{i}.\mathrm{i}.\mathrm{d}.\sim Q_{X{Y}_1{Y}_2},\end{array}$$

(2)

for two given pmfs $P_{X{Y}_1{Y}_2}$ and $Q_{X{Y}_1{Y}_2}$. The transmitter can communicate with the receivers over n uses of a discrete memoryless broadcast channel $(\mathcal{W},{\mathcal{V}}_1\times {\mathcal{V}}_2,P_{V_1{V}_2|W})$ where $\mathcal{W}$ denotes the finite channel input alphabet and ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ the finite channel output alphabets. Specifically, the transmitter feeds inputs

$$W^n=f^{\left(n\right)}\left(X^n\right),$$

(3)

to the channel, where $f^{\left(n\right)}$ denotes the chosen (possibly stochastic) encoding function

$$f^{\left(n\right)}:{\mathcal{X}}^n\to {\mathcal{W}}^n.$$

(4)

Each Receiver $i\in \{1,2\}$ observes the BC ouputs $V_i^n$, where for a given input $W_t=w_t$,

$$\begin{array}{c}\hfill (V_{1,t},V_{2,t})\sim {\mathsf{\Gamma }}_{V_1{V}_2|W}(·,·|w_t),t\in \{1,\dots ,n\}.\end{array}$$

(5)

Based on the sequence of channel outputs $V_i^n$ and the source sequence $Y_i^n$, Receiver i decides on the hypothesis $\mathcal{H}$. That means it produces the guess

$${\widehat{\mathcal{H}}}_i=g^{\left(n\right)}(V_i^n,Y_i^n),$$

(6)

for a chosen decoding function

$$g_i^{\left(n\right)}:{\mathcal{V}}_i^n\times {\mathcal{Y}}_i^n\to \{0,1\}.$$

(7)

There are different possible scenarios regarding the requirements on error probabilities. We assume that each receiver is interested in only one of the two exponents. For each $i\in \{1,2\}$, let ${\mathsf{h}}_i\in \{0,1\}$ be the hypothesis whose error exponent Receiver i wishes to maximize, and ${\overline{\mathsf{h}}}_i$ the other hypothesis, i.e., ${\overline{\mathsf{h}}}_i\in \{0,1\}$ and ${\mathsf{h}}_i\ne {\overline{\mathsf{h}}}_i$. (The values of ${\mathsf{h}}_1$ and ${\mathsf{h}}_2$ are fixed and part of the problem statement.) We then have:

Definition 1.

An exponent pair $({\theta }_1,{\theta }_2)$ is said to be achievable over a BC, if for each ${ϵ}_1,{ϵ}_2\in (0,1)$ and sufficiently large blocklengths n, there exist encoding and decoding functions $(f^{\left(n\right)},g_1^{\left(n\right)},g_2^{\left(n\right)})$ such that:

$$\begin{array}{cc}\hfill {\alpha }_{1,n}& \stackrel{\Delta }{=}Pr[{\widehat{\mathcal{H}}}_1={\mathsf{h}}_1|\mathcal{H}={\overline{\mathsf{h}}}_1],{\alpha }_{2,n}\stackrel{\Delta }{=}Pr[{\widehat{\mathcal{H}}}_2={\mathsf{h}}_2|\mathcal{H}={\overline{\mathsf{h}}}_2],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\beta }_{1,n}& \stackrel{\Delta }{=}Pr[{\widehat{\mathcal{H}}}_1={\overline{\mathsf{h}}}_1|\mathcal{H}={\mathsf{h}}_1],{\beta }_{2,n}\stackrel{\Delta }{=}Pr[{\widehat{\mathcal{H}}}_2={\overline{\mathsf{h}}}_2|\mathcal{H}={\mathsf{h}}_2],\hfill \end{array}$$

(9)

satisfy

$$\begin{array}{cc}\hfill {\alpha }_{i,n}& \le {ϵ}_i,i\in \{1,2\},\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill -\underset{n\to \infty }{\overline{lim}}\frac{1}{n}log{\beta }_{i,n}& \ge {\theta }_i,i\in \{1,2\}.\hfill \end{array}$$

(11)

Definition 2.

The fundamental exponents region$\mathcal{E}$is the set of all exponent pairs$({\theta }_1,{\theta }_2)$that are achievable.

Remark 1.

Notice that both ${\alpha }_{1,n}$ and ${\beta }_{1,n}$ depend on the BC law ${\mathsf{\Gamma }}_{V_1{V}_2|W}$ only through the conditional marginal distribution ${\mathsf{\Gamma }}_{V_1|W}$. Similarly, ${\alpha }_{2,n}$ and ${\beta }_{2,n}$ only depend on ${\mathsf{\Gamma }}_{V_2|W}$. As a consequence, also the fundamental exponents region $\mathcal{E}$ depends on the joint laws $P_{X{Y}_1{Y}_2}$ and $Q_{X{Y}_1{Y}_2}$ only through their marginal laws $P_{X{Y}_1}$, $P_{X{Y}_2}$, $Q_{X{Y}_1}$, and $Q_{X{Y}_2}$.

Remark 2.

As a consequence to the preceding Remark 1, when $P_X=Q_X$, one can restrict attention to a scenario where both receivers aim at maximizing the error exponent under hypothesis $\mathcal{H}=1$, i.e., ${\mathsf{h}}_1={\mathsf{h}}_2=1$. In fact, under $P_X=Q_X$, the fundamental exponents region $\mathcal{E}$ for arbitrary ${\mathsf{h}}_1$ and ${\mathsf{h}}_2$ coincides with the fundamental exponents region $\mathcal{E}$ for ${\mathsf{h}}_1^{\prime }=1$ and ${\mathsf{h}}_2^{\prime }=1$ if one exchanges pmfs $P_{X{Y}_1}$ and $Q_{X{Y}_1}$ in case ${\mathsf{h}}_1=0$ and one exchanges pmfs $P_{X{Y}_2}$ and $Q_{X{Y}_2}$ in case ${\mathsf{h}}_2=0$.

To simplify the notation in the sequel, we use the following shorthand notations for the pmfs $P_{X{Y}_1{Y}_2}$ and $Q_{X{Y}_1{Y}_2}$.

For each $i\in \{1,2\}$:

$$\mathrm{if}{\overline{\mathsf{h}}}_i=0⟹\left(p_{X{Y}_1{Y}_2}^i:=P_{X{Y}_1{Y}_2}\mathrm{and}{q}_{X{Y}_1{Y}_2}^i:=Q_{X{Y}_1{Y}_2}\right)$$

(12a)

and

$$\mathrm{if}{\overline{\mathsf{h}}}_i=1⟹\left(p_{X{Y}_1{Y}_2}^i:=Q_{X{Y}_1{Y}_2}\mathrm{and}{q}_{X{Y}_1{Y}_2}^i:=P_{X{Y}_1{Y}_2}\right).$$

(12b)

We propose two coding schemes yielding two different exponent regions, depending on whether

$$\forall x\in \mathcal{X}:p_X^1\left(x\right)=p_X^2\left(x\right),$$

(13)

or

$$\exists x\in \mathcal{X}:p_X^1\left(x\right)\ne p_X^2\left(x\right).$$

(14)

Notice that (13) always holds when ${\mathsf{h}}_1={\mathsf{h}}_2$. In contrast, given (14), then obviously ${\mathsf{h}}_1\ne {\mathsf{h}}_2$.

3. Results on Exponents Region

Before presenting our main results, we recall the achievable error exponent over a discrete memoryless channel reported in [15] (Theorem 1).

3.1. Achievable Exponent for Point-to-Point Channels

Consider a single-receiver setup with only Receiver 1 that wishes to maximize the error exponent under hypothesis ${\mathsf{h}}_1=1$. For simplicity then, we drop the user index 1 and simply call the receiver’s source observation $Y^n$ and its channel outputs $V^n$.

Theorem 1

(Theorem 1 in [15]). Any exponent θ satisfying the following condition is achievable:

$$\begin{array}{cc}\hfill \theta & \le maxmin\{{\theta }_{\mathit{standard}}\left(P_{S|X}\right),{\theta }_{\mathit{dec}}(P_{S|X},P_T,P_{W|T}),{\theta }_{\mathit{miss}}(P_{S|X},P_T,P_{W|T})\},\hfill \end{array}$$

(15)

where the maximization is over pmfs $P_{S|X}$, $P_T$, and $P_{W|T}$ such that the joint law $P_{STWVXY}:=P_{XY}{P}_{S|X}{P}_T{P}_{W|T}{P}_{V|W}$ satisfies

$$I(S;X|Y)\le I(W;V\left|T\right),$$

(16)

and where the exponents in (15) are defined as:

$$\begin{array}{cc}\hfill {\theta }_{\mathit{standard}}\left(P_{S|X}\right)& :=\underset{\begin{array}{c}{\tilde{P}}_{SXY}:\\ {\tilde{P}}_{SX}=P_{SX}\\ {\tilde{P}}_{SY}=P_{SY}\end{array}}{min}D({\tilde{P}}_{SXY}\parallel P_{S|X}{Q}_{XY}),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{dec}}(P_{S|X},P_T,P_{W|T})& :=\underset{\begin{array}{c}{\tilde{P}}_{SXY}:\\ {\tilde{P}}_{SX}=P_{SX}\\ {\tilde{P}}_Y=P_Y\\ H_P\left(S\right|Y)\le H_{\tilde{P}}\left(S\right|Y)\end{array}}{min}D({\tilde{P}}_{SXY}\parallel P_{S|X}{Q}_{XY})-I(S;X|Y)+I(W;V|T),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{miss}}(P_{S|X},P_T,P_{W|T})& :=D(P_Y\parallel Q_Y)+{\mathbb{E}}_{P_T}\left[D\left(P_{V|T}\parallel {\mathsf{\Gamma }}_{V|W=T}\right)\right]-I(S;X|Y)+I(W;V|T).\hfill \end{array}$$

(19)

Here, all mutual information terms are calculated with respect to the joint pmf $P_{STWVXY}$ defined above.

The exponent in Theorem 1 is obtained by the following scheme, which is also depicted in Figure 2.

The transmitter attempts to quantize the source sequence $X^n$ using a random codebook consisting of codewords $\left\{S^n(m,\ell )\right\}$. If the quantization fails because no codeword is jointly typical with the source sequence, then the transmitter applies the UEP mechanism in [17] by sending an IID $P_T$-sequence $T^n$ over the channel. Otherwise, it sends the codeword $W^n\left(m\right)$ for m indicating the first index of the $S^n(m,\ell )$ codeword that is jointly typical with its source observation $X^n$. The receiver jointly decodes the channel and source codeword by verifying the existence of indices $(m^{\prime },{\ell }^{\prime })$ such that $W^n=W^n\left(m^{\prime }\right)$ is jointly typical with its channel outputs $V^n$ and there is no other codeword $S^n(m^{\prime },\tilde{\ell })$ with smaller conditional empirical entropy given $Y^n$ than $S^n(m^{\prime },{\ell }^{\prime })$. If the decoded codeword $S^n(m^{\prime },{\ell }^{\prime })$ is jointly typical with the receiver’s observation $Y^n$, then it produces $\widehat{\mathcal{H}}=0$, and otherwise $\widehat{\mathcal{H}}=1$.

The three competing type-II error exponents in Theorem 1 can be understood in view of this coding scheme as follows. Exponent ${\theta }_{\mathit{standard}}$ indicates the event that a random codeword $S^n(m,\ell )$ is jointly typical with the transmitter’s observation $X^n$ and with the receiver’s observation $Y^n$ while being under $\mathcal{H}=1$. This is also the error exponent in Han’s scheme [2] over a noiseless communication link and does not depend on the channel law ${\mathsf{\Gamma }}_{V|W}$. Exponent ${\theta }_{\mathit{dec}}$ is related to the joint decoding that checks the joint typicality of the source codeword, as well as of the channel codeword, and applies a conditional minimum entropy decoder. A similar error exponent is observed in the SHA scheme [3,4] over a noiseless link if the mutual information $I(W;V|T)$ is replaced by the rate of the link. The third exponent ${\theta }_{miss}$ finally indicates an event where the transmitter sends $T^n$ (so as to indicate the receiver to decide for $\widehat{\mathcal{H}}=1$) but the receiver detects a channel codeword $W^n\left(m^{\prime }\right)$ and a corresponding source codeword $S^n(m^{\prime },{\ell }^{\prime })$. This exponent is directly related to the channel transition law ${\mathsf{\Gamma }}_{V|W}$ and not only to the mutual information of the channel and does not occur when transmission is over a noiseless link. Interestingly, it is redundant in view of exponent ${\theta }_{dec}$ whenever $Q_{XY}=P_X{Q}_Y$ because in this case the minimization in (18) evaluates to $D(P_Y\parallel Q_Y)$. In this special case, the exponent can also be shown to be optimal, see [15].

We now present our achievable exponents region, where we distinguish the two cases (1) ${\mathsf{h}}_1\ne {\mathsf{h}}_2$ and $P_X\ne Q_X$; and (2) $({\mathsf{h}}_1={\mathsf{h}}_2)$ or $P_X=Q_X$.

3.2. Achievable Exponents Region When ${\mathsf{h}}_1\ne {\mathsf{h}}_2$ and $P_X\ne Q_X$

Theorem 2.

If ${\mathsf{h}}_1\ne {\mathsf{h}}_2$ and $P_X\ne Q_X$, i.e., (14) holds, then all error exponent pairs $({\theta }_1,{\theta }_2)$ satisfying the following condition are achievable:

$$\begin{array}{cc}\hfill {\theta }_i& \le min\{{\theta }_{\mathit{standard},i}{\theta }_{\mathit{dec},i},{\theta }_{\mathit{cross},i},{\theta }_{\mathit{miss},i}\},i\in \{1,2\},\hfill \end{array}$$

(20)

where the union is over pmfs $p_{S|X}^i$, $p_T$, $p_{T_i|T}^i$, and $p_{W|T_i}^i$, for $i\in \{1,2\}$, so that the joint pmfs $p^1,p^2$ defined through (12) and

$$\begin{array}{cc}\hfill p_{SX{Y}_1{Y}_{2}T{T}_{i}W{V}_1{V}_2}^i& :=p_{S|X}^i·p_{X{Y}_1{Y}_2}^i·p_T·p_{T_i|T}^i·p_{W|T{T}_i}^i·{\mathsf{\Gamma }}_{V_1{V}_2|W},i\in \{1,2\},\hfill \end{array}$$

(21)

satisfy constraints

$$I_{p^i}(S;X|Y_i)<I_{p^i}(W;V_i|T,T_i),i\in \{1,2\},$$

(22)

and where the exponents in (20) are defined as follows, where we set $q^1=p^2$ and $q^2=p^1$:

$$\begin{array}{cc}\hfill {\theta }_{\mathit{standard},i}& :=\underset{\begin{array}{c}{\tilde{P}}_{SX{Y}_i}:\\ {\tilde{P}}_{SX}=p_{SX}^i\\ {\tilde{P}}_{S{Y}_i}=p_{S{Y}_i}^i\end{array}}{min}D({\tilde{P}}_{SX{Y}_i}\parallel p_{S|X}^i{q}_{X{Y}_i}^i),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{dec},i}& :=\underset{\begin{array}{c}{\tilde{P}}_{SX{Y}_i}:\\ {\tilde{P}}_{SX}=p_{SX}^i\\ {\tilde{P}}_{Y_i}=p_{Y_i}^i\\ H_{p^i}\left(S\right|Y_i)\le H_{\tilde{P}}\left(S\right|Y_i)\end{array}}{min}D({\tilde{P}}_{SX{Y}_i}\parallel p_{S|X}^i{q}_{X{Y}_i}^i)-I_{p^i}(S;X|Y_i)+I_{p^i}(W;V_i|T,T_i),\hfill \end{array}$$

(24)

$${\theta }_{\mathit{miss},i}:=D(p_{Y_i}^i\parallel q_{Y_i}^i)+{\mathbb{E}}_{p_T}\left[D\left(p_{V_i|T}^i\parallel {\mathsf{\Gamma }}_{V_i|W=T}\right)\right]-I_{p^i}(S;X|Y_i)+I_{p^i}(W;V_i|T,T_i),$$

(25)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{cross},i}& :=\underset{\begin{array}{c}{\tilde{P}}_{SX{Y}_i}:\\ {\tilde{P}}_{Y_i}=p_{Y_i}^i\\ H_{p^i}\left(S\right|Y_i)\le H_{\tilde{P}}\left(S\right|Y_i)\end{array}}{min}{\mathbb{E}}_{{\tilde{P}}_{SX}}\left[D\left({\tilde{P}}_{Y_i|XS}\parallel q_{Y_i|X}^i\right)\right]+\underset{\begin{array}{c}{\tilde{P}}_{T{T}_{i}W}:\\ {\tilde{P}}_{TW}=q_{TW}^i\\ {\tilde{P}}_{T{T}_i}=p_{T{T}_i}^i\end{array}}{min}{\mathbb{E}}_{{\tilde{P}}_{T{T}_{i}W}}\left[D(p_{V_i|T{T}_i}^i\parallel {\mathsf{\Gamma }}_{V_i|W})\right]\hfill \\ & -I_{p^i}(S;X|Y_i)+I_{p^i}(W;V_i|T,T_i).\end{array}$$

(26)

Proof. 

See Appendix A. □

In Theorem 2, the exponent triple ${\theta }_{\mathit{standard},1},{\theta }_{\mathit{dec},1},{\theta }_{\mathit{miss},1}$ can be optimized over the pmfs $p_{S|X}^1$, $p_{T_1|T}^1$ and $p_{W|T{T}_1}^1$ and independently thereof the exponent triple ${\theta }_{\mathit{standard},2},{\theta }_{\mathit{dec},2},{\theta }_{\mathit{miss},2}$ can be optimized over the pmfs $p_{S|X}^2$, $p_{T_2|T}^2$ and $p_{W|T,T_2}^2$. The pmf $p_T$ is common to both optimizations. However, whenever the exponents ${\theta }_{\mathit{cross},1}$ and ${\theta }_{\mathit{cross},2}$ are not active, Theorem 2 depends only on $p_{S|X}^i$, $p_{T_i}^i$ and $p_{W|T_i}^i$, for $i=1,2$, and there is thus no tradeoff between the two exponents ${\theta }_1$ and ${\theta }_2$. In other words, the same exponents ${\theta }_1$ and ${\theta }_2$ can be attained as in a system where the transmitter communicates over two individual DMCs ${\mathsf{\Gamma }}_{V_1|W}$ and ${\mathsf{\Gamma }}_{V_2|W}$ to the two receivers, or equivalently each receiver achieves the same exponent as if the other receiver was not present in the system.

The scheme achieving the exponents region in Theorem 2 is described in detail in Section 4 and analyzed in Appendix A. The main feature is that the sensor makes a tentative decision on $\mathcal{H}$ and conveys this decision to both receivers through its choice of the codebooks and a special coded time-sharing sequence indicating this choice. The receiver that wishes to maximize the error exponent corresponding to the hypothesis guessed at the sensor directly decides on this hypothesis. The other receiver should compare its own observation to a quantized version of the source sequence observed at the sensor. The sensor uses the quantization and binning scheme presented in [15] tailored to this latter receiver using either coded time-sharing sequence $T_1^n$ and codebooks $\left\{S^n(1;m,\ell )\right\}$ and $\left\{W^n(1;m)\right\}$ or coded time-sharing sequence $T_2^n$ and codebooks $\left\{S^n(2;m,\ell )\right\}$ and $\left\{W^n(2;m)\right\}$, respectively. The overall scheme is illustrated in Figure 3.

Exponents ${\theta }_{\mathit{standard},i}$, ${\theta }_{\mathit{dec},i}$, and ${\theta }_{\mathit{miss},i}$ have similar explanations as in the single-user case. Exponent ${\theta }_{\mathit{cross},i}$ corresponds to the event that the transmitter sends a codeword from $\left\{W\right(j;m\left)\right\}$, for $j=3-i$, but Receiver i decides that a codeword from $\left\{W\right(i;m\left)\right\}$ was sent and a source codeword $S(i;m,\ell )$ satisfies the minimum conditional entropy condition and the typicality check with the observed source sequence $Y_i^n$. Notice that setting $T_i$ as a constant decreases the error exponent ${\theta }_{\mathit{cross},i}$.

For the special case where the BC consists of a common noiseless link, Theorem 2 has been proved in [12,13]. (More precisely, [12] considers the more general case with $K\ge 2$ receivers and $M\ge K$ hypotheses.) In this case, the exponents $({\theta }_{\mathit{miss},1},{\theta }_{\mathit{cross},1})$ and $({\theta }_{\mathit{miss},2},{\theta }_{\mathit{cross},2})$ are not active and there is no tradeoff between ${\theta }_1$ and ${\theta }_2$.

3.3. Achievable Exponents Region for ${\mathsf{h}}_1={\mathsf{h}}_2$ or $P_X=Q_X$

Define for any pmfs $P_T$, $P_{S{U}_1{U}_2|XT}$ and function

$$\begin{array}{c}\hfill f:\mathcal{S}\times {\mathcal{U}}_1\times {\mathcal{U}}_2\times \mathcal{X}\to \mathcal{W}\end{array}$$

(27)

the joint pmfs

$$\begin{array}{cc}\hfill p_{S{U}_1{U}_{2}X{Y}_1{Y}_{2}T{V}_1{V}_2}^i& :=P_{S{U}_1{U}_2|XT}·p_{X{Y}_1{Y}_2}^i·P_T·{\mathsf{\Gamma }}_{V_1{V}_2|S{U}_1{U}_{2}X},i\in \{1,2\},\hfill \end{array}$$

(28)

and

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_{V_1{V}_2|S{U}_1{U}_{2}X}:={\mathsf{\Gamma }}_{V_1{V}_2|W}(v_1,v_2|f(s,u_1,u_2,x)),\forall s\in \mathcal{S},u_1\in {\mathcal{U}}_1,u_2\in {\mathcal{U}}_2,x\in \mathcal{X},\end{array}$$

(29)

and for each $i\in \{1,2\}$, the four exponents

$$\begin{array}{cc}\hfill {\theta }_{\mathit{standard},i}& :=\underset{\begin{array}{c}{\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}:\\ {\tilde{P}}_{S{U}_{i}XT}=p_{S{U}_{i}XT}^i\\ {\tilde{P}}_{S{U}_i{Y}_{i}T{V}_i}=p_{S{U}_i{Y}_{i}T{V}_i}^i\end{array}}{min}D\left({\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}\parallel p_{S{U}_i|X}^i{q}_{X{Y}_i}^i{P}_T{\mathsf{\Gamma }}_{V_i|S{U}_1{U}_{2}X}\right),\hfill \end{array}$$

(30a)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{dec},i}^a& :=\underset{\begin{array}{c}{\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}:\\ {\tilde{P}}_{S{U}_{i}XT}=p_{S{U}_{i}XT}^i\\ {\tilde{P}}_{Y_{i}T{V}_i}=p_{Y_{i}T{V}_i}^i\\ H_{p^i}(S,U_i|Y_i,T,V_i)\le H_{\tilde{P}}(S,U_i|Y_i,T,V_i)\end{array}}{min}D\left({\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}\parallel p_{S{U}_i|X}^i{q}_{X{Y}_i}^i{P}_T{\mathsf{\Gamma }}_{V_i|S{U}_1{U}_{2}X}\right)-I_{p^i}(S,U_i;X|T)+I_{p^i}(S,U_i;Y_i,V_i|T),\hfill \end{array}$$

(30b)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{dec},i}^b& :=\underset{\begin{array}{c}{\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}:\\ {\tilde{P}}_{S{U}_{i}XT}=p_{S{U}_{i}XT}^i\\ {\tilde{P}}_{S{Y}_{i}T{V}_i}=p_{S{Y}_{i}T{V}_i}^i\\ H_{p^i}\left(U_i\right|S,Y_i,T,V_i)\le H_{\tilde{P}}\left(U_i\right|S,Y_i,T,V_i)\end{array}}{min}D\left({\tilde{P}}_{S{U}_{i}X{Y}_{i}T{V}_i}\parallel p_{S{U}_i|X}^i{q}_{X{Y}_i}^i{P}_T{\mathsf{\Gamma }}_{V_i|S{U}_1{U}_{2}X}\right)-I_{p^i}(U_i;X|S,T)+I_{p^i}(U_i;Y_i,V_i|S,T),\hfill \end{array}$$

(30c)

$$\begin{array}{cc}\hfill {\theta }_{\mathit{miss},i}& :={\mathbb{E}}_{P_T}\left[D\left(p_{Y_i{V}_i|T}^i\parallel q_{Y_i}^i{\mathsf{\Gamma }}_{V_i|W=T}\right)\right]-I_{p^i}(S,U_i;X|T)+I_{p^i}(S,U_i;Y_i,V_i|T).\hfill \end{array}$$

(30d)

Theorem 3.

If ${\mathsf{h}}_1={\mathsf{h}}_2$ or $P_X=Q_X$, i.e., (13) holds, then the union of all nonnegative error exponent pairs $({\theta }_1,{\theta }_2)$ satisfying the following conditions is achievable:

$$\begin{array}{cc}\hfill {\theta }_i& \le min\left\{{\theta }_{\mathit{standard},i},{\theta }_{\mathit{dec},i}^a,{\theta }_{\mathit{dec},i}^b,{\theta }_{\mathit{miss},i}\right\},i\in \{1,2\},\hfill \\ \hfill {\theta }_1+{\theta }_2& \le min\{{\theta }_{\mathit{standard},1}+{\theta }_{\mathit{standard},2},{\theta }_{\mathit{standard},1}+{\theta }_{\mathit{dec},2}^a,{\theta }_{\mathit{standard},1}+{\theta }_{\mathit{dec},2}^b,\hfill \\ & {\theta }_{\mathit{standard},2}+{\theta }_{\mathit{dec},1}^a,{\theta }_{\mathit{standard},2}+{\theta }_{\mathit{dec},1}^b,{\theta }_{\mathit{miss},1}+{\theta }_{\mathit{miss},2}\}\hfill \end{array}$$

(31a)

$$\begin{array}{cc}\hfill & -I_{p^1}(U_1;U_2|S,T),\hfill \end{array}$$

(31b)

$$\begin{array}{cc}\hfill {\theta }_1+{\theta }_2& \le min\left\{{\theta }_{\mathit{dec},1}^a,{\theta }_{\mathit{dec},1}^b\right\}+min\left\{{\theta }_{\mathit{dec},2}^a,{\theta }_{\mathit{dec},2}^b\right\}-2I_{p^1}(U_1;U_2|S,T),\hfill \end{array}$$

(31c)

where the union is over pmfs $P_T$, $P_{S{U}_1{U}_2|XT}$ and functions f as in (27) so that the pmfs (28) and (29) satisfy for $i\in \{1,2\}$:

$$\begin{array}{cc}\hfill I_{p^i}(S,U_i;X|T)& \le I_{p^i}(S,U_i;Y_i,V_i|T),\hfill \end{array}$$

(32a)

$$\begin{array}{cc}\hfill I_{p^i}(U_i;X|S,T)& \le I_{p^i}(U_i;Y_i,V_i|S,T),\hfill \end{array}$$

(32b)

$$\begin{array}{c}{I}_{p^1}(S,U_1;X|T)+I_{p^1}(S,U_2;X|T)+I_{p^1}(U_1;U_2|S,T)\hfill \\ \hfill \le I_{p^1}(S,U_1;Y_1,V_1|T)+I_{p^2}(S,U_2;Y_2,V_2|T),\end{array}$$

(32c)

$$\begin{array}{c}{I}_{p^1}(U_1;X|S,T)+I_{p^1}(U_2;X|S,T)+I_{p^1}(U_1;U_2|S,T)\hfill \\ \hfill \le I_{p^1}(U_1;Y_1,V_1|S,T)+I_{p^2}(U_2;Y_2,V_2|S,T),\end{array}$$

(32d)

$$\begin{array}{c}{I}_{p^1}(U_1;X|S,T)+I_{p^1}(S,U_2;X|T)+I_{p^1}(U_1;U_2|S,T)\hfill \\ \hfill \le I_{p^1}(U_1;Y_1,V_1|S,T)+I_{p^2}(S,U_2;Y_2,V_2|T),\end{array}$$

(32e)

$$\begin{array}{c}{I}_{p^1}(S,U_1;X|T)+I_{p^1}(U_2;X|S,T)+I_{p^1}(U_1;U_2|S,T)\hfill \\ \hfill \le I_{p^1}(S,U_1;Y_1,V_1|T)+I_{p^2}(U_2;Y_2,V_2|S,T),\end{array}$$

(32f)

Proof. 

The coding and testing scheme achieving these exponents is described in Section 5. The analysis of the scheme is similar to the proof of [15] (Theorem 4) and omitted for brevity. In particular, error exponent ${\theta }_{\mathit{standard},i}$ corresponds with the event that Receiver i decodes the correct cloud and satellite codewords but wrongly decides on ${\widehat{\mathcal{H}}}_i=0$. In contrast, error exponents ${\theta }_{\mathit{dec},i}^a$ and ${\theta }_{\mathit{dec},i}^b$ correspond to the events that Receiver i wrongly decides on ${\widehat{\mathcal{H}}}_i=0$ after wrongly decoding both the cloud center and the satellite or only the satellite. Error exponent ${\theta }_{\mathit{miss},i}$ corresponds to the miss-detection event. Due to the implicit rate constraints in (46), the final constraints in (31) are obtained by eliminating the rates $R_0,R_1,R_2$ by means of Fourier–Motzkin elimination. Notice that in constraint (31c), the mutual information $I_{p^1}(U_1;U_2|S,T)$ is multiplied by a factor 2, whereas in (31b), it appears without a factor. The reason is that the error analysis includes union bounds over the codewords in a bin and when wrongly decoding the satellite codewords (which is the case of exponents ${\theta }_{\mathit{dec},i}^a$ and ${\theta }_{\mathit{dec},i}^b$) then the union bound is over pairs of codewords, whereas under correct decoding, it is over single codewords. In the former case, we have the factor $2^{2n{R}_i^{\prime }}$ in the error probability, and, in the latter case, the factor $2^{n{R}_i^{\prime }}$. The auxiliary rates $R_1^{\prime }$ and $R_2^{\prime }$ are then eliminated using the Fourier–Motzkin elimination algorithm. □

For each $i\in \{1,2\}$, exponents ${\theta }_{\mathit{standard},i},{\theta }_{\mathit{dec},i}^a,{\theta }_{\mathit{dec},i}^b$, and ${\theta }_{\mathit{miss},i}$ have the same form as the three exponents in [15] (Theorem 1) for the DMC. There is, however, a tradeoff between the two exponents ${\theta }_1$ and ${\theta }_2$ in the above theorem because they share the same choice of the auxiliary pmfs $P_T$ and $P_{S{U}_1{U}_2|XT}$ and the function f. In [10], the above setup is studied in the special case of testing against conditional independence, and the mentioned tradeoff is illustrated through a Gaussian example.

4. Coding and Testing Scheme When ${\mathit{p}}_{\mathit{X}}^{\mathbf{1}}\ne {\mathit{p}}_{\mathit{X}}^{\mathbf{2}}$

Fix $\mu >0$, a sufficiently large blocklength n, auxiliary distributions $p_T$, $p_{T_1|T}^1$ and $p_{T_2|T}^2$ over $\mathcal{W}$, conditional channel input distributions $p_{W|T{T}_1}^1$ and $p_{W|T{T}_2}^2$, and conditional pmfs $p_{S|X}^1$ and $p_{S|X}^2$ over a finite auxiliary alphabet $\mathcal{S}$ such that for each $i\in \{1,2\}$:

$$I_{p^i}(S;X|Y_i)<I_{p^i}(W;V_i|T,T_i).$$

(33)

The mutual information in (33) is calculated according to the joint distribution:

$$\begin{array}{cc}\hfill p_{SX{Y}_1{Y}_{2}T{T}_{i}W{V}_1{V}_2}^i& =p_{S|X}^i·p_{X{Y}_1{Y}_2}^i·p_T·p_{T_i|T}^i·p_{W|T{T}_i}^i·{\mathsf{\Gamma }}_{V_1{V}_2|W}.\hfill \end{array}$$

(34)

For each $i\in \{1,2\}$, if $I_{p^i}(S;X)<I_{p^i}(W;V_i|T,T_i)$, choose rates

$$\begin{array}{cc}\hfill R_i& :=I_{p^i}(S;X)+\mu ,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill R_i^{\prime }& :=0.\hfill \end{array}$$

(36)

If $I_{p^i}(S;X)\ge I_{p^i}(W;V_i|T,T_i)$, then choose rates

$$\begin{array}{cc}\hfill R_i& :=I_{p^i}(W;V_i|T,T_i)-\mu ,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill R_i^{\prime }& :=I_{p^i}(S;X)-I_{p^i}(W;V_i|T,T_i)+2\mu .\hfill \end{array}$$

(38)

Again, all mutual informations in (35)–(38) are calculated with respect to the pmf in (34).

Code Construction: Generate a sequence $T^n=(T_1,\dots ,T_n)$ by independently drawing each component $T_k$ according to $p_T$. For each $i\in \{1,2\}$, generate a sequence $T_i^n=(T_{i,1},\dots ,T_{i,n})$ by independently drawing each $T_{i,k}$ according to $p_{T_i|T}^i(.|t)$ when $T_k=t$. In addition, construct a random codebook

$${\mathcal{C}}_W^i=\left\{W^n(i;m):m\in \{1,...,\lfloor 2^{n{R}_i}\rfloor \}\right\}$$

(39)

superpositioned on $(T^n,T_i^n)$ where the k-th symbol $W_k(i;m)$ of codeword $W^n(i;m)$ is drawn independently of all codeword symbols according to $p_{W|T{T}_i}^i(·|t,t_i)$ when $T_k=t$ and $T_{i,k}=t_i$. Finally, construct a random codebook

$$\begin{array}{cc}\hfill {\mathcal{C}}_S^i& =\{S^n(i;m,\ell ):m\in \{1,\dots ,\lfloor 2^{n{R}_i}\rfloor \},\ell \in \{1,\dots ,\lfloor 2^{n{R}_i^{\prime }}\rfloor \}\},i\in \{1,2\},\hfill \end{array}$$

(40)

by independently drawing the k-th component $S_k(i;m,\ell )$ of codeword $S^n(i;m,\ell )$ according to the marginal pmf $p_S^i$.

Reveal all codebooks and the realizations $t^n,t_1^n,t_2^n$ of the sequences $T^n,T_1^n,T_2^n$ to all terminals.

Transmitter: Given source sequence $X^n=x^n$, the transmitter looks for indices $(i,m,\ell )\in \{1,2\}\times \{1,\dots ,\lfloor 2^{n{R}_1}\rfloor \}\times \{1,\dots ,\lfloor 2^{n{R}_i^{\prime }}\rfloor \}$ such that codeword $s^n(i;m,\ell )$ from codebook ${\mathcal{C}}_S^i$ satisfies

$$\begin{array}{c}\hfill (s^n(i;m,\ell ),x^n)\in {\mathcal{T}}_{\mu /2}^n\left(p_{SX}^i\right).\end{array}$$

(41)

and the corresponding codeword $w^n(i;m)$ from codebook ${\mathcal{C}}_W^i$ satisfies

$$\begin{array}{c}\hfill (t^n,t_i^n,w^n(i;m))\in {\mathcal{T}}_{\mu /2}^n\left(p_{T{T}_{i}W}^i\right).\end{array}$$

(42)

(Notice that when $\mu$ is sufficiently small, then Condition (41) can be satisfied for at most one value $i\in \{1,2\}$, because $p_X^1\ne p_X^2$.) If successful, the transmitter picks uniformly at random one of the triples $(i,m,\ell )$ that satisfy (41), and it sends the sequence $w^n(i;m)$ over the channel. If no triple satisfies Condition (41), then the transmitter sends the sequence $t^n$ over the channel.

Receiver $i\in \{1,2\}$: Receives $v_i^n$ and checks whether there exist indices $(m^{\prime },{\ell }^{\prime })$ such that the following three conditions are satisfied:

• $$\begin{array}{c}\hfill (t^n,t_i^n,w^n(i;m^{\prime }),v_i^n)\in {\mathcal{T}}_{\mu }^n\left(p_{T{T}_{i}W{V}_i}^i\right),\end{array}$$

  (43)
• $$\begin{array}{c}\hfill H_{\mathrm{tp}(s^n(i;m^{\prime },{\ell }^{\prime }),y_i^n)}\left(S\right|Y_i)=\underset{\tilde{\ell }}{min}{H}_{\mathrm{tp}(s^n(i;m^{\prime },\tilde{\ell }),y_i^n)}\left(S\right|Y_i),\end{array}$$

  (44)
• $$\begin{array}{c}\hfill (s^n(i;m^{\prime },{\ell }^{\prime }),y_i^n)\in {\mathcal{T}}_{\mu }^n\left(p_{S{Y}_i}^i\right).\end{array}$$

  (45)

If successful, it declares ${\widehat{\mathcal{H}}}_i={\overline{\mathsf{h}}}_i$. Otherwise, it declares ${\widehat{\mathcal{H}}}_i={\mathsf{h}}_i$.

Analysis: See Appendix A.

5. Coding and Testing Scheme When ${\mathit{p}}_{\mathit{X}}^{\mathbf{1}}={\mathit{p}}_{\mathit{X}}^{\mathbf{2}}$

In this case, the scheme is based on hybrid source-channel coding. Choose a large positive integer n, auxiliary alphabets $\mathcal{S}$, ${\mathcal{U}}_1,$ and ${\mathcal{U}}_2$, and a function f as in (27).

Choose an auxiliary distribution $P_T$ over $\mathcal{W}$, and a conditional distribution $P_{S{U}_1{U}_2|XT}$ over $\mathcal{S}\times {\mathcal{U}}_1\times {\mathcal{U}}_2$ so that for $i\in \{1,2\}$ inequalities (32) are satisfied with strict inequality.

Then, choose a positive $\mu$ and rates $R_0,R_1,R_2$ so that

$$\begin{array}{cc}\hfill R_0& =I_{p^1}(S;X|T)+\mu ,\hfill \end{array}$$

(46a)

$$\begin{array}{cc}\hfill R_i& >I_{p^1}(U_i;X|S,T),i\in \{1,2\},\hfill \end{array}$$

(46b)

$$\begin{array}{cc}\hfill R_1+R_2& >I_{p^1}(U_1;X|S,T)+I_{p^1}(U_2;X|S,T)+I_{p^1}(U_1;U_2|S,T),\hfill \end{array}$$

(46c)

and

$$\begin{array}{cc}\hfill R_0+R_i& <I_{p^i}(S,U_i;Y_i,V_i|T),\hfill \end{array}$$

(46d)

$$\begin{array}{cc}\hfill R_i& <I_{p^i}(U_i;Y_i,V_i|S,T).\hfill \end{array}$$

(46e)

Generate a sequence $T^n$ i.i.d. according to $P_T$ and construct a random codebook

$${\mathcal{C}}_S=\left\{S^n\left(m_0\right):m_0\in \{1,...,\lfloor 2^{n{R}_0}\rfloor \}\right\}$$

superpositioned on $T^n$ where each codeword is drawn independently according to $p_{S|T}^1$ conditioned on $T^n$. Then, for each index $m_0$ and $i\in \{1,2\}$, randomly generate a codebook

$${\mathcal{C}}_{U_i}\left(m_0\right)=\left\{U_i^n(m_0,m_i):m_i\in \{1,...,\lfloor 2^{n{R}_i}\rfloor \}\right\}$$

superpositioned on $(T^n,S^n\left(m_0\right))$ by drawing each entry of the n-length codeword $U_i^n(m_0,m_i)$ i.i.d. according to the conditional pmf $p_{U_i|ST}^1(·|S_k\left(m_0\right),T)$ where $S_k\left(m_0\right)$ denotes the k-th symbol of $S^n\left(m_0\right)$. Reveal the realizations of the codebooks and the sequence $T^n$ to all terminals.

Transmitter: Given that it observes the source sequence $X^n=x^n$, the transmitter looks for indices $(m_0,m_1,m_2)$ that satisfy

$$\begin{array}{c}\hfill \left(s^n\left(m_0\right),u_1^n(m_0,m_1),u_2^n(m_0,m_2),x^n,t^n\right)\in {\mathcal{T}}_{\mu /2}^n\left(p_{S{U}_1{U}_{2}XT}^1\right).\end{array}$$

(47)

If successful, it picks one of these indices uniformly at random and sends the codeword $w^n$ over the channel, where

$$\begin{array}{c}\hfill w_k=f\left(s_k\left(m_0\right),u_{1,k}(m_0,m_1),u_{2,k}(m_0,m_2),x_k\right),k\in \{1,\dots ,n\},\end{array}$$

(48)

and where $(s_k\left(m_0\right),u_{1,k}(m_0,m_1),u_{2,k}(m_0,m_2))$ denote the k-th components of codewords $(s^n\left(m_0\right),u_1^n(m_0,m_1),u_2^n(m_0,$$m_2\left)\right)$. Otherwise, it sends the sequence of inputs $t^n$ over the channel.

Receiver $i\in \{1,2\}$: After observing $V_i^n=v_i^n$ and $Y_i^n=y_i^n$, Receiver $i\in \{1,2\}$ looks for indices $m_0^{\prime }\in \{1,\dots ,\lfloor 2^{n{R}_0}\rfloor \}$ and $m_i^{\prime }\in \{1,\dots ,\lfloor 2^{n{R}_i}\rfloor \}$ that satisfy the following conditions:

• $$\begin{array}{c}\hfill (s^n\left(m_0^{\prime }\right),u_i^n(m_0^{\prime },m_i^{\prime }),y_i^n,t^n,v_i^n)\in {\mathcal{T}}_{\mu }^n\left(p_{S{U}_i{Y}_{i}T{V}_i}^i\right).\end{array}$$

  (49)
• $$\begin{array}{c}{H}_{\mathrm{tp}\left(s^n\left(m_0^{\prime }\right),u_i^n(m_0^{\prime },m_i^{\prime }),y_i^n,t^n,v_i^n\right)}(S,U_i|Y_i,T,V_i)\hfill \\ =\underset{{\tilde{m}}_0,{\tilde{m}}_i}{min}{H}_{\mathrm{tp}\left(s^n\left({\tilde{m}}_0\right),u_i^n({\tilde{m}}_0,{\tilde{m}}_i),y_i^n,t^n,v_i^n\right)}(S,U_i|Y_i,T,V_i),\end{array}$$

  (50)

If successful, Receiver i declares ${\widehat{\mathcal{H}}}_i={\overline{\mathsf{h}}}_i$. Otherwise, it declares ${\widehat{\mathcal{H}}}_i={\mathsf{h}}_i$.

Analysis: Similar to [15] (Appendix D) and omitted.

6. Summary and Conclusions

The paper proposed and analyzed general distributed hypothesis testing schemes both for the case where the sensor can distinguish the two null hypotheses and where it cannot. Our general schemes recover all previously studied special cases. Moreover, our schemes illustrate a similar phenomenon for setups with common noisefree communication links from the sensor to all decision centers: while a tradeoff arises when the transmitter cannot distinguish the alternate hypotheses at the two decision centers, such a tradeoff can almost completely be mitigated when the transmitter can distinguish the alternate hypotheses. In contrast to the noise-free link scenario, under a noisy broadcast channel model, a tradeoff can still arise in this case because decision centers can confuse the decision taken at the transmitter, and thus misinterpret to whom the communication is dedicated.

Interesting directions for future research include information-theoretic converse results and extensions to multiple sensors or more than two decision centers.