TraceAll: A Real-Time Processing for Contact Tracing Using Indoor Trajectories
Abstract
1. Introduction
- We develop a novel technique TraceAll for efficiently answering the contact tracing queries.
- We reduce the total processing time to answer the queries by not scanning all the suspected trajectories but scanning only suspected parts.
- We adapt the three-dimensional R-Tree for fast retrieval purposes concerning the trajectories of suspected cases that may hold the infection.
- We evaluate our technique on real data based on multiple metrics and present that they achieve our objectives.
2. Related Work
2.1. Contact Tracing Methods
2.2. Contact Tracing Applications
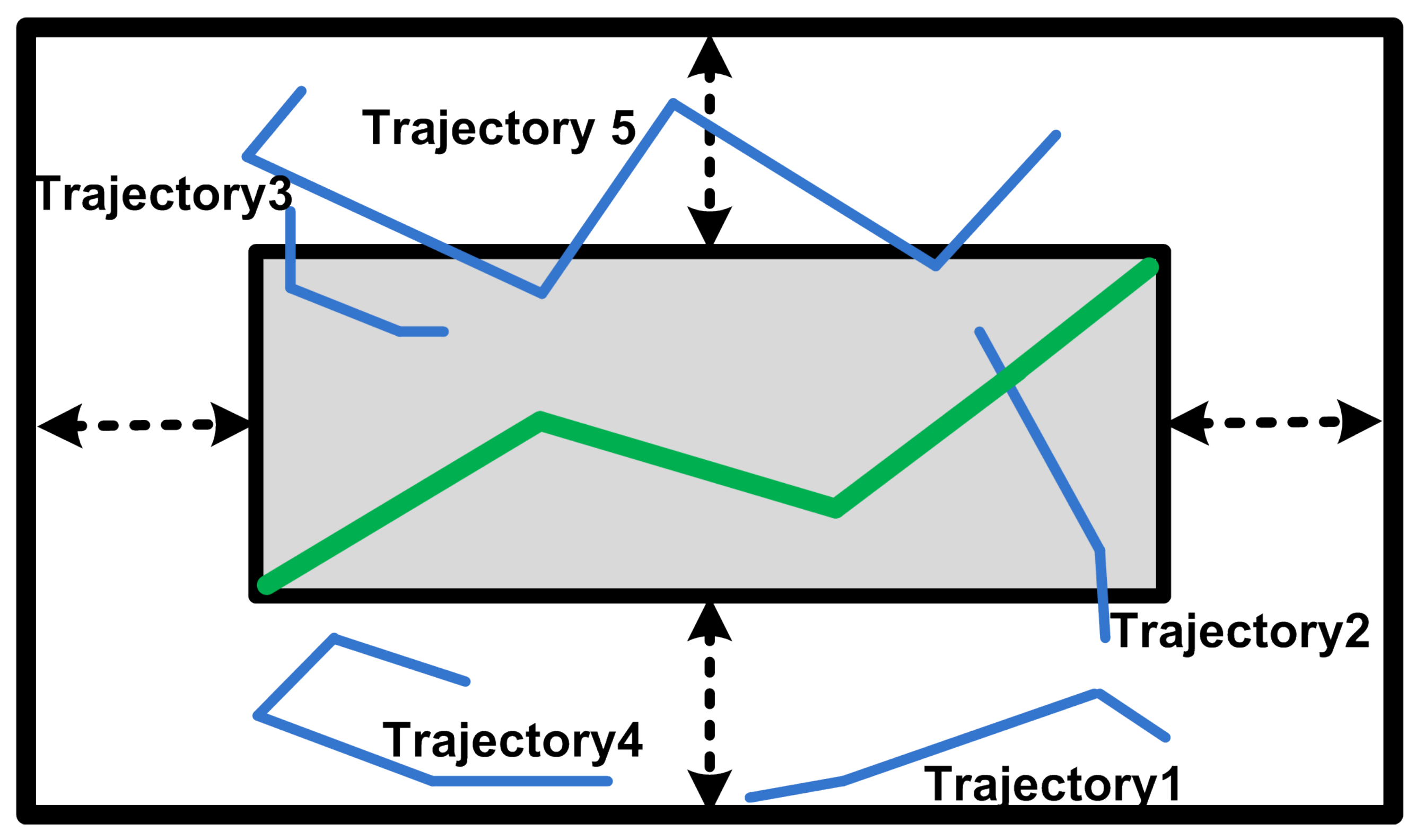
3. Problem Setting
3.1. Preliminaries
3.2. Problem Statement
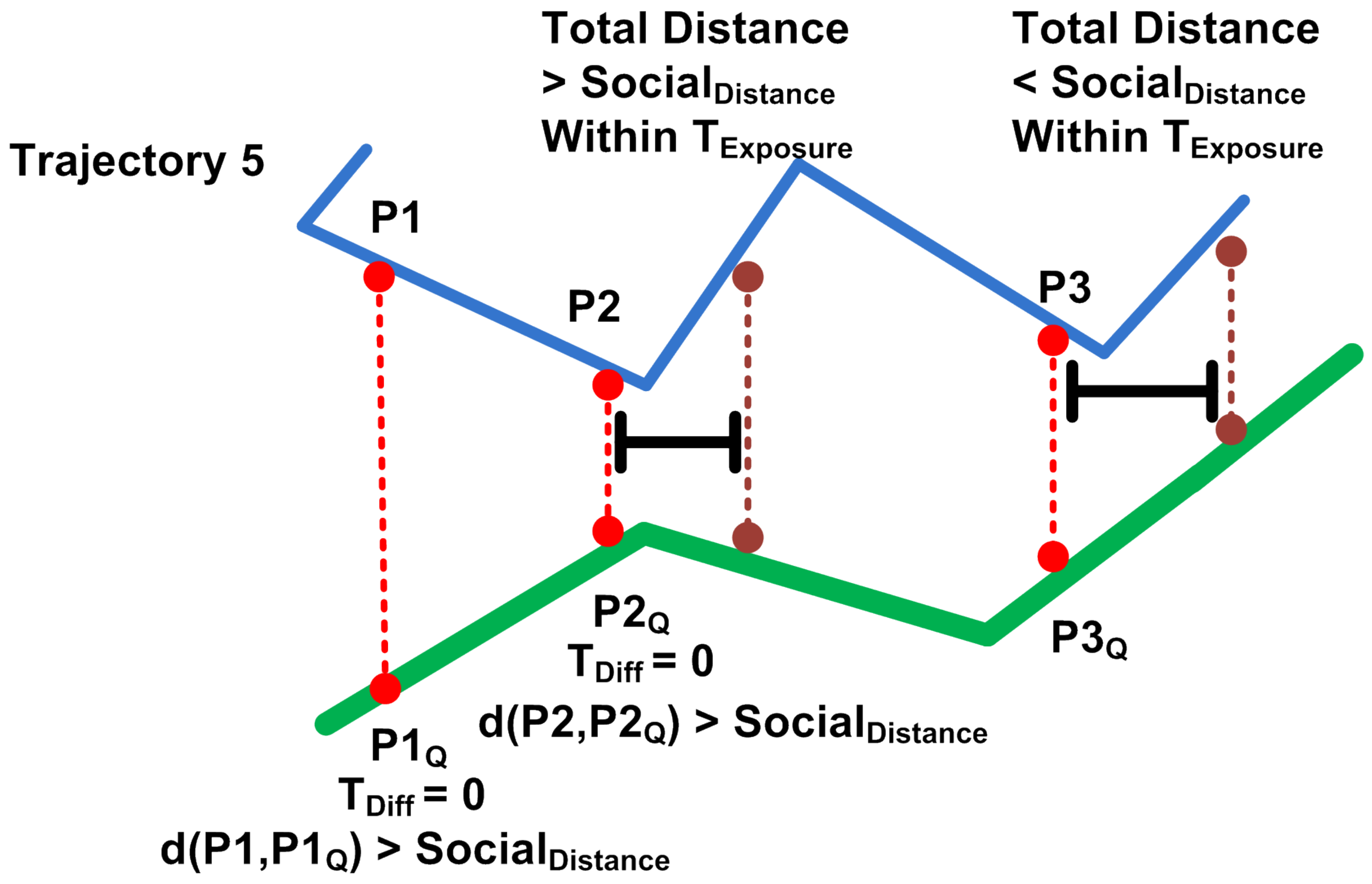
4. Proposed Solution
4.1. Main Idea
4.2. Solution Overview
| Algorithm 1 TraceAll: Contact Tracer Technique |
|
| Algorithm 2 Is Exposed |
|
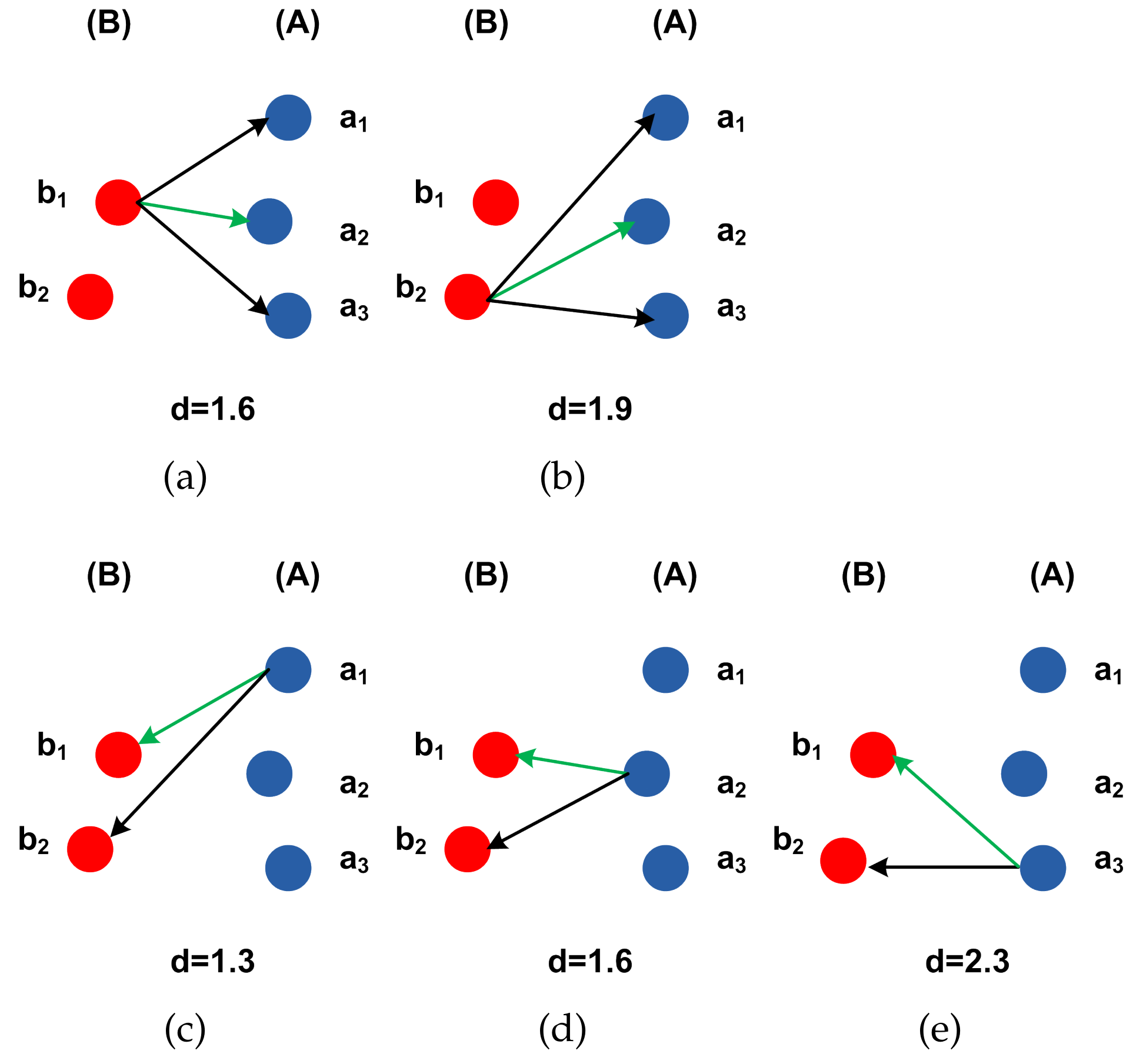
4.3. Hausdorff Distance Calculation.
4.4. Summary
5. Experiments
5.1. Experimental Setup
5.1.1. Data Set
5.1.2. Environment Settings
5.2. Performance Metrics
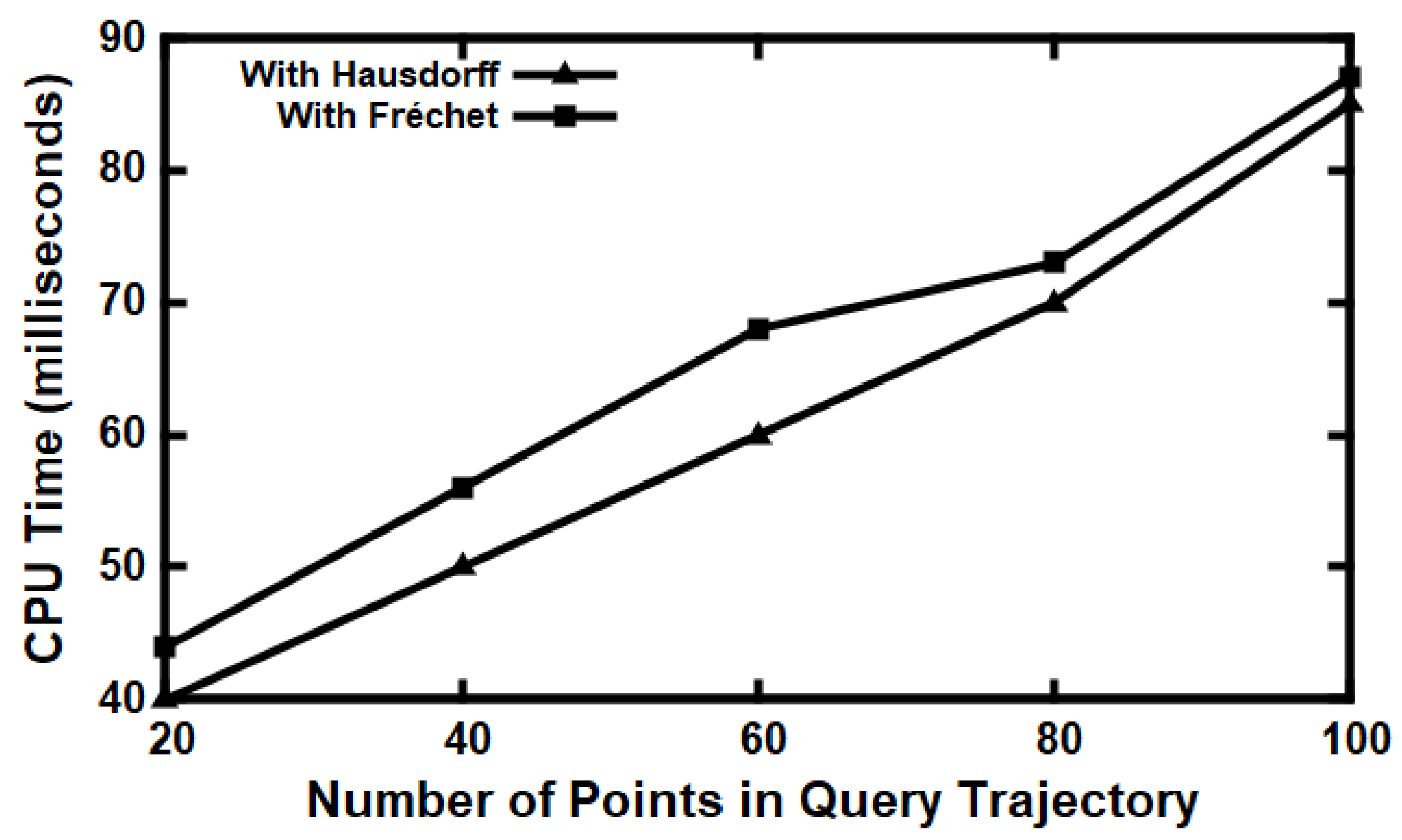
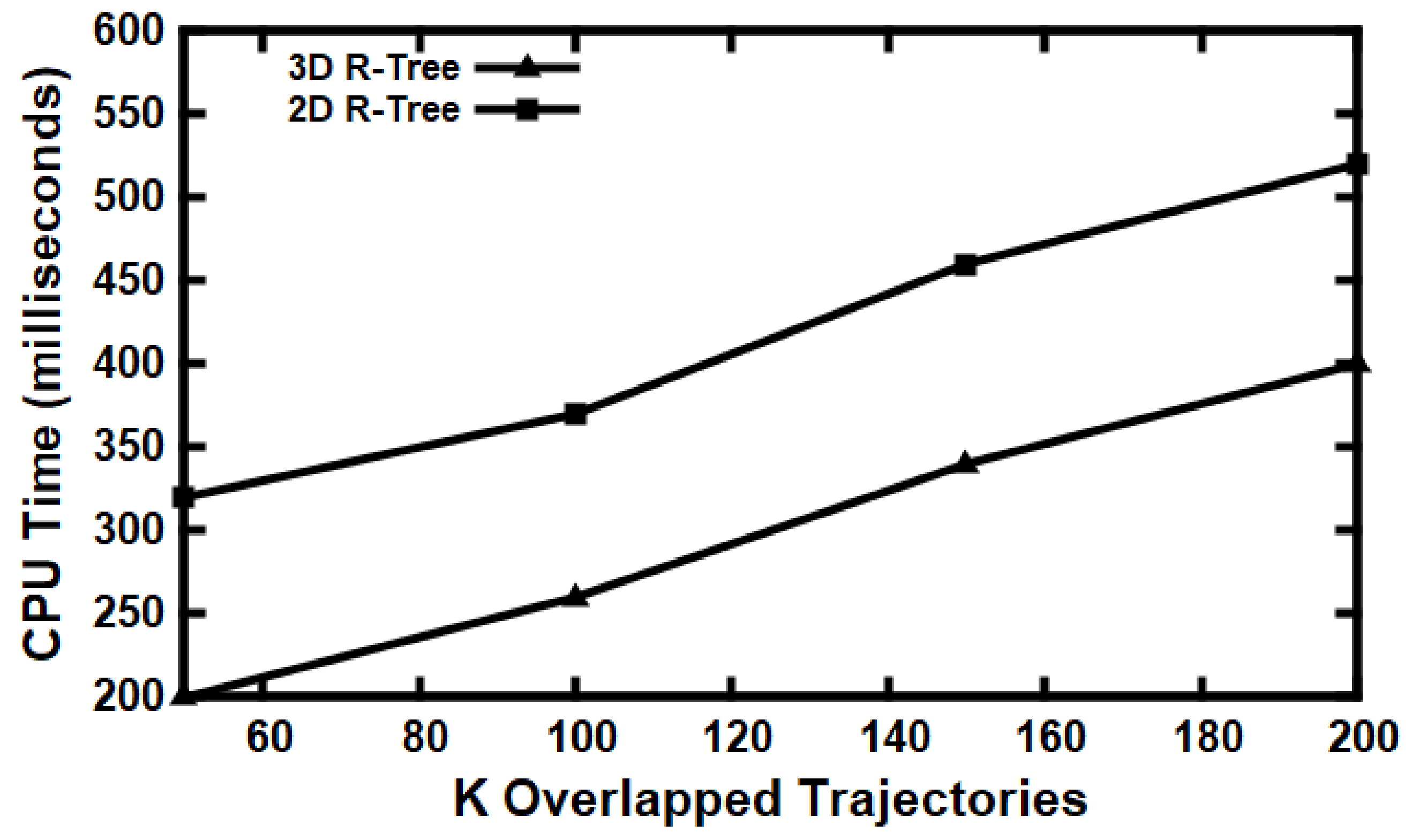
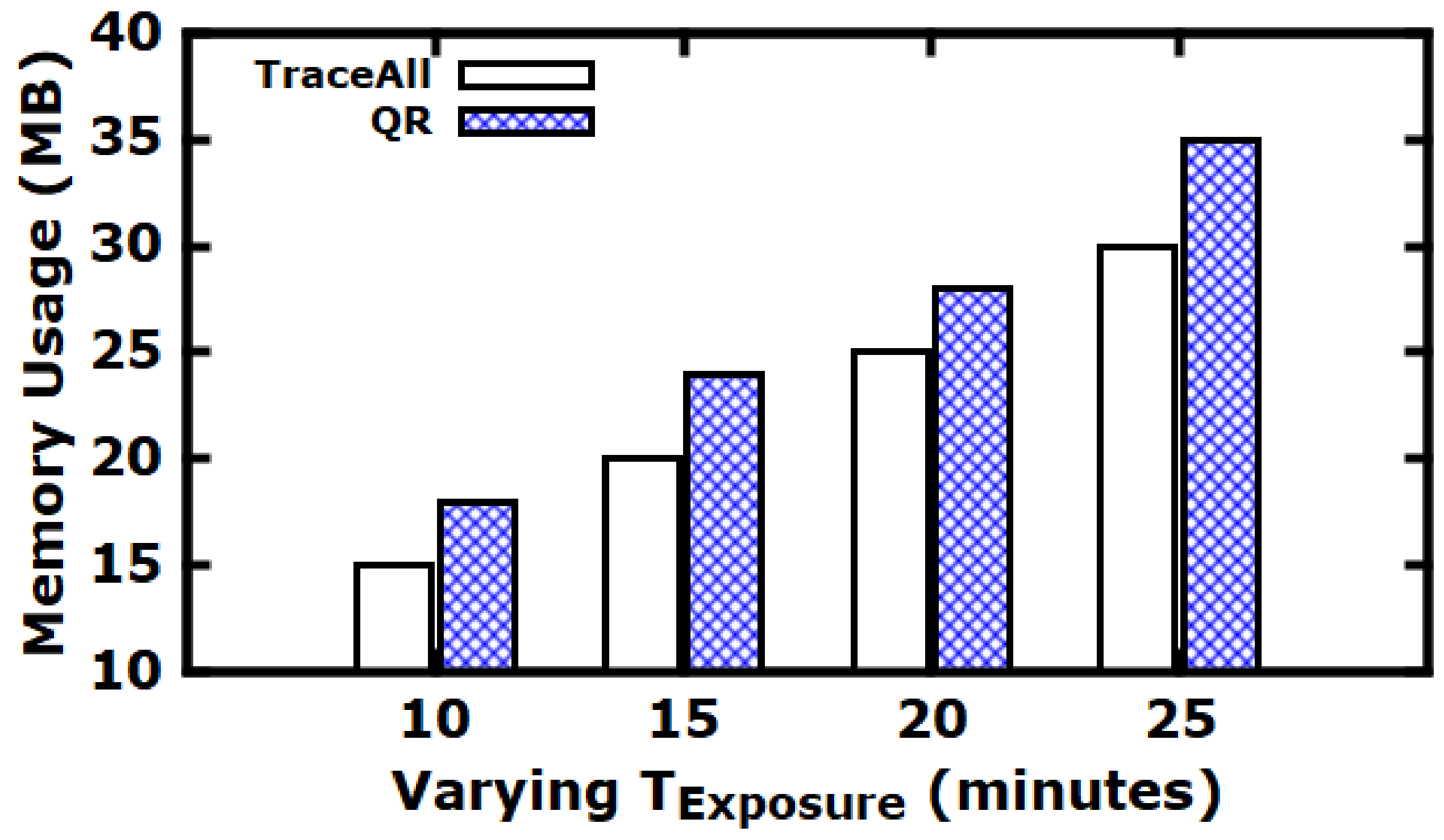
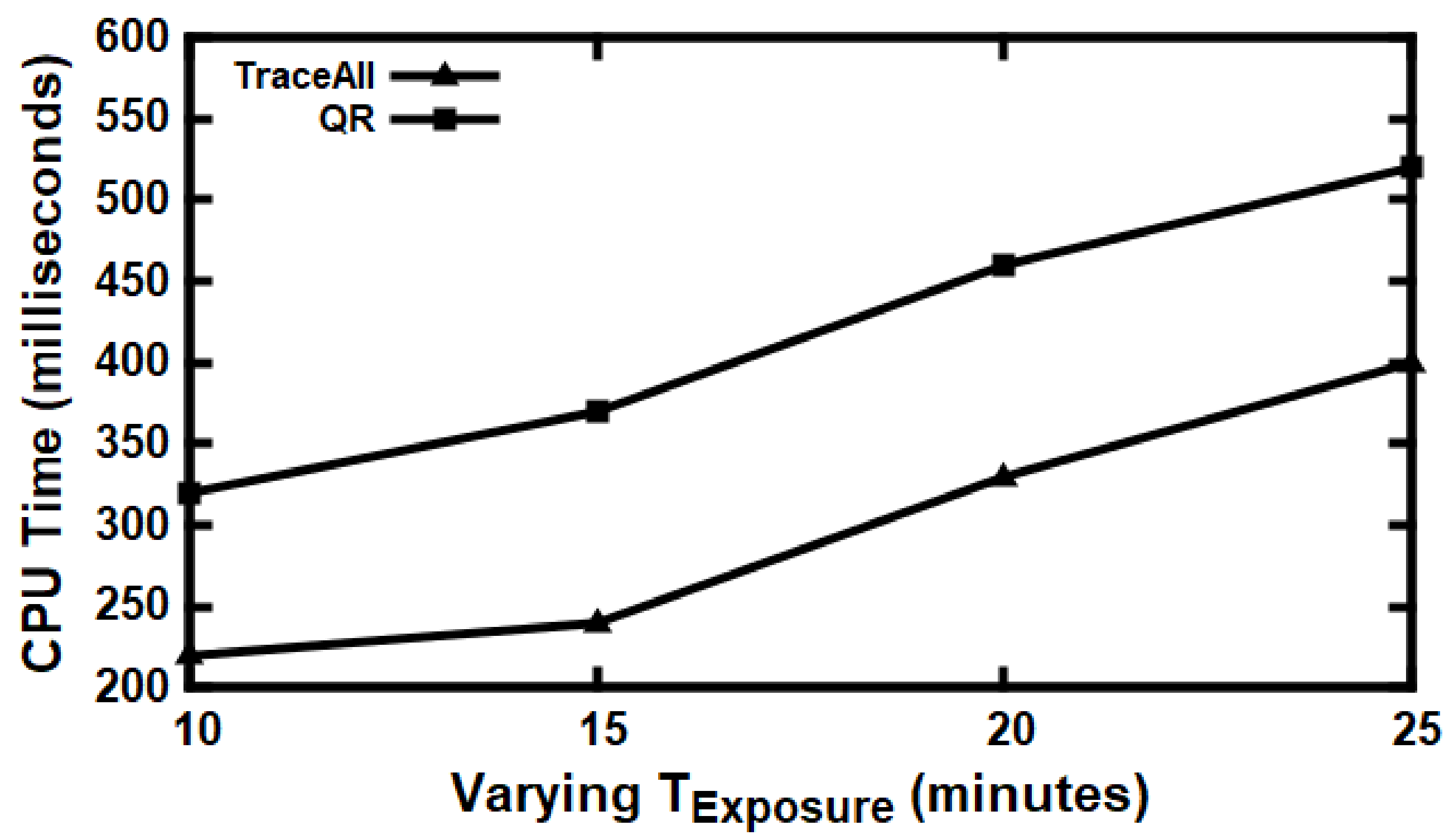
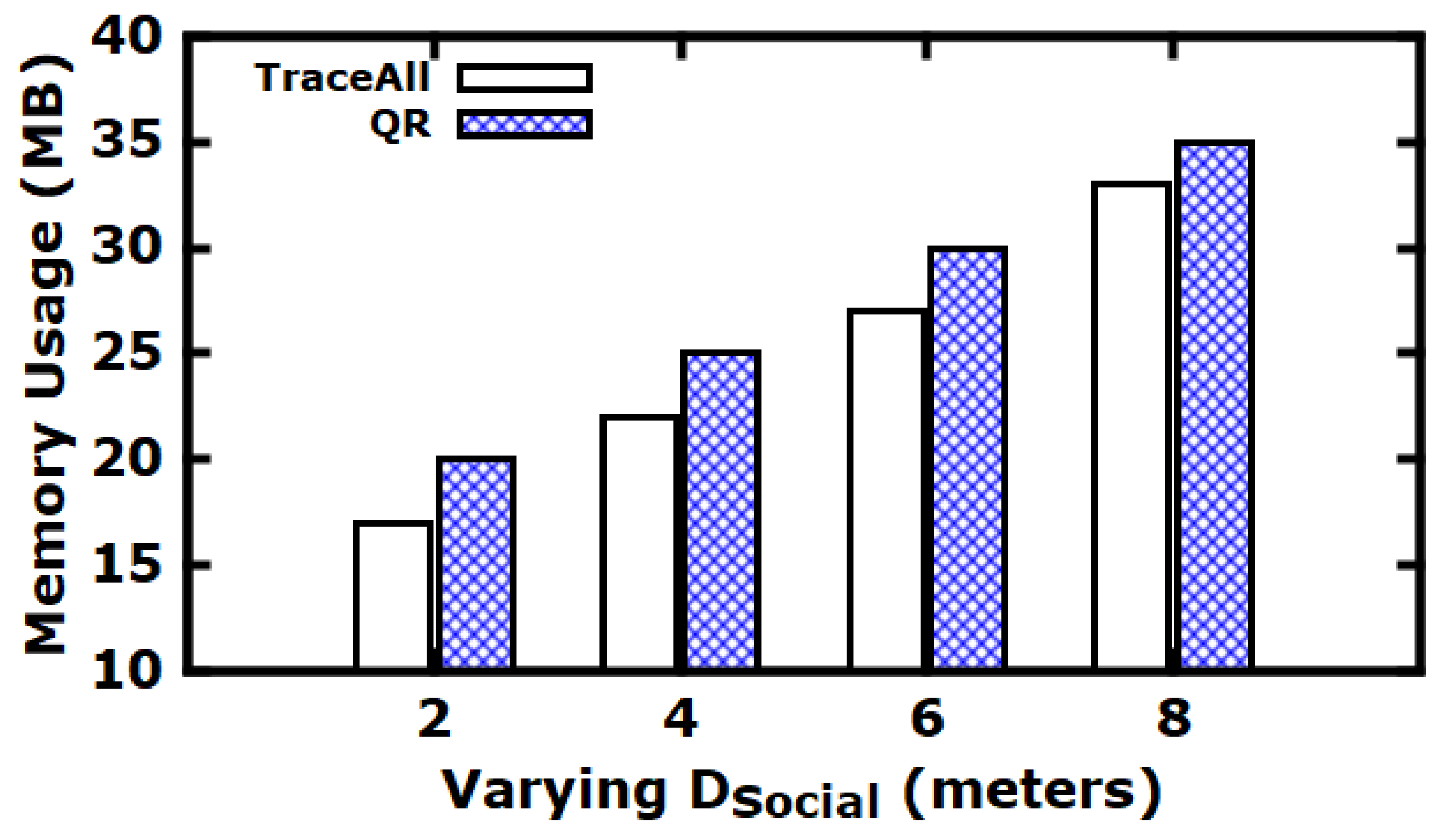
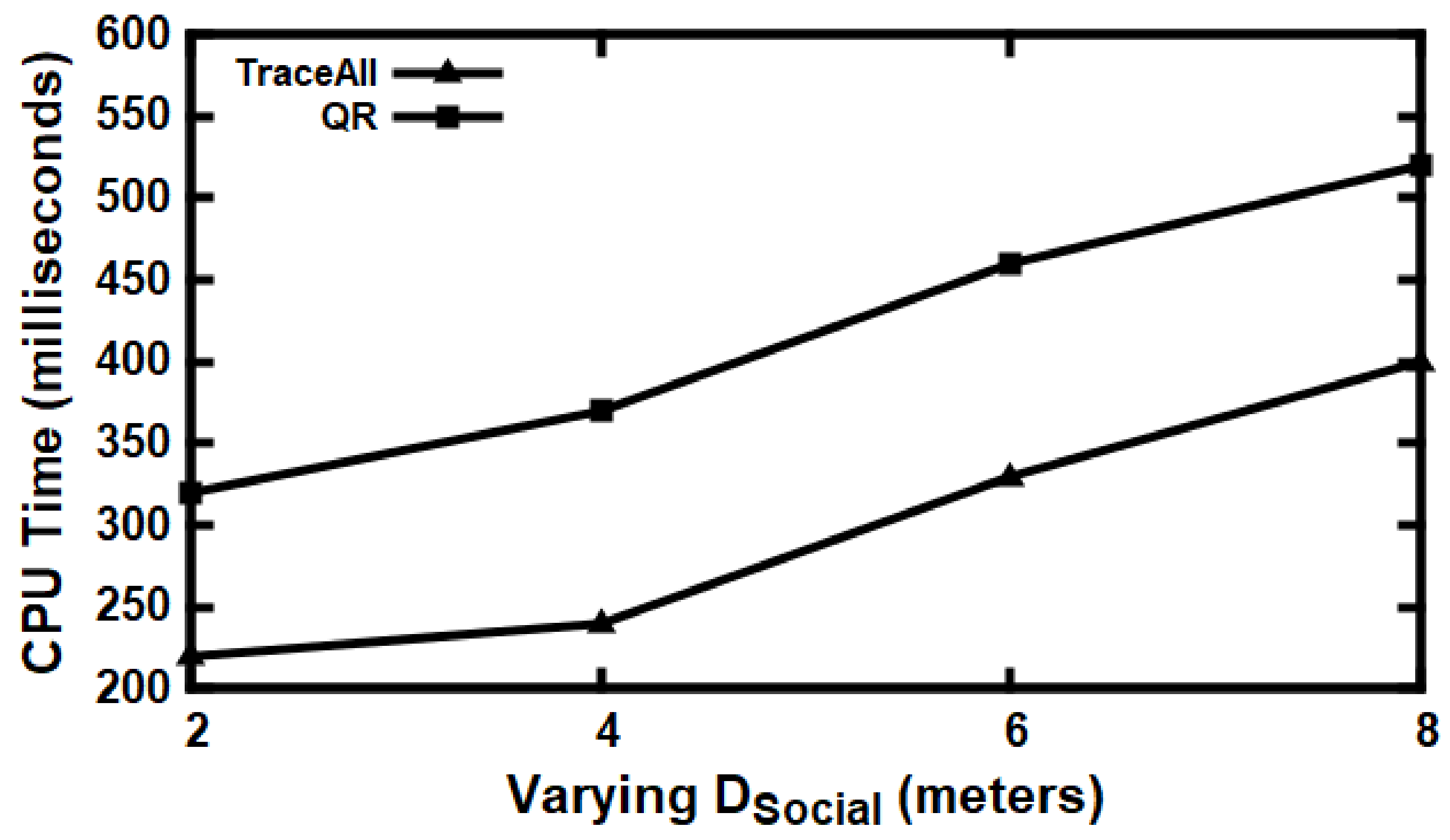
5.3. Experimental Evaluation
Baseline Comparisons
5.4. Experiments Summary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Vazquez-Prokopec, G.M.; Montgomery, B.L.; Horne, P.; Clennon, J.A.; Ritchie, S.A. Combining contact tracing with targeted indoor residual spraying significantly reduces dengue transmission. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef]
- Eames, K.T.D. Contact tracing strategies in heterogeneous populations. Epidemiol. Infect. 2007, 135, 443–454. [Google Scholar] [CrossRef]
- Armbruster, B.; Brandeau, M.L. Contact tracing to control infectious disease: When enough is enough. Health Care Manag. Sci. 2007, 10, 341–355. [Google Scholar] [CrossRef]
- Zhang, Z.T. Optimization of History Tree in 3DR-Tree Index Structure. Appl. Mech. Mater. 2013, 347–350, 2521–2523. [Google Scholar] [CrossRef]
- Guttman, A. R-Trees: A Dynamic Index Structure for Spatial Searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984. [Google Scholar]
- Shi, Y.; Hendawi, A.M.; Fattah, H.; Ali, M. RxSpatial: Reactive Spatial Library for Real-Time Location Tracking and Processing. In Proceedings of the International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 2165–2168. [Google Scholar]
- Shahtori, N.M.; Ferdousi, T.; Scoglio, C.; Sahneh, F.D. Quantifying the impact of early-stage contact tracing on controlling ebola diffusion. Math. Biosci. Eng 2018, 15, 1165–1180. [Google Scholar] [CrossRef] [PubMed]
- Dixon, M.G.; Schafer, I.J. Ebola Viral Disease OutbreakWest Africa, 2014. Ann. Emerg. Med. 2015, 65, 114–115. [Google Scholar]
- Eames, K.T.D.; Keeling, M.J. Contact tracing and disease control. Proc. R. Soc. Lond. B Biol. Sci. 2003, 270, 2565–2571. [Google Scholar] [CrossRef] [PubMed]
- Fraser, D.K.C.; Heesterbeek, H. The effectiveness of contact tracing in emerging epidemics. PLoS ONE 2006, 1, 1–7. [Google Scholar]
- Anglemyer, A.; Moore, T.H.M.; Parker, L.; Chambers, T.; Grady, A.; Chiu, K.; Parry, M.; Wilczynska, M.; Flemyng, E.; Bero, L. Digital contact tracing technologies in EPIDEMICS: A rapid review. Cochrane Database Syst. Rev. 2020, 8. [Google Scholar] [CrossRef]
- Braithwaite, I.; Callender, T.; Bullock, M.; Aldridge, R.W. Automated and Partially-automated Contact TRACING: A rapid systematic review to inform the control of covid-19. Lancet Digit. Health 2020, 2, e607–e621. [Google Scholar] [CrossRef]
- Juneau, C.E.; Briand, A.S.; Pueyo, T.; Collazzo, P.; Potvin, L. Effective Contact Tracing for Covid-19: A Systematic Review. Available online: https://www.medrxiv.org/content/10.1101/2020.07.23.20160234v2 (accessed on 20 September 2020).
- Garg, L.; Chukwu, E.; Nasser, N.; Chakraborty, C.; Garg, G. Anonymity Preserving IoT-Based COVID-19 and Other Infectious Disease Contact Tracing Model. IEEE Access 2020, 8, 59402–159414. [Google Scholar] [CrossRef]
- Hu, P. IoT-based Contact Tracing Systems for Infectious Diseases: Architecture and Analysis. Available online: https://arxiv.org/pdf/2009.01902.pdf (accessed on 20 September 2020).
- Lombardi, M.; Pascale, F.; Santaniello, D. Internet of Things: A General Overview between Architectures, Protocols and Applications. Information 2021, 12, 87. [Google Scholar] [CrossRef]
- Amato, F.; Moscato, F.; Moscato, V.; Pascale, F.; Picariello, A. An agent-based approach for recommending cultural tours. Pattern Recognit. Lett. 2020, 131, 341–347. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, M.; Yang, J.; Zhang, Q.; Zhang, X. Improvement of Generalization Ability of Deep CNN via Implicit Regularization in Two-Stage Training Process. IEEE Access 2018, 6, 15844–15869. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, M.; Tian, X.; Jiang, N.; Wang, D. A full stage data augmentation method in deep convolutional neural network for natural image classification. Discrete Dyn. Nat. Soc. 2020. [Google Scholar] [CrossRef]
- Woodley, M. RACGP Releases COVIDSafe Factsheet. Royal Australian College of General Practitioners. Available online: https://www1.racgp.org.au/newsgp/professional/racgp-releasescovidsafe-fact-sheet (accessed on 20 September 2020).
- Australian Government Department of Health: COVIDSafe App. Available online: https://www.health.gov.au/resources/apps-and-tools/covidsafe-app (accessed on 20 September 2020).
- Maddocks. The COVIDSafe Application Privacy Impact Assessment. 2020. Available online: https://www.health.gov.au/sites/default/files/documents/2020/04/covidsafe-application-privacy-impact-assessment-covidsafe-application-privacy-impactassessment.pdf (accessed on 20 September 2020).
- Help Speed up Contact Tracing with Tracetogether. Available online: https://www:gov:sg/article/help-speed-upcontact-tracing-with-tracetogether (accessed on 20 September 2020).
- Berke, A.; Bakker, M.; Vepakomma, P.; Larson, K.; Pentland, A.S. Assessing disease exposure risk with location histories and protecting privacy: A cryptographic approach in response to a global pandemic. arXiv 2020, arXiv:2003.14412. [Google Scholar]
- Reichert, S.B.L.; Scheuermann, B. Decentralized Contact Tracing Using a DHT and Blind Signatures. Available online: https://eprint.iacr.org/2020/398.pdf (accessed on 20 September 2020).
- Lee, Y. Taiwan’s Carrot-and-Stick Approach to Virus Fight Wins Praise, but Strains Showing. Available online: https://www.reuters.com/article/us-health-coronavirus-taiwan-quarantine-idUSKBN21E0EE (accessed on 20 September 2020).
- Yasaka, T.M.; Lehrich, B.M.; Sahyouni, R. Peer-to-Peer Contact Tracing: Development of a Privacy-Preserving Smartphone App. App. JMIR Mhealth Uhealth 2020, 8, e18936. [Google Scholar] [CrossRef]
- World Health Organization. Contact Tracing during an Outbreak of Ebola Virus Disease. 2014. Available online: https://apps.who.int/iris/bitstream/handle/10665/159040/9789290232575.pdf (accessed on 20 September 2020).
- World Health Organization. Surveillance Strategy during Phase 3 of the Ebola Response. 2015. Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/WHO_EVD_Guidance_Sur_15.1_eng.pdf (accessed on 20 September 2020).
- Danquah, L.O.; Hasham, N.; MacFarlane, M.; Conteh, F.E.; Momoh, F.; Tedesco, A.A.; Jambai, A.; Ross, D.A.; Weiss, H.A. Use of a mobile application for Ebola contact tracing and monitoring in northern Sierra Leone: A proof-of-concept study. BMC Infect. Dis. 2019, 19, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Stein, M.L.; Rump, B.O.; Kretzschmar, M.E.E.; Steenbergen, J.E.V. Social Networking Sites as a Tool for Contact Tracing: Urge for Ethical Framework for Normative Guidance. Public Health Ethics 2014, 7, 57–60. [Google Scholar] [CrossRef]
- Mandeville, K.L.; Harris, M.; Thomas, H.L.; Chow, Y.; Seng, C. Using social networking sites for communicable disease control: Innovative contact tracing or breach of confidentiality? Public Health Ethics 2014, 7, 47–50. [Google Scholar] [CrossRef]
- Mcmullen, P. The Hausdorff distance between compact convex sets. Mathematika 1984, 31, 76–82. [Google Scholar] [CrossRef]
- Atallah, M.J. A linear time algorithm for the Hausdorff distance between convex polygons. Inform. Process. 1983, 17, 207–209. [Google Scholar] [CrossRef]
- Kim, I.S.; Mclean, W. Computing The Hausdorff Distance Between Two Sets Of Parametric Curves. Available online: http://koreascience.or.kr/article/JAKO201334064306689.pdf (accessed on 20 September 2020).
- Torres-Sospedra, J.; Montoliu, R.; Martínez-Usó, A.; Avariento, J.P.; Arnau, T.J.; Benedito-Bordonau, M.; Huerta, J. UJIIndoorLoc: A New Multi-building and Multi-floor Database for WLAN Fingerprint-based Indoor Localization Problems. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, South Korea, 27–30 October 2014. [Google Scholar]
- Ali, M.E.; Eusuf, S.S.; Islam, K.A. An Efficient Index for Contact Tracing Query in a Large Spatio-Temporal Database. arXiv 2020, arXiv:2006.12812. [Google Scholar]
- Lee, W.K.H.; Chung, Y.D. Safe contact tracing for COVID-19: A method without privacy breach using functional encryption techniques based-on spatio-temporal trajectory data. PLoS ONE 2020, 15, e0242758. [Google Scholar]
- Cao, F.K.Y.; Masatoshi, Y. PCT-TEE: Trajectory-based Private Contact Tracing System with Trusted Execution Environment. Available online: https://arxiv.org/pdf/2012.03782.pdf (accessed on 20 September 2020).
- Alt, H.; Godau, M. Computing The Frechet Distance Between Two Polygonal Curves. Int. J. Comput. Geom. Appl. 1995, 5, 75–91. [Google Scholar] [CrossRef]

| Parameter Name | Value |
|---|---|
| 14 days | |
| 10 min | |
| 2 m | |
| Direct |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alarabi, L.; Basalamah, S.; Hendawi, A.; Abdalla, M. TraceAll: A Real-Time Processing for Contact Tracing Using Indoor Trajectories. Information 2021, 12, 202. https://doi.org/10.3390/info12050202
Alarabi L, Basalamah S, Hendawi A, Abdalla M. TraceAll: A Real-Time Processing for Contact Tracing Using Indoor Trajectories. Information. 2021; 12(5):202. https://doi.org/10.3390/info12050202
Chicago/Turabian StyleAlarabi, Louai, Saleh Basalamah, Abdeltawab Hendawi, and Mohammed Abdalla. 2021. "TraceAll: A Real-Time Processing for Contact Tracing Using Indoor Trajectories" Information 12, no. 5: 202. https://doi.org/10.3390/info12050202
APA StyleAlarabi, L., Basalamah, S., Hendawi, A., & Abdalla, M. (2021). TraceAll: A Real-Time Processing for Contact Tracing Using Indoor Trajectories. Information, 12(5), 202. https://doi.org/10.3390/info12050202







