Combining Network Coding and Retransmission Techniques to Improve the Communication Reliability of Wireless Sensor Network
Abstract
1. Introduction
- An extensive state-of-the-art study concerning relay selection and NC techniques, presenting relevant and current works;
- A simulation assessment of both proposed schemes, relay selection and the NC, working together in the communication. In addition, we will present an analysis of the advantages and drawbacks of the combined implementation of both schemes;
- A discussion about some of the negative results obtained when combining the ORST technique with specific NC approaches.
2. Related Work
2.1. Relay Selection Related Work
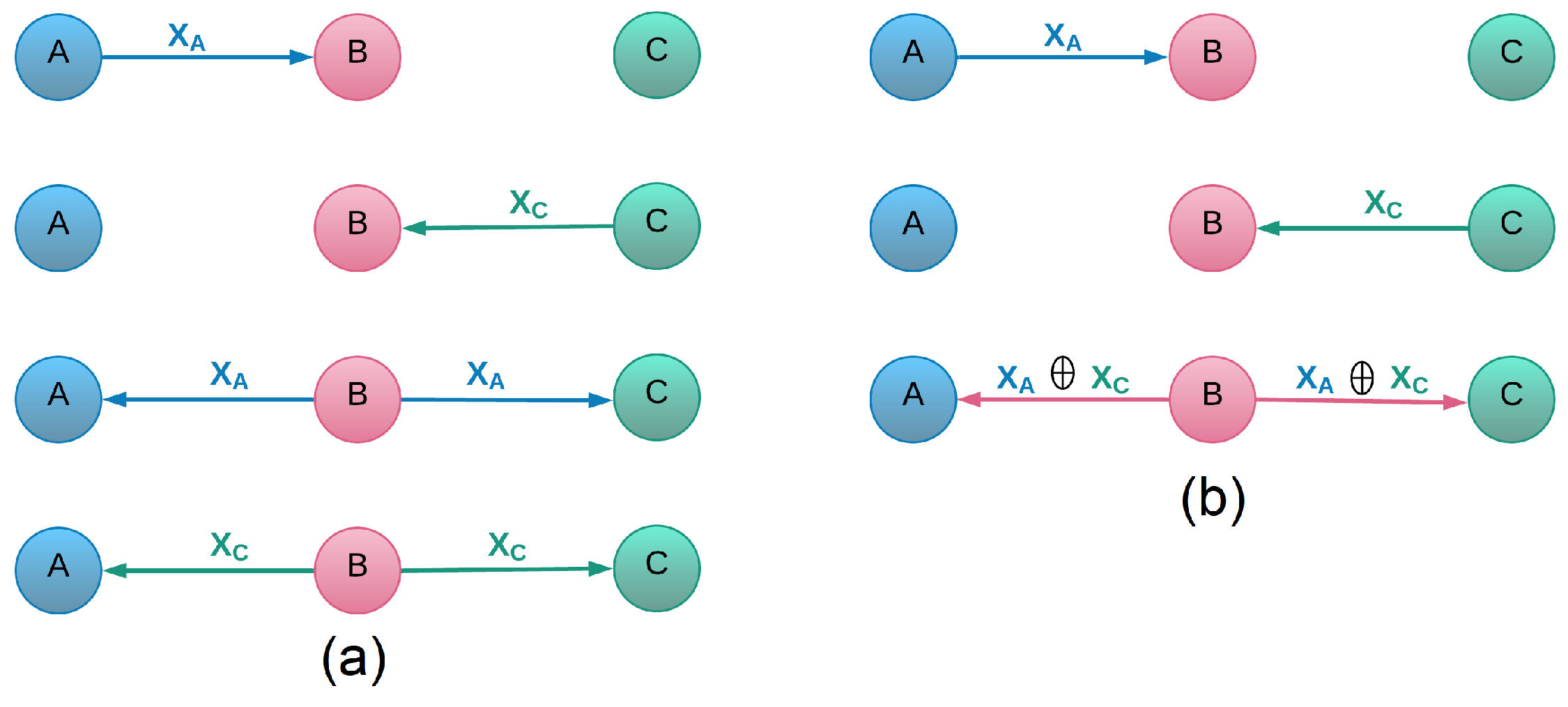
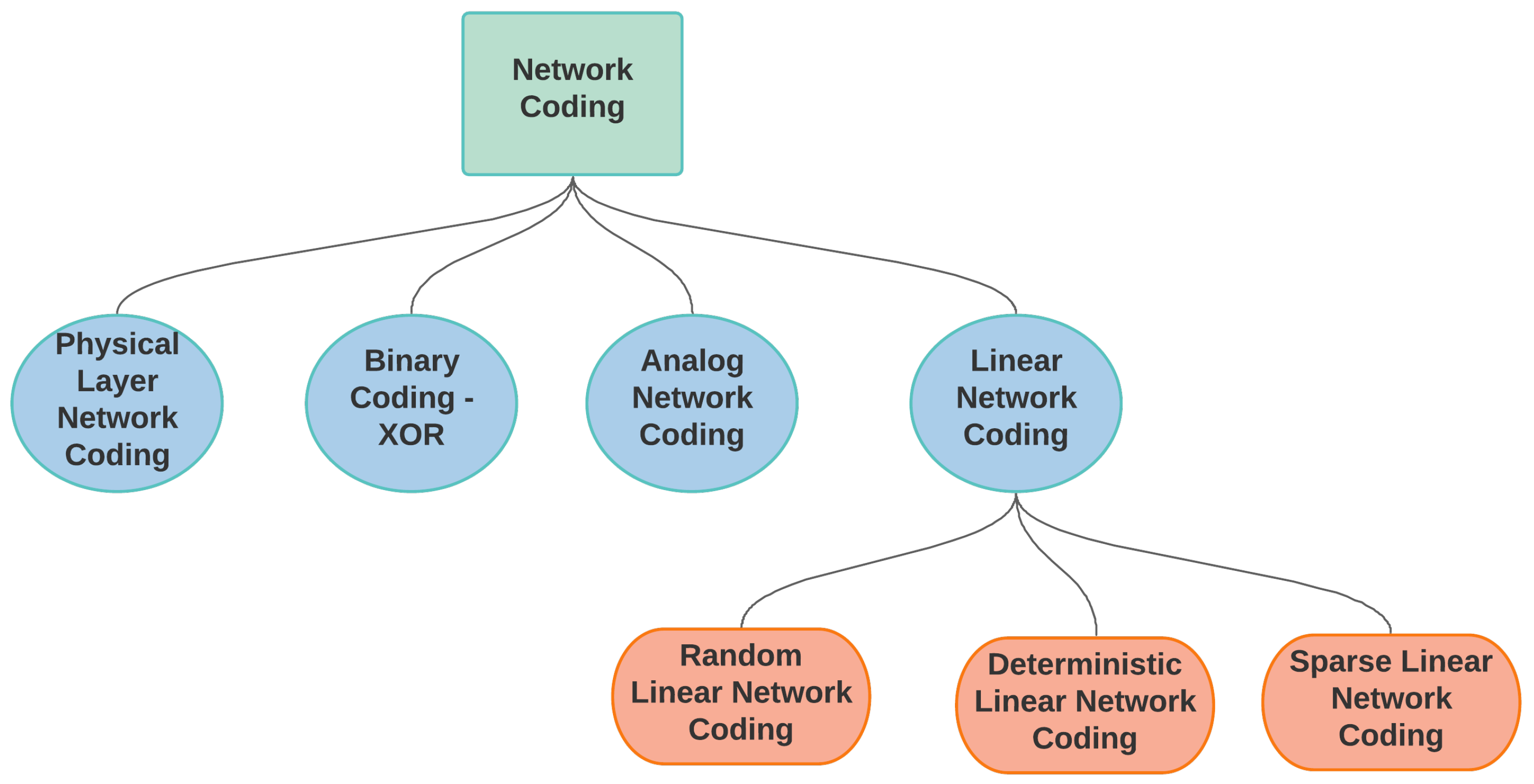
2.2. Brief Explanation of the Main Types of Network Coding
2.3. Network Coding Related Work
2.4. Wrap-Up
3. WSN Communication
3.1. System Model
3.2. The Optimized Relay Selection Technique
- , being the remaining energy and is the initial energy of node , respectively. The value is the normalized remaining energy of node (a real number between 0 and 1);
- the expression is used so that the node with the largest amount of energy has the lowest cost in the objective function.
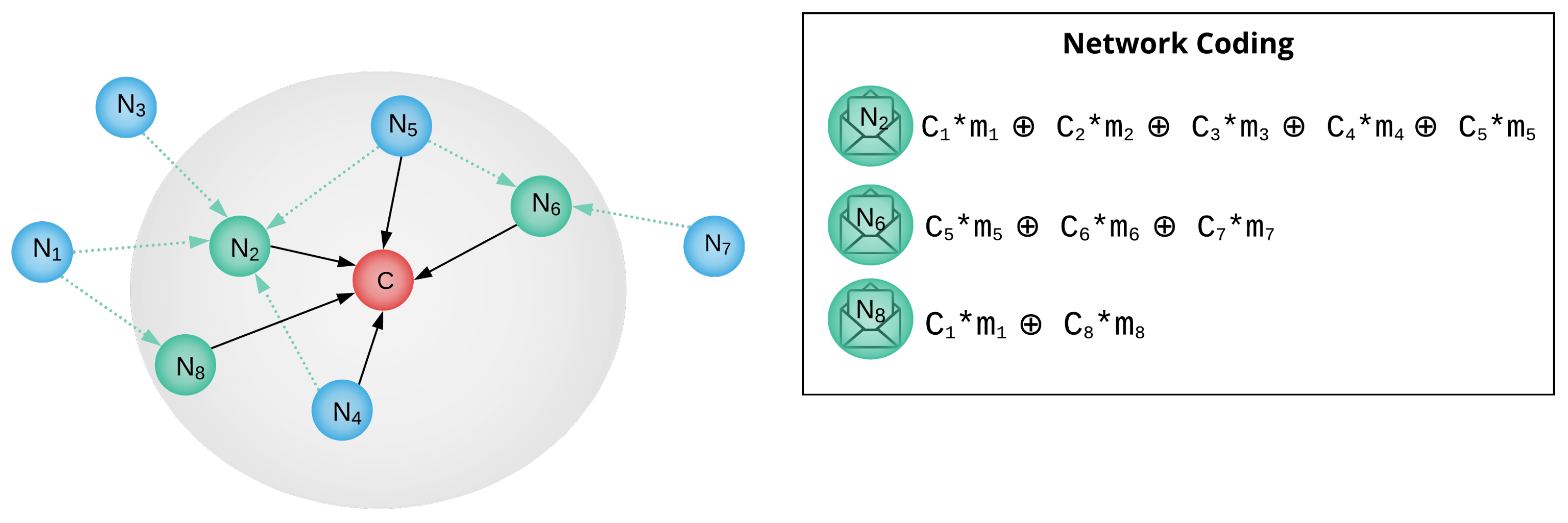
3.3. Network Coding Technique
4. Simulation Assessments
4.1. Simulation Settings
4.2. Network Coding Technique Application Scenarios
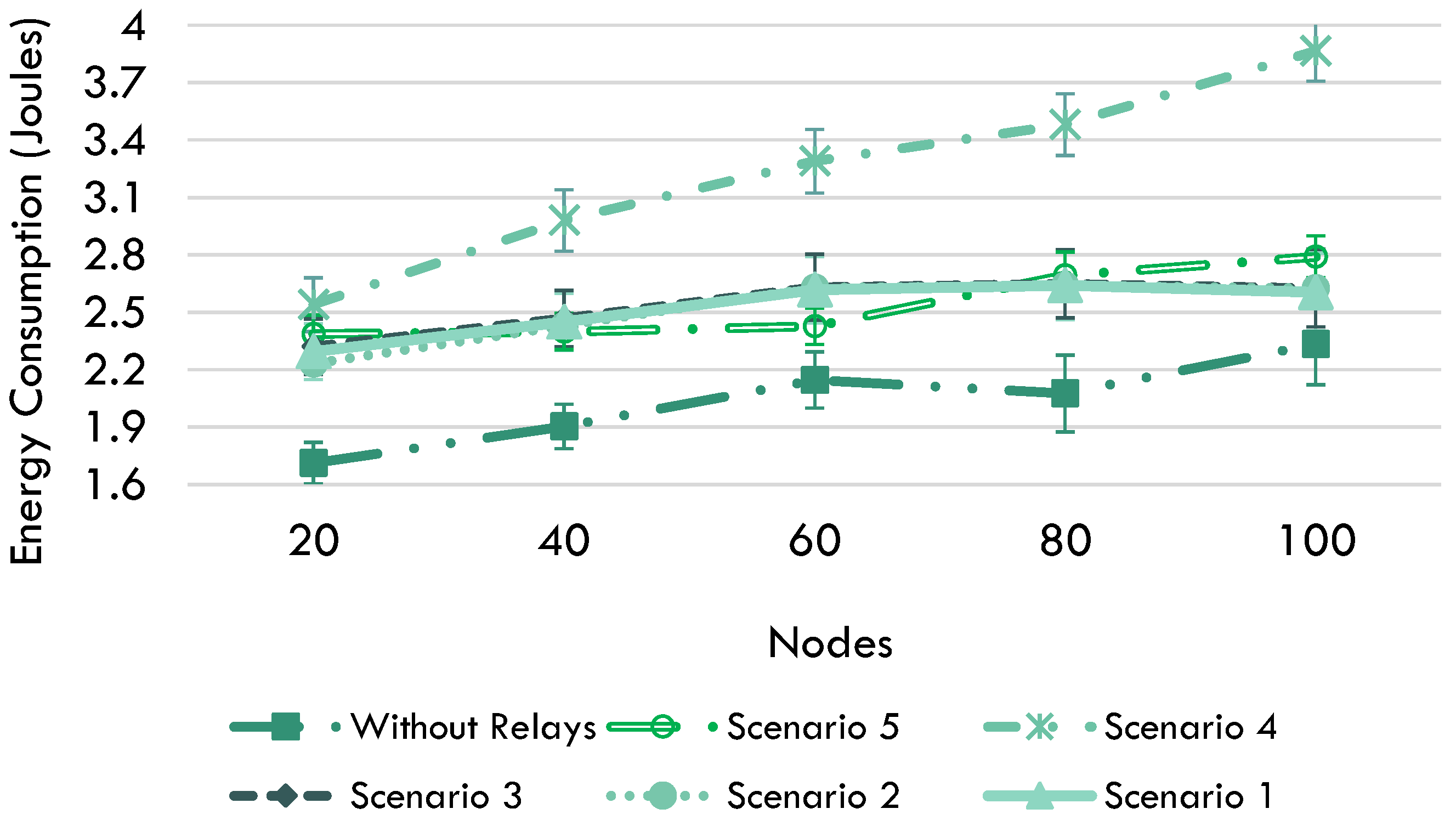
4.3. Simulation Assessment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adriano, J.D.; do Rosario, E.C. Wireless Sensor Networks in Industry 4.0: WirelessHART and ISA100. 11a. In Proceedings of the 13th IEEE International Conference on Industry Applications (INDUSCON), Sao Paulo, Brazil, 11–14 November 2018; pp. 924–929. [Google Scholar]
- Ez-Zazi, I.; Arioua, M.; El Oualkadi, A.; Lorenz, P. A hybrid adaptive coding and decoding scheme for multi-hop wireless sensor networks. Wirel. Pers. Commun. 2017, 94, 3017–3033. [Google Scholar] [CrossRef]
- Gungor, V.C.; Hancke, G.P. Industrial wireless sensor networks: Challenges, design principles, and technical approaches. IEEE Trans. Ind. Electron. 2009, 56, 4258–4265. [Google Scholar] [CrossRef]
- Rodrigues, L.M.; Montez, C.; Budke, G.; Vasques, F.; Portugal, P. Estimating the lifetime of wireless sensor network nodes through the use of embedded analytical battery models. J. Sens. Actuator Netw. 2017, 6, 8. [Google Scholar] [CrossRef]
- Rodrigues, L.M.; Montez, C.; Moraes, R.; Portugal, P.; Vasques, F. A temperature-dependent battery model for wireless sensor networks. Sensors 2017, 17, 422. [Google Scholar] [CrossRef]
- Valle, O.T.; Montez, C.; de Araujo, G.; Vasques, F.; Moraes, R. NetCoDer: A Retransmission Mechanism for WSNs Based on Cooperative Relays and Network Coding. Sensors 2016, 16, 799. [Google Scholar] [CrossRef]
- Fragouli, C.; Le Boudec, J.Y.; Widmer, J. Network coding: An instant primer. ACM SIGCOMM Comput. Commun. Rev. 2006, 36, 63–68. [Google Scholar] [CrossRef]
- Valle, O.T.; Budke, G.; Montez, C.; Moraes, R.; Vasques, F. Experimental assessment of LNC-based cooperative communication schemes using commercial off-the-shelf wireless sensor network nodes. Int. J. Commun. Syst. 2018, 31, e3508. [Google Scholar] [CrossRef]
- Lu, X.; Cheng, W.; He, Q.; Xie, X. Cooperative communication based regular topology to achieve coverage and K-connectivity for WSNs. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2514–2518. [Google Scholar]
- Bletsas, A.; Khisti, A.; Reed, D.P.; Lippman, A. A simple cooperative diversity method based on network path selection. IEEE J. Sel. Areas Commun. 2006, 24, 659–672. [Google Scholar] [CrossRef]
- Bhute, Y.; Raut, A. A survey on relay selection strategies in cooperative wireless network for capacity enhancement. Int. J. Comput. Appl. 2013, 65, 12–17. [Google Scholar]
- Laurindo, S.; Moraes, R.; Nassiffe, R.; Montez, C.; Vasques, F. An Optimized Relay Selection Technique to Improve the Communication Reliability in Wireless Sensor Networks. Sensors 2018, 18, 3263. [Google Scholar] [CrossRef] [PubMed]
- Asam, M.; Haider, Z.; Jamal, T.; Ghuman, K.; Ajaz, A. Novel Relay Selection Protocol for Cooperative Networks. arXiv 2019, arXiv:1911.07764. [Google Scholar]
- Chen, Y.; Liu, W.; Wang, T.; Deng, Q.; Liu, A.; Song, H. An adaptive retransmit mechanism for delay differentiated services in industrial WSNs. Eurasip J. Wirel. Commun. Netw. 2019, 2019. [Google Scholar] [CrossRef]
- Hossain, M.A.; Noor, R.M.; Yau, K.L.A.; Ahmedy, I.; Anjum, S.S. A Survey on Simultaneous Wireless Information and Power Transfer with Cooperative Relay and Future Challenges. IEEE Access 2019, 7, 19166–19198. [Google Scholar] [CrossRef]
- Ho, T.; Lun, D. Network Coding: An Introduction; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Fragouli, C.; Soljanin, E. Network Coding Fundamentals. Found. Trends Netw. 2007, 2, 1–133. [Google Scholar] [CrossRef]
- Ostovari, P.; Wu, J.; Khreishah, A. Network coding techniques for wireless and sensor networks. In The Art of Wireless Sensor Networks; Springer: Berlin/Heidelberg, Germany, 2014; pp. 129–162. [Google Scholar] [CrossRef]
- Yue, J.; Girs, S.; Akerberg, J.; Bjorkman, M.; Lin, Z. Network coding for reliable downlink transmissions in industrial wireless sensor and actuator networks. In Proceedings of the International Symposium on Wireless Communication Systems, Poznań, Poland, 20–23 September 2016; pp. 560–565. [Google Scholar] [CrossRef]
- Liu, X.; Gong, X.; Zheng, Y. Reliable cooperative communications based on random network coding in multi-hop relay WSNs. IEEE Sens. J. 2014, 14, 2514–2523. [Google Scholar] [CrossRef]
- Laurindo, S.; Moraes, R.; Montez, C.; Vasques, F. Multi-criteria Analysis to Select Relay Nodes in the ORST Technique. Int. Conf.-Hoc Netw. Wirel. 2019, 11803, 167–182. [Google Scholar]
- Laurindo, S.; Moraes, R.; Montez, C.; Vasques, F. Assessment of Different Algorithms to Solve the Set-Covering Problem in a Relay Selection Technique. In Proceedings of the 25th International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020. [Google Scholar]
- Tripathi, Y.; Prakash, A.; Tripathi, R. An Energy Balanced Load Aware Relay Selection in Cooperative Routing for Wireless Sensor Network. In Proceedings of the 9th Annual Information Technology, Electromechanical Engineering and Microelectronics Conference (IEMECON), Jaipur, India, 13–15 March 2019; pp. 223–231. [Google Scholar]
- Yang, K.; Zhu, S.; Dan, Z.; Tang, X.; Wu, X.; Ouyang, J. Relay Selection for Wireless Cooperative Networks using Adaptive Q-learning Approach. In Proceedings of the 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Taiyuan, China, 18–21 July 2019; pp. 1–5. [Google Scholar]
- Mei, Z.; Lu, Y. Performance Analysis of Several Relay Node Selection Schemes for Cooperative Communications. In Proceedings of the 11th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 14–16 June 2019; pp. 41–45. [Google Scholar]
- Zhang, J.; Tang, J.; Wang, F. Cooperative relay selection for load balancing with mobility in hierarchical WSNs: A multi-armed bandit approach. IEEE Access 2020, 8, 18110–18122. [Google Scholar] [CrossRef]
- Su, Y.; Lu, X.; Zhao, Y.; Huang, L.; Du, X. Cooperative Communications with Relay Selection Based on Deep Reinforcement Learning in Wireless Sensor Networks. IEEE Sens. J. 2019, 19, 9561–9569. [Google Scholar] [CrossRef]
- Elsamadouny, A.; Hasna, M.; Khattab, T.; Abualsaud, K.; Yaacoub, E. On the delay of finite buffered multi-hop relay wireless internet of things. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–7. [Google Scholar]
- Huang, J.; Gharavi, H.; Yan, H.; Xing, C.C. Network Coding in Relay-Based Device-to-Device Communications. IEEE Netw. 2017, 31, 102–107. [Google Scholar] [CrossRef][Green Version]
- Katti, S.; Gollakota, S.; Katabi, D. Embracing wireless interference: Analog network coding. ACM SIGCOMM Comput. Commun. Rev. 2007, 37, 397–408. [Google Scholar] [CrossRef]
- Basaran, S.T.; Kurt, G.K. Wireless Channel Induced Coding. IEEE Commun. Lett. 2019, 23, 1688–1691. [Google Scholar] [CrossRef]
- Dong, D.S.; Pokhrel, Y.M.; Gachhadar, A.; Maharjan, R.K.; Qamar, F.; Amiri, I.S. Resource tuned optimal random network coding for single hop multicast future 5g networks. Int. J. Electron. Telecommun. 2019, 65, 463–469. [Google Scholar] [CrossRef]
- Ho, T.; Medard, M.; Koetter, R.; Karger, D.R.; Effros, M.; Shi, J.; Leong, B. A Random Linear Network Coding Approach to Multicast. IEEE Trans. Inf. Theory 2006, 52, 4413–4430. [Google Scholar] [CrossRef]
- Migabo, M.E.; Olwal, T.O.; Djouani, K.; Kurien, A.M. Cooperative and Adaptive Network Coding for Gradient Based Routing in Wireless Sensor Networks with Multiple Sinks. J. Comput. Netw. Commun. 2017. [Google Scholar] [CrossRef]
- Feizi, S.; Lucani, D.E.; Sørensen, C.W.; Makhdoumi, A.; Médard, M. Tunable sparse network coding for multicast networks. In Proceedings of the International Symposium on Network Coding (NetCod), Aalborg Oest, Denmark, 27–28 June 2014; pp. 1–6. [Google Scholar]
- Sehat, H.; Pahlevani, P. On the Probability of Partial Decoding in Sparse Network Coding. arXiv 2019, arXiv:1907.12051. [Google Scholar]
- Zarei, A.; Pahlevani, P.; Davoodi, M. On the partial decoding delay of sparse network coding. IEEE Commun. Lett. 2018, 22, 1668–1671. [Google Scholar] [CrossRef]
- Bao, X.; Li, J. Matching code-on-graph with network-on-graph: Adaptive network coding for wireless relay networks. In Proceedings of the 43rd Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 28–30 September 2005; pp. 386–395. [Google Scholar]
- Bao, X.; Li, J. Adaptive Network Coded Cooperation (ANCC) for Wireless Relay Networks: Matching Code-on-Graph with Network-on-Graph. IEEE Trans. Wirel. Commun. 2008, 7, 574–583. [Google Scholar] [CrossRef]
- Chebli, L.; Hausl, C.; Zeitler, G.; Koetter, R. Cooperative uplink of two mobile stations with network coding based on the WiMax LDPC code. In Proceedings of the Global Telecommunications Conference (GLOBECOM), Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Han, C.; Yang, Y.; Han, X. A fast network coding scheme for mobile wireless sensor networks. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef][Green Version]
- Hao, K.; Jin, Z. A New Deterministic Linear Network Coding and Its Application on Multicast Network. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Heide, J.; Pedersen, M.V.; Fitzek, F.H.; Médard, M. On code parameters and coding vector representation for practical RLNC. IEEE Int. Conf. Commun. 2011. [Google Scholar] [CrossRef]
- Akhtari, S.; Moghim, N.; Mahdavi, M. Middleman covert channel establishment based on MORE routing protocol using network coding in ad hoc networks. Int. J. Commun. Syst. 2020, 33, 1–14. [Google Scholar] [CrossRef]
- Wu, H.; Li, Y.; Hu, Y.; Tang, B.; Bao, Z. On Optimizing Effective Rate for Random Linear Network Coding over Burst-Erasure Relay Links. IEEE Wirel. Commun. Lett. 2019, 8, 588–591. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Wang, J.; Ji, X.; Wu, H.; Bao, Z. A Low-Complexity Coded Transmission Scheme over Finite-Buffer Relay Links. IEEE Trans. Commun. 2018, 66, 2873–2887. [Google Scholar] [CrossRef]
- Xu, C.; Wang, P.; Xiong, C.; Wei, X.; Muntean, G.M. Pipeline network coding-based multipath data transfer in heterogeneous wireless networks. IEEE Trans. Broadcast. 2017, 63, 376–390. [Google Scholar] [CrossRef]
- Guo, B.; Liu, Y.; Zhou, C. Exploit network coding over GF(2q) for multi-user cooperative wireless networks. Int. J. Wirel. Inf. Netw. 2014, 21, 1–14. [Google Scholar] [CrossRef]
- Chen, F.; Wang, N.; German, R.; Dressler, F. Performance Evaluation of IEEE 802.15.4 LR-WPAN for Industrial Applications. In Proceedings of the Fifth Annual Conference on Wireless on Demand Network Systems and Services, Garmisch-Partenkirchen, Germany, 23–25 January 2008; pp. 89–96. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Pattanaik, S.R.; Wu, S.L. Design and analysis of a low latency deterministic network MAC for wireless sensor networks. Sensors 2017, 17, 2185. [Google Scholar] [CrossRef]
- Xu, K.; Wang, Q.; Hassanein, H.; Takahara, G. Optimal wireless sensor networks (WSNs) deployment: Minimum cost with lifetime constraint. Wirel. Mob. Comput. Netw. Commun. 2005, 3, 454–461. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Srinivasan, K.; Levis, P. RSSI is Under Appreciated. In Proceedings of the Third Workshop on Embedded Networked Sensors (EmNets 2006), Cambridge, MA, USA, 30–31 May 2006; pp. 239–242. [Google Scholar]
- Karp, R. Reducibility among combinatorial problems. In Complexity of Computer Computations; Miller, R., Thatcher, J., Eds.; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Wolsey, L.A. Integer Programming; Wiley: New York, NY, USA, 1998; p. 288. [Google Scholar]
- Morrison, D.R.; Jacobson, S.H.; Sauppe, J.J.; Sewell, E.C. Branch-and-Bound Algorithms: A Survey of Recent Advances in Searching, Branching, and Pruning. Discret. Optim. 2016, 19, 79–102. [Google Scholar] [CrossRef]
- Community, O. OMNET++. Available online: https://omnetpp.org/ (accessed on 8 April 2020).
- Castalia. Framerwork Castalia. Available online: https://github.com/boulis/Castalia (accessed on 8 April 2020).
- Lp Solve. lp solve Library. Available online: http://lpsolve.sourceforge.net/ (accessed on 5 April 2020).







| State-of-the-Art | Classification | Send the Coefficients | Coefficient Submission Strategy | Exchange of Additional Messages |
|---|---|---|---|---|
| Migabo et al. [34] | RLNC | √ | ||
| Heide et al. [43] | RLNC | √ | ||
| Akhtari et al. [44] | RLNC | √ | ||
| Wu et al. [45] | RLNC | √ | ||
| Dong et al. [32] | RLNC | √ | √ | |
| Li et al. [46] | SLNC | √ | ||
| Xu et al. [47] | RLNC | √ | √ | |
| Guo et al. [48] | RLNC | √ | ||
| Bao and Li [38,39] | SLNC | √ | ||
| Han et al. [41] | DLNC | √ | ||
| Valle et al. [6] | RLNC | √ |
| Parameters | Values |
|---|---|
| Node distribution | Random with coordinator in center |
| Radio | CC2420 |
| MAC layer | IEEE 802.15.4e |
| Number of superframe slots | 140 |
| Data rate | 250 kbps |
| Initial energy per node | 18,720 J |
| TxOutputPower | 0 dBm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laurindo, S.; Moraes, R.; Montez, C.; Vasques, F. Combining Network Coding and Retransmission Techniques to Improve the Communication Reliability of Wireless Sensor Network. Information 2021, 12, 184. https://doi.org/10.3390/info12050184
Laurindo S, Moraes R, Montez C, Vasques F. Combining Network Coding and Retransmission Techniques to Improve the Communication Reliability of Wireless Sensor Network. Information. 2021; 12(5):184. https://doi.org/10.3390/info12050184
Chicago/Turabian StyleLaurindo, Suelen, Ricardo Moraes, Carlos Montez, and Francisco Vasques. 2021. "Combining Network Coding and Retransmission Techniques to Improve the Communication Reliability of Wireless Sensor Network" Information 12, no. 5: 184. https://doi.org/10.3390/info12050184
APA StyleLaurindo, S., Moraes, R., Montez, C., & Vasques, F. (2021). Combining Network Coding and Retransmission Techniques to Improve the Communication Reliability of Wireless Sensor Network. Information, 12(5), 184. https://doi.org/10.3390/info12050184









