Abstract
By only storing a unique copy of duplicate data possessed by different data owners, deduplication can significantly reduce storage cost, and hence is used broadly in public clouds. When combining with confidentiality, deduplication will become problematic as encryption performed by different data owners may differentiate identical data which may then become not deduplicable. The Message-Locked Encryption () is thus utilized to derive the same encryption key for the identical data, by which the encrypted data are still deduplicable after being encrypted by different data owners. As keys may be leaked over time, re-encrypting outsourced data is of paramount importance to ensure continuous confidentiality, which, however, has not been well addressed in the literature. In this paper, we design SEDER, a SEcure client-side Deduplication system enabling Efficient Re-encryption for cloud storage by (1) leveraging all-or-nothing transform (), (2) designing a new delegated re-encryption (), and (3) proposing a new proof of ownership scheme for encrypted cloud data (). Security analysis and experimental evaluation validate security and efficiency of SEDER, respectively.
1. Introduction
Cloud storage services are widely deployed nowadays. Popular services include Amazon S3 [1], Apple iCloud [2], and Microsoft Azure [3]. By using cloud services, data owners pay for storage they use, eliminating expensive costs of maintaining dedicated infrastructures.
As more and more users turn to public clouds for storage, the amount of data stored in clouds grows rapidly. Conventionally, the clouds simply store what have been sent by the data owners. This unfortunately will lead to a significant waste of storage space, as different data owners may upload identical data. A remediation is to perform deduplication, in which clouds only store a unique copy of duplicate data from different data owners to reduce unnecessary waste of storage space. For example, research from Microsoft [4] showed that deduplication can achieve 50% and 90–95% storage savings in the standard file systems and backup systems, respectively. Almost all the existing popular file hosting services like Dropbox [5] and Box [6] perform data deduplication.
There are two popular data deduplication mechanisms: server-side deduplication and client-side deduplication. Their main differences are: in server-side deduplication, servers perform deduplication on the outsourced data, transparently to the clients (data owners); in client-side deduplication, the servers and the clients cooperate to perform deduplication. Compared to the server-side deduplication, the client-side deduplication has a significant benefit that the clients do not need to upload those data that have been stored at servers, significantly reducing bandwidth consumption. Therefore, the client-side deduplication is used more broadly in public file hosting services [5,6].
As public cloud providers are usually untrusted [7], data owners hesitate to outsource sensitive data to them due to various concerns. First, data owners fear ownership loss of critical assets. This is because, once the attacker can obtain a data copy, it can simply claim ownership of the data and it is hard to differentiate who originally owns the data. Second, data owners worry about unauthorized access of their sensitive data. Since the data are now hosted by the cloud providers, no guarantees can be provided to data owners that their sensitive information is under strict control and will not be abused. A common solution which can mitigate the aforementioned concerns is to encrypt data using a secret key before outsourcing them. In this way, the provider only “owns” the meaningless encrypted data rather than the original sensitive data. In addition, without having access to the key, unauthorized users can only have access to the encrypted data.
Encryption, however, creates a severe obstacle for deduplication, as identical plaintext may be encrypted into different ciphertext by different data owners who usually use different keys. To resolve this issue, a cryptographic primitive called Message-Locked Encryption () [8,9,10,11,12] was proposed, which derives encryption keys based on the plaintext being encrypted. Using , different data owners can generate identical encryption keys for the same content, leading to deduplicable (One implied assumption for is that the same encryption algorithm will be used by different data owners.) ciphertexts. In practice, encryption keys may be leaked [13,14] and those keys should not be used any more, or data may be deleted by some users and ownership of those users on the data should be revoked [15]. Under such circumstance, to ensure continuous confidentiality of sensitive data, re-encrypting the data using a new key is necessary. Li et al. proposed REED [15] to address the re-encryption problem for deduplication-based encrypted storage systems, which is specifically designed for the server-side deduplication. On the contrary, our design in this work specifically targets the client-side deduplication.
Compared to the design for the server-side deduplication (e.g., REED [15]), ours faces various new challenges especially for the encrypted data. In the server-side deduplication, the client simply uploads the encrypted file to the server and does not get involved in the deduplication process; in the client-side deduplication, however, upon uploading a new file, the client needs to first check whether the file has been stored in the server and, if the file has been stored, the server needs to verify whether the client actually owns the file before adding it to the owner list of the file. This raises a few issues especially for the encrypted data: (1) The server stores an encrypted version of the file, but the client stores a plaintext version of the file. It is non-trivial for the client to efficiently check whether there are identical files stored in both parties. (2) To allow the server to verify whether the client owns the file, the conventional proof of ownership (PoW [16]) protocol requires both the server and the client possessing the same file format (e.g., both are plaintext). It clearly cannot be applied here since the server and the client do not possess the same file format. In addition, since the outsourced data are encrypted and the server does not have access to the encryption key, in both the server-side and the client-side deduplication, the re-encryption process needs to involve the client or a trusted third party who manages clients’ keys. However, the existing designs for the client-side deduplication [17,18] require re-encrypting the entire file whenever the re-encryption happens. The more efficient design for the server-side deduplication [15] simply requires the client to conduct the re-encryption process, which may impose a significant burden on the client.
This paper addresses the aforementioned issues by proposing the first SEcure client-side Deduplication system enabling Efficient Re-Encryption (SERER) for cloud storage. The key insights are threefold: First, we design a novel technique which can allow efficiently detecting duplicate files between two parties even if the file is in different file formats (i.e., a plaintext file format and an encrypted file format). Second, we adapt the traditional PoW scheme, such that it can work correctly even when the server and the client possess different file formats, i.e., the new PoW design can allow the server, which possesses the encrypted version of the file, to efficiently verify whether the client possesses the plaintext of the file. Third, by leveraging all-or-nothing transform and delegated re-encryption, we enable secure re-encryption without imposing a heavy load on the client side. Specifically, by introducing all-or-nothing transform, we make it possible to re-encrypt a file by only re-encrypting a small portion of it; in addition, by adapting proxy re-encryption, we delegate the re-encryption to the cloud server, which possesses a large amount of computational power. Compared to our conference version [19], major differences of this article are: (1) We propose a new approach which can efficiently detect duplicate files between the client and the server even if each stores the file in a different format, i.e., the client stores the plaintext file while the server stores the encrypted file. On the contrary, in the conference version, the client needs to first encrypt the entire plaintext file which incurs a large overhead. (2) We simplify the design of delegated re-encryption, incurring less overhead compared to the conference version. (3) We design , a new PoW scheme that can work correctly even if the server and the client possess different file formats. On the contrary, the conference version directly relies on the original PoW protocol and can only ensure that the prover (i.e., the client) possesses an encrypted version of the original file, rather than the actual original file. (4) We provide a more thorough and formal security analysis. (5) We implement the new designs and re-evaluate the performance of SEDER.
- Contributions. We summarize our contributions as follows:
- We initiate research of the re-encryption problem for secure client-side deduplication in public clouds. The resulted design, SEDER, is a SEcure client-side Deduplication system allowing Efficient Re-encryption.
- We have designed a new delegated re-encryption () scheme and a novel proof of ownership (PoW) scheme for ciphertext (). We also propose a new approach that can securely and efficiently detect duplicate files between the client and the server even though they store the files in a different format. The re-encryption for secure client-side deduplication is enabled by smartly leveraging the aforementioned schemes as well as all-or-nothing transform ().
- We theoretically analyze security of SEDER. We also experimentally evaluate its performance.
2. Backgroud
2.1. Deduplication and Proofs of Ownership (PoWs)
Deduplication is a widely used technique in the cloud environment [4], aiming at removing cross-user duplicates. Note that the deduplication does not contradict with the known durability technique, which replicates data redundantly [20,21,22,23] such that data can be always recoverable upon being corrupted. This is because the redundant data created for durability purposes usually belong to a single user, and the deduplication technique removes redundant data cross users, which were unknown by users and have not been used for durability purposes. Based on granularity of duplicates, deduplication can be categorized as file-level [9] (i.e., duplicates in files) and block-level [24] (i.e., duplicates in blocks/chunks) deduplication. Another categorization of deduplication is based on where deduplication is performed. In a server-side deduplication, all files are uploaded to a cloud server, and the cloud server performs deduplication transparently to clients. In a client-side deduplication, the client first checks whether the file has been stored in the server by uploading a checksum of the file. If the file already exists in the server side, there is no need to upload the file (bandwidth saving), and the server simply adds the client as the owner of this file. In this paper, we focus on client-side deduplication, which is used broadly in practice (e.g., Dropbox [5], Box [6]). In addition, we use the file-level deduplication for simplicity, but the idea could be applicable to the block-level deduplication.
One attack faced by the client-side deduplication is that an adversary that obtains the file checksum can simply claim ownership of this file. Proofs of Ownership (PoWs) have been explored to mitigate this attack. A typical PoW protocol based on Merkle-tree was proposed by Halevi et al. [16], in which the prover answers with the sibling-path for each leaf node being challenged and the verifier checks: (1) whether every sibling-path is valid or not based on the stored root; and (2) whether each leaf node being challenged is a correct hash value of the corresponding file block.
2.2. Message-Locked Encryption (MLE)
[8] is a scheme designed to derive encryption keys from messages being encrypted. In , different data owners are able to generate the same key for identical data. Existing schemes include CE [9], DupLESS [10], Duan Scheme [11], and the LAP scheme [12]. A secure scheme ensures that only the data owners who possess the exact same content can obtain the corresponding encryption key.
2.3. All-Or-Nothing Transform (AONT)
[25] is an unkeyed, invertible, and randomized transformation. No one can succeed in performing the inverse transformation without knowing the entire output of the . Specifically, given message m of l-blocks, where denotes block concatenation, transforms m into message of -blocks, , where . The transformation satisfies the following properties:
- Given m, can be computed efficiently. That is, the complexity of is polynomial to the length of m.
- Given , can be computed efficiently.
- Without knowing the entire (i.e., if one block is missing), the probability of recovering m is negligibly small.
2.4. Discrete Logarithm Problem (DLP)
We have a finite cyclic group G of order q, and the corresponding generator is denoted as g. For a given element , the discrete logarithm problem is to find an integer such that . The discrete logarithm problem is hard, i.e., there is no known algorithm that can compute x in polynomial time [26].
3. Model and Assumptions
- System model. We consider two entities, cloud server () and data owner (). The cloud server offers storage services and wants to perform client-side deduplication to reduce storage and bandwidth cost. The data owners outsource their file to the cloud server. To maintain data confidentiality of their outsourced file, they will encrypt the file before outsourcing them. Note that, when the data owner tries to upload a file that has been stored in the cloud server, will append this data owner to the owner list of the corresponding file without requiring uploading the entire file again.
- Adversarial model. All the data owners are assumed to be fully trusted. In addition, it is an authentic data owner that uploads the original file initially. However, the cloud server is honest-but-curious [7,27]. will honestly store the encrypted files uploaded by the data owner, perform data deduplication, and respond to requests from data owners. Moreover, will not disclose data to anyone who fails to prove ownership of the data. However, it is curious and attempts to infer sensitive information about the encrypted file. We assume there is a malicious entity () which attempts to recover sensitive data in the file using key materials obtained, or to pass the ownership verification during the client-side deduplication without really possessing the file.
The cannot be a special attacker, which is a revoked data owner who still keeps the original file, but it can be an attacker, which is a revoked data owner who has completely removed the original file.
- Assumptions. We assume that is secure (The has been well investigated in the literature. For instance, DupLESS [10], Duan Scheme [11], and LAP scheme [12] are resistant to offline brute-force attack.). The PKI can function securely and each entity has an asymmetric key pair, in which the private key is well protected. All the communication channels are protected by SSL/TLS, so that any eavesdroppers cannot infer information about messages being exchanged. There is no collusion between and since neither of them can obtain any advantages through collusion.
4. SEDER
In this section, we introduce SEDER, a SEcure client-side Deduplication system enabling Efficient Re-encryption for cloud storage. We first design two new building blocks (Section 4.1), a delegated re-encryption scheme () which allows delegating re-encryption to an untrusted third party and, a new PoW scheme which can allow a verifier (i.e., the cloud server) to check ownership of the original file by only having access to the ciphertext of the file. Based on the newly designed building blocks, we present the detailed design of SEDER (Section 4.2 and Section 4.3).
4.1. Building Blocks
4.1.1. Delegated Re-Encryption
Proxy re-encryption () [28,29] allows a proxy to convert the ciphertext, which can only be decrypted by the delegator, into another ciphertext that can be decrypted by the delegatee, without leaking the plaintext to the proxy. Proxy re-encryption has several promising features, such as uni-direction, transparency to the proxy, and non-interaction between the delegator and the delegatee during the re-encryption process. However, the traditional proxy re-encryption [30] does not suit our scenario well because: first, we require that the re-encryption process can be repeated again and again, but traditional proxy re-encryption cannot support this requirement well. Second, in the traditional proxy re-encryption [30], the delegator and the delegatee do not share the secret key used for encryption, which is not true in our scenario. Our new design, Delegated Re-Encryption (), works as follows:
- : G is a multiplicative cyclic group of prime order p (p is an -bit prime number, which should be large enough). g is chosen from G at random and is known to all the parties.
- : Given data owner , this algorithm generates a secret key , which is a number selected randomly from .
- : Message m is encrypted into , where m is from .
- : Given the data owner ’s secret key , the data owner generates a re-encryption key based on its own secret key (which is a random number , being generated by running ) as well as : . This is specific for our design which is different from the traditional proxy re-encryption. In our design, all the data owners will share the secret keys, and hence data owner knows ’s secret key . The purpose of the proxy here is to simply help perform the re-encryption, once the secret key is leaked. This purpose is slightly different from traditional proxy re-encryption, and we therefore use delegated re-encryption for differentiation.
- : Given the re-encryption key , the proxy can re-encrypt the ciphertext to by computing: .
- : Given the ciphertext , the data owner decrypts it using by computing: . This is because: .
4.1.2. A PoW Scheme for Ciphertexts ()
The traditional PoW scheme [16] requires the verifier (e.g., the cloud server) to have access to the plaintext of the original file (Section 2.1). This requirement, however, cannot be satisfied in our scenario, in which the cloud server can only have access to the ciphertext of the outsourced file. We therefore need a new PoW protocol specifically for Ciphertext ( for short), which can allow the verifier to check whether the prover (i.e., the client) really owns the original file by only having access to the corresponding ciphertext. You et al. [31] proposed a design by leveraging Intel SGX, which, however, requires the verifier to be equipped with the SGX security feature in the processor.
Our design of here aims to remove the assumption on the secure hardware. Motivated by DEW [32], we ask the initial data owner, who first uploads the ciphertext of the file, to compute and upload some auxiliary data which can be used later by the cloud server to verify ownership of the original file. Note that, for security, the auxiliary data should satisfy two properties: (1) They can be used by the cloud server to correctly verify the PoW proof, which is computed over the original file by the client. (2) The cloud server should not learn anything about the original file by utilizing the auxiliary data. For performance, the auxiliary data should consume significantly less storage space compared to the original data to avoid cancelling benefits of deduplication. Note that we are not able to compute the auxiliary data simply following the DEW [32], since their auxiliary data are specifically computed from the watermarked version of multimedia files. In our scenario, we do not have “watermarks”.
To construct the auxiliary data, we start from the PoR (Proofs of Retrievability [33]) tags which support private verifiability, which can be constructed as [33]: , where denote the index of each file block, and the index of each symbol (each symbol is from , where q is a large prime) in the block, respectively, and “PRF” is a pseudo-random function with a secret key , and is a set of s secret coefficients in . Note that and need to be known by the verifier.
However, we observed that the privately verifiable PoR tags cannot be directly used for our purpose because: In traditional PoR scenarios, the client is the verifier and the cloud server is the prover; in our scenario, on the contrary, the cloud server is the verifier and the client is the prover, i.e., the cloud server needs to know and to perform verification. This could be problematic since, by knowing and , the honest but curious cloud server (Section 3) may brute-force the original file content from the PoR tags due to the limited content space of a file.
Therefore, we need to allow the cloud server to verify the PoW proof without being able to brute-force the original file content. Our solution is: (1) We slightly change the construction of the tag to , where y is a secret random number unknown to the cloud server. Specifically, y can be derived from a pseudo-random function with a secret key , and can be generated by applying on the original file. The server does not have the original file, and is not able to derive y. (2) We disclose to the cloud server, but keep secret from it. An issue remaining unsolved is, without knowing , how can the cloud server verify the PoW proof? To address this issue, we generate by applying on the original file. The server does not have the original file, and is not able to derive . When generating the PoW proof, the prover which actually possesses the original file will be able to compute , and then compute assisting information which assists the server to check the PoW proof. Note that should be kept secret from the prover, and the assisting information should be able to be computed without knowing . In addition, to prevent the cloud server from learning the original file content from the PoW proof, the prover will mask each proof using randomness. The detailed design of our is elaborated as follows:
- The data owner chooses a set of secret coefficients from . Given a file (f), the data owner pre-processes it and computes auxiliary data . By applying over the file f, the data owner generates two keys and . Using , the data owner derives a random number y in . The data owner splits the file into n blocks, each of which contains s symbols in , and derives a tag for each file block (for ):The will be sent to the cloud server.
- : The verifier checks whether the prover really possesses a file f. Checking each file block will be expensive, especially when the file is large in size. Instead, the verifier can check a random subset of c blocks (The verifier will check all the blocks if the file is small in size, e.g., having no more than 460 4 KB blocks.), which can ensure with high probability that the prover will not be able to pass the verification if it does not possess the entire file, when c is large enough [34]. The verifier picks a random c-element subset I of the set [1, n] and, for each , a random element is picked from . The will be sent to the prover. To prevent the prover from knowing , the cloud server sends to the prover.
- The prover applies over the file f, generating and . Using , the prover computes y. Based on the received Q, the prover computes a proof as (for ):where is a random number picked by the prover for masking the proof. The prover also computes:Then, is returned to the verifier.
- : The algorithm returns “1” if the equationholds taking and as input. Otherwise, the algorithm returns “0”.
4.2. Design Rationale of SEDER
There are several key designs in SEDER, as listed in the following:
First, we rely on to ensure a file encrypted by different data owners is always deduplicable. guarantees that different data owners who possess an identical file can always generate an identical encryption key.
Second, we design novel techniques that can allow the client and the server to identify duplicate content stored in them even though they hold the content in a different format, i.e., the client stores plaintext of the content while the server stores ciphertext of the content. An immediate solution is, during deduplication, the client encrypts the plaintext of the file, computes a checksum over the encrypted file, and sends this checksum to the server for comparison. This could be very expensive especially when the file is large in size. An improvement could be that the initial data owner who uploads the file initially also computes a checksum over the plaintext of the file, and stores this checksum in the server, and, during deduplication, the client can simply send the checksum computed from the plaintext of the data. This improvement, however, is insecure because, by knowing the checksum of the original data, the server may brute-force the file content due to the limited content space of a file. Fortunately, the encryption key derived through can be used to protect the checksum value of plaintext as well. Our solution is that the initial data owner encrypts the checksum (which is usually small in size) over the plaintext using the key, and the encrypted checksum will be sent to the server. This can prevent the server from performing the brute-force attack since it cannot have access to the key. In addition, during the deduplication, the client can compute the checksum over the plaintext of the data, encrypt it using the derived key, and send the encrypted checksum to the server for comparison.
Third, we use and together to support efficient re-encryption of the outsourced file. Specifically, given a file, we apply , obtaining the ciphertext. ensures that the same ciphertext will be generated from different users if the file content is the same. Then, is applied to ciphertext, generating a set of data blocks. Note that without fetching all the data blocks, the ciphertext cannot be recovered thanks to the interesting property of . In this way, to re-encrypt a file, the data owner only needs to re-encrypt one data block, rather than all the data blocks. In addition, by leveraging , we can delegate the re-encryption process to the untrusted cloud server, without leaking the plaintext of the file. This is advantageous as we can eliminate the burden on the client who is supposed to be kept lightweight.
Finally, to ensure only the valid data owners are able to decrypt the data being re-encrypted, we perform the following: (1) We leverage to distinguish valid and invalid data owners. A valid data owner should be able to prove his/her ownership as he/she really possesses the file. When a data owner passes the verification, the cloud server will add him/her to the owner list of the file and provide him/her the assisting information needed for decrypting the file. (2) The data owner who re-encrypts the file will compute new assisting information that is needed to decrypt the file. The new assisting information will be re-propagated to the users in the owner list. The unauthorized users (e.g., the hackers which obtain the secret key) do not have the original file and will not be able to pass the to be added to the owner list.
4.3. Design Details of SEDER
Let , and be the security parameters, be a delegated re-encryption scheme that , , ,
. is a symmetric encryption scheme such that , , and is an asymmetric encryption scheme such that . Let P denote the scheme such that . Let be a cryptographic hash function: . In the following, we describe the design details of SEDER, which contains six phases: , , , , and .
- : This is to bootstrap the system parameters, and to initialize cryptographic parameters for data owners and cloud server. The system runs to initialize the system parameters. In addition,
- Data owner (): Each data owner runs the key generation algorithm of asymmetric encryption scheme to generate the public and private key pair by running the algorithm: .
- Cloud server (): It generates the public/private key pair by running the key generation algorithm of the asymmetric encryption scheme:.
- : The phase is run by the data owner before uploading a file f to . derives two keys and by applying over f. computes a checksum of f by: .
- : Data owner sends an upload request (, ) to the cloud server , indicating that he/she wants to upload f. and interact to perform the following operations:
- Case 1— does not exist in : In this case, will upload the entire file f to following these steps:
- runs , generating .
- encrypts f by running .
- generates a secret key by running: .
- splits into l blocks: , and applies transform on , generating blocks, such that where and .
- randomly selects a data block from and encrypts it by running: . The final ciphertext is: .
- encrypts using symmetric encryption with :, and further encrypts using asymmetric encryption with ’s public key: .
- sends to the cloud server , , and .
- organizes the received information in the format , , , , owner list . By decrypting using , obtains the assisting information The owner list is initialized as .
- Case 2— exists in : Since the file has been stored by , it is necessary to perform to verify whether really possesses this file:
- runs , and sends Q and to . Note that is part of the (Section 4.1.1).
- computes a proof by running , and sends back to .
- verifies by running . If the output is ‘1’, appends to the owner list () and sends the assisting information of f, i.e., , to . Otherwise, rejects . Note that will be encrypted using ’s public key and securely distributed to , and can use private key for decryption.
- : When , a data owner in the owner list , suspects or (i.e., the old secret key used for encrypting in ) is leaked, only a small part of ciphertext rather than the entire file will be re-encrypted by as follows:
- decrypts using , obtaining , where i denotes the data owner which encrypts the file before re-encryption.
- By using and his/her own secret key , generates the re-encryption key by running . encrypts using : , and then encrypts using ’s public key: . and are sent to .
- runs and replaces c with . In addition, replaces with , which is decrypted from , and distributes to valid owners in . Note that a revoked owner will not be able to obtain , and is not able to decrypt the re-encrypted data any more.
- : sends a download request (, ) to if he/she wants to retrieve f. then checks whether is in the owner list or not. If is in the owner list, will respond with , and uses the file key and the assisting information (e.g., , or if the data have been re-encrypted) to decode . Otherwise, will reject this download request.
- : When receives a delete request (, ) from a data owner , if is in the owner list, will remove from the owner list of file f, i.e., has been revoked. If turns empty, will delete and , . Otherwise, the re-encryption process (i.e., ) should be invoked so that the revoked data owner is not able to decrypt the data any more.
5. Analysis and Discussion
5.1. Security Analysis
Security of SEDER is captured in the following Lemmas and Theorems.
Lemma 1.
The cloud server cannot learn the original file by having access to its ciphertext and the encrypted assisting information.
Proof. (Sketch) The encrypted file after transform, i.e., , and the assisting information, i.e., or , are stored in the cloud storage. Without having access to the file key derived through , the cloud server cannot decrypt any assisting information, and hence cannot have access to the secret key which is required to decrypt block c (or ). Due to , without having obtained all the blocks, the cloud server will not be able to decode to obtain the encrypted original file , let alone the original file f. □
Lemma 2.
The cloud server cannot learn the original file from .
Proof. (Sketch) is obtained by encrypting the hash value of the file f using a file key . Since the cloud server is not able to have access to (the used to derive is assumed to be secure, and without having access to the original file, the cloud server will not be able to derive ), it will not be able to decrypt the cipher to obtain the hash value of f, considering the symmetric encryption is secure. Without the hash value of the file, the cloud server is not able to perform the brute-force attack to infer the file. □
Lemma 3.
The cloud server cannot learn the original file when performing .
Proof. (Sketch) During each run of proxy re-encryption, the cloud server (as a re-encryption proxy here) can observe: (1) ; and (2) . There are two potential attack cases. Case 1: the cloud server tries to learn m using knowledge obtained from one run of proxy re-encryption. The cloud server will not be able to have access to , , , , and it is clear that the cloud server cannot learn m from the knowledge of (1) and (2) since there are three unknowns and two equations. The probability of guessing m will be no larger than for a q-bit m, which is negligibly small for a large enough q. Case 2: the cloud server tries to learn m by accumulating knowledge from multiple runs of proxy re-encryption. By accumulating knowledge from the first run of the proxy re-encryption, the cloud server cannot learn m since there are three unknowns but only two equations. For each following run, the data owner will pick a completely different random key, and send a new re-encryption key to the cloud server. Therefore, the cloud server will obtain an additional equation, along with a new unknown. In other words, the additional knowledge accumulated from each following run of proxy re-encryption will not provide the cloud server with any additional advantage of computing m. □
Lemma 4.
The cloud server cannot learn the original file through performing .
Proof. (Sketch) The cloud server can have access to: (1) , which consists of tags and , provided by the data owner who initially uploads the file; (2) , which includes and , obtained during each execution.
(1) We first show that, by having access to , the cloud server cannot obtain the original file. By having access to the set of n tags and , equivalently, the cloud server can have access to n linear equations and unknowns (i.e., , ,…, , , ,…, ,…, , ,…, , , ,…, , y). The cloud server is not able to compute the unknowns using the n linear equations. The cloud server may try to guess the file content (due to the limited content space of a file) in a brute-force manner and, to use each guessed file content to derive and y using . This will not be feasible since both and y are directly or indirectly derived by , which can resist against the offline brute-force attack. The only option for the cloud server is to guess each file content, and to utilize the n linear equations to compute the remaining , ,…, , and y based on the guessed file content. However, the number of unknowns (i.e., n + 1) is more than the number of linear equations (i.e., n), which makes the n linear equations unsolvable.
(2) We then show that, by accumulating PoW proofs after each PoW execution, the cloud server is still not able to learn the original file. A few key points are important for our security: First, If the PoW check fails, the accumulated PoW proof should not help the server, since the data owner is not supposed to possess the original file. Second, the cloud server will strictly follow the PoW protocol during each PoW execution (i.e., honest). This includes generating a random challenge during each PoW execution. Third, the prover will not collude with the verifier, and will mask each (where ) with a newly generated random number. After each successful PoW execution, the cloud server will accumulate a new PoW proof, which includes , ,…, as well as :
…
Since () is masked by newly generated random number , the number of new linear equations brought by , ,…, is equal to the number of new unknowns. Therefore, the set of alone does not bring any advantage to the cloud server for computing . We further show that, by utilizing , the cloud server also gains negligible advantage of computing . Because of hardness of DLP, to use , the cloud server needs to guess () and , and to verify correctness of each guessing using . The probability for a successful guessing will be smaller than , which is negligibly small if q is large enough. □
Lemma 5.
A malicious entity which does not possess the entire file cannot pass the verification.
Proof. (Sketch) In the following, we first prove that the PoW verification process is correct. We further show that, by checking a random subset of the entire file, the verifier can ensure that the prover really possesses the entire file with a high probability (note that, if the file size is small, the verifier will check all the file blocks, which can always ensure that the prover really possesses the entire file). Lastly, we show that, if the PoW verification can be passed successfully, the verifier can always ensure that the prover possesses the challenged blocks.
We first show correctness of the verification process as follows:
We then show that, by challenging a random subset of blocks among the entire file, and if a malicious data owner does not possess the entire file, the cloud server can detect it with a high probability. According to PDP [34], if the adversary only possesses w proportion of an n-block file, when being challenged, a random subset of c blocks out of n blocks, the probability that the verifier can detect the misbehavior is: , and . The lower bound of the P is , which means, when c is large enough, , and .
Finally, we show that, if the prover loses one of the challenged blocks, it will not be able to pass the PoW check. During the PoW verification, all the PoW tags , where are unknown to the prover, and hence is also unknown. If the prover is missing one block being challenged, it needs to guess this block when computing the PoW proof , ,…, .
The resulting PoW proof can successfully pass the PoW check with a probability no more than . This probability is negligibly small for a large enough prime q. Therefore, we can conclude that the prover is not able to pass the PoW check without actually possessing all the blocks being challenged during each PoW execution. □
Theorem 1.
SEDER is secure under our adversarial model.
Proof. (Sketch) SEDER is secure since the following security goals can be achieved: (1) the cloud server cannot learn anything about the original file f; and (2) a malicious entity which does not possess f cannot pass the check; and (3) a malicious entity cannot learn anything about f. The first security goal can be captured by Lemmas 1–4, and the second security goal can be ensured by Lemma 5. For the last security goal, since a malicious entity (including a revoked data owner which has deleted the original file) cannot pass the check, it can obtain neither the encrypted data nor the updated decryption key, and hence is not able to learn the original file f. □
5.2. Discussion
- Zero-day attack. SEDER is vulnerable to the zero-day attack, in which the key is leaked and the re-encryption has not been performed. During this period, the adversary can have access to the original file using the obtained key materials. This seems to be unavoidable and currently not a good solution for mitigating such a strong attack.
- The nature of the storage being supported by SEDER. Currently, SEDER only supports archival storage [20,34,35,36]. It can be extended to support dynamic storage (i.e., supporting dynamic operations like insert, delete, and modify [27,37,38,39]) in the future.
6. Experimental Evaluation
6.1. Experimental Setup
We have experimentally evaluated overhead of each major operation in SEDER. We chose the security parameters as: , , and . The length of the file key and is 128 bits. The symmetric and asymmetric encryption were instantiated by AES-128 and RSA-1024, respectively. The hash function was instantiated using SHA-256. We instantiated the secure following the idea of DupLESS [10]. OpenSSL-1.1.0e [40] was used for the major cryptographic operations. Throughout the experiment, the client and the cloud server both ran on a local computer with Intel i5-6300 (2.5 GHz) CPU and 8 GB RAM. The computational overhead in , , , and phases are evaluated for different file sizes, and the experimental results are averaged over 10 runs. When evaluating the phase, we varied a and b, where a is the file block size (in bytes) and b is the symbol size (in bytes).
6.2. Experimental Results
In the following, we evaluate the performance of SEDER in different phases. To the best of our knowledge, among existing PoW schemes on encrypted cloud data [17,18,31], as shown in Table 1, PoWIS is the solely proposal that can achieve the same security level with our . First, due to relying on the hash value of the original file to find out whether the file has existed in the cloud server before uploading, the PoW process in [17,18] are vulnerable to the brute-force attack. In addition, since the PoW design in [17] works relying on the hash value of the file, it cannot provide concrete ownership guarantees (the vulnerability has been identified in [16]). In this case, the PoWIS [31] and our are the two more secure PoW schemes on encrypted cloud data than the counterparts [17,18] for the client-side deduplication system. Therefore, for the phase, we compare our PoWC with the existing scheme PoWIS [31], which can also enable the PoW over the outsourced encrypted data securely. For the phase, we compare the performance of our re-encryption process (i.e., DRE) with that in REED [15], which consumes much less bandwidth and computational resources compared to the existing re-encryption designs in [17,18,41] by taking full advantage of , but completely relies on the client for the re-encryption process due to the nature of the server-side deduplication.

Table 1.
Comparison with other deduplication schemes. (Hur [41] and REED [15] are server-side deduplication schemes which do not include the PoW process).
- PreUpload. The data owner obtains secure keys in this phase. The secure , i.e., DupLESS, requires interactions between the data owner and an independent key server. We therefore assessed the computational overhead in both the data owner and the key server. As shown in Figure 1, the computational cost in the key server is constant. On the contrary, the computational cost for the client (i.e., the data owner) is linear with the file size. This is because the data owner needs to first compute a hash value of the original file, and such a cost depends on the file size.
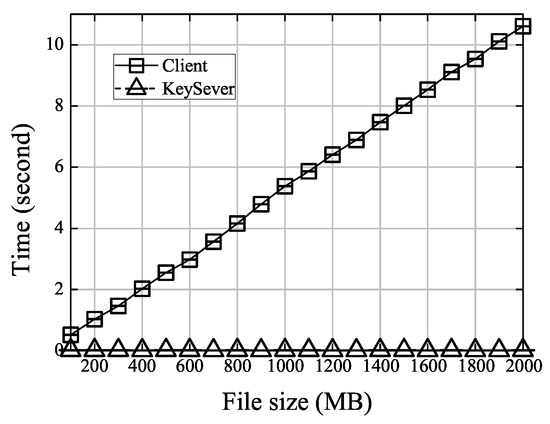 Figure 1. Computational cost for the phase.
Figure 1. Computational cost for the phase. - Upload. The computational cost for Case 1 and Case 2 of the phase (Section 4.3) are shown in Figure 2 and Figure 3, respectively.
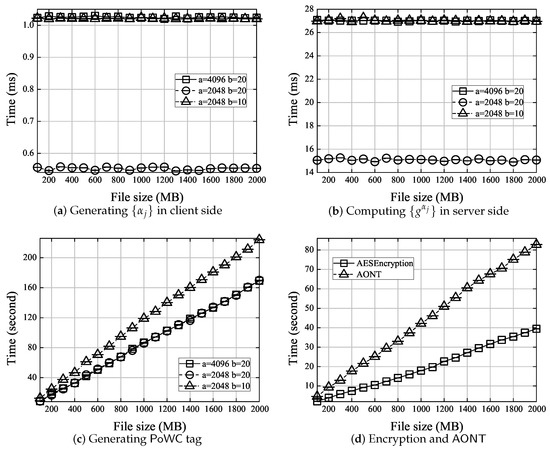 Figure 2. Computational cost for various components in Case 1 of phase.
Figure 2. Computational cost for various components in Case 1 of phase.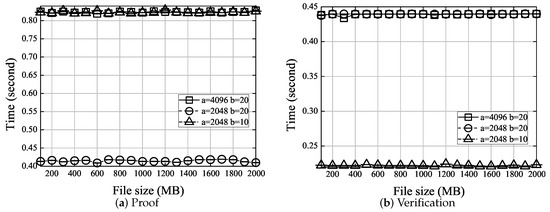 Figure 3. Computational cost for various components in Case 2 of phase.
Figure 3. Computational cost for various components in Case 2 of phase.
In Case 1, to enable , the initial data owner needs to select a set of secret coefficients and to compute tags. Then, the data owner encrypts the file and performs on the encrypted file. From Figure 2, we can observe that: (1) The computation for generating the secret coefficients and computing is independent from the file size. In addition, this computation is mainly determined by s, which is . (2) The computation for generating tags grows linearly with the file size. Additionally, for the fixed file size, the computation for different testing cases is: . This is because, the computation for generating tags depends on the total number of symbols in a file, which . (3) The computation for AES encryption and transform is determined by the file size and approximately grow linearly with the file size.
In Case 2, the prover (i.e., a potential data owner) computes the proof, and the verifier (i.e., the cloud server) verifies correctness of the proof. From Figure 3, we can observe that: (1) Both the proof generation and verification can be performed in constant time thanks to the use of spot checking (i.e., only 460 randomly picked blocks instead of the entire file are checked [34]. (2) For the fixed file size, the computation needed for different testing cases are . This is because both the proof generation and verification are mainly determined by the number of symbols in a block, i.e., s, which is .
Considering security, we compare the performance of our and PoWIS [31], which both allow PoW to be performed on the encrypted data with sufficient ownership guarantees and resistance to the brute-force attack. The comparison is shown in Table 2. We can observe that PoWIS is much more efficient than in tag generation, proof generation, and verification. This is mainly due to the support of secure hardware (i.e., Intel SGX) in PoWIS. On the contrary, is purely based on cryptography and does not require secure hardware as well as the trust on the secure hardware manufacturer. Secure hardware may not be equipped with the server, and hence PoWIS will have limited applications, but is a general solution which can be deployed on any general computing device. In addition, using secure hardware like Intel SGX will introduce extra overhead for performing platform attestation [42] to ensure the usage of secure hardware. This overhead may be large, e.g., more than 1 s [31].

Table 2.
Performance comparison between PoWIS and in this work. PoWIS has a much better performance by using dedicated secure hardware, but it relies on the assumption that the cloud server has secure hardware equipped. The is purely based on cryptography, and does not rely on the aforementioned assumption.
- Update. A valid data owner will cooperate with the cloud server to re-encrypt the file if the key is leaked. The results for this phase are shown in Figure 4a.
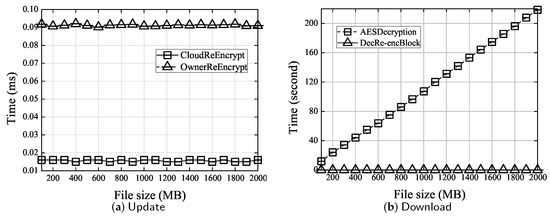 Figure 4. Computational cost for and phase.
Figure 4. Computational cost for and phase.
We can observe that the computation in both the data owner and the cloud server is rather small (less than ms), compared to actually re-encrypting the entire file (which is 10–200 s as estimated from Figure 4b). In addition, both are independent from the file size because only a fixed part of the entire data needs to be re-encrypted.
Considering significant computational and bandwidth saving, we compare the performance of and REED [15], both of which support the re-encryption in a cloud storage system by re-encrypting a small file block with fixed size rather than the entire file in [17,18,41]. The results are shown in Table 3. We can observe that our , although introduces computational overhead to the server, has significantly less computation in the client side. This is because: (1) In our , the client only needs to re-encrypt the key, rather than the data; on the contrary, the client needs to re-encrypt the data in REED. (2) REED uses cipertext-policy attribute-based encryption (CP-ABE) in the re-encryption process, which contains computationally expensive pairing operations for fine-grained access control; on the contrary, our re-encryption process does not contain these expensive pairing operations to support a coarse-grained access control in re-encryption. A more fine-grained re-encryption scheme for SEDER could be our future work by taking fully advantage of the nature of the client-side deduplication.

Table 3.
Performance comparison between REED and our DRE. Note that the re-encrypted block is 64 bytes in size.
- Download. To retrieve the file, a data owner needs to decrypt the re-encrypted block (the process is denoted as - in Figure 4b), to perform the reverse operation of , and to further decrypt the resulted data to obtain the original file (denoted as in Figure 4b). From Figure 4b, we can observe that: (1) The computation of decrypting the re-encrypted block is small (less than 6 ms) and remains constant. (2) The computation for grows linearly with the file size.
7. Related Work
- Message-Locked Encryption (). is a set of encryption algorithm that the encryption key is derived from the message being encrypted, which is formalized by Bellare et al. in [8]. Douceur et al. [9] proposed convergent encryption (CE), the first scheme, in which the encryption key is the hash value of the file being encrypted, such that the same file possessed by different users can be encrypted to be same ciphertexts by identical encryption key. CE has been adopted in several online backup systems [43,44,45,46,47,48,49] for facilitating the performance of deduplication over data encrypted by different data owners. However, CE is vulnerable to the offline dictionary attack, since content space is usually predictable. To mitigate this security issue, several schemes were proposed. Bellare et al. proposed DupLESS [10] by introducing an independent key server and limiting times for accessing the key server. Duan [11] proposed another secure scheme based on distributed oblivious key generation. Liu et al. [12] proposed a scheme without relying on any independent server by requiring the valid data owner to participate in authentication and use a same input Password-Authenticated-Key-Exchange (PAKE) to derive the final key. The online dictionary attack is mitigated for the first time by allowing the valid data owner to limit times for performing key exchange with them.
- Proxy Re-Encryption. Blaze et al. [28] proposed proxy re-encryption for the first time, which requires a mutual trust between the delegator and its delegatees. Ateniese et al. [30] released a trust requirement with the cost that the re-encrypted ciphertext cannot be re-encrypted repeatedly. Canetti and Hohenberger [50] pointed out that the proxy re-encryption is vulnerable to the chosen-ciphertext attack (CCA) and the chosen-plaintext attack (CPA), and proposed a CCA-secure proxy re-encryption scheme, which, however, requires bidirectional trust among delegator and delegatees. Davidson et al. [51] presented two proxy re-encryption schemes based on matrix transformation, one is secure under standard CPA model requiring unidirectional trust between delegator and its delegatees, and the other one is secure in a stricter CCA model when the delegator and its delegatees can establish bidirectional trust. More recently, Ref. [52] identified a new security level for proxy re-encryption and adjusted existing schemes to fit in this new security definition. There are several works focusing on enhancing usability of existing proxy re-encryption schemes. For example, the a proxy re-encryption scheme in [53] is compatible with the hybrid encryption scenario at the cost of additional storage space for the proxy to store encrypted random masks for each delegatee.
- Deduplication and Proofs of Ownership (PoWs). Deduplication has been widely used in cloud storage. For significant bandwidth and storage saving, the client-side deduplication schemes [41,47,54,55,56] is investigated and used more than the server-side deduplication schemes in practice. ClearBox [57] is a transparent deduplication scheme, in which storage service providers can attest to users the number of owners of specific file transparently, so that users can share the fee for storing the same file. Li et al. [58] proposed to achieve data integrity and deduplication simultaneously. Tang et al. [59] performed data deduplication on a backup system with ciphertext-policy attribute based encryption (CP-ABE) enabled. For protecting privacy, the Message-Locked Encryption [8,9] was used in server-side deduplication. To mitigate the offline dictionary attack faced by CE, which is one of the most widely used schemes, Bellare et al. proposed DupLESS [10] by introducing a key server and limiting the number of requests for obtaining a key within a fixed time interval, which can mitigate the brute-force attack faced by the . Liu et al. [12] removed the additional independent key server at the cost of requiring at least one valid data owner to stay online when performing deduplication. Li et al. [47] proposed a deduplication scheme taking advantage of the hybrid cloud environment, in which the encryption keys are generated and managed by the private cloud server owned by the users, while the public cloud server provides storage service and server-side deduplication. Yao et al. [60] proposed a Hierarchical Privilege-Based Predicate Encryption () scheme based on the hierarchical encryption, which introduces a deduplication provider to check duplication based on user dynamic privileges of users without revealing any information about privilege to the cloud server. To further enhance the effectiveness of deduplication, some generalized deduplication schemes [61,62,63] are proposed by detecting and removing “similar” data rater than “identical” data using transformation functions, e.g., the Hamming code and the Revealing Encryption (RE), in traditional deduplication schemes.
To enable a secure client-side deduplication, the proof of ownership protocol is necessary since the cloud server needs to check whether the prover really possesses the file that has existed in the cloud storage without requiring the prover to upload the entire file again to manage ownership of the file correctly. The traditional Merkle tree based PoW [16] assumes that the cloud server is fully trusted and has access to the original file, which is not applicable to scenarios where the data owners have advanced security requirements, e.g., protecting confidentiality and copyright against the untrusted cloud server. To ensure data confidentiality, Puzio et al. proposed a client-side deduplication scheme [64] to remove redundant data by introducing a trusted third party (which is called “Metadata Magager”) to authenticate users that can perform deduplication checking for, however, specific users rather than across multiple users. In 2018, Xiong et al. [65] designed an authenticated deduplication by leveraging a role symmetric encryption (RSE) algorithm to accomplish fine-grained access control for deduplication. Xiong et al. [18,65], Ding et al. [17], and our previous work [19] proposed several client-side deduplication schemes including proofs of ownership on the encrypted cloud data, which, however, are problematic in security or performance due to using irrational commitment in ownership validation, e.g., the encrypted file blocks in [18,65], the hash value of the original file in [17], and the Merkle tree derived from the encrypted data. You et al. noticed this conflict and proposed a deduplication-friendly watermarking [32], in which the untrusted cloud server can validate ownership of the original file by having access to the watermarked file. An implementation of PoW [31] for encrypted cloud data by leveraging trusted hardware was proposed, which, however, requires the cloud server to support and enable specific trusted features.
However, data owner revocation is not well considered in the above deduplication schemes, which is quite common in the cloud storage environment. In this case, Kwon et al. [66] then designed a deduplication scheme specific for multimedia data based on randomized convergent encryption and privilege-based encryption. Hur et al. [41] proposed a novel server-side deduplication to support dynamic ownership management by leveraging the group key distribution techniques and randomized convergent encryption. Xiong et al. proposed a client-side deduplication scheme [18] allowing changing ownership dynamically based on their previous work [65]. Ding et al. proposed a client-side deduplication scheme [17] that enables dynamic ownership based on homomorphic encryption. However, the aforementioned schemes are expensive in computation and communication since the entire encrypted file needs to be updated when the re-encryption happens. REED [15,67] aimed at addressing the key revocation problem for the secure server-side deduplication in cloud storage efficiently. In order to efficiently replace old keys and re-encrypt the data, REED introduced two special transforms derived from CAONT (CANOT is a special case of transforms in which the key used for transform is the hash value of the message being processed). Different from REED, our SEDER resolves the re-encryption problem for the client-side deduplication and further optimizes the performance of the re-encryption process by taking full advantage of the nature of the client-side deduplication.
Overall, our SEDER enables secure and efficient re-encryption for a cloud storage, in which the data owner collaborates with the cloud server to re-encrypt a small file block when the key needs to be updated, resulting in significant bandwidth and computational saving. The client-side deduplication is enabled in SEDER as well, which ensures data ownership and is resistant to the brute-force attack.
8. Conclusions
In this paper, we propose SEDER to enable an efficient and secure re-encryption scheme for client-side deduplication in cloud storage. We achieve efficiency by only re-encrypting a small proportion of the file and delegating the re-encryption process to the cloud server. We achieve security by incorporating a secure duplicate detection approach and a PoW scheme specifically for encrypted data. Security analysis and experimental results show that our design is applicable to the cloud storage system, since it ensures continuous data confidentiality with modest computational and communication overhead, which, specifically, is for the test data set. The prover and the cloud server spend no more than 0.85 s and 0.45 s, respectively, in performing the PoW, and the re-encryption process requires at most 0.092 milliseconds and 0.014 milliseconds for the users and the cloud server, respectively.
Author Contributions
Conceptualization, B.C.; Data curation, W.Y.; Formal analysis, W.Y. and B.C.; Funding acquisition, L.L. (Limin Liu); Investigation, W.Y.; Methodology, W.Y.; Resources, L.L. (Lei Lei); Software, W.Y.; Supervision, L.L. (Limin Liu); Writing—original draft, W.Y.; Writing—review & editing, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
Data Assurance and Communications Security Center: 2018YFB0804402.
Acknowledgments
We would like to thank Quanwei Cai and Jingqiang Lin for their early contribution to this work. This work was supported by the National Key R&D Program of China under Award No. 2018YFB0804402.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Amazon Simple Storage Service. Available online: http://aws.amazon.com/cn/s3/ (accessed on 25 March 2021).
- Icloud. Available online: https://www.icloud.com/ (accessed on 25 March 2021).
- Microsoft Azure. Available online: http://www.windowsazure.cn/?fb=002 (accessed on 25 March 2021).
- Meyer, D.T.; Bolosky, W.J. A Study of Practical Deduplication. ACM Trans. Storage 2012, 7, 4. [Google Scholar] [CrossRef]
- Dropbox. Available online: https://www.dropbox.com/ (accessed on 25 March 2021).
- Box. Available online: https://www.box.com/ (accessed on 25 March 2021).
- Yu, S.; Wang, C.; Ren, K.; Wenjing, L. Achieving Secure, Scalable, and Fine-Grained Data Access Control in Cloud Computing. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Bellare, M.; Keelveedhi, S.; Ristenpart, T. Message-locked encryption and secure deduplication. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, 26–30 May 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 296–312. [Google Scholar]
- Douceur, J.R.; Adya, A.; Bolosky, W.J.; Dan, S.; Theimer, M. Reclaiming space from duplicate files in a serverless distributed file system. In Proceedings of the International Conference on Distributed Computing Systems, Vienna, Austria, 2–5 July 2002; pp. 617–624. [Google Scholar]
- Bellare, M.; Keelveedhi, S.; Ristenpart, T. DupLESS: Server-Aided Encryption for Deduplicated Storage. In Proceedings of the USENIX Conference on Security, Washington, DC, USA, 14–16 August 2013; pp. 179–194. [Google Scholar]
- Duan, Y. Distributed Key Generation for Encrypted Deduplication: Achieving the Strongest Privacy. In Proceedings of the CCS’14: 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 57–68. [Google Scholar]
- Liu, J.; Asokan, N.; Pinkas, B. Secure Deduplication of Encrypted Data without Additional Independent Servers. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 874–885. [Google Scholar]
- Debian Security Advisory. Available online: https://www.debian.org/security/2008/dsa-1571 (accessed on 25 March 2021).
- These Are Not the Certs You’re Looking for. Available online: http://dankaminsky.com/2011/08/31/notnotar/ (accessed on 25 March 2021).
- Li, J.; Qin, C.; Lee, P.P.C.; Li, J. Rekeying for Encrypted Deduplication Storage. In Proceedings of the IEEE/IFIP International Conference on Dependable Systems and Networks, Toulouse, France, 28 June–1 July 2016. [Google Scholar]
- Halevi, S.; Harnik, D.; Pinkas, B.; Shulman-Peleg, A. Proofs of ownership in remote storage systems. In Proceedings of the CCS’11: The ACM Conference on Computer and Communications Security, Chicago, IL, USA, 17–21 October 2011; pp. 491–500. [Google Scholar]
- Ding, W.; Yan, Z.; Deng, R.H. Secure Encrypted Data Deduplication with Ownership Proof and User Revocation. In Algorithms and Architectures for Parallel Processing, Proceedings of the 17th International Conference, Helsinki, Finland, 21–23 August 2017; Ibrahim, S., Choo, K.R., Yan, Z., Pedrycz, W., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switerland, 2017; Volume 10393, pp. 297–312. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, Y.; Tang, S.; Liu, X.; Yao, Z. Secure Encrypted Data With Authorized Deduplication in Cloud. IEEE Access 2019, 7, 75090–75104. [Google Scholar] [CrossRef]
- Lei, L.; Cai, Q.; Chen, B.; Lin, J. Towards Efficient Re-encryption for Secure Client-Side Deduplication in Public Clouds. In Proceedings of the 18th International Conference on Information and Communications Security, Singapore, 29 November–2 December 2016; pp. 71–84. [Google Scholar]
- Chen, B.; Curtmola, R.; Ateniese, G.; Burns, R. Remote data checking for network coding-based distributed storage systems. In Proceedings of the 2010 ACM Workshop on Cloud Computing Security Workshop, Chicago, IL, USA, 8 October 2010; pp. 31–42. [Google Scholar]
- Chen, B.; Curtmola, R. Towards self-repairing replication-based storage systems using untrusted clouds. In Proceedings of the Third ACM Conference on Data and Application Security and Privacy, San Antonio, TX, USA, 18–20 February 2013; pp. 377–388. [Google Scholar]
- Chen, B.; Ammula, A.K.; Curtmola, R. Towards server-side repair for erasure coding-based distributed storage systems. In Proceedings of the 5th ACM Conference on Data and Application Security and Privacy, San Antonio, TX, USA, 2–4 March 2015; pp. 281–288. [Google Scholar]
- Chen, B.; Curtmola, R. Remote data integrity checking with server-side repair 1. J. Comput. Secur. 2017, 25, 537–584. [Google Scholar] [CrossRef]
- Quinlan, S.; Dorward, S. Venti: A New Approach to Archival Storage. In Proceedings of the FAST ’02 Conference on File and Storage Technologies, Monterey, CA, USA, 28–30 January 2002; Volume 2, pp. 89–101. [Google Scholar]
- Rivest, R.L. All-or-nothing encryption and the package transform. In Proceedings of the International Workshop on Fast Software Encryption, Haifa, Israel, 20–22 January 1997; pp. 210–218. [Google Scholar]
- Gordon, D. Discrete Logarithm Problem. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011; pp. 352–353. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.; Li, J.; Ren, K.; Lou, W. Enabling Public Verifiability and Data Dynamics for Storage Security in Cloud Computing. In Proceedings of the European Conference on Research in Computer Security, Saint-Malo, France, 21–23 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 355–370. [Google Scholar]
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Espoo, Finland, 31 May–4 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 127–144. [Google Scholar]
- Ivan, A.A.; Dodis, Y. Proxy Cryptography Revisited. In Proceedings of the Network and Distributed System Security Symposium (NDSS 2003), San Diego, CA, USA, 23–26 February 2003. [Google Scholar]
- Ateniese, G.; Fu, K.; Green, M.; Hohenberger, S. Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. 2006, 9, 1–30. [Google Scholar] [CrossRef]
- You, W.; Chen, B. Proofs of Ownership on Encrypted Cloud Data via Intel SGX. In Proceedings of the First ACNS Workshop on Secure Cryptographic Implementation, Rome, Italy, 19–22 October 2020. [Google Scholar]
- You, W.; Chen, B.; Liu, L.; Jing, J. Deduplication-friendly watermarking for multimedia data in public clouds. In Proceedings of the European Symposium on Research in Computer Security, Guildford, UK, 14–18 September 2020; Springer: Cham, Switzerland, 2020; pp. 67–87. [Google Scholar]
- Shacham, H.; Waters, B. Compact proofs of retrievability. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 90–107. [Google Scholar]
- Ateniese, G.; Burns, R.; Curtmola, R.; Herring, J.; Kissner, L.; Peterson, Z.; Song, D. Provable data possession at untrusted stores. In Proceedings of the CCS07: 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007; pp. 598–609. [Google Scholar]
- Curtmola, R.; Khan, O.; Burns, R.; Ateniese, G. MR-PDP: Multiple-replica provable data possession. In Proceedings of the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008; pp. 411–420. [Google Scholar]
- Bowers, K.D.; Juels, A.; Oprea, A. HAIL: A high-availability and integrity layer for cloud storage. In Proceedings of the CCS ’09: 16th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 9–13 November 2009; pp. 187–198. [Google Scholar]
- Erway, C.C.; Küpçü, A.; Papamanthou, C.; Tamassia, R. Dynamic provable data possession. ACM Trans. Inf. Syst. Secur. (TISSEC) 2015, 17, 15. [Google Scholar] [CrossRef]
- Chen, B.; Curtmola, R. Robust dynamic provable data possession. In Proceedings of the 2012 32nd International Conference on Distributed Computing Systems Workshops, Macau, China, 18–21 June 2012; pp. 515–525. [Google Scholar]
- Chen, B.; Curtmola, R. Robust dynamic remote data checking for public clouds. In Proceedings of the ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; pp. 1043–1045. [Google Scholar]
- OpenSSL. Available online: https://www.openssl.org/ (accessed on 25 March 2021).
- Hur, J.; Koo, D.; Shin, Y.; Kang, K. Secure data deduplication with dynamic ownership management in cloud storage. IEEE Trans. Knowl. Data Eng. 2016, 28, 3113–3125. [Google Scholar] [CrossRef]
- Remote Attestation in Intel Software Guard Extensions. 2020. Available online: https://software.intel.com/content/www/us/en/develop/articles/code-sample-intel-software-guard-e/xtensions-remote-attestation-end-to/-end-example.html (accessed on 25 March 2021).
- Cox, L.P.; Murray, C.D.; Noble, B.D. Pastiche: Making backup cheap and easy. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 285–298. [Google Scholar] [CrossRef]
- Killijian, M.O.; Powell, D.; Courtès, L. A Survey of Cooperative Backup Mechanisms, 2006. Available online: https://hal.archives-ouvertes.fr/hal-00139690/document (accessed on 25 March 2021).
- Storer, M.W.; Greenan, K.; Long, D.D.E.; Miller, E.L. Secure data deduplication. In Proceedings of the ACM Workshop on Storage Security and Survivability, Alexandria, VA, USA, 31 October 2008; pp. 1–10. [Google Scholar]
- Xu, J.; Chang, E.C.; Zhou, J. Weak leakage-resilient client-side deduplication of encrypted data in cloud storage. In Proceedings of the ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 8–10 May 2013; pp. 195–206. [Google Scholar]
- Li, J.; Li, Y.K.; Chen, X.; Lee, P.P.C.; Lou, W. A Hybrid Cloud Approach for Secure Authorized Deduplication. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1206–1216. [Google Scholar] [CrossRef]
- Stanek, J.; Sorniotti, A.; Androulaki, E.; Kencl, L. A Secure Data Deduplication Scheme for Cloud Storage. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 99–118. [Google Scholar]
- Li, J.; Chen, X.; Li, M.; Li, J.; Lee, P.P.C.; Lou, W. Secure Deduplication with Efficient and Reliable Convergent Key Management. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1615–1625. [Google Scholar] [CrossRef]
- Canetti, R.; Hohenberger, S. Chosen-ciphertext secure proxy re-encryption. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007; pp. 185–194. [Google Scholar]
- Phong, L.; Wang, L.; Aono, Y.; Nguyen, M.; Boyen, X. Proxy Re-Encryption Schemes with Key Privacy from LWE; 2016. Available online: https://eprint.iacr.org/2016/327.pdf (accessed on 25 March 2021).
- Davidson, A.; Deo, A.; Lee, E.; Martin, K. Strong post-compromise secure proxy re-encryption. In Proceedings of the Australasian Conference on Information Security and Privacy, Christchurch, New Zealand, 3–5 July 2019; Springer: Cham, Switerland, 2019; pp. 58–77. [Google Scholar]
- Myers, S.; Shull, A. Efficient Hybrid Proxy Re-Encryption for Practical Revocation and Key Rotation; 2017. Available online: https://eprint.iacr.org/2017/833.pdf (accessed on 25 March 2021).
- Leesakul, W.; Townend, P.; Xu, J. Dynamic data deduplication in cloud storage. In Proceedings of the 2014 IEEE 8th International Symposium on Service Oriented System Engineering, Oxford, UK, 7–11 April 2014; pp. 320–325. [Google Scholar]
- Liu, H.; Chen, L.; Zeng, L. Cloud Data Integrity Checking with Deduplication for Confidential Data Storage. In Proceedings of the International Symposium on Cyberspace Safety and Security, Xi’an, China, 23–25 October 2017; Springer: Cham, Switerland, 2017; pp. 460–467. [Google Scholar]
- Liu, X.; Sun, W.; Lou, W.; Pei, Q.; Zhang, Y. One-tag checker: Message-locked integrity auditing on encrypted cloud deduplication storage. In Proceedings of the INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Armknecht, F.; Bohli, J.M.; Karame, G.O.; Youssef, F. Transparent Data Deduplication in the Cloud. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 886–900. [Google Scholar]
- Li, J.; Li, J.; Xie, D.; Cai, Z. Secure Auditing and Deduplicating Data in Cloud. IEEE Trans. Comput. 2016, 65, 2386–2396. [Google Scholar] [CrossRef]
- Tang, H.; Cui, Y.; Guan, C.; Wu, J.; Weng, J.; Ren, K. Enabling Ciphertext Deduplication for Secure Cloud Storage and Access Control. In Proceedings of the ACM on Asia Conference on Computer and Communications Security, Xi’an, China, 30 May–3 June 2016. [Google Scholar]
- Yao, X.; Lin, Y.; Liu, Q.; Zhang, Y. A secure hierarchical deduplication system in cloud storage. In Proceedings of the IEEE/ACM International Symposium on Quality of Service, Beijing, China, 20–21 June 2016; pp. 1–10. [Google Scholar]
- Nielsen, L.; Vestergaard, R.; Yazdani, N.; Talasila, P.; Sipos, M. Alexandria: A Proof-of-Concept Implementation and Evaluation of Generalised Data Deduplication. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Vestergaard, R.; Zhang, Q.; Lucani, D.E. Generalized Deduplication: Bounds, Convergence, and Asymptotic Properties. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM 2019), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lucani, D.E.; Nielsen, L.; Orlandi, C.; Pagnin, E.; Vestergaard, R. Secure Generalized Deduplication via Multi-Key Revealing Encryption. In Security and Cryptography for Networks, Proceedings of the 12th International Conference (SCN 2020), Amalfi, Italy, 14–16 September 2020; Galdi, C., Kolesnikov, V., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12238, pp. 298–318. [Google Scholar] [CrossRef]
- Puzio, P.; Molva, R.; Önen, M.; Loureiro, S. ClouDedup: Secure Deduplication with Encrypted Data for Cloud Storage. In Proceedings of the 2013 IEEE 5th International Conference on Cloud Computing Technology and Science, Bristol, UK, 2–5 December 2013; Volume 1, pp. 363–370. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, Y.; Li, X.; Lin, M.; Yao, Z.; Liu, G. RSE-PoW: A Role Symmetric Encryption PoW Scheme with Authorized Deduplication for Multimedia Data. Mob. Netw. Appl. 2018, 23, 650–663. [Google Scholar] [CrossRef]
- Kwon, H.; Hahn, C.; Kim, D.; Hur, J. Secure deduplication for multimedia data with user revocation in cloud storage. Multimed. Tools Appl. 2017, 76, 5889–5903. [Google Scholar] [CrossRef]
- Qin, C.; Li, J.; Lee, P.P.C. The Design and Implementation of a Rekeying-Aware Encrypted Deduplication Storage System. ACM Trans. Storage 2017, 13, 1–30. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).