Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases
Abstract
1. Introduction
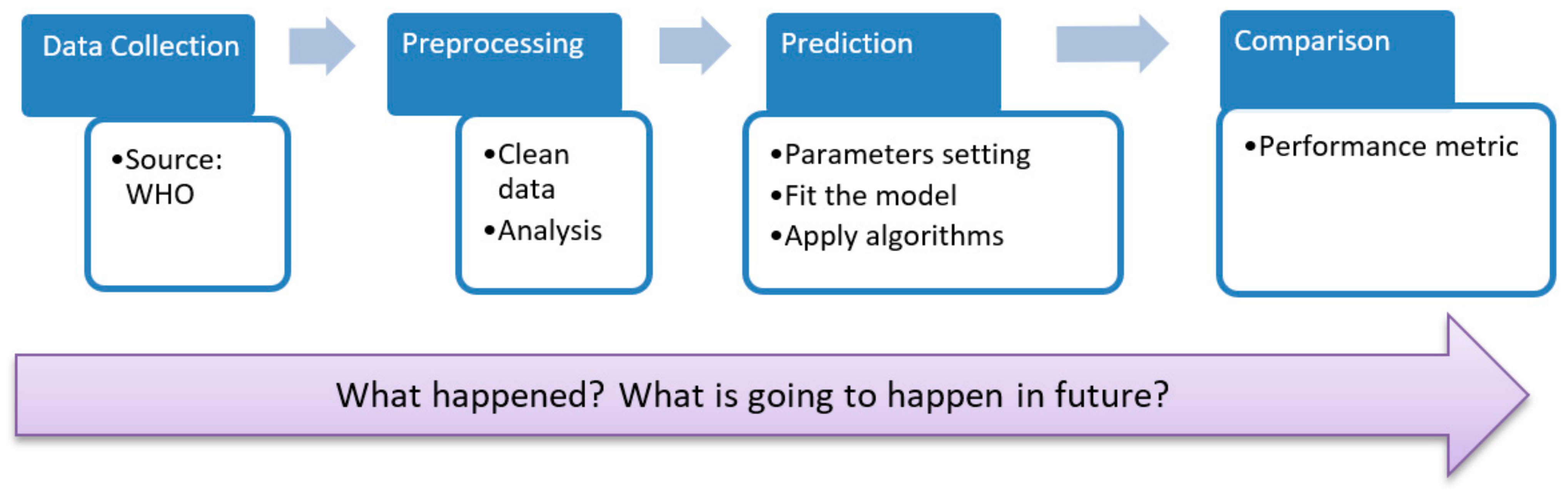
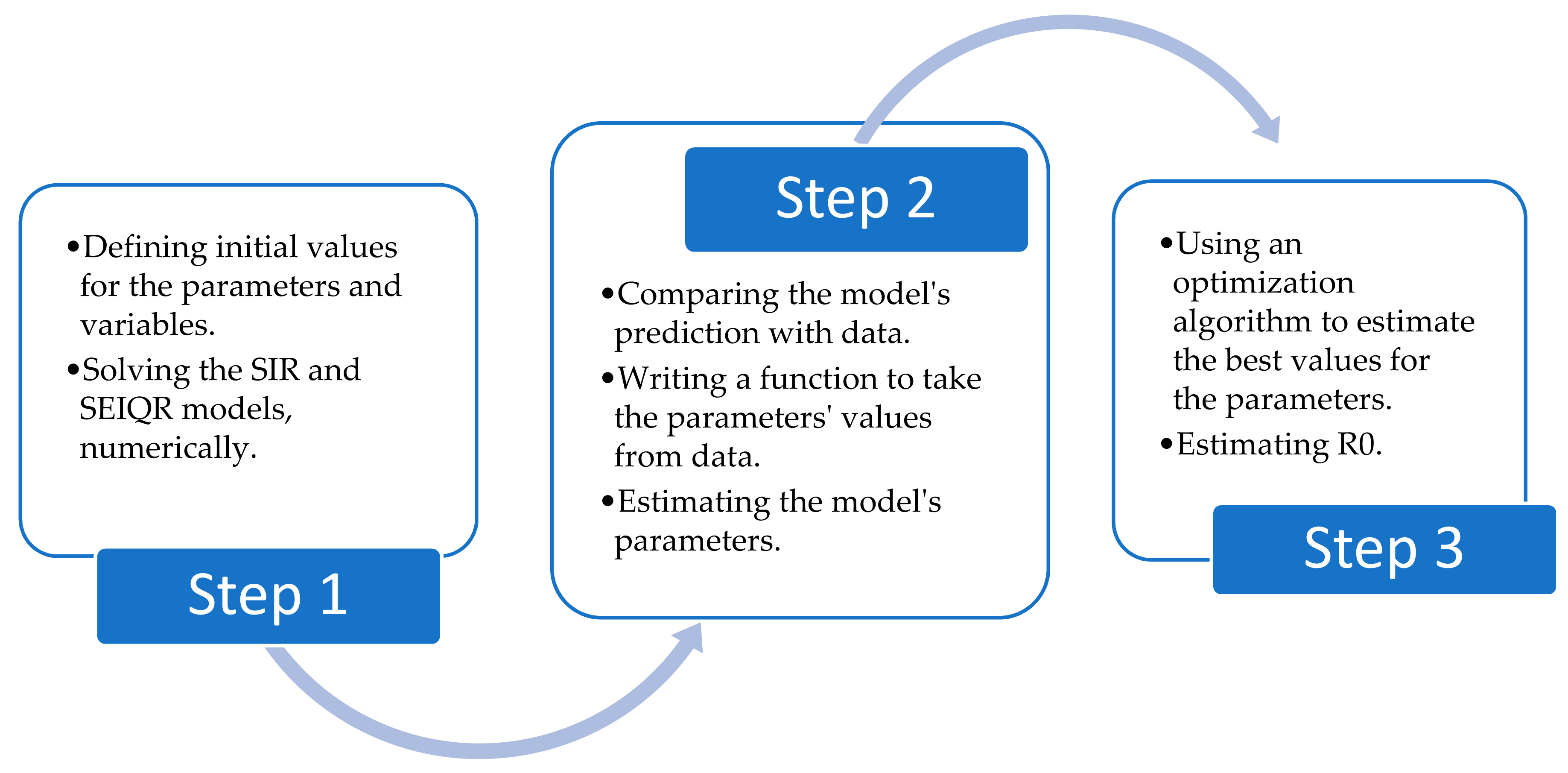
2. Research Methodology
3. SIR Model
- S is the number of susceptible individuals at time t;
- I is the number of infected individuals at time t;
- R is the number of recovered individuals at time t;
- and are the transmission rate and rate of recovery (removal), respectively.
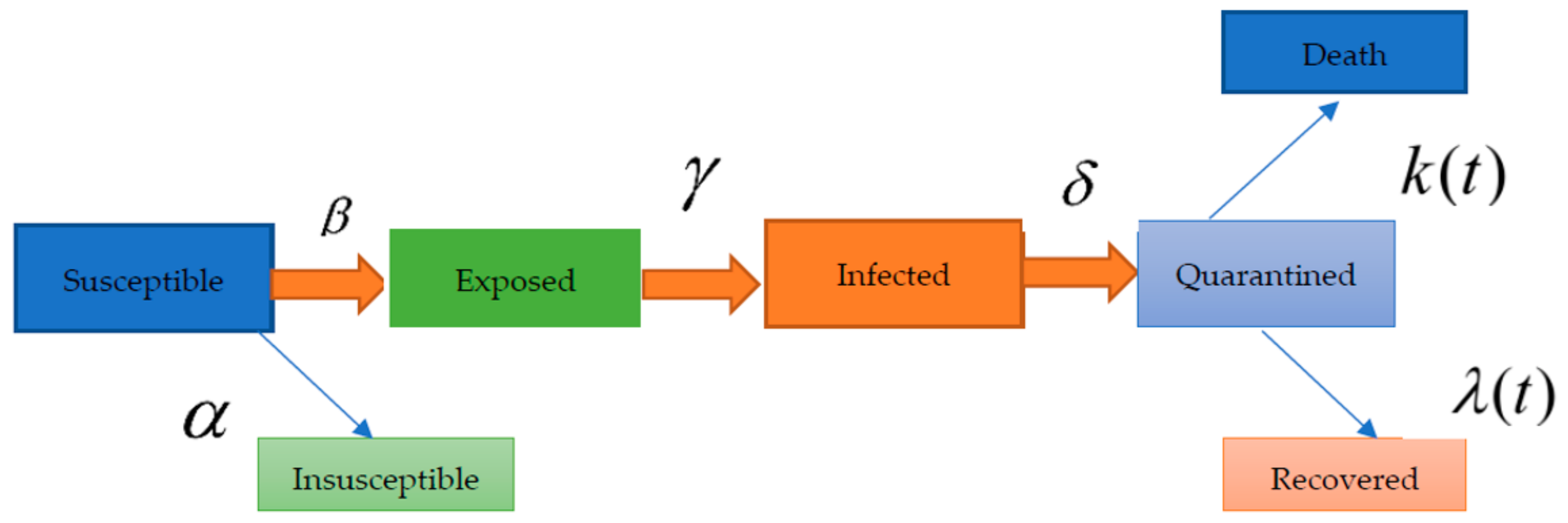
4. SEIQR Model
5. Prediction
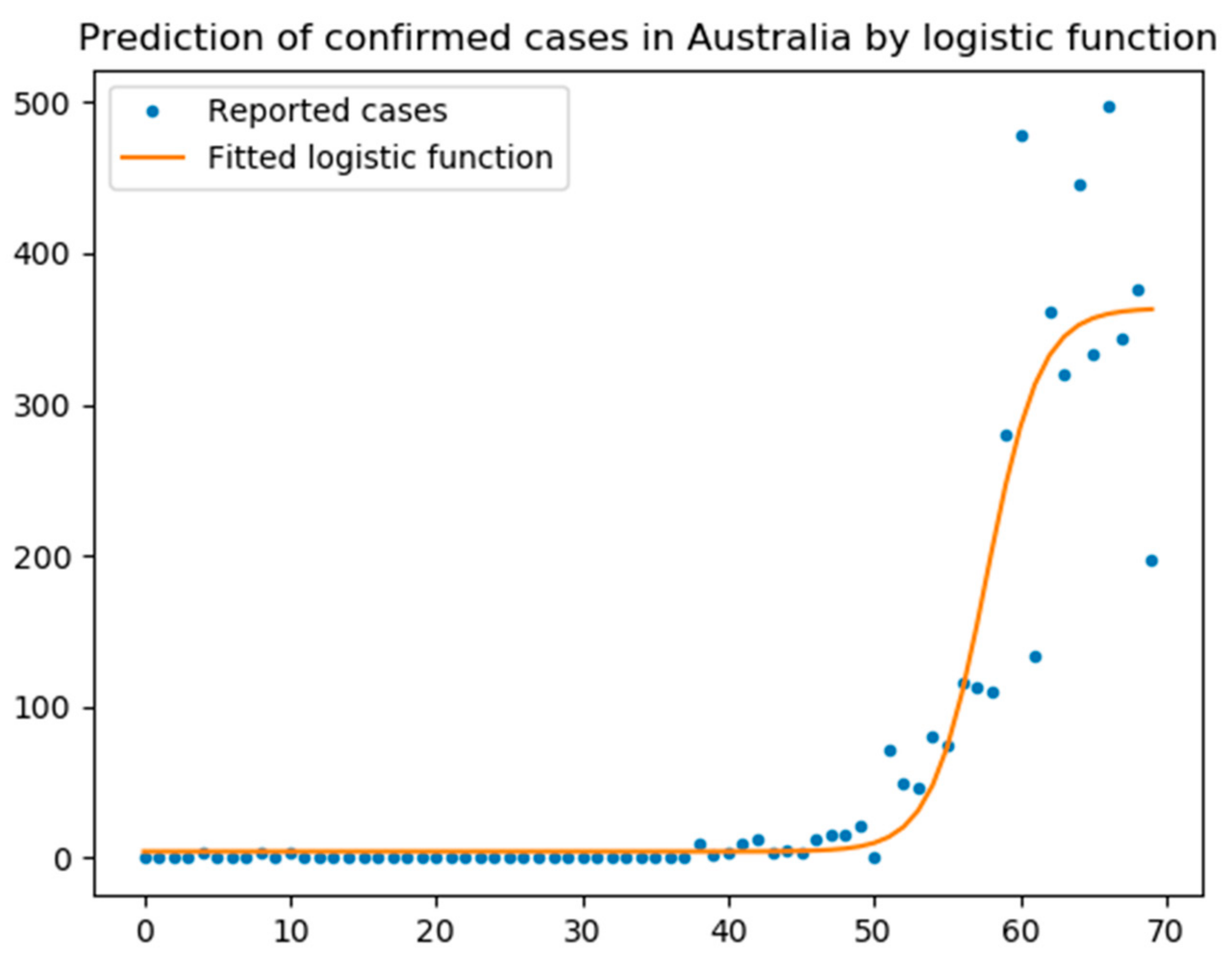
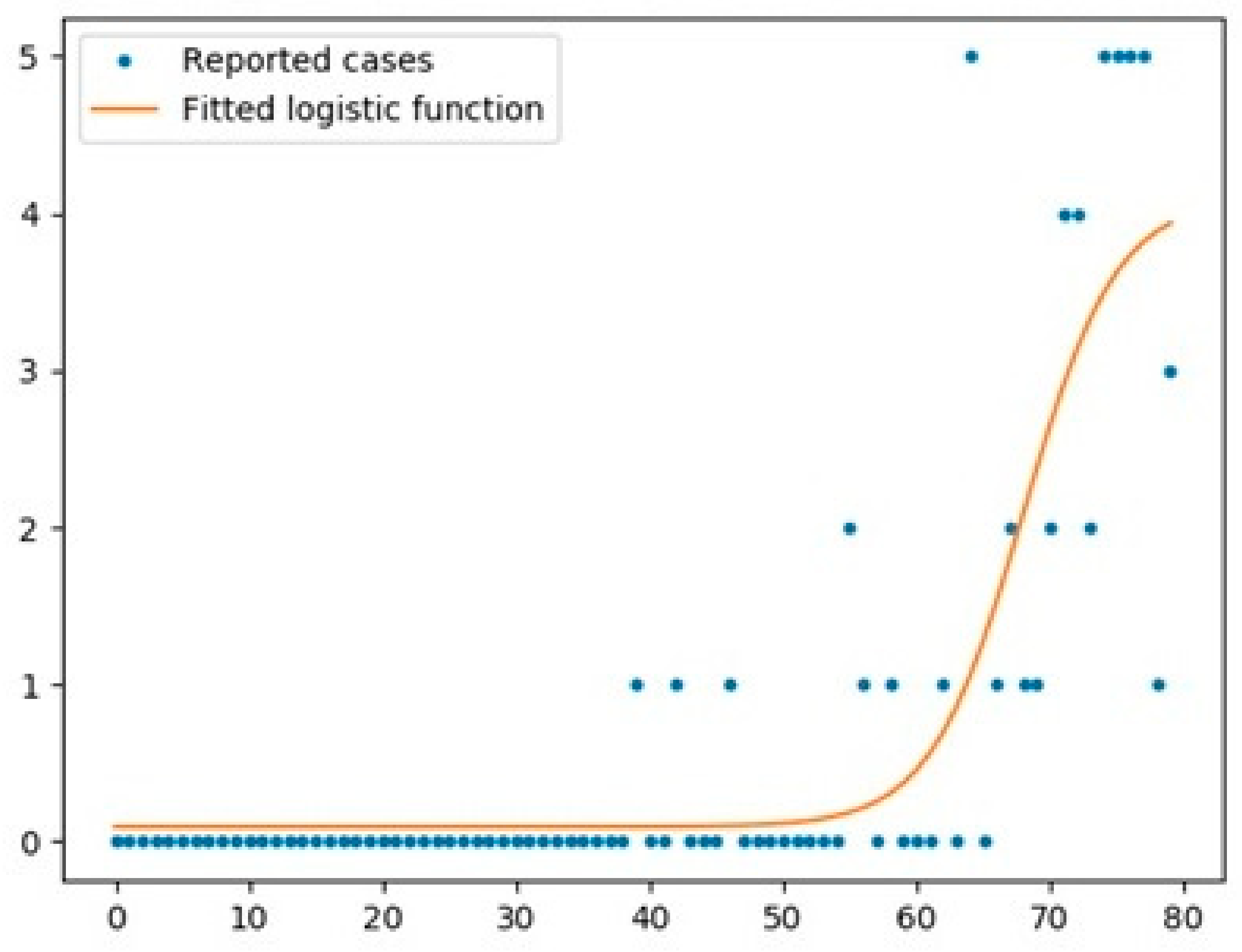
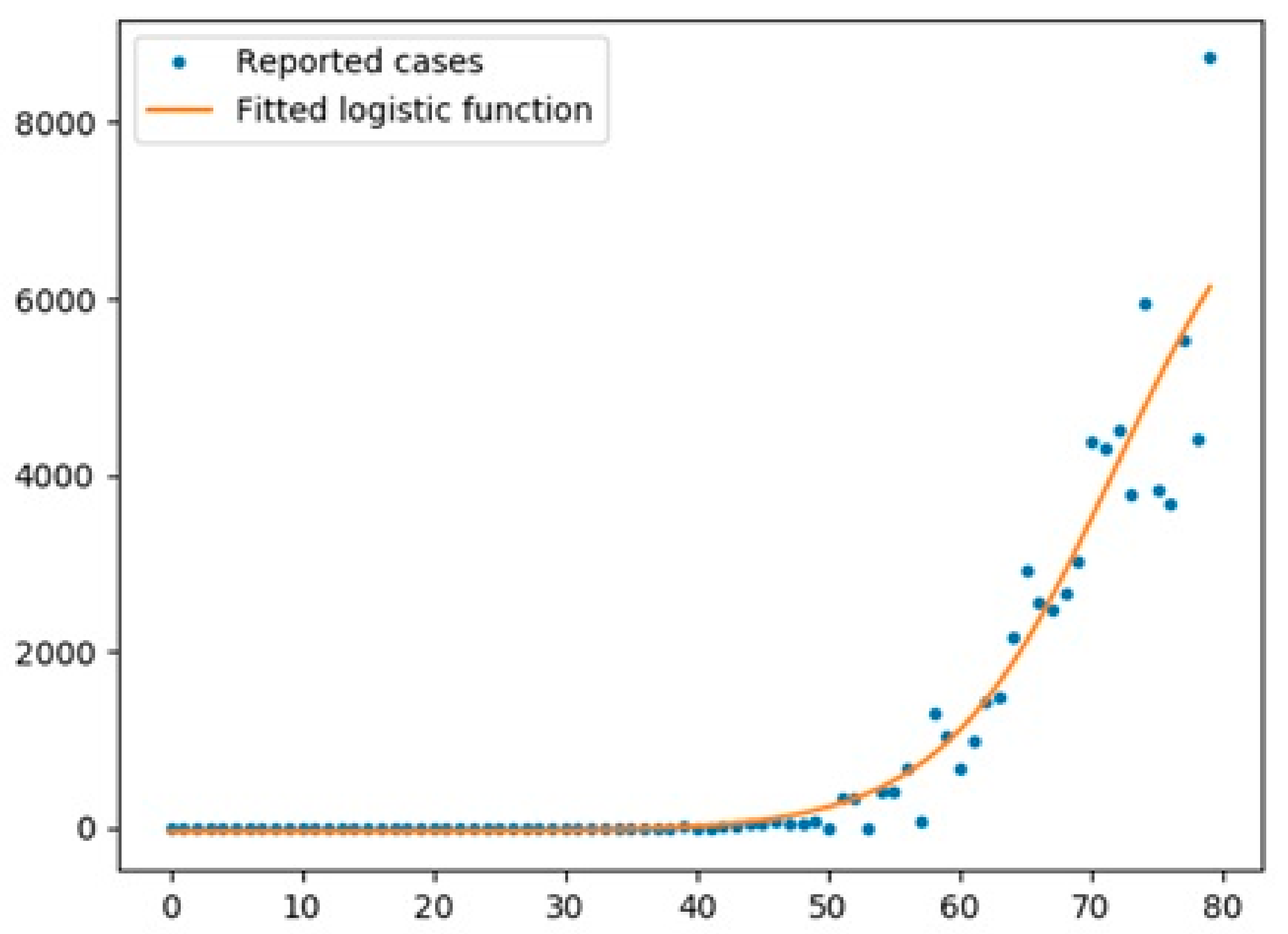
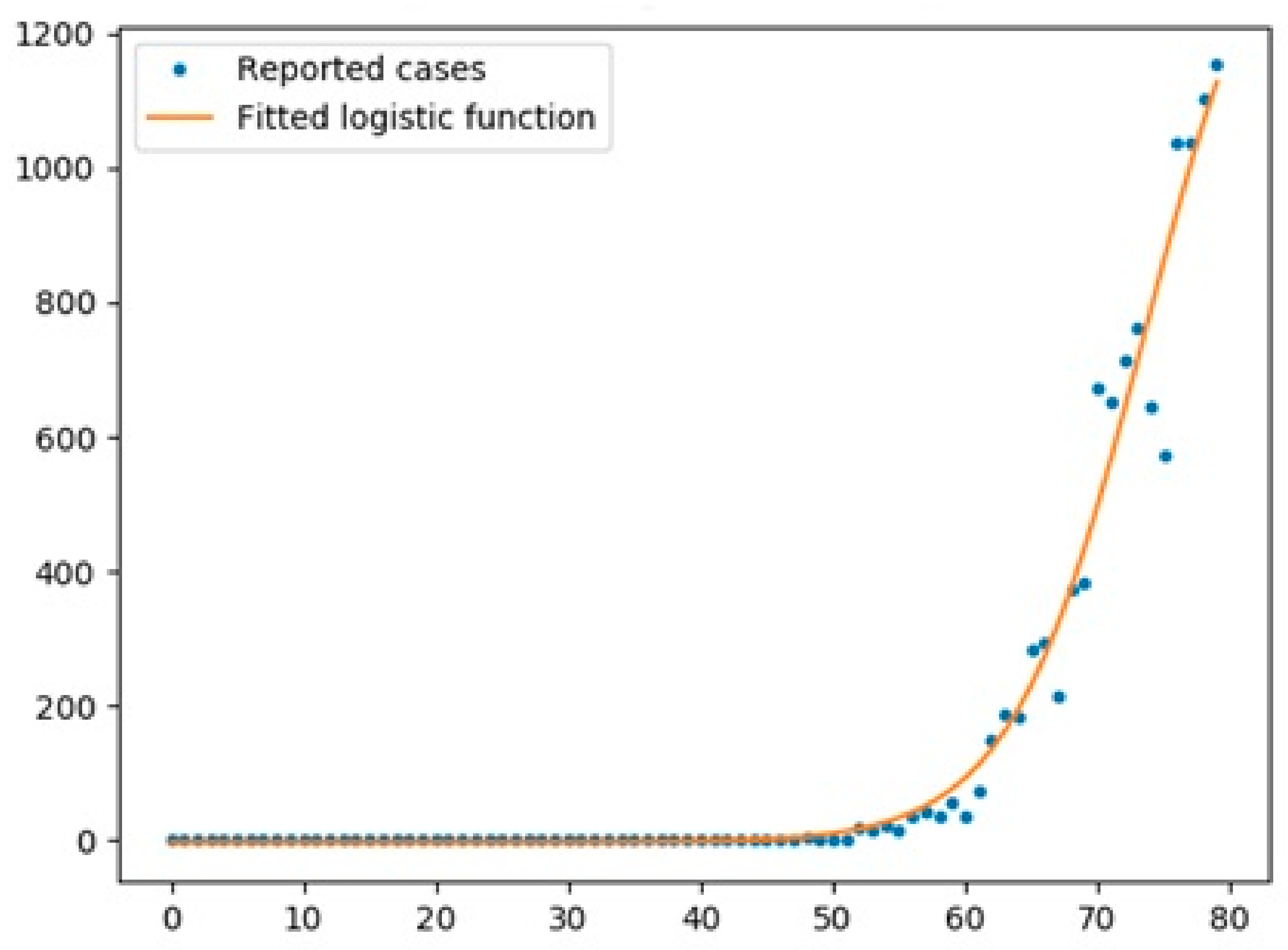
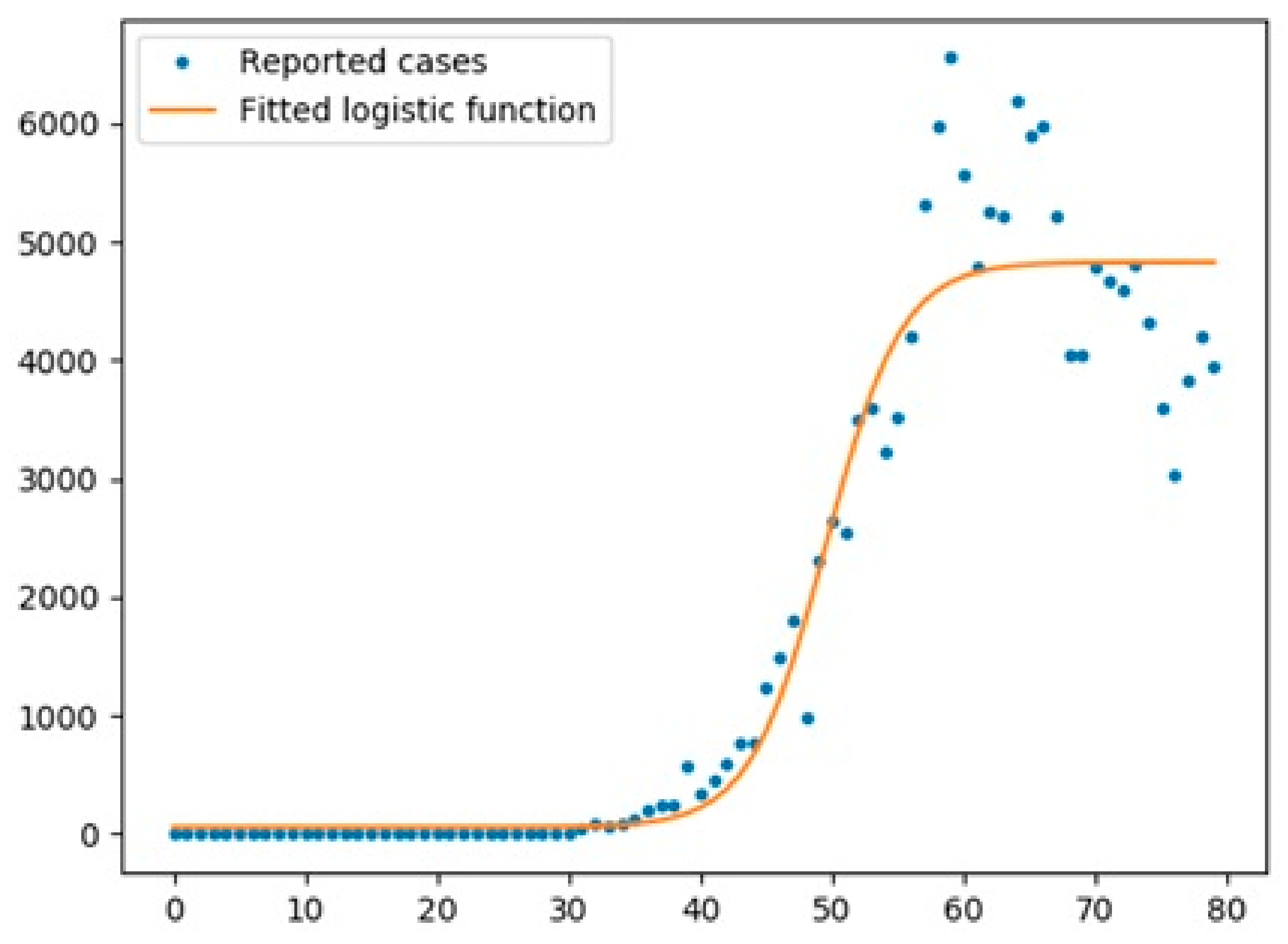
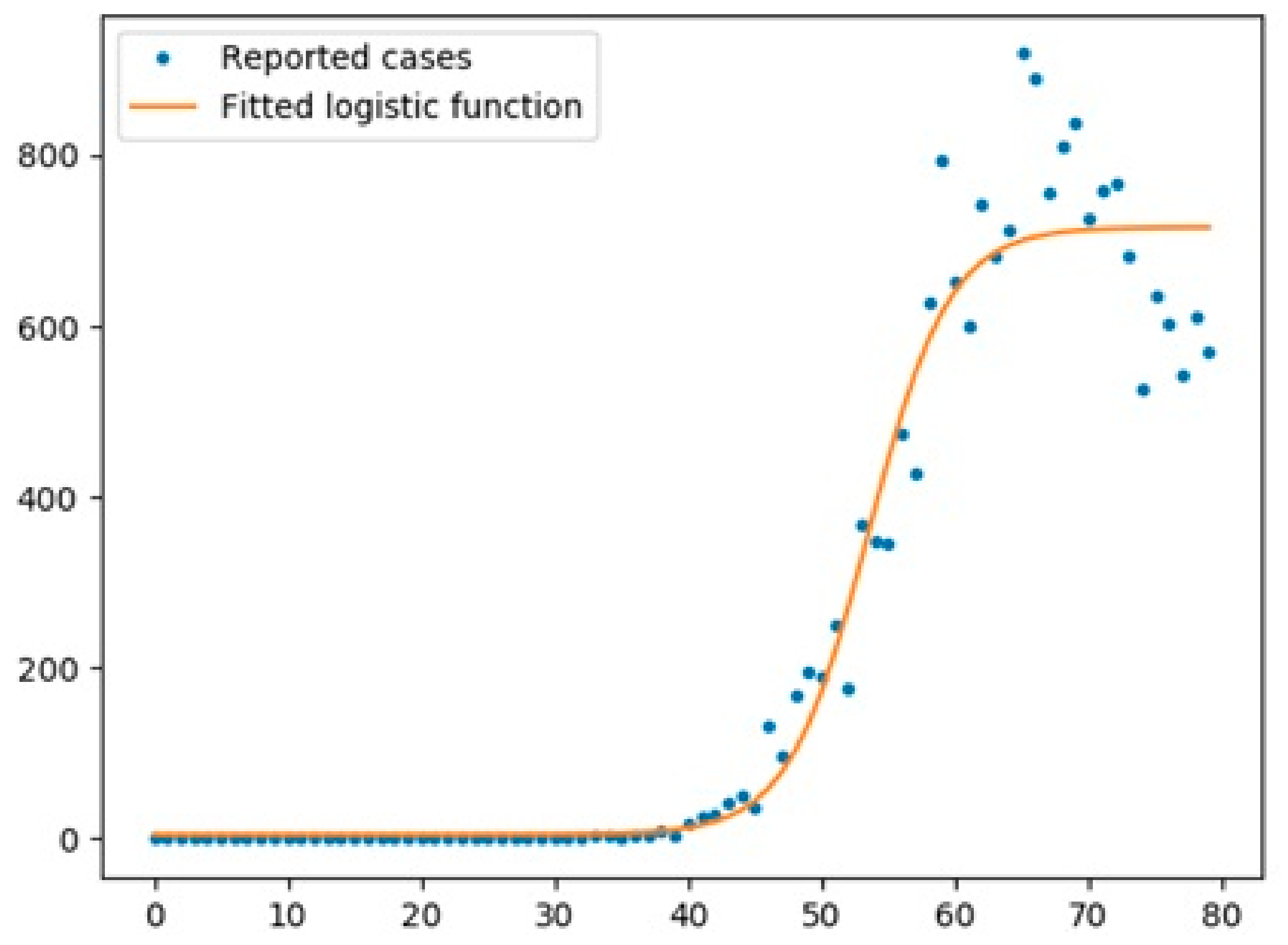
5.1. Logistic Function
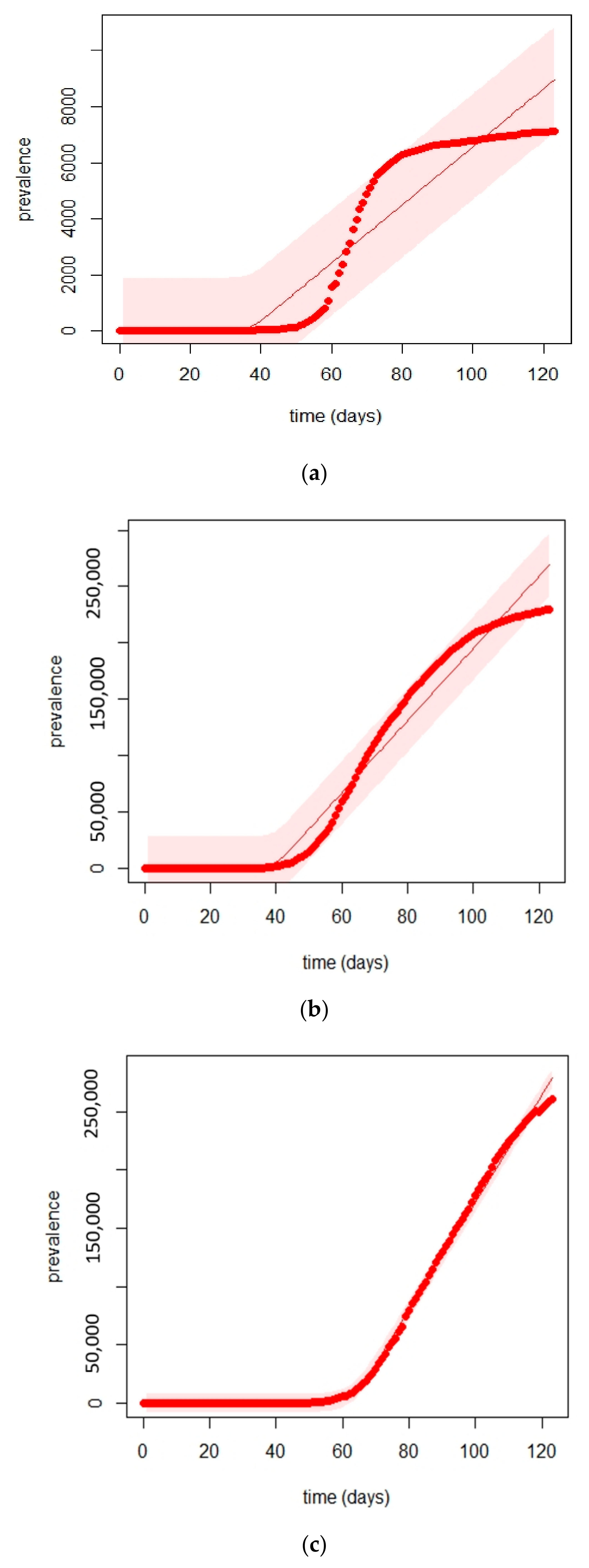
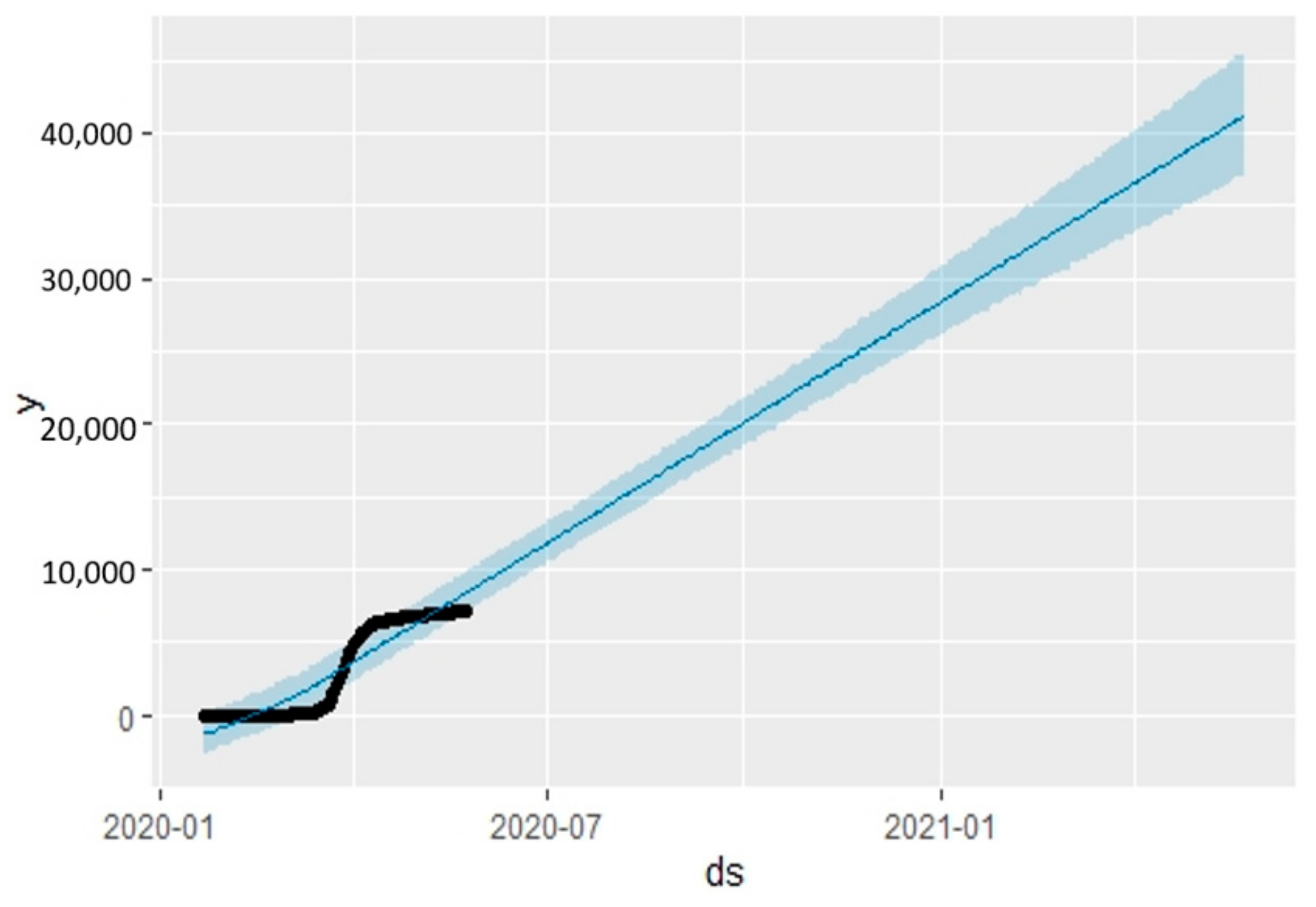
5.2. Times Series Forecasting with the Prophet Algorithm
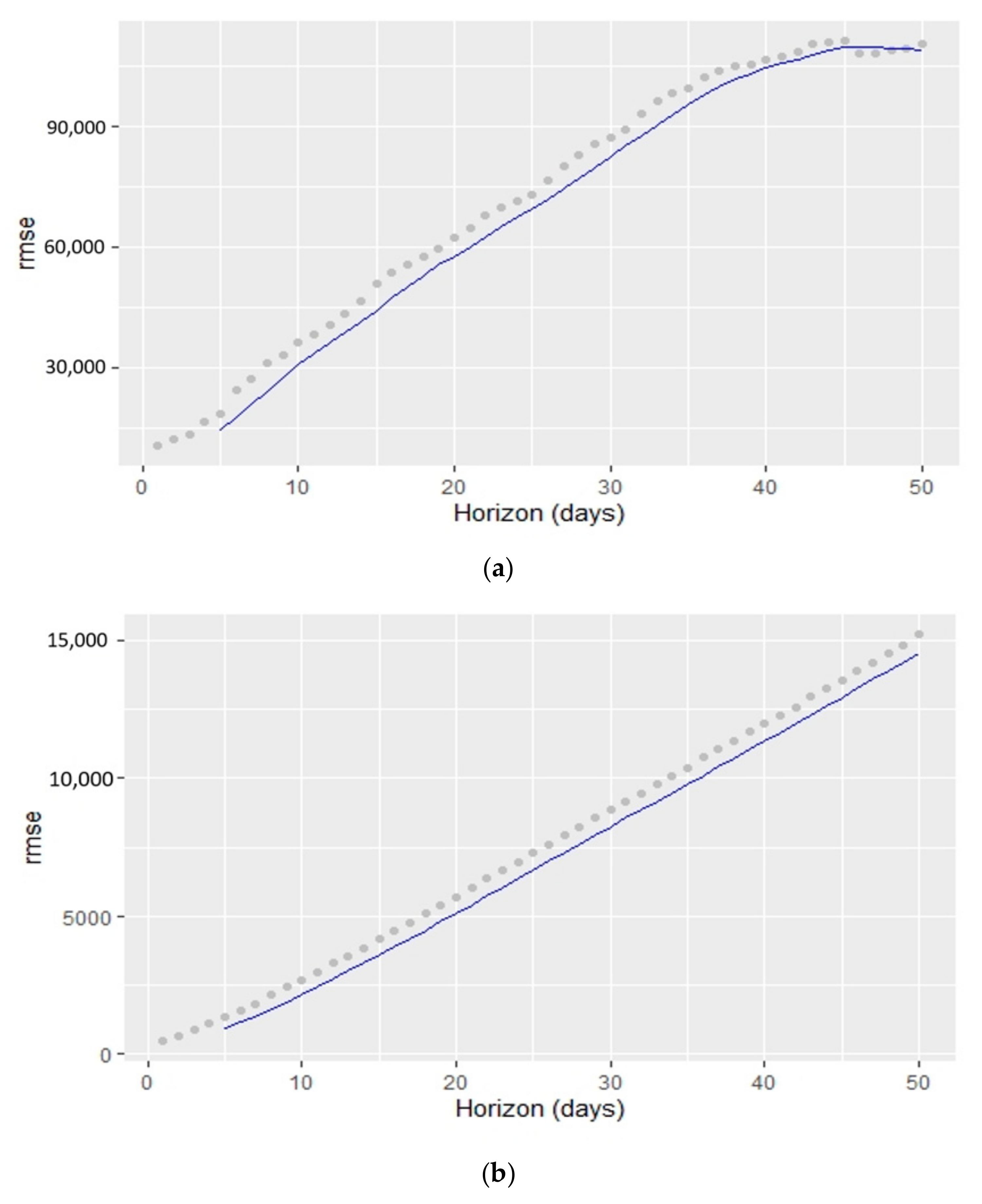
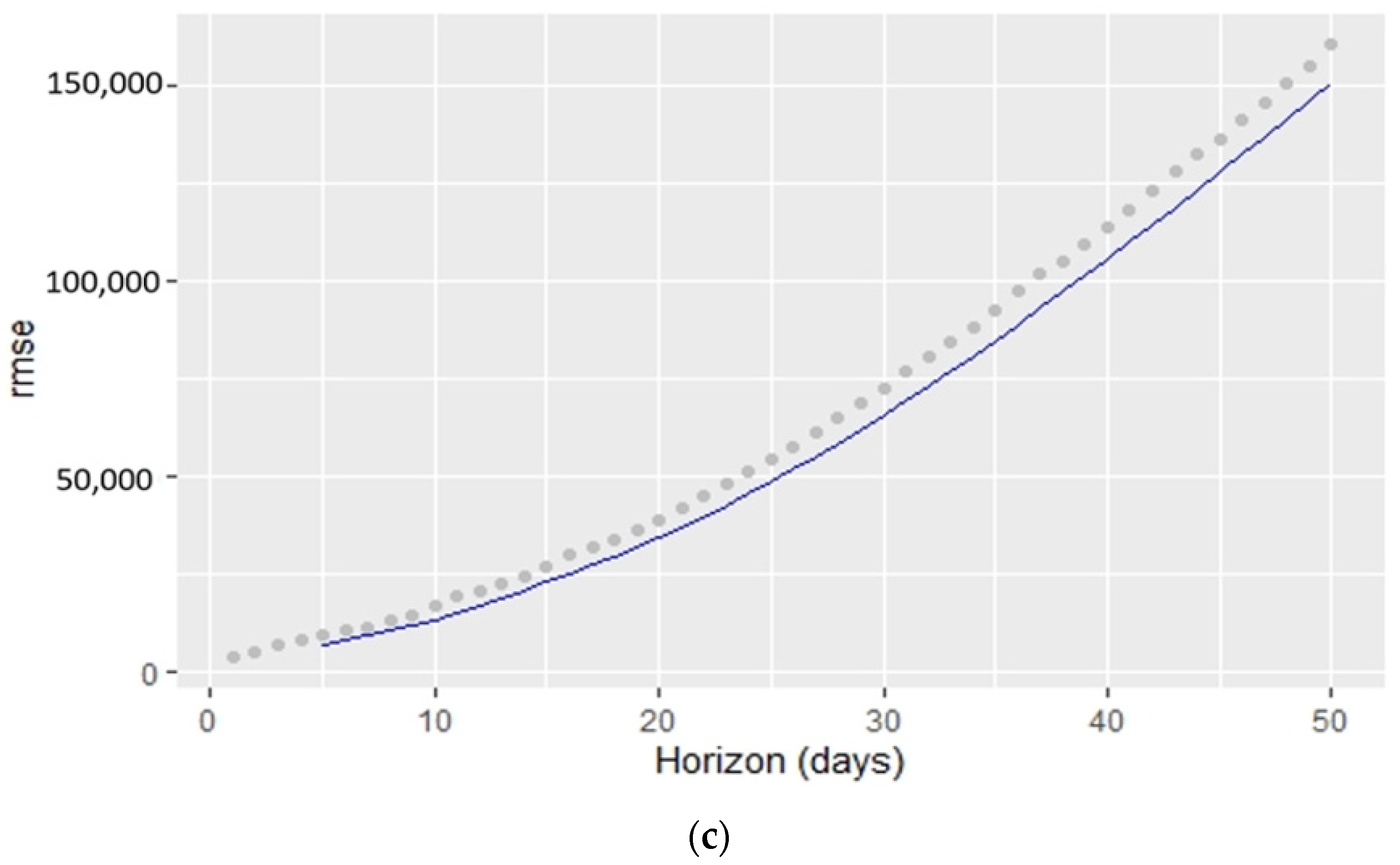
6. Results
6.1. Analysis
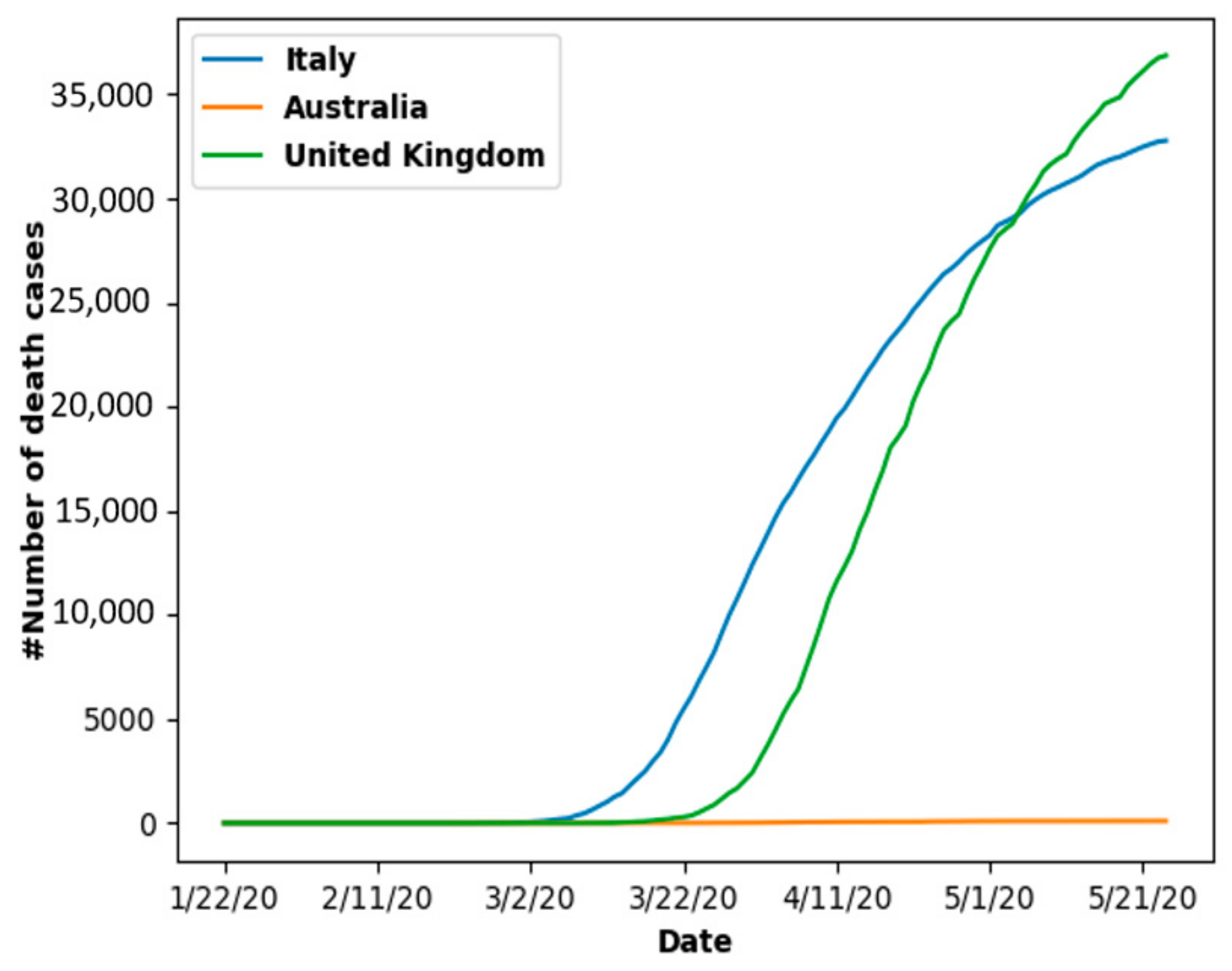
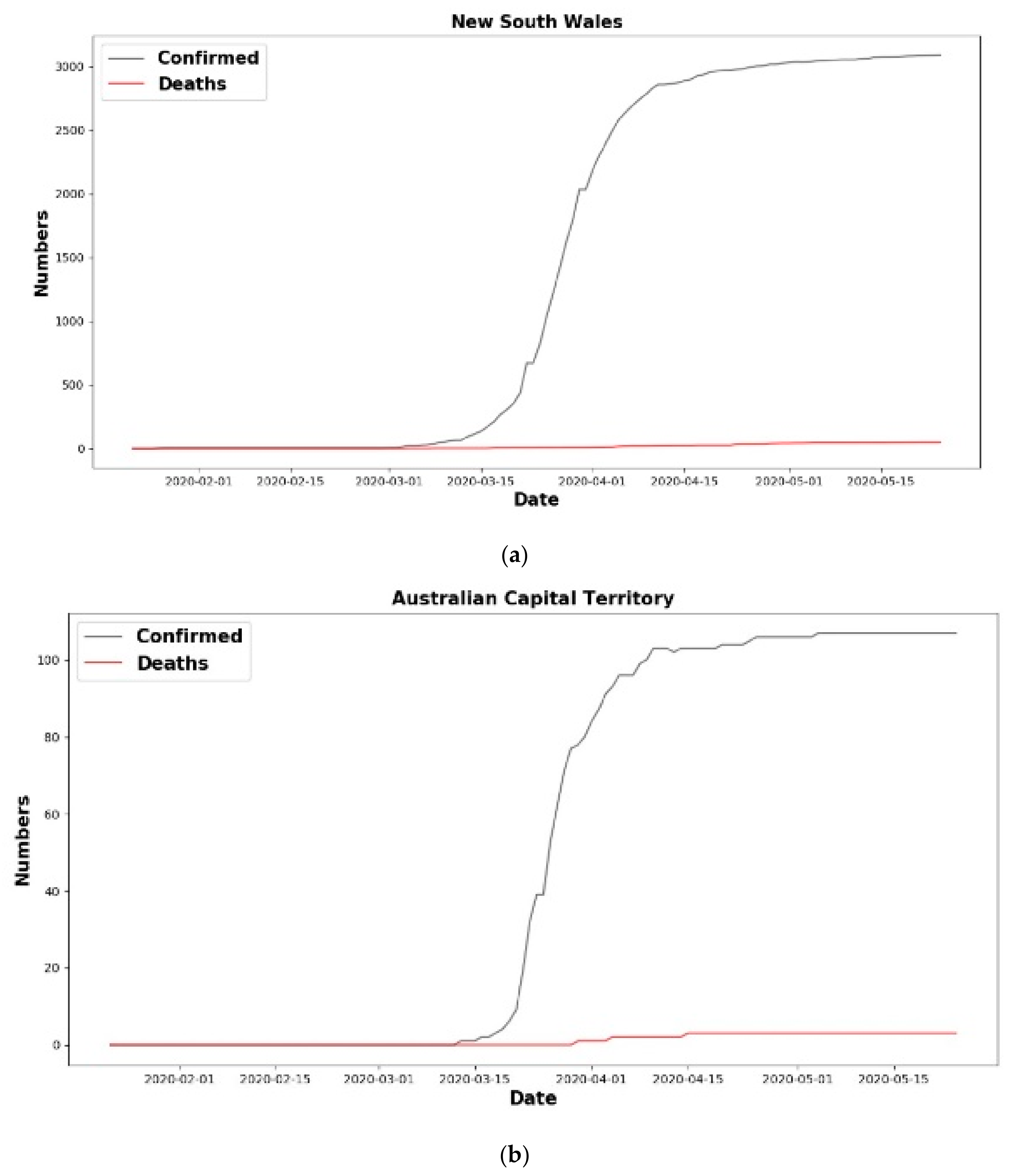
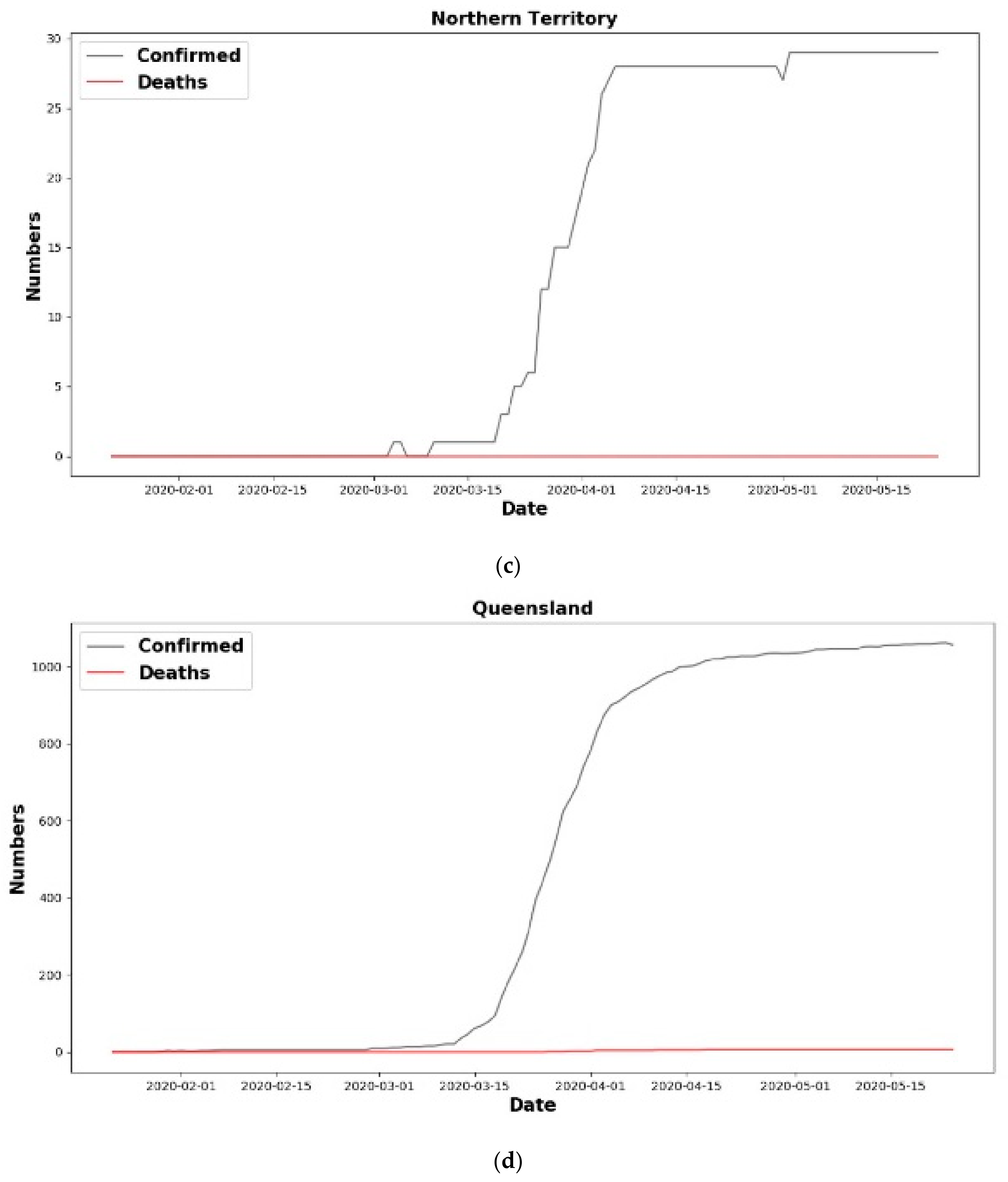
6.1.1. New Cases
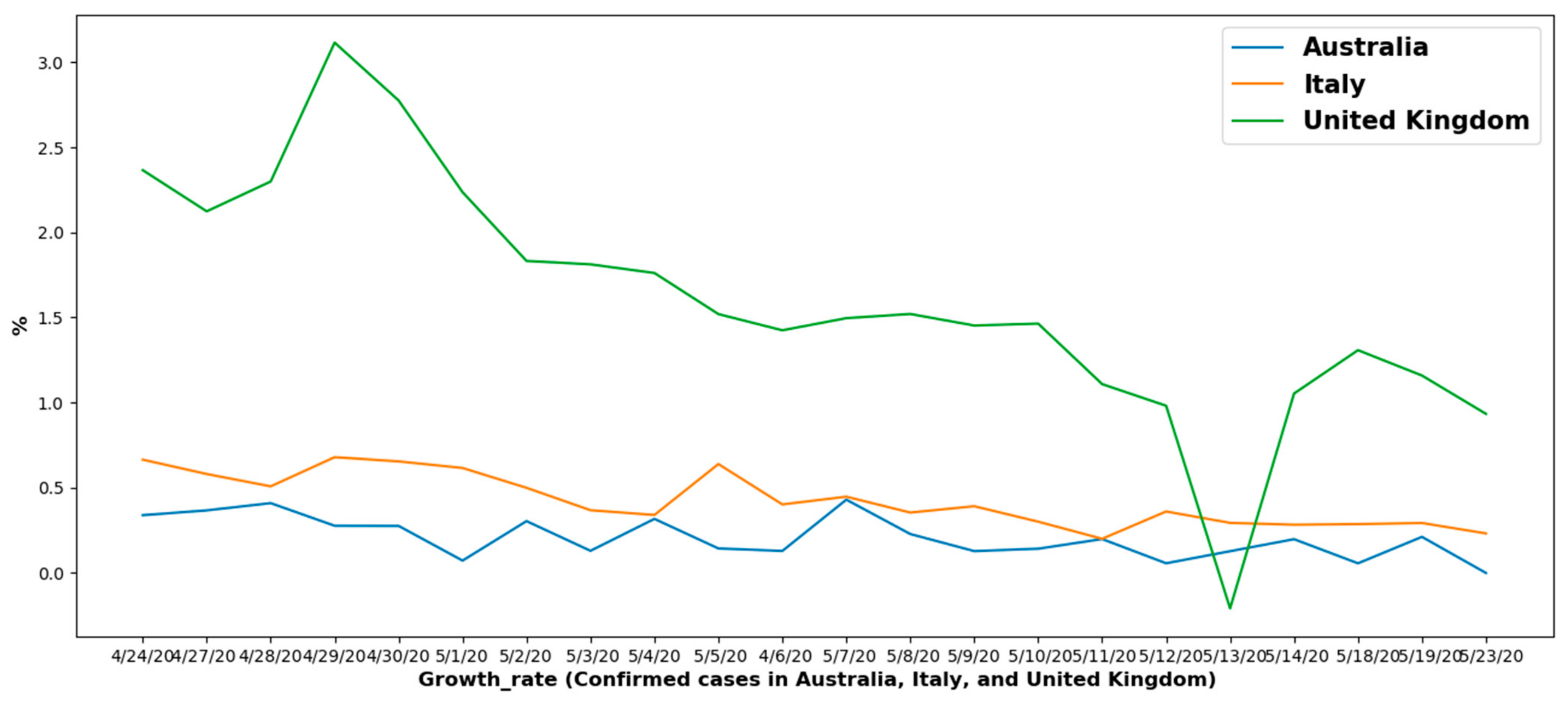
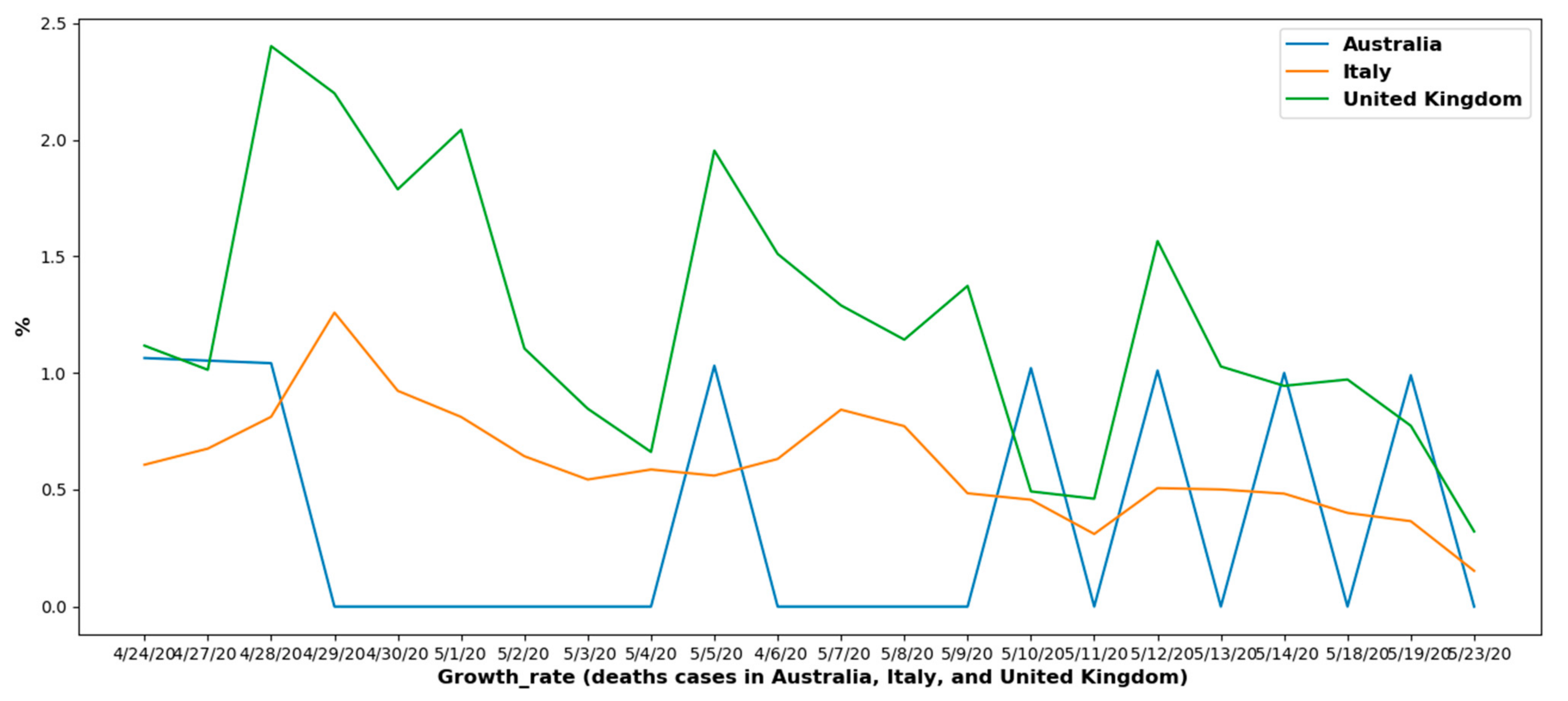
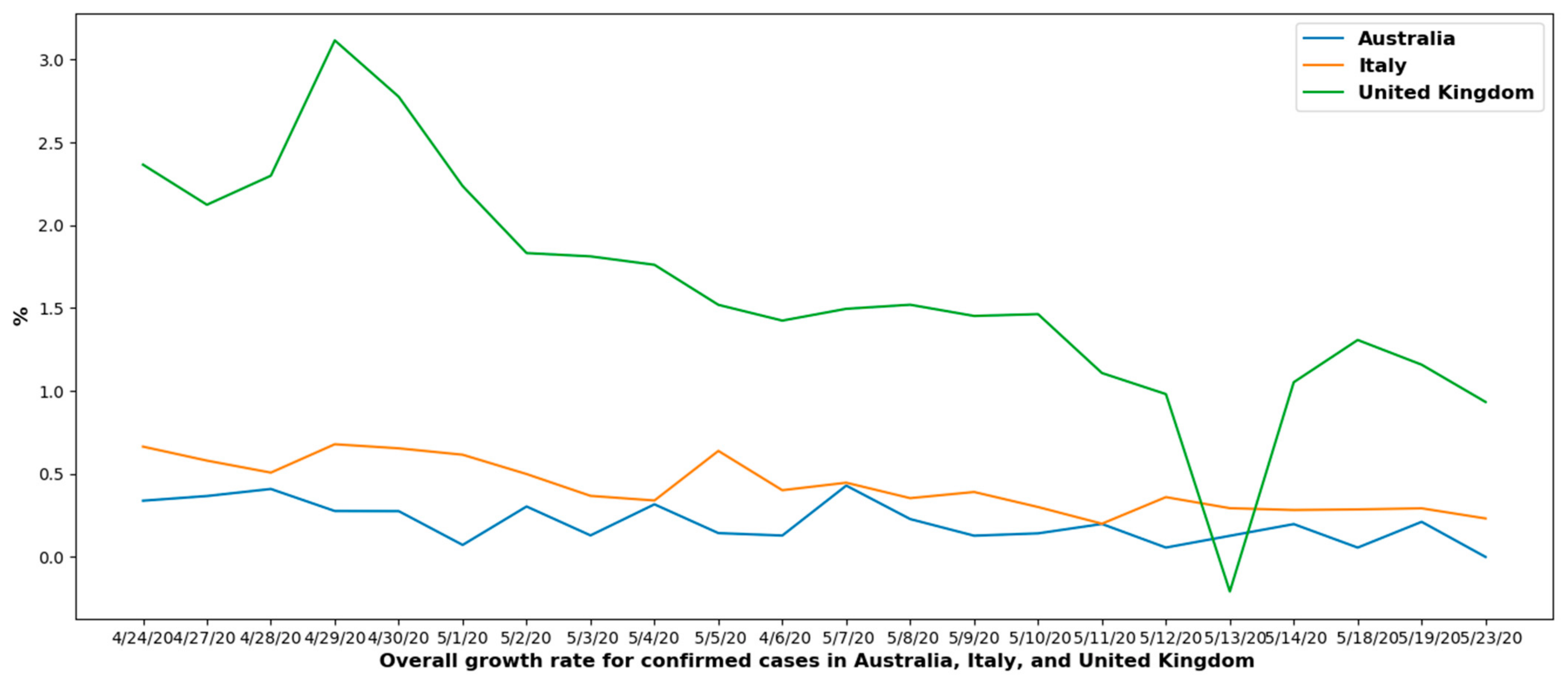
6.1.2. Overall Growth Rate
7. Discussion and Conclusions
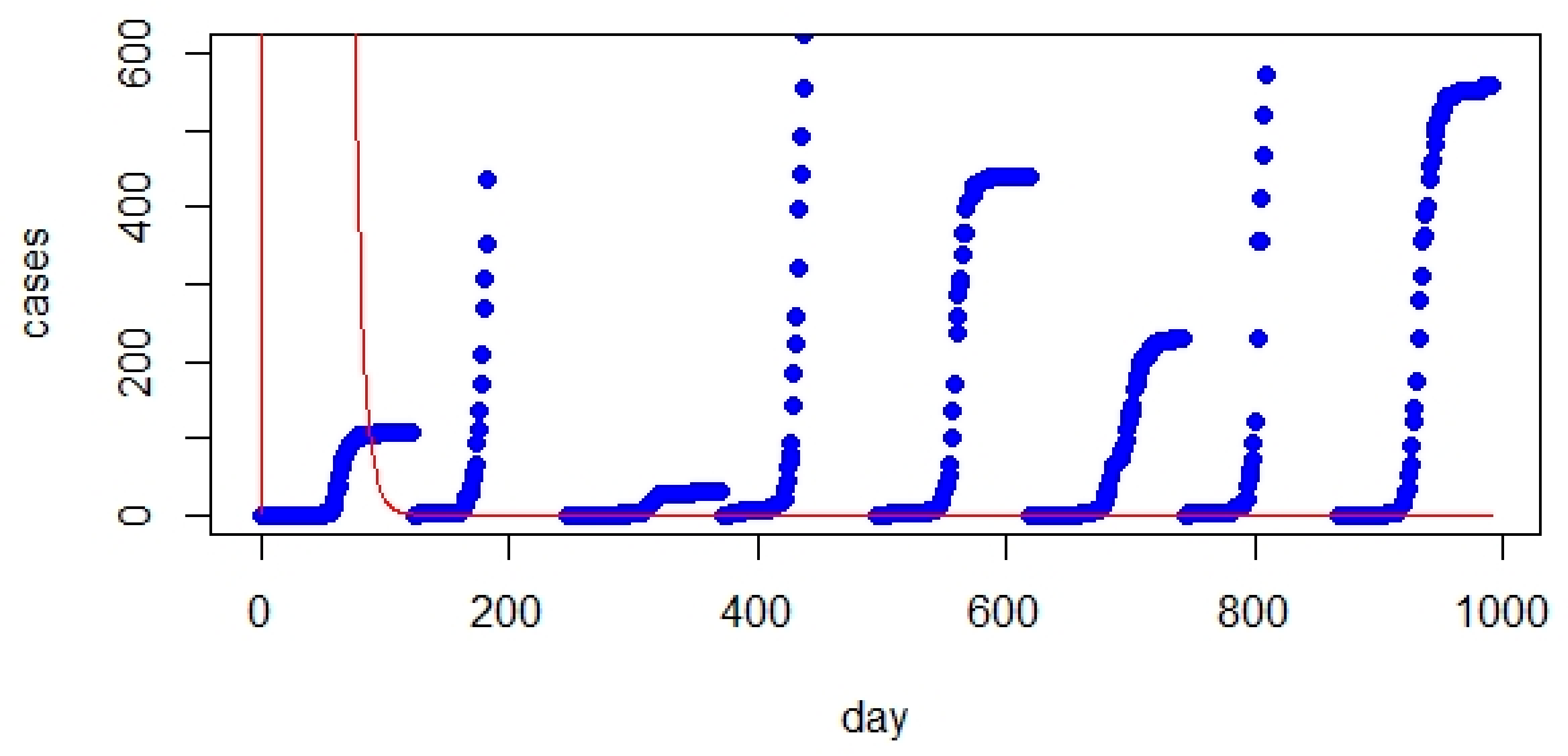
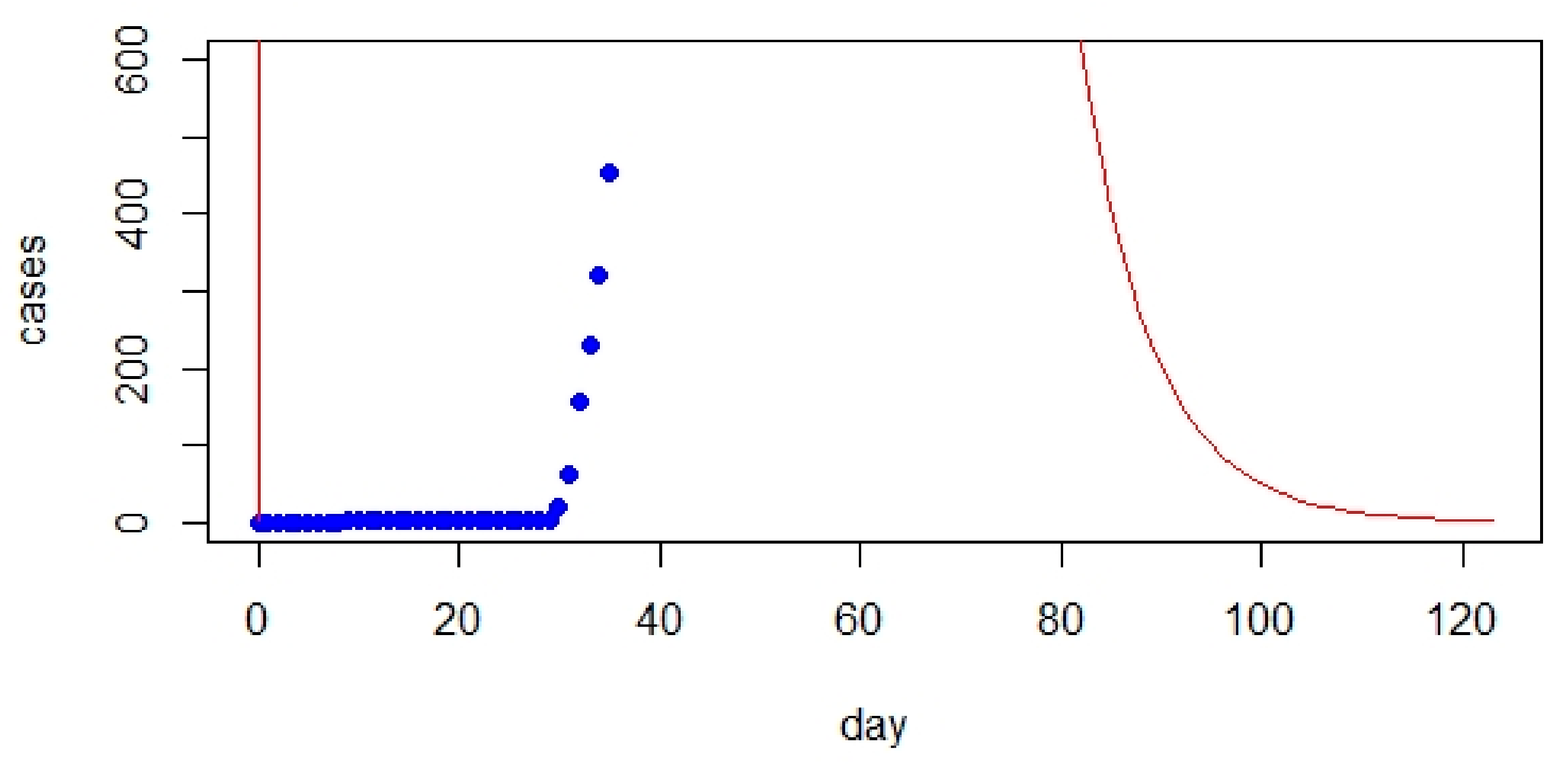
- The comparison between the classic SIR model and real data showed a significant gap. However, initializing the parameters of the SIR model significantly improved the prediction.
- The classic SIR model worked best for UK but was not suitable for Australia based on RMSE values.
- The logistic function was a good model for UK with an R2 score of 0.97, while the scores for Australia and Italy were 0.67 and 0.95, respectively.
- The best RMSE value belonged to the Australian cases (confirmed and deaths).
- Parameter optimization for the SIR and SEIQR models significantly improved their prediction accuracy.
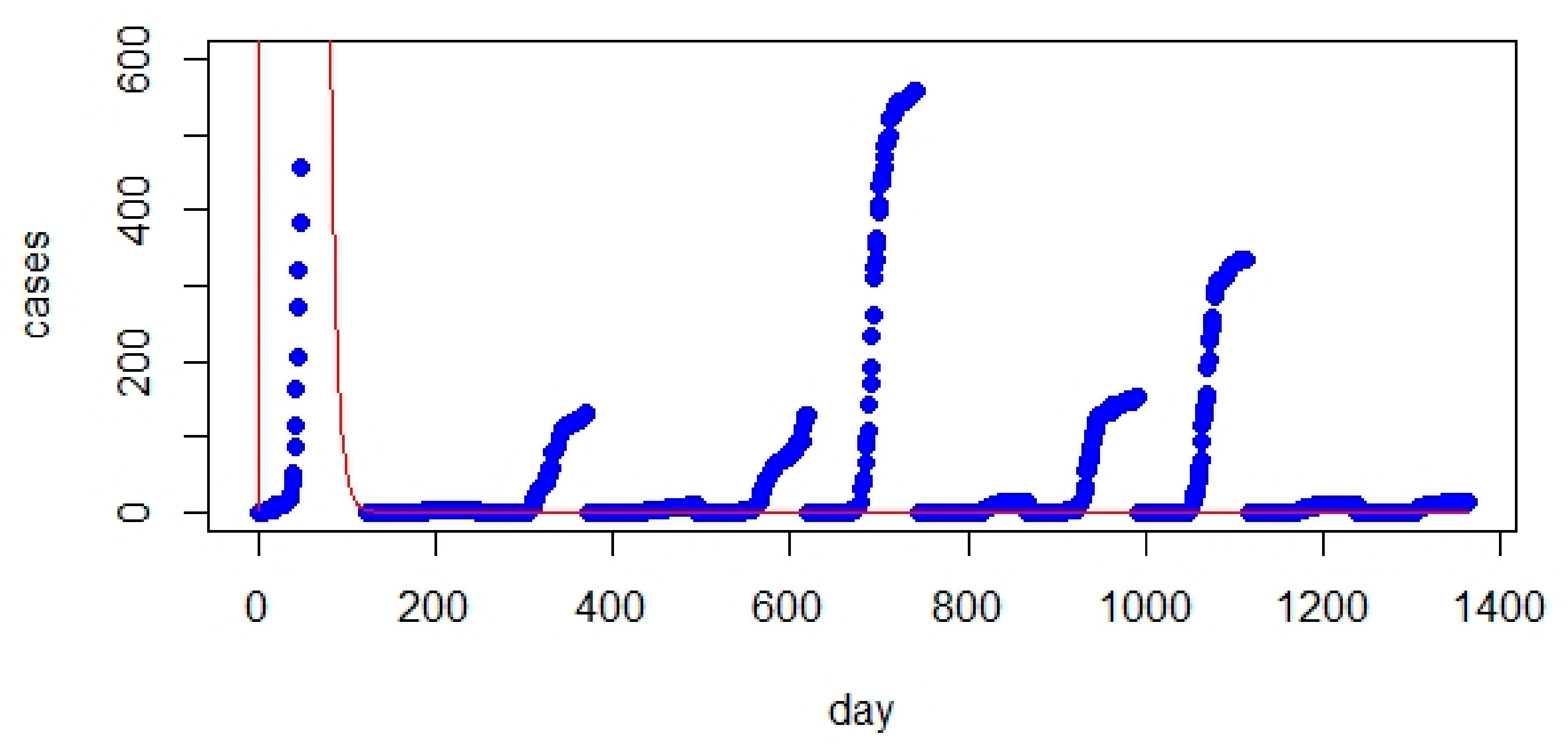
- The improved version of SEIQR exhibited better performance than the SIR model (regarding RMSE values and figures).
- The optimized SEIQR model has better prediction for UK and Italy compared with Australia.
- The best values for the parameters were determined using the Nelder–Mead algorithm for the SIR model and the L-BFGS-B algorithm for the SEIQR model.
- The Prophet algorithm worked better for Italy and UK cases than for Australian cases.
- The logistic function had a better performance for cases in all three countries compared with the Prophet algorithm.
- The improved versions of the SIR and SEIQR models exhibited a better performance than the logistic function, Prophet algorithm, and classic SIR model.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aràndiga, F.; Baeza, A.; Cordero-Carrión, I.; Donat, R.; Martí, M.C.; Mulet, P.; Yanez, D.F. A Spatial-Temporal Model for the Evolution of the COVID-19 Pandemic in Spain Including Mobility. Mathematics 2020, 8, 1677. [Google Scholar] [CrossRef]
- Putra, S.; Mu’tamar, Z.K. Estimation of Parameters in the SIR Epidemic Model Using Particle Swarm Optimization. Am. J. Math. Comput. Model. 2019, 4, 83–93. [Google Scholar] [CrossRef]
- Mbuvha, R.R.; Marwala, T. On Data-Driven Management of the COVID-19 Outbreak in South Africa. medRxiv 2020. [Google Scholar] [CrossRef]
- Qi, H.; Xiao, S.; Shi, R.; Ward, M.P.; Chen, Y.; Tu, W.; Su, Q.; Wang, W.; Wang, X.; Zhang, Z. COVID-19 transmission in Mainland China is associated with temperature and humidity: A time-series analysis. Sci. Total Environ. 2020, 728, 138778. [Google Scholar] [CrossRef]
- Asteris, P.G.; Douvika, M.G.; Karamani, C.A.; Skentou, A.D.; Chlichlia, K.; Cavaleri, L.; Daras, T.; Armaghani, D.J.; Zaoutis, T.E. A Novel Heuristic Algorithm for the Modeling and Risk Assessment of the COVID-19 Pandemic Phenomenon. Comput. Model. Eng. Sci. 2020, 125, 815–828. [Google Scholar] [CrossRef]
- Salgotra, R.; Gandomi, M.; Gandomi, A.H. Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming. Chaos Solitons Fractals 2020, 138, 109945. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2021, 1–11. [Google Scholar] [CrossRef]
- Reno, C.; Lenzi, J.; Navarra, A.; Barelli, E.; Gori, D.; Lanza, A.; Valentini, R.; Tang, B.; Fantini, M.P. Forecasting COVID-19-Associated Hospitalizations under Different Levels of Social Distancing in Lombardy and Emilia-Romagna, Northern Italy: Results from an Extended SEIR Compartmental Model. J. Clin. Med. 2020, 9, 1492. [Google Scholar] [CrossRef] [PubMed]
- Santosh, K.C. COVID-19 Prediction Models and Unexploited Data. J. Med. Syst. 2020, 44, 1–4. [Google Scholar] [CrossRef]
- Putra, M.; Kesavan, M.M.; Brackney, K.; Hackney, D.N.; Roosa, M.K.M. Forecasting the impact of coronavirus disease during delivery hospitalization: An aid for resource utilization. Am. J. Obstet. Gynecol. MFM 2020, 2, 100127. [Google Scholar] [CrossRef] [PubMed]
- Nabi, K.N. Forecasting COVID-19 pandemic: A data-driven analysis. Chaos Solitons Fractals 2020, 139, 110046. [Google Scholar] [CrossRef]
- Fenga, L. Forecasting the COVID-19 Diffusion in Italy and the Related Occupancy of Intensive Care Units. J. Probab. Stat. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Gaglione, D.; Braca, P.; Millefiori, L.M.; Soldi, G.; Forti, N.; Marano, S.; Willett, P.K.; Pattipati, K.R. Adaptive Bayesian Learning and Forecasting of Epidemic Evolution—Data Analysis of the COVID-19 Outbreak. IEEE Access 2020, 8, 175244–175264. [Google Scholar] [CrossRef]
- Berta, P.; Lovaglio, P.G.; Paruolo, P.; Verzillo, S. Real Time Forecasting of Covid-19 Intensive Care Units Demand; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Dean, N.E.; Piontti, A.P.Y.; Madewell, Z.J.; Cummings, D.A.; Hitchings, M.D.; Joshi, K.; Kahn, R.; Vespignani, A.; Halloran, M.E.; Longini, I.M. Ensemble forecast modeling for the design of COVID-19 vaccine efficacy trials. Vaccine 2020, 38, 7213–7216. [Google Scholar] [CrossRef]
- Kane, P.B.; Moyer, H.; MacPherson, A.; Papenburg, J.; Ward, B.J.; Broomell, S.B.; Kimmelman, J. Expert Forecasts of COVID-19 Vaccine Development Timelines. J. Gen. Intern. Med. 2020, 35, 3753–3755. [Google Scholar] [CrossRef]
- Keeling, M.J.; Hill, E.M.; Gorsich, E.E.; Penman, B.; Guyver-Fletcher, G.; Holmes, A.; Leng, T.; McKimm, H.; Tamborrino, M.; Dyson, L.; et al. Predictions of COVID-19 dynamics in the UK: Short-term forecasting and analysis of potential exit strategies. PLoS Comput. Biol. 2021, 17, e1008619. [Google Scholar] [CrossRef] [PubMed]
- Brand, S.P.C.; Aziza, R.; Kombe, I.K.; Agoti, C.N.; Hilton, J.; Rock, K.S.; Parisi, A.; Nokes, D.J.; Keeling, M.J.; Barasa, E.W. Forecasting the scale of the COVID-19 epidemic in Kenya. MedRxiv 2020. [Google Scholar] [CrossRef]
- Massonnaud, C.; Roux, J.; Crépey, P. COVID-19: Forecasting short term hospital needs in France. medrxiv 2020. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics—II. The problem of endemicity. Bull. Math. Biol. 1991, 53, 57–87. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Weiss, H.H. The SIR model and the foundations of public health. Mater. Mat. 2013, 2013, 1–17. [Google Scholar]
- Peng, L.; Yang, W.; Zhang, D.; Zhuge, C.; Hong, L. Epidemic analysis of COVID-19 in China by dynamical modeling. arXiv 2020, arXiv:2002.06563. [Google Scholar]
- Mitchell, T.M. Machine learning and data mining. Commun. ACM 1999, 42, 30–36. [Google Scholar] [CrossRef]
- Arkes, H.R. Overconfidence in Judgmental Forecasting. In Harvey J. Greenberg; Springer International Publishing: Berlin/Heidelberg, Germany, 2001; pp. 495–515. [Google Scholar]
- Armstrong, J.S. Standards and Practices for Forecasting. In Harvey J. Greenberg; Springer International Publishing: Berlin/Heidelberg, Germany, 2001; pp. 679–732. [Google Scholar]
- Maleki, M.; Mahmoudi, M.R.; Wraith, D.; Pho, K.-H. Time series modelling to forecast the confirmed and recovered cases of COVID-19. Travel Med. Infect. Dis. 2020, 37, 101742. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Ndiaye, B.M.; Tendeng, L.; Seck, D. Analysis of the COVID-19 pandemic by SIR model and machine learning technics for forecasting. arXiv 2020, arXiv:2004.01574v1. [Google Scholar]
- Chambers, L.G.; Fletcher, R. Practical Methods of Optimization. Math. Gaz. 2001, 85, 562. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Merow, C.; Urban, M.C. Seasonality and uncertainty in global COVID-19 growth rates. Proc. Natl. Acad. Sci. USA 2020, 117, 27456–27464. [Google Scholar] [CrossRef] [PubMed]
- Kindler, O.; Pulkkinen, O.; Cherstvy, A.G.; Metzler, R. Burst statistics in an early biofilm quorum sensing model: The role of spatial colony-growth heterogeneity. Sci. Rep. 2019, 9, 1–19. [Google Scholar] [CrossRef] [PubMed]

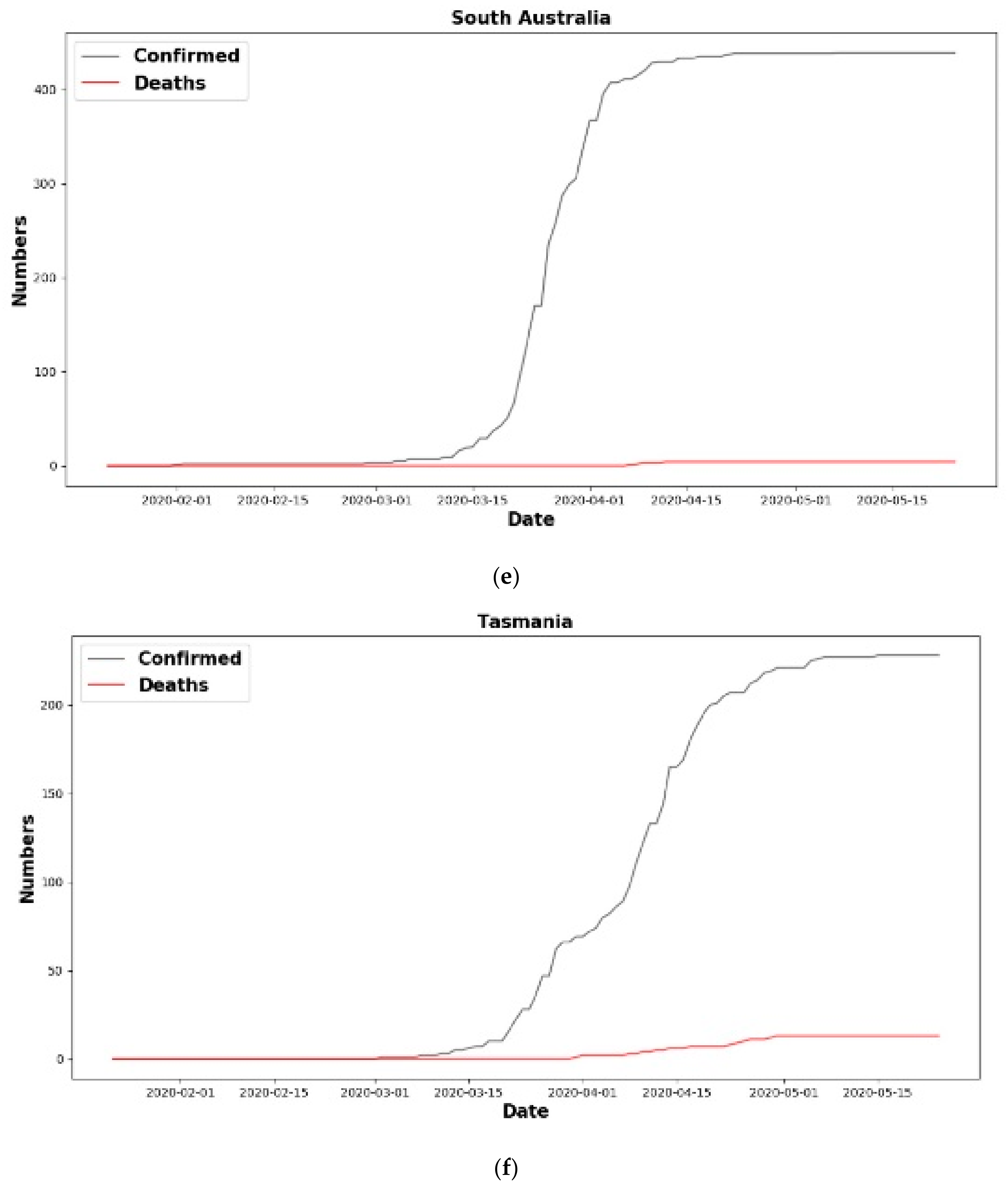
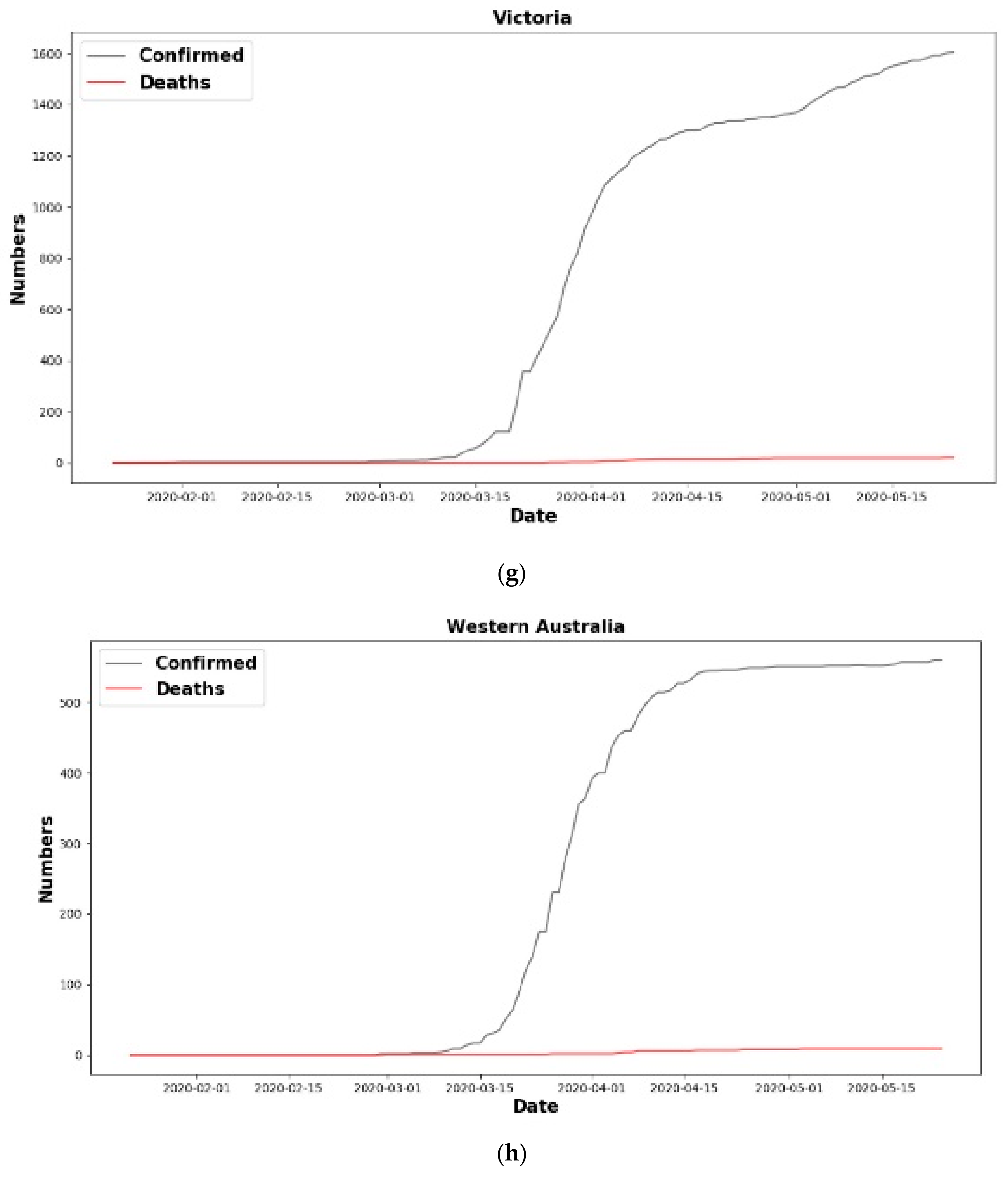

| Country | Confirmed Cases | Death Cases |
|---|---|---|
| Australia | 0.87 | 0.67 |
| UK | 0.92 | 0.97 |
| Italy | 0.93 | 0.95 |
| Country | Confirmed Cases | Death Cases |
|---|---|---|
| Australia | 8.22 | 0.88 |
| UK | 21.94 | 6.97 |
| Italy | 23.24 | 8.00 |
| Italy | UK | Australia |
|---|---|---|
| 18.75 | 15.45 | 831.84 |
| Algorithm | Parameter Setting |
|---|---|
| BFGS | Maxit = 100, reltol * = 10−8 |
| Nelder–Mead | Maxit = 500, reltol = 10−8, alpha = 1, beta = 0.5, gamma = 2.0 |
| L-BFGS-B | Maxit = 100, reltol = 10−8, lmm ** = 5, factr *** = 107 |
| CG | Maxit = 100, reltol = 10−8 |
| Country | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | BFGS | Nelder–Mead | L-BFGS-B | CG | BFGS | Nelder–Mead | L-BFGS-B | CG | BFGS | Nelder–Mead | L-BFGS-B | CG |
| Australia | 0.014 | 0.014 | 0.378 | 0.37 | 0.22 | 0.22 | 0.14 | 0.14 | 0.063 | 0.063 | 2.64 | 2.64 |
| UK | 0.37 | 3.84701−3 | 0.37 | 0.37 | 0.14 | 1.94−1 | 0.14 | 0.14 | 2.64 | 0.02 | 2.64 | 2.64 |
| Italy | 0.37 | 1.083555−3 | 0.37 | 0.37 | 0.14 | 3.9088−1 | 0.14 | 0.37 | 2.64 | 0.01 | 2.64 | 2.64 |
| Model | Italy | UK | Australia |
|---|---|---|---|
| SIR model | 1.41 | 1.01 | 1.13 |
| SEIR model | 1.12 | 1.23 | 1.04 |
| y | ds | Cutoff | |||
|---|---|---|---|---|---|
| 7095 | 21 May 2020 | 21,309.752 | 18,998.140 | 23,829.955 | 4 April 2020 |
| 7099 | 22 May 2020 | 21,630.708 | 19,245.072 | 24,269.904 | 4 April 2020 |
| 7114 | 23 May 2020 | 21,959.985 | 19,424.097 | 24,640.939 | 4 April 2020 |
| 7114 | 24 May 2020 | 22,326.688 | 19,766.194 | 25,093.353 | 4 April 2020 |
| y | ds | Cutoff | |||
|---|---|---|---|---|---|
| 252,246 | 21 May 2020 | 143,776.53 | 126,702.28 | 162,413.93 | 4 April 2020 |
| 255,544 | 22 May 2020 | 146,462.83 | 128,526.68 | 165,539.80 | 4 April 2020 |
| 258,504 | 23 May 2020 | 148,818.88 | 130,813.85 | 168,216.41 | 4 April 2020 |
| 260,916 | 24 May 2020 | 150,344.39 | 131,476.87 | 170,004.00 | 4 April 2020 |
| y | ds | Cutoff | |||
|---|---|---|---|---|---|
| 228,006 | 21 May 2020 | 373,982.5 | 336,940.1 | 415,612.7 | 4 April 2020 |
| 228,658 | 22 May 2020 | 379,300.7 | 340,862.6 | 422,338.4 | 4 April 2020 |
| 229,327 | 23 May 2020 | 384,792.4 | 344,957.8 | 429,120.3 | 4 April 2020 |
| 229,858 | 24 May 2020 | 390,481.8 | 349,482.8 | 436,663.2 | 4 April 2020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahimi, I.; Gandomi, A.H.; Asteris, P.G.; Chen, F. Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases. Information 2021, 12, 109. https://doi.org/10.3390/info12030109
Rahimi I, Gandomi AH, Asteris PG, Chen F. Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases. Information. 2021; 12(3):109. https://doi.org/10.3390/info12030109
Chicago/Turabian StyleRahimi, Iman, Amir H. Gandomi, Panagiotis G. Asteris, and Fang Chen. 2021. "Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases" Information 12, no. 3: 109. https://doi.org/10.3390/info12030109
APA StyleRahimi, I., Gandomi, A. H., Asteris, P. G., & Chen, F. (2021). Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models: Australia, Italy, and UK Cases. Information, 12(3), 109. https://doi.org/10.3390/info12030109









