Abstract
The internet of things (IoT) devices are expected to collect vast amounts of data that support different kinds of applications such as health monitor, smart home, and traffic management. However, its characteristics such as resource-constrained nature, dynamicity, and large-scale growth bring challenges to secure IoT data sharing. Nowadays, blockchain-based ciphertext-policy attribute-based encryption (CP-ABE) was proposed to realize secure IoT data sharing. In blockchain-based CP-ABE data sharing schemes, the data are encrypted and stored in the cloud. Once users want to process the data, they should download and then decrypt the ciphertext in the client-end, and after processing the data, users encrypt and upload the ciphertext onto the cloud. This outweighs the advantage of using cloud computing resources. Fully homomorphic encryption (FHE) and homomorphic signature technology may be adopted to realize ciphertext computation and for correctness checking of ciphertext computation results. In this paper, we propose a secure and computable IoT data sharing system to ensure users enjoying the computation convenience of the cloud-end. Specifically, the proposed system integrates CP-ABE and FHE to realize secure IoT data sharing and ciphertext computation. In addition, we generated homomorphic signatures of ciphertexts to enable users to check the correctness of the ciphertext computation results. Moreover, to supervise the cloud, providing the honest IoT data access control, storage, and computing services for users, we recorded the access policy of the data, the hash of the data, the signature of the ciphertext, and the homomorphic signature of the ciphertext on the blockchain. The performance evaluation and security analysis show the proposed scheme is practical and secure.
1. Introduction
The internet of things (IoT) is one of the most promising technologies in recent years. It is a distributed system equipped with IoT devices, such as sensors and actuators. According to the forecast, more than 8.4 billion connected IoT devices joined the network in 2017, and will reach 20.4 billion by 2020 [1]. IoT devices are expected to collect and exchange vast amounts of data, which can be useful for different stakeholders. Many challenges arise when organizing the IoT data sharing, because the resource-constrained IoT devices cannot process the data securely and efficiently.
Currently, the cloud-edge-collaborative (CEC) framework is widely used in IoT data processing [2]. In the framework, edge servers act as intermediaries between IoT devices and the cloud and allow IoT devices to share data with low latency, while the cloud with unlimited storage capability stores the IoT data [3]. However, sharing IoT data in CEC suffers from the risk of data tampering, data leakage, and ungranted access. Hence, secure data sharing in CEC is capturing increasing attention. The simplest and most direct approach to solve these problems is to encrypt the IoT data with other users’ public keys. However, this is inefficient and cannot support fine-grained access control for IoT data sharing [4,5,6,7,8,9].
Ciphertext-policy attribute-based encryption (CP-ABE) [10,11,12] is a public-key encryption technology for fine-grained access control and data sharing. In CP-ABE schemes, the private key of users is associated with their own attributes, and the data owner specifies the access policy for the ciphertext. A user could decrypt the ciphertext, only when his/her attributes of private key satisfy the access policy of the ciphertext. There are many data sharing approaches based on CP-ABE, these schemes upload access policy and encrypted data onto the cloud, thus the cloud is the single-server that grants users access to data. However, the cloud may tamper with the encrypted data or deny granted users from accessing data. Therefore, blockchain-based CP-ABE schemes are proposed. These schemes store the access policy in the blockchain [13,14], and due to the blockchain’s openness characteristics, users can verify whether their attributes are satisfied with the ciphertext’s access policy independently. Thus, the cloud cannot deny authorized users access to the data.
The blockchain-based CP-ABE scheme ensures the security of IoT data sharing. However, when users process the data, they should download and decrypt the ciphertext, and then process the data at the client-end, which wastes cloud computing resources. The fully homomorphic encryption (FHE) is known as a mechanism for computing encrypted data without decrypting it. For example, Alice encrypts the plaintexts with FHE and uploads her ciphertexts onto the cloud. When Alice wants to compute , she only needs to send the computation function to the cloud. Once the cloud receives , it calculates and returns c to Alice. Finally, Alice decrypts c with her private key to get . In a homomorphic encryption scheme, ciphertexts are stored on and calculated by the cloud. As a third party, the cloud server is not fully trusted because it may return incorrect ciphertext, , or ciphertext calculation result, c, to users.
Homomorphic signature schemes are designed to verify the correctness of outsourcing computation to address the problem [15] mentioned above. However, the homomorphic signature is a kind of data or information, and it also faces the risk of information tampering.
To get better use advantages of FHE and homomorphic signature, we also record the hash of IoT data and the homomorphic signature of the ciphertext on the blockchain. The openness and non-tampering characteristics of blockchain enable it to act as a supervisor to confirm whether the cloud is storing and calculating ciphertext correctly.
To sum up, we extend the blockchain-based CP-ABE scheme to realize ciphertext computation by combining FHE and CP-ABE algorithms. In our proposed system, the blockchain-based CP-ABE scheme enjoys the computation convenience of the cloud server. To avoid the cloud tampering with the ciphertexts and providing incorrect ciphertext calculation results, we generated the homomorphic signatures of ciphertexts and uploaded the hash of the data and the homomorphic signature of the ciphertext onto the blockchain. Our contributions are as follows:
- (1)
- We construct a computable IoT data sharing system based on FHE and CP-ABE. In the system, we extended the blockchain-based CP-ABE IoT data sharing scheme to realize ciphertext computable by reconstructing its encryption algorithm and decryption algorithm based on FHE.
- (2)
- Moreover, we use the homomorphic signature algorithm to sign the ciphertext, realizing the computation result verifiable. Thus, the cloud cannot return the incorrect ciphertext calculation results for users.
- (3)
- Finally, we upload the access policy of data, the hash of data, the signature of ciphertext, and the homomorphic signature of ciphertext onto the blockchain. Due to the openness characteristics of the blockchain, users can get the access policy of IoT data to verify whether they are the authorized ones to access the data. Thus, the cloud cannot deny authorized users’ access requests. In addition, the non-tampering characteristics of blockchain guarantee that users get the integrity hash, signature of IoT data, and homomorphic signature of ciphertext to verify the correctness of the ciphertext and ciphertext computation result returned from the cloud.
The remainder of this paper is organized as follows: The background and related works are introduced in Section 2. Section 3 introduces the proposed scheme, security assumptions, and security goals. The design detail of the proposed scheme is described in Section 4. Section 5 and Section 6 describe the security and evaluation of our scheme. Finally, Section 7 gives the conclusion of this paper.
2. Background and Related Work
2.1. Blockchain
Blockchain technology got introduced as a decentralized cryptocurrency, such as Bitcoin [16]. Nowadays, the blockchain is more used as the underlying technology to provide decentralized, distributed anti-destruction, traceability, and tamper-resistant services, than as a decentralized electronic currency trading system.
Blockchain can be divided into two types: permissioned blockchain and permissionless blockchains [17]. In the permissionless blockchain network, anyone can join, quit, and obtain data at any time, and every participant is anonymous. While the permissioned blockchain needs identity authentication before users joining the blockchain network and provides a secure way for a group of entities that have a common goal, to communicate with each other. Common blockchain platforms include Bitcoin [16], Ethereum [18], EOS [19], and Hyperledger Fabric [20].
2.2. Fully Homomorphic Encryption
The fully homomorphic encryption (FHE) scheme supports arbitrary function computation on encrypted data without decrypting it. This technology enables the cloud to process the ciphertext directly, which allows users to enjoy the convenience of shared resources while ensuring the confidentiality of the data [21,22].
An FHE scheme consists of four parts: KeyGen, Encrypt, Decrypt, and Evaluate. Consider the messages , which are encrypted to the ciphertext , where , . Given a computable function, , anyone could compute the ciphertext that decrypts to .
• Ciphertext Flatten
The flatten technique modifies vectors that keep ciphertext bounded to realize leveled FHE.
Let x, y be two vectors whose dimension is k, and set , .
- -
- is a vector , where is the -th bit in . binary representation.
- -
- = .
- -
- = .
- -
- = ().
So that the following equalities to hold,
=
For any dimension vector ,
= = hold.
2.3. Ciphertext-Policy Attribute-Based Encryption
Ciphertext-policy attribute-based encryption (CP-ABE) is a type of public-key encryption and has been widely applied and employed in cloud storage systems [14,23]. In CP-ABE schemes, a user’s secret key is associated with the attributes, and ciphertext is associated with the access policy. Thus, a user can decrypt a ciphertext only if the attributes of his/her secret key match the access policies of the ciphertext. Therefore, data owners can define access policies to achieve fine-grained data sharing [24,25]. Thus, how to construct the access policy structure is the core of the CP-ABE scheme.
• Bilinear Mapping
Suppose and are two cyclic groups whose order p is prime, and the generator of is g. A bilinear map should satisfy the following properties:
- (1)
- Bilinear: For , .
- (2)
- Non-degeneracy: There exists , such that e()1.
- (3)
- Computability: For , e() could be computed easily.
• Linear secret sharing scheme
In the proposed system, we use a linear secret sharing scheme (LSSS) to define the access policy structure of the ciphertext. An LSSS scheme over with a set of parties, P is linear, if:
- (1)
- Each party shares a secret number that forms a secret vector over .
- (2)
- There exists matrix for with columns and rows. For , the M’s th row is defined as a function . Let a vector , where s is a shared secret, and each is randomly chosen. Thus, , , is the shared secret of s for . There exists , where to make holds.
2.4. Homomorphic Signature Schemes
Homomorphic signature schemes are designed to verify the correctness of outsourcing computation to address pollution attacks [15]. The cost of the computation and communication of homomorphic signature is independent of the amount of data input by the verifier, and the time complexity of the algorithm within the O(1). A homomorphic signature scheme is a polynomial-time algorithm [26] and can be described as follows:
- Setup (){sk, pk}. Suppose is a security parameter and is an integer. The algorithm output a key pair {}, where is a secret key and is the corresponding public key.
- HSign (sk, m) . The algorithm generates a signature for the message m, computed with the secret key .
- Eval (pk, , ) . The algorithm takes a public key, a computable function, and a signature tuple, as input. Then it outputs a signature, which is a result of the function, over the signature tuple, .
- Vrf (pk,, ) . The algorithm takes a public key, ; a signature, and a message, which is the result of the function, over the message tuple, as input. It outputs 1, if is valid for the message, otherwise it outputs 0.
2.5. Related Works
There are many cryptographic techniques proposed to solve the security problem in IoT applications, Saračević et al. designed a data encryption technique and key exchange model for a smart city [27,28]. To provide secure IoT data sharing, Mollah et al. [3] proposed a secure IoT data-sharing scheme based on the CEC framework that utilizes public key encryption and symmetric encryption, but the scheme supposes that the edge servers must share their data-search secret keys to retrieve the requested data for users, which causes communication overheads in practice. To address the above problem, Tao et al. [1] proposed a new CEC scheme that allows users to generate keyword search trapdoors based on the keywords and private key. However, they all assumed that the cloud server cloud does not tamper with users’ data.
While Fan et al. [13] proposed a secure and verifiable data sharing scheme to realize data sharing in VSNs. They upload the data’s access policy onto a blockchain, realizing the self-certification of users, data confidentiality, and cloud attack resistance. Wang et al. [14] proposed a framework that combines Ethereum and ABE to realize fine-grained access control of the data in IPFS. Through the decentralization, verifiability, and immutability properties of blockchain, these schemes ensure the integrity of the data stored on the server. Although ABE technology enables data owners to define the data access policy and ensure data security, the computing resource of the cloud is not utilized. It should be highlighted to provide verifiable data outsourcing computation without compromising data privacy.
Nowadays, cloud data computation privacy has become a focus of research [4,29]. FHE is one of the important technologies to ensure cloud data computing security, ciphertext retrieval, etc. The first FHE scheme was proposed by Gentry [30,31] in 2009. After Gentry’s proposition, there were several notable works on FHE over integers [32,33]. Some other works focused on improving the FHE scheme’s performance [34,35]. López-Alt et al. [36] implemented FHE on multi-party computation. Micciancio [37] and Boneh et al. [38] proposed the FHE is an important solution in the cloud computing area.
The FHE scheme ensures the privacy of data outsourcing computation, but it cannot verify the correctness of the ciphertext calculation results. In 2002, Johnson et al. [39] introduced a definition for homomorphic signatures. After that, many homomorphic signature schemes were proposed that improved efficiency, security, and privacy [40,41] of homomorphic signatures. To allow multi-private key signatures to do the homomorphic evaluation, Zhang et al. [42] added the homomorphic property to the aggregate signature schemes.
3. The Proposed System
3.1. System Architecture
The system consists of the following entities: an attribute authority (AA), IoT devices, edge servers, a cloud server, blockchain, and users.
AA is responsible for generating decryption keys as well as to evaluate keys for users. Additionally, the AA generates a public key for each IoT device.
IoT devices are data collectors that define the access policy of the data.
Edge servers are responsible for encrypting the IoT data and sending the ciphertext to the cloud. In addition, edge servers verify the correctness of the ciphertext stored on the cloud server (actually, edge servers verify the signatures signed by the cloud). All edge servers jointly maintain the blockchain. They run smart contact (described in Section 4.3.) to record the valid IoT data information on the blockchain. Moreover, during the ciphertext computation stage, edge servers run Pre-compute (described in Section 4.2) and Final-compute (described in Section 4.2.) to process the ciphertexts.
The cloud server stores the encrypted IoT data and computes ciphertexts for users. Moreover, it signs the ciphertexts via a signature algorithm (such as ECDSA) and a homomorphic signature algorithm separately.
The blockchain records the hash of the data, the cloud server’s signatures, and the access policy of the data.
Users are data and computation requesters.
As shown in Figure 1, the description of the step numbers are as follows:
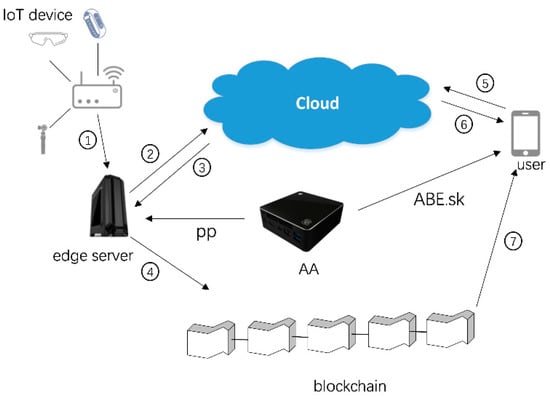
Figure 1.
System model.
- IoT devices send the collected data, their public key, and the access policy to the nearby edge server via a secure channel.
- The edge server encrypts the IoT data and sends the ciphertexts to the cloud server. Concretely, the edge server selects a secret message and then uses the attribute-based encryption scheme with the access policy as input to encrypt the trapdoor, r. Then, the edge server uses fully homomorphic encryption to encrypt the data with the trapdoor, r. Finally, the edge server sends the ciphertexts, c and c’, to the cloud server.
- The cloud server signs the hash of ciphertext, c, via a traditional signature algorithm and signs the hash of ciphertext, c’, via a homomorphic signature algorithm. Then, the cloud server returns the signatures to the edge server.
- The edge server verifies the signatures and records the valid signatures, the hash of data, and the access policies of the data on the blockchain.
- A user sends the access request or computation request to the cloud.
- The cloud server retrieves the ciphertext or computes the ciphertexts, then sends the ciphertext or ciphertext computation result to the user.
- The user decrypts the ciphertext and downloads the data from the blockchain. Then, the user verifies the validity of the data via the hash of the data or computation result via the homomorphic signatures.
3.2. Security Assumption
To ensure our system is secure, we make the security assumptions as follows:
Assumption 1. Edge servers may be compromised. Thus, an edge server may become a Byzantine node. Hence, we assume that the number of Byzantine nodes does not exceed one-third of the number of edge servers.
Assumption 2. We assume that IoT devices are not capable of encrypting data and calculating the hash value. Thus, we assume the IoT devices trust their nearby edge servers and send their data and access policies through a secure channel. In addition, we assume that users are capable of decrypting and computing the hash value.
Assumption 3. We assume that the cloud server is not fully trusted, which means it will provide services honestly but may tamper with the ciphertext. The AA is fully trusted. Users are dishonest to obtain ungranted access to data.
3.3. Security Goals
3.3.1. Cloud Attack Resistance
The proposed system should guarantee the cloud server could not deny the granted users access to the data.
3.3.2. Data Confidentiality and Integrity
The proposed system should ensure that only the granted users whose attributes of the secret key satisfy the access policy of the ciphertext could be able to decrypt and compute the ciphertext. In addition, the proposed system should guarantee the integrity of the ciphertext stored on the cloud.
3.3.3. Computation Privacy and Verifiability
To take advantage of the powerful computing capability of the cloud, the system should ensure the privacy of data during the computation process. Moreover, the computation result should be verifiable.
4. System Design
4.1. Construction
In this section, we introduce the processing of building a secure IoT data sharing system that supports ciphertexts computation. Concretely, as shown in Figure 2, the AA generates global parameters to set up the system by running Global Setup. Then AA generates data encryption keys for IoT devices by running IoT Devices Registration and generates decryption keys and evaluate keys based on the attributes of users by running Users Registration. To realize secure IoT data sharing and realize computable ciphertexts, edge devices share a random trapdoor under the IoT data access policy by encrypting the trapdoor via the PolicyEnc algorithm. Thus, only users whose attributes meet the access policy can obtain the trapdoor. Then, edge devices use the trapdoor to encrypt IoT data via the PlaintextEnc algorithm, which realizes data security and supports the ciphertext computation. We store the ciphertexts of IoT data, generated by edge devices, on the cloud. To confirm the reception and storage of the corresponding ciphertext correctly, the cloud server runs Cloud Signature to calculate the ordinary signature and homomorphic signature of the ciphertexts separately. Then, the cloud server sends the signatures to the edge server. The edge server runs Blockchain Record to record the IoT data information via invoking smart contract (described in Section 4.3) after verifying that the signatures are valid and the ciphertexts have not been tampered with. When users want to obtain IoT data, they send an access request to the cloud server by running Users Retrieve. The cloud server determines whether to return the corresponding ciphertexts via evaluating whether the attributes of the users meet the access policy of the IoT data. After obtaining the ciphertexts, users decrypt the trapdoor with their attribute private keys by running the PolicyDec algorithm and then running the PlaintextDec algorithm to get the IoT data by inputting the trapdoor. Finally, the user verifies the plaintext by comparing the data information downloaded from the blockchain via running Verify Data.
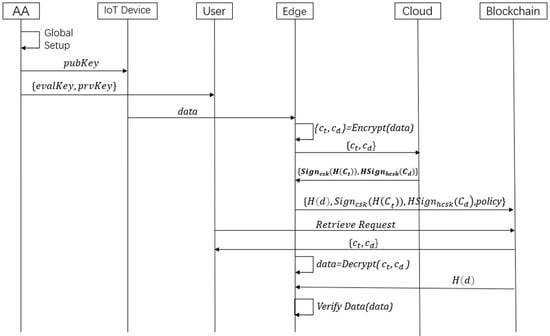
Figure 2.
Data storage and retrieval process.
- Global Setup() : The AA chooses as the security parameter, , are cyclic groups whose order are prime p, g is a generator of , is a bilinear map, and is a hash function. Then AA choose two random numbers , and computes , . In addition, the AA takes a lattice dimension , an error distribution , and an integer q as input. Then, AA sets , , and constructs a uniform distribution matrix . Finally, AA outputs the global parameter .
- IoT Devices Registration(pp) pubKey: AA generates encryption public key for IoT devices. Specifically, is a matrix, and is a vector, AA computes the vector , where , and let , then it outputs pubKey = (mpk, , A).
- Users Registration(pp, msk, attrs) {evalKey, prvKey}: In this algorithm, AA generates evaluate keys and decryption keys for users. Upon receiving the attributes, , of a user, the AA chooses two random numbers , and then generates the attribute key . After that, the AA choose , where , and computes . Finally, the AA outputs the evaluate key as evalKey = (ABE.sk, ) and the decryption key as prvKey = (ABE.sk, , ).
- Encrypt (pp, pubKey, policy, d){}: Once an edge server receives the access policy of data, the public key of IoT device, and the data. The edge server encryptions a trapdoor, which is used for encrypting the IoT data, under the policy of IoT data.PolicyEnc(pp, policy): During the policy encryption phase, the edge server chooses a random trapdoor , an encryption exponent , and a vector . Let policy = (M, ), the edge server computes , for = 1 to ( is the number of the matrix M’s rows and is the M’s th row), and outputs .
- PlaintextEnc (pp, pubKey, d): During the data encryption phase, the edge server chooses a unique distribution matrix, , and computes .
Finally, the edge server sends {} to the cloud server.
- Cloud Signature{} }: On receiving the {} from an edge server, the cloud stores the ciphertexts on the cloud. Then, the cloud signs the hash of the ciphertext, via a signature algorithm with its secret key, csk, that is, , and signs the ciphertext, via a homomorphic signature algorithm with its homomorphic secret key, hcsk, that is, . Finally, the cloud returns the signatures to the edge server.
- Blockchain Record (): On receiving from the cloud, the edge server first verifies the signatures. If the signatures are invalid and the ciphertexts have been tampered with, the edge server sends error information to the cloud. Otherwise, the edge server constructs a transaction = {, (M, )}. Then the edge server signs the transaction’s hash with its secret key, edev, that is, . Finally, the edge server packages the transaction and the signature and then broadcasts them in the edge server network.
- Users Retrieve: Users send the data requests to the cloud. The cloud decides whether to return the ciphertext () to users by evaluating whether the attributes of users meet the access policy of the IoT data.
- Decrypt(pp, prvKey,): This algorithm consists of PolicyDec and PlaintextDec and is run by users.
- (1)
- PolicyDec(pp, prvKey,): When users receive the ciphertext, it means there exist satisfying . Thus, users calculate Formula (1).Then, users obtain . by calculating Formula (2).
- (2)
- PlaintextDec (pp, prvKey,) : Users compute , and . Then users process vector as: . Finally, users get the plaintext by computing d + = , where .
- Verify Data() → 0/1: When a user gets the plaintext of the data, d, he computes d’s hash value. Then the user verifies whether the hash value is equal to the H(d) stored on the blockchain. If they are not equal, the user outputs 0. Otherwise, the user outputs 1.
4.2. Ciphertext Calculation
In some cases, users want to process the data stored on the cloud. Therefore, we add ciphertext computation (i.e., Pre-Compute, Compute, and Final-Compute) and Computation Correct Verify processes to the system.
As shown in Figure 3, users could outsource their computing to the cloud as follows:
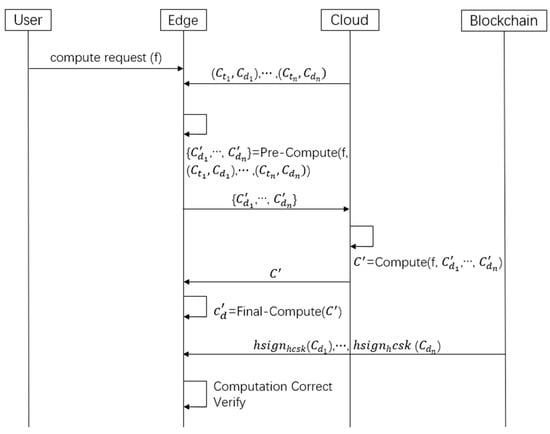
Figure 3.
Ciphertext calculation process.
- Pre-Compute(pp, f, (),(), ) {}: Once the edge server receives a user’s computation request, it downloads the ciphertexts from the cloud. Then it calls the PolicyDec algorithm to decrypt the ciphertexts to get (,n). Finally, the edge server computes , (,n) and sends , to the cloud server.
- Compute(f, ,,) : Once the cloud server receives the and , it computes and returns to the edge server.
- Final-Compute() : On receiving , the edge server selects a random r and calls PolicyEnc(pp, policy) to encrypt the trapdoor, r. Then the edge server computes and returns to the user.
- Computation Correct Verify(hcpk, policy, f, ): On receiving , the user downloads homomorphic signatures from blockchain and computes Eval(hcpk, f, (),, ()) , and then verifies whether Vrf(hcpk, , ) = 1 holds. If the signature is invalid, the user sends error information to the edge server and cloud server. Otherwise, the user decrypts the ciphertext to obtain the calculated plaintext, .
4.3. Smart Contract
In our scheme, the blockchain acts as a trusted party to record the data information, which consists of the hash of data, the signature of the ciphertext signed by the cloud, and the access policy of the data. Users could supervise the cloud server to return the correct ciphertexts and the correct ciphertext calculation results based on the data information.
Edge servers use the smart contract to upload the data information. Specifically, after verifying the signature and the homomorphic signature signed by the cloud (described in Section 4.1. Blockchain Record), the edge server uploads IoT data information onto the blockchain via invoking uploadDataInfo described in Algorithm 1.
| Algorithm 1. UploadDataInfo |
|
In addition, during the verification phase (described in Section 4.1. Verify Data and Section 4.2. Computation Correct Verify) users get the IoT data information via invoking getDataInfo described in Algorithm 2.
| Algorithm 2. GetDataInfo |
|
5. Security Analysis
This section presents security analyses of the proposed system in both formal and informal ways.
5.1. Formal Security Analysis
Theorem 1.
Assume that the digital signature, and the homomorphic signature,are unforgeable under chosen message attacks, and the hash function,is second pre-image resistant, and the blockchain can resist tampering attacks. Then the proposed system is secure for static cloud adversaries.
Adversary Model: Let be a cloud adversary, we assume to have (1) capability to decide whether to return the ciphertexts to users; (2) ful control over the ciphertext of IoT data. Thus may launch attacks such as denying authorized users to access IoT data, data forgery, and data tampering.
Lemma 1.
It is not possible forto record illegal signatures of ciphertexts on the blockchain and change the blockchain data as long as he/she corrupted no more than 1/3 of blockchain nodes or controls not more than 50% of the total computation power.
Proof.
Before the information of IoT data is uploaded to the blockchain, the cloud signs the ciphertexts via digital signature and homomorphic signature. The edge server verifies the signatures and only records the valid IoT data information on the blockchain. Thus cannot record illegal on the blockchain by forging wrong signatures. Furthermore, the blockchain consists of blocks connected by the hash of the former block. To change the blockchain data, needs to successfully corrupt more than 1/3 of blockchain nodes (based on the PBFT consensus algorithm) or have more than 50% of the total computational power of the network (based on the POW consensus algorithm). □
Lemma 2.
It is not possible forto return incorrect ciphertext and incorrect ciphertext calculation results to requesters (or users), named R.
Definition 1.
Consider that the cloud returns a ciphertext, (to R. R runs Dec(pp, prvKey,) (described in Section 4.1.) and gets the plaintext, d. Then R gets the data information {H(d),, (M, )} via invoking getDataInfo (described in Algorithm 2). Finally, R checks the signatures and and computes the hash of plaintext, d, denoted by H′(d), and then compares H′(d) with H(d). If the signature is valid and H′(d) is equal to H(d), R regards () as the correct ciphertext.
Definition 2.
Consider that the cloud returns a calculated ciphertext result, (), whereandto R. Then R gets the data information {H(), , (M, )} via invoking getDataInfo (described in Algorithm 2). Finally, R computes Eval(hcpk, f, (),, ()) , and then verifies whether Vrf(hcpk, , ) = 1 holds. If the equation holds, R regards () as the correct ciphertext computation result.
Proof.
If wants to return an incorrect ciphertext, (), or an incorrect ciphertext computation result, (), to R. needs to tamper the hash, H(d), and forge signatures recorded on the blockchain. As shown in Lemma 1, it is not possible for to record illegal IoT information on the blockchain. □
Theorem 2.
The proposed system cannot deny the authorized users’ access requests and can protect the privacy of IoT data from being disclosed to unauthorized users.
Proof.
The proposed system algorithm encrypts the IoT data under the access policy of the IoT data, and generates the users’ private key, which is associated with users’ attributes. Thus, a user could decrypt the ciphertext, only when the attributes of his/her private key satisfy the access policy of the ciphertext. (1) Suppose a cloud adversary, refuses to return ciphertext to authorized users. Users can propose an objection and get the corresponding access policy in the blockchain to prove the illegal behavior of . Thus, cannot deny authorized users’ access requests. (2) Suppose a cloud adversary, returns ciphertexts to unauthorized users. Because the attributes of users do not satisfy the access policy of the ciphertexts, users cannot decrypt the ciphertext. Thus, our system can protect the privacy of IoT data from being disclosed to unauthorized users. □
5.2. Informal Security Analysis
We will informally explain how the system achieves the security goals described in Section 3.3.
- (1)
- Cloud attack resistance: We have assumed that the cloud server may tamper with data and deny granted users access to data. In our scheme, we upload the data’s access policy onto the blockchain. The user can determine whether his/her attributes are satisfied with the access policies of the ciphertext. Therefore, the cloud server cannot deny the granted user access to the IoT data.
- (1)
- Data confidentiality: In our system, we use FHE to encrypt the data and the trapdoor, to make data computable. Then we use ABE to encrypt the trapdoor, thus only the users whose attributes satisfy the access policies of the ciphertext could get the trapdoor. Therefore, our scheme satisfies the data confidentiality.
- (3)
- Data integrity: We also upload the data’s hash onto the blockchain. When users obtain data from the cloud server, they can execute Verify Data (described in Section 4.1) to ensure the integrity of the IoT data. Therefore, the cloud server cannot tamper with the data in our scheme.
- (4)
- Computation privacy: The computation privacy of our scheme is based on FHE, which allows arbitrary computation on the encrypted data without decrypting it. The cloud computes the ciphertext for users with an evaluate key that satisfies the access policies who could not get any information of data due to the security of FHE. Therefore, our scheme could ensure the privacy of the data during the processing.
- (5)
- Computation verifiability: The cloud uses a homomorphic signature algorithm to sign the encrypted data, so users can verify whether the ciphertext computation result is correct by verifying the homomorphic signature.
To show the advantage of our system, we compared the proposed system with the existing IoT data protection system in terms of the following features. “Privacy” represents the protection of IoT data against unauthorized access, “fine-grained access control” means each data item has its own access control policy, “integrity” refers to the accuracy and consistency of data over its lifecycle, “ciphertext calculation” is the ability to compute the ciphertext, and “trustworthiness” represents that the required data and calculation results can be verified by the user. Table 1 illustrates that our system not only owns the functionalities of ciphertext calculation but also provides privacy, fine-grained access control, integrity, and trustworthiness of the IoT data.

Table 1.
Comparison between our system with other data protection system in the internet of things (IoT).
6. Performance Evaluation
In this section, we implemented and evaluated the performance of the proposed scheme. The performance evaluation was broken into two parts. The time cost for processing the cryptographic schemes is studied in the first part. The blockchain efficiency is studied in the second part.
6.1. System Settting
The efficiency of the scheme mainly depends on the blockchain platform, computing platform, and performance of the cryptographic scheme. For instance, in this paper, we use the Hyperledger Fabric (HLF) as the blockchain platform, since HLF is a platform for permissioned distributed ledger solutions, underpinned by a modular architecture delivering high degrees of confidentiality, resiliency, flexibility, and scalability. In addition, we use a popular cryptography library Pairing-Based Cryptography (PBC) [45], which implements pairing-based cryptosystems (described in Section 2.3.). Thus, we can realize CP-ABE by choosing an elliptic curve group. Moreover, based on the public HElib [46], which implements various forms of homomorphic encryption with many optimizations to make homomorphic evaluation run faster, we implement the FHE algorithm.
Specifically, Table 2 shows the hardware and software environments, and we used HLF v1.2 to initialize a permissioned blockchain in the edge server which was configured cpabe-0.11 [47], while we configured could server with HElib to implement the homomorphic calculation.

Table 2.
Configuration of system parameters.
6.2. Proccessing Time of Cryptogrphic Shceme
6.2.1. ABE Overhead
We evaluate the ABE performance on a personal computer based on PBC library (version 0.5.14). Specifically, we use a 160-bit elliptic curve group based on the supersingular curve over a 512-bit finite field. We consider a user with a different number of attributes to generate ABE.sk. Figure 4a shows the time for AA to generate attribute keys is approximately 0.021–0.104 s. Figure 4b,c shows the time for edge servers’ encryption and users’ decryption in our scheme.
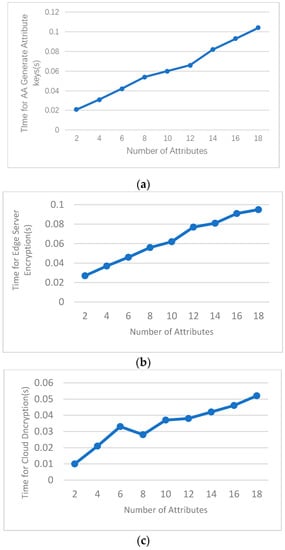
Figure 4.
Time cost for (a) AA to generate attribute keys; (b) edge server encryption; and (c) cloud decryption; with different number of attributes.
6.2.2. FHE Overhead
We evaluate the FHE performance on a personal computer based on HElib, which is a software library that implements BGV [48]. Specifically, we choose different security parameters, plaintext spaces, and evaluation function levels, . Table 3 shows the measured values (average of 100 runs) of the key generation time, encryption time, ciphertext addition calculation time (two ciphertext addition), ciphertext multiplication calculation time (two ciphertext multiplication), and decryption time.

Table 3.
Time cost for fully homomorphic encryption (FHE, s).
6.2.3. Homomorphic Signature Overhead
We suggest using Wang’s scheme [49] to test the efficiency of the homomorphic signature. The signing cost of running one-time signature is 1psf. The psf denotes the computation cost of running the PFS algorithm.
6.3. Smart Contract
We use HLF v1.2 to realize the designed smart contract (chaincode) described in Algorithms 1 and 2 and build a five-node PC test environment. Specifically, one PC acts as the orderer node with a Kafka/Zoomkeeper, and only one channel was established. We use the default endorsement policy of HLF and fixed the complexity of the transaction’s payload field as 1000 bytes. Inspired by [50], we study the latency and throughput of each smart contract for different block sizes and various transaction arrival rates. Table 4 shows the block sizes and transaction arrival rates used in our tests.

Table 4.
Block size (#tansactions) and transaction arrival rate.
After deploying the smart contract (chaincode) on the blockchain, we simulated different transaction arrival rates by triggering smart contracts different times per second and conducted 1000 s of experiments.
Figure 5 shows uploadDataInfo average latency (i.e., time taken from uploadDataInfo trigging to DataInfo committed to the blockchain ledger) and throughput (i.e., the rate at which DataInfo are committed to the blockchain) for different parameters referred to in Table 4.
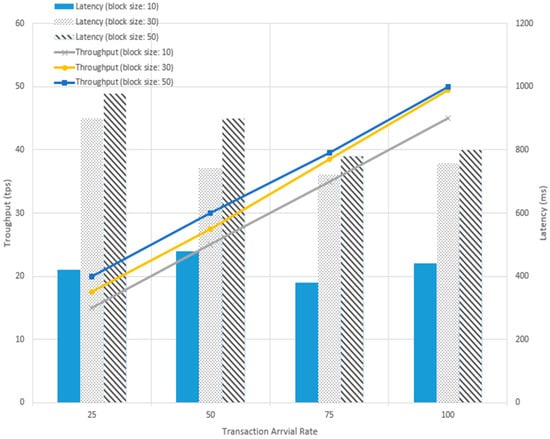
Figure 5.
Time cost of storing data information on the blockchain for different block sizes and transaction arrival rates.
Figure 6 shows getDataInfo’s average latency (i.e., time taken from getDataInfo trigging to DataInfo being returned to users) and throughput (i.e., rate of getting DataInfo from the blockchain) for different parameters referred to in Table 4.
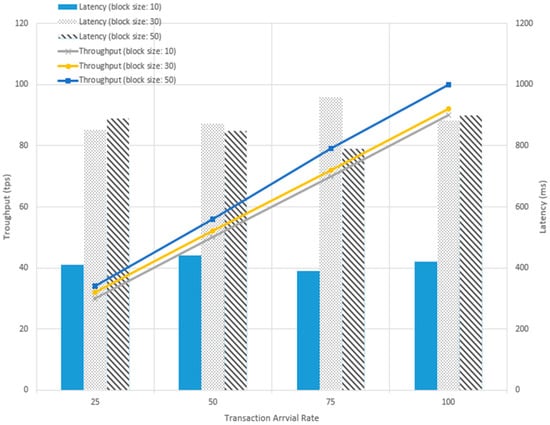
Figure 6.
Time cost of getting data information from the blockchain for different block sizes and transaction arrival rates.
6.4. System Performance
To show the utility of our system, we evaluate the communication and computation costs of each phase of the system. Table 5 shows the cost of the IoT data sharing process described in Section 4.1. Table 6 shows the cost of the IoT data computation process described in Section 4.1.

Table 5.
Communication and computation cost(s) of IoT data sharing.

Table 6.
Communication and computation cost(s) of IoT data computation.
6.5. System Limitation
Since the homomorphic signature scheme does not support the verification of arbitrary computation, our system can only verify the ciphertexts calculated on the polynomial function, . In addition, our system needs multiple times of interact and ciphertext pre-process between edge servers and cloud server. It is not suitable for application scenarios with real-time requirements.
7. Conclusions
In this article, we proposed a computable and secure IoT data sharing scheme, which is based on blockchain, ABE, FHE, and homomorphic encryption. In the scheme, we use FHE to encrypt the data, realizing secure data computation. Then we used ABE to realize fine-granted IoT data sharing. In addition, we upload the data’s access policy onto the blockchain, which allows any user to verify whether their attributes satisfied the access policy at any time. To ensure the correctness of the ciphertext computation, we used a homomorphic signature algorithm to sign ciphertexts. The security analysis proved that the proposed scheme is secure, and the performance evaluation experiments show that the scheme is practical.
Our solution can be deployed in IoT architectures that require trusted storage and computation. For example, in the smart hospital scenario, the data collected by medical equipment can be encrypted by PCs and stored in the cloud server. The corresponding access-control policies can be formulated by patients. Doctors can access and process the data according to their authorities and outsource complex data calculation requests to the cloud.
In future research, we are looking for alternatives to homomorphic signatures to verify ciphertext calculation results. Moreover, we will reduce the number of interactions between the cloud server and the edge server in the ciphertext calculation process.
Author Contributions
Scheme design, S.S. and R.D.; implementation, S.S.; writing—original draft preparation, S.S.; writing—review and editing, R.D.; supervision, S.C.; project administration, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Leading Special project of the Chinese Academy of Science (Class C), grant number XDC02070600.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Ding, S.; Jin, C.; Li, C.; Fan, K.; Li, H. A Novel Attribute-Based Access Control Scheme using Blockchain for IoT. IEEE Access 2019, 7, 38431–38441. [Google Scholar] [CrossRef]
- Tao, Y.; Xu, P.; Jin, H. Secure Data Sharing and Search for Cloud-Edge-Collaborative Storage. IEEE Access 2020, 8, 15963–15972. [Google Scholar] [CrossRef]
- Mollah, M.B.; Azad, M.A.K.; Vasilakos, M.A.K. Secure Data Sharing and Searching at the Edge of Cloud-Assisted Internet of Things. IEEE Cloud Comput. 2017, 4, 34–42. [Google Scholar] [CrossRef]
- Xu, G.W.; Li, H.W.; Ren, H.; Yang, K.; Deng, R.H. Data Security Issues in Deep Learning: Attacks, Countermeasures, and Opportunities. IEEE Commun. Mag. 2019, 57, 116–122. [Google Scholar] [CrossRef]
- Sun, S.; Chen, S.D.; Du, R.; Li, W.W.; Qi, D.L. Blockchain Based Fine-Grained and Scalable Access Control for IoT Security and Privacy. In Proceedings of the International Conference on Data Science in Cyberspace (DSC), Hangzhou, China, 23–25 June 2019; pp. 598–603. [Google Scholar]
- Bahgat, M.M.; Farag, H.H.; Mokhtar, B. IoT-Based Online Access Control System for Vehicles in Truck-Loading Fuels Terminals. In Proceedings of the 30th International Conference on Microelectronics (ICM), Sousse, Tunisia, 16–19 December 2018; pp. 1–4. [Google Scholar]
- Maia, N.A.L.; Pereira, Y.L.; Souza, A.L.F.; Cunha, I.; Oliveira, L.B. Demo Abstract: Attributed-Based Authentication and Access Control for IoT Home Devices. In Proceedings of the International Conference on Information Processing in Sensor Networks (IPSN), Porto, Portugal, 11–13 April 2018; pp. 112–113. [Google Scholar]
- Hofmann, C.A.; Knopp, A. Ultranarrow Band Wave Form for IoT Direct Random Multiple Access to GEO Satellites. IEEE Internet Things J. 2019, 6, 10134–10149. [Google Scholar] [CrossRef]
- Meneghello, F.; Calore, M.; Zucchetto, D.; Polese, M.; Zanella, A. IoT: Internet of Threats? A Survey of Practical Security Vulnerabilities in Real IoT Devices. IEEE Internet Things J. 2018, 6, 8182–8201. [Google Scholar] [CrossRef]
- Gunjal, Y.S.; Gunjal, M.S.; Tambe, A.R. Hybrid Attribute Based Encryption and Customizable Authorization in Cloud Computing. In Proceedings of the International Conference on Advances in Communication and Computing Technology (ICACCT), Sangamner, India, 8–9 February 2018; pp. 187–190. [Google Scholar]
- Porwal, S.; Mittal, S. Design of Concurrent Ciphertext Policy-Attribute Based Encryption Library for Multilevel Access of Encrypted Data. In Proceedings of the International Conference on Parallel, Distributed and Grid Computing (PDGC), Solan Himachal Pradesh, India, 20–22 December 2018; pp. 42–47. [Google Scholar]
- Jiang, Y.; Du, M. Provable Security Analysis on Unbounded Hierarchical Identity-Based Encryption and Attribute-Based Encryption. In Proceedings of the International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; pp. 510–513. [Google Scholar]
- Fan, K.; Pan, Q.; Zhang, K.; Bai, Y.H.; Sun, S.L.; Li, H.; Yang, Y.T. A Secure and Verifiable Data Sharing Scheme Based on Blockchain in Vehicular Social Networks. IEEE Trans. Veh. Technol. 2020, 69, 5826–5835. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.L.; Zhang, Y.L. A Blockchain-Based Framework for Data Sharing with Fine-Grained Access Control in Decentralized Storage Systems. IEEE Access 2018, 6, 38437–38450. [Google Scholar] [CrossRef]
- Freeman, D.M. Improved Security for Linearly Homomorphic Signatures: A Generic Framework. In Proceedings of the International Conference on Public Key Cryptography–PKC, Taormina, Italy, 6–9 March 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 697–714. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitco.in/pdf/bitcoin.pdf (accessed on 10 January 2021).
- A Blockchain Platform for the Enterprise. Available online: https://hyperledger-fabric.readthedocs.io/en/latest/index.html (accessed on 10 January 2021).
- Ethereum Smart Contract Platform. Available online: https://www.ethereum.org/ (accessed on 10 January 2021).
- EOS.IO Technical White Paper v2. Available online: https://github.com/EOSIO/Documentation/blob/master/TechnicalWhitePaper.md (accessed on 10 January 2021).
- Cachin, C. Architecture of the Hyperledger Blockchain Fabric. In Proceedings of the Workshop on Distributed Cryptocurrencies and Consensus Ledgers, Chicago, IL, USA, 25 July 2016; Volume 310. [Google Scholar]
- Li, X.; Mou, H.; Lu, D. An Improved Ciphertext Retrieval Scheme Based on Fully Homomorphic Encryption. Wuhan Univ. J. Nat. Sci. 2019, 24, 218–222. [Google Scholar] [CrossRef]
- Chatterjee, A.; Aung, K.M.M. Fully Homomorphic Encryption in Real World Applications; Springer: Singapore, 2019. [Google Scholar]
- Ding, Y.; Li, X. Policy Based on Homomorphic Encryption and Retrieval Scheme in Cloud Computing. In Proceedings of the IEEE International Conference on Computational Science & Engineering & IEEE International Conference on Embedded & Ubiquitous Computing, Guangzhou, China, 21–24 July 2017. [Google Scholar]
- Hur, J. Improving Security and Efficiency in Attribute-Based Data Sharing. IEEE Trans. Knowl. Data Eng. 2013, 25, 2271–2282. [Google Scholar] [CrossRef]
- Sahaiand, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar]
- Traverso, G.; Demirel, D.; Buchmann, J. Homomorphic Signature Schemes; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–21. [Google Scholar]
- Saračević, M.; Adamović, S.Z.; Miškovic, V.A.; Elhoseny, M.; Maček, N.D.; Selim, M.M.; Shankar, K. Data Encryption for Internet of Things Applications Based on Catalan Objects and Two Combinatorial Structures. IEEE Trans. Reliab. 2020. [Google Scholar] [CrossRef]
- Saračević, M.; Adamović, S.; Macek, N.; Elhoseny, M.; Sarhan, S. Cryptographic Keys Exchange Model for Smart City Applications. IET Intell. Transp. Syst. 2020, 14, 1456–1464. [Google Scholar] [CrossRef]
- Rass, S.; Slamanig, D. Cryptography for Security and Privacy in Cloud Computing; Artech House Inc.: Norwood, MA, USA, 2013. [Google Scholar]
- Gentry, C. A Fully Homomorphic Encryption Scheme. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Gentry, C. Fully Homomorphic Encryption using Ideal Lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, STOC ’09, Bethesda, MD, USA, 31 May–2 June 2009; Mitzenmacher, M., Ed.; ACM: New York, NY, USA, 2009; pp. 169–178. [Google Scholar]
- Cheon, J.H.; Coron, J.; Kim, J.; Lee, M.S.; Lepoint, T.; Tibouchi, M.; Yun, A. Batch Fully Homomorphic Encryption over the Integers. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, 26–30 May 2013; pp. 315–335. [Google Scholar]
- Coron, J.; Lepoint, T.; Tibouchi, M. Scale-Invariant Fully Homomorphic Encryption over the Integers. In Proceedings of the International Conference on Practice and Theory in Public-Key Cryptography, Darmstadt, Germany, 21–23 May 2014; pp. 311–328. [Google Scholar]
- Ducas, L.; Micciancio, D. FHEW: Bootstrapping Homomorphic Encryption in Less than a Second. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; pp. 26–30. [Google Scholar]
- Eric, C.; Chris, P.; Chad, S. A Language and Compiler for Homomorphic Encryption Made Easy. In Proceedings of the ACM Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 1020–1037. [Google Scholar]
- López-Alt, A.; Tromer, E.; Vaikuntanathan, V. On-the-Fly Multiparty Computation on the Cloud via Multikey Fully Homomorphic Encryption. In Proceedings of the 44th Annual ACM Symposium on Theory of Computing Conference, STOC, New York, NY, USA, 20–22 May 2013; pp. 1219–1234. [Google Scholar]
- Micciancio, D. A First Glimpse of Cryptography is Holy Grail. Commun. ACM 2010, 53, 96. [Google Scholar] [CrossRef]
- Boneh, D.; Gentry, C.; Halevi, S.; Wang, F.; Wu, D.J. Private Database Queries using Somewhat Homomorphic Encryption. In Proceedings of the International Conference on Applied Cryptography and Network Security, Banff, AB, Canada, 25–28 June 2013; Springer: Berlin, Heidelberg, 2013; pp. 102–118. [Google Scholar]
- Johnson, R.; Molnar, D.; Song, D.X.; Wagner, D. Homomorphic Signature Schemes. In Proceedings of the Cryptographer’s Track at the RSA Conference, San Jose, CA, USA, 18–22 February 2002; pp. 244–262. [Google Scholar]
- Libert, B.; Peters, T.; Joye, M.; Yung, M. Linearly Homomorphic Structure-Preserving Signatures and their Applications. Des. Codes Cryptogr. 2015, 77, 441–477. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, J.; Ling, Y.; Ji, M.; Wei, G.; Ying, B. Efficient Multiple Sources Network Coding Signature in the Standard Model. Concurr. Comput. Pract. Exp. 2015, 27, 2616–2636. [Google Scholar] [CrossRef]
- Zhang, P.; Yu, J.; Wang, T. A Homomorphic Aggregate Signature Scheme based on Lattice. Chin. J. Electron. 2012, 21, 701–704. [Google Scholar]
- Manzoor, A.; Liyanage, M.; Braeken, A. Blockchain based Proxy Re-Encryption Scheme for Secure IoT Data Sharing. In Proceedings of the IEEE International Conference on Blockchain and Cryptocurrency, Seoul, Korea, 14–17 May 2019. [Google Scholar]
- Truong, H.T.T.; Almeida, M.; Karame, G. Towards Secure and Decentralized Sharing of IoT Data. In Proceedings of the IEEE International Conference on Blockchain, Atlanta, GA, USA, 14–17 July 2019. [Google Scholar]
- Ben, L. The PBC (Pairing-Based Cryptography) Library. Available online: https://crypto.stanford.edu/pbc/ (accessed on 10 January 2021).
- Shai, H. An Implementation of Homomorphic Encryption. Available online: https://github.com/shaih/HElib (accessed on 10 January 2021).
- John, B.; Amit, S.; Brent, W. Ciphertext-Policy Attribute-Based Encryption. Available online: http://acsc.cs.utexas.edu/cpabe/ (accessed on 10 January 2021).
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (leveled) Fully Homomorphic Encryption without Bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8−10 January 2012; pp. 309–325. [Google Scholar]
- Wang, F.H.; Hu, Y.P.; Wang, B.C. Lattice-based Linearly Homomorphic Signature Scheme over Binary Field. Sci. China Inf. Sci. 2013, 56, 1–9. [Google Scholar] [CrossRef][Green Version]
- Nathan, S.; Thakkar, P.; Vishwanathan, B. Performance Benchmarking and Optimizing Hyperledger Fabric Blockchain Platform. In Proceedings of the International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS), Milwaukee, WI, USA, 25–28 September 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).