Learnable Leaky ReLU (LeLeLU): An Alternative Accuracy-Optimized Activation Function
Abstract
:1. Introduction
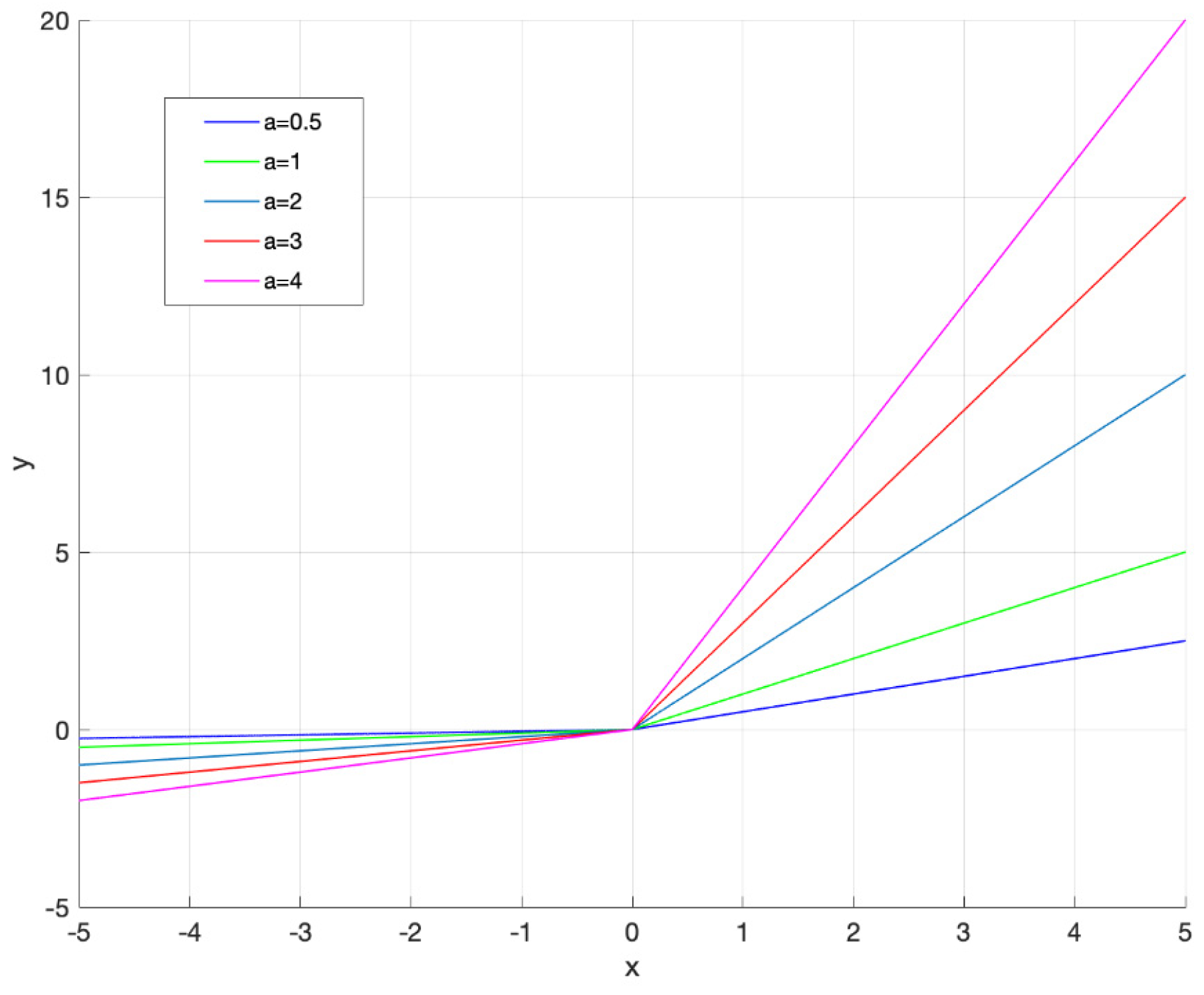
2. The Proposed Activation Function
3. Parameter Adaptation and Network Regularization
4. Results
4.1. Datasets and Network Topologies
4.2. Numerical Results
4.3. LeLeLU Performance in Larger Deep Neural Networks
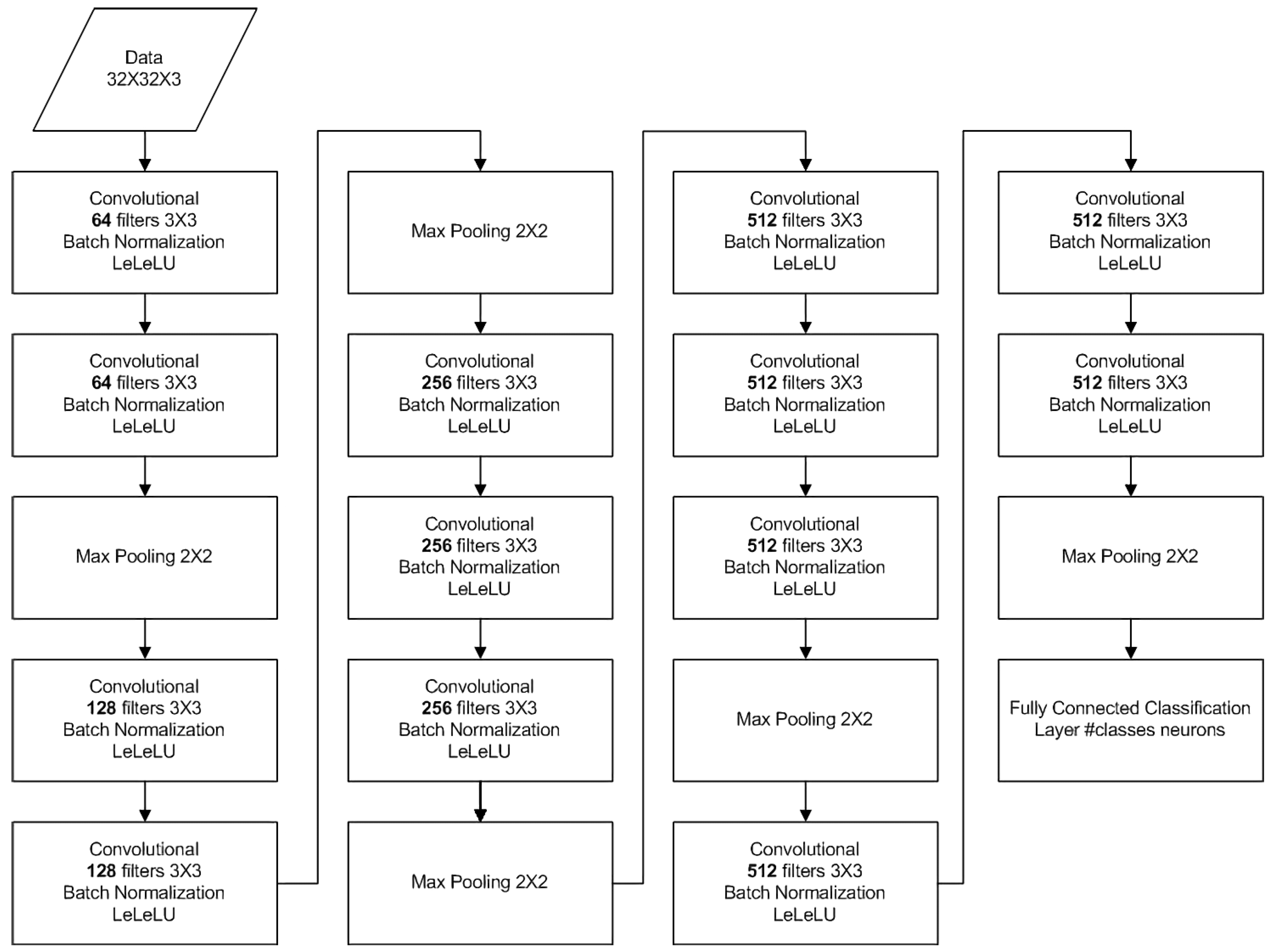
4.3.1. VGG-16 with LeLeLU
4.3.2. ResNet-v1-56 with LeLeLU
4.4. LeLeLU Performance vs. Dataset Complexity
| Algorithm 1 Dataset Complexity Estimation |
| Input: X_train data, number_of_classes Output: Dataset_complexity 1 x_matrix is initialized to the X_train data 2 set number_of_classes to the number of classes of the classification problem 3 set number_of_training_files N to the number of training examples contained in the dataset 4 T ← 0 5 for each data sample in x_matrix 6 calculate the entropy E of the corresponding data sample 7 T ← T + E 8 end for 9 calculate mean entropy (ME): ME ← T/N 10 calculate the bits Q required to represent the number of classes 11 Dataset_complexity = ME × Q |
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, 2010 ICML’10, Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA; pp. 807–814, ISBN 9781605589077. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv 2015, arXiv:1502.01852. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dugas, C.; Bengio, Y.; Bélisle, F.; Nadeau, C.; Garcia, R. Incorporating second-order functional knowledge for better option pricing. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2001; pp. 472–478. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 972–981. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.-P. BinaryConnect: Training deep neural networks with binary weights during propagations. In Proceedings of the NIPS’15: Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 2, pp. 3123–3131. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A Self-Gated Activation Function. arXiv 2017, arXiv:1710.05941v1. [Google Scholar]
- Misra, D.M. A self regularized non-monotonic neural activation function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Maguolo, G.; Nanni, L.; Ghidoni, S. Ensemble of convolutional neural networks trained with different activation functions. Expert Syst. Appl. 2021, 166, 114048. [Google Scholar] [CrossRef]
- Liang, S.; Lyu, L.; Wang, C.; Yang, H. Reproducing Activation Function for Deep Learning. arXiv 2021, arXiv:2101.04844. [Google Scholar]
- Zhou, Y.; Zhu, Z.; Zhong, Z. Learning specialized activation functions with the Piecewise Linear Unit. arXiv 2021, arXiv:2104.03693. [Google Scholar]
- Shridhar, K.; Lee, J.; Hayashi, H.; Mehta, P.; Iwana, B.K.; Kang, S.; Uchida, S.; Ahmed, S.; Dengel, A. ProbAct: A Probabilistic Activation Function for Deep Neural Networks. arXiv 2020, arXiv:1905.10761v2. [Google Scholar]
- Bingham, G.; Miikkulainen, R. Discovering Parametric Activation Functions. arXiv 2021, arXiv:2006.03179v4. [Google Scholar]
- Burgin, M. Generalized Kolmogorov complexity and duality in theory of computations. Not. Russ. Acad. Sci. 1982, 25, 19–23. [Google Scholar]
- Kaltchenko, A. Algorithms for Estimating Information Distance with Application to Bioinformatics and Linguistics. arXiv 2004, arXiv:cs.CC/0404039. [Google Scholar]
- Vitányi, P.M.B. Conditional Kolmogorov complexity and universal probability. Theor. Comput. Sci. 2013, 501, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Solomonoff, R. A Preliminary Report on a General Theory of Inductive Inference; Report V-131; Office of Scientific Research, United States Air Force: Washington, DC, USA, 1960. [Google Scholar]
- Jorma, R. Information and Complexity in Statistical Modeling; Springer: New York, NY, USA, 2007; p. 53. ISBN 978-0-387-68812. [Google Scholar]



| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| ReLU | 0.9875 | 100% |
| PReLU | 0.9861 | 99.9% |
| Tanh | 0.9835 | 99.6% |
| ELU | 0.9879 | 100% |
| SELU | 0.9878 | 100.04% |
| HardSigmoid | 0.9756 | 98.79% |
| Mish | 0.9881 | 100.06% |
| Swish | 0.9878 | 100.04% |
| LeLeLU | 0.9897 | 100.23% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| ReLU | 0.8956 | 100% |
| PReLU | 0.8961 | 100.06% |
| Tanh | 0.8979 | 100.2% |
| ELU | 0.9071 | 101.2% |
| SELU | 0.8959 | 100.03% |
| HardSigmoid | 0.8704 | 97.19% |
| Mish | 0.9037 | 100.9% |
| Swish | 0.9019 | 100.7% |
| LeLeLU | 0.912 | 101.8% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| ReLU | 0.9073 | 100% |
| PReLU | 0.8815 | 97.2% |
| Tanh | 0.8522 | 93.9% |
| ELU | 0.8721 | 96.1% |
| SELU | 0.8196 | 93% |
| HardSigmoid | 0.8586 | 97.4% |
| Mish | 0.8974 | 101.8% |
| Swish | 0.8947 | 101.5% |
| LeLeLU | 0.9353 | 103.2% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| ReLU | 0.6829 | 100% |
| PReLU | 0.7094 | 103.5% |
| Tanh | 0.6785 | 99.3% |
| ELU | 0.7065 | 103.4% |
| SELU | 0.7103 | 104% |
| HardSigmoid | 0.6652 | 97.4% |
| Mish | 0.6938 | 101.6% |
| Swish | 0.6890 | 100.9% |
| LeLeLU | 0.7166 | 104.9% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| Sigmoid | 0.1 | 11.46% |
| Tanh | 0.1 | 11.46% |
| ReLU | 0.8727 | 100% |
| Leaky ReLU | 0.8649 | 99.1% |
| PReLU | 0.8635 | 98.94% |
| ELU | 0.8765 | 100.44% |
| SELU | 0.8665 | 99.29% |
| Swish | 0.8655 | 99.17% |
| LeLeLU | 0.8792 | 100.74% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| Sigmoid | 0.01 | 1.99% |
| Tanh | 0.01 | 1.99% |
| ReLU | 0.5294 | 100% |
| Leaky ReLU | 0.4944 | 93.39% |
| PReLU | 0.4630 | 87.46% |
| ELU | 0.5660 | 106.91% |
| SELU | 0.5152 | 97.31% |
| Swish | 0.5401 | 102.02% |
| LeLeLU | 0.5632 | 106.38% |
| Activation Function | Accuracy | Normalized Accuracy |
|---|---|---|
| Sigmoid | 0.3647 | 52.37% |
| HardSigmoid | 0.3255 | 46.74% |
| ReLU | 0.6964 | 100% |
| Leaky ReLU | 0.6978 | 100.2% |
| GELU | 0.7019 | 100.79% |
| PReLU | 0.7223 | 103.72% |
| ELU | 0.6967 | 100.04% |
| SELU | 0.6852 | 98.39% |
| Mish | 0.6988 | 100.34% |
| Swish | 0.6968 | 100.06% |
| Softplus | 0.6971 | 100.1% |
| Softsign | 0.5838 | 83.83% |
| Tanh | 0.6388 | 91.73% |
| LeLeLU | 0.7283 | 104.58% |
| Dataset | Complexity | LeLeLU Accuracy Improvement |
|---|---|---|
| MNIST | 6.41 | 100.23% |
| Fashion MNIST | 16.466 | 101.8% |
| Sign Language | 33.584 | 103.2% |
| CIFAR-10 | 83.993 | 104.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maniatopoulos, A.; Mitianoudis, N. Learnable Leaky ReLU (LeLeLU): An Alternative Accuracy-Optimized Activation Function. Information 2021, 12, 513. https://doi.org/10.3390/info12120513
Maniatopoulos A, Mitianoudis N. Learnable Leaky ReLU (LeLeLU): An Alternative Accuracy-Optimized Activation Function. Information. 2021; 12(12):513. https://doi.org/10.3390/info12120513
Chicago/Turabian StyleManiatopoulos, Andreas, and Nikolaos Mitianoudis. 2021. "Learnable Leaky ReLU (LeLeLU): An Alternative Accuracy-Optimized Activation Function" Information 12, no. 12: 513. https://doi.org/10.3390/info12120513
APA StyleManiatopoulos, A., & Mitianoudis, N. (2021). Learnable Leaky ReLU (LeLeLU): An Alternative Accuracy-Optimized Activation Function. Information, 12(12), 513. https://doi.org/10.3390/info12120513







