Passive Fault-Tolerant Control of a 2-DOF Robotic Helicopter

Abstract

The presence of faults in dynamic systems causes the potential loss of some of the control objectives. For that reason, a fault-tolerant controller is required to ensure a proper operation, as well as to reduce the risk of accidents. The present work proposes a passive fault-tolerant controller that is based on robust techniques, which are utilized to adjust a proportional-derivative scheme through a linear matrix inequality. In addition, a nonlinear term is included to improve the accuracy of the control task. The proposed methodology is implemented in the control of a two degrees of a freedom robotic helicopter in a simulation environment, where abrupt faults in the actuators are considered. Finally, the proposed scheme is also tested experimentally in the Quanser^® 2-DOF Helicopter, highlighting the effectiveness of the proposed controller.

1. Introduction

The main objective of a fault-tolerant controller is to preserve stability and a proper performance, even when there is a malfunction in some of the system components. A suitable controller is essential to maintain a correct and safe operation. Besides, with the objective of assuring the suitability of a proposed scheme, it is required to settle on adequate methods of analysis. In this fashion, different techniques have been proposed to analyze the stability of the closed-loop system, as well as to guarantee a required performance. Nevertheless, with the automation of internal processes, the occurrence of faults is prone to increase. In addition, it is usual that the system components yield a natural degradation in performance over time, a fact that can lead to instability or to irreversible damage. Even under a wide range of tolerable faults, the controller must be designed to ensure proper operation, or at least an adequate degree of command to set the system to rest, with minimal potential risk.

As mentioned in [1], some outstanding control approaches have been considered to operate in the presence of faults, maintaining desirable properties of stability and performance. In particular, in scenarios where safety is essential, such as aircraft vehicle navigation, power plant control, or chemical process regulation, where any slight failure could cause catastrophic results.

A failure can be defined as a deviation of a system’s response from its nominal behavior, or the deviation of the system parameters from their nominal values [2]. Most of the literature concerning fault detection considers the case of linear systems [3,4,5]. Nonetheless, for the case of nonlinear systems, some results are available in [6]. For these systems, the fault is represented as an exogenous input or deviation in the dynamic response from the expected value. Besides, when the failures are considered as additive external signals, they are called additive faults.

1.1. Fault Tolerance Control

Tolerance describes the idea of alleviating the consequences of a failure, so that the components remain functional. This can be attained by the principle of fault tolerance [7]. The control technique, in which the occurrence of failures is taken into account for control purposes, is known as Fault-Tolerant Control (FTC) [8]. Some FTC systems employ analytical or hardware redundancy. Those systems where people’s safety is involved use hardware redundancy due to its superb effectiveness; nevertheless, its financial cost is inherently high. It is worth commenting that analytical redundancy reduces instrumentation and maintenance costs, and this approach can be carried out by using control laws that are designed to be robust against known or unknown faults [9].

A well-designed robust controller can ensure stability and maintain an acceptable closed-loop performance in a large number of circumstances, event in the presence of some actuator faults. Recently proposed FTC methods are based on robust techniques such as those shown in [10,11]. FTC strategies are classified into two categories: The first one is named Active Fault-Tolerant Control (AFTC) which consists of reacting to a component’s malfunction (e.g., actuators, sensors, and even the system itself) by reconfiguring the system’s controller. To do so, the system’s controller needs to be a reconfigurable one. Moreover, it needs to use the information from a Fault Detection and Diagnostic scheme (FDD) and a device to reconfigure the controller. All this requires redundancy in different components that make up the control system. Moreover, the second one is called Passive Fault-Tolerant Control (PFTC) which consists of designing, a priori, a controller that supports a certain number of known faults and does not require additional mechanisms or a reconfiguration of the controller. Therefore, since in PTFC no additional mechanisms or reconfigurations of the controller are needed, the probability of presenting a lack of stability or poor performance of automatic control system diminishes, see [12,13]. According to [14], PFTC does not involve the combined estimation of control signals and faults. Compared to the AFTC method, the PFTC control uses the same control strategy before and after faults [15]. Besides, under the presence of a passive fault, the PFTC requires neither fault diagnosis nor controller redesign [16]. The basic idea of PFTC is to make the closed-loop system robust against uncertainties, as well as to a restrictive set of probable failures, assuming that it is possible to guarantee that a fault acts as an uncertainty to the system, in a way that can be limited. In that case, a carefully designed robust controller can achieve tolerance to a wide range of faults.

1.2. Main Contribution

The simple structure and reliability of classical linear controllers, such as PID (proportional-integral-derivative) control algorithms, have been widely considered [17], inducing a robust behavior in several circumstances, such as in the presence of a large variety of uncertainties. In this work, a PD controller strategy is considered, whose feedback gains are adjusted through the solution of a convex optimization problem, which is used in turn to demonstrate the suitability of a given linear matrix inequality (LMI), as shown in [18]. The faults can be considered as additive failures in the actuators, causing a deviation from the nominal behavior of the system response. These types of failures can occur due to wear, changes in the actuator structure, or damage. Furthermore, the presence of these faults produces an impact on the the performance of the closed-loop system, leading to a potential degradation or even lack in operation of the aircraft system, which motivates the design of a PFTC, which is able to operate in a broad class of scenarios, including the presence of disturbances and dynamic uncertainties.

The robust control formulation that is proposed in this paper consists of a passive approach, which attempts to minimize the output discrepancy over the control objective, as it was previously studied in [19]. A classical approach, in robust control, considers the discrepancy caused by the deviation of the systems parameters as an apparent input disturbance, see Figure 1. Thus, the control objective is to get rid of, or minimize, such a deviation.

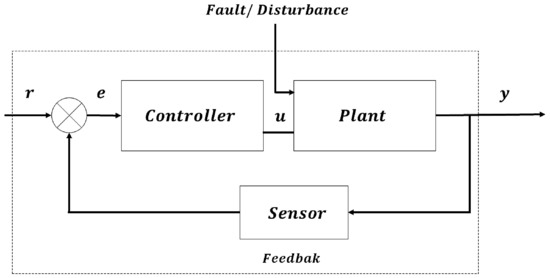
Figure 1. Block diagram representing the dynamic system under the presence of faults. Here, r is the reference signal, u is the control input, y is the output and e is the regulation or tracking error.

There are three fundamental advantages of the method used in this paper. The first one is that, PFTC is much less expensive than the AFTC method because it does not require the incorporation of additional redundant devices to maintain a good performance of the closed-loop control system in the presence of failures that occur in the system. The second one is that the strategy for designing the robust controller of the system, based on LMIs, considers an extensive list of potential system malfunctions and, additionally, measurement noise and disturbances, guaranteeing with this to preserve an adequate performance in adverse conditions. Finally, the third one is that the time required to make adjustments to the controller is not a limitation because it is adjusted once the system’s operation starts; therefore, the controller remains fixed in real-time. These advantages were verified by applying the previous method to a 2-DOF helicopter under the presence of two tolerable faults, corroborating its effectiveness through experimental tests presented in Section 5.

The rest of this paper is organized as follows. The next Section presents the dynamic model of the 2-DOF helicopter. The proposed FTC is presented in Section 3. The control design implementation is shown in Section 4. The numerical results based on simulations and experiments are given in Section 5. Finally, the discussions and main conclusions are presented in Section 6 and Section 7.

2. Dynamic Model of the 2-Dof Helicopter

This section presents the case of study. The system is composed of a laboratory device, consisting in a two degree of freedom helicopter, made by Quanser^®, See Figure 2.

Figure 2. Helicopter 2-DOF Quanser^®.

The 2-DOF helicopter is a dynamic system that consists of two motors, the first or lift is considered as the actuator one and causes the pitching movement, and a tail motor or actuator two, which produces the yaw movement; both direct current motors are driven with a nominal voltage of 12 volts. The platform dimensions are shown in Appendix A. For more system specifications and their components, as well as the system setup, see [20,21].

An Arduino^® Mega 2560 is used to communicate with the physical system, where the pulse width modulation method is implemented to command the motor. For the power part, a Monster Moto Shield is utilized, with a voltage capacity of 16 volts and 30 amperes of current, with a 20 KHz PWM frequency. The sensing was carried out by two rotary optical encoders, one placed at the base of the platform, which allows the yaw angle $\psi$ to be measured, and the other one is placed in the center of the platform which measures the pitch angle $\varphi$. The acquired data is processed in Matlab^®. The experimental platform is shown in Figure 2 and its corresponding schematic diagram in Figure 3.

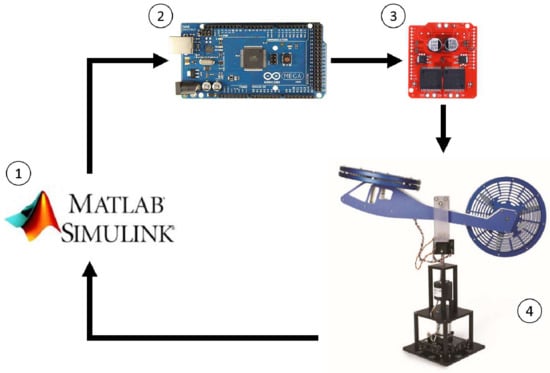
Figure 3. Experimental platform.

The dynamic model that describes the equations of motion is obtained by using the Euler–Lagrange formalism. The system model can be written through the following nonlinear second-order equation:

$$D\left(q\right)\ddot{q}+C(q,\dot{q})+G\left(q\right)=\tau ,$$

(1)

where q is the vector of generalized coordinates, $\tau$ is the input vector, $G\left(q\right)$ is the vector of gravitational torques, $C(q,\dot{q})$, models the quadratic effects of the velocity generated by the Coriolis and centripetal forces and $D\left(q\right)$ is the inertia matrix, which is a symmetric positive definite matrix. Specifically:

$$\begin{array}{c}\hfill \begin{array}{ccc}D\left(q\right)& =& (m_1{l_1}^2+m_2{l_2}^2)\left[\begin{array}{cc}1& 0\\ 0& {cos}^2\left(\varphi \right)\end{array}\right],\\ \\ G\left(q\right)& =& \left[\begin{array}{c}{m}_{1}g{l}_{1}cos\left(\varphi \right)-m_{2}g{l}_{2}cos\left(\varphi \right)\\ 0\end{array}\right],\\ \\ C(q,\dot{q})& =& (m_1{l}_1^2+m_2{l}_2^2){\dot{\psi }}^{2}cos\left(\varphi \right)sin\left(\varphi \right)\left[\begin{array}{c}1\\ -2\dot{\varphi }\dot{\psi }\end{array}\right]\end{array}\end{array}$$

The structure of the matrices $D\left(q\right)$, $C(q,\dot{q})$, and $G\left(q\right)$ depend on the kinematic parameters of the mechanical system, as well as on the masses of the rigid bodies and their geometric distributions. For the Quanser^® 2-DOF, it is convenient to define the generalized coordinate vector and its derivative:

$$q=\left[\begin{array}{c}\varphi \\ \psi \end{array}\right],\dot{q}=\left[\begin{array}{c}\dot{\varphi }\\ \dot{\psi }\end{array}\right],$$

(2)

where $\varphi$, $\psi$ are the Pitch and Yaw angles, respectively, and $\dot{\psi }$, $\dot{\varphi }$ their angular velocities, see Figure 4.

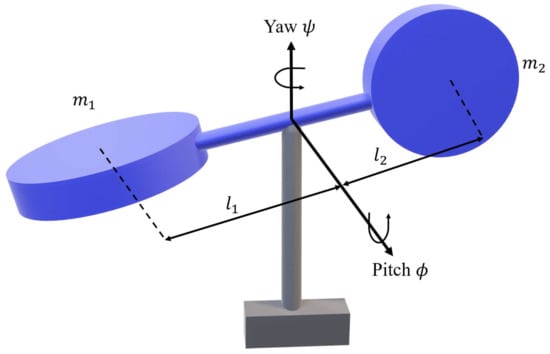
Figure 4. 2-DOF Quanser Helicopter Schematic.

Note that the use of system identification techniques has not been required because of the well-know dynamic structure of the helicopter model. The viability of the considered model has been tested with comparisons between simulations and experiments on the physical system; nonetheless, the formulation of novel modeling approaches is beyond the scope of this paper.

3. Fault-Tolerant Control Scheme

The nominal dynamics of a 2-DOF helicopter is described by Equation (1). In the presence of additive failures in actuators the dynamic model becomes,

$$D\left(q\right)\ddot{q}+C(q,\dot{q})+G\left(q\right)=\tau +f_a,$$

(3)

for

$$f_a=\left[\begin{array}{c}{f}_{a1}\\ f_{a2}\end{array}\right]$$

the failure vector, with $f_{a1}$ and $f_{a2}$ being the failures in each of the actuators. It is worth mentioning that these failures affect the aircraft performance by reducing the thrust force of the motors.

The control law for the regulation of the 2-DOF helicopter with the presence of additive failures in the actuators is defined as

$$\tau =D_o\left(q\right)\left[u_{PD}+u_{NL}\right]+C_o(q,\dot{q})+G_o\left(q\right),$$

(4)

where $\tau$ is the feedback control law, $G_o$ is the vector of gravitational torques, $D_o$ and $C_o$ are the nominal inertia and Coriolis effects, respectively. These differ from those of the actual helicopter model due to parametric uncertainties. The function $u_{PD}$ denotes the linear PD controller, where the gains $K_p$ and $K_d$ are tuned through the LMI-based convex optimization techniques proposed in [22]. The nonlinear controller $u_{NL}$ aims to compensate gravitational torques. LMI based robust controllers with a nonlinear compensation of uncertainties have been proposed in [23], for the case of fractional-order systems, and without considering the presence of faults.

By substituting the controller (4) into (3), one obtains

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \ddot{q}& =D^{-1}\left(q\right)\left\{\tau +f_a-[C(q,\dot{q})+G\left(q\right)]\right\},\hfill \\ \hfill & =D^{-1}\left(q\right)D_o\left(q\right)\left[u_{PD}+u_{NL}\right]+D^{-1}\left(q\right)f_a+D^{-1}\left(q\right)[\Delta C(q,\dot{q})+\Delta G\left(q\right)],\hfill \\ \hfill & =u_{PD}+u_{NL}+D^{-1}\left(q\right)f_a+\phi ,\hfill \end{array}\end{array}$$

(5)

for $\phi =D^{-1}\left(q\right)\Delta D\left(q\right)\left[u_{PD}+u_{NL}\right]+D^{-1}\left(q\right)[\Delta C(q,\dot{q})+\Delta G\left(q\right)]$ a term that condenses the effect of dynamic uncertainties and other disturbances, with $\Delta$, the deviation operator, such that $\Delta M=M_0-M$ is the difference between the nominal $M_0$ and the real M, where M is an arbitrary matrix/vector, and $M_0$ its nominal value.

4. Control Design and Implementation

Considering the state vector $x={[q^T,{\dot{q}}^T]}^T\in {\Re }^4$, one has that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_1& =\varphi ⟹{\dot{x}}_1=\dot{\varphi }=x_3\hfill \\ \hfill x_2& =\psi ⟹{\dot{x}}_2=\dot{\psi }=x_4\hfill \\ \hfill x_3& =\dot{\varphi }⟹{\dot{x}}_3=\ddot{\varphi }\hfill \\ \hfill x_4& =\dot{\psi }⟹{\dot{x}}_4=\ddot{\psi }\hfill \end{array}\end{array}$$

(6)

Therefore, by considering the linear PD controller as $u_{PD}=-Kx$, for a constant matrix gain K, the model described in (1) can be transformed into

$$\dot{x}=(A-BK)x+B(u_{NL}+\phi )+E_f{f}_a,$$

(7)

for matrices

$$A=\left[\begin{array}{cc}0& I\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ I\end{array}\right],\mathrm{and}{E}_f=\left[\begin{array}{c}0\\ D^{-1}\left(q\right)\end{array}\right].$$

Besides, the following assumption is considered with respect to the failure vector

$$∥F∥\le \gamma ∥x∥,$$

(8)

with $F=E_f{f}_a$, which means that the effect of the failure is upper bounded by a linear term that is proportional to the configuration and speed of the robotic system. This assumption is well funded by noticing that the failure impacts directly in the evolution of the state vector x.

The above condition prevents the equilibrium point of the nominal system, with $u_{NL}+\phi =0$ from deviating in the presence of tolerable faults. The proposed method assumes that the equilibrium of the nominal system is exponentially stable under the action of the linear controller $u_{PD}$.

The following result provides sufficient conditions to verify the robust stability of Equation (7), [24].

Theorem 1.

Consider system (7), with linear and nonlinear controllers

$$u_{PD}=-Kxand{u}_{NL}=-k_{nl}\frac{B^{T}Px}{∥B^{T}Px∥},$$

such that $k_{nl}>∥\phi ∥$, and $K=\left[K_p{K}_d\right]$ satisfies

$$\left[\begin{array}{cc}A\Xi +\Xi A^T+B{\rm Y}+{{\rm Y}}^T{B}^T& 0\\ 0& -\Xi \end{array}\right]⪯0,$$

(9)

with matrices $\Xi =P^{-1}$ and ${\rm Y}=-K\Xi$, for P symmetric. Then if γ in (8) fulfills

$$\gamma <\frac{{\lambda }_{min}\left(Q\right)}{2{\lambda }_{max}\left(P\right)},$$

(10)

for $Q=-PA-A^{T}P+PBK+K^T{B}^{T}P$, which is clearly symmetric and positive definite by virtue of (9), and ${\lambda }_{min}(-)$ and ${\lambda }_{max}(-)$ the minimum and maximum proper value functions, respectively. Then, $x=0$ is asymptotically stable. Furthermore, if all the above assumptions are globally valid, then the equilibrium $x=0$ is globally exponentially stable.

Proof. 

Since P is positive definite, it is possible to consider the candidate Lyapunov function $V=x^{T}Px$, whose time derivative along the closed-loop path becomes

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{V}& =x^{T}P\dot{x}+{\dot{x}}^{T}Px\hfill \\ \hfill & =2x^{T}P\dot{x}\hfill \\ \hfill & =2x^{T}P(A-BK)x+2x^{T}PB(u_{NL}+\phi )+2x^{T}PF.\hfill \end{array}\end{array}$$

(11)

Besides, using the fact that, for any arbitrary square matrix M and vector x, one has that $2x^{T}Mx=x^{T}Mx+x^T{M}^{T}x$; this results in

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{V}& =x^T\left[P(A-BK)+{(A-BK)}^{T}P\right]x+2x^{T}PB(u_{NL}+\phi )+2x^{T}PF\hfill \\ \hfill & =x^T\left(PA-PBK+A^T-K^T{B}^{T}P\right)x+2x^{T}PB(u_{NL}+\phi )+2x^{T}PF\hfill \\ \hfill & =-x^{T}Qx+2x^{T}PB(u_{NL}+\phi )+2x^{T}PF\hfill \\ \hfill & \le -{\lambda }_{min}{\left(Q\right)\left|\right|x\left|\right|}^2+2x^{T}PB(u_{NL}+\phi )+2x^{T}PF\hfill \end{array}\end{array}$$

(12)

In order to simplify the analysis, let us focus firstly on the term $x^{T}PB(u_{NL}+\phi )=x^{T}PB{u}_{NL}+x^{T}PB\phi$. Thereby, by substituting the definition of the nonlinear controller, one has

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x^{T}PB(u_{NL}+\phi )& =-x^{T}PB\left(k_{nl}\frac{B^{T}Px}{∥B^{T}Px∥}\right)+x^{T}PB\phi \hfill \\ \hfill & =-k_{nl}\left|\right|B^{T}Px\left|\right|+x^{T}PB\phi ,\hfill \end{array}\end{array}$$

(13)

and thus, by using the Cauchy–Schwartz inequality $x^{T}PB\phi \le \left|\right|B^{T}Px\left|\right|\left|\right|\phi \left|\right|$, one gets

$$x^{T}PB(u_{NL}+\phi )=-(k_{nl}-\left|\right|\phi \left|\right|\left)\right||B^{T}Px\left|\right|\le 0$$

since $k_{nl}>\left|\right|\phi \left|\right|$. Therefore, it is clear that

$$\dot{V}\le -{\lambda }_{min}{\left(Q\right)\left|\right|x\left|\right|}^2+2x^{T}PF.$$

(14)

It is also possible to simplify the above inequality, by noticing that

$$x^{T}PF\le \gamma {\lambda }_{max}{\left(P\right)\left|\right|x\left|\right|}^2,$$

(15)

which leads to

$$\dot{V}\le -[{\lambda }_{min}\left(Q\right)-2\gamma {\lambda }_{max}\left(P\right)]{\left|\right|x\left|\right|}^2.$$

(16)

Hence, by virtue of ${\lambda }_{min}\left(Q\right)-2\gamma {\lambda }_{max}\left(P\right)>0$, it can be concluded that $x=0$ is asymptotically stable. Moreover,

$$\dot{V}\le -\frac{{\lambda }_{min}\left(Q\right)-2\gamma {\lambda }_{max}\left(P\right)}{{\lambda }_{max}\left(P\right)}V,$$

(17)

and it is evident that $x\to 0$ with an exponential rate. □

As is conventional in a Lyapunov based control design, a heuristic process is conducted. This consists in gradually increasing the gain $k_{nl}$ until achieving an acceptable performance, with manageable frequency of commutation and control-signal amplitude in the actuators.

The structure of the controller is shown in Figure 5. It should be noticed that, under the conditions imposed by the proposed design, a failure is tolerable if condition (10) is fulfilled, while the converse cannot be stated.

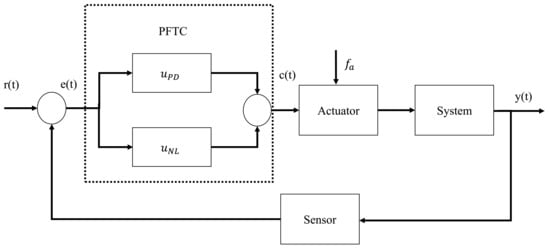
Figure 5. PFTC controller structure.

5. Numerical Results

In order to test the proposed algorithm, the simulation was carried out in Simulink^®. The parameters shown in Appendix A were used in the simulations. The controller gains were obtained by solving the LMI in Matlab^®.

$$Kp=\left[\begin{array}{cc}12.2668& 0\\ 0& 12.2668\end{array}\right],$$

$$Kd=\left[\begin{array}{cc}6.71320& 0\\ 0& 6.7132\end{array}\right],$$

$$P=\left[\begin{array}{cccc}0.0186& 0& 0.0062& 0\\ 0& 0.0186& 0& 0.0062\\ 0.0062& 0& 0.0186& 0\\ 0& 0.0062& 0& 0.0186\end{array}\right],$$

$$Q=-30.2586\left[\begin{array}{ccc}\begin{array}{c}2\\ 0\end{array}& \begin{array}{c}0\\ 2\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\right].$$

Two types of results are provided in this section. First, the simulation results are used to verify the fault tolerance scheme. Subsequently, the 2-DOF helicopter platform is used to implement the proposed controller. The Table 1 shows the case considered.

Table 1. Cases considered.

Case	Description
1	Nominal behaviour, without faults
2	fault in actuator 1 $25\%$
3	fault in actuator 1 $50\%$
4	fault in actuator 2 $25\%$
5	fault in actuator 2 $50\%$

5.1. Simulation Test

For simulations, the following initial conditions are considered $\varphi =0.1$ rad and $\psi =0.1$ rad. The appearance of abrupt faults in the system is considered, where the faults are modeled as step functions, the time of occurrence of the failure is the time for the step. The graphs show the behavior of the error, the time in which the fault occurs is denoted by a red vertical dotted line, while ${\tau }_{\varphi }=U_p$ and ${\tau }_{\psi }=U_y$ show the control signal in response to the presence of the fault, for the pitch and yaw angles.

Actuator $f_{a1}$ Fault 25%

The presence of a partial abrupt failure of $25\%$ is considered in actuator one at 20 s. Figure 6 shows the result obtained from the test. Note that when the failure occurs, the speed in actuator one decreases which can translate into a partial loss of efficiency in the motor, affecting the lift generated by the rotors. Therefore, the controller increases the input values $U_p$ to compensate the effect of failures and meet the control objective.

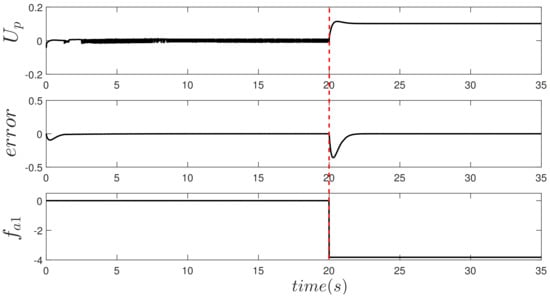
Figure 6. Behavior of the control signal, regulation error and fault in both states, where the fault is present in the actuator one, that is, $f_{a1}$.

Actuator $f_{a2}$ Fault 50%

The presence of a partial abrupt failure of $50\%$ is considered in actuator two (actuator two produces the $\psi$ motion); the dotted red line indicates the time of occurrence of the fault at 20 s. A fault greater than that of actuator one is considered; for this test, the failure considered is $50\%$; this is to make it more noticeable. The Figure 7 shows the error, the control signal for actuator two ($U_y$), and the fault behavior ($f_{a2}$). In the presence of the fault, the error is different from zero, which physically indicates that the angle yaw has changed with respect to the desired one; therefore, the fault-tolerant control algorithm reacts by increasing the control signal, trying to compensate for the presence of the failure, causing the error to return to the desired value or very close to this.

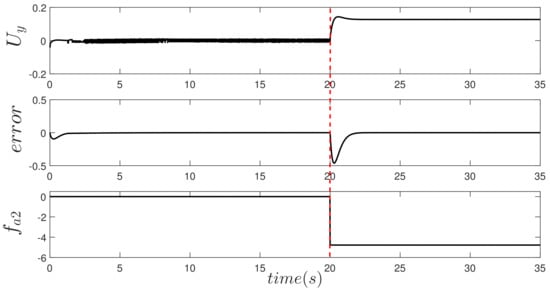
Figure 7. Behavior of the control signal, regulation error and fault in both states, where the fault is present in the actuator two, that is, $f_{a2}$.

5.2. Physical Test

Figure 8 and Figure 9 show the schematic diagram and the experimental platform of the closed-loop control system, respectively. The fault was produced by decreasing the thrust force by means of a series of covers of different size, such that, when a cover is placed on the thruster, it reduces the airflow, and in turns lift force. These covers were designed from the area of the rotating disk by varying its size. The masks cover from 100% of the surface to 25% of it.

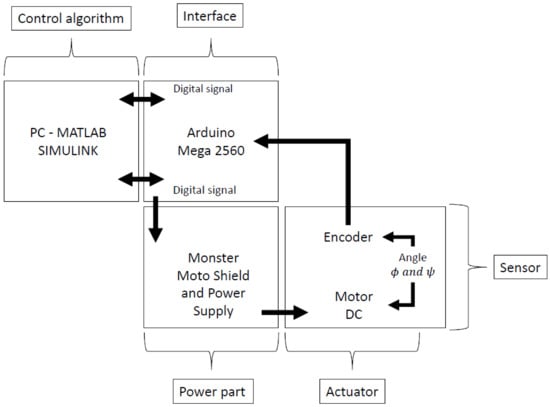
Figure 8. Schematic diagram of the 2-DOF helicopter closed-loop control system.

Figure 9. Experimental platform of the 2-DOF helicopter closed-loop control system.

For physical tests, the input to the plant is saturated, which influences the input voltage range at the actuators. Pulse Width Modulation or PWM is a technique used to transmit analog signals whose carrier signal is digital; in this technique, the duty cycle of a periodic signal is modified and is used to establish the amount of power that is sent to the actuators. This helps us to operate with the plant’s minimum and maximum intake values; for this case, the pulse width modulation (PWM) range values were: 150 PWM for the lower limit and 255 PWM for the upper limit.

In the case of regulation, the following initial conditions are given $\varphi$ = ${-42}^{\circ }$, $\psi$ = ${-20}^{\circ }$. Under nominal conditions, the implemented control fulfills the control objective. Figure 10 shows the evolution in time of the error in angles.

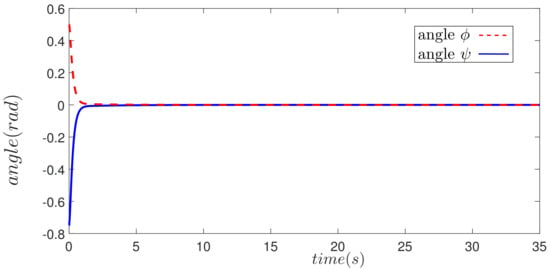
Figure 10. Time evolution of the error angles.

Actuator $f_{a1}$ Fault 25%

Figure 11 shows the evolution in time of the error in the angles $\varphi$, $\psi$, and the control signal provided by the PFTC. It is considered an abrupt failure of $25\%$ at 14 s. In the interval from one to six seconds oscillations of the system are shown, this is because the initial conditions are different from zero. The fault appears at second fourteen. While the fault acts directly on the lift motor, it also affects the angle $\varphi$. Once the failure occurs, both angles present a deviation; however, the proposed PFTC acts to compensate for this effect, maintaining the control objective.

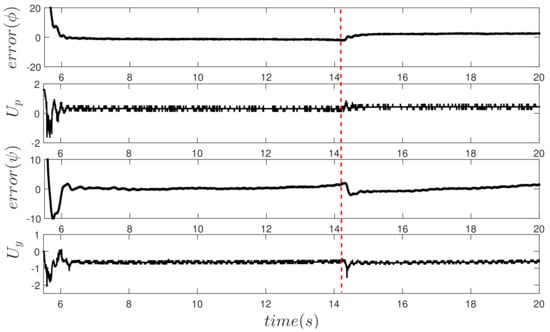
Figure 11. Response to the presence of failure in actuator $f_{a1}$ of $25\%$.

Actuator $f_{a1}$ Fault 50%

Figure 12 shows the evolution in time of the error in the angles $\varphi$, $\psi$, and the control signal provided by the PFTC. It is considered an abrupt failure of $50\%$ at 14 s. Due to the magnitude of the fault, the angle $\varphi$ presents deviation, which is reflected in the position error (error $\varphi$) and the increase of the controller signal. While the PFTC control compensates for the error, it does not maintain the desired position; however, the system can continue to operate safely, with a mild deviation.

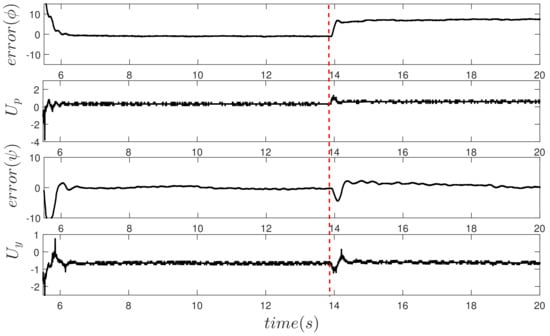
Figure 12. Response to the presence of failure in actuator $f_{a1}$ of $50\%$.

Actuator $f_{a2}$ Fault $25\%$ and $50\%$

Figure 13 and Figure 14 show the results when actuator faults occurred $f_{a2}$, the first one with a magnitude of $25\%$ at 11 s. The second with a failure magnitude of $50\%$ at 14 s. As can be noticed in Figure 13, in the event of a fault of 25%, the control algorithm presents a good performance since the error in both $\varphi$ and $\psi$ is minimal. However, when a 50% fault occurs, as seen in Figure 14, although the controller signals $U_y$ increases to compensate the fault, the algorithm cannot tolerate it; this is reflected in the behavior of the error $\psi$. Physically, this causes control of the rear engine to be lost, and therefore it is impossible to regulate the yaw movement, considering that the platform is fixed on a pedestal, the helicopter rotates without control on its axis.

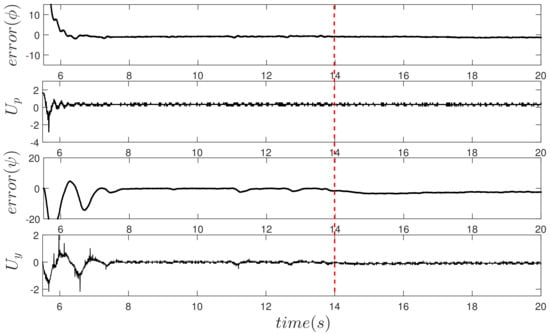
Figure 13. Response to the presence of failure in actuator $f_{a2}$ of $25\%$.

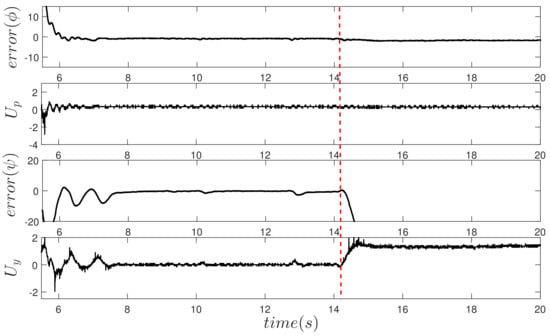
Figure 14. Response to the presence of failure in actuator $f_{a2}$ of $50\%$.

6. Discussions

6.1. Results

The coupling of the state variables is notorious in the obtained results. In each of the experimental tests, an encoder-sensor adjustment was necessary to set the angles $\varphi$ and $\psi$ to zero from the beginning, taking a few seconds. Therefore, the time on the plots does not start exactly at zero. Passive fault tolerant control provides tools to counteract the action of a large group of faults; nevertheless, the control objective cannot be guaranteed if these exceed the theoretical limits. In addition, only failures in the actuators are considered in this paper.

The method proposed in this work was compared with other control schemes. The first was based on the pole placement design, which is a design methodology based on the knowledge of the system’s transfer function, where the objective is to determine the closed-loop pole locations on the complex plane, thus establishing the controller gains. Besides, PI and PID controllers can be used with the pole placement design, as long as the plant transfer function system is of first or second order [17]. The second method was based on the Cohen–Coon method [25]. From the experimentation, the response of the plant to an input of the unit scale type is obtained; thus, it is intended to obtain a maximum overpass of $25\%$ in closed-loop, presenting a dead time and considering that the process is self-regulated. Table 2 shows the values of the gains used in the comparison, while Figure 15 shows the comparison results, in which it is clear that the proposed controller produces the best performance among all the tested methodologies.

Table 2. Controller gain values.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{d}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{k}}_{\mathit{n}}\mathit{l}$
Proposed method
$\varphi$	12.2668	6.71320	-	0.54
$\psi$	12.2668	6.7132	-	0.54
Pole placement
$\varphi$	6.28	3.0483	-	-
$\psi$	4.1229	3.0235	-	-
Cohen-Coon
$\varphi$	0.0375	0.827	1.072	-
$\psi$	0.0040	0.668	0.8	-

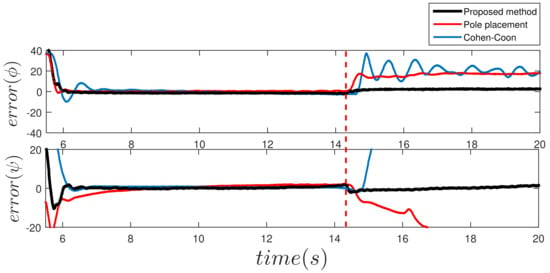
Figure 15. Response to the presence of failure in actuator $f_1$ of $25\%$.

6.2. Limitations

The proposed approach has shown some important (practical) robustness properties. However, there are also two main limitations. The first of them is with respect to the size of tolerable faults, that is, considering that the upper limit of the perturbations (for which the designed robust control is effective) is a fixed value, the size of the tolerable faults is reduced as more uncertainties are presents. Furthermore, given a control adjustment through $K_p$ and $K_d$, there are faults that cannot be tolerated, for which, the robustness condition is not satisfied. Then, the case of arbitrarily large faults is not treatable with the proposed approach. The second limitation is related to the design of the controller, which is obtained through an optimization algorithm; thus, there is only a small room for post-adjustment. As a consequence of the above limitations, it is difficult to analytically determine the size of tolerable failures, even if the upper limit of the uncertainties/disturbances, plus the magnitude of the failure, is known; this is due to the admissible controller existence conditions.

7. Conclusions

A passive fault tolerant controller is proposed, based on robust control techniques such as PD through linear matrix inequalities, and solved using convex optimization. Furthermore, to further improve the closed-loop performance, a nonlinear control is included. The methodology has been validated through numerical simulations and experiments on the Quanser^® 2-DOF Helicopter platform. Some issues associated with the physical implementation are resolved. The experimental test shows the effectiveness of the proposed approach in the presence of actuator failures, demonstrating fault tolerance. It is worth mentioning that the proposed technique can be extended to a broader class of aerodynamic robots such as fixed wing drones and quadcopters, among others. Future work will consider including nonlinear techniques, data-driven, artificial intelligence schemes, and fractional calculus based methods.