Algebraic Fault Analysis of SHA-256 Compression Function and Its Application
Abstract
1. Introduction
1.1. Background
1.2. Related Work
1.3. Our Contribution
1.4. Organization
2. Materials and Methods
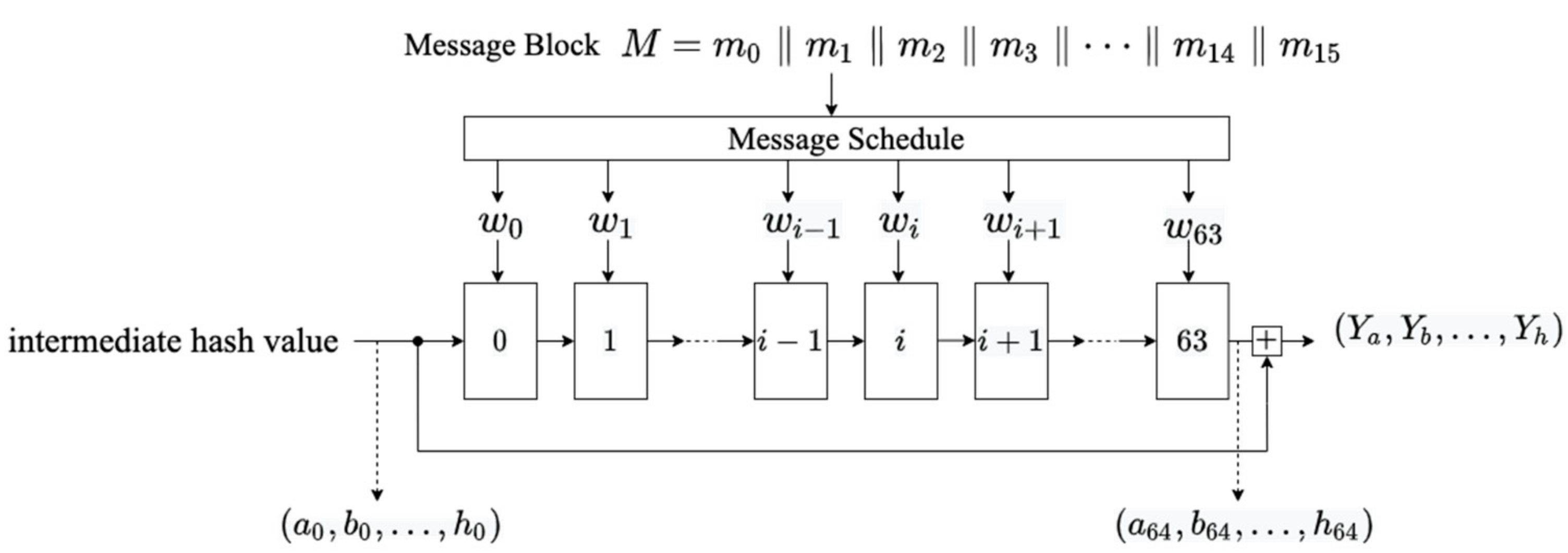
2.1. SHA-256 Compression Function
2.2. SHACAL-2
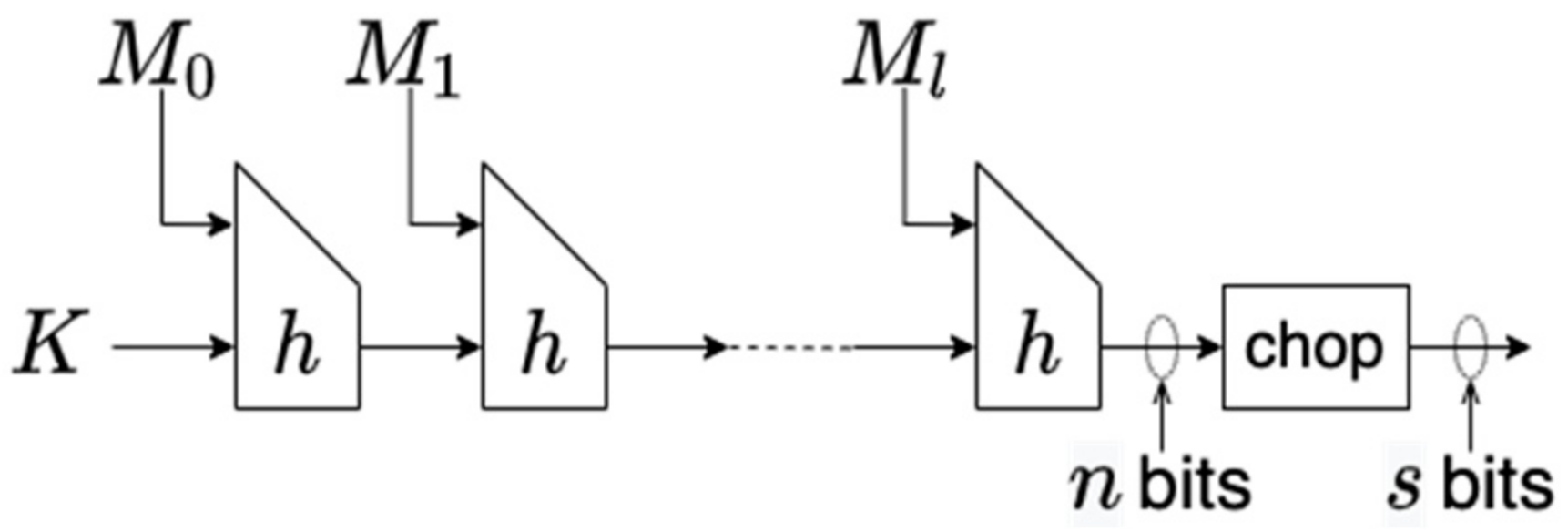
2.3. ChopMD-MAC
2.4. Algebraic Fault Analysis for the SHA-256 Compression Function by Hao et al.
2.4.1. Phase 1
2.4.2. Phase 2
3. Results
3.1. Detailed Examination of AFA
- (1)
- Inject three faults into and recover , , , and .
- (2)
- Inject three faults into and recover , , and .
- (3)
- Inject three faults into and recover , , , and .
- (4)
- Inject three faults into and recover , , , and .
- (5)
- Calculate the input message block and intermediate hash value.
3.2. AFA for SHACAL-2
- (1)
- Inject three faults into and recover , , , and .
- (2)
- Inject three faults into and recover , , , and .
- (3)
- Inject three faults into and recover , , , and .
- (4)
- Inject three faults into and recover , , , and .
- (5)
- Calculate the input message.
3.3. AFA for Almost Universal Forgery of chopMD-MAC
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the Importance of Checking Cryptographic Protocols for Faults (Extended Abstract). In Advances in Cryptology-EUROCRYPT ‘97, International Conference on the Theory and Application of Cryptographic Techniques, Konstanz, Germany, 11–15 May 1997; Fumy, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1233, pp. 37–51. [Google Scholar]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the Importance of Eliminating Errors in Cryptographic Computations. J. Cryptol. 2001, 14, 101–119. [Google Scholar] [CrossRef]
- Biham, E.; Shamir, A. Differential fault analysis of secret key cryptosystems. In Advances in Cryptology-CRYPTO ‘97, 17th Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 1997; Kaliski, B.S., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1294, pp. 513–525. [Google Scholar]
- Dusart, P.; Letourneux, G.; Vivolo, O. Differential Fault Analysis on A.E.S. In Applied Cryptography and Network Security, First International Conference, ACNS 2003, Kunming, China, 16–19 October 2003; Zhou, J., Yung, M., Han, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2846, pp. 293–306. [Google Scholar]
- Li, R.; Li, C.; Gong, C. Differential Fault Analysis on SHACAL-1. In Sixth International Workshop on Fault Diagnosis and Tolerance in Cryptography, FDTC 2009, Lausanne, Switzerland, 6 September 2009; Breveglieri, L., Koren, I., Naccache, D., Oswald, E., Seifert, J.P., Eds.; IEEE Computer Society: Washington, DC, USA, 2009; pp. 120–126. [Google Scholar]
- Kitae, J.; Lee, C. Differential Fault Analysis on Block Cipher LED-64. In Future Information Technology, Application, and Service; Hyuk, J., Park, J., Leung, V., Wang, C.L., Shon, T., Eds.; Springer: Dordrecht, The Netherland, 2012; Volume 164, pp. 747–755. [Google Scholar]
- Hemme, L.; Hoffmann, L. Differential Fault Analysis on the SHA1 Compression Function. In 2011 Workshop on Fault Diagnosis and Tolerance in Cryptography, FDTC 2011, Tokyo, Japan, 29 September 2011; Breveglieri, J., Guilley, S., Koren, I., Naccache, D., Takahashi, J., Eds.; IEEE Computer Society: Washington, DC, USA, 2011; pp. 54–62. [Google Scholar]
- Jinkeon, K.; Kitae, J.; Jaechul, S.; Seokhie, H. Differential Fault Analysis on HAS-160 Compression Function. In Computer Science and Its Applications; Yeo, S.S., Pan, Y., Lee, Y., Chang, H., Eds.; Springer: Dordrecht, The Netherland, 2012; Volume 203, pp. 97–105. [Google Scholar]
- Li, W.; Tao, Z.; Gu, D.; Wang, Y.; Liu, Z.; Liu, Y. Differential Fault Analysis on the MD5 Compression Function. J. Comput. 2013, 8, 2888–2894. [Google Scholar] [CrossRef]
- Courtois, N.; Ware, D.; Jackson, K. Fault-Algebraic Attacks on Inner Rounds of DES. In Proceedings of the eSmart 2010 European Smart Card Security Conference, Sophia Antipolis, France, 22–24 September 2010. [Google Scholar]
- Bouillaguet, C.; Derbez, P.; Fouque, P.A. Automatic Search of Attacks on Round-Reduced AES and Applications. In Advances in Cryptology-CRYPTO 2011—31st Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Rogaway, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6841, pp. 169–187. [Google Scholar]
- Zhao, X.; Guo, S.; Zhang, F.; Shi, Z.; Ma, C.; Wang, T. Improving and Evaluating Differential Fault Analysis on LED with Algebraic Techniques. In 2013 Workshop on Fault Diagnosis and Tolerance in Cryptography, Los Alamitos, CA, USA, 20 August 2013; Fischer, W., Schmidt, J.M., Eds.; IEEE Computer Society: Washington, DC, USA, 2013; pp. 41–51. [Google Scholar]
- Ganesh, V.; Dill, D.L. A Decision Procedure for Bit-Vectors and Arrays. In Computer Aided Verification, 19th International Conference, CAV 2007, Berlin, Germany, 3–7 July 2007; Damm, W., Hermanns, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4590, pp. 519–531. [Google Scholar]
- CryptoMiniSat5. Available online: https://www.msoos.org/cryptominisat5/ (accessed on 23 August 2021).
- National Institute of Standards and Technology. Secure Hash Standard (SHS). FIPS PUB 180-4; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- National Institute of Standards and Technology. The Keyed-Hash Message Authentication Code (HMAC). FIPS PUB 198-1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008. [Google Scholar]
- Jeong, K.; Lee, Y.; Sung, J.; Hong, S. Security Analysis of HMAC/NMAC by Using Fault Injection. J. Appl. Math. 2013, 2013, 101907:1–101907:6. [Google Scholar] [CrossRef]
- Hao, R.; Li, B.; Ma, B.; Song, L. Algebraic Fault Attack on the SHA-256 Compression Function. IJORCS 2014, 4, 1–9. [Google Scholar] [CrossRef][Green Version]
- Nejati, S.; Horáček, J.; Gebotys, C.; Ganesh, V. Algebraic Fault Attack on SHA Hash Functions Using Programmatic SAT Solvers. In Principles and Practice of Constraint Programming—24th International Conference, CP 2018, Lille, France, 27–31 August 2018; Hooker, J., Ed.; Springer: Cham, Switzerland, 2018; Volume 11008, pp. 737–754. [Google Scholar]
- Modifications to NESSIE Submissions Selected for 2nd Phase. Available online: https://www.cosic.esat.kuleuven.be/nessie/tweaks (accessed on 23 August 2021).
- Naito, Y.; Sasaki, Y.; Wang, L.; Yasuda, K. Generic State-Recovery and Forgery Attacks on ChopMD-MAC and on NMAC/HMAC. In Advances in Information and Computer Security—8th International Workshop on Security, IWSEC 2013, Okinawa, Japan, 18–20 November 2013; Sakiyama, K., Terada, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8231, pp. 83–98. [Google Scholar]

| Fault Position | Recovered Chaining Values | Computation Time [s] |
|---|---|---|
| none | - | |
| none | - | |
| 20.3 | ||
| 176.5 | ||
| 66.7 | ||
| 82.0 | ||
| 109.6 | ||
| 110.0 |
| Phase 1 | Fault Position | |||
|---|---|---|---|---|
| Number of Faults | Success Rate [%] | Average Time [s] | Success Rate [%] | Average Time [s] |
| 14 | 100 | 11.6 | 100 | 39.9 |
| 13 | 97 | 11.0 | 100 | 41.7 |
| 12 | 98 | 10.9 | 100 | 41.0 |
| 11 | 100 | 11.2 | 100 | 37.4 |
| 10 | 96 | 10.5 | 99 | 47.4 |
| 9 | 93 | 11.2 | 100 | 45.5 |
| 8 | 88 | 10.8 | 100 | 59.3 |
| 7 | 80 | 10.3 | 96 | 44.5 |
| 6 | 75 | 12.6 | 89 | 88.0 |
| 5 | 50 | 13.7 | 82 | 123.9 |
| 4 | 30 | 31.3 | - | - |
| 3 | 1 | 112.5 | - | - |
| Phase 2 | Fault Position | |||
|---|---|---|---|---|
| Number of Faults |
Success Rate [%] |
Average Time [s] | Success Rate [%] | Average Time [s] |
| 14 | 100 | 1.00 | 100 | 81.34 |
| 13 | 97 | 0.93 | 100 | 83.48 |
| 12 | 98 | 0.91 | 100 | 89.20 |
| 11 | 100 | 0.86 | 100 | 95.11 |
| 10 | 96 | 0.84 | 100 | 67.34 |
| 9 | 93 | 0.76 | 100 | 72.71 |
| 8 | 88 | 0.77 | 100 | 102.73 |
| 7 | 80 | 0.73 | 100 | 98.08 |
| 6 | 75 | 0.70 | 100 | 102.01 |
| 5 | 50 | 0.64 | 100 | 87.25 |
| 4 | 30 | 0.77 | 100 | 121.75 |
| 3 | 1 | 0.78 | 100 | 492.76 |
| Output of Chop Function | Average Time [s] | Success Rate [%] |
|---|---|---|
| 1072 | 100 | |
| 46,344 | 80 | |
| 37,574 | 100 | |
| 49,950 | 70 | |
| 2012 | 90 | |
| 15,444 | 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K.; Hori, K.; Hirose, S. Algebraic Fault Analysis of SHA-256 Compression Function and Its Application. Information 2021, 12, 433. https://doi.org/10.3390/info12100433
Nakamura K, Hori K, Hirose S. Algebraic Fault Analysis of SHA-256 Compression Function and Its Application. Information. 2021; 12(10):433. https://doi.org/10.3390/info12100433
Chicago/Turabian StyleNakamura, Kazuki, Koji Hori, and Shoichi Hirose. 2021. "Algebraic Fault Analysis of SHA-256 Compression Function and Its Application" Information 12, no. 10: 433. https://doi.org/10.3390/info12100433
APA StyleNakamura, K., Hori, K., & Hirose, S. (2021). Algebraic Fault Analysis of SHA-256 Compression Function and Its Application. Information, 12(10), 433. https://doi.org/10.3390/info12100433






