1. Introduction
The vast advances made in wireless technology and electronics have enabled the emergence of wireless sensor networks (WSN) which have received much attention recently and are expected to become commonplace due to playing a major role in various applications such as industrial monitoring, health care monitoring, environmental sensing, target tracking, etc. Since sensors are usually small low-power devices powered by batteries that have limited lifetime, they are usually designed to send data to a fusion center at which most of the energy-consuming computations are performed. An example of data sent to the fusion center for processing are the time-of-arrival (TOA) samples needed for range-based anchor-based localization, which is the application considered in this work. The TOA data obtained at the anchors and sent to the fusion center for processing are indicative of the distance between an anchor and the target sensor to be localized or tracked. However, data processing is not the only energy-consuming process encountered. In fact, communication energy consumption in WSNs is greater than computational energy consumption [
1]. Thus, in the present work, we focus on minimizing the energy expenditure in data communication between the anchors and the fusion center by minimizing the data volume undergoing transmission without significantly affecting the transmitted information.
The work in [
1] suggests two approaches for energy-efficient data processing and communication in WSNs. The first direction is to use short word-length (SWL) techniques such as delta modulation (DM) [
2] and sigma-delta modulation (SDM) [
3] in order to reduce the number of bits that represent a signal sample by exploiting the difference between adjacent samples. This is beneficial in reducing both computational and communication power. The second approach is to use compressive sensing (CS) [
4,
5] to reduce the communication power. CS compresses transmitted data by sampling randomly at a sub-Nyquist rate. Reconstruction of the original signal can generally be achieved by powerful optimization techniques such as
-minimization [
4]. CS with random sampling is effective in avoiding aliasing in reconstruction due to sub-Nyquist sampling of sparse signals [
6,
7].
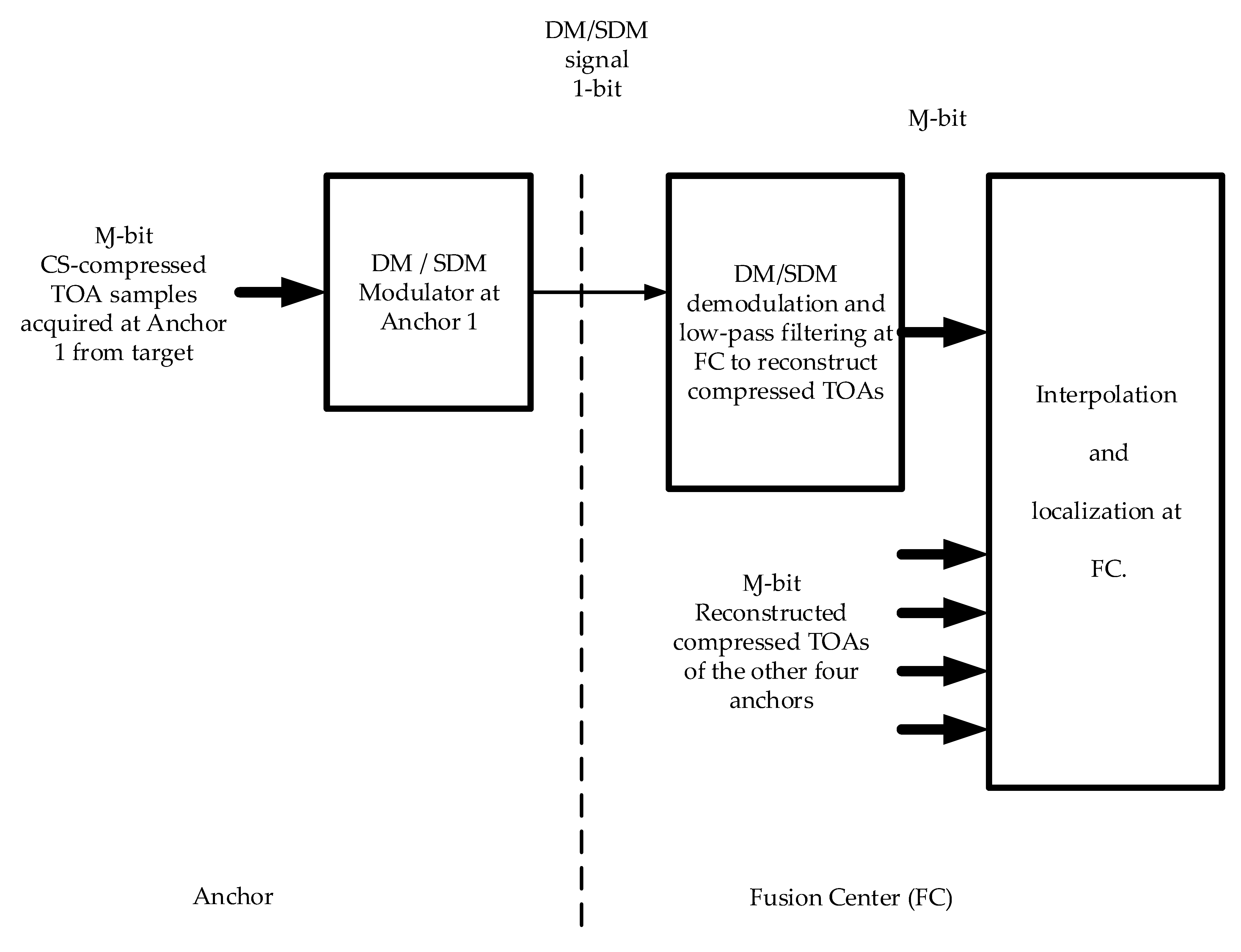
The present work attempts both CS and SWL directions simultaneously to reduce the communication energy expenditure by first applying CS to the data to be transmitted so as to reduce the number of samples and then applying DM or SDM to achieve a 1-bit representation per sample. We demonstrate the performance of this approach in the context of target tracking in WSNs as depicted in the block diagram of
Figure 1. The CS-compressed TOA data are DM/SDM-modulated at the anchors before transmission to the fusion center where they are DM/SDM-demodulated, LP-filtered and interpolated to restore the original uncompressed TOA values. Then, localization or target tracking is achieved at the fusion center.
To the best of our knowledge, combining CS with SWL techniques has not been attempted in the literature. There are, however, several works on 1-bit CS [
8,
9,
10] that are quite different from the present approach. In 1-bit CS, the limiting case of 1-bit measurements is considered by preserving just the sign information of random samples or measurements and treating the measurements as sign constraints to be enforced in reconstruction. The original signal is then recovered by constrained optimization to within a scaling factor since sign information does not include amplitude information. To resolve this ambiguity, reconstruction is constrained to be on the unit sphere to reduce the search space [
8]. However, it has been shown in [
11,
12] that for target localization or tracking in WSNs, the computationally expensive recovery by convex optimization can be replaced by simple linear interpolation due to the usually low frequency content of TOA measurements from moving targets. In addition to its computational efficiency, linear interpolation can be made to operate in real time or with small delay whereas other optimization techniques such as
-minimization are batch processing techniques requiring the whole or a considerably large part of the signal to be available to be processed for optimized reconstruction [
4,
13]. The proposed combined CS-SWL method suits the simple linear interpolation recovery scheme.
Referring to the system in
Figure 1, some computation is still needed in the anchor nodes to implement a random number generator for CS random acquisition of the TOA samples, in addition to the simple hardware of the DM/SDM modulator. However, this is more than compensated for by the achieved communication energy efficiency. Localization at the fusion center is performed by the method of gradient descent (GD) [
11,
12,
14].
The remainder of the paper is organized as follows.
Section 2 discusses GD localization in WSNs based on CS.
Section 3 overviews DM and SDM, whereas
Section 4 explains their incorporation in the overall localization system and the ensuing parameter adjustments. Simulation results are presented in
Section 5, and
Section 6 concludes the paper.
2. CS-Based Gradient Descent Localization in WSNs
Localization in WSNs usually involves distance measurements between a target node and a number of reference nodes or anchors. Computing these distances by TOA data is most commonly adopted in low-density WSNs due to their insensitivity to inter-device distances compared to other types of data used in range-based localization such as time-difference-of-arrival (TDOA), received-signal-strength (RSS) or angle-of-arrival (AOA) data [
15]. Iterative localization methods using GD are widely used due to their noise immunity compared to analytical methods [
16] and low computational complexity [
17].
We consider GD localization in three dimensions as in [
11,
12]. The error function to be minimized in this optimization problem is given by
with
where the target node
needs
N anchor nodes to be localized. For three dimensions,
N is at least 4. The anchor nodes are
with
. The distance between the
i-th anchor node and the target is
, the receive time of the
i-th anchor is
, and the transmit time of the target is
. Thus,
is the TOA measurement acquired at the
i-th anchor. Finally,
c is the speed of light when RF or UWB signals are used in ranging.
GD minimization of the error function in Equation (1) is achieved by
where
and
are the vectors of position and gradient at the
k-th iteration respectively, and
α is the convergence factor. The iteration index
k is also the time index when tracking is performed for a moving target.
The gradient vector at the
k-th iteration is given by
CS can be used to acquire the TOA data for energy-efficient localization. Following is a brief overview of CS.
In compressive sensing, a discrete-time signal vector
can be acquired or sampled compressively by a measurement or sampling matrix
to yield the vector
,
, according to
Clearly, the above is an underdetermined system of equations in terms of the recovery of
from
. We assume that
is
K-sparse in the
M-dimensional space spanned by the
M basis vectors
such that
where
is the matrix whose columns consist of the
M basis vectors, and
s is the transform vector containing only
K non-zero elements and
K << M. In our case,
is the DFT matrix. Therefore, Equation (5) becomes
CS theory states that the vector
is recoverable from
if the sparsity information of the former is preserved in the latter. This is possible if matrix
satisfies the restricted isometry property (RIP) [
18] which dictates the incoherence of
with
. This incoherence can be established by ensuring that
is a random matrix which results in the vector
being fully recoverable from
when the following inequality is satisfied:
where
C is a constant and by solving the convex optimization problem of the underdetermined system of equations using
-minimization [
4,
19].
For localization in WSNs, CS can therefore be applied by random acquisition or sampling of the TOA data at the anchors at a rate below the Nyquist rate. It has been demonstrated in [
11] that the TOA data associated with helical motion of the target node, for instance, is sufficiently sparse in frequency, thereby justifying the use of CS for energy-efficient tracking. Moreover, it has also been shown that the computationally complex and batch-processing
-minimization can be replaced by simple linear interpolation of the compressed TOA data received at the fusion center as a computationally efficient and almost real-time recovery scheme of the original TOA data. This is possible because of the usually low-frequency content of TOA data, taking into account that interpolation is a low-pass filtering operation.
Thus far, a means to reduce communication energy consumption has been ensured by using CS to reduce the number of TOA samples transmitted from the anchors to the fusion center. A further reduction of this energy consumption component is to achieve a 1-bit representation per TOA sample by using DM before transmission. DM techniques are overviewed in the following section.
4. CS-DM/SDM Localization in WSNs
Both DM and SDM systems are considered for the application of WSN node localization and tracking employing CS in the anchor acquisition of the TOA samples sent from the target. Referring to
Figure 1 of the introduction section, let us assume that the sample reduction ratio
R regarding the CS operation is given by
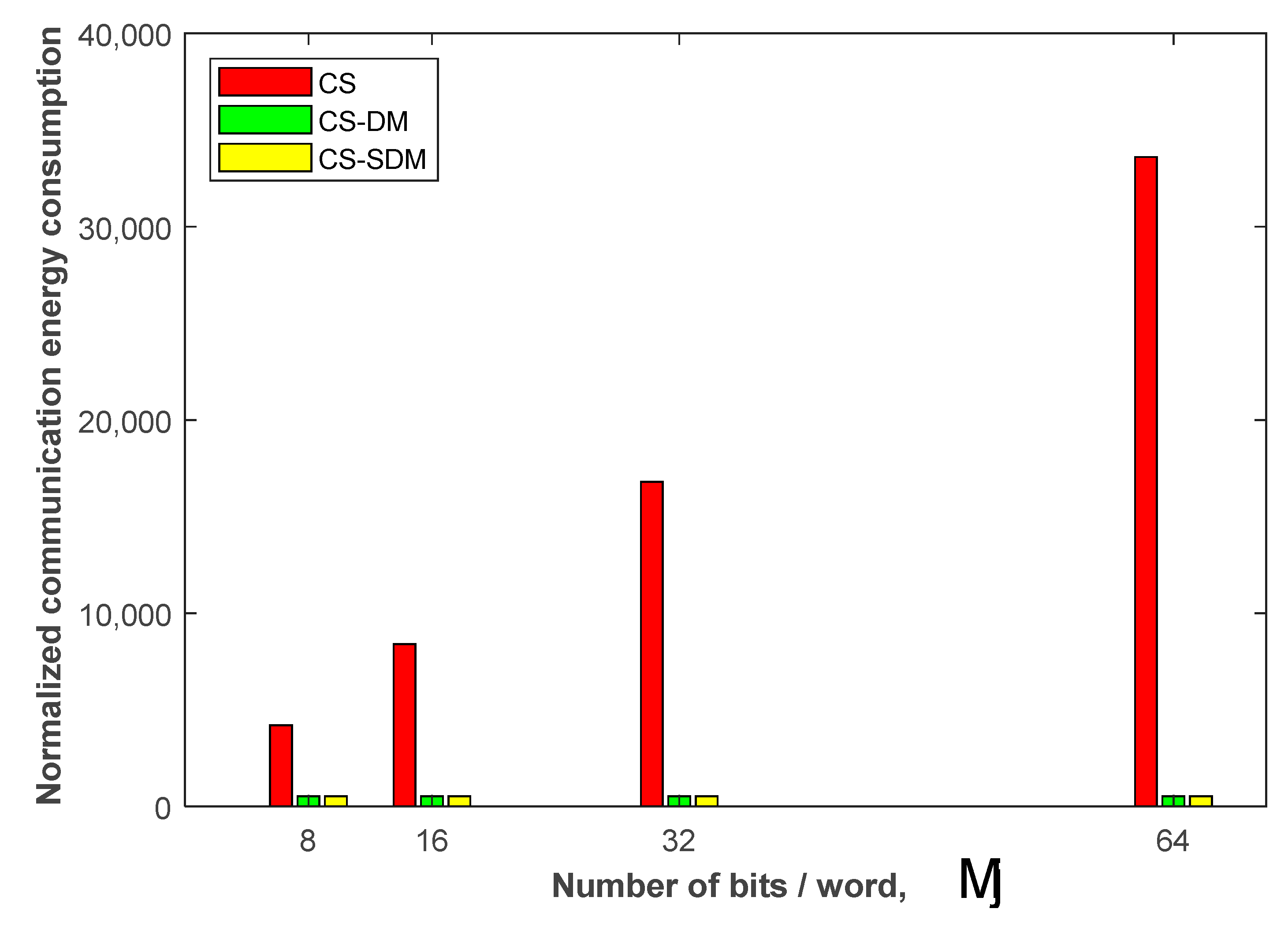
Therefore, CS reduces the number of transmitted samples by R. If we further assume that each sample is represented by an Ɱ-bit word, then the total communication energy from anchor to fusion center, after applying CS and DM/SDM, is reduced by (R. Ɱ) owing to the 1-bit-per-sample representation enabled by DM/SDM.
The localization error criterion used to assess performance is chosen as the normalized error measure (NEM) given in dBs. This is a relative error measure involving the localization error function
and the true distances
of Equation (1), and is given by
where
K is the iteration number, Ҡ is the total number of target path points, and
N is the number of anchors.
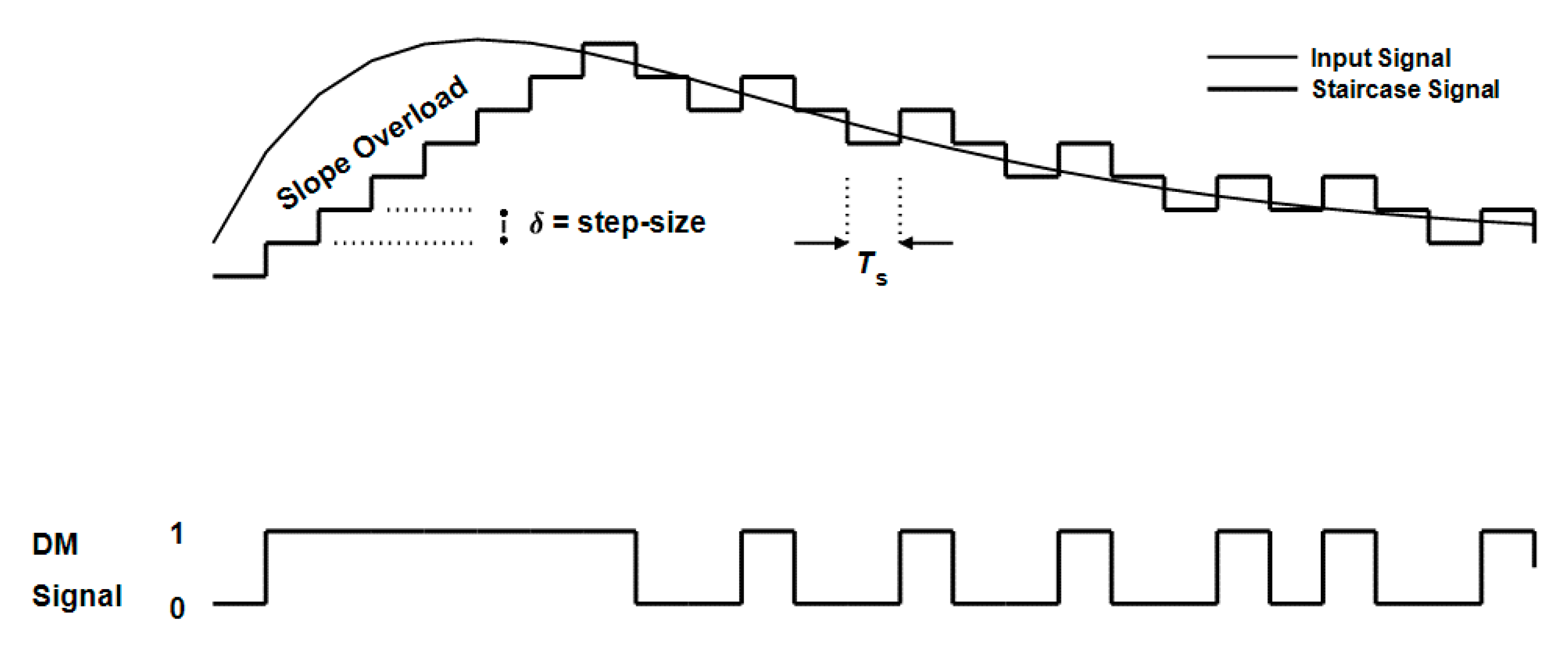
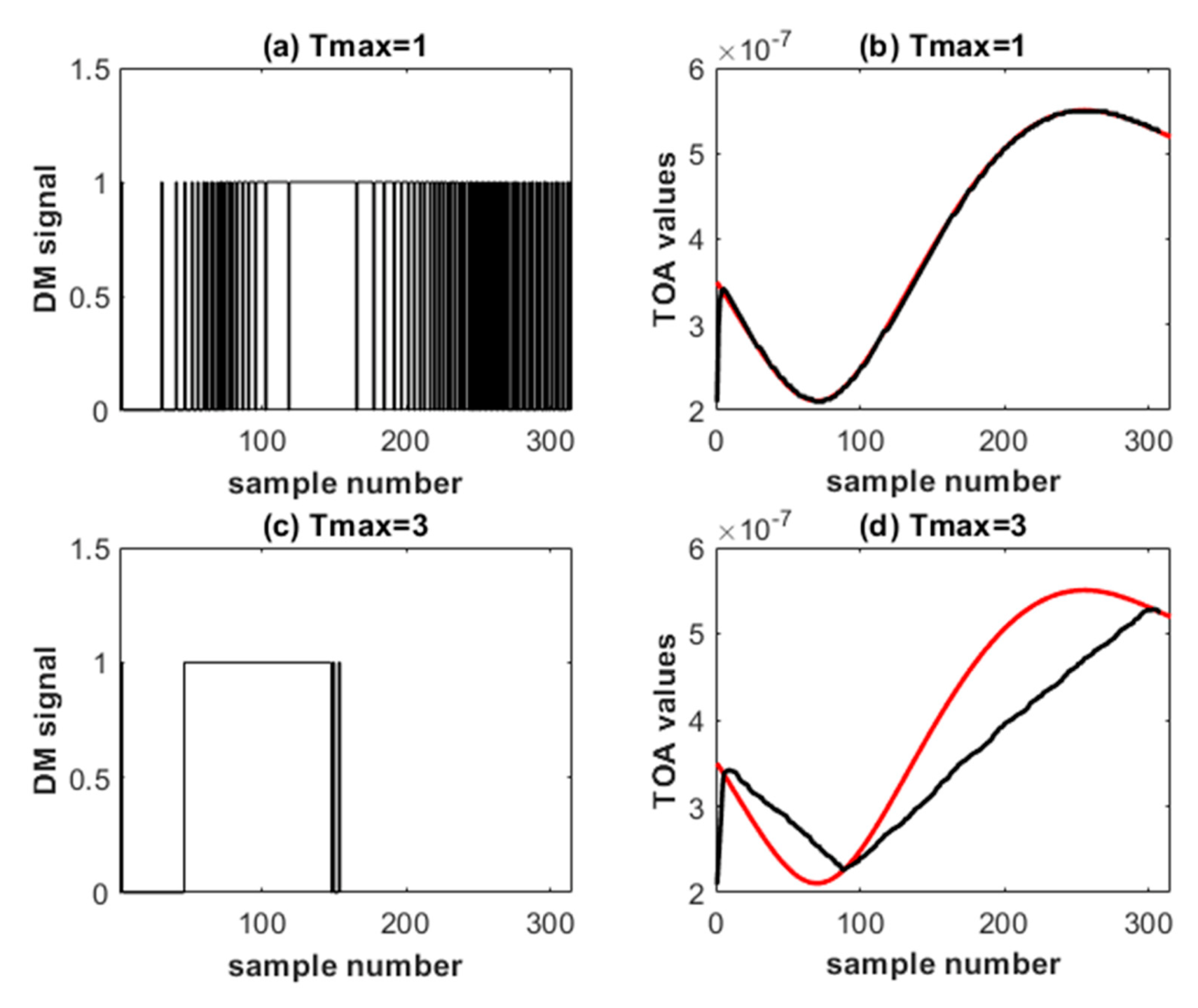
Let us first consider the DM-based localization system. Under no-compression conditions (R = 1), operation can be almost free from quantization noise when the step size is optimized for best performance measured by NEM. Introducing CS to the system by randomly acquiring TOA values at the anchors and gradually increasing the maximum random sampling interval, we find that the succeeding DM system will exhibit slope overload because the input samples change abruptly in magnitude between successive randomly spaced samples. Thus, the effect of CS on the original uncompressed slowly varying TOA sequence is to introduce higher frequencies due to abrupt transitions caused by compression, thereby leading to slope overload. This necessitates re-optimizing (increasing) the DM step size every time the maximum sampling interval is increased until normal operation is resumed with no slope overload. The increasing step size will increase the quantization noise and hence decrease the localization accuracy at the fusion center. This is the major disadvantage of the DM system when used in conjunction with CS.
Noting the noise shaping property of the SDM system, its use instead of the DM system is expected to improve the overall performance or localization accuracy measured by NEM. However, the reconstruction LPF at the fusion center must be carefully designed. Moreover, the phase introduced by this filter introduces additional localization error. In contrast, the reconstruction filter used with CS-DM localization can be simple and does not introduce significant distortion; the reason is that the reconstruction filter filters the staircase waveform which is mainly of low frequency content, whereas in SDM, it filters the SDM signal itself which has a wider-range spectral content. Therefore, the filter to be used in this work in conjunction with CS-SDM will be chosen as a linear-phase optimal finite impulse response (FIR) digital filter employing the Parks–McClellan filter design algorithm [
21]. The equiripple method of designing this type of filter is an optimization problem that adjusts the coefficient values to create an optimal filter such that the transition width is minimized along with the stopband and passband ripple.
In this work, we consider tracking a target moving along a helical path in three dimensions representing the moving-target position. These dimensions are described by the following equations:
We assume that the angle
takes on the values from zero to 2π, and
r and
are constants. All anchors are assumed to be in the radio range of the target path. In [
11,
12], a helical path with
r = 40 and
= 20 was considered. It was shown that the TOA values as a function of time had low frequency content. Therefore, we consider 315 points in the path are enough to yield acceptable localization error.
To achieve CS, the complete vector of 315 discrete TOA samples is input to a random sampling algorithm to yield a shorter vector of TOA measurements as in Equation (5), only to be reconstructed later by interpolation at the fusion center. In Equation (5), the sampling matrix Φ has at most one non-zero value (unity) in each row. The random sampling that generates the compressed vector is based on the selection of samples separated by random periods. The random variable representing these random periods is uniformly distributed over the time interval [
]. Thus, the sampling instants indexed by the integer
, are given by
where
is the initial time instant,
is the original sampling period and
, is the discrete uniform distribution over the integer interval
.
It is assumed that the fusion center knows the distribution generating the random sampling instants in order to maintain the structure of the original TOA samples. The interpolated or reconstructed TOA values are then used to localize the target path by gradient descent.
In the following section on simulation results, both localization systems employing CS-DM and CS-SDM will be simulated, discussed and compared.
Author Contributions
Conceptualization, Z.M.H. and N.A.S.A.; methodology, N.A.S.A. and Z.M.H.; software, N.A.S.A. and Z.M.H.; formal analysis, N.A.S.A. and Z.M.H.; investigation, N.A.S.A. and Z.M.H.; resources, N.A.S.A. and Z.M.H.; writing—original draft preparation, N.A.S.A.; writing—review and editing, Z.M.H. and N.A.S.A.; supervision, Z.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially funded by Edith Cowan University via the ASPIRE Program.
Data Availability Statement
The MATLAB code for this work is available from the authors on request.
Acknowledgments
The authors would like to thank Edith Cowan University for supporting this project via the ASPIRE Program. Thanks and appreciation are also due to the anonymous reviewers for their constructive comments and to the MDPI office for prompt response and valuable guidance throughout the review process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hussain, Z.M. Energy-Efficient Systems for Smart Sensor Communications. In Proceedings of the 2020 30th International Telecommunication Networks and Applications Conference (ITNAC), IEEE, Melbourne, Australia, 25–27 November 2020; pp. 1–4. [Google Scholar]
- Stallings, W. Data and Computer Communications, 9th ed.; Pearson: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Aziz, P.M.; Sorensen, H.V.; Van der Spiegel, J. An overview of sigma-delta converters. IEEE Signal Process. Mag. 1996, 13, 61–84. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Qaisar, S.; Bilal, R.M.; Iqbal, W.; Naureen, M.; Lee, S. Compressive sensing; from theory to applications, a survey. J. Commun. Netw. 2013, 15, 443–456. [Google Scholar] [CrossRef]
- Bilinskis, I.; Selavo, L.; Sudars, K. Method for sensor data alias-free acquisition from wideband signal sources and their asymmetric compression reconstruction. Balt. J. Mod. Comput. 2013, 1, 199–209. [Google Scholar]
- Tarczynski, A.; Allay, N. Spectral analysis of randomly sampled signals: Suppression of aliasing and sample jitter. IEEE Trans. Signal Process. 2004, 12, 3324–3334. [Google Scholar] [CrossRef]
- Boufounos, P.T.; Baraniuk, R.G. 1-Bit Compressive Sensing. In Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS’08), Princeton, NJ, USA, 19–21 March 2008; IEEE: Princeton, NJ, USA; pp. 16–21. [Google Scholar]
- Yin, M.; Yu, K.; Wang, Z. Compressive sensing based sampling and reconstruction for wireless sensor array network. Math. Probl. Eng. 2016, 2016, 11. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Suter, B.W. One-Bit compressive sensing via lo-minimization. EURASIP J. Adv. Signal Process. 2016. [Google Scholar] [CrossRef] [Green Version]
- Alwan, N.A.S.; Hussain, Z.M. Compressive sensing for localization in wireless sensor networks: An approach for energy and error control. IET Wirel. Sens. Syst. 2018, 8, 116–120. [Google Scholar] [CrossRef]
- Alwan, N.A.S.; Hussain, Z.M. Compressive sensing with chaotic sequences: An application to localization in wireless sensor networks. Wirel. Pers. Commun. 2019, 105, 941–950. [Google Scholar] [CrossRef]
- Chen, W.; Wassell, I.J. Energy-efficient signal acquisition in wireless sensor networks: A compressive sensing framework. IET Wirel. Sens. Syst. 2012, 2, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Qiao, D.; Pang, G.K.H. Localization in Wireless Sensor Networks with Gradient Descent. In Proceedings of the IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 23–26 August 2011. [Google Scholar]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O., III; Moses, R.L.; Correal, N.S. Locating the nodes. IEEE Signal Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Zhang, L.; Tao, C.; Yang, G. Wireless positioning: Fundamentals, systems and state-of-the-art signal processing techniques. In Cellular Networks- Positioning, Performance Analysis, Reliability; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Alwan, N.A.S.; Hussain, Z.M. Gradient descent localization in wireless sensor networks. In Wireless Sensor Networks, Insights and Innovations; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Candes, E.J.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles; exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Flood, J.E. Digital Modulation. In Telecommunications Engineer’s Reference Book; Elsevier Ltd.: Oxford, UK, 1993. [Google Scholar]
- Lyons, R.G. Understanding Digital Signal Processing, 3rd ed.; Prentice-Hall, Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Molisch, A.F. Wireless Communications, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
Figure 1.
Combined CS-SWL communication-energy-efficient localization wireless sensor system using five anchor or reference nodes. Note that thick arrows are used for multibit connections.
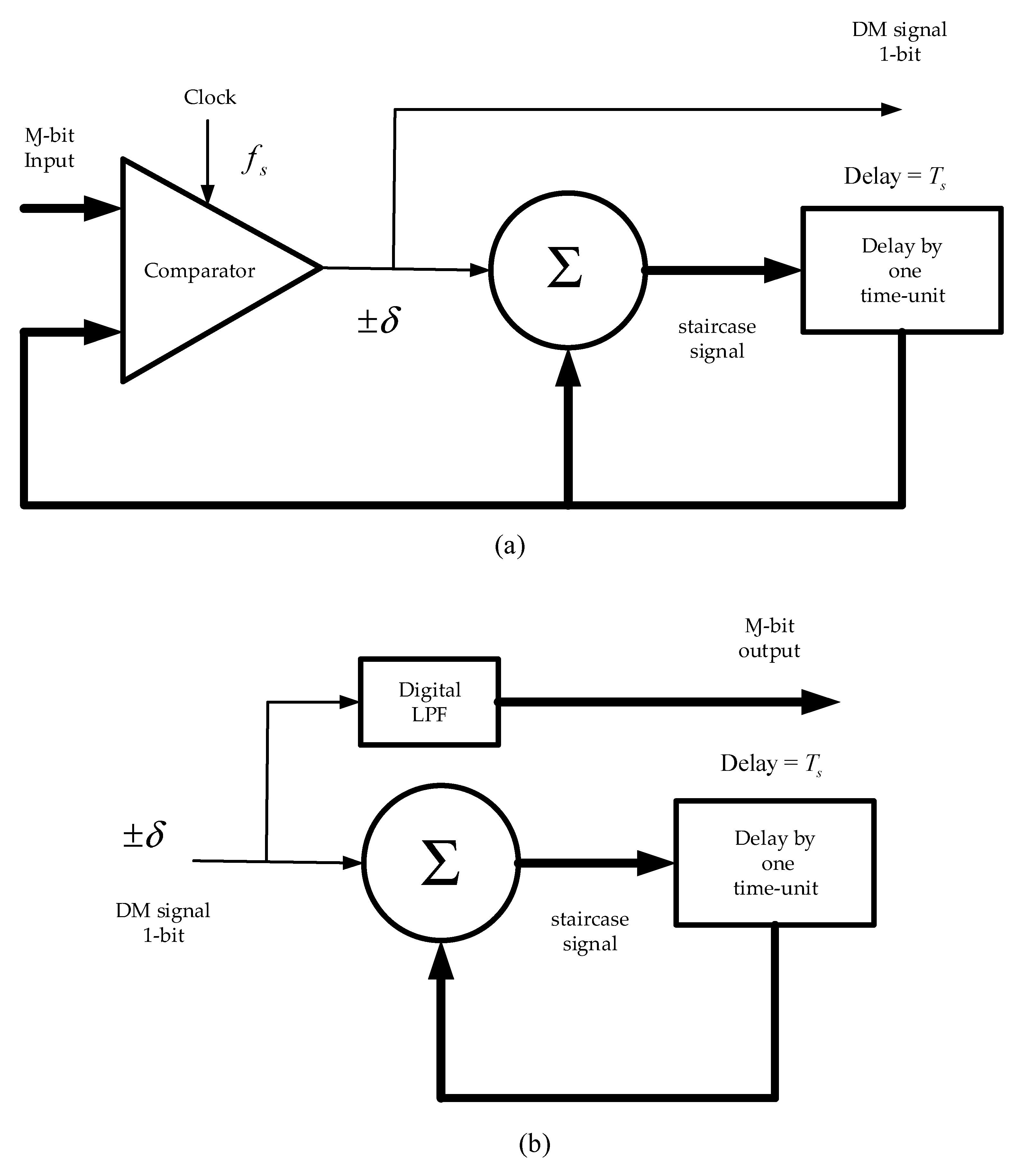
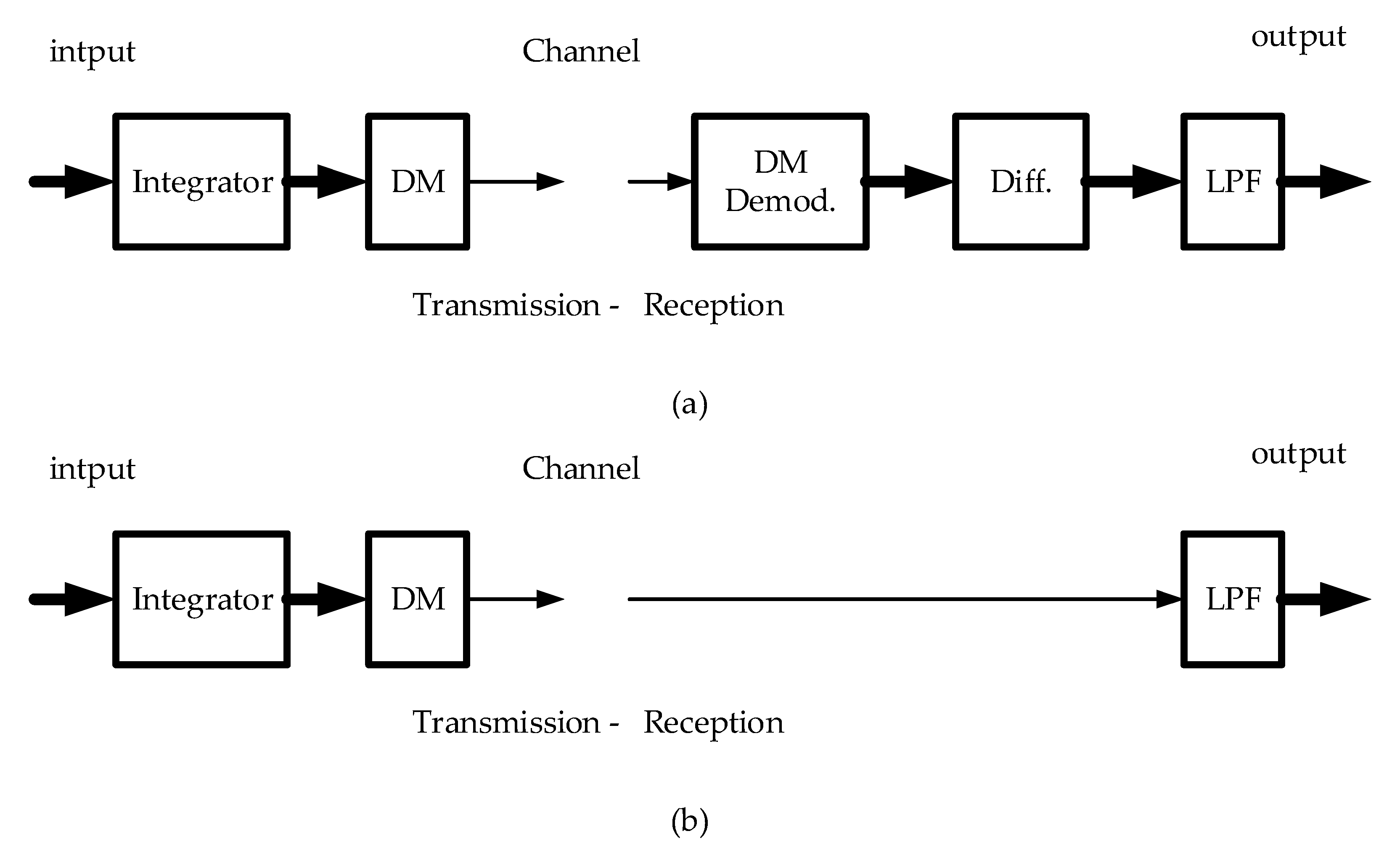
Figure 2.
Delta modulation: (a) Transmission (DM modulator as a comparator and integrator in a feedback loop); (b) Reception (DM demodulator as an integrator and LPF).
Figure 3.
Example of delta modulation operation.
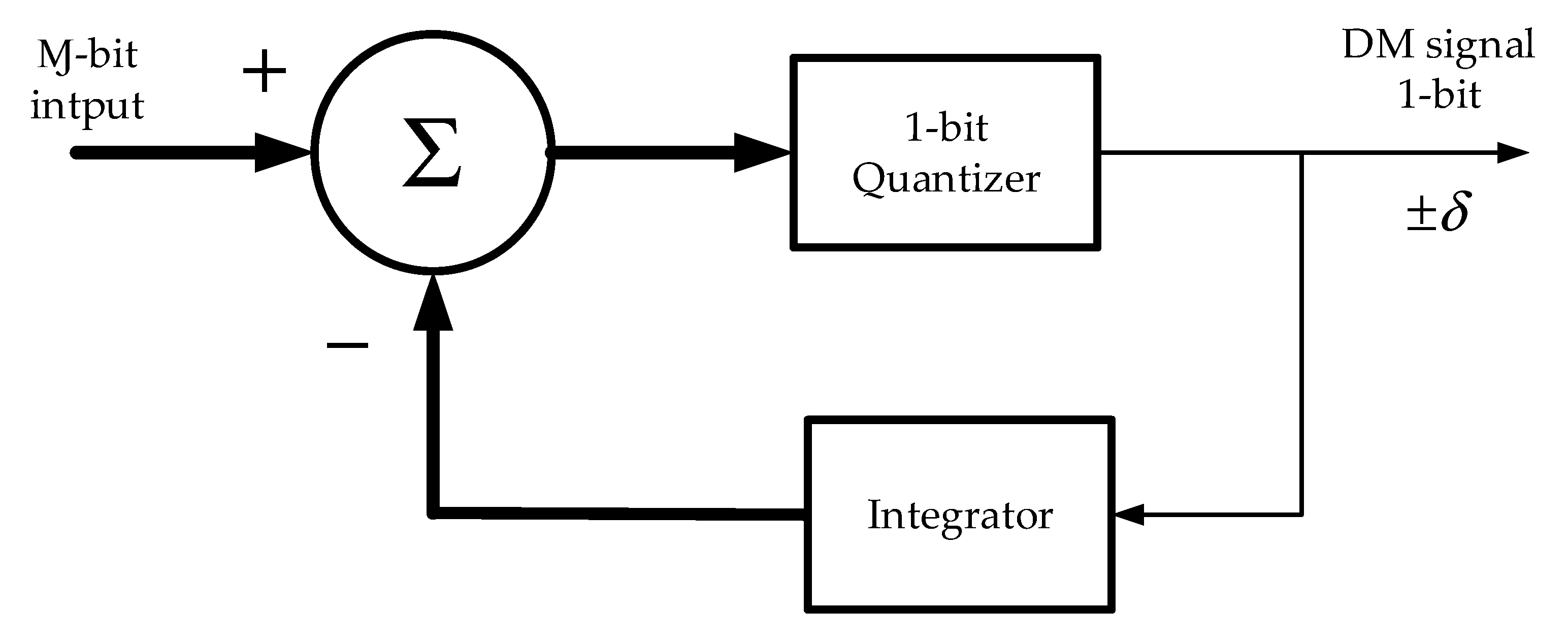
Figure 4.
Block diagram of the DM modulator of
Figure 2a.
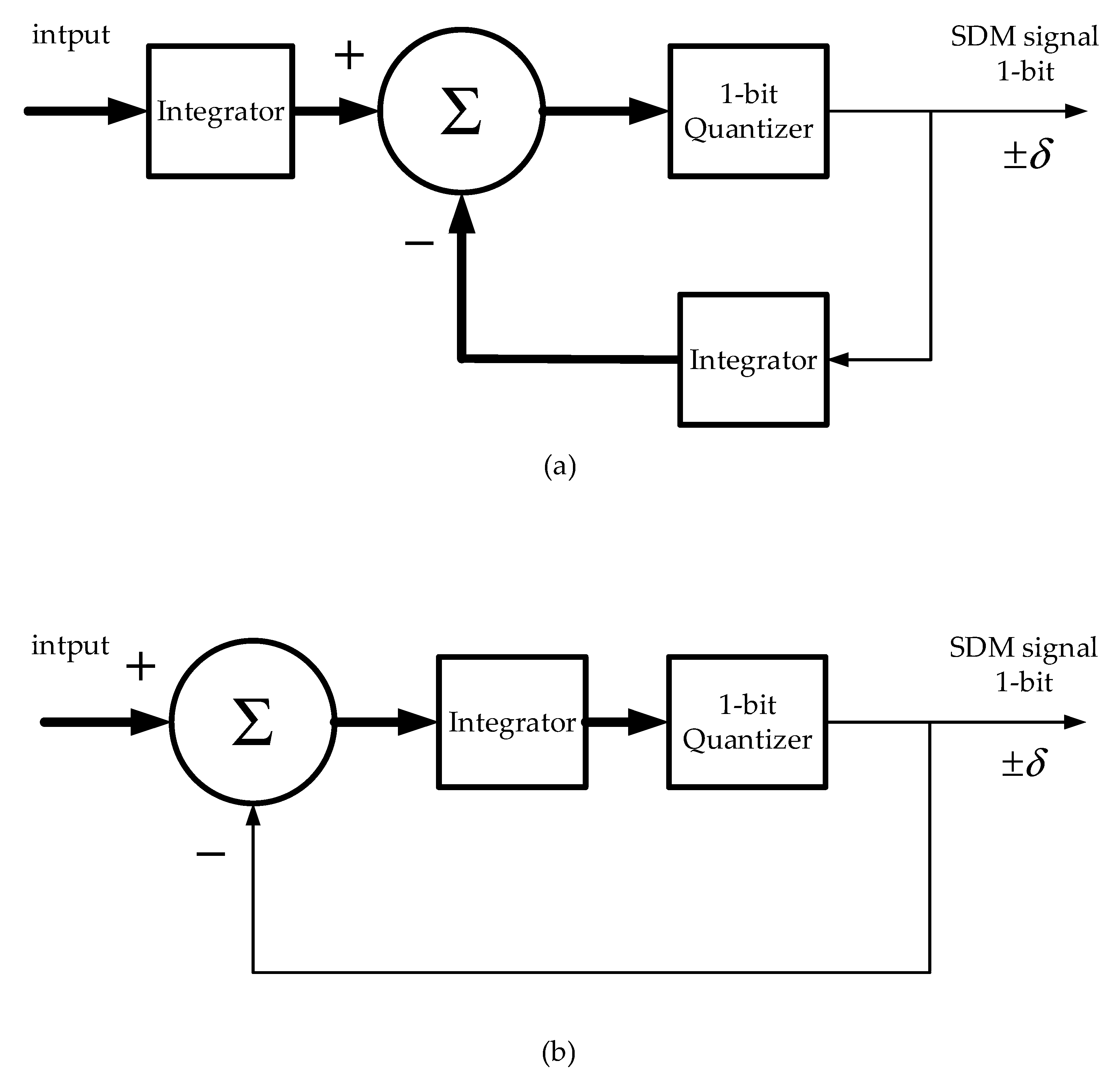
Figure 5.
Sigma-delta modulation (SDM): (a) derivation of SDM; (b) SDM system.
Figure 6.
SDM modulator: (a) as a DM modulator preceded by an integrator; (b) equivalent SDM modulator block diagram.
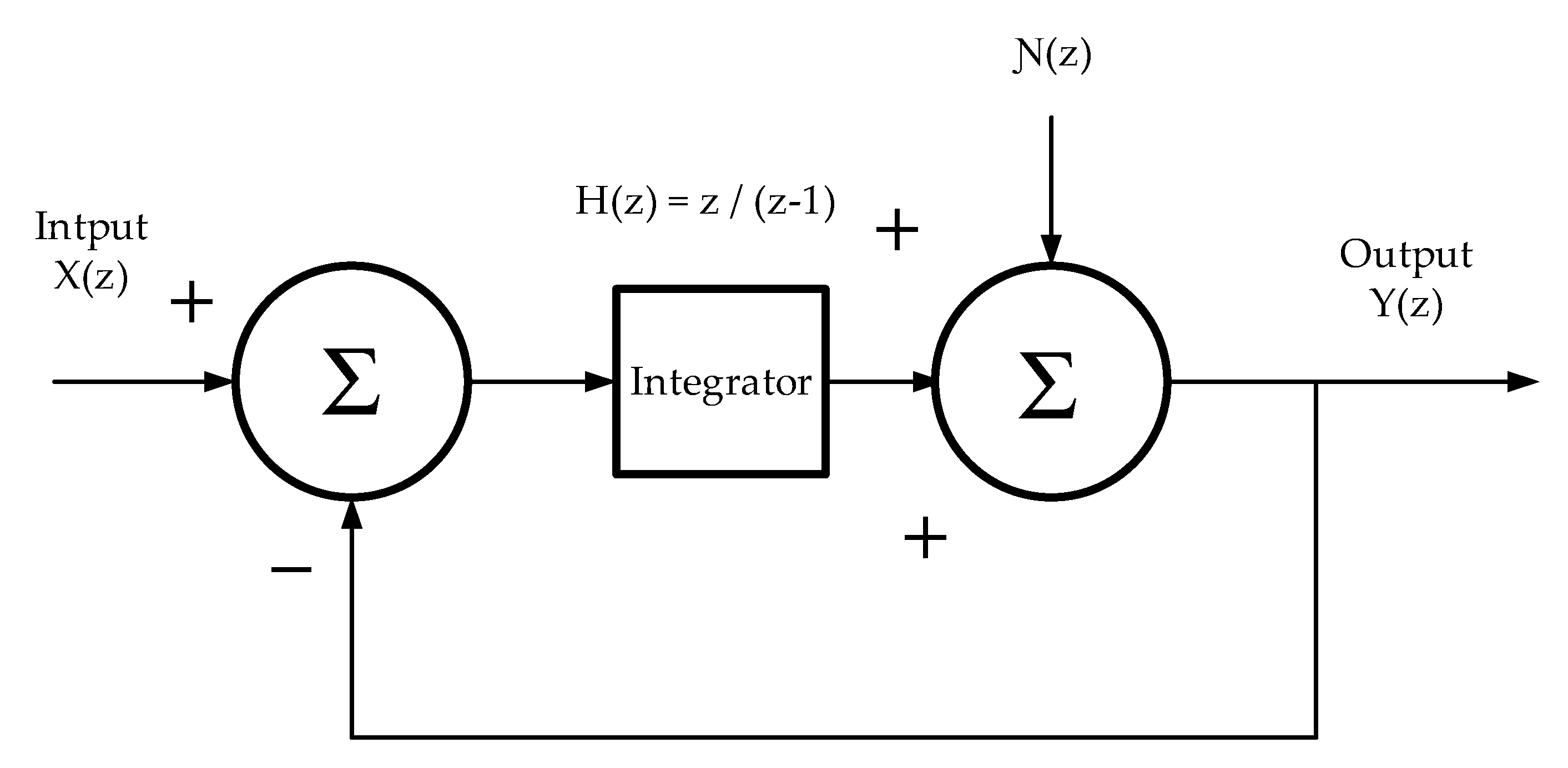
Figure 7.
SDM modulator in the z-domain.
Figure 8.
DM signals with original and reconstructed TOA values for the CS-DM localization system. The original TOA values are shown in red, the reconstructed in black. Results are averaged over 100 realizations.
Figure 9.
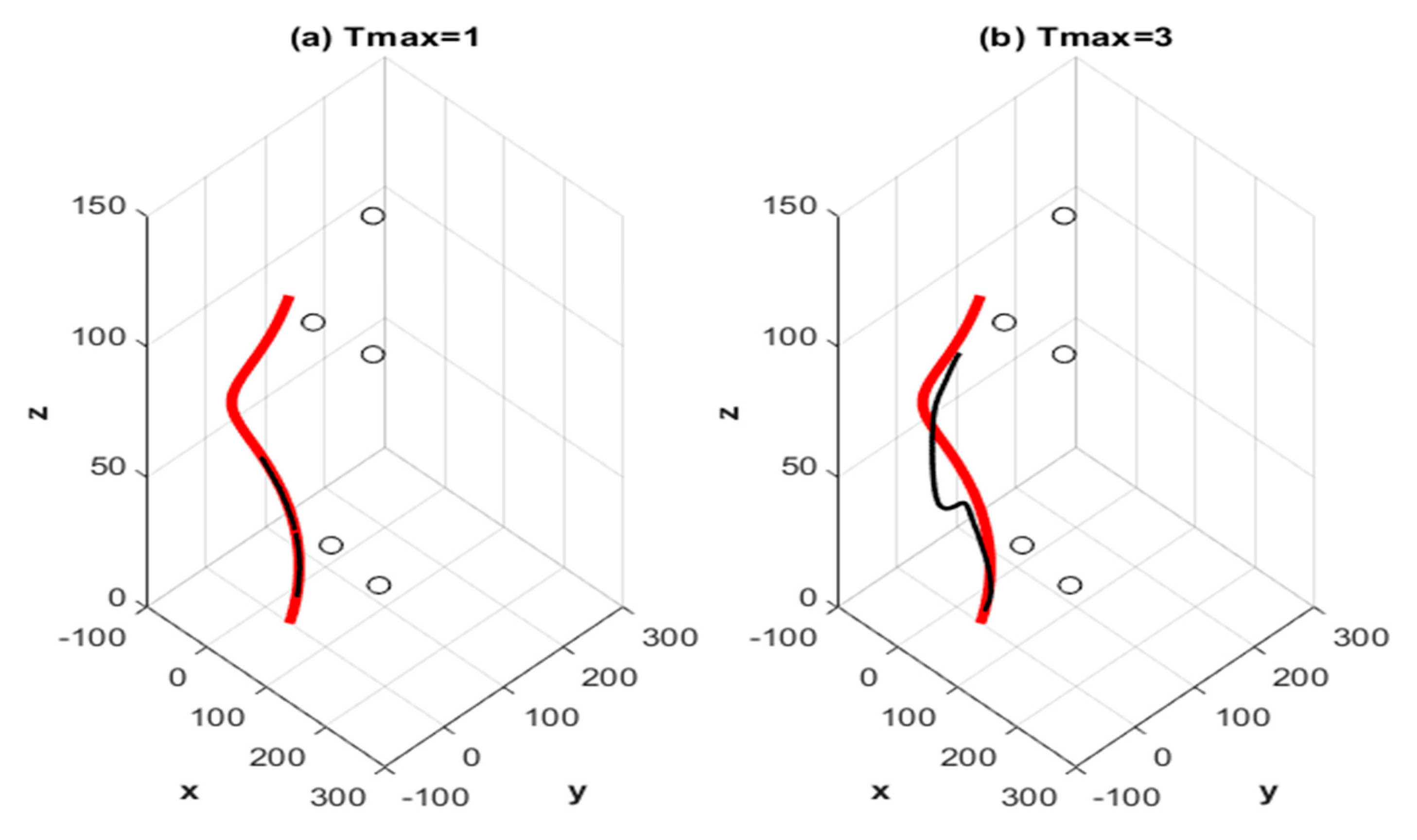
True and localized helical paths for the cases = 1 and 3. The true path is shown in bold red. The small circles indicate the five anchor positions. Results are averaged over 100 realizations.
Figure 10.
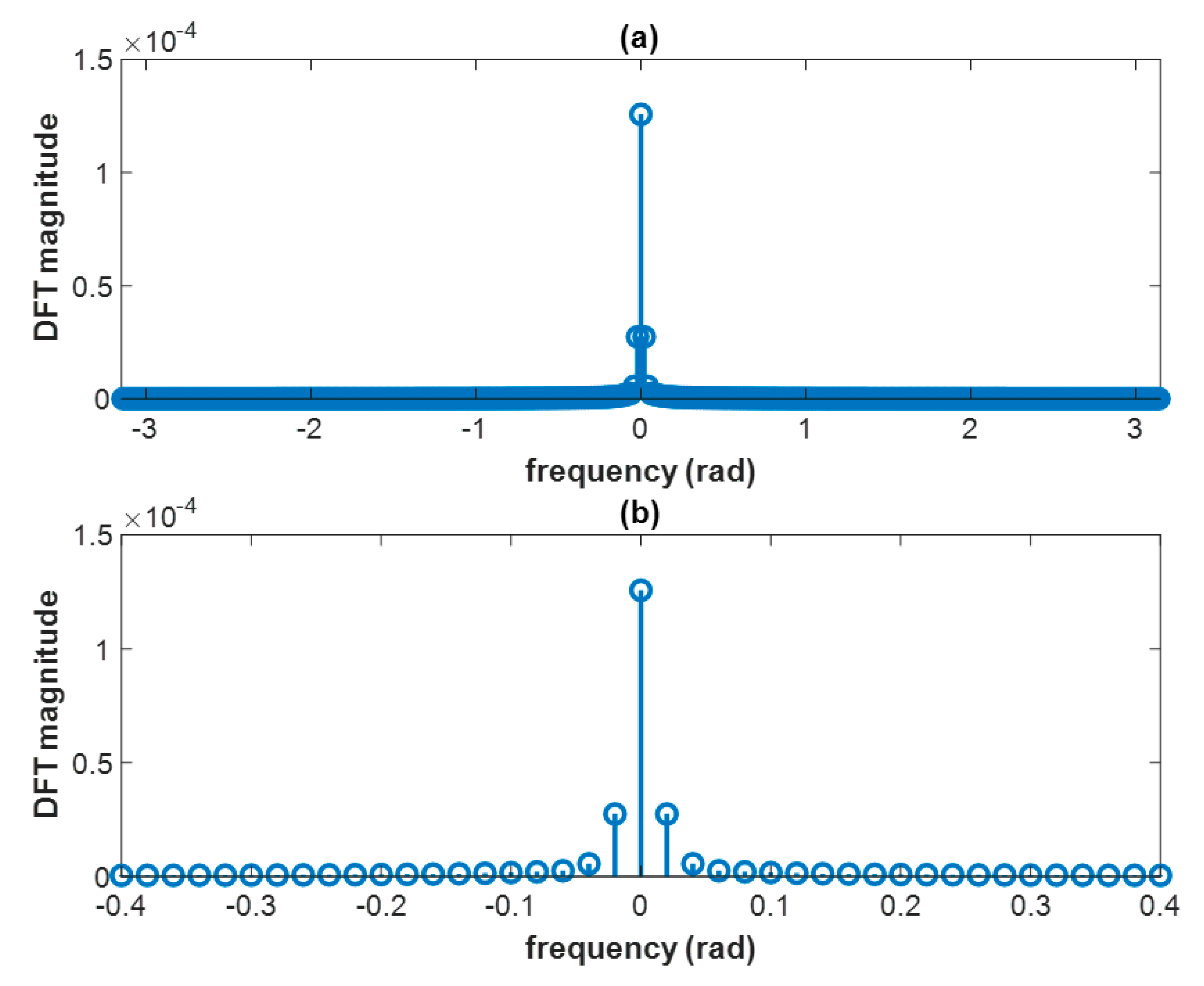
(a) The DFT magnitude of the TOA sequence seen by Anchor 1. (b) A magnified view.
Figure 11.
Demodulation LPF transfer function for the CS-SDM localization system.
Figure 12.
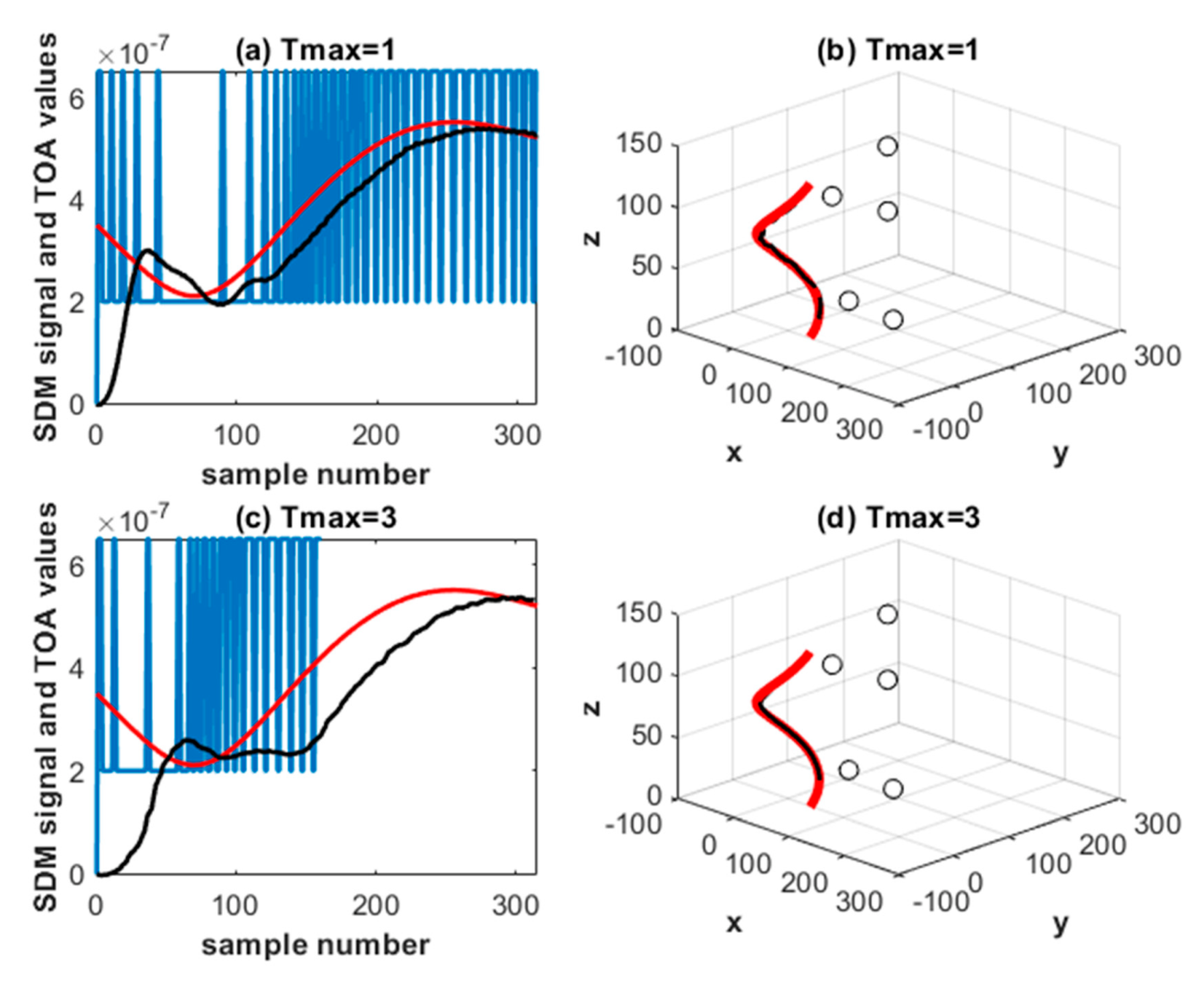
SDM signals, original and reconstructed TOA values and localized paths for the CS-SDM localization system. The original TOA values are shown in red and the reconstructed in black. True and localized helical paths are also shown. The true path is shown in bold red. The small circles indicate the five anchor positions. Results are averaged over 100 realizations.
Figure 13.
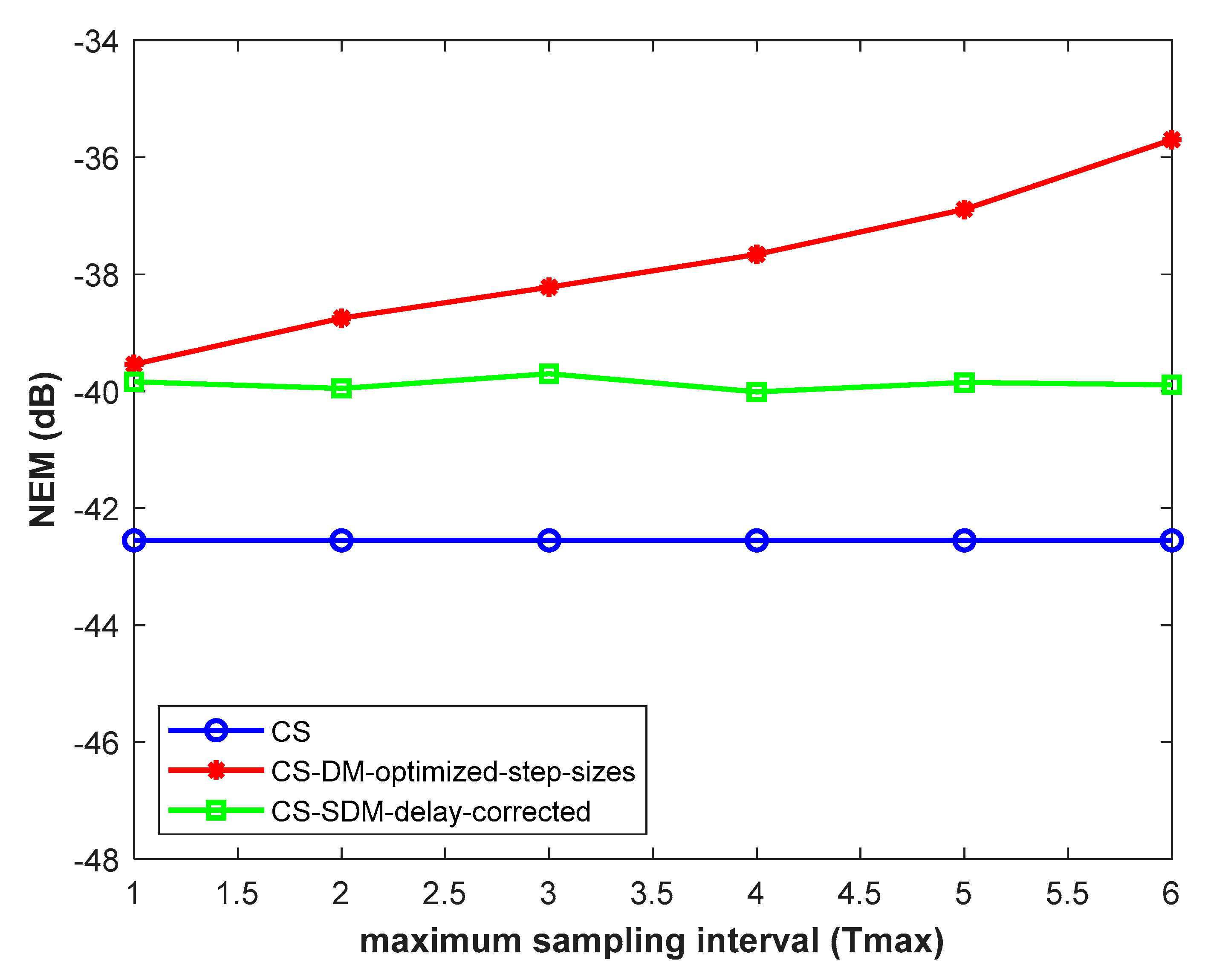
Performance of CS-SWL localization systems in terms of localization NEM versus maximum sampling interval () under noise-free conditions (neither measurement nor transmission noise). Results are averaged over 100 realizations.
Figure 14.
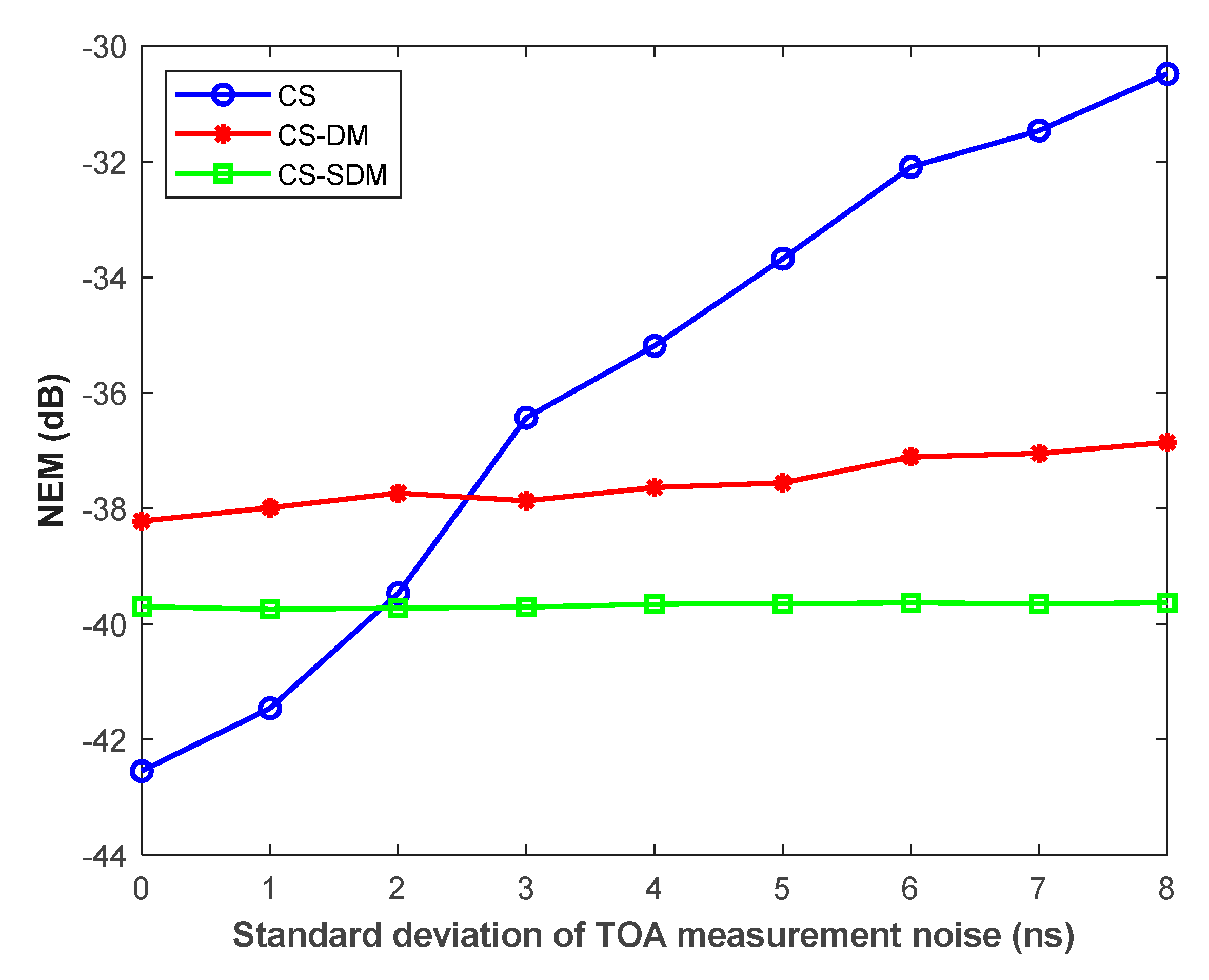
Localization NEM versus standard deviation of TOA measurement noise (SD1) for the three localization systems. = 3. Results are averaged over 100 realizations.
Figure 15.
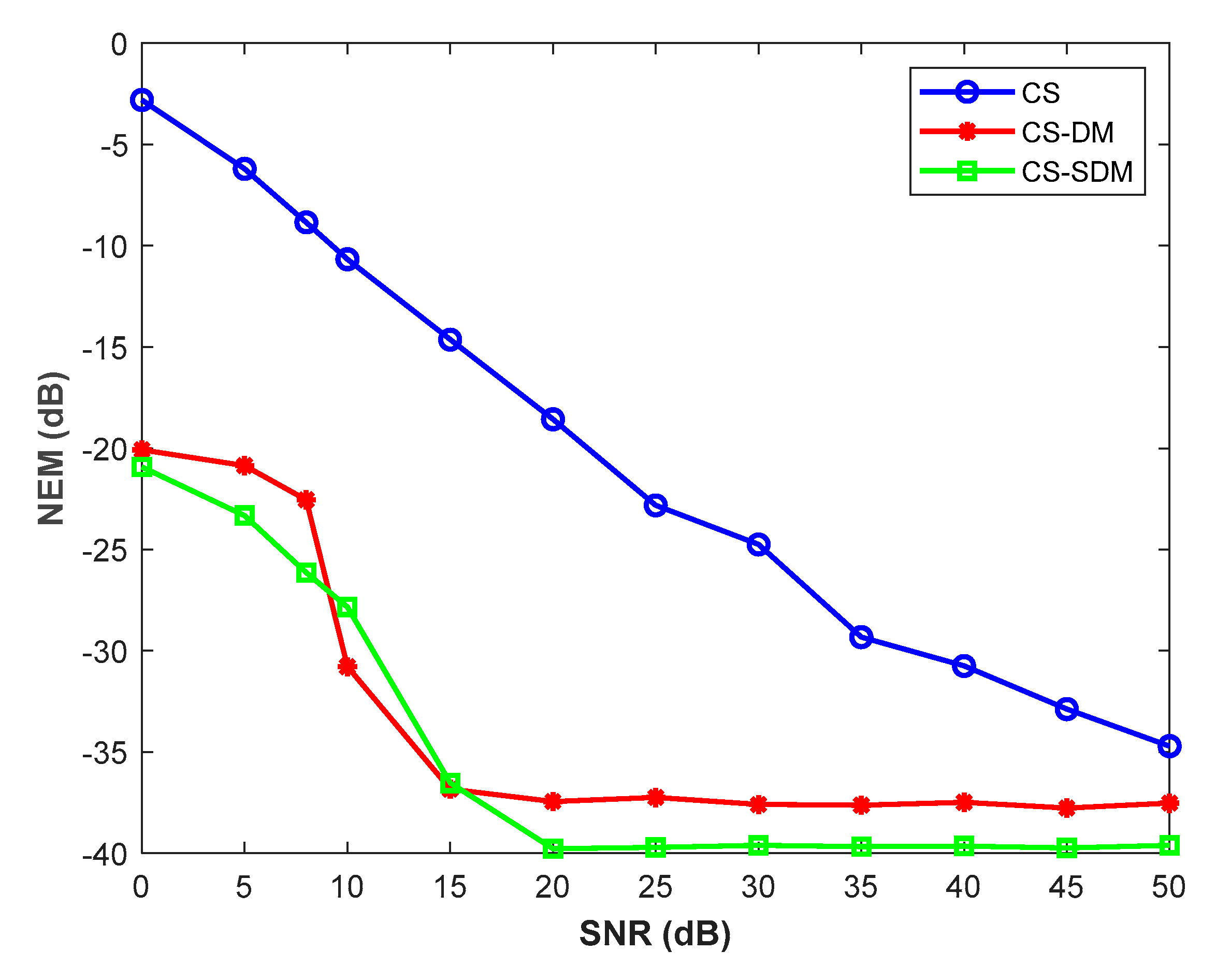
Localization NEM versus SNR for the three localization systems. = 3, standard deviation of TOA measurement noise SD1 = 5 ns. Results are averaged over 15 realizations.
Figure 16.
Normalized communication energy consumption for the three localization systems versus the number of bits/word (Ɱ) of the original TOA samples. R = 3, N = 5, path length = 315.
Table 1.
SDM reconstruction LPF specifications.
| Band (rad) | Gain | Ripple |
|---|
Passband: (0–0.04π) or
(0–0.126 rad) | 1 | 5 dB |
Stopband: (0.1π–π) or
(0.314–3.14 rad) | 0 | −40 dB |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).