Abstract
Biological tissue damage monitoring is an indispensable part of high-intensity focused ultrasound (HIFU) treatment. As a nonlinear method, multi-scale permutation entropy (MPE) is widely used in the monitoring of biological tissue. However, the traditional MPE method neglects the amplitude information when calculating the time series complexity, and the stability of MPE is poor due to the defects in the coarse-grained process. In order to solve the above problems, the method of improved coarse-grained multi-scale weighted permutation entropy (IMWPE) is proposed in this paper. Compared with the MPE, the IMWPE method not only includes the amplitude of signal when calculating the signal complexity, but also improves the stability of entropy value. The IMWPE method is applied to the HIFU echo signals during HIFU treatment, and the probabilistic neural network (PNN) is used for monitoring the biological tissue damage. The results show that compared with multi-scale sample entropy (MSE)-PNN and MPE-PNN methods, the proposed IMWPE-PNN method can correctly identify all the normal tissues, and can more effectively identify damaged tissues and denatured tissues. The recognition rate for the three kinds of biological tissues is higher, up to 96.7%. This means that the IMWPE-PNN method can better monitor the status of biological tissue damage during HIFU treatment.
1. Introduction
Currently, high-intensity focused ultrasound (HIFU) is widely used in tumor therapy [1,2,3]. HIFU treatment is noninvasive and safe compared with traditional tumor therapy (surgical resection, chemotherapy, and radiotherapy) [4,5,6]. HIFU focuses high-intensity ultrasound on the target area of the tumor, making the temperature of the target area rise continuously, thus causing damage to the biological tissues in the target area. When the temperature of the target area exceeds 63 °C, the tissues in the target area become denatured [7,8,9]. The technique does not damage the normal tissues and cells outside the target area, so as to achieve the purpose of destroying cancer cells. Thus, accurate monitoring of the biological tissue damage in the target area is the key to ensure the safety and efficiency of HIFU treatment.
So far, HIFU researchers have generally used ultrasound to monitor the entire process of HIFU treatment [10,11,12]. Ralf Seip et al. used the energy characteristics of ultrasonic signals to monitor the damage of biological tissue during HIFU treatment. The experimental results showed that the recognition accuracy based on energy characteristics reached 82% [13]. In [14], the sound velocity characteristics of ultrasonic signals were used to monitor the damage of biological tissues during HIFU treatment, and the results showed that the sound velocity of damaged biological tissues was higher than that of non-damaged tissues. However, the sound velocity measurement of biological tissues is easily affected by environmental noise, which leads to the inaccuracy of the monitoring results of biological tissue damage. From the perspective of nonlinear analysis, HIFU treatment can change the entropy value of the ultrasonic signal in biological tissue [15,16,17]. Tsui et al. used the Shannon entropy of ultrasound signals to monitor the damage of liver tissues [18]. The results showed that there was a big difference between the Shannon entropy value of the ultrasonic signal of the normal biological tissues and the damaged biological tissues. In [19], the multi-scale sample entropy (MSE) of the radio frequency ultrasonic signals was employed to monitor the damage of porcine tissues. Compared with the Shannon entropy and MSE mentioned above, multi-scale permutation entropy (MPE) has the advantages including strong noise resistance and robustness, so the MPE is often employed to analyze the complexity of ultrasonic time series [20,21,22]. In [23], MPE, as the characteristic of the ultrasonic scattering echo signal, was used to distinguish the non-denatured biological tissue and denatured biological tissue during HIFU treatment. However, MPE also has some shortcomings, such as, it loses information about the signal amplitude due to that MPE does not analyze the amplitude difference between the same ordinal modes in analyzing signal complexity. At the same time, the traditional coarse-grained method in the MPE easily causes the fluctuation of MPE value, which reduces the stability of MPE [24,25,26]. In order to solve the above problems, the traditional MPE method was improved and a new nonlinear analysis method was proposed, called improved coarse-grained multi-scale weighted permutation entropy (IMWPE). IMWPE introduces a weighted algorithm on the basis of MPE, which effectively solves the problem that the MPE method loses information about the signal amplitude in analyzing signal complexity. In addition, IMWPE reduces entropy fluctuations and improves the stability of entropy by improving the coarse-grained process of multi-scale calculation.
In this paper, we consider the advantages of IMWPE in analyzing signal complexity, IMWPE is used to extract the damage characteristics of HIFU echo signals from biological tissues. Then, the probabilistic neural network (PNN) is employed to realize the identification of three kinds of biological tissues (including normal tissues, damaged tissues and denatured tissues) during HIFU treatment. In addition, the advantages of the IMWPE-PNN method are illustrated compared with MSE-PNN and MPE-PNN methods. The outline of this paper is as follows: Section 1 is the introduction; Section 2 is the materials and methods, which includes the MPE, IMWPE, PNN methods, the process of IMWPE-PNN method and the experimental system; Section 3 includes the analyzed results of simulated signals and actual HIFU echo signals; Section 4 is the discussion; Section 5 is the conclusion.
2. Materials and Methods
2.1. Multi-Scale Permutation Entropy
Multi-scale permutation entropy (MPE) combines coarse-graining and permutation entropy method to extract nonlinear features of time series. The specific calculation steps are as follows:
- (1)
- For embedding dimension , delay time τ, time series can be reconstructed in phase space as
can be defined as
where .
- (2)
- The time reconstruction sequence is arranged in ascending order. The symbol sequence is obtained. Where has possible values and can be expressed as
- (3)
- can be defined as
- (4)
- According to Equation (4), permutation entropy (PE) can be defined as
- (5)
- The time series with sequence length N was coarsely granulated, and the coarse-grained sequence is obtained aswhere .
- (6)
- Multi-scale permutation entropy (MPE) can be defined as
2.2. Improved Coarse-Grained Multi-Scale Weighted Permutation Entropy
MPE does not analyze the amplitude difference between the same ordinal modes in analyzing signal complexity, resulting in the MPE feature not containing signal amplitude information. In addition, the traditional coarse-grained process method is employed in MPE analysis, as shown in Figure 1. In the traditional coarse-grained process, the number of elements in the coarse-grained sequence will continue to decrease as the scale factor increases. For example, when the scale factor is selected as 3, the number of elements in the traditional coarse-grained sequence is only 1/3 of the original time series at most (considering the rounding situation). In this case, the entropy value of the analyzed signal will fluctuate, and the characteristics are unstable.
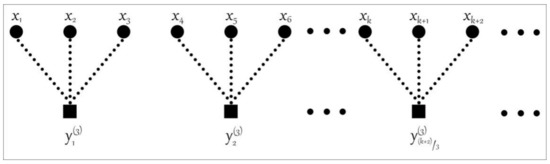
Figure 1.
The traditional coarse-grained process with the scale factor s = 3.
In order to solve the above problems, an improved coarse-grained multi-scale weighted permutation entropy (IMWPE) is proposed based on the MPE method. The specific calculation steps are as follows
- (1)
- According to the definition of permutation entropy in Formula (5), the can be obtained by weighting in the formula. The is defined aswhere can be defined aswhere
Thus, the weighted permutation entropy is calculated according to Equations (5) and (8).
- (2)
- In the coarse-grained process, the coarse-grained process is improved by the overlapping sliding average method. Each sliding length is set to a sampling point. The original signal will be transformed into the groups of coarse-grained sequence through the overlapping sliding windows under the same scale factor , which can avoid the loss of elements in a coarse-grained sequence. Where is expressed as
- (3)
- When the scale factor and embedding dimension are determined, we calculate the WPE entropy value of each coarse-grained sequence. Then, the entropy values of WPE of the coarse-grained sequence are averaged to obtain the improved coarse-grained multi-scale weighted permutation entropy (IMWPE). The IMWPE is defined as
2.3. Probabilistic Neural Network
A probabilistic neural network (PNN) is developed on the basis of radial basis neural network, which integrates Parzen window probability density function estimation and Bayes classification criterion, and can achieve arbitrary nonlinear approximation and converge to the optimal solution of Bayesian classification [27,28]. The specific learning steps are as follows:
- (1)
- The sample data is normalized and then input into the pattern layer of PNN, and the Euclidean distance between the normalized sample data and the training sample data is calculated as
- (2)
- The radial basis function (RBF) is selected as the activation function to process the normalized samples and training samples to be identified, so as to obtain the initial probability matrix P.
- (3)
- The output value of the pattern layer is calculated. Then, the initial probability sum of the type of the sample to be identified is calculated according to the Formula (15), so as to realize the PNN pattern recognition.
2.4. The Process of IMWPE-PNN Method
A new biological tissue damage monitoring method based on IMWPE and PNN during HIFU treatment is proposed in this section. Figure 2 is the flow chart of the proposed IMWPE-PNN method. The process is as follows.
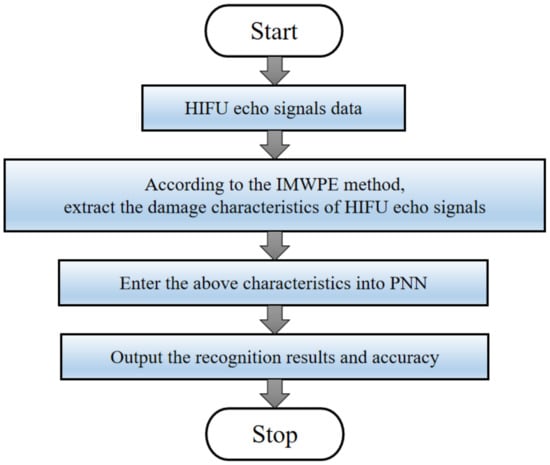
Figure 2.
Flow chart of the proposed method.
- (1)
- The HIFU echo signals data were collected in real-time through the HIFU irradiation experimental system.
- (2)
- The damage characteristics of HIFU echo signals are extracted by IMWPE methods. The damage characteristics sets are randomly divided into training samples sets and test samples sets. The training samples sets are input into the PNN for establishing the PNN prediction model.
- (3)
- The test samples sets are entered into the PNN prediction model to realize pattern recognition and the recognition results and accuracy are obtained.
2.5. Experimental System
The HIFU irradiation experiment system is shown in Figure 3. Before the irradiation experiment, povidone was added to remove air bubbles in the water, so as not to affect the results of the experiment. Then, fresh in vivo porcine muscle tissue (thickness: 40 mm) was fixed on a rubber plate and placed directly under the HIFU transducer (PRO2008, Shenzhen, China). The HIFU system was operated to adjust the irradiation position of the HIFU transducer by computer, and the HIFU transducer was used to irradiate porcine muscle tissue. The pictures of porcine muscle tissue sample and B-mode ultrasonography are shown in Figure 4. The irradiation power of the HIFU transducer was 210–300 W and the center frequency of the HIFU transducer is 1.39 MHz. The fiber optical hydrophone (FOPH2000, Leutenbach, Germany) was used to receive the HIFU echo signal. The received HIFU echo signals were transformed into the digital signals through the digital oscilloscope (MDO3032, Tektronix, Beaverton, OR, USA), and stored in the computer. Meanwhile, the thermometer at the HIFU irradiation target area was used to measure the temperature of the irradiation area. The B-ultrasound probe of the B-mode ultrasonography was used to monitor the HIFU irradiation area. The subtraction images of the irradiation area are shown in Figure 5. According to the reference [23,26], the actual damaged status of biological tissues were determined by the temperature and subtraction image of the irradiation area. The porcine muscle tissue before HIFU irradiation is normal tissue, and the tissue subtraction image shows that there is no white bright block in the irradiated area according to Figure 5a. After HIFU irradiation, when the temperature of the irradiated area exceeds 63 °C and the irradiated area presents a large number of white bright blocks as shown in Figure 5c, the tissue has been denatured. When the temperature of the irradiated area does not exceed 63 °C, but white bright blocks appear in the irradiated area, the tissue has been damaged.
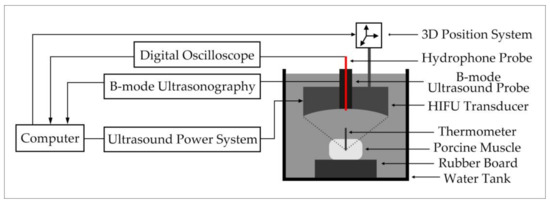
Figure 3.
HIFU irradiation experiment system.
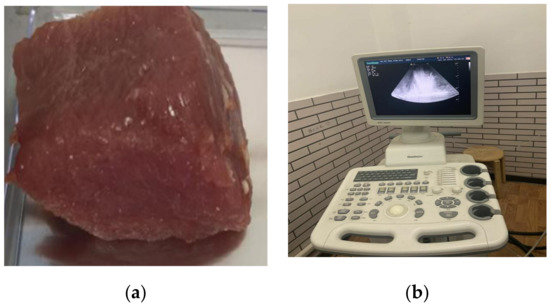
Figure 4.
The pictures of porcine muscle tissue sample and B-mode ultrasonography. (a) porcine muscle tissue sample; (b) B-mode ultrasonography.
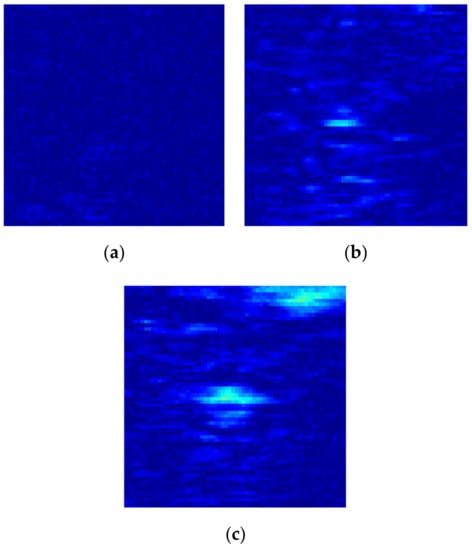
Figure 5.
Subtraction images of irradiation area. (a) Normal tissue; (b) Damaged tissue; (c) Denatured tissue.
3. Results
3.1. The Analyzed Results of Simulated Signals
According to the reference [29], Gaussian white noise with 5000 sampling points is used as a simulation signal to prove the advantages of IMWPE compare with the MPE method. Both MPE and IMWPE methods are analyzed for the simulation signal. The embedding dimension is selected as 4, 5, 6, 7 and 8. The delay time is selected as 2 and the maximum scale factor is 50. The entropy values of MPE and IMWPE are shown in Figure 6. When the embedded dimensions are 4 and 5, the downward trend of the entropy values of MPE and IMWPE is still not obvious, and the advantages of multi-scale entropy are not effectively exploited. When the embedding dimensions are 6, 7 and 8, with the increase in scale factor, the entropy values of MPE and IMWPE show an obvious downward trend. In addition, the IMWPE value decreases faster than MPE, which means that IMWPE includes amplitude information when analyzing the complexity of the signal. Compared with MPE, the entropy value of IMWPE have less fluctuation and better stability, which means that the IMWPE method can effectively improve the stability and reliability of the entropy value by improving the coarse-grained process.
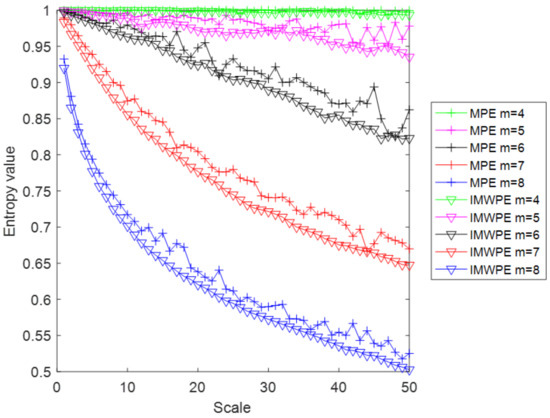
Figure 6.
The entropy values of MPE and IMWPE under different dimension.
In order to further illustrate the advantages of the IMWPE method over the traditional MPE method, we also analyze the Gaussian white noise with 500, 1000, and 3000 sampling points. Table 1 shows the comparison results between MPE and IMWPE of Gaussian white noise with different sampling points. As demonstrated, the standard deviation of IMWPE is lower than that of MPE under different sampling points conditions, which means that the stability of IMWPE is better than that of MPE. In addition, the running time of the IMWPE method is slightly higher than that of the MPE. This is because the IMWPE method averages the new coarse-grained sequence and also weights the signal amplitude, which slightly increases the computational complexity of the algorithm.

Table 1.
The comparison results between MPE and IMWPE with different sampling points.
3.2. The Analyzed Results of Actual HIFU Echo Signals
The time–domain diagram and frequency spectrum of HIFU echo signals are shown in Figure 7. The center frequency of the HIFU echo signals is 1.39 MHz. The MSE, MPE and IMWPE methods are used to calculate the entropy values of 240 HIFU echo signals (including 80 normal status, 80 damaged status and 80 denatured status). The delay time is selected as 2 and the embedding dimension is selected as 7. Probabilistic neural network (PNN) is used to recognize the extracted features. 150 HIFU echo signals (including 50 normal status, 50 damaged status and 50 denatured status) are randomly selected as the training set, and the remaining 90 HIFU echo signals (including 30 normal status, 30 damaged status and 30 denatured status) are selected as the test set.
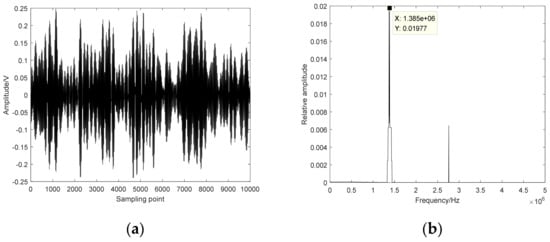
Figure 7.
The time–domain diagram and frequency spectrum of HIFU echo signal. (a) Time–domain diagram; (b) Frequency spectrum.
After cross-validation, the smoothing factor parameter of PNN is determined to be 1.5. Figure 8 shows the damaged recognition results of biological tissue based on MSE-PNN, MPE-PNN and IMWPE-PNN. Abscissa 1 to 30 are normal tissue samples, 31 to 60 are damaged tissue samples, and 61 to 90 are denatured tissue samples. The ordinate type 1 represents the normal tissue status, type 2 represents the damaged tissue status, and type 3 represents the denatured tissue status. It can be seen that the identification ability of MPE-PNN method is superior to MSE-PNN method. The damaged recognition rate of biological tissue based on MPE-PNN is 88.9%. Compared with MSE-PNN and MPE-PNN methods, the IMWPE-PNN method can correctly identify all the normal tissues to be identified. In addition, IMWPE-PNN has fewer misidentification samples of damaged tissues and denatured tissues. The sensitivity and specificity of IMWPE-PNN are higher than MSE-PNN and MPE-PNN methods, reaching 0.933 and 0.967, respectively. The damaged recognition rate of biological tissue based on IMWPE-PNN reaches 96.7%.
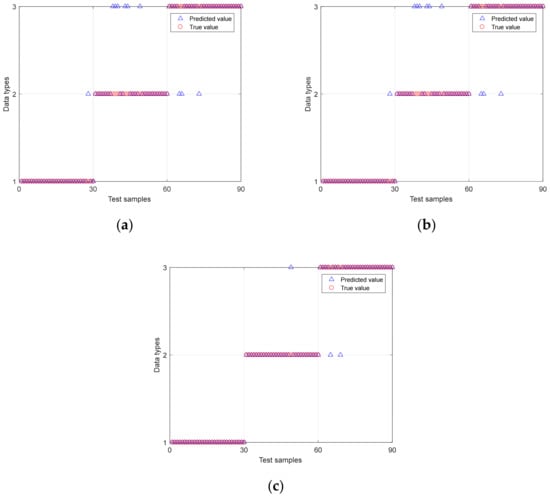
Figure 8.
The damaged recognition results of biological tissue based on MSE-PNN, MPE-PNN and IMWPE-PNN. (a) MSE-PNN; (b) MPE-PNN; (c) IMWPE-PNN.
4. Discussion
In HIFU treatment, MPE was widely used in the damaged monitoring of biological tissue. However, the traditional MPE method loses information about the signal amplitude when analyzing the complexity of the signals, and the stability of MPE is poor due to the defects in the traditional coarse-grained process, which will reduce the separability. To solve the above problems, the IMWPE method is proposed based on MPE. IMWPE introduces a weighted algorithm on the basis of MPE, which effectively solves the problem that the MPE loses information about the signal amplitude due to that MPE does not analyze the amplitude difference between the same ordinal modes in analyzing signal complexity. In addition, IMWPE reduces entropy fluctuations and improves the stability of entropy compare MPE. The analyzed results of simulated signals show that the IMWPE method not only contains the amplitude information of the signal when analyzing the complexity of the signal, but also improves the stability of the entropy value compared with MPE (Figure 6 and Table 1). The MSE, MPE and IMWPE methods are applied to the HIFU echo signals during HIFU treatment, and the probabilistic neural network (PNN) is used to recognize the status of biological tissue. Compared with MSE-PNN and MPE-PNN methods, the IMWPE-PNN method can correctly identify all the normal tissues to be identified. In addition, IMWPE-PNN has fewer misidentification samples of damaged tissues and denatured tissues (Figure 8). The analyzed results of actual HIFU echo signals show that the IMWPE-PNN method has a better recognition effect on the state of biological tissues (including normal tissues, damaged tissues and denatured tissues) than MSE-PNN and MPE-PNN. The damaged recognition rate of biological tissue based on IMWPE-PNN reaches 96.7%. The above results support the hypothesis that the IMWPE-PNN method has a better identification effect to monitor the HIFU treatment. Finally, we may consider combining entropy theory and advanced signal processing technology to further improve the recognition accuracy and anti-noise ability.
5. Conclusions
This paper realizes biological tissue damage monitoring based on IMWPE and PNN during HIFU treatment. To solve the defects of MPE, an IMWPE method is put forward. The analyzed results of simulated signals prove the superiority of the IMWPE method. The MSE, MPE and IMWPE methods are applied to calculate the entropy value of the actual HIFU echo signals of three types of tissues. PNN is used to recognize the extracted features. The results show that the IMWPE-PNN method has a better recognition effect to monitor the state of biological tissues than MSE-PNN and MPE-PNN. The damaged recognition rate of biological tissue based on IMWPE-PNN reaches 96.7%. In future research, the second harmonic characteristics of the HIFU echo signal may be extracted to monitor the biological tissue damage during HIFU treatment.
Author Contributions
Conceptualization, B.L.; methodology, B.L. and J.C.; software, B.L. and X.Z. (Xian Zhang); validation, B.L., Z.P. and J.C.; formal analysis, B.L.; investigation, B.L.; resources, X.Z. (Xiao Zou); data curation, B.L. and X.Z. (Xian Zhang); writing—original draft preparation, B.L.; writing—review and editing, X.Z. (Xiao Zou); visualization, B.L. and J.C.; supervision, B.L.; project administration, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by Natural Science Foundation of China (U2031112), Natural Science Youth Foundation of Hunan Province (2020JJ5396), Excellent Young Scientist Foundation of Hunan Provincial Education Department (20B405) and the Research Foundation for Advanced Talents (E07020006 and E07021011).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable, the study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cranston, D. A review of high intensity focused ultrasound in relation to the treatment of renal tumours and other malignancies. Ultrason. Sonochem. 2015, 27, 654–658. [Google Scholar] [CrossRef] [PubMed]
- Ramaekers, P.; De Greef, M.; Van Breugel, J.M.M.; Moonen, C.T.W.; Ries, M. Increasing the HIFU ablation rate through an MRI-guided sonication strategy using shock waves: Feasibility in the in vivo porcine liver. Phys. Med. Biol. 2016, 61, 1057–1077. [Google Scholar] [CrossRef] [PubMed]
- Tsang, S.H.; Ma, K.W.; She, W.H.; Chu, F.; Lau, V.; Lam, S.W.; Lo, C.M. High-intensity focused ultrasound ablation of liver tumors in difficult locations. Int. J. Hyperth. 2021, 38, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Diana, M.; Schiraldi, L.; Liu, Y.Y.; Memeo, R.; Mutter, D.; Pessaux, P.; Marescaux, J. High intensity focused ultrasound (HIFU) applied to hepato-bilio-pancreatic and the digestive system-current state of the art and future perspectives. Hepatobiliary Surg. Nutr. 2016, 5, 329–344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hallez, L.; Touyeras, F.; Hihn, J.Y.; Bailly, Y. Characterization of HIFU transducers designed for sonochemistry application: Acoustic streaming. Ultrason. Sonochemistry 2016, 29, 420–427. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Wong, F.; Wang, Y.; Cheng, Y.; Yang, L. Preliminary study on ultrasound-guided high-intensity focused ultrasound ablation for treatment of broad ligament uterine fibroids. Int. J. Hyperth. 2021, 38, 18–23. [Google Scholar] [CrossRef]
- Lang, B.H.H.; Woo, Y.-C.; Wong, C.K.H. High-Intensity Focused Ultrasound for Treatment of Symptomatic Benign Thyroid Nodules: A Prospective Study. Radiology 2017, 284, 897–906. [Google Scholar] [CrossRef]
- Feijoo, E.R.C.; Sivaraman, A.; Barret, E.; Sanchez-Salas, R.; Galiano, M.; Rozet, F.; Prapotnich, D.; Cathala, N.; Mombet, A.; Cathelineau, X. Focal High-intensity Focused Ultrasound Targeted Hemiablation for Unilateral Prostate Cancer: A Prospective Evaluation of Oncologic and Functional Outcomes. Eur. Urol. 2016, 69, 214–220. [Google Scholar] [CrossRef]
- Wust, P.; Cho, C.H.; Hildebrandt, B. Thermal monitoring: Invasive minimal-invasive and non-invasive approaches. Int. J. Hyperth. 2006, 22, 255–262. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, T.E.; Kim, J.H.; Park, B.J. Unintended pregnancies with term delivery following ultrasound-guided high-intensity focused ultrasound (USgHIFU) ablation of uterine fibroid and adenomyosis. Clin. Exp. Obstet. Gynecol. 2018, 45, 842–844. [Google Scholar]
- Rahimian, S.; Tavakkoli, J. Estimating dynamic changes of tissue attenuation coefficient during high-intensity focused ultrasound treatment. J. Ther. Ultrasound 2013, 1, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.; Liu, G.; Tong, X. Influence of temperature-dependent acoustic and thermal parameters and nonlinear harmonics on the prediction of thermal lesion under HIFU ablation. Math. Biosci. Eng. MBE 2021, 18, 1340–1351. [Google Scholar] [CrossRef]
- Seip, R.; Ebbini, E.S. Noninvasive estimation of tissue temperature response to heating fields using diagnostic ultrasound. IEEE Trans. Biomed. Eng. 1995, 42, 828–839. [Google Scholar] [CrossRef] [PubMed]
- Shishitani, T.; Yoshizawa, S.; Umemura, S. Change in acoustic impedance and sound speed of HIFU-exposed chicken breast muscle. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, 11–14 October 2010; pp. 1384–1387. [Google Scholar]
- Luo, L.; Molnar, J.; Ding, H.; Lv, X.; Spengler, G. Ultrasound absorption and entropy production in biological tissue: A novel approach to anticancer therapy. Diagn. Pathol. 2006, 1, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, L.F. Entropy production in a cell and reversal of entropy flow as an anticancer therapy. Front. Phys. China 2009, 4, 122. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.Q.; Zhang, H.; Liu, B.; Tang, H.; Qian, S.Y. Identification of denatured and normal biological tissues based on compressed sensing and refined composite multi-scale fuzzy entropy during high intensity focused ultrasound treatment. Chin. Phys. B 2021, 30, 028704. [Google Scholar] [CrossRef]
- Tsui, P.H. Ultrasound detection of scatterer concentration by weighted entropy. Entropy 2015, 17, 6598–6616. [Google Scholar] [CrossRef] [Green Version]
- Mobasheri, S.; Behnam, H.; Rangraz, P.; Tavakkoli, J. Radio Frequency Ultrasound Time Series Signal Analysis to Evaluate High-intensity Focused Ultrasound Lesion Formation Status in Tissue. J. Med. Signals Sens. 2016, 6, 91–98. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Liu, D.; Yan, T.; Ji, Y.; Fu, Q.; Li, M.; Faiz, M.A.; Khan, M.I. Novel method for measuring regional precipitation complexity characteristics based on multiscale permutation entropy combined with CMFO-PPTTE model. J. Hydrol. 2021, 592, 125801. [Google Scholar] [CrossRef]
- Liu, B.; Hu, W.P.; Zou, X.; Ding, Y.J.; Qian, S.Y. Recognition of denatured biological tissue based on variational mode decomposition and multi-scale permutation entropy. Acta Phys. Sin. 2019, 68, 028702. [Google Scholar]
- Zhang, X.; Li, J.; Li, D.Q.; Li, Y.; Liu, B.; Hu, Y.F. Separation of magnetotelluric signals based on refined composite multiscale dispersion entropy and orthogonal matching pursuit. Earth Planets Space 2021, 73, 76. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Liu, B.; Qian, S.; Hu, W. Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment. Entropy 2019, 21, 666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Ma, J.; Li, Z.; Li, C.; Zhan, L.; Zhang, G.Z. Rolling Bearing Fault Diagnosis Based on Refined Composite Multi-Scale Approximate Entropy and Optimized Probabilistic Neural Network. Entropy 2021, 23, 259. [Google Scholar] [CrossRef]
- Liu, B.; Wang, R.; Peng, Z.; Qin, L. Identification of Denatured Biological Tissues Based on Compressed Sensing and Improved Multiscale Dispersion Entropy during HIFU Treatment. Entropy 2020, 22, 944. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).