A Workflow for Synthetic Data Generation and Predictive Maintenance for Vibration Data
Abstract
1. Introduction
- A method for building a digital twin model (of a motor and gearbox circuit specifically in this study) and generating synthetic healthy and faulty data using this model is proposed.
- A predictive maintenance algorithm to estimate the current state of the machine/digital twin is presented for all types of periodic signal (vibration data specifically in this study), and steps of this algorithm are described in detail to ensure reproducibility. The proposed predictive maintenance algorithm can work with both synthetic data and suitable real-life data.
- A publicly accessible vibration dataset and digital twin model-generated synthetic data were used to test the classification accuracy of the proposed predictive maintenance algorithm, in terms of correctly classifying healthy and faulty data.
2. Methodology
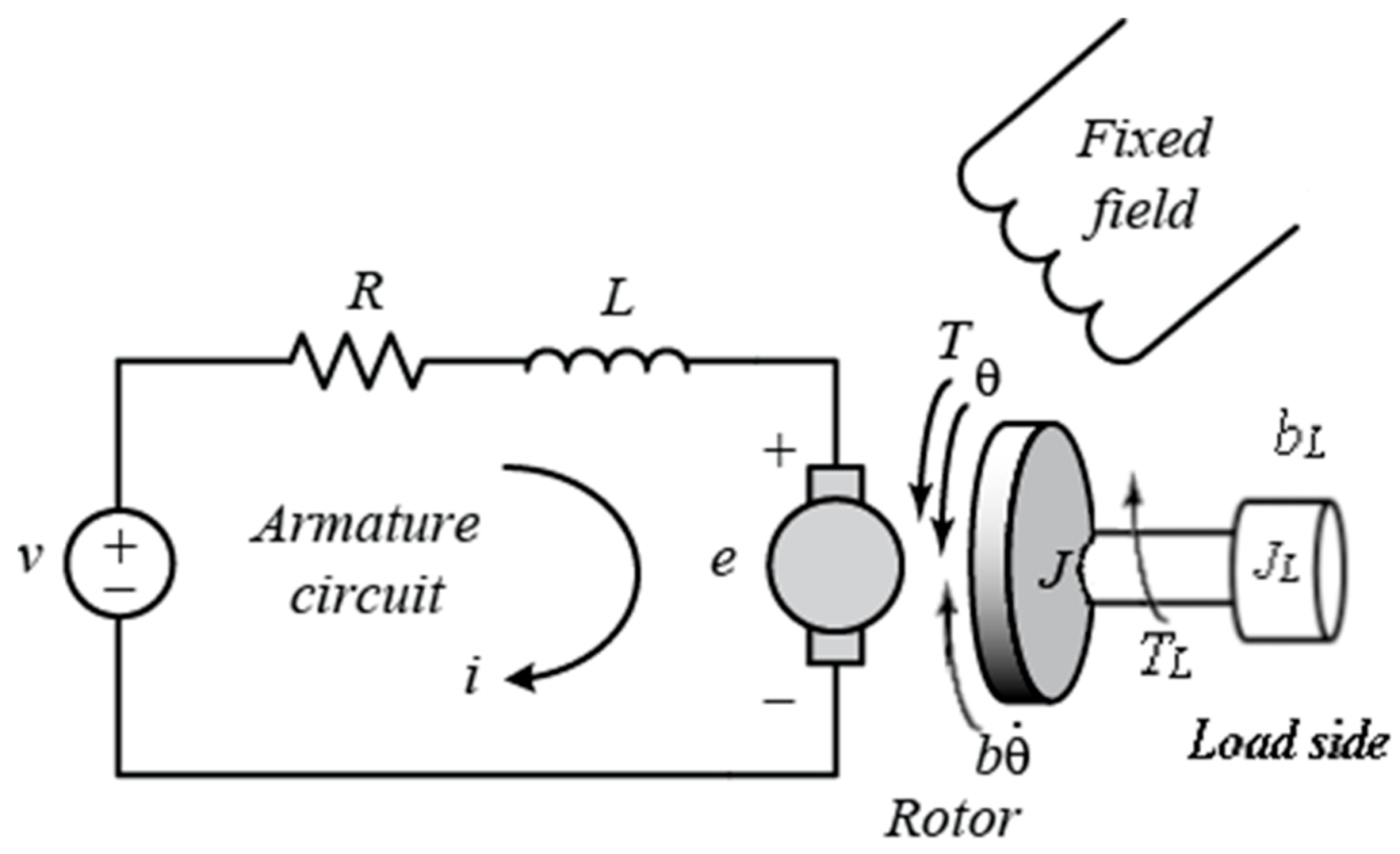
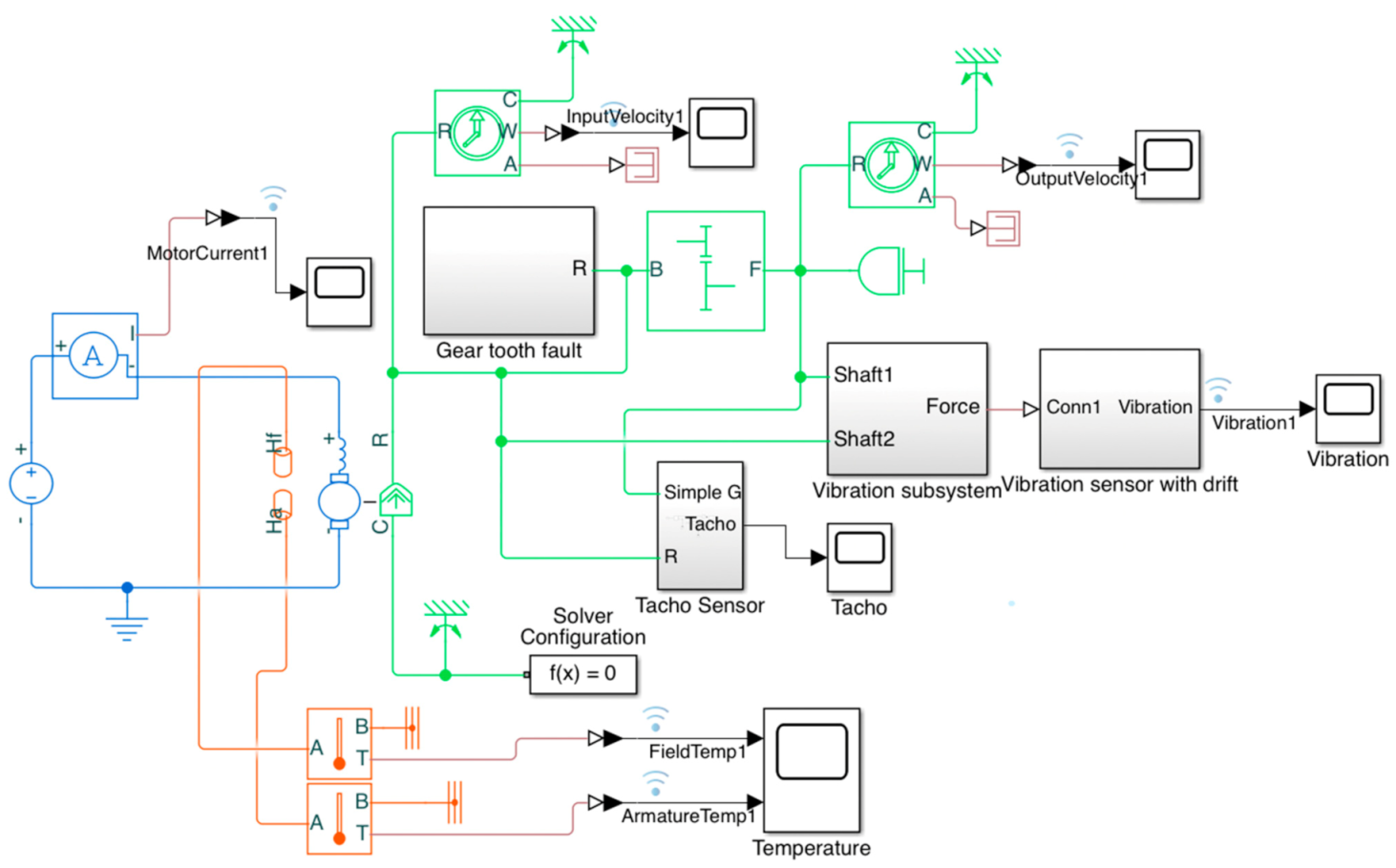
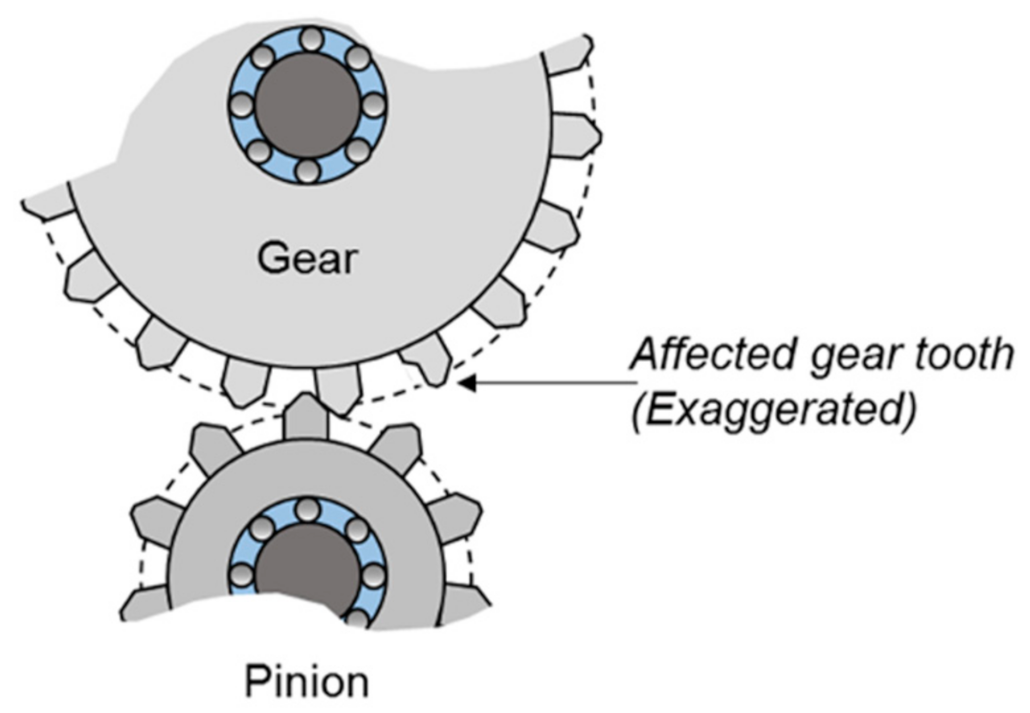
2.1. Creating the Digital Twin Model
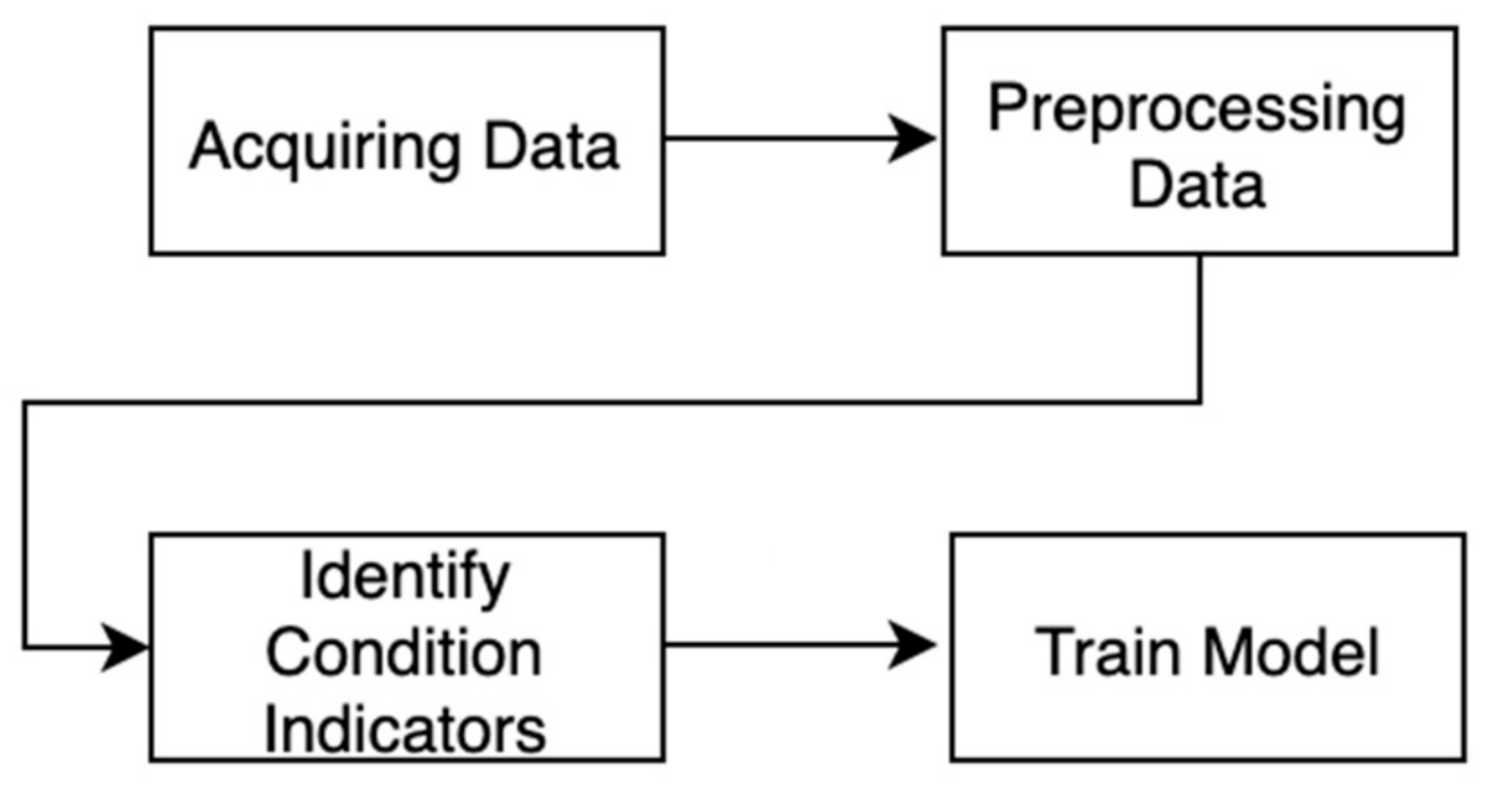
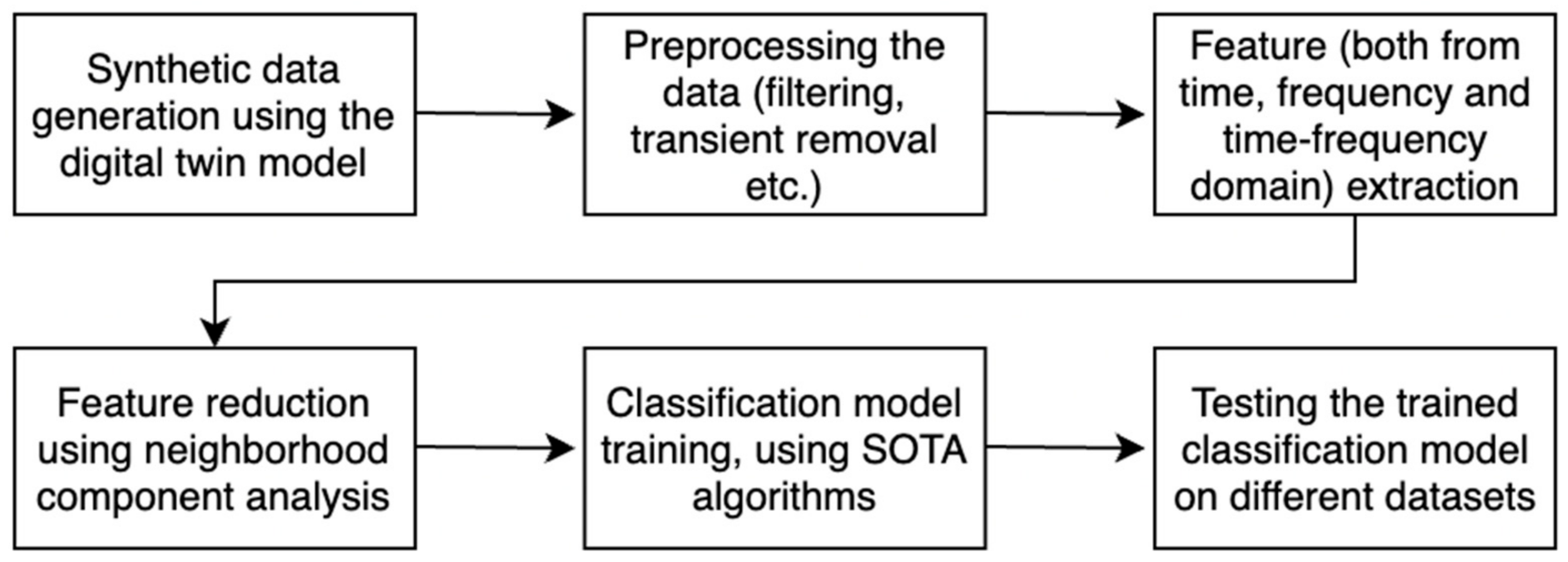
2.2. Predictive Maintenance Workflow
| Algorithm 1 Synthetic Data Generation Algorithm |
| Input: Description of the List of Failures |
| (1) Develop Detailed Physics-Based Model of the Process |
| (2) Develop and Implement Modelling Strategies of the Failures |
| (3) Input Realistic Range of Variables Responsible of the Failures |
| Randomly vary the Variables Responsible of the Failures |
| Run Until Enough Data |
| Output: Supervised Dataset for Predictive Maintenance |
2.3. Testing the Predictive Maintenance Algorithm
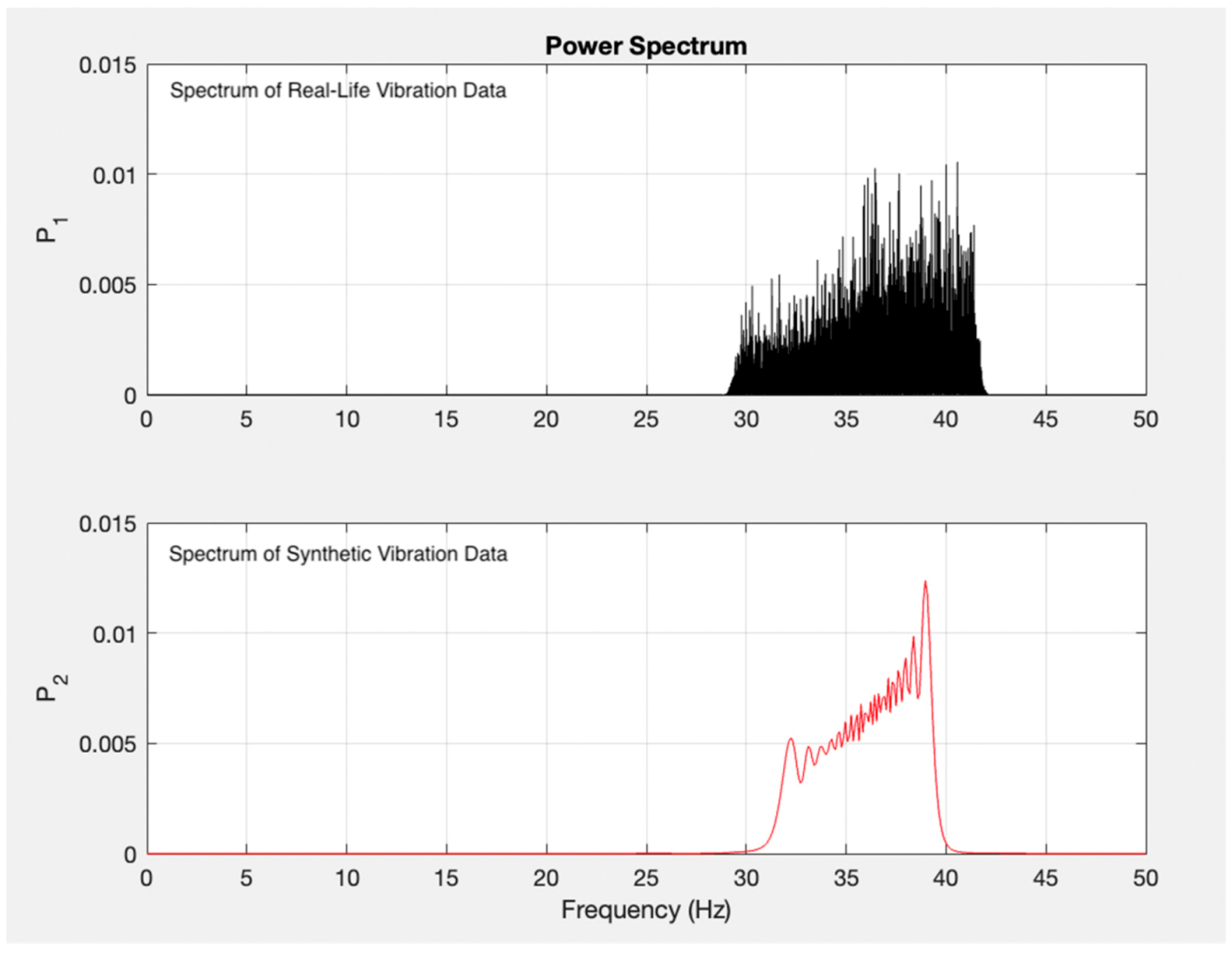
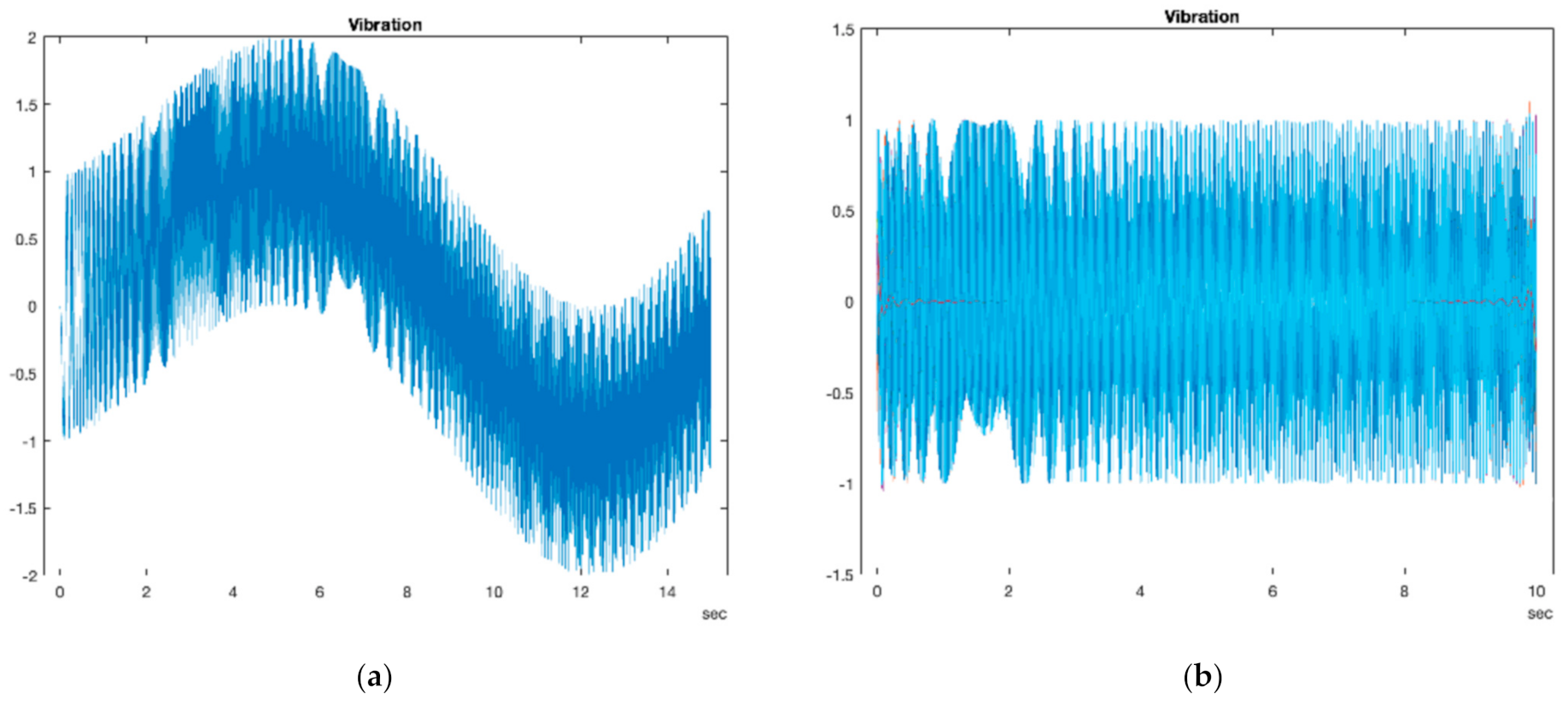
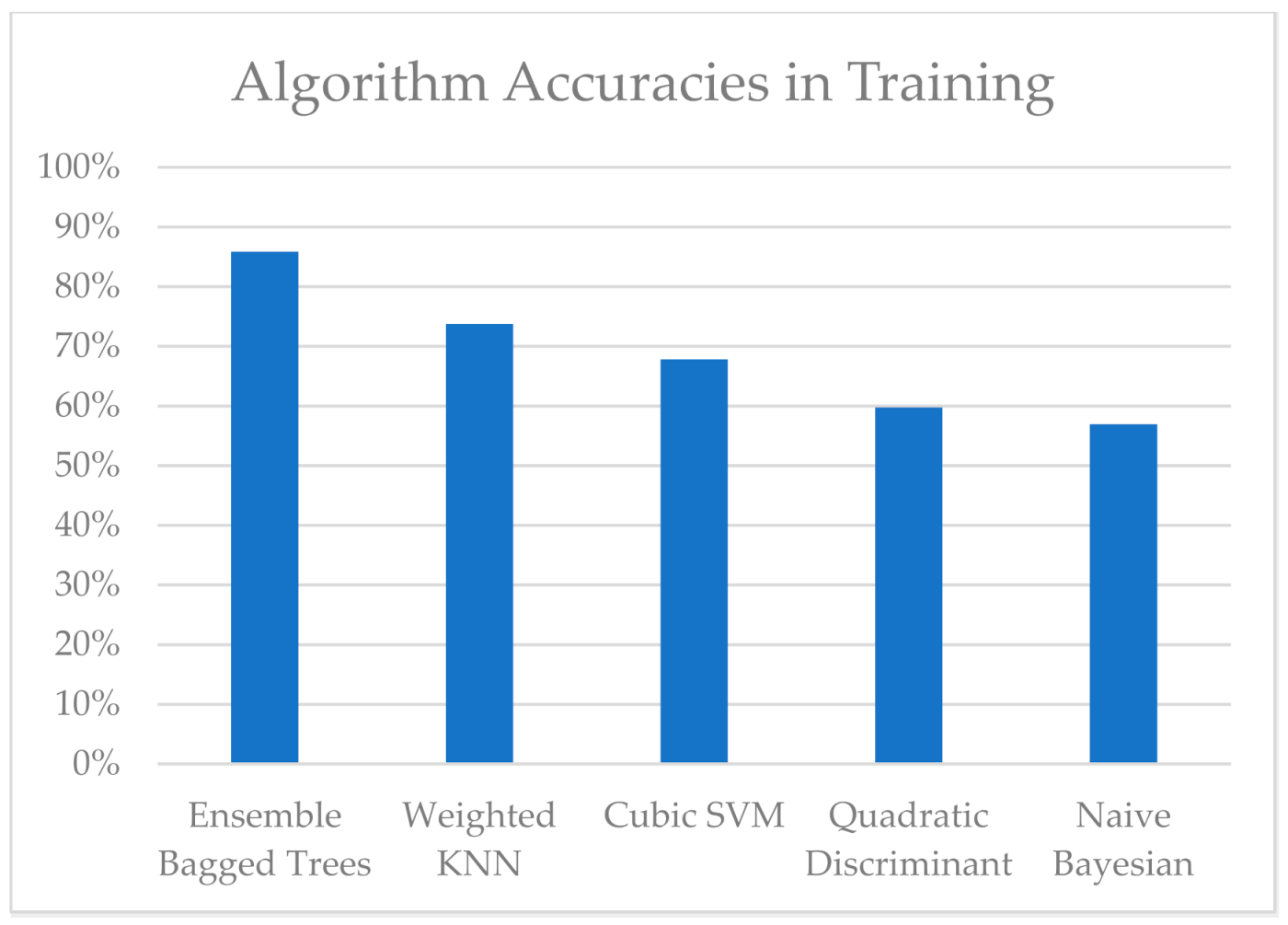
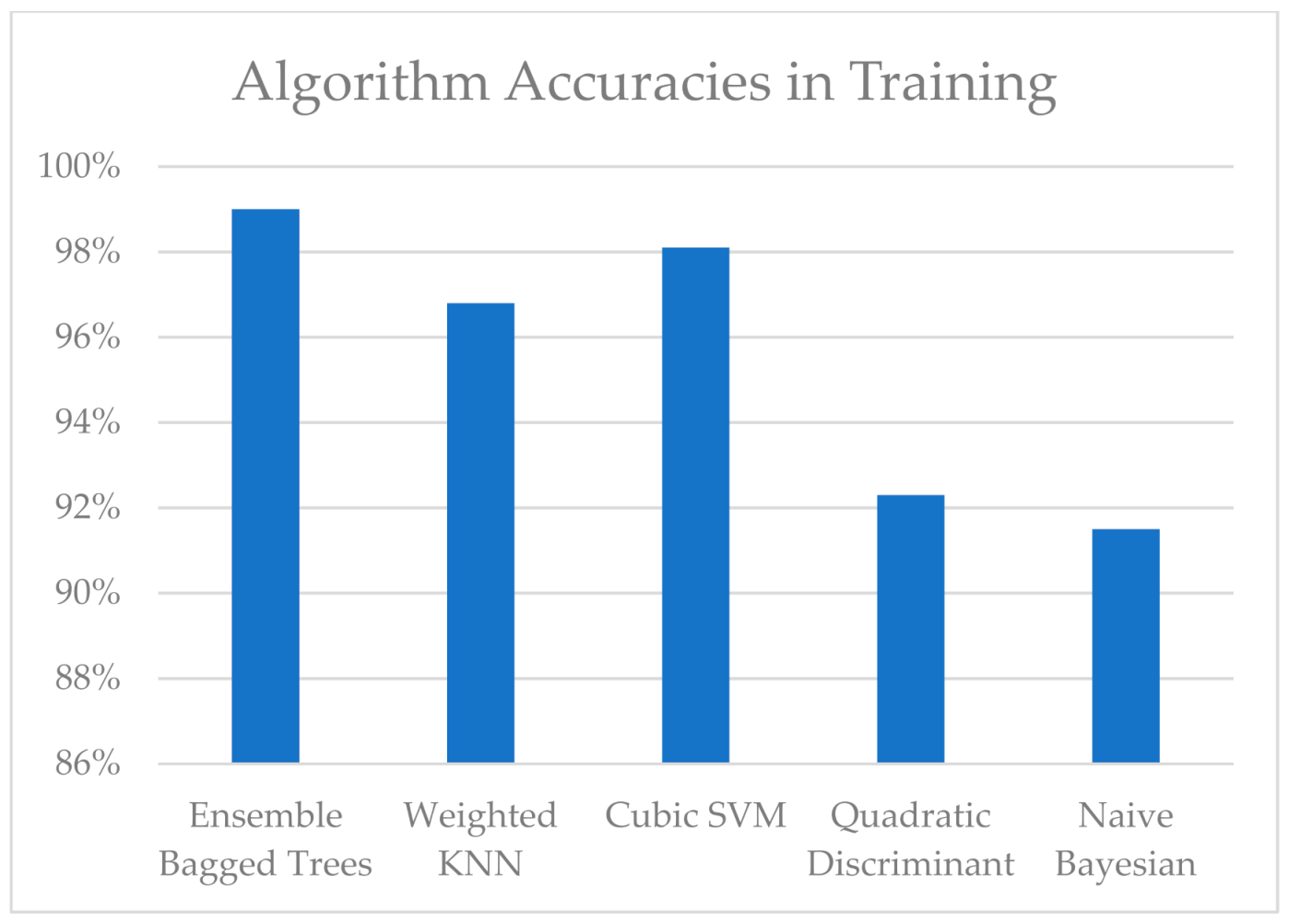
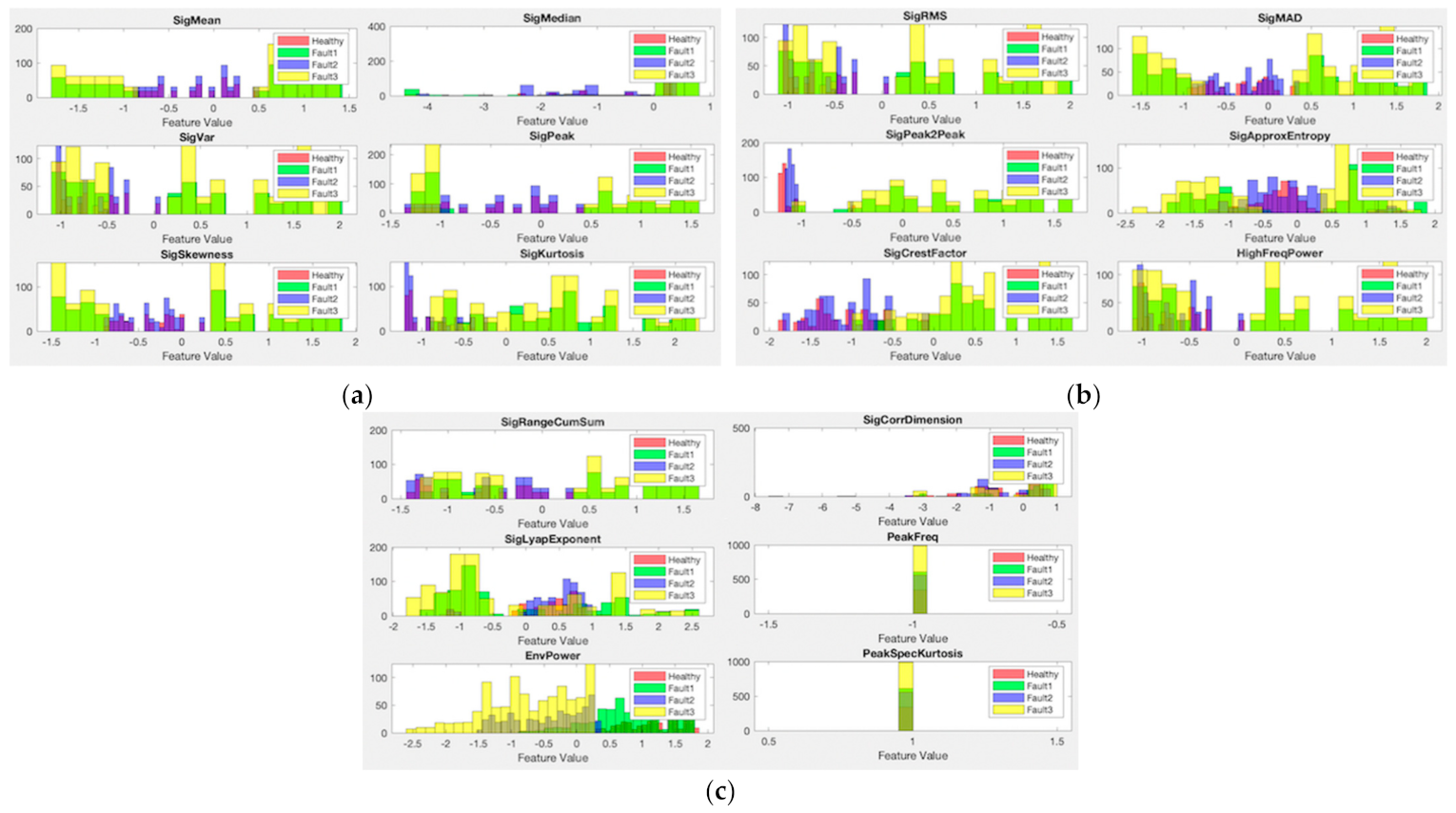
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krupitzer, C.; Wagenhals, T.; Züfle, M.; Lesch, V.; Schäfer, D.; Mozaffarin, A.; Edinger, J.; Becker, C.; Kounev, S. A survey on predictive maintenance for industry 4.0. arXiv 2020, arXiv:2002.08224. [Google Scholar]
- Jimenez, J.J.M.; Schwartz, S.; Vingerhoeds, R.; Grabot, B.; Salaün, M. Towards multi-model approaches to predictive maintenance: A systematic literature survey on diagnostics and prognostics. J. Manuf. Syst. 2020, 56, 539–557. [Google Scholar] [CrossRef]
- Baidya, R.; Ghosh, S.K. Model for a Predictive Maintenance System Effectiveness Using the Analytical Hierarchy Process as Analytical Tool. IFAC-PapersOnLine 2015, 48, 1463–1468, ISSN 2405-8963. [Google Scholar] [CrossRef]
- Deloux, E.; Castanier, B.; Bérenguer, C. Predictive maintenance policy for a gradually deteriorating system subject to stress. Reliab. Eng. Syst. Saf. 2009, 94, 418–431. [Google Scholar] [CrossRef][Green Version]
- Aivaliotis, P.; Georgoulias, K.; Chryssolouris, G. The Use of Digital Twin for Predictive Maintenance in Manufacturing. Int. J. Comput. Integr. Manuf. 2019, 32, 1067–1080. Available online: https://www.researchgate.net/profile/Luca-Romeo-2/publication/327334242_Machine_Learning_approach_for_Predictive_Maintenance_in_Industry_40/links/5e15db8792851c8364badb48/Machine-Learning-approach-for-Predictive-Maintenance-in-Industry-40.pdf (accessed on 3 August 2021). [CrossRef]
- Melesse, T.Y.; Di Pasquale, V.; Riemma, S. Digital Twin models in industrial operations: State-of-the-art and future research directions. IET Collab. Intell. Manuf. 2021, 3, 37–47. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Werner, A.; Zimmermann, N.; Lentes, J. Approach for a holistic predictive maintenance strategy by incorporating a digital twin. Procedia Manuf. 2019, 39, 1743–1751. [Google Scholar] [CrossRef]
- Melesse, T.Y.; Di Pasquale, V.; Riemma, S. Digital twin models in industrial operations: A systematic literature review. Procedia Manuf. 2020, 42, 267–272. [Google Scholar] [CrossRef]
- Dalzochio, J.; Kunst, R.; Pignaton, E.; Binotto, A.; Sanyal, S.; Favilla, J.; Barbosa, J. Machine learning and reasoning for predictive maintenance in Industry 4.0: Current status and challenges. Comput. Ind. 2020, 123, 103298. [Google Scholar] [CrossRef]
- Nacchia, M.; Fruggiero, F.; Lambiase, A.; Bruton, K. A Systematic Mapping of the Advancing Use of Machine Learning Techniques for Predictive Maintenance in the Manufacturing Sector. Appl. Sci. 2021, 11, 2546. [Google Scholar] [CrossRef]
- Klein, P.; Bergmann, R. Data Generation with a Physical Model to Support Machine Learning Research for Predictive Maintenance. LWDA 2018, 2191, 179–190. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Transfer learning using deep representation regularization in remaining useful life prediction across operating conditions. Reliab. Eng. Syst. Saf. 2021, 211, 107556. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Li, X. Deep learning-based prognostic approach for lithium-ion batteries with adaptive time-series prediction and on-line validation. Measurement 2020, 164, 108052. [Google Scholar] [CrossRef]
- J Humaidi, A.; Kasim Ibraheem, I. Speed Control of Permanent Magnet DC Motor with Friction and Measurement Noise Using Novel Nonlinear Extended State Observer-Based Anti-Disturbance Control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Vibration Analysis of Rotating Machinery. Mathworks Help Center. 2021. Available online: https://uk.mathworks.com/help/signal/ug/vibration-analysis-of-rotating-machinery.html (accessed on 9 August 2021).
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Designing Algorithms for Condition Monitoring and Predictive Maintenance; Mathworks Help Center: Natick, MA, USA, 2021; Available online: https://uk.mathworks.com/help/predmaint/gs/designing-algorithms-for-condition-monitoring-and-predictive-maintenance.html (accessed on 8 August 2021).
- Using Simulink to Generate Fault Data; Mathworks Help Center: Natick, MA, USA, 2021; Available online: https://uk.mathworks.com/help/predmaint/ug/Use-Simulink-to-Generate-Fault-Data.html (accessed on 8 August 2021).
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. signal Process 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Bearing Data Center. Case Western Reserve University Bearing Data Center Website. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 10 August 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selçuk, Ş.Y.; Ünal, P.; Albayrak, Ö.; Jomâa, M. A Workflow for Synthetic Data Generation and Predictive Maintenance for Vibration Data. Information 2021, 12, 386. https://doi.org/10.3390/info12100386
Selçuk ŞY, Ünal P, Albayrak Ö, Jomâa M. A Workflow for Synthetic Data Generation and Predictive Maintenance for Vibration Data. Information. 2021; 12(10):386. https://doi.org/10.3390/info12100386
Chicago/Turabian StyleSelçuk, Şahan Yoruç, Perin Ünal, Özlem Albayrak, and Moez Jomâa. 2021. "A Workflow for Synthetic Data Generation and Predictive Maintenance for Vibration Data" Information 12, no. 10: 386. https://doi.org/10.3390/info12100386
APA StyleSelçuk, Ş. Y., Ünal, P., Albayrak, Ö., & Jomâa, M. (2021). A Workflow for Synthetic Data Generation and Predictive Maintenance for Vibration Data. Information, 12(10), 386. https://doi.org/10.3390/info12100386





