1. Introduction
The demand for fast and accurate tracking of the targets is increasing day by day. Under water, noise corrupted angle measurements are available from noise radiated from the target and processed from a single observer platform operating in passive mode [
1]. Passive target tracking is more popular as it helps the tracker from being tracked. In the ocean environment, target motion analysis is generally performed in a two-dimensional plane using angles-only measurements. The angles generated by the sensors are well known as bearing angles. The observer with the single sensor array, say hull-mounted array (HMA), in a passive mode, determines parameters of target motion like its range, course, bearing angle, speed, etc. As the range of the target is not available and bearing being nonlinearly related to target motion parameters, nonlinearity in the process is high [
2]. In addition to this, measurements from a single sensor array are only considered to be available, which makes the process unobservable and the observer must perform a proper maneuver to make the process observable [
3,
4,
5].
The ocean environment is unstable all the time and this makes the bearing measurements from a single sensor array unreliable in obtaining all the required information about the target. Moreover, an increase in system complexity increases the need for more input from different sensor arrays to obtain complete information on the system. According to the application and need, a system with multiple sensors can choose different sensors with the required characteristics and based on the environmental conditions for obtaining the target information. Information from these sensors is then consistently combined coherently to obtain the parameters like range, course, velocity, and acceleration of the target during its movement. This is known as data fusion problem. As the bearing measurements are taken from two sensors, in this work, the maneuver of the observer to obtain the observability of the target is reduced in most of the scenarios.
Angles-only tracking, commonly known as bearings-only tracking, used classical filters like maximum likelihood estimator, pseudo linear estimator, etc. in the early 19th century [
1,
6] and these were batch processing filters. In real-time scenarios, these batch processing estimators need a lot of time for obtaining the estimated results. This led to the evolution of recursive estimators like least square estimator, Kalman filter (KF), etc. KF being a linear filter was not suitable for nonlinear bearings-only tracking [
3]. The nonlinearity in the process leads to the evolution of extended KF (EKF), unscented KF (UKF), particle filter (PF), etc. to deal with the nonlinearities in the process and measurements [
7]. EKF reduces the nonlinearities by linearizing the measurement equation using Taylor series expansion and updates the state and covariance matrices and calculates the filter gain. The filter is mostly dependent on the initializations and due to the linearization process; information is lost making the solution unreliable. In UKF, the probability density function of the state vector is propagated through a set of carefully chosen sample points, called sigma points, using unscented transform [
8,
9]. This helps in possession of posterior mean and covariance up to second order for any type of nonlinearity. Hence, unlike EKF, UKF can provide improved stability, accuracy, and better convergence in solution [
10,
11,
12].
Y. Bar-Shalom, in [
13], gave a deep insight regarding data association and data fusion of multiple sensors in multiple target environment using radar measurements. Several filtering algorithms were utilized including EKF, UKF, and PF. Data fusion for underwater surveillance was presented in [
14,
15,
16], in which the technique was evaluated only using MGBEKF and UKF algorithms. In [
17], the author used a data fusion technique to evaluate the performance of the fusion technique for two and more than two sensors of data fusion. It is an extensive work for the work presented by Bar-Shalom on data fusion. In [
18], the authors applied a data fusion technique using a PF for estimation of robot motions. In [
19], the authors analyzed the fusion technique for batch processing using the maximum likelihood estimator and analyzed the same with recursive processing with an unscented Gauss–Helmert Kalman filter. The observability of the system is further discussed in the paper. In [
18], a data fusion algorithm was used along with a data association algorithm to detect multiple targets. It deals with the hardware complexity in target detection. In [
19], data fusion was used to detect the target in a properly designed underwater network. In [
20], authors used interacting multiple model techniques combined with EKF and UKF for tracking the single as well as multiple targets and compared two different data fusion techniques that involve fusion using nearest neighborhood calculation and fusion using probabilistic data association. The data fusion techniques in literature are extended to robotics, in air surveillance, and underwater surveillance applications. However, there is a necessity to explore the fusion techniques in detail for underwater surveillance applications.
The filters considered for evaluation of fusion algorithm are further compared with theoretical Cramer–Rao lower bound (CRLB). The mathematical modelling of CRLB for tracking algorithms using a single sensor array is in [
9,
21] and that for tracking algorithms using two sensor arrays is represented in
Section 2.6.
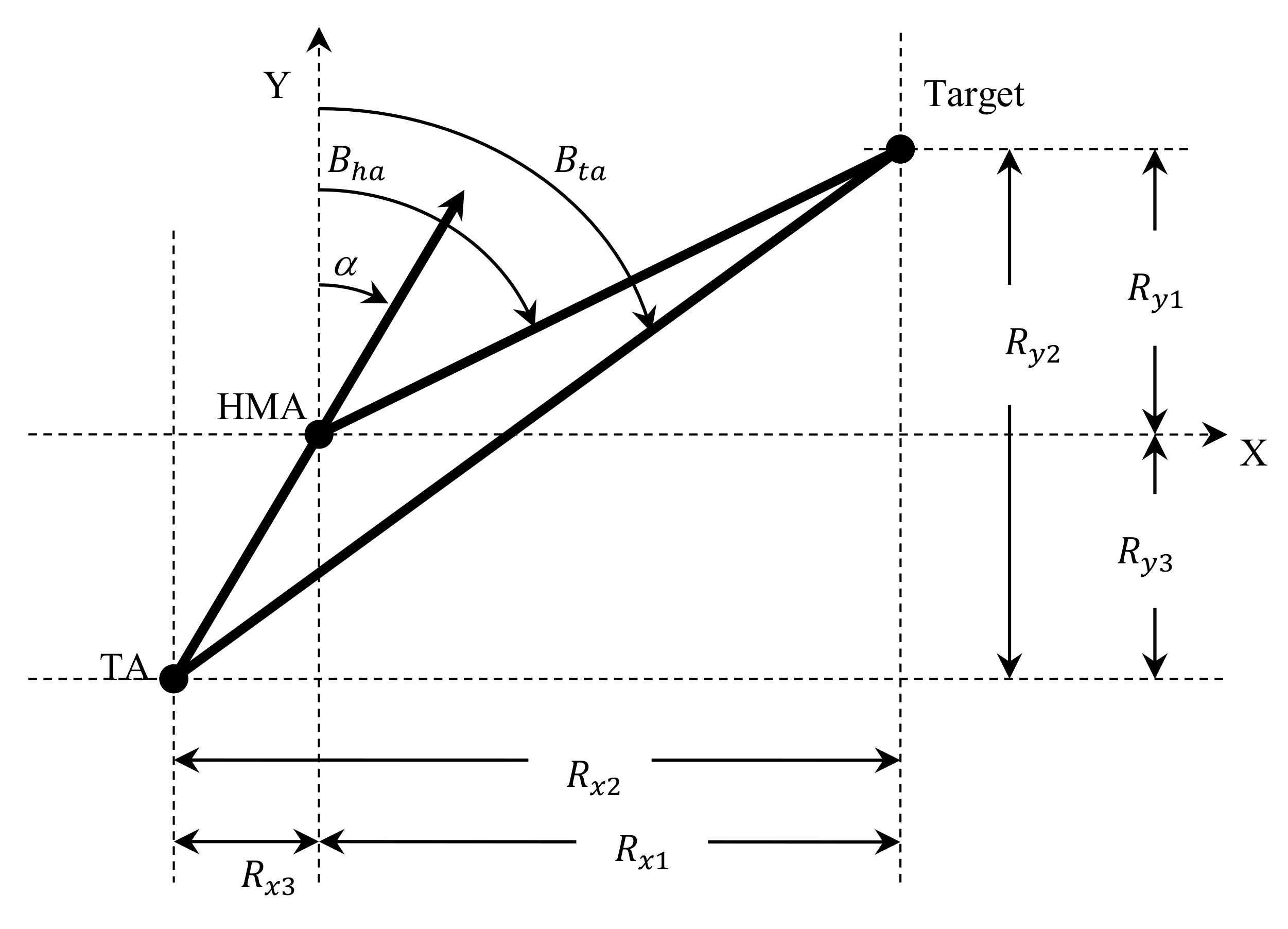
In this paper, a single target following the constant velocity model is considered for simplicity. The fusion of measurement information from two sensor arrays, HMA and towed array (TA) is considered without maneuver. TA is towed behind the observer at a certain distance away from the observer. This helps in the reduction of self-noise from the observer and allows it to operate at very low frequencies. Hence, the TA will be capable of even tracking the target at great distances. The algorithm is evaluated for several scenarios in Monte Carlo simulations.
In this paper, the performance of BOT with a single sensor (HMA) and two sensors (HMA and TA) using different filters is evaluated. The mathematical modelling of all the algorithms is described in
Section 2. The results obtained from the simulation of the algorithms and discussion on the results is given in
Section 3. This paper is concluded in
Section 4.
3. Implementation and Simulation
Scenarios that are considered for evaluating the algorithms are as shown in
Table 1. The bearing measurements from HMA and TA are assumed to be available continuously for every second for TST and SST.
In an underwater environment, a submarine in a passive mode of operation can track a target at 4 to 5 kilometers. However, this changes with the environmental conditions underwater. Scenarios with different target courses are considered to track the target moving in different directions. Scenario with an initial bearing of 20° is like the scenario with an initial bearing of 0° with coordinates frame turned by 20°. Hence the bearing value is chosen as 0° for simplicity. Target is also assumed to be a submarine, so, the speed of the target is chosen accordingly [
24].
For SST, the observer is presumed to maneuver following the famous S-maneuver in its course. Therefore, for two minutes, the observer follows the current course it is i.e, 90°. Now it slowly turns 180° at the rate of 0.5° per second to attain 270°. With 0.5° per second turn rate, the observer takes 6 minutes to complete the maneuver. For TST, the observer is presumed to be traveling at a constant speed and with a constant course of 90° i.e., without any maneuver in course or speed. The noise in measurements is assumed to follow Gaussian distribution and is additive. The initializations of the target state vector and its covariance matrices are chosen as in Equations (33)–(35). The speed of the target is difficult to estimate and is assumed to be 5m/s, as the submarine travels at very low speeds. Sonar range of the day, which gives the minimum range of target detection with a 50 percent probability of detection, of 5000 m is considered in target state vector initializations.
For SST, the initial state vector is given in Equation (61) and for TST it is given in Equation (62).
Initial target state estimate
is assumed to be distributed uniformly and elements of the state covariance matrix are initialized accordingly as Equation (63).
Here for TST and for SST
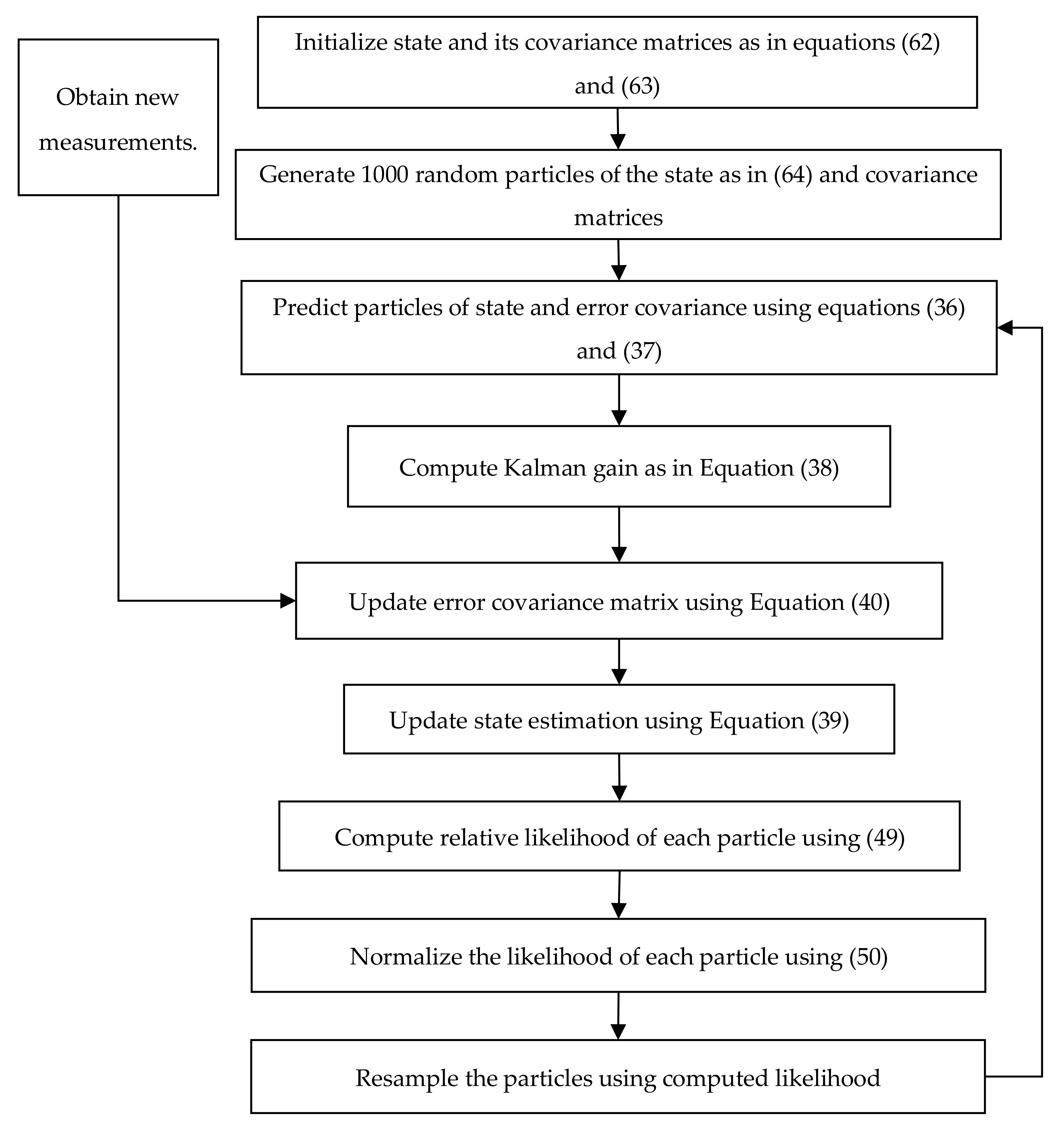
The particles of the target state vector for PFEKF and PFMGBEKF filters are generated by adding random noise to the initial state vector as in (58) for TST. Similarly, for SST the initial state vector is added with a column matrix of random numbers with four rows as in Equation (64) [
22].
Here, represents the particle number and . The covariance matrix for each particle of the target state vector for PFEKF and PFMGBEKF filters are generated based on each particle generated.
It is not genuine to evaluate the performance of the algorithm on a run basis, as randomness exists in the experiment. Therefore, Monte Carlo simulation of 100 runs is performed for each filtering in MATLAB [
6] for both SST and TST algorithms. The maximum (3σ) error acceptable in estimated range, course and speeds are 8% of true range, 3° and 1m/s, the root-mean-squared (RMS) (1σ) error allowed for the acceptance of the solution are 2.66% of true range, 1° and 0.33m/s respectively. The errors in the estimation of target parameters are root-mean-squared and the solution is assessed on the error acceptance levels mentioned above.
RMSE is nothing but root mean squared error and it is, in general, called standard deviation. It is implemented as follows. The difference between the true target parameter and the estimated target parameter is taken as error and it is squared. The mean of the squared error for all the 100 runs is then calculated and square rooted. This provides the RMSE of the estimated target parameters. Let
be the number of Monte Carlo runs and
be the total time in seconds for which the simulation is carried out. Then the error is mathematically given as Equation (65) and the RMSE as Equation (66).
The error in the estimated target parameters must be within the vicinity range of the weapon that has to be fired onto the target. The error in estimated target parameters is calculated based on Monte Carlo runs. Therefore, the RMSE values of the estimated target parameters are considered. With Monte Carlo simulations with 100 different noise sequences (maintaining same PDF), the outputs are root mean squared to obtain a single value. The acceptance criteria are chosen based on the weapon homing zone. The solution is said to be obtained only when the error in the estimated target parameters is less than the given values in acceptance criteria. Once the solution is obtained, the estimated target parameters can be used to release weapon onto the target.
The convergence time of the solutions for the three scenarios based on the above-mentioned acceptance criteria for 100 runs is tabulated in
Table 2 for different filtering algorithms. In a Monte Carlo simulation, it is observed that UKF converges faster than other filters for BOT. Moreover, with single bearing measurement, the observer needs to follow S-maneuver, which can be avoided while using bearing measurements from two sensors.
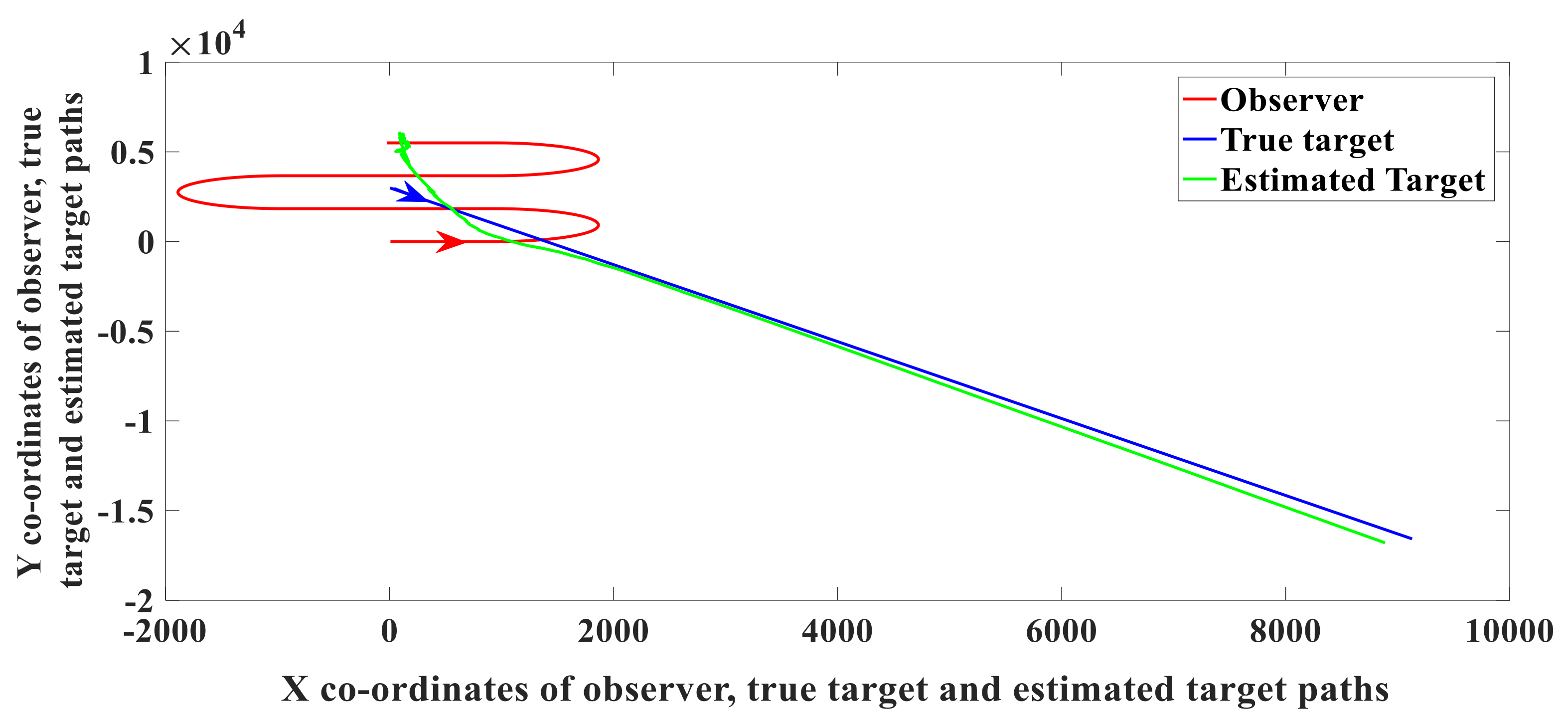
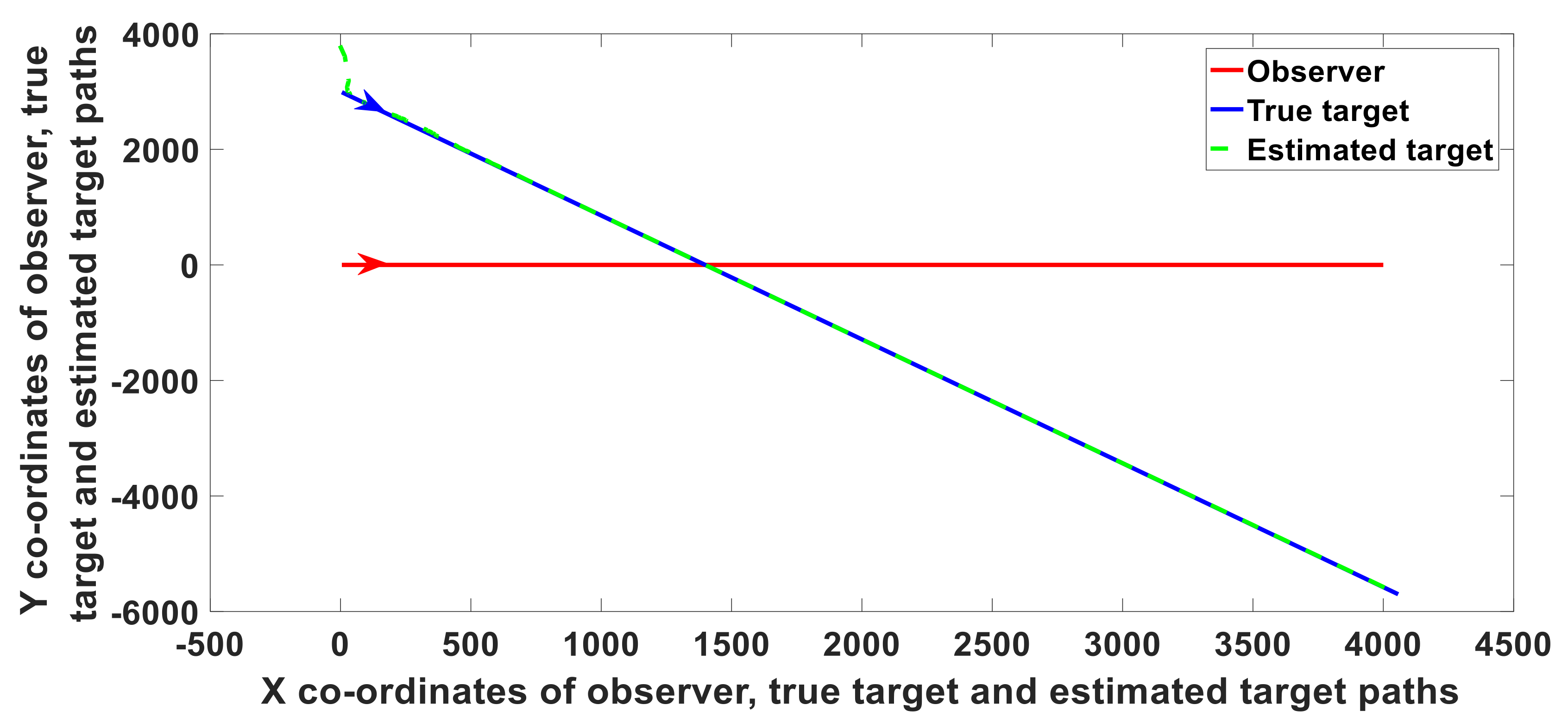
The simulation is carried out for 30 minutes. Results obtained with UKF for scenario 1 in
Table 1 with SST and TST, are presented in
Figure 3 and
Figure 4 respectively. For SST, the observer needs to perform S-maneuver to obtain the observability of the process and hence to obtain a solution. With TST, the observability and solution are obtained even without observer maneuver as it uses bearing measurements from two sensors.
Table 3 gives the total convergence times of the solution with various filtering algorithms for TST. The solution is said to be converged if the acceptance criteria are achieved in all the three parameters at a time and the solution does not diverge for the rest of the simulation time. It can be observed from the table data that the solution convergence time is only for a short period with some of the scenarios and not for the entire simulated time for EKF. For scenario 2, the solution is converged from 227 to 447th second and then the solution diverged for the rest of the simulation time. The solution is not obtained for some of the scenarios with EKF. With MGBEKF, the same trend of solution-divergence persists. With UKF, the solution is obtained earlier than other filters for most of the scenarios. As shown in
Table 3, UKF for scenario 1 has convergence time of 235 seconds whereas PFEKF and PFMGBEKF have convergence times of 337 and 237 seconds respectively. It can also be observed from
Table 2 and
Table 3 data that the convergence times for TST are obtained faster than SST.
As the measurements are taken from two different sensor arrays and both the measurements are nonlinearly related to the target state vector elements, the process nonlinearity will be very high. Therefore, sub-optimal nonlinear filters, EKF and MGBEKF, failed to give proper solutions. Particle filter deals with complete non-linearity and is suitable for highly nonlinear systems. However, to avoid the sample degeneracy problem it is combined with other filters and hence gives better results than EKF and MGBEKF.
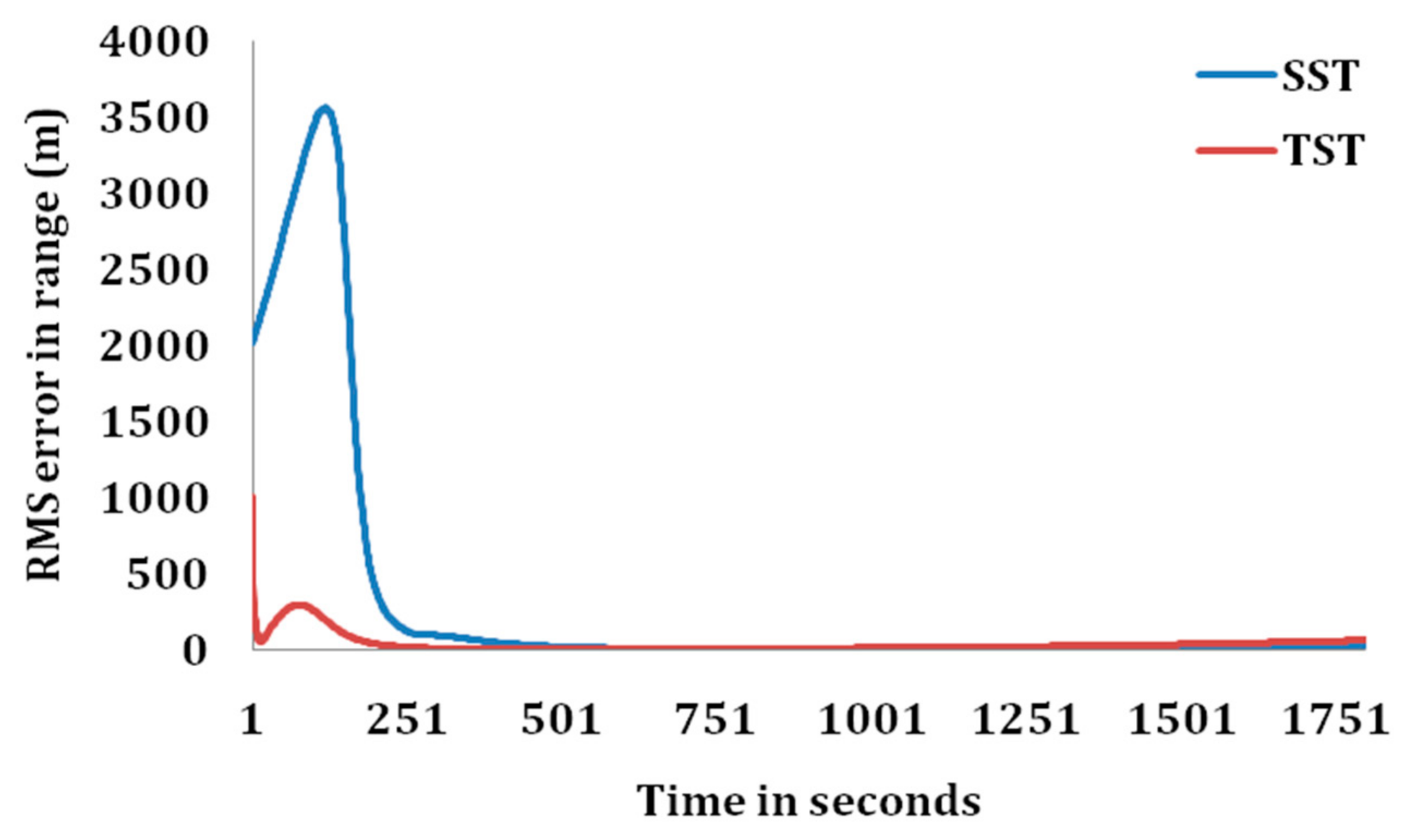
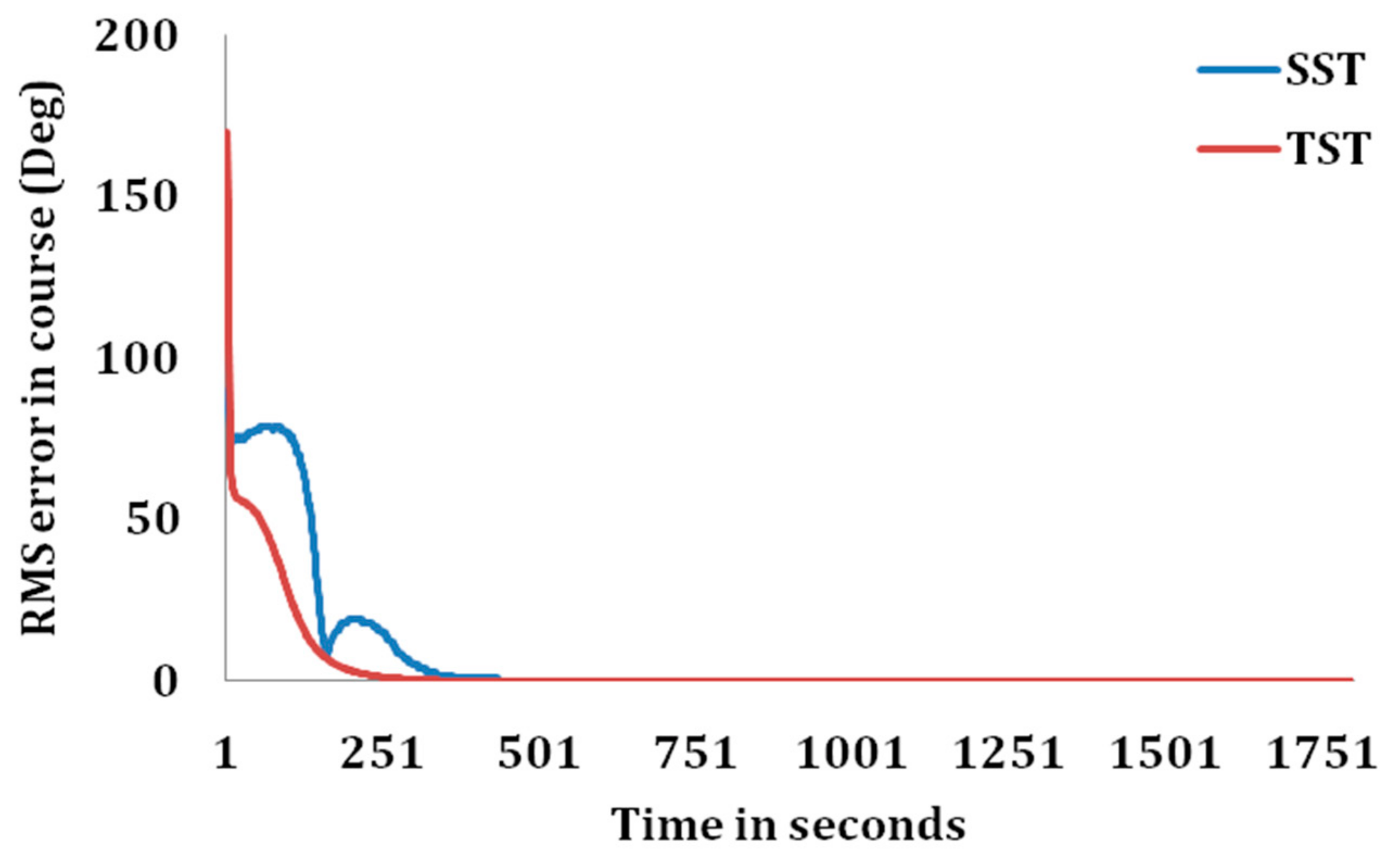
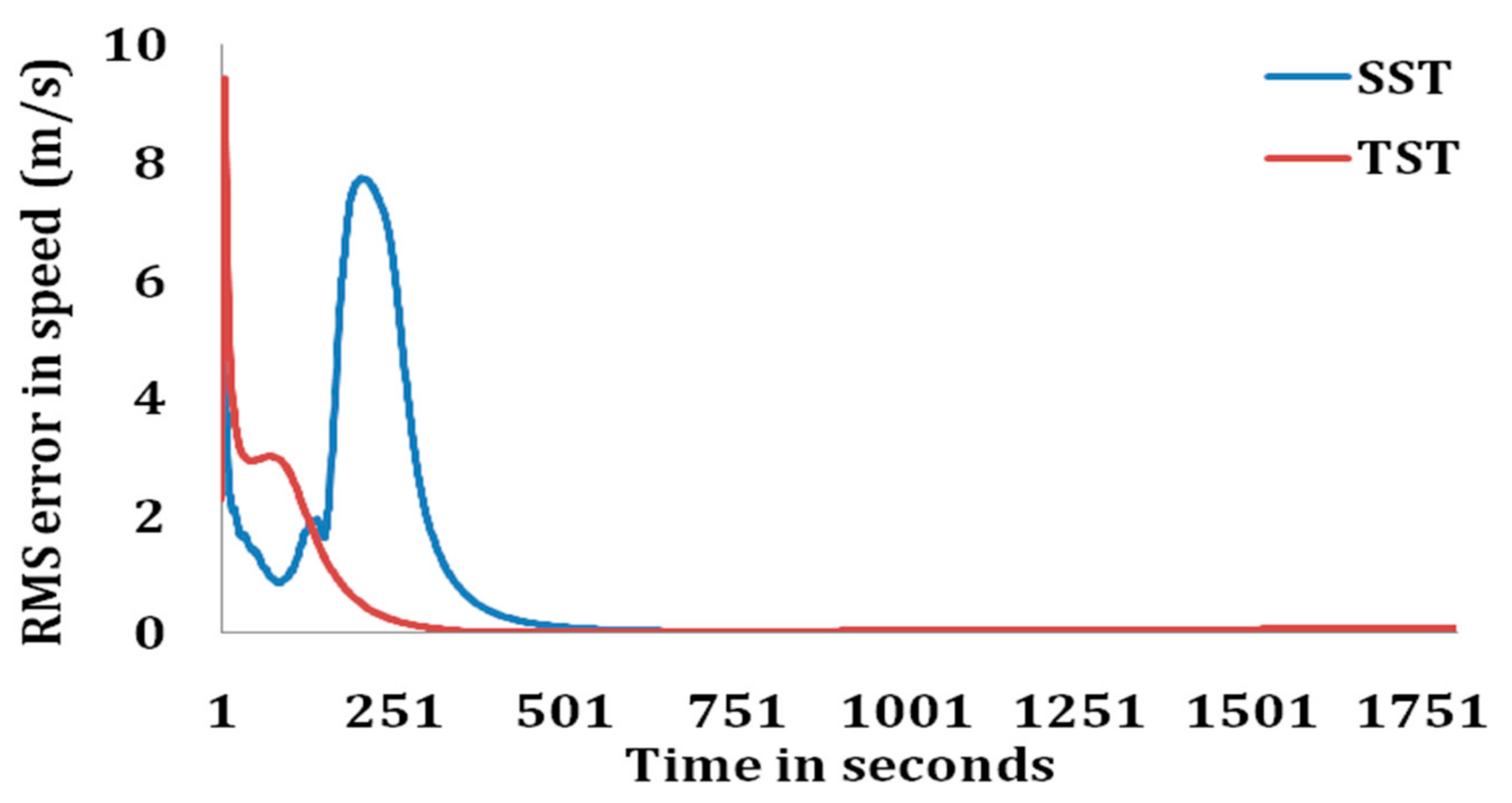
RMS errors in range, course, and speed estimates of the target are represented in
Figure 5,
Figure 6 and
Figure 7. It can be observed from the figures that the RMS errors in estimated target parameters are less in case of TST than that with SST. RMS errors in estimated parameters are obtained within the acceptance criteria for TST much earlier than that of SST. However, as the range between observer and target increases, the RMS errors in estimated target parameters increases slightly for TST than that of SST.
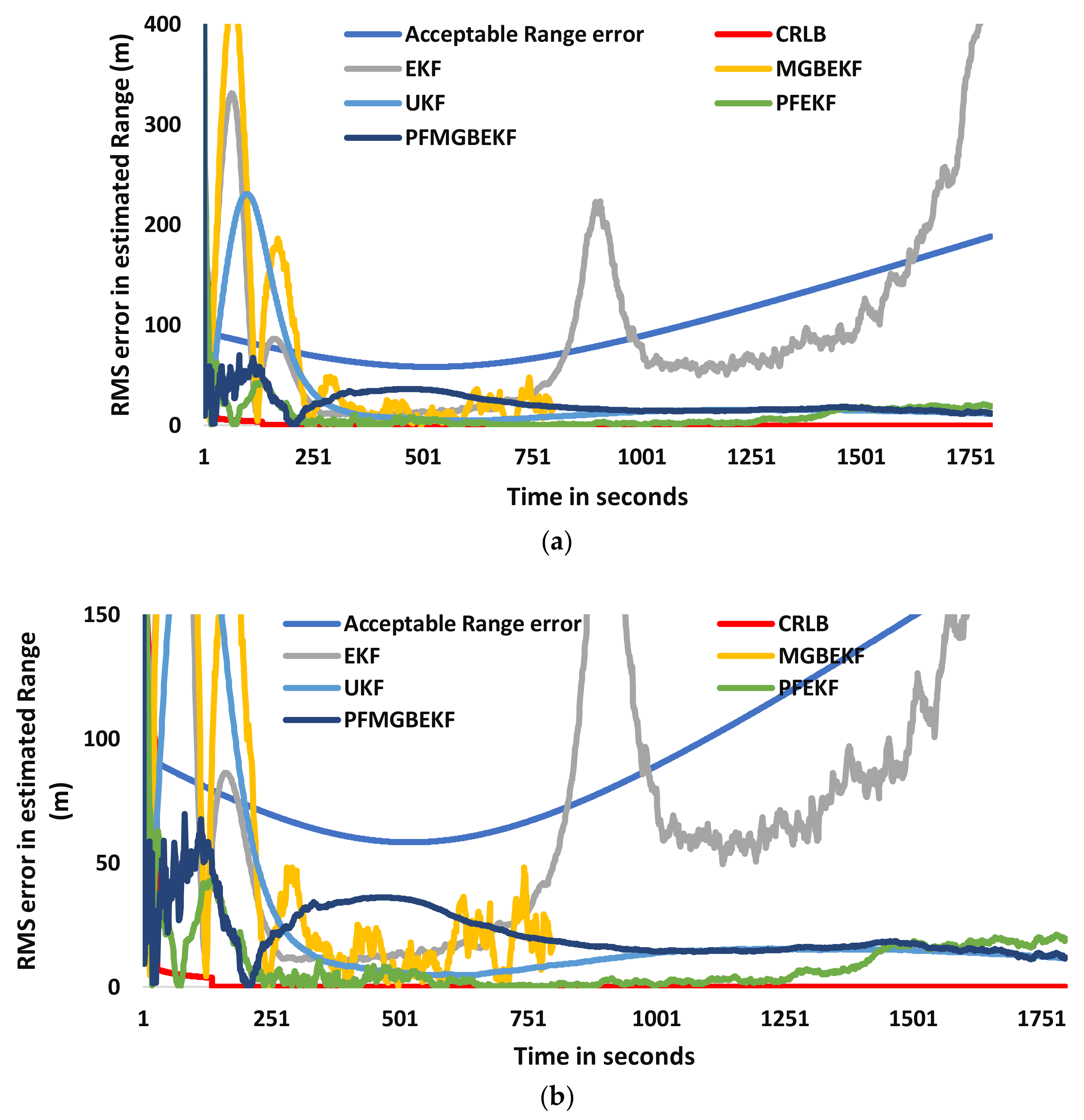
Figure 8 shows the acceptable error in range along with CRLB values for scenario 3, according to the acceptance criteria mentioned above, which is 2.667% of true range. RMS errors in the range of the target for different filters are also shown in
Figure 8. It can be observed from the figure that lower RMS error is obtained earlier with PFEKF and PFMGBEKF filters than that of EKF, MGBEKF, and UKF filters. It can be seen from
Figure 8b that the lowest RMS error is obtained with PFEKF. Though the error is below the acceptable error values, there is an effect of EKF that makes the error to vary in an unstable manner, which can be seen in the form of spikes in the plot. Similarly, with PFMGBEKF, the instability in error is reduced when compared to PFEKF.
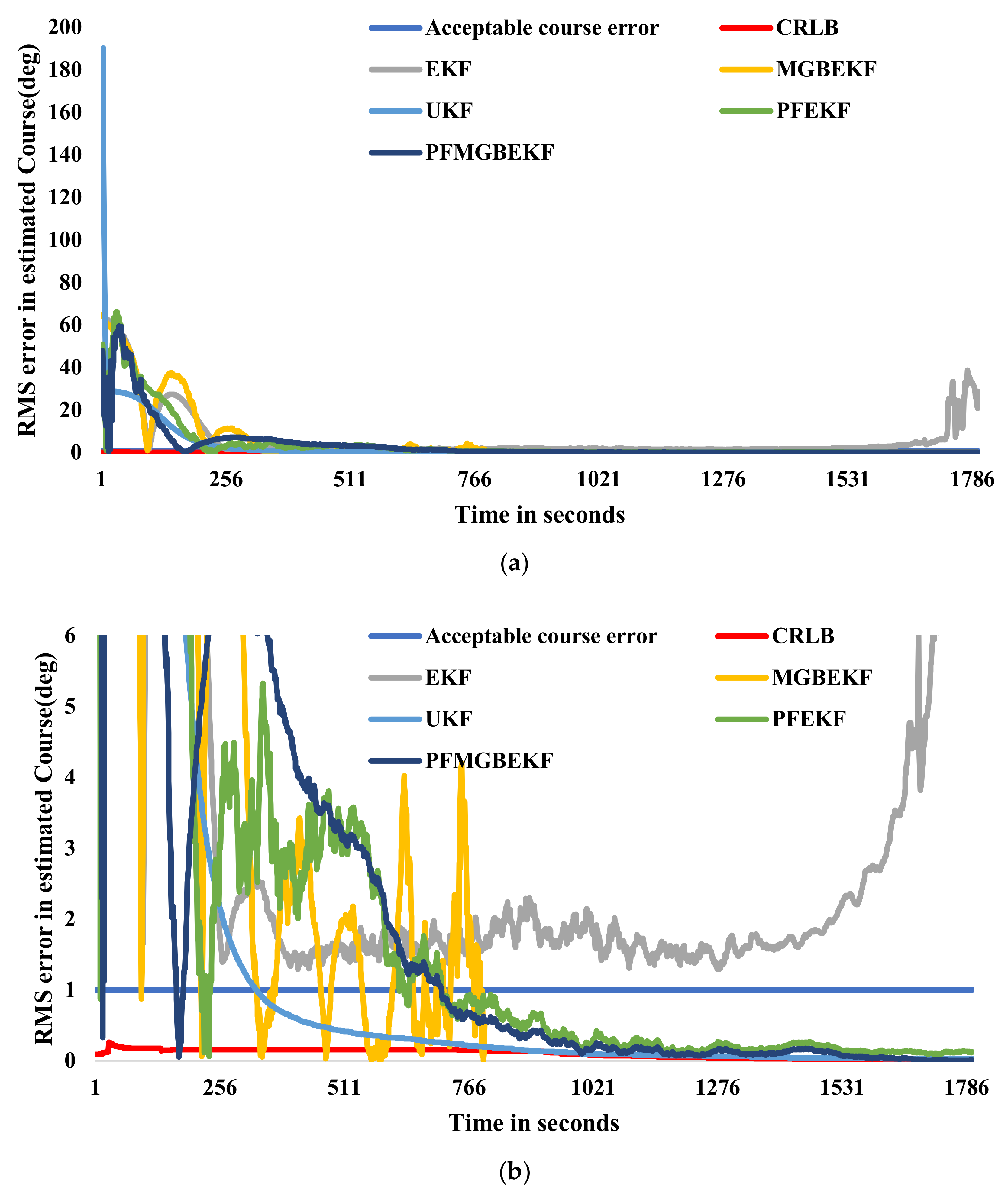
Figure 9 shows the acceptable error in the course for the same scenario 3, according to the acceptance criteria mentioned above, which is less than 1°. RMS errors in the course of the target for different filters are also shown in
Figure 9. From
Figure 9a, it can be observed that the error in the course is not obtained within acceptance criteria with EKF and MGBEKF. However, the fastest convergence in the target course was observed to be obtained with UKF, which can be seen from
Figure 9b. PFEKF and PFMGBEKF also have convergence in the target course at 562 and 550 s respectively.
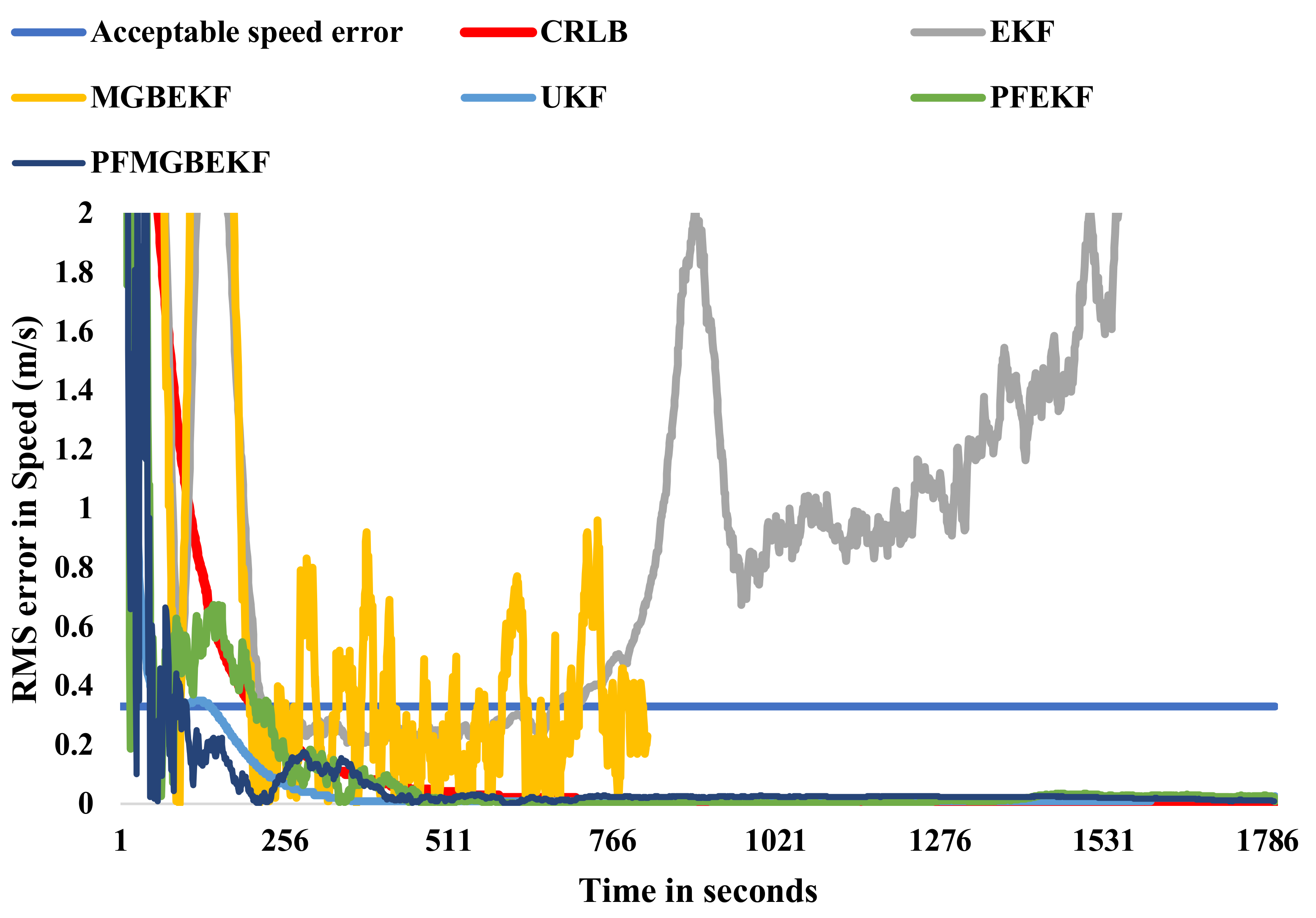
Figure 10 shows the acceptable error in speed for the same scenario 3, according to the acceptance criteria mentioned above, which is less than 0.33 m/s. RMS errors in the speed of the target for different filters are also shown in
Figure 10. It can be observed from the figure that RMS error in speed with EKF and MGBEKF are varying in an unstable manner and are out of bounds after a certain time. With UKF, the convergence of speed error within acceptable criteria takes a shorter time than other filters and has a stable pattern. With PFMGBEKF, the lowest values in error are obtained. The overall convergence times were observed to be shorter for UKF than other filters and hence UKF performs well for TST than other filters.