Measurement of Text Similarity: A Survey
Abstract
1. Introduction
Motivation of the Survey
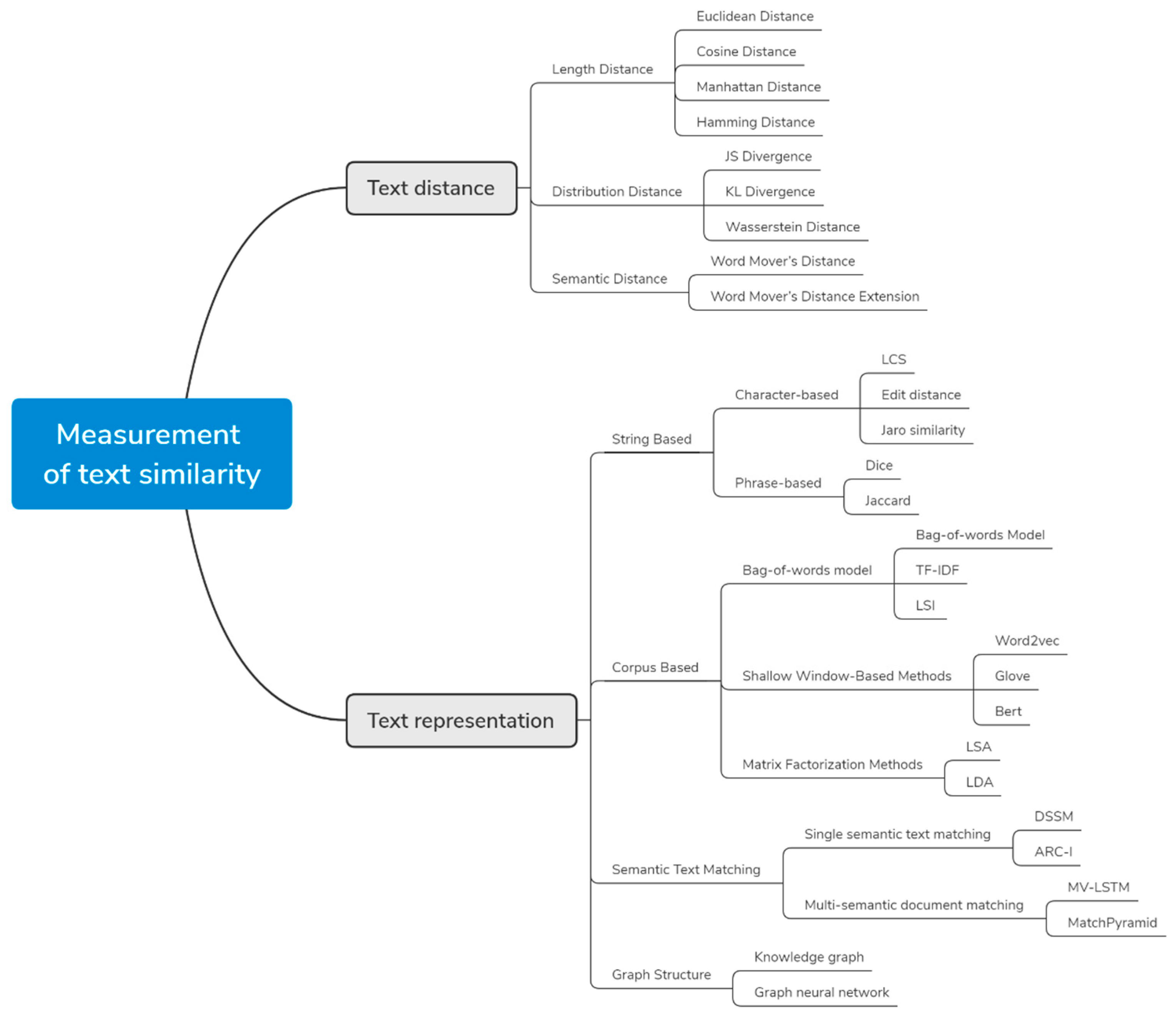
2. Text Distance
2.1. Length Distance
2.1.1. Euclidean Distance
2.1.2. Cosine Distance
2.1.3. Manhattan Distance
2.1.4. Hamming Distance
2.2. Distribution Distance
2.2.1. JS Divergence
2.2.2. KL Divergence
2.2.3. Wasserstein Distance
2.3. Semantic Distance
2.3.1. Word Mover’s Distance
2.3.2. Word Mover’s Distance Extension
3. Text Representation
3.1. String-Based
3.1.1. Character-Based
3.1.2. Phrase-Based
3.2. Corpus-Based
3.2.1. Bag-of-Words Model
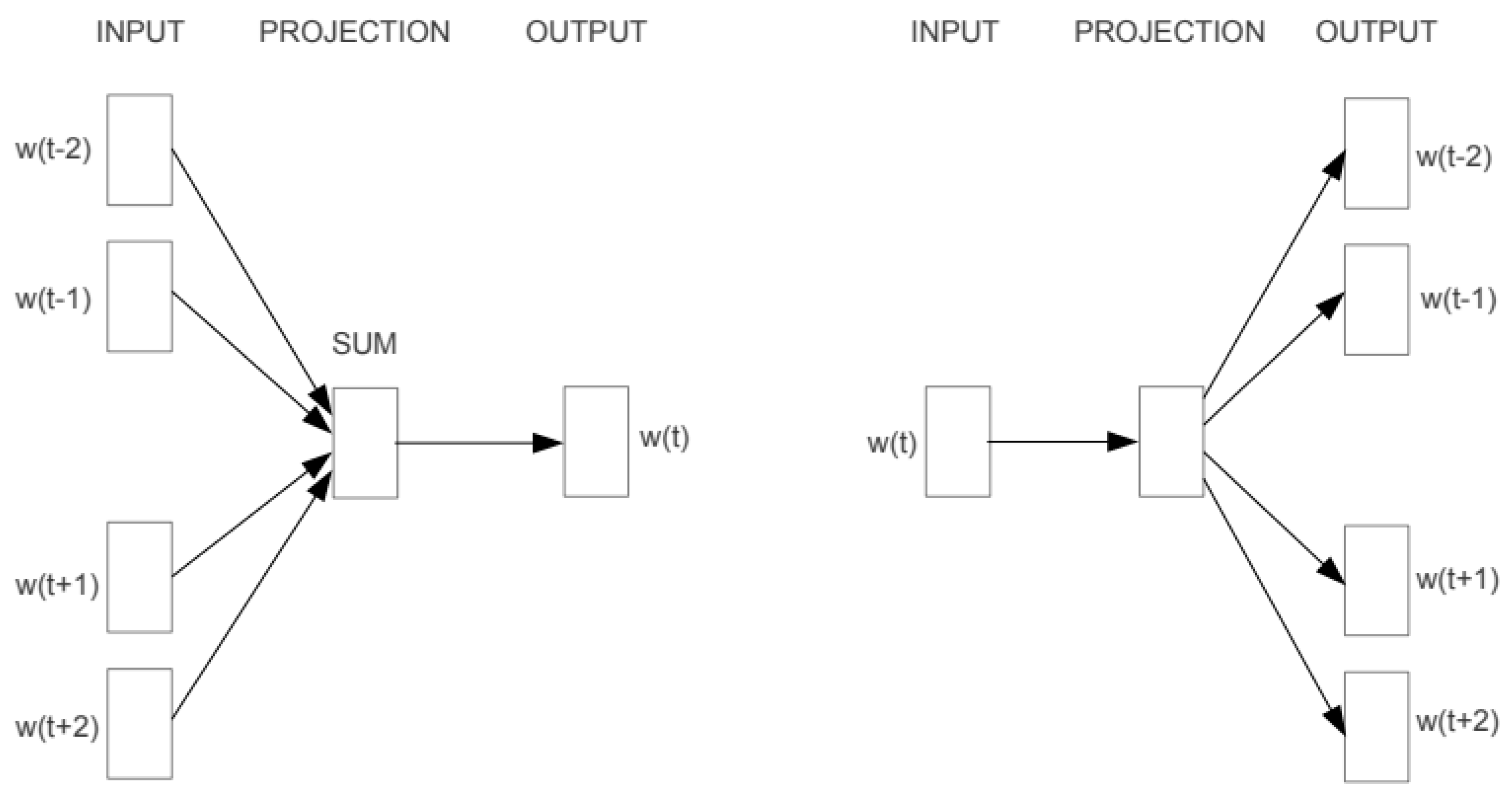
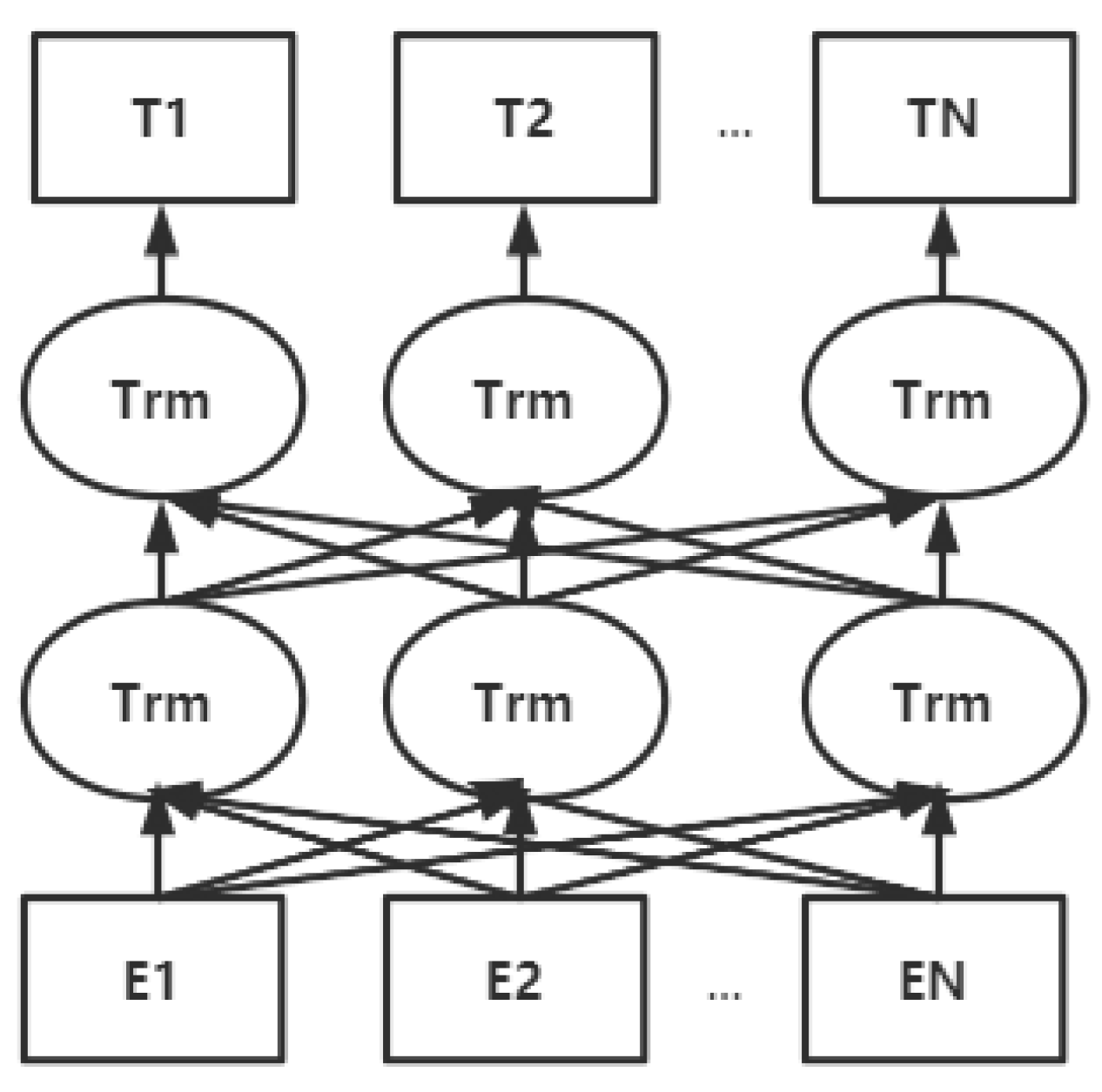
3.2.2. Shallow Window-Based Methods
3.2.3. Matrix Factorization Methods
3.3. Semantic Text Matching
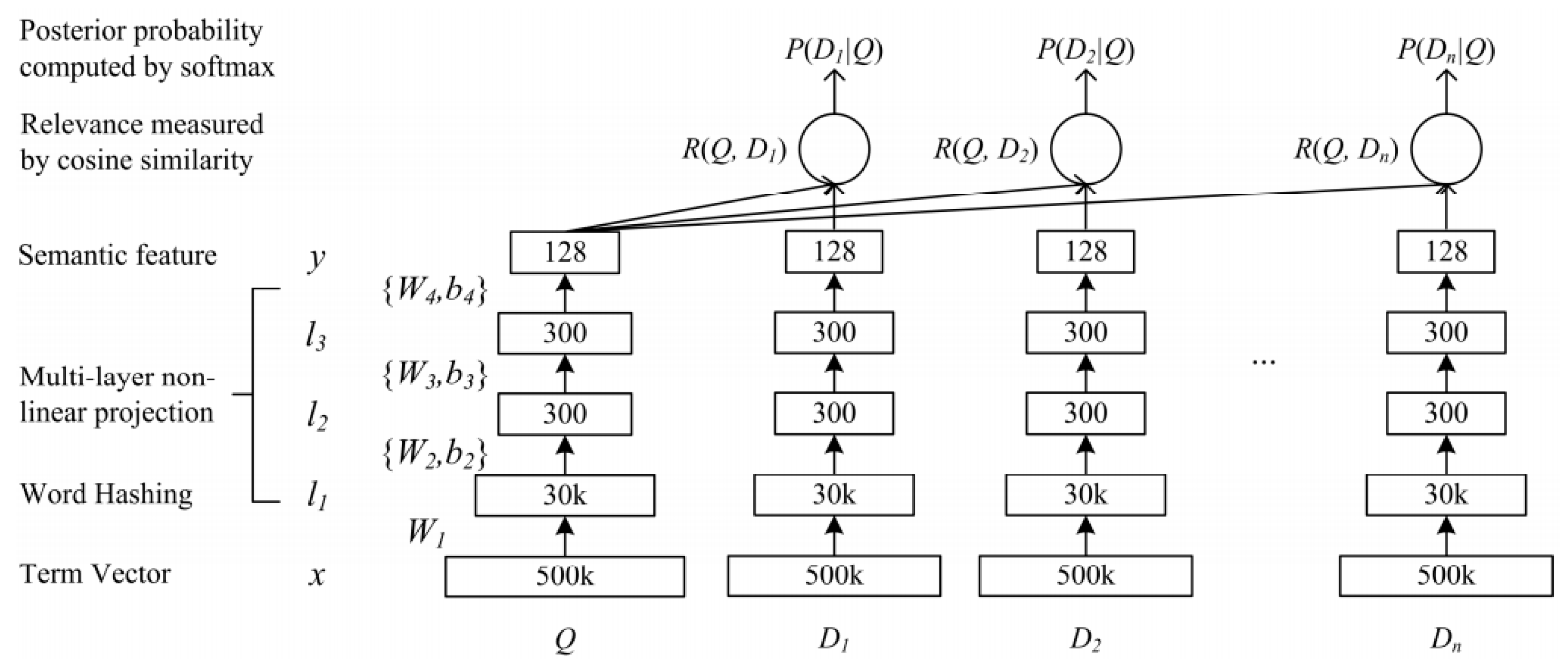
3.3.1. Single Semantic Text Matching
- (a)
- The embedding layer mainly includes: TermVector and WordHashing. TermVector uses the bag-of-words model, but this can easily lead to OOV (out of vocabulary) problems. Then, it uses word hashing to combine words with n-gram, which effectively reduces the possibility of OOV.
- (b)
- The feature extraction layer mainly includes: Multi-layer, semantic feature, cosine similarity. Its main function is to extract the semantic feature of two text sequences through three full connection layers to calculate the cosine similarity.
- (c)
- The similarity is judged by the output layer through SoftMax binary classification.
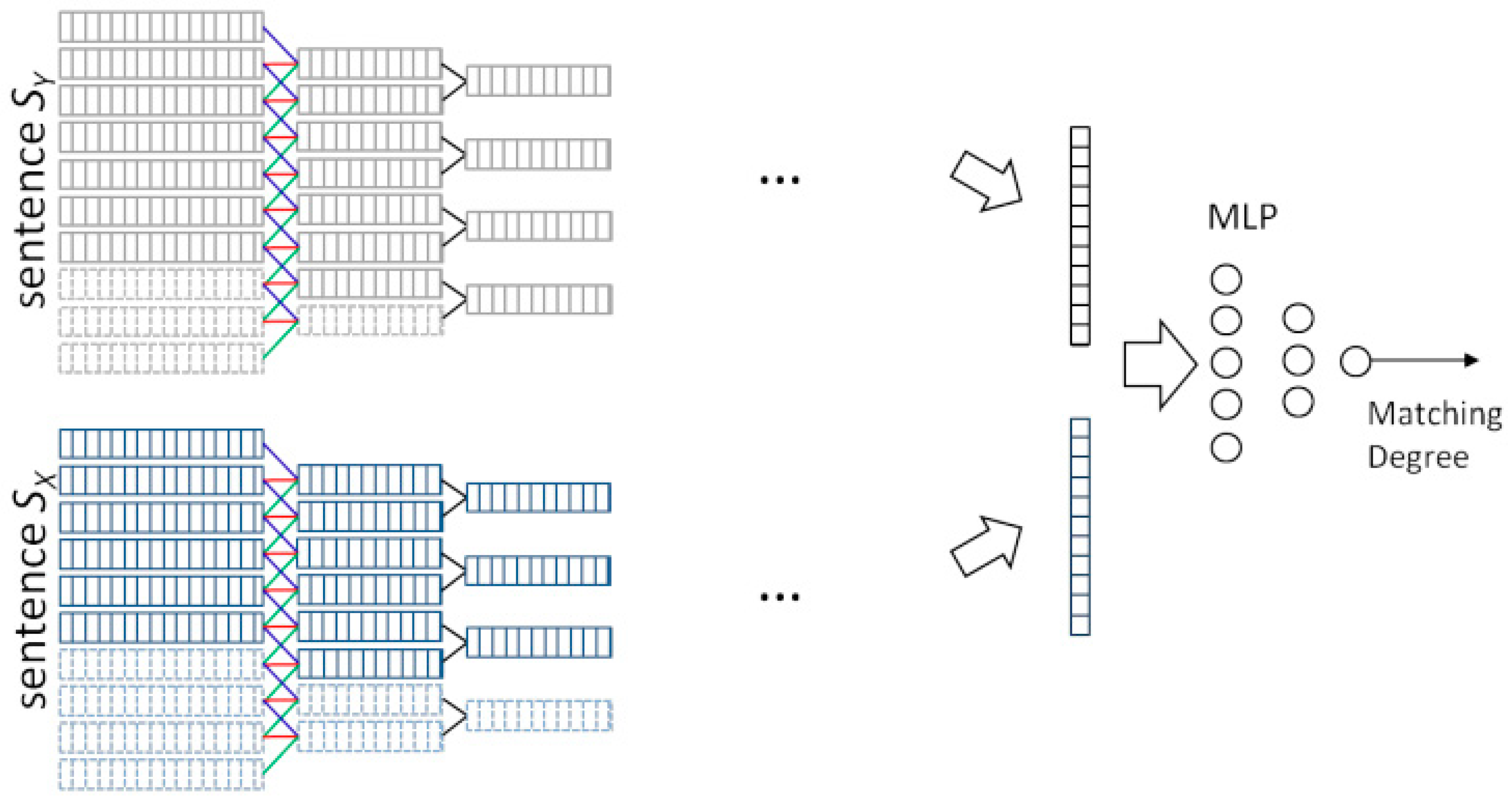
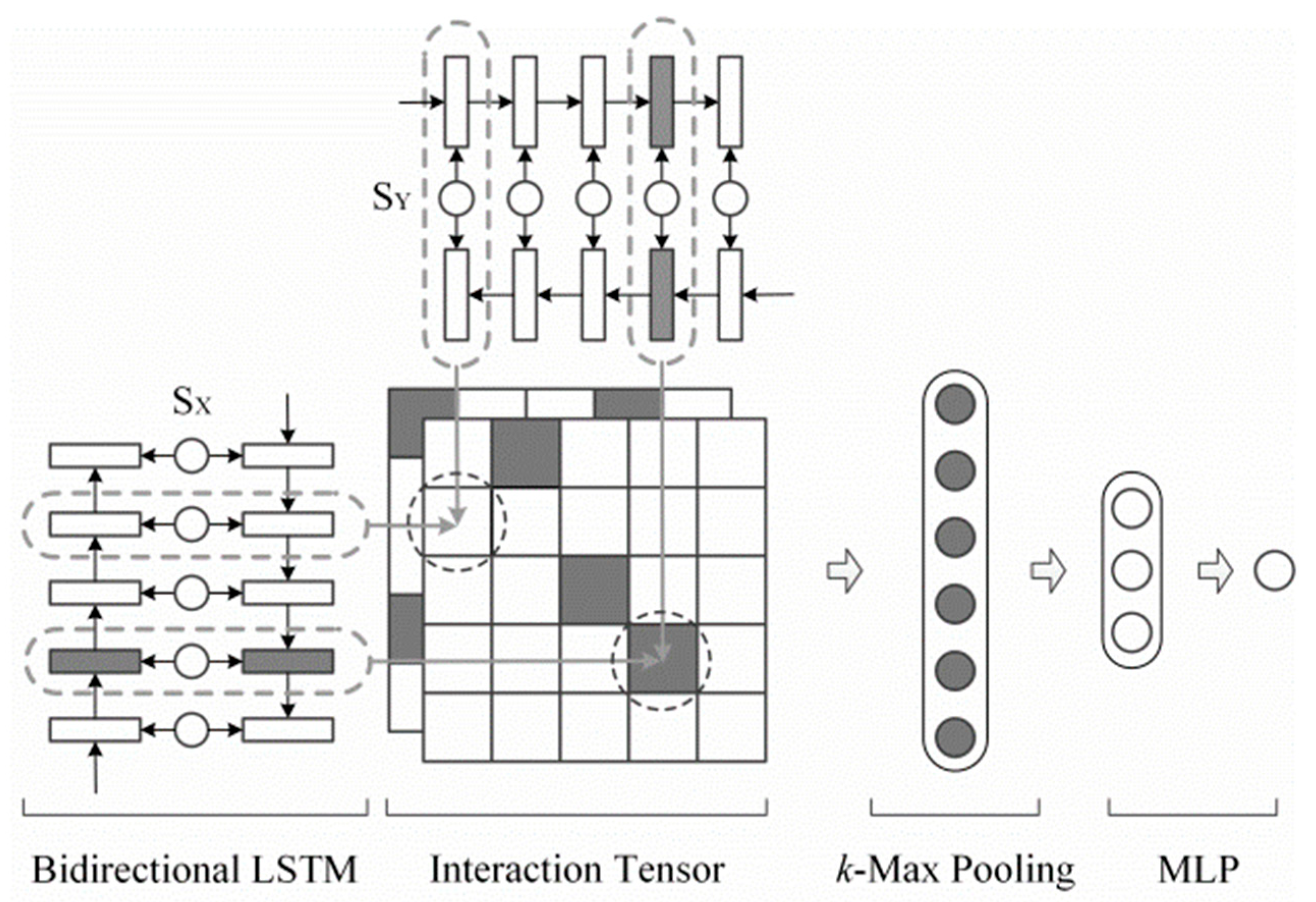
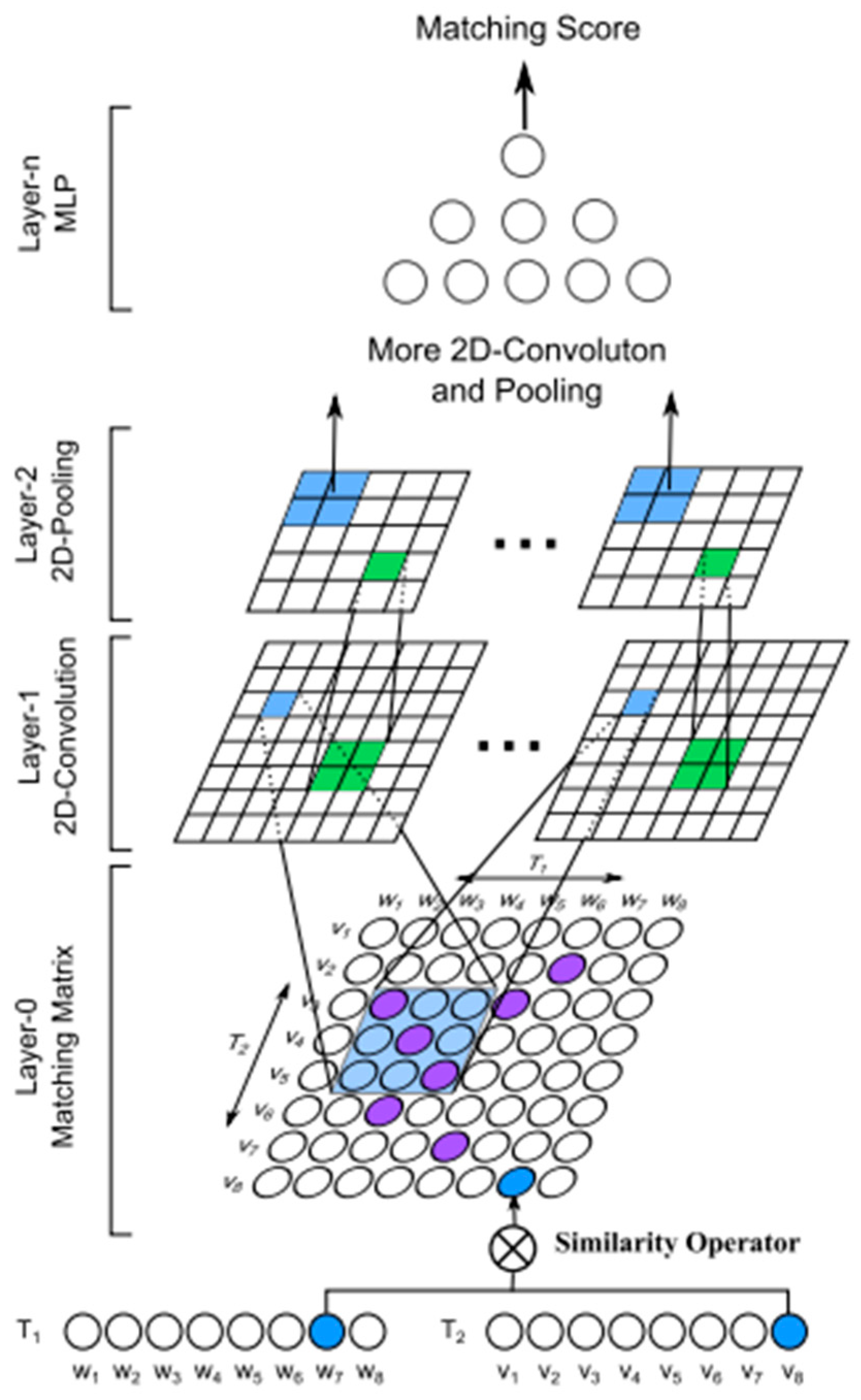
3.3.2. Multi-Semantic Document Matching
3.4. Based on Graph Structure
3.4.1. Knowledge Graph
3.4.2. Graph Neural Network
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, D. An information-theoretic definition of similarity. In Proceedings of the International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; pp. 296–304. [Google Scholar]
- Li, H.; Xu, J. Semantic matching in search. Found. Trends Inf. Retr. 2014, 7, 343–469. [Google Scholar] [CrossRef]
- Jiang, N.; de Marneffe, M.C. Do you know that Florence is packed with visitors? Evaluating state-of-the-art models of speaker commitment. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 4208–4213. [Google Scholar]
- Wang, Q.; Li, B.; Xiao, T.; Zhu, J.; Li, C.; Wong, D.F.; Chao, L.S. Learning deep transformer models for machine translation. arXiv 2019, arXiv:1906.01787. [Google Scholar]
- Serban, I.V.; Sordoni, A.; Bengio, Y.; Courville, A.; Pineau, J. Building end-to-end dialogue systems using generative hierarchical neural network models. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Pham, H.; Luong, M.T.; Manning, C.D. Learning distributed representations for multilingual text sequences. In Proceedings of the 1st Workshop on Vector Space Modeling for Natural Language Processing, Denver, CO, USA, 5 June 2015; pp. 88–94. [Google Scholar]
- Gomaa, W.H.; Fahmy, A.A. A survey of text similarity approaches. Int. J. Comput. Appl. 2013, 68, 13–18. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of distances. In Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–583. [Google Scholar]
- Norouzi, M.; Fleet, D.J.; Salakhutdinov, R.R. Hamming distance metric learning. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1061–1069. [Google Scholar]
- Manning, C.D.; Manning, C.D.; Schütze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Nielsen, F. A family of statistical symmetric divergences based on Jensen’s inequality. arXiv 2010, arXiv:1009.4004. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Weng, L. From GAN to WGAN. arXiv 2019, arXiv:1904.08994. [Google Scholar]
- Vallender, S. Calculation of the Wasserstein distance between probability distributions on the line. Theory Probab. Appl. 1974, 18, 784–786. [Google Scholar] [CrossRef]
- Kusner, M.; Sun, Y.; Kolkin, N.; Weinberger, K. From word embeddings to document distances. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 957–966. [Google Scholar]
- Andoni, A.; Indyk, P.; Krauthgamer, R. Earth mover distance over high-dimensional spaces. In Proceedings of the Symposium on Discrete Algorithms, San Francisco, CA, USA, 20–22 January 2008; pp. 343–352. [Google Scholar]
- Wu, L.; Yen, I.E.; Xu, K.; Xu, F.; Balakrishnan, A.; Chen, P.Y.; Ravikumar, P.; Witbrock, M.J. Word mover’s embedding: From word2vec to document embedding. arXiv 2018, arXiv:1811.01713. [Google Scholar]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D.L. The mahalanobis distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Huang, G.; Guo, C.; Kusner, M.J.; Sun, Y.; Sha, F.; Weinberger, K.Q. Supervised word mover’s distance. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 4862–4870. [Google Scholar]
- Hunt, J.W.; Szymanski, T.G. A fast algorithm for computing longest common subsequences. Commun. ACM 1977, 20, 350–353. [Google Scholar] [CrossRef]
- Tsai, Y.T. The constrained longest common subsequence problem. Inf. Process. Lett. 2003, 88, 173–176. [Google Scholar] [CrossRef]
- Iliopoulos, C.S.; Rahman, M.S. New efficient algorithms for the LCS and constrained LCS problems. Inf. Process. Lett. 2008, 106, 13–18. [Google Scholar] [CrossRef]
- Irving, R.W.; Fraser, C.B. Two algorithms for the longest common subsequence of three (or more) strings. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching, Tucson, AZ, USA, 29 April–1 May 1992; pp. 214–229. [Google Scholar]
- Levenshtein, V.I. Binary codes capable of correcting deletions, insertions, and reversals. Sov. Phys. Dokl. 1966, 10, 707–710. [Google Scholar]
- Damerau, F.J. A technique for computer detection and correction of spelling errors. Commun. ACM 1964, 7, 171–176. [Google Scholar] [CrossRef]
- Winkler, W.E. String Comparator Metrics and Enhanced Decision Rules in the Fellegi-Sunter Model of Record Linkage. 1990. Available online: https://files.eric.ed.gov/fulltext/ED325505.pdf (accessed on 31 August 2020).
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone. 1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Wang, S.; Manning, C.D. Baselines and bigrams: Simple, good sentiment and topic classification. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics: Short Papers, Jeju Island, Korea, 8–14 July 2012; Volume 2, pp. 90–94. [Google Scholar]
- Salton, G.; Buckley, C. Term-weighting approaches in automatic text retrieval. Inf. Process. Manag. 1988, 24, 513–523. [Google Scholar] [CrossRef]
- Robertson, S.E.; Walker, S. Some simple effective approximations to the 2-poisson model for probabilistic weighted retrieval. In Proceedings of the International ACM Sigir Conference on Research and Development in Information Retrieval SIGIR’94, Dublin, Ireland, 3–6 July 1994; pp. 232–241. [Google Scholar]
- Rong, X. word2vec parameter learning explained. arXiv 2014, arXiv:1411.2738. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed representations of sentences and documents. In Proceedings of the International Conference on Machine Learning, Bejing, China, 22–24 June 2014; pp. 1188–1196. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Deerwester, S.; Dumais, S.T.; Furnas, G.W.; Landauer, T.K.; Harshman, R. Indexing by latent semantic analysis. J. Am. Soc. Inf. Sci. 1990, 41, 391–407. [Google Scholar] [CrossRef]
- Kontostathis, A.; Pottenger, W.M. A framework for understanding Latent Semantic Indexing (LSI) performance. Inf. Process. Manag. 2006, 42, 56–73. [Google Scholar] [CrossRef]
- Landauer, T.K.; Dumais, S.T. A solution to Plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychol. Rev. 1997, 104, 211. [Google Scholar] [CrossRef]
- Landauer, T.K.; Foltz, P.W.; Laham, D. An introduction to latent semantic analysis. Discourse Process. 1998, 25, 259–284. [Google Scholar] [CrossRef]
- Grossman, D.A.; Frieder, O. Information Retrieval: Algorithms and Heuristics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 15. [Google Scholar]
- Hofmann, T. Probabilistic latent semantic analysis. arXiv 2013, arXiv:1301.6705. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Wei, X.; Croft, W.B. LDA-based document models for ad-hoc retrieval. In Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Seattle, WA, USA, 6–11 August 2016; pp. 178–185. [Google Scholar]
- Sahami, M.; Heilman, T.D. A web-based kernel function for measuring the similarity of short text snippets. In Proceedings of the 15th International Conference on World Wide Web, Edinburgh, Scotland, UK, 23–26 May 2006; pp. 377–386. [Google Scholar]
- Li, Q.; Wang, B.; Melucci, M. CNM: An Interpretable Complex-valued Network for Matching. arXiv 2019, arXiv:1904.05298. [Google Scholar]
- Shen, Y.; He, X.; Gao, J.; Deng, L.; Mesnil, G. A latent semantic model with convolutional-pooling structure for information retrieval. In Proceedings of the 23rd ACM International Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 101–110. [Google Scholar]
- Huang, P.S.; He, X.; Gao, J.; Deng, L.; Acero, A.; Heck, L. Learning deep structured semantic models for web search using clickthrough data. In Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, Burlingame, CA, USA, 27 October–1 November 2013; pp. 2333–2338. [Google Scholar]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Hu, B.; Lu, Z.; Li, H.; Chen, Q. Convolutional neural network architectures for matching natural language sentences. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2042–2050. [Google Scholar]
- Wan, S.; Lan, Y.; Guo, J.; Xu, J.; Pang, L.; Cheng, X. A deep architecture for semantic matching with multiple positional sentence representations. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Pang, L.; Lan, Y.; Guo, J.; Xu, J.; Wan, S.; Cheng, X. Text matching as image recognition. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Liu, Z.; Xiong, C.; Sun, M.; Liu, Z. Entity-duet neural ranking: Understanding the role of knowledge graph semantics in neural information retrieval. arXiv 2018, arXiv:1805.07591. [Google Scholar]
- Chen, X.; Jia, S.; Xiang, Y. A review: Knowledge reasoning over knowledge graph. Expert Syst. Appl. 2020, 141, 112948. [Google Scholar] [CrossRef]
- Zhu, G.; Iglesias, C.A. Computing semantic similarity of concepts in knowledge graphs. IEEE Trans. Knowl. Data Eng. 2016, 29, 72–85. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 2787–2795. [Google Scholar]
- Dong, L.; Wei, F.; Zhou, M.; Xu, K. Question answering over freebase with multi-column convolutional neural networks. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Beijing, China, 26–31 July 2015; pp. 260–269. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Zhou, J.; Cui, G.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. arXiv 2018, arXiv:1812.08434. [Google Scholar]
- Vashishth, S.; Yadati, N.; Talukdar, P. Graph-based Deep Learning in Natural Language Processing. In Proceedings of the 7th ACM IKDD CoDS and 25th COMAD, Hyderabad, India, 5–7 January 2020; pp. 371–372. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef] [PubMed]
- Sultan, M.A.; Bethard, S.; Sumner, T. Dls@ cu: Sentence similarity from word alignment and semantic vector composition. In Proceedings of the 9th International Workshop on Semantic Evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 148–153. [Google Scholar]
- Liu, B.; Guo, W.; Niu, D.; Wang, C.; Xu, S.; Lin, J.; Lai, K.; Xu, Y. A User-Centered Concept Mining System for Query and Document Understanding at Tencent. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1831–1841. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Dong, Y. Measurement of Text Similarity: A Survey. Information 2020, 11, 421. https://doi.org/10.3390/info11090421
Wang J, Dong Y. Measurement of Text Similarity: A Survey. Information. 2020; 11(9):421. https://doi.org/10.3390/info11090421
Chicago/Turabian StyleWang, Jiapeng, and Yihong Dong. 2020. "Measurement of Text Similarity: A Survey" Information 11, no. 9: 421. https://doi.org/10.3390/info11090421
APA StyleWang, J., & Dong, Y. (2020). Measurement of Text Similarity: A Survey. Information, 11(9), 421. https://doi.org/10.3390/info11090421



