Model for Collaboration among Carriers to Reduce Empty Container Truck Trips †
Abstract
1. Introduction
2. Literature Review
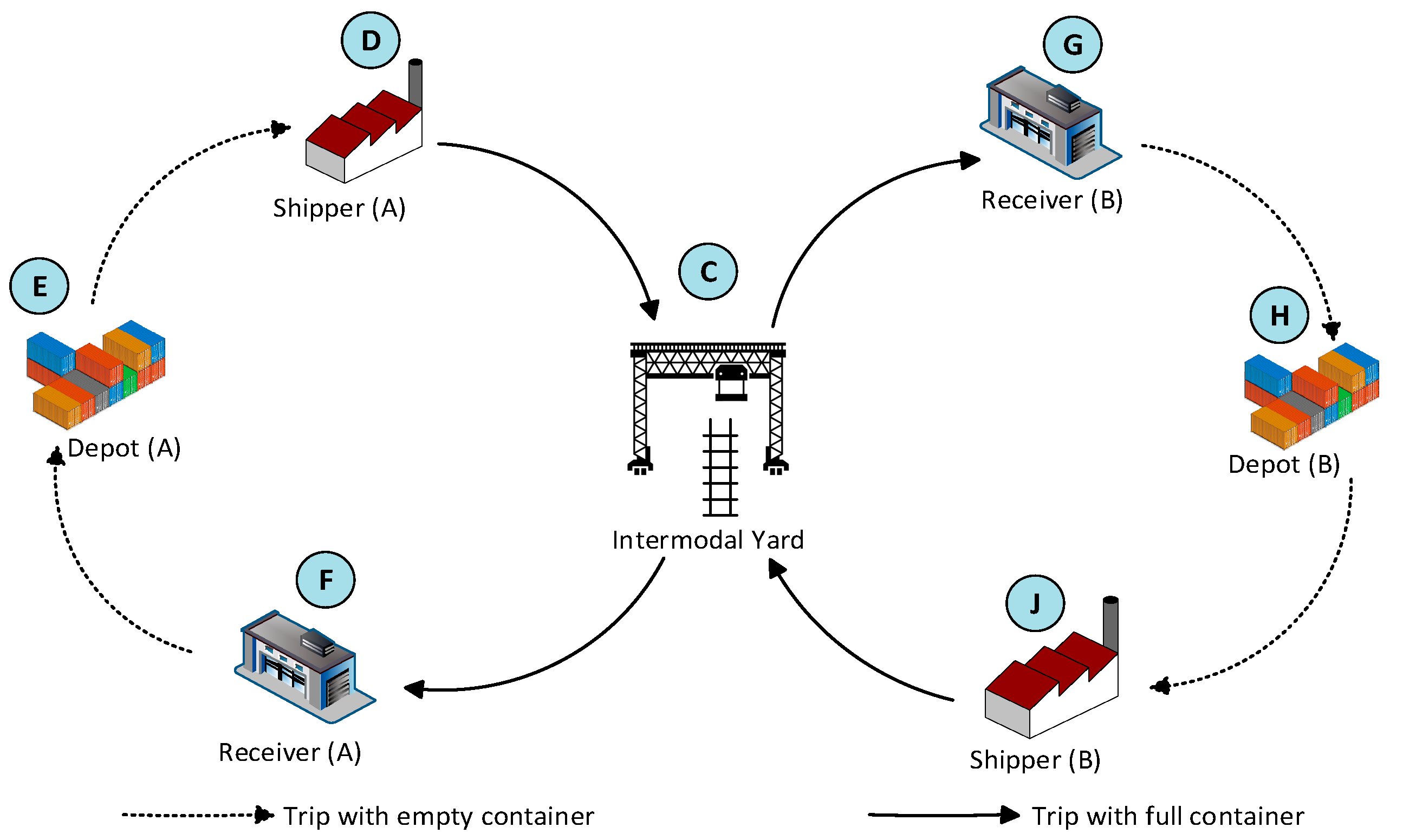
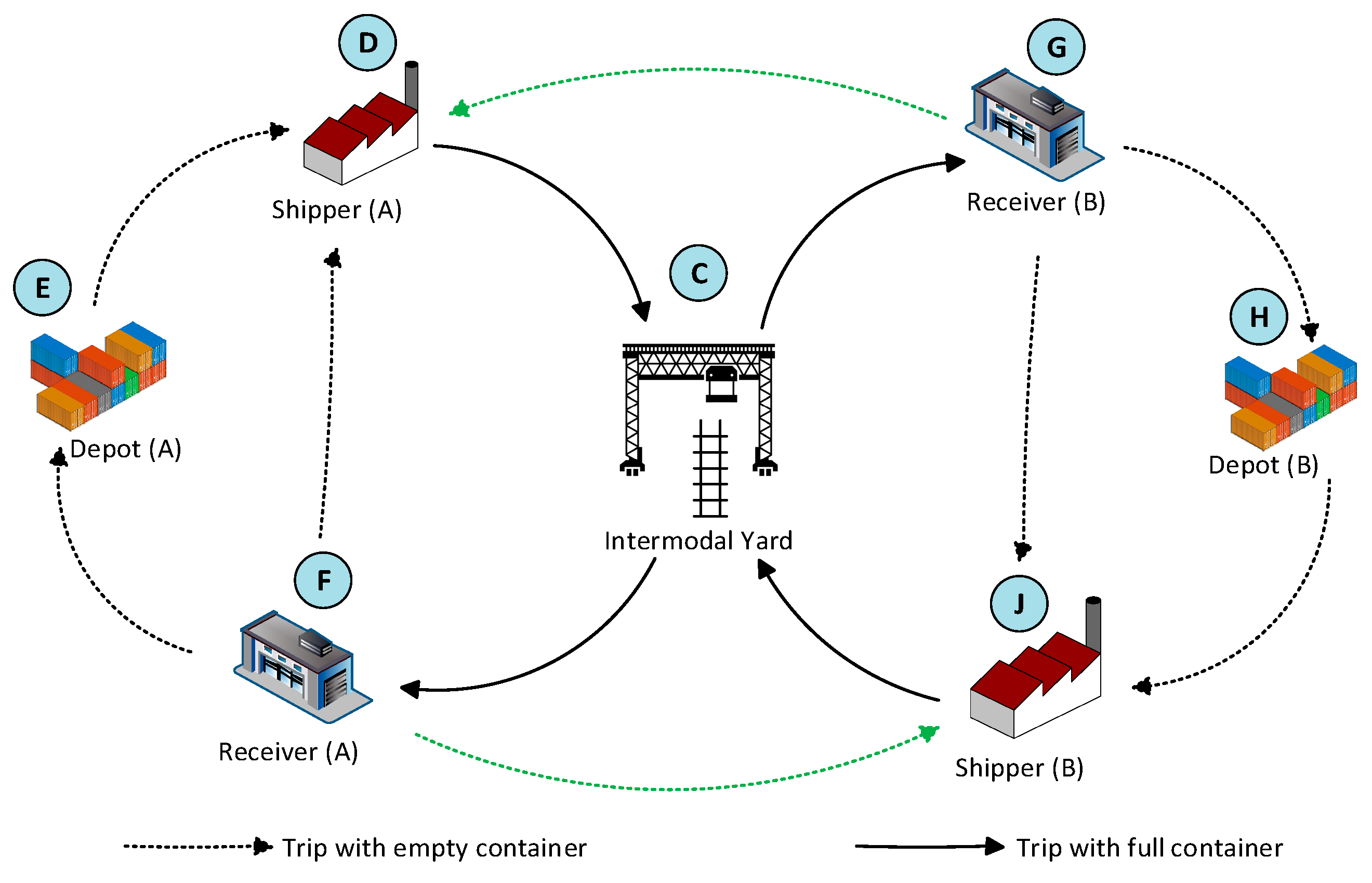
3. Intermodal Freight Transport Model with Collaboration
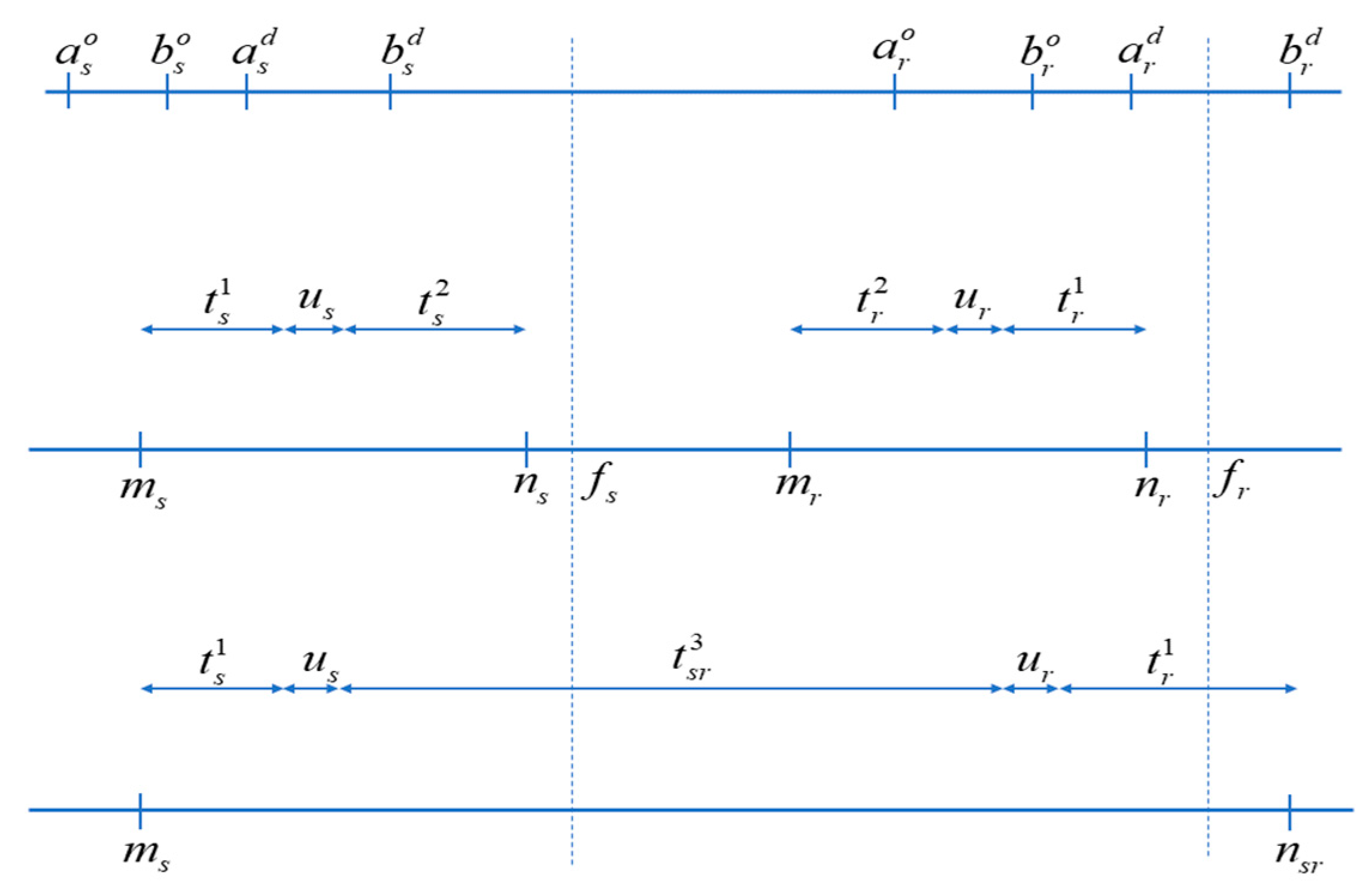
4. Stochastic Model
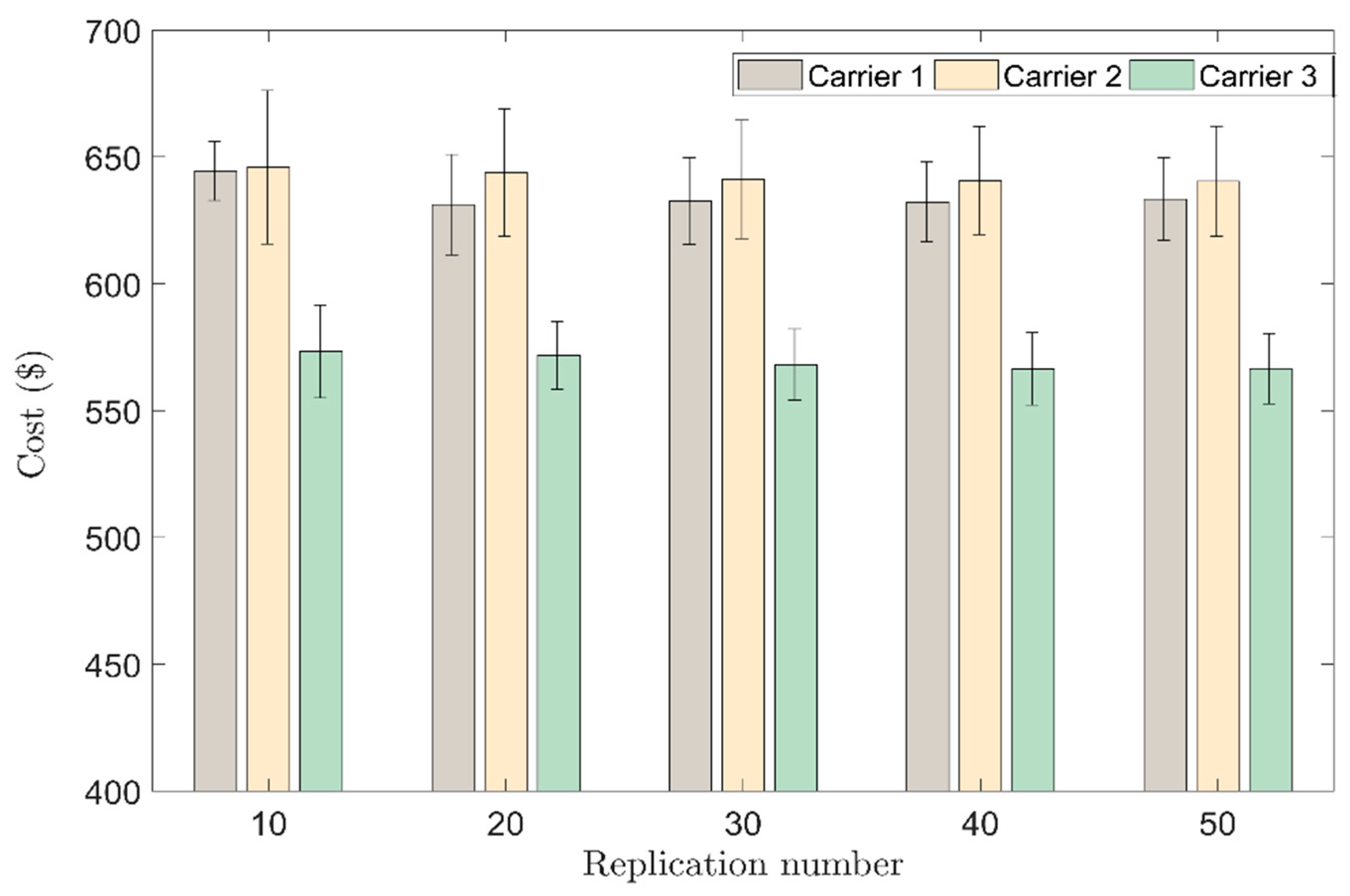
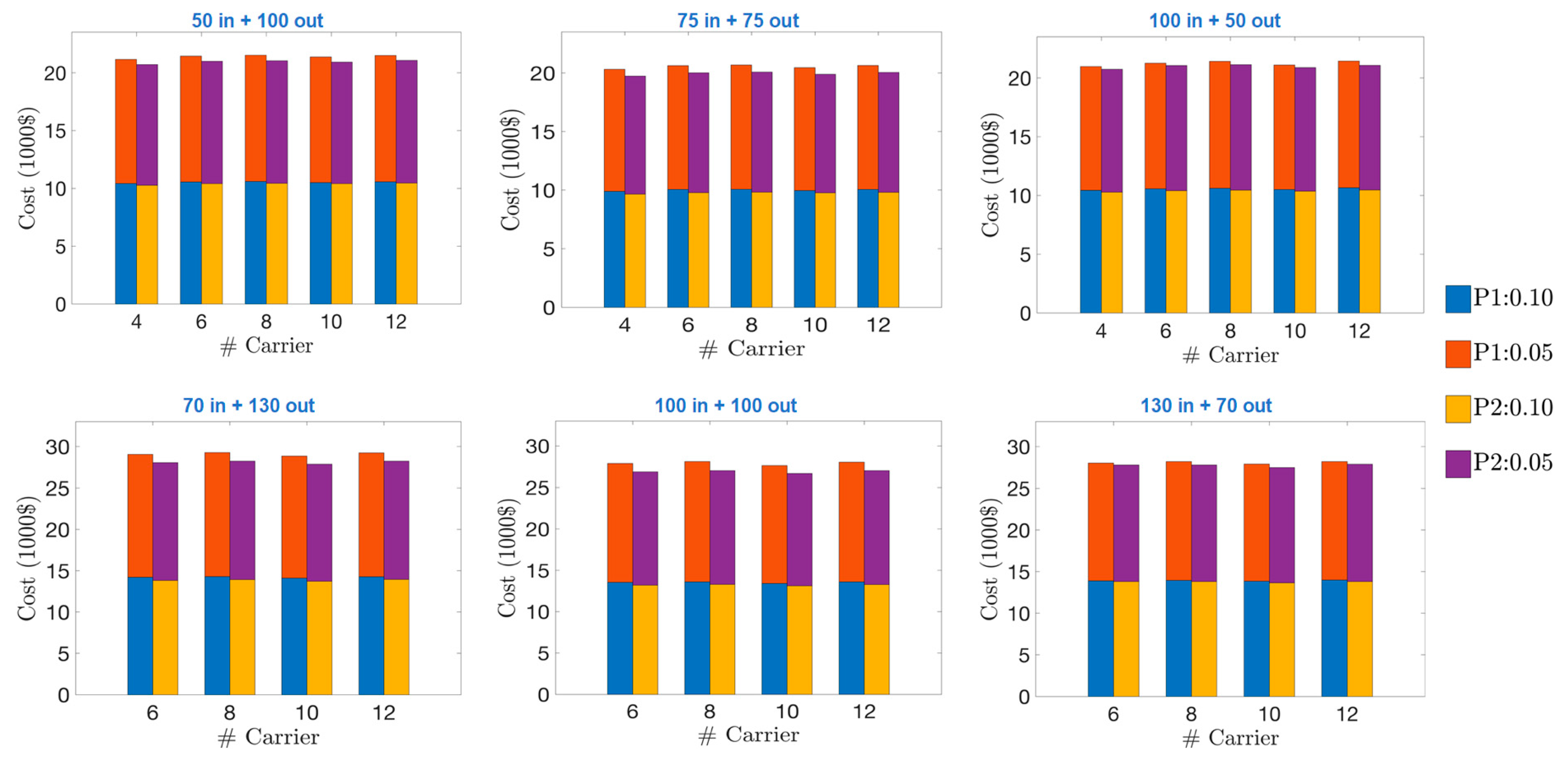
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jennings, B.; Holcomb, M.C. Beyond containerization: The broader concept of intermodalism. Transp. J. 1996, 35, 5–13. [Google Scholar]
- Huynh, N.; Uddin, M.; Minh, C.C. Data analytics for intermodal freight transportation applications. In Data Analytics for Intelligent Transportation Systems; Elsevier: Cambridge, MA, USA, 2017; pp. 241–262. [Google Scholar]
- IANA. Data & Statistics. Available online: https://www.intermodal.org/resource-center/data-statistics (accessed on 15 January 2020).
- Caballini, C.; Sacone, S.; Saeednia, M. Cooperation among truck carriers in seaport containerized transportation. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 38–56. [Google Scholar] [CrossRef]
- Schulte, F.; Lalla-Ruiz, E.; González-Ramírez, R.G.; Voß, S. Reducing port-related empty truck emissions: A mathematical approach for truck appointments with collaboration. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 195–212. [Google Scholar] [CrossRef]
- Guajardo, M.; Rönnqvist, M. A review on cost allocation methods in collaborative transportation. Int. Trans. Oper. Res. 2016, 23, 371–392. [Google Scholar] [CrossRef]
- Krajewska, M.A.; Kopfer, H.; Laporte, G.; Ropke, S.; Zaccour, G. Horizontal cooperation among freight carriers: Request allocation and profit sharing. J. Oper. Res. Soc. 2008, 59, 1483–1491. [Google Scholar] [CrossRef]
- Chen, L.; Miller-Hooks, E. Resilience: An indicator of recovery capability in intermodal freight transport. Transp. Sci. 2012, 46, 109–123. [Google Scholar] [CrossRef]
- Uddin, M.; Huynh, N. Reliable routing of road-rail intermodal freight under uncertainty. Netw. Spat. Econ. 2019, 19, 929–952. [Google Scholar] [CrossRef]
- Uddin, M.M.; Huynh, N. Routing model for multicommodity freight in an intermodal network under disruptions. Transp. Res. Rec. 2016, 2548, 71–80. [Google Scholar] [CrossRef]
- Simatupang, T.M.; Sridharan, R. The collaborative supply chain. Int. J. Logist. Manag. 2002, 13, 15–30. [Google Scholar] [CrossRef]
- Cruijssen, F.; Cools, M.; Dullaert, W. Horizontal cooperation in logistics: Opportunities and impediments. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 129–142. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Collaborative vehicle routing: A survey. Eur. J. Oper. Res. 2018, 268, 1–12. [Google Scholar] [CrossRef]
- Cong, L.; Zhibin, J.; Feng, C.; Xiao, L.; Liming, L.; Zhou, X. Empty container repositioning—A review. In Proceedings of the WCICA 2010: 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 3028–3033. [Google Scholar]
- Özener, O.Ö.; Ergun, Ö. Allocating costs in a collaborative transportation procurement network. Transp. Sci. 2008, 42, 146–165. [Google Scholar] [CrossRef]
- Ergun, Ö.; Kuyzu, G.; Savelsbergh, M. Shipper collaboration. Comput. Oper. Res. 2007, 34, 1551–1560. [Google Scholar] [CrossRef]
- Yilmaz, O.; Savasaneril, S. Collaboration among small shippers in a transportation market. Eur. J. Oper. Res. 2012, 218, 408–415. [Google Scholar] [CrossRef]
- Kuyzu, G. Lane covering with partner bounds in collaborative truckload transportation procurement. Comput. Oper. Res. 2017, 77, 32–43. [Google Scholar] [CrossRef]
- Agarwal, R.; Ergun, Ö. Network design and allocation mechanisms for carrier alliances in liner shipping. Oper. Res. 2010, 58, 1726–1742. [Google Scholar] [CrossRef]
- Atasoy, B.; Schulte, F.; Steenkamp, A. Platform-based collaborative routing using dynamic prices as incentives: The case of Quicargo. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 12–16 January 2020. [Google Scholar]
- Chan, F.T.; Zhang, T. The impact of Collaborative Transportation Management on supply chain performance: A simulation approach. Expert Syst. Appl. 2011, 38, 2319–2329. [Google Scholar] [CrossRef]
- Frisk, M.; Göthe-Lundgren, M.; Jörnsten, K.; Rönnqvist, M. Cost allocation in collaborative forest transportation. Eur. J. Oper. Res. 2010, 205, 448–458. [Google Scholar] [CrossRef]
- Dai, B.; Chen, H. A multi-agent and auction-based framework and approach for carrier collaboration. Logist. Res. 2011, 3, 101–120. [Google Scholar] [CrossRef]
- Los, J.; Schulte, F.; Spaan, M.T.J.; Negenborn, R.R. Collaborative vehicle routing when agents have mixed information sharing attitudes. Transp. Res. Procedia 2020, 44, 94–101. [Google Scholar] [CrossRef]
- Quintero-Araujo, C.L.; Gruler, A.; Juan, A.A. Quantifying Potential Benefits of Horizontal Cooperation in Urban Transportation under Uncertainty: A Simheuristic Approach. In Proceedings of the Advances in Artificial Intelligence, Salamanca, Spain, 14–16 September 2016; pp. 280–289. [Google Scholar]
- Sterzik, S.; Kopfer, H.; Yun, W.-Y. Reducing hinterland transportation costs through container sharing. Flex. Serv. Manuf. J. 2015, 27, 382–402. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, C.; Lin, W.-H.; Miao, L.; Yang, P. A tabu search heuristic for the local container drayage problem under a new operation mode. Transp. Res. Part E Logist. Transp. Rev. 2014, 62, 136–150. [Google Scholar] [CrossRef]
- Islam, S.; Olsen, T.; Ahmed, M.D. Reengineering the seaport container truck hauling process. Bus. Process Manag. J. 2013, 19, 752–782. [Google Scholar] [CrossRef]
- Tawfik, C.; Limbourg, S. Pricing problems in intermodal freight transport: Research overview and prospects. Sustainability 2018, 10, 3341. [Google Scholar] [CrossRef]
- Tawfik, C.; Limbourg, S. A bilevel model for network design and pricing based on a level-of-service assessment. Transp. Sci. 2019, 53, 1609–1626. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 28. [Google Scholar]
- Ghosh, B.K. Probability inequalities related to Markov’s theorem. Am. Stat. 2002, 56, 186–190. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Heuristic-based truck scheduling for inland container transportation. OR Spectr. 2010, 32, 787–808. [Google Scholar] [CrossRef]
- USDOT. Freight Facts and Figures; USDOT: Washington, DC, USA, 2017.
- Li, R.; Chai, H.; Tang, J. Empirical study of travel time estimation and reliability. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Rakha, H.A.; El-Shawarby, I.; Arafeh, M.; Dion, F. Estimating path travel-time reliability. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 236–241. [Google Scholar]
- Fazili, M.; Venkatadri, U.; Cyrus, P.; Tajbakhsh, M. Physical Internet, conventional and hybrid logistic systems: A routing optimisation-based comparison using the Eastern Canada road network case study. Int. J. Prod. Res. 2017, 55, 2703–2730. [Google Scholar] [CrossRef]
- Ferrell, W.; Ellis, K.; Kaminsky, P.; Rainwater, C. Horizontal collaboration: Opportunities for improved logistics planning. Int. J. Prod. Res. 2020, 58, 4267–4284. [Google Scholar] [CrossRef]

| Focus | Reference | Method | Problem | UC | IM | Equal Profit Share | Shipment/Transport Planning | ||
|---|---|---|---|---|---|---|---|---|---|
| Opt | Game | Sim | |||||||
| Shipper | Ergun et al. [16] | √ | LCP | √ | |||||
| Kuyzu [18] | √ | LCP | √ | ||||||
| Özener and Ergun [15] | √ | √ | LCP | √ | |||||
| Yilmaz and Savasaneril [17] | √ | √ | AP | √ | |||||
| Carrier | Agarwal and Ergun [19] | √ | √ | IP | √ | ||||
| Atasoy et al. [20] | √ | VRP | √ | ||||||
| Caballini et al. [4] | √ | IP | √ | √ | |||||
| Chan and Zhang [21] | √ | AP | |||||||
| Dai and Chen [23] | √ | √ | VRP | √ | |||||
| Frisk et al. [22] | √ | MCFP | √ | √ | |||||
| Islam et al. [28] | √ | AP | √ | ||||||
| Krajewska et al. [7] | √ | √ | VRP | √ | √ | ||||
| Los et al. [24] | √ | VRP | √ | ||||||
| Quintero-Araujo et al. [25] | √ | VRP | √ | √ | |||||
| Schulte et al. [5] | √ | TSP | √ | √ | |||||
| Sterzik et al. [26] | √ | VRP | √ | √ | |||||
| Xue et al. [27] | √ | VRP | √ | √ | |||||
| This study | √ | IP | √ | √ | √ | √ | |||
| Node | Distance | Travel Time | ||||
|---|---|---|---|---|---|---|
| Intermodal Terminal/ Yard | Shipper/ Receiver | Empty Container Depot | Intermodal Terminal/ Yard | Shipper/ Receiver | Empty Container Depot | |
| Intermodal Terminal/ Yard | 0 | 0 | ||||
| Shipper/Receiver | ||||||
| Empty Container Depot | ||||||
| Notation | Explanation |
|---|---|
| Sets | |
| Set of inbound and outbound shipments | |
| Set of all freight carriers | |
| Set of shipments owned by carrier where | |
| Parameters related to shipments | |
| Origin of shipment | |
| Destination of shipment | |
| Distance traveled by truck when performing shipment ; | |
| Packing/unpacking time at shipper/receiver location related to shipment | |
| Time required when performing shipment ; | |
| Starting time of shipment | |
| Finishing time of shipment ; | |
| Deadline for shipment | |
| Parameters related to carriers | |
| Unit cost of freight carrier , expressed in $/mile | |
| ; this parameter is known in advance | |
| Operating cost of carrier without collaboration | |
| Final operating cost of carrier when performing shipments by itself as well as using HST and VST (with collaboration) | |
| Number of trucks available to carrier | |
| Available time for each truck | |
| Sharing factor, | |
| Parameters related to combined shipments | |
| ; is a sufficiently large number | |
| Distance traveled by truck when performing a pair of shipments ; | |
| Time required when performing a pair of shipments ; | |
| Unit penalty cost of delay | |
| Penalty cost for the delay arising when performing a pair of shipments and violating the deadline of shipment | |
| Finishing time of a pair of shipments ; | |
| Parameters related to time windows | |
| Time windows at the terminal/yard, shippers, and receivers where shipment starts | |
| Time windows at the terminal/yard, shippers, and receivers where shipment ends |
| Shipment ID | d1 | d2 | Origin | Destination | Carrier | Deadline |
|---|---|---|---|---|---|---|
| 1 | 40 | 35 | Y | ED | 1 | 2 p.m. |
| 2 | 45 | 35 | ED | Y | 1 | 2 p.m. |
| 3 | 55 | 35 | Y | ED | 1 | 2 p.m. |
| 4 | 50 | 33 | ED | Y | 1 | 2 p.m. |
| 5 | 42 | 37 | Y | ED | 1 | 2 p.m. |
| 6 | 37 | 46 | ED | Y | 1 | 2 p.m. |
| 7 | 35 | 32 | Y | ED | 1 | 2 p.m. |
| 8 | 33 | 26 | ED | Y | 1 | 2 p.m. |
| 9 | 40 | 30 | Y | ED | 1 | 2 p.m. |
| 10 | 35 | 28 | ED | Y | 1 | 2 p.m. |
| 11 | 40 | 25 | Y | ED | 2 | 2 p.m. |
| 12 | 35 | 35 | ED | Y | 2 | 2 p.m. |
| 13 | 50 | 40 | Y | ED | 2 | 2 p.m. |
| 14 | 55 | 33 | ED | Y | 2 | 3 p.m. |
| 15 | 61 | 37 | Y | ED | 2 | 2 p.m. |
| 16 | 47 | 46 | ED | Y | 2 | 2 p.m. |
| 17 | 55 | 32 | Y | ED | 2 | 2 p.m. |
| 18 | 63 | 26 | ED | Y | 2 | 3 p.m. |
| 19 | 40 | 30 | Y | ED | 2 | 2 p.m. |
| 20 | 60 | 28 | ED | Y | 2 | 2 p.m. |
| 21 | 30 | 25 | Y | ED | 3 | 2 p.m. |
| 22 | 35 | 40 | ED | Y | 3 | 2 p.m. |
| 23 | 40 | 45 | Y | ED | 3 | 2 p.m. |
| 24 | 60 | 35 | ED | Y | 3 | 2 p.m. |
| 25 | 52 | 47 | Y | ED | 3 | 2 p.m. |
| 26 | 47 | 36 | ED | Y | 3 | 2 p.m. |
| 27 | 40 | 22 | Y | ED | 3 | 2 p.m. |
| 28 | 53 | 24 | ED | Y | 3 | 2 p.m. |
| 29 | 30 | 40 | Y | ED | 3 | 2 p.m. |
| 30 | 42 | 45 | ED | Y | 3 | 2 p.m. |
| Shipment Type & Cost | CM | ||
|---|---|---|---|
| Carrier 1 | Carrier 2 | Carrier 3 | |
| Single | 6 | 11, 16, 19 | 26, 27 |
| Combined | (1, 28) | (5, 12) | (7, 14) |
| (3, 20) | (17, 2) | (13, 18) | |
| (9, 8) | (21, 24) | (25, 10) | |
| (15, 4) | (23, 22) | (29, 30) | |
| Cost with collaboration ($) | 654.50 | 690.00 | 595.65 |
| Cost without collaboration ($) | 823.90 | 838.00 | 748.60 |
| Savings ($) | 169.40 | 148.00 | 152.95 |
| % Savings | 23.4 | 23.2 | 23.6 |
| Problem Size 1 | Variables # | Constraints # | Cost ($) | Savings ($) | % Savings | Time (s) |
|---|---|---|---|---|---|---|
| 10–20–2 | 1800 | 15,727 | 1872.79 | 534.57 | 22.2 | 4.1 |
| 10–20–4 | 3600 | 29,653 | 1919.15 | 435.55 | 18.5 | 16.0 |
| 10–20–6 | 5400 | 43,579 | 1911.49 | 424.37 | 18.2 | 763.8 |
| 15–15–2 | 1800 | 15,727 | 1771.18 | 636.18 | 26.4 | 3.5 |
| 15–15–4 | 3600 | 29,653 | 1809.45 | 545.25 | 23.2 | 125.0 |
| 15–15–6 | 5400 | 43,579 | 1791.40 | 544.45 | 23.2 | 318.1 |
| 20–10–2 | 1800 | 15,727 | 1903.31 | 504.04 | 20.9 | 31.6 |
| 20–10–4 | 3600 | 29,653 | 1941.00 | 413.70 | 17.6 | 65.0 |
| 20–10–6 | 5400 | 43,579 | 1932.42 | 403.68 | 17.3 | 156.8 |
| 20–30–2 | 5000 | 44,207 | 3120.05 | 909.90 | 22.6 | 8.9 |
| 20–30–4 | 10,000 | 83,413 | 3153.20 | 820.20 | 20.6 | 22.2 |
| 20–30–6 | 15,000 | 122,619 | 3166.97 | 819.54 | 20.5 | 58.6 |
| 20–30–8 | 20,000 | 161,825 | 3105.14 | 802.76 | 20.5 | 1009.6 |
| 25–25–2 | 5000 | 44,207 | 3016.79 | 1013.16 | 25.1 | 9.8 |
| 25–25–4 | 10,000 | 83,413 | 3044.78 | 928.62 | 23.4 | 25.7 |
| 25–25–6 | 15,000 | 122,619 | 3063.56 | 922.94 | 23.2 | 71.2 |
| 25–25–8 | 20,000 | 161,825 | 2998.03 | 909.87 | 23.3 | 217.0 |
| 30–20–2 | 5000 | 44,207 | 3121.63 | 908.33 | 22.5 | 11.8 |
| 30–20–4 | 10,000 | 83,413 | 3153.85 | 819.55 | 20.6 | 28.0 |
| 30–20–6 | 15,000 | 122,619 | 3171.37 | 815.13 | 20.4 | 105.3 |
| 30–20–8 | 20,000 | 161,825 | 3105.80 | 802.00 | 20.5 | 498.0 |
| 30–50–4 | 25,600 | 215,053 | 5208.49 | 1263.76 | 19.5 | 72.7 |
| 30–50–6 | 38,400 | 316,179 | 5204.29 | 1248.21 | 19.3 | 174.0 |
| 30–50–8 | 51,200 | 417,305 | 5213.63 | 1270.77 | 19.6 | 698.6 |
| 30–50–10 | 64,000 | 518,431 | 5195.75 | 1237.06 | 19.2 | 7031.0 |
| 40–40–4 | 25,600 | 215,053 | 4974.91 | 1497.34 | 23.1 | 66.7 |
| 40–40–6 | 38,400 | 316,179 | 4963.40 | 1489.11 | 23.0 | 146.6 |
| 40–40–8 | 51,200 | 417,305 | 4971.60 | 1494.80 | 23.1 | 287.8 |
| 40–40–10 | 64,000 | 518,431 | 4953.96 | 1478.84 | 23.0 | 1082.5 |
| 50–30–4 | 25,600 | 215,053 | 5204.65 | 1267.61 | 19.6 | 72 |
| 50–30–6 | 38,400 | 316,179 | 5192.70 | 1259.80 | 19.5 | 138.8 |
| 50–30–8 | 51,200 | 417,305 | 5201.97 | 1264.43 | 19.5 | 692.9 |
| 50–30–10 | 64,000 | 518,431 | 5181.13 | 1251.67 | 19.4 | 5624.8 |
| 40–60–4 | 40,000 | 336,813 | 6564.33 | 1624.08 | 19.8 | 109.1 |
| 40–60–6 | 60,000 | 495,219 | 6569.62 | 1609.74 | 19.7 | 200.8 |
| 40–60–8 | 80,000 | 653,625 | 6577.55 | 1611.71 | 19.7 | 604.3 |
| 40–60–10 | 100,000 | 812,031 | 6492.52 | 1583.03 | 19.6 | 5798.7 |
| 40–60–12 | 120,000 | 970,437 | 6586.13 | 1606.98 | 19.6 | 39,133.1 |
| 50–50–4 | 40,000 | 336,813 | 6326.87 | 1861.54 | 22.7 | 124.7 |
| 50–50–6 | 60,000 | 495,219 | 6328.50 | 1850.85 | 22.6 | 229.1 |
| 50–50–8 | 80,000 | 653,625 | 6338.15 | 1851.10 | 22.6 | 550.6 |
| 50–50–10 | 100,000 | 812,031 | 6255.36 | 1820.19 | 22.5 | 4106.2 |
| 50–50–12 | 120,000 | 970,437 | 6336.42 | 1856.69 | 22.7 | 8388.2 |
| 60–40–4 | 40,000 | 336,813 | 6559.34 | 1629.06 | 19.9 | 119.7 |
| 60–40–6 | 60,000 | 495,219 | 6568.35 | 1611.01 | 19.7 | 222.2 |
| 60–40–8 | 80,000 | 653,625 | 6574.38 | 1614.87 | 19.7 | 695.7 |
| 60–40–10 | 100,000 | 812,031 | 6486.94 | 1588.61 | 19.7 | 7371.4 |
| 60–40–12 | 120,000 | 970,437 | 6582.86 | 1609.94 | 19.6 | 29,051.1 |
| 50–100–4 | 90,000 | 760,213 | 9954.96 | 2182.49 | 18.0 | 287.2 |
| 50–100–6 | 135,000 | 1,117,819 | 10,092.44 | 2194.51 | 17.9 | 425.1 |
| 50–100–8 | 180,000 | 1,475,425 | 10,136.31 | 2190.89 | 17.8 | 996.6 |
| 50–100–10 | 225,000 | 1,833,031 | 10,042.13 | 2146.98 | 17.6 | 8067.0 |
| 50–100–12 | 270,000 | 2,190,637 | 10,132.66 | 2189.79 | 17.8 | 33,092.3 |
| 75–75–4 | 90,000 | 760,213 | 9398.99 | 2886.15 | 23.5 | 341.8 |
| 75–75–6 | 135,000 | 1,117,819 | 9418.87 | 2868.08 | 23.3 | 485.7 |
| 75–75–8 | 180,000 | 1,475,425 | 9457.52 | 2869.68 | 23.3 | 1078.7 |
| 75–75–10 | 225,000 | 1,833,031 | 9352.02 | 2729.09 | 22.6 | 9700.5 |
| 75–75–12 | 270,000 | 2,190,637 | 9456.35 | 2866.11 | 23.3 | 13,450.2 |
| 100–50–4 | 90,000 | 760,213 | 10,091.23 | 2193.92 | 17.9 | 334.3 |
| 100–50–6 | 135,000 | 1,117,819 | 10,105.71 | 2181.24 | 17.8 | 446.5 |
| 100–50–8 | 180,000 | 1,475,425 | 10,159.74 | 2167.46 | 17.6 | 1022.0 |
| 100–50–10 | 225,000 | 1,833,031 | 10,043.48 | 2145.62 | 17.6 | 8096.7 |
| 100–50–12 | 270,000 | 2,190,637 | 10,153.28 | 2169.17 | 17.6 | 45,806.4 |
| 70–130–6 | 240,000 | 1,990,419 | 13,465.66 | 3123.39 | 18.8 | 1052.6 |
| 70–130–8 | 320,000 | 2,627,225 | 13,561.14 | 3111.52 | 18.7 | 1164.6 |
| 70–130–10 | 400,000 | 3,264,031 | 13,380.36 | 3059.89 | 18.6 | 12,405.4 |
| 70–130–12 | 480,000 | 3,900,837 | 13,567.21 | 3098.04 | 18.5 | 23,480.4 |
| 100–100–6 | 240,000 | 1,990,419 | 12,695.04 | 3894.01 | 23.4 | 1095.8 |
| 100–100–8 | 320,000 | 2,627,225 | 12,773.86 | 3898.80 | 23.4 | 1214.9 |
| 100–100–10 | 400,000 | 3,264,031 | 12,614.22 | 3835.03 | 23.3 | 21,798.7 |
| 100–100–12 | 480,000 | 3,900,837 | 12,791.33 | 3873.93 | 23.2 | 28,036.5 |
| 130–70–6 | 240,000 | 1,990,419 | 13,533.84 | 3055.21 | 18.4 | 1204.5 |
| 130–70–8 | 320,000 | 2,627,225 | 13,638.23 | 3034.42 | 18.2 | 1292.7 |
| 130–70–10 | 400,000 | 3,264,031 | 13,453.29 | 2983.97 | 18.2 | 18,121.4 |
| 130–70–12 | 480,000 | 3,900,837 | 13,648.33 | 3016.92 | 18.1 | 30,413.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uddin, M.; Huynh, N. Model for Collaboration among Carriers to Reduce Empty Container Truck Trips. Information 2020, 11, 377. https://doi.org/10.3390/info11080377
Uddin M, Huynh N. Model for Collaboration among Carriers to Reduce Empty Container Truck Trips. Information. 2020; 11(8):377. https://doi.org/10.3390/info11080377
Chicago/Turabian StyleUddin, Majbah, and Nathan Huynh. 2020. "Model for Collaboration among Carriers to Reduce Empty Container Truck Trips" Information 11, no. 8: 377. https://doi.org/10.3390/info11080377
APA StyleUddin, M., & Huynh, N. (2020). Model for Collaboration among Carriers to Reduce Empty Container Truck Trips. Information, 11(8), 377. https://doi.org/10.3390/info11080377






