Abstract
A novel bit reduced fuzzy clustering method applied to segment high resolution massive images is proposed. The image is decomposed in blocks and compressed by using the fuzzy transform method, then adjoint pixels with same gray level are binned and the fuzzy c-means algorithm is applied on the bins to segment the image. This method has the advantage to be applied to massive images as the compressed image can be stored in memory and the runtime to segment the image are reduced. Comparison tests are performed with respect to the fuzzy c-means algorithm to segment high resolution images; the results shown that for not very high compression the results are comparable with the ones obtained applying to the fuzzy c-means algorithm on the source image and the runtimes are reduced by about an eighth with respect to the runtimes of fuzzy c-means.
1. Introduction
The management of massive data represents a serious problem in image data clustering both in terms of memory allocation and execution times. In order to overcome this problem, it is necessary to reduce the size of the image, without producing information losses that affect the results of the clustering process. An idea to reduce the image size is to aggregate similar adjoint pixels into bins, using these bins as input data in the clustering process.
Bit-reduced fuzzy c-means (for short, brFCM) is an extension of the fuzzy c-means (for short FCM) algorithm [1,2] proposed in [3] in order to cluster large images. The image is binned removing the least significant bits in the pixels and binning adjoining identical pixel; then, a weighted FCM is applied to the binned image considering as weight the number of pixels in each bin.
In [4] brFCM is applied in very large (VL) image data clustering; the image is reduced by removing the least significant bits in the pixel values and binning adjoint pixel with identical grey level values; the weights are given by the number of pixels in each bin; the data assigned to the bin is the average of the pixel values of its pixels. The authors show that its performances are better than the ones of other FCM variations proposed in literature to cluster large and very large data.
An extension of the brFCM is proposed in [5] in hotspot detection from massive event spatial datasets. The binning strategy was to reduce the spatial scale and aggregating in a bin data points included in a determined convex region in the map; a bin is given by the centroid of the event points included in that region and its weight is given by the number of data points located inside this region.
A serious problem in applying the brFCM algorithm to massive images is the difficulty in storing in memory the entire image for binning similar adjoint pixels.
To solve this problem in this research we propose a new image bit reduction FCM clustering algorithm, called FTbrFCM, for segmenting massive image datasets in which the brFCM algorithm is applied to images compressed via F-transform.
The fuzzy transform technique [6] (for short, F-transform) is a consolidated method applied for lossy image compression [6,7,8]. In particular, in [7,8] is proposed a F-transform image compression method in which the image s decomposed in blocks; each block is compressed via F-transform and the compressed image is obtained merging the compressed blocks. In [9] the block F-transform image compression method is applied in image segmentation.
In FTbrFCM we apply this block F-transform image compression method to compress the image, then, the bit reduction method is executed to the compressed image, removing the least significant bits and merging adjoining identical pixels.
In this way, the whole image is not loaded in memory, but only some of its blocks; each block is compressed using the F-transform algorithm and, subsequently, the compressed image is recomposed in memory and the brFCM algorithm is applied.
In this way we obtain the following advantages:
- -
- The clustering algorithm can be applied to the entire compressed image stored in memory;
- -
- The runtime of the image segmentation algorithm is reduced, since it is applied on the compressed image;
- -
- It is not necessary to remove the least significant bits in the pixels for bin the image, as the F-transform algorithm used to compress the image has already smoothed the image and the bins can be obtained spatially adjacent merging pixels with the same gray value.
The FTbrFCM algorithm is schematized in Figure 1.
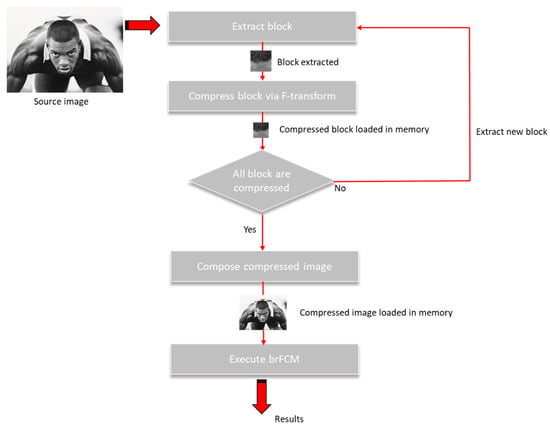
Figure 1.
Schema of the image bit reduction fuzzy c-means (FCM) clustering algorithm (FTbrFCM).
After the compressed image is constructed merging adjoint compressed blocks, the brFCM algorithm is executed aggregating in a bin identical adjoint pixels and then running the weighted FCM in which the weight of a bin is given by the number of pixels aggregated in it.
The results are given by C segmented images, where C is the number of clusters; the value assigned to a pixel in the ith segmented image is given by the membership degree of its bin to the ith cluster.
We test our algorithm on high resolution color images comparing the performances with the ones measured executing FCM on the source not compressed image.
This document is structured as follows: in Section 2 the bi-dimensional F-transform concept and the block-wise F-transform image compression method are introduced; a detailed discussion of the bidimensional F-transform and its application in image compression is in [6,7,8]. The brFCM algorithm is descripted in Section 3. In Section 4 the FTbrFCM algorithm is presented in detail. In Section 5 are shown the results of comparison test applied in image. Final discussions are in Section 6.
2. F-Transform Image Compression
Let [a, b] ⊂ R be a closed interval, n ≥ 2 and {x1, x2, …, xn} ⊂ [a, b] be a set of points called nodes, such that a ≤ x1 < x2 < … < xn ≤ b. The family of fuzzy sets A1, …, An: [a, b] → [0, 1] is a fuzzy partition of [a, b] if for every i = 1, 2, …, n the following conditions hold:
- Ai(xi) = 1
- Ai(x) = 0 if x ∉ (xi−1, xi+1), where x0 = a and xn+1 = b
- Ai(x) is a continuous function on [a, b];
- Ai(x) strictly increases on [xi−1, xi] and strictly decreases on [xi, xi+1];
- ∀ x ∈ [a, b] . A1(x) + A2(x) + … + An(x) = 1 (Ruspini condition).
The fuzzy sets {A1, …, An} are called basic functions. They form an uniform fuzzy partition of [a, b] if n ≥ 3 and for every i = 1, 2, …, n the following conditions hold:
- 6.
- xi = a + h ∙ i, where h = (b − a)/(n + 1) (that is, the nodes are equidistant);
- 7.
- Ai(xi − x) = Ai(xi + x) for every x in [0, h]
- 8.
- Ai+1(x) = Ai(x − h) for every x in [xi, xi+1] and i = 1, 2, …, n − 1.
Let f be a function continuous in [a, b] and let P = {p1, …, pm} be a discrete set of points in [a, b] in which the function f is known. We assume that the set P of these points is sufficiently dense with respect to the fixed uniform fuzzy partition, that is for each i = 1, …, n there exists an index j in {1, …, m} such that Ai(pj) > 0. Then we can define the n-tuple {F1, …, Fn} as the discrete F-transform of f with respect to {A1, A2, …, An}, where each Fi is given by:
for k = 1, …, n. Now we define the discrete inverse F-transform of f with respect to {A1, A2, …, An} to be the following function defined in the same points p1, …, pm of [a, b]:
The (2) approximate the function f in the interval [a, b] (cfr. [5], Theorem 18).
2.1. F-Transforms in Two Variables
The discrete direct and inverse fuzzy transforms of a function f continuous in [a, b] can be extended to functions in two variables. Assume that our universe of discourse is the rectangle [a, b] × [c, d] and let m,n ≥ 2, {x1, x2, …, xm} ⊂ [a, b] be a set of nodes in [a, b] and {y1, y2, …, yn} ⊂ [c, d] be a set of nodes in [a, b], such that x1 ≤ a < x2 < … < xm ≤ b and y1 ≤ c < … < yn ≤ d. Furthermore, let A1, …, Am: [a, b] → [0, 1] be a fuzzy partition of [a, b] and B1, …, Bn: [c, d] → [0, 1] be a fuzzy partition of [c, d].
Let f be a function continuous in [a, b] × [c, d] known in a discrete set of points (pj,qj) ∈ [a, b] × [c, d], where i = 1, …, M and j = 1, …, N, P = {p1, …, pM} sufficiently dense with respect to {A1, …, Am} and Q = {q1, …, qN} sufficiently dense with respect to {B1, …, Bn}.
Then, generalizing the Equation (1), we can define the discrete F-transform matrix of f [Fkl], with respect to {A1, …, Am} and {B1, …, Bn} with components k = 1, …, m and l = 1, …, n:
By extending Equation (2) to the case of two variables, we define the discrete bi-dimensional inverse F-transform of f with respect to {A1, A2, …, An} and {B1, …, Bm} to be the following function defined in the same points (pi,qj) in [a, b] × [c, d], with i in {1, …, N} and j in {1, …, M}, as:
The inverse F-transform (4) approximate the bidimensional function f in [a, b] × [c, d].
2.2. F-Transforms in Two Variables for Image Compression
Let I(x,y) an image function discretized in a digital gray M × N image composed of M × N pixels with coordinates (pi,qj) ∈ {1, …, M} × {1, …, N}. For brevity of notation, we put pi = i, qj = j and [a, b] × [c, d] = [1, N] × [1, M].
The matrix I is divided in submatrices of identical size MC × NC called blocks, where MC < M, NC < N, MC is a divisor of M and NC is a divisor of N. The image I is then composed of (MC × NC)/(M × N) blocks of equal size MC × NC.
Each block is composed of MC × NC pixels with coordinates (pi,qj) ∈ {1, …, MC } × {1, …, NC }. For brevity of notation, we put pi = i, qj = j and [a, b] × [c, d] = [1, MC] × [1, NC].
Let A1, …, Am: [1, MC] → [0, 1] be a fuzzy partition of [1, MC] with mC < MC and let B1, …, Bn: [1, NC] ⭢ [0, 1] a fuzzy partition of [1, NC] with nC < NC.
Each block of sizes MC × NC is compressed in a block of sizes mC × nC via the discrete bi-dimensional F-transform [FklC] with components given by:
for each k = 1, …, mC and l = 1, …, nC. As above, naturally we do in such a way that the set{1, …, M(C) (resp., {1, …, N(C)})} is sufficiently dense to the fuzzy partition of the basic functions {A1, …, Am(C)} defined (resp., {B1, …, Bn(C)}) in the interval [1, M(C)] (resp., [1, N(C)]) considered.
The parameter ρ: = (mC∙× nC)/(MC × NC) is the compression rate of the block.
Afterwards, we decode the compressed blocks via the discrete inverse F-transform :{1, …, M(C)} × {1, …, N(C)} → [0, 1] defined as:
which approximates IC with arbitrary precision.
The tests conducted in [10 14] have shown that the best performances are obtained by using a symmetric fuzzy partition of [1, MC] whose fuzzy sets A1, …, Am(C):[1, MC] → [0, 1]] are defined as
where k =1, 2, …, mC, h = (MC − 1)/(mC + 1), x0 = 1 and xmC + 1 = mC, and by using a symmetric fuzzy partition of [1, NC] whose fuzzy sets B1, …, BnC:[1, NC] → [0, 1] are defined as:
where l = 1, 2, …, nC, s = (NC − 1)/(nC +1), y0 = 1 and xnC + 1 = nC.
The compressed image Iρ of I obtained using the compression ratio ρ is constructed merging the compressed blocks where each compressed block is given by the direct F-transform matrix [FklC] calculated by (5).
Algorithm 1 shows in pseudocode the block F-transform image compression algorithm.
| Algorithm 1. Block F-Transform Image Compression. | |
| Input: | Source Image I |
| Output: | Compressed image Iρ |
| 1 | Set MC,NC,nC,mC where ρ := mC∙nC / MC NC |
| 2 | Set the basic functions A1, A2, …, An as in (7) and B1, B2, …, Bn as in (8) |
| 3 | For each block IC |
| 4 | For k = 1 to mC |
| 5 | For l = 1 to nC |
| 6 | Numkl := 0 // Numerator of the Ftransform component (5) |
| 7 | Denkl := 0 // Denominator of the Ftransform component (5) |
| 8 | For i = 1 to MC |
| 9 | For j = 1 to NC |
| 10 | Numkl := IC(i,j)∙Ak(i) Bl(j) |
| 11 | Denkl := Ak(i) Bl(j) |
| 12 | Next j |
| 13 | Next i |
| 14 | FklC := Numkl / Denkl // Ftransform component (5) |
| 15 | Next l |
| 16 | Next k |
| 17 | Next block |
| 18 | Merge the compressed block to obtain the compressed image Iρ |
| 19 | Store the compressed image Iρ |
The compressed image Iρ can be decompressed dividing it in MC × NC blocks and decoding every block in a MC × NC block by (6); finally, the decoded blocks are merged to form the decompressed image.
3. The brFCM Algorithm
Let X = {x1, …, xN} ⊂ Rn be a set of data Np data points: each data point xj = (xj1, …, xjn) is a vector in the space Rn.
FCM is a partitive fuzzy clustering algorithm aimed to find as set of points in Rn the set of C fuzzy cluster centers V = {v1, …, vC} where vi = (vi1, …, vjn) (i = 1, …, C). The C × Np partition matrix U with components uij i = 1, …, C; j = 1, …, Np give the membership degree of the jth data point to the ith cluster.
FCM find V and U minimizing the following objective function:
where dij = is the Euclidean distance between vi and xja.
The parameter γ ∈ [1, +∝) is called fuzzifier parameter; it determines the fuzziness degree of the fuzzy partition. (a constant which affects the membership values and determines the degree of fuzziness of the partition).
By applying the Lagrange multipliers, and considering the constraints:
are obtained for U and V the following solutions
and
FCM is an iterative algorithm in which initially the membership degrees (or the cluster centers) are assigned randomly; in any cycle the cluster centers and the membership degrees are calculated via (12) and (13). The algorithm stops after t iterations if:
where ε > 0 is a parameter assigned a priori to stop the iteration process and
The pseudocodes of the FCM is given in Algorithm 2.
| Algorithm 2. FCM. | |
| Input: | Input Dataset D with Np Data Points |
| Output: | Partition matrix U and cluster centers V |
| |
A variation of the FCM algorithm is the weighted FCM (wFCM) algorithm [10] in which a weight defines the influence of the data point to the solutions; data points with higher weights influence the determination of location of the cluster centers more than the others.
We can consider FCM a special case of wFCM where wj = 1 for each j = 1, …, Np, in which each data point influences the determination of cluster centers in the same way.
wFCM minimize the following objective function:
Using the Lagrange multipliers, and considering the constraints (10) and (11), are obtained for the cluster centers the solutions:
The solutions obtained for the membership degrees are given by (13).
The pseudocode of wFCM is shown in Algorithm 3.
| Algorithm 3. WFCM. | |
| Input: | Input dataset D with NP data points |
| Output: | Partition matrix U and cluster centers V |
| |
A density-based wFCM was proposed in [11] for reducing the size of the input dataset. In [12,13] two weighted FCM algorithms are used for image segmentation. In [14] a wFCM algorithm is applied to solve the Source Location problem.
The brFCM algorithm is proposed in [3] to handle massive datasets. It uses a wFCM algorithm in which the weight is given by the number of data points merged in a bin.
The pseudocode of brFCM is shown in Algorithm 4.
| Algorithm 4. BRFCM. | |
| Input: | Input dataset D with Np data points |
| Output: | Partition matrix U and cluster centers V |
| |
4. F-Transform brFCM Algorithm
The FTbrFCM algorithm is made up of two phases. In the first phase, the F-transform algorithm is applied by acquiring in memory and compressing the individual blocks of the image I and, finally, merging the compressed blocks to form the compressed image Ip, stored in memory.
In the second phase the brFCM algorithm is executed on the compressed image Ip. The bins are made up of sets of adjacent pixels with the same gray value in the compressed image and the weight of each bin is given by the number of these pixels.
The binning process is accomplished by examining the pixels of the image. If the pixel value is identical to that of a neighboring pixel already binned, then the pixel is merged into that bin and the weight value associated with the bin is increased; otherwise, a new bin is created to which the pixel value is assigned and the weight of this bin is initialized to 1.
The pseudocode of FTbrFCM is shown in Algorithm 5.
| Algorithm 5. FTBRFCM. | |
| Input: | Source image I with size M × N |
| Output: | Partition matrix U and cluster centers V |
| |
The results can be treated as a set of C images with size m × n. In fact, we assign the membership degree of a bin to a cluster to every pixel belonging to this bin, obtaining a m × n matrix; then we normalize the values of the pixels in the number of grey levels (for example, multiplying the pixel values by 255, considering 256 grey levels, and approximating the value obtained to the nearest integer).
To measure the performance of FTbrFCM, we test the FTbrFCM algorithm in image segmentation of high-resolution images. Then a comparison with the results obtained applying FCM is performed.
To carry out this comparison, after obtained the image corresponding
- (1)
- The m × n image corresponding to the membership degree to the cth cluster with c = 1, …, C, is decompressed in a M × N image by applying the block- inverse F-transform (6) and merging the decoded blocks to form a decompressed N × M image Ic.
- (2)
- Let I0c be, the N × M resultant image correspondent to the cth cluster obtained executing FCM on the original image, the root mean square error (RMSE) index of Ic with respect to I0c is given by:
- (3)
- The final RMSE index is given by the average of the RMSE measures calculated for all the clusters:
We compress the image with different compression rates, measuring the trend of the RMSE error varying the compression rate.
In next section we show the results of our tests performed applying the FTbrFCM algorithm on massive image datasets.
5. Test Results
The FTbrFCM is applied to a set about 200 color high-resolution images of paintings by famous painters in the Google Art & culture web page (https://artsandculture.google.com); the mean resolution of these images is of 108 pixels. Each image is decomposed in the three bands R, G and B, then, FTbrFCM is executed on the image in each band. The Xie-Beni validity index [15] is used to find the optimal number of clusters.
We apply FTbrFCM on the image on each band by using various compression rates. We execute FTbrFCM on an Intel core I5 3.2 GHz processor.
For brevity we present the detailed results obtained for the color images Mona Lisa, which represents the homonymous oil painting by Leonardo da Vinci preserved in the Louvre, and Sunflowers, which represents the Van Gogh’s the painting on canvas, Vase with 15 Sunflowers, preserved at Van Gogh Museum
In Figure 2a–d is shown the high-resolution image Mona Lisa decomposed in the three band R, G and B.


Figure 2.
(a) Mona Lisa; (b) Mona Lisa R Band; (c) Mona Lisa G Band; and (d) Mona Lisa B Band.
The images in the three bands are been compressed and segmented setting C = 3 clusters.
Figure 3, Figure 4 and Figure 5 show, respectively, the segmented images obtained in the bands R, G and B, compressing the original image with a compression rate ρ = 0.25, obtained compressing each block 4 × 4 in a block 2 × 2.

Figure 3.
Mona Lisa R Band—compression rate 0.25—segmented images.

Figure 4.
Mona Lisa G Band—compression rate 0.25—segmented images.

Figure 5.
Mona Lisa B Band—compression rate 0.25—segmented images.
A segmented image can be subsequently processed to be classified. As an example, the binary image in Figure 6 show the results of the classification of the second segmented image in the G band and the pixel values frequency histogram used to classify the pixels.
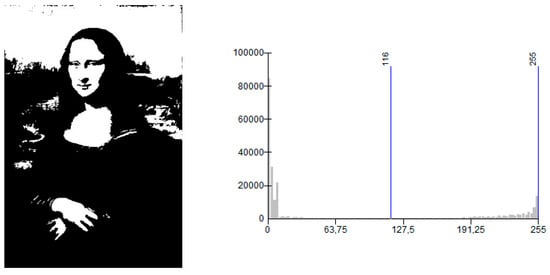
Figure 6.
Classified frequency image and its pixel values frequency histogram.
We calculate the RMSE index of the segmented image obtained in a band with respect to the correspondent segmented image obtained applying FCM on the source image in that band. To perform these measures, we decompress the segmented images obtained by executing the FTbrFCM algorithm using the bidimensional inverse F-transform.
In Table 1 are shown the RMSE measures obtained in each band changing the compression rate.

Table 1.
Root mean square error (RMSE) measures for the image Mona Lisa.
The trend of RMSE varying the compression rate is shown in Figure 7.
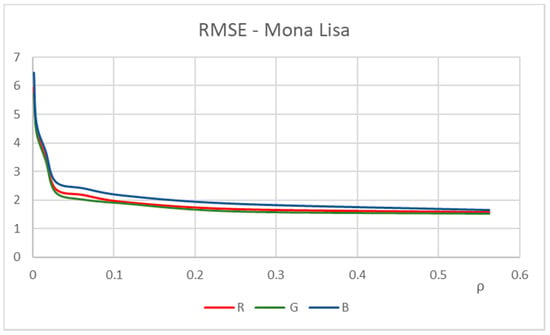
Figure 7.
Mona Lisa—RMSE trend in the three band.
This results show that for not high compressions (ρ greater than 0.016), the RMSE index is less than 3, i.e., the average difference of the pixel values between the segmented image obtained using the FTbrFCM algorithm and the corresponding one obtained using the FCM algorithm is less than 3, therefore the loss of information due to the compression of the source image can be considered acceptable. In fact, if the mean square error obtained is less than 3 the average absolute difference between the membership degree of a pixel to the cluster obtained with the two algorithms is less than 3/255 ≈ 1.2 × 10−2 and the loss of information can be neglected. For strong compressions (ρ < 0.1), however, the RMSE value rises rapidly and the average differences between the membership degree values assigned to each pixel become significant.
In Figure 8a–d are shown the image Sunflowers and its decomposition in the three bands R, G and B.
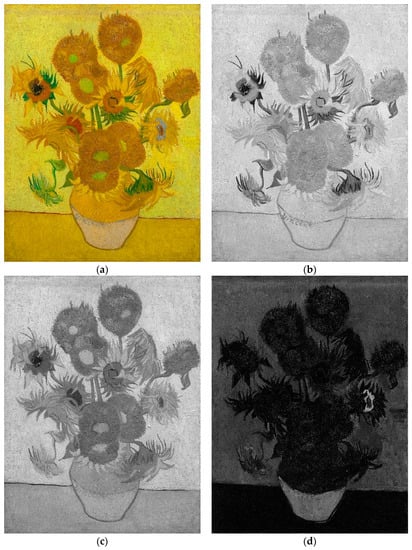
Figure 8.
(a) Sunflowers; (b) Sunflowers R Band; (c) Sunflowers G Band; (d) Sunflowers B Band.
This image in each band is compressed using various compression rates and segmented setting the number of clusters (C) to 3. In Figure 9, Figure 10 and Figure 11 shown the segmented images obtained using a compression rate = 0.25, respectively, in the R, G and B bands.

Figure 9.
Sunflowers R Band—compression rate 0.25—segmented images.
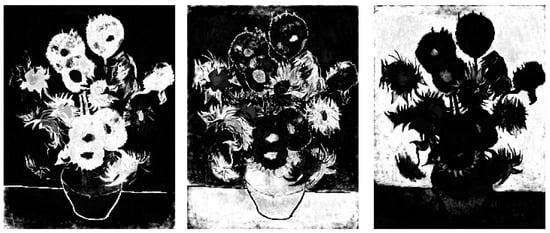
Figure 10.
Sunflowers G Band—compression rate 0.25—segmented images.
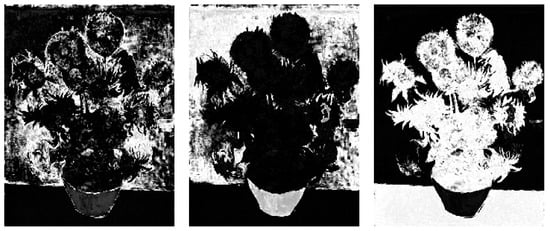
Figure 11.
Sunflowers B Band—compression rate 0.25—segmented images.
To measure the RMSE index of each segmented image with respect to the correspondent one obtained executing FCM on the source image, we decompress the segmented image via the bidimensional inverse F-transform.
In Table 2 are shown the RMSE measures obtained in each band changing the compression rate.

Table 2.
RMSE measures for the image Sunflowers.
The trend of the RMSE index in the three bands is shown in Figure 12.
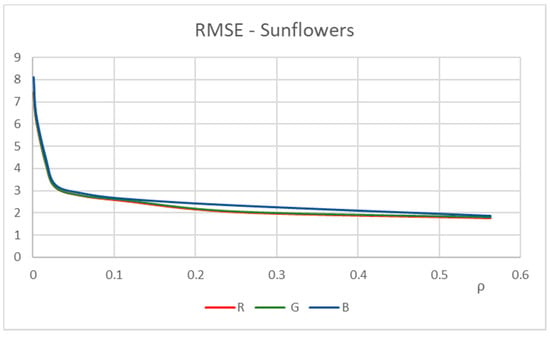
Figure 12.
Sunflowers—RMSE trend in the three band.
The results in Figure 13 show that for compression rates greater or equal to 0.063 the value of the RMSE index is less than 3 in each band and the segmented images obtained executing FtbrFCM are comparable with the ones obtained executing FCM on the source images; conversely, for compression rates less than 0.063 the RMSE index rises rapidly and the loss of information due to compression becomes significant.
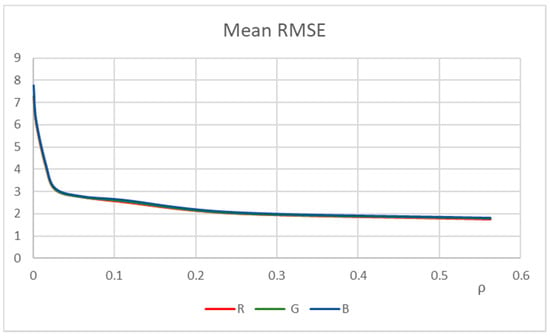
Figure 13.
Mean RMSE trend in the three band.
In Figure 12 is shown the mean trend of the RMSE measured for all the images in the dataset in the three bands varying the compression rate.
For a compression rate ρ less than 0.11 the mean RMSE is greater than 3 and increases exponentially for higher compression. For compression rates greater than 0.11 the mean RMSE is less than 3 and the results obtained running FTbrFCM are comparable with the ones obtained running FCM on the source images.
To compare the performances of FTbrFCM also with other image segmentation methods in literature we measure also the RMSE of FTbrFCM with respect to two fast FCM image segmentation variations called fuzzy generalized fuzzy c-means (for short FGFCM) [16] and improved intuitionistic fuzzy c-means (for short IIFCM) [17]; both these two FCM-based algorithms incorporate local spatial information considering spatial relations between near pixels and are more robust to noise than FCM improving its performances.
Figure 14 shows the trend of the mean RMSE calculated in any band varying the compression rate with respect to FCM, FGFCM and IIFCM.
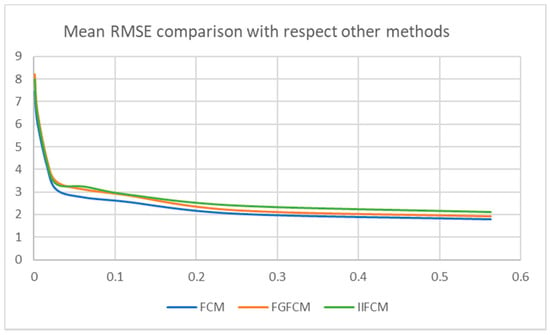
Figure 14.
Mean RMSE trend with respect to FCM, fuzzy generalized fuzzy c-means (FGFCM) [16] and improved intuitionistic fuzzy c-means (IIFCM).
Even if the average RMSE obtained with respect to FGFCM and IIFCM is greater than the average RMSE obtained with respect to FCM as the compression rate changes, the average RMSE obtained with respect to FGFCM and IIFCM remains below the threshold 3 for compression rates not lower than 0.1. These results show that for not substantial compression (ρ ≥ 0.1) the quality of the segmented images obtained executing FTbrFCM is also comparable with the ones obtained executing. FGFCM and IIFCM.
In Figure 15 is shown the mean runtime in seconds, varying the compression rate. The run time measured where ρ = 1 is the one obtained executing FCM on the source image.
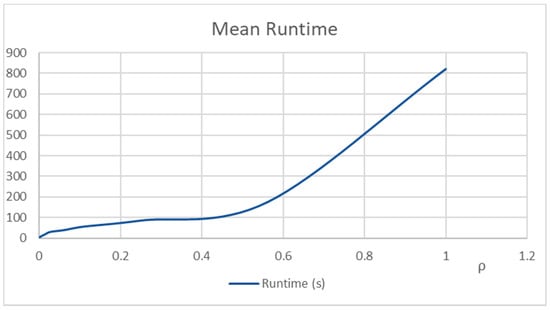
Figure 15.
Mean runtime trend.
Figure 15 show that for ρ ≤ 0.25 the runtimes are less than 1/8 of the runtime of FCM applied on the source image. Since in our tests for all the images and in all bands using compression rates greater than ρ = 0.11 the RMSE is less than 3, we deduce that using compression rates ρ = 0.11 and ρ = 0.25 all the segmented images are comparable with the ones obtained by executing FCM, and the runtimes are on average reduced to 1/8 with respect to the ones obtained executing FCM.
6. Conclusions
In order to handle massive data in image segmentation, we propose a bit reduced FCM algorithm applied on images compressed by bi-dimensional F-transforms. To perform the compression of the image, the block F-transform compression method is used in which each block of the image is acquired sequentially and compressed; when all the blocks have been compressed the compressed image is reconstructed and is binned by merging all adjacent pixels with the same gray value in a bin. FTbrFCM is tested on a set of high definition color images; the results show that for not excessively high compressions (ρ ≥ 0.11) the results are comparable with the ones obtained applying FCM and other FCM-based more robust image segmentation algorithms on the source images; in addition, for ρ ≤ 0.25 the runtimes are not exceeding one eighth of the runtimes measured using FCM on the source images.
In the future, we intend to further increase the performance of this method by exploring the use of variations of the FCM algorithm that are more robust than the presence of noise in the data and the initialization of clusters, to be applied to binned datasets for the segmentation of the compressed image. In addition, we intend to carry out further tests considering different types of massive image data such as high-resolution multiband satellite data and high-resolution diagnostic images used in many medical fields, varying the size of the image.
Author Contributions
Conceptualization, B.C. and F.D.M.; methodology, B.C. and F.D.M.; software, B.C. and F.D.M.; validation, B.C. and F.D.M.; formal analysis, B.C. and F.D.M.; investigation, B.C. and F.D.M.; resources, B.C. and F.D.M.; data curation, B.C. and F.D.M.; writing—original draft preparation, B.C. and F.D.M.; writing—review and editing, B.C. and F.D.M.; visualization, B.C. and F.D.M.; supervision, B.C. and F.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dunn, C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981; p. 272. [Google Scholar]
- Eschrich, S.; Ke, L.; Hall, L.; Goldgof, D. Fast accurate fuzzy clustering through data reduction. IEEE Trans. Fuzzy Syst. 2003, 11, 262–269. [Google Scholar] [CrossRef]
- Havens, T.C.; Bezdek, J.C.; Leckie, C.R.; Hall, L.O.; Palaniswami, M. Fuzzy C-means algorithms for very large data. IEEE Trans. Fuzzy Syst. 2012, 20, 1130–1146. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. Extended Fuzzy C-Means Hotspot Detection Method for Large and Very Large Event Datasets. Inf. Sci. 2018, 441, 198–215. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transforms. Fuzzy Sets Syst. 2006, 157, 993−1023. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. Compression and decompression of images with discrete fuzzy transforms. Inf. Sci. 2007, 177, 2349−2362. [Google Scholar]
- Di Martino, F.; Loia, V.; Sessa, S. An image coding/decoding method based on direct and inverse fuzzy trans-forms. Int. J. Approx. Reason. 2008, 48, 110−131. [Google Scholar] [CrossRef]
- Di Martino, F.; Loia, V.; Sessa, S. A segmentation method for images compressed by fuzzy transforms. Fuzzy Sets Syst. 2010, 161, 56–74. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley-Blackwell: New York, NY, USA, 2005; p. 342. [Google Scholar]
- Hathaway, R.; Hu, Y. Density-Weighted Fuzzy c -Means Clustering. IEEE Trans. Fuzzy Syst. 2008, 17, 243–252. [Google Scholar] [CrossRef]
- Ji, Z.; Xia, Y.; Chen, Q.; Sun, Q.-S.; Xia, D.; Feng, D.D. Fuzzy c-means clustering with weighted image patch for image segmentation. Appl. Soft Comput. 2012, 12, 1659–1667. [Google Scholar] [CrossRef]
- Gong, M.; Liang, Y.; Shi, J.; Ma, W.; Ma, J. Fuzzy C-Means Clustering with Local Information and Kernel Metric for Image Segmentation. IEEE Trans. Image Process. 2012, 22, 573–584. [Google Scholar] [CrossRef] [PubMed]
- Nadalin, E.Z.; Silva, R.C.; Attux, R.; Romano, J.M.T. Analysis of the Weighted Fuzzy C-means in the Problem of Source Location. In Proceedings of the ESANN 2014, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 23–25 April 2014; pp. 219–224. [Google Scholar]
- Xie, X.L.; Beni, G. A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- Cai, W.; Chen, S.; Zhang, D. Fast and robust fuzzy c-means clustering algorithm incorporating local information for image segmentation. Pattern Recognit. 2007, 40, 825–838. [Google Scholar] [CrossRef]
- Verma, H.; Agrawal, R.K.; Sharan, A. An improved intuitionistic fuzzy c-means clustering algorithm incorporating local information for brain image segmentation. Appl. Soft Comput. 2016, 46, 543–557. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).