Modeling Web Client and System Behavior
Abstract
1. Introduction
- How many nodes do we need to run handling different customer workloads?
- Which is the best client scheduling discipline?
- Are the system resources enough to serve clients’ requests?
- How long is a client waiting time?
- How much will clients’ waiting time reduce if more nodes would are deployed?
1.1. Motivation
- a review of the most modern methods for estimating the performance of an Internet system,
- a classification scheme of approaches to estimating resource requirements,
- an experimental comparison of a subset of the estimation approaches.
1.2. Organization
2. Related Works
2.1. Works Based on Various Formalisms
2.2. Previous Works Based on Queueing Net, Time Colored Petri Net and QPN Formalisms
2.3. Current Work Based on QPN Formalism
3. Web System Architecture
3.1. Clustering
- High Availability also known as Fail-over Clusters,
- Load Balancing,
- High Performance.
3.2. Nodes in Cluster-Based Web Architecture
3.3. Distributed Computing
3.4. Different Customers
4. Queueing Nets and Petri Nets Models
4.1. Queueing Nets and Petri Nets in the Same Model
- Arrival process is a mathematical model for the time between request arrivals to the system e.g.,: Poisson, Erlang, hyper-exponential, general. (We analyzed queueing systems without external clients arrival.)
- Service time is defined as the time required to serve a customer request e.g.,: logarithmic, chi-square, hyper-exponential, exponential. Service times are Independent and Identically Distributed (IID). (We analyzed queueing systems with the exponential clients’ service time.)
- Scheduling strategies define the strategies used to allocate the processor e.g.,: First In First Out (FIFO), Last In First Out (LIFO), Last In First Out with Preempt and Resume (LIFO-PR), Round Robin (RR) with a fixed quantum, Small Quantum ⇒ Processor Sharing (PS), Infinite Server (IS) = fixed delay, Shortest Processing Time first (SPT). (We used IS for clients machine, PS for FE nodes and FIFO for BE nodes.)
- Number of processors. (This paper considers a single server queue.)
- Number of buffers is waiting room size. (Size of the queue is infinite.)
- set of places,
- set of transactions,
- initial marking (number of tokens),
- incidence function (routing probability),
- token color function.
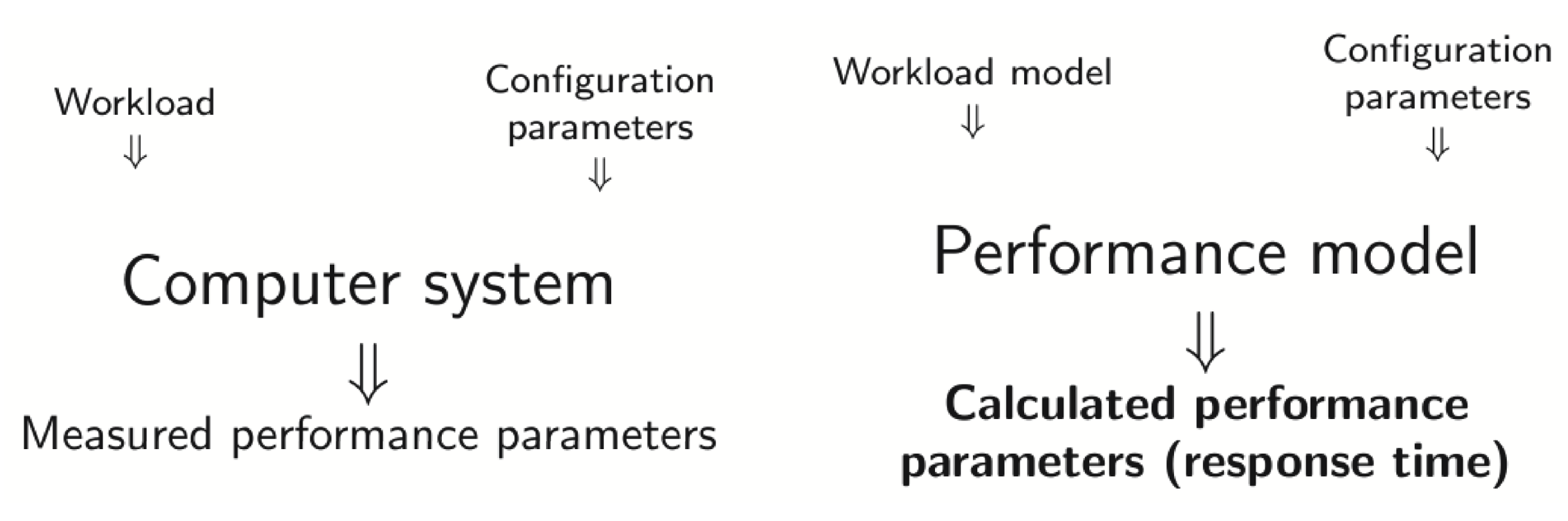
4.2. Theoretical Introduction
- understanding the operation of the system,
- determine the system load,
- measure system parameters,
- build a performance model,
- model verification and validation,
- load changes,
- predicting system performance,
- analysis of various scenarios.
- number of clients, workload intensity (think time (The think time adds delay in between successive requests to the system from populated concurrent clients.), different types of arriving requests of clients are different behaviours) for the client.
- number of hardware elements (nodes in FE and BE layer), hardware connections (routing), software parameters (service resources as threads and connection pools), scheduling strategy, service demand (Service demand in milliseconds is the time needed to serve one request at the station.) for the selected class in a specific resource (1), excluding the waiting time for a resource (it does not depend on the load) for the system.
4.3. Client Model
- —client service type,
- —time limit, i.e., time interval in which the client has to be serviced,
- —function describing arrivals of a particular type of clients.
- —servicing on a Www Server,
- —servicing on an Application Server,
- —servicing on a Database Server.
- —total time of servicing for clients of type,
- —time of servicing for client of type on a www server,
- —time of servicing for clients of type on an application server,
- —time of servicing for clients of type on a database server.
- —distribution of probability of clients’ arrivals (degenerate/determined (A determined distribution means that the times are constant and there is no variance.), Poisson, etc.),
- —average intensity of arrivals,
- —another parameter of distribution (if it exist).
- —time of task execution,
- —period of task occurrence,
- ,
- —time limits of the task.
- x—random variable (amount of tasks in t time),
- —intensity of task arrivals.
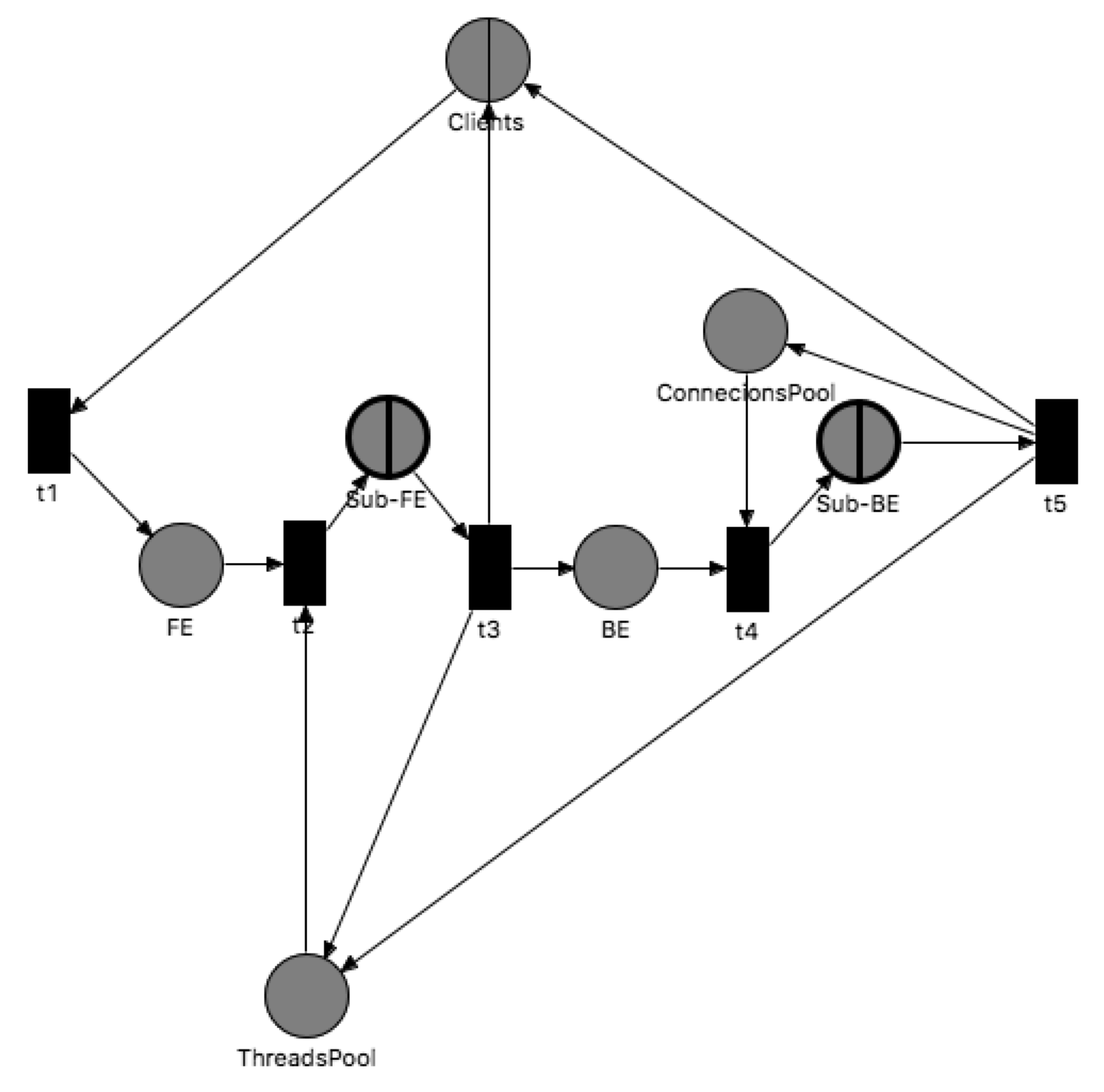
5. System Model
QP Net
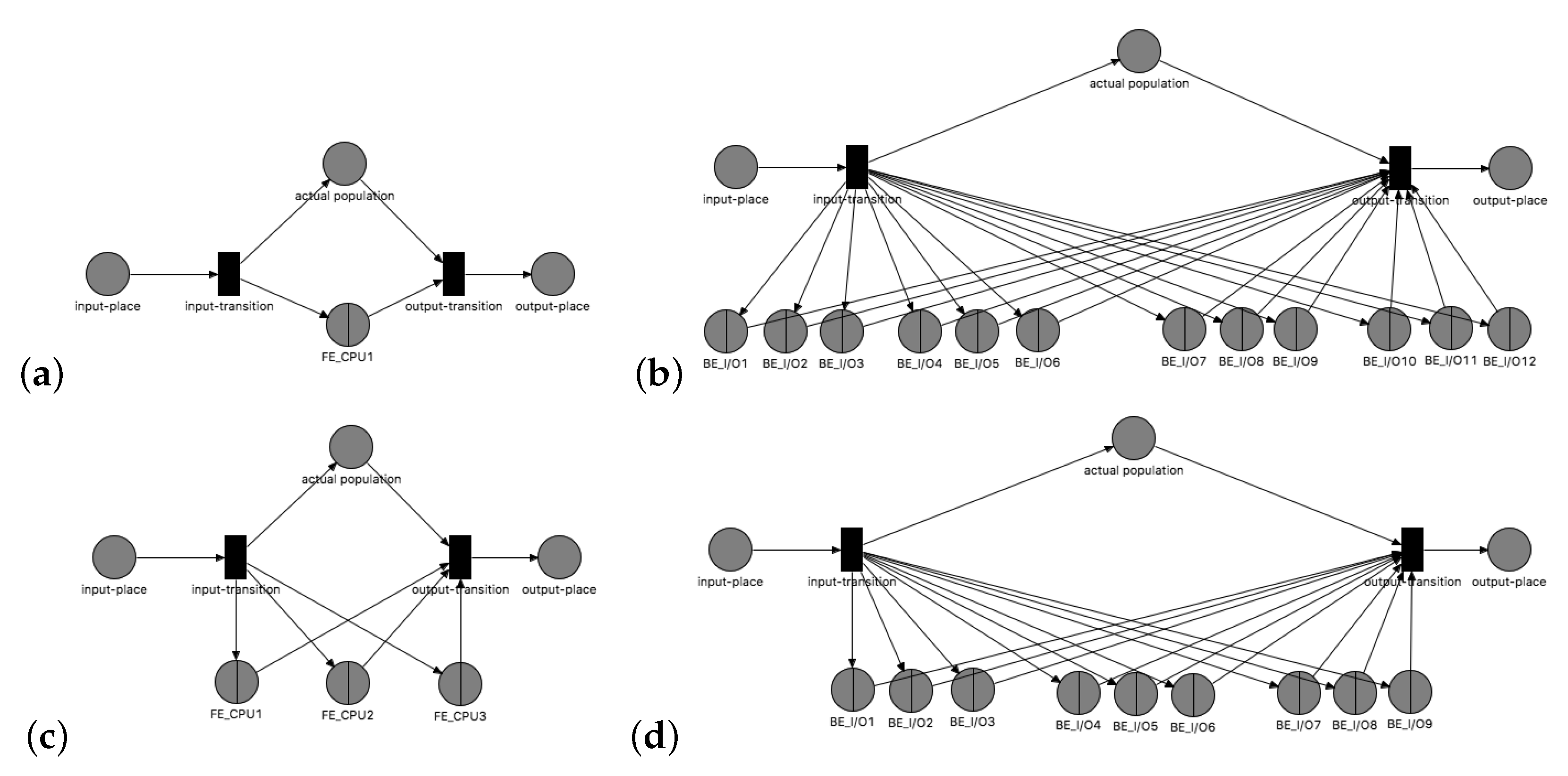
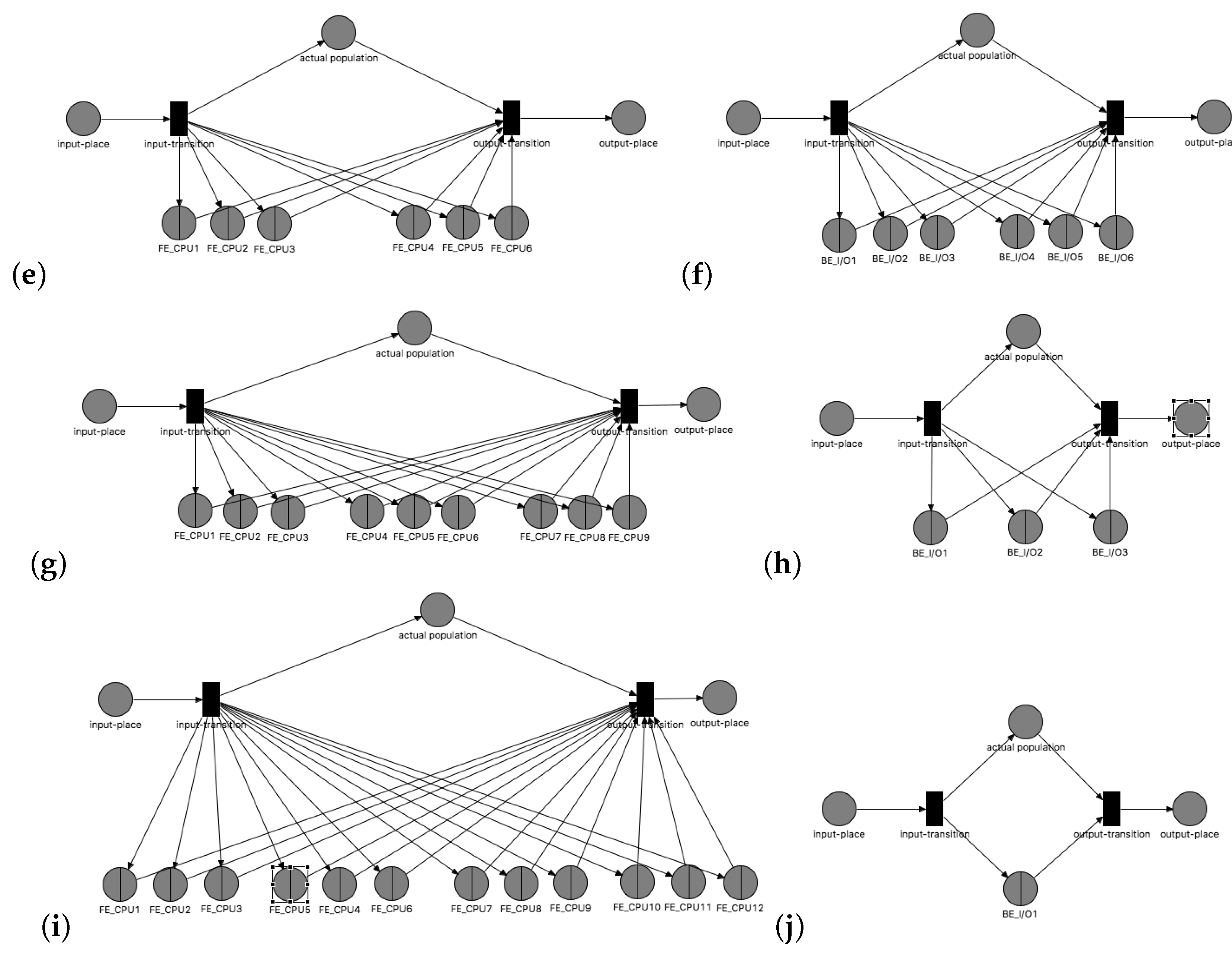
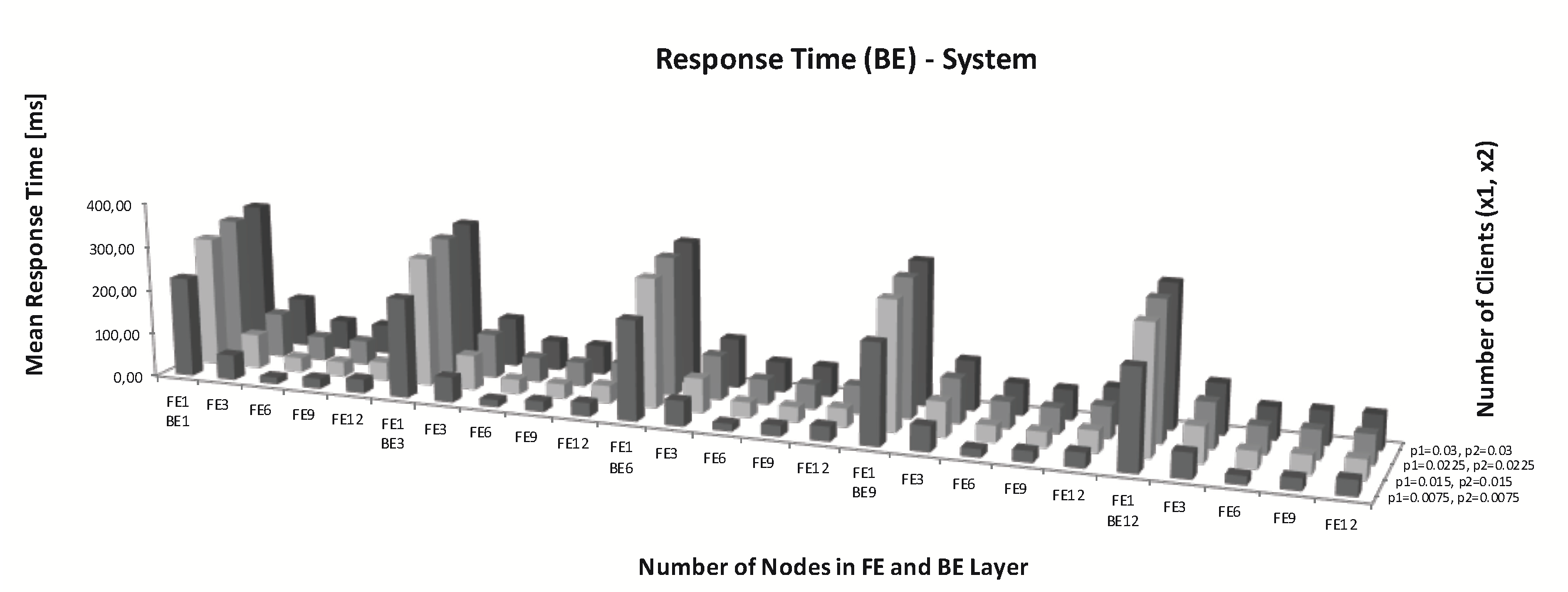
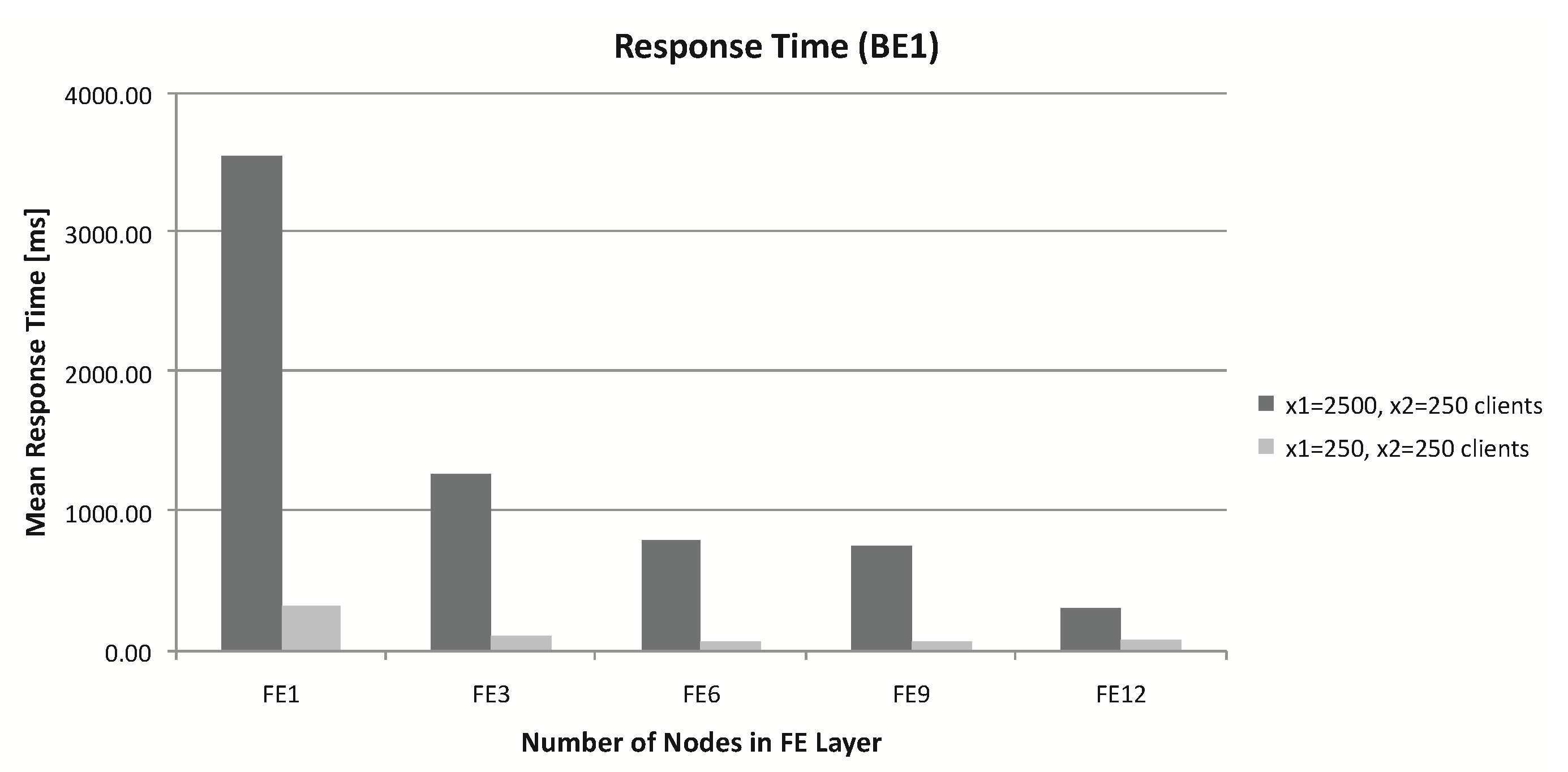
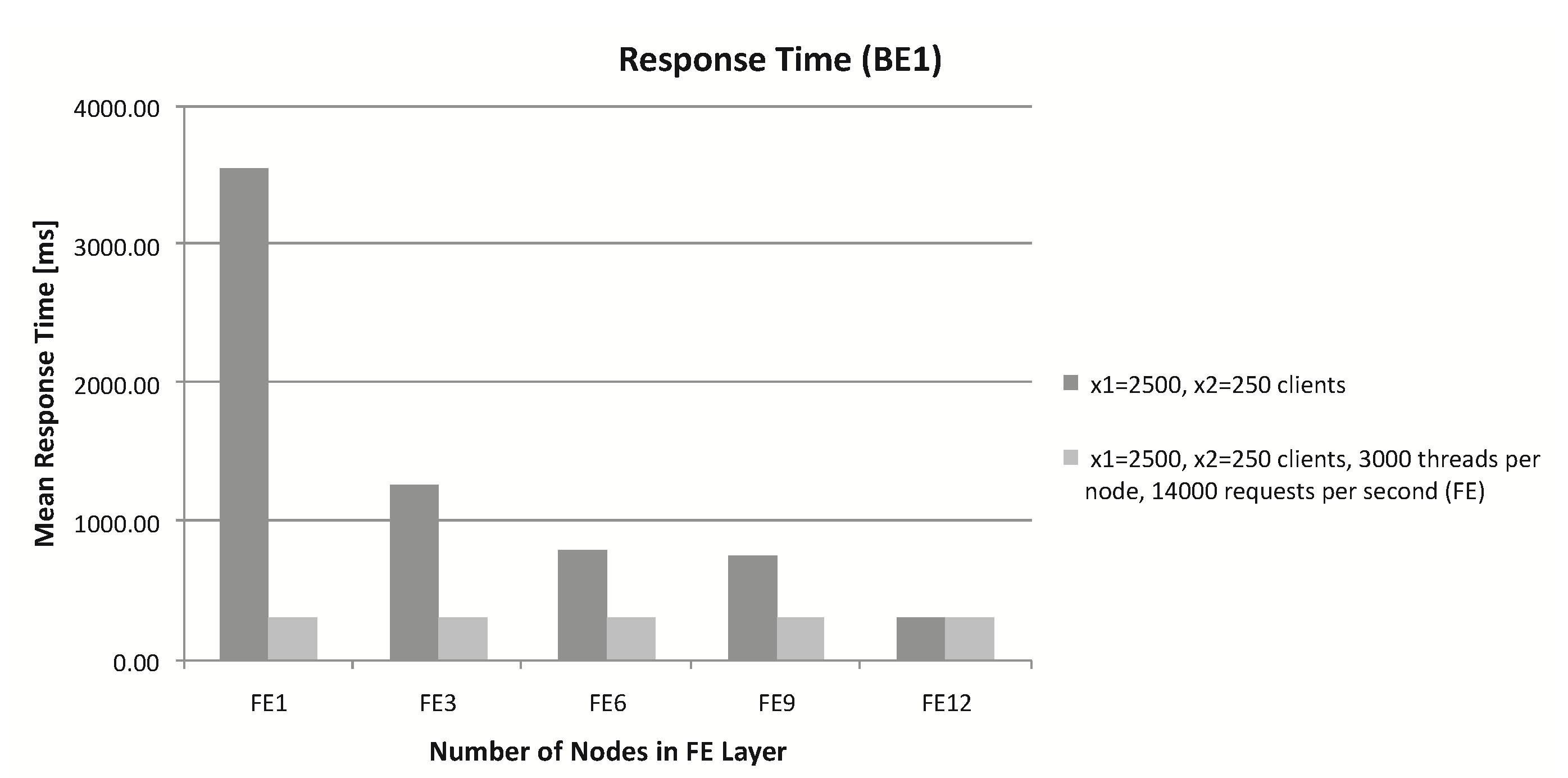
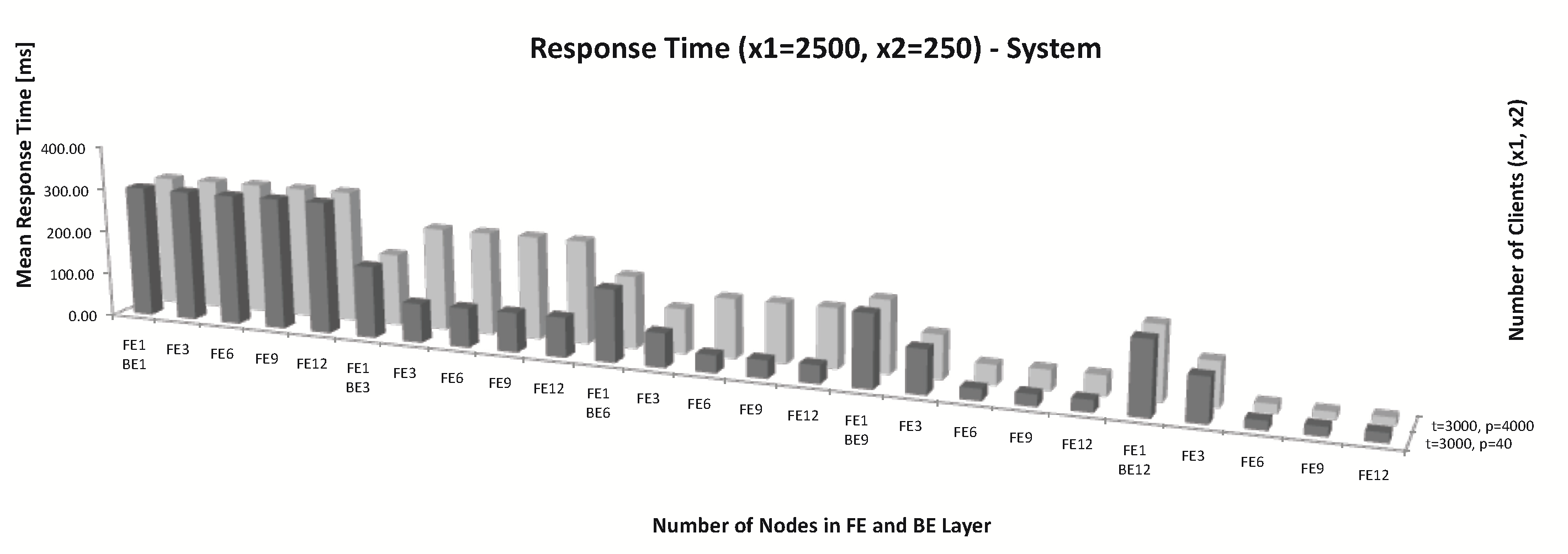
6. Simulations with Different Parameters
Simulation with Changed Parameters
7. Summary
Funding
Conflicts of Interest
References
- Li, Z.; Jiao, L.; Hu, X. Performance Analysis for Job Scheduling in Hierarchical HPC Systems: A Coloured Petri Nets Method. In Algorithms and Architectures for Parallel Processing; Wang, G., Zomaya, A., Martinez, G., Li, K., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 259–280. [Google Scholar]
- Rak, T. Response Time Analysis of Distributed Web Systems Using QPNs. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Buchmann, A.; Dutz, C.; Kounev, S.; Buchmann, A.; Dutz, C.; Kounev, S. QPME-Queueing Petri Net Modeling Environment. In Proceedings of the Third International Conference on the Quantitative Evaluation of Systems-(QEST’06), Riverside, CA, USA, 11–14 September 2006; pp. 115–116. [Google Scholar] [CrossRef]
- Rak, T. Cluster-Based Web System Models for Different Classes of Clients in QPN. In Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 1039, pp. 347–365. [Google Scholar]
- Rak, T. Performance Analysis of Cluster-Based Web System Using the QPN Models. In Information Sciences and Systems 2014; Czachórski, T., Gelenbe, E., Lent, R., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 239–247. [Google Scholar]
- Rzonca, D.; Rzasa, W.; Samolej, S. Consequences of the Form of Restrictions in Coloured Petri Net Models for Behaviour of Arrival Stream Generator Used in Performance Evaluation. In Computer Networks. CN 2018. Communications in Computer and Information Science; Gaj, P., Sawicki, M., Suchacka, G., Kwiecień, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 860, pp. 300–310. [Google Scholar]
- Kounev, S.; Buchmann, A. On the Use of Queueing Petri Nets for Modeling and Performance Analysis of Distributed Systems. In Petri Net; Kordic, V., Ed.; IntechOpen: Rijeka, Croatia, 2008; Chapter 8. [Google Scholar] [CrossRef]
- Eismann, S.; Grohmann, J.; Walter, J.; von Kistowski, J.; Kounev, S. Integrating Statistical Response Time Models in Architectural Performance Models. In Proceedings of the 2019 IEEE International Conference on Software Architecture (ICSA), Hamburg, Germany, 25–29 March 2019; pp. 71–80. [Google Scholar] [CrossRef]
- Kattepur, A.; Nambiar, M. Service Demand Modeling and Performance Prediction with Single-user Tests. Perform. Eval. 2017, 110, 1–21. [Google Scholar] [CrossRef]
- Rak, T. Performance Modeling Using Queueing Petri Nets. In Communications in Computer and Information Science, Proceedings of the 24th International Conference on Computer Networks (CN), Ladek Zdroj, Poland, 20–23 June 2017; Gaj, P., Kwiecien, A., Sawicki, M., Eds.; IEEE Polish Section Chapter; Institute of Informatics, Silesian University of Technology; Springer International Publishing AG: Cham, Switzerland, 2017; Volume 718, pp. 321–335. [Google Scholar] [CrossRef]
- Nalepa, F.; Batko, M.; Zezula, P. Performance Analysis of Distributed Stream Processing Applications Through Colored Petri Nets. In Mathematical and Engineering Methods in Computer Science; Kofroň, J., Vojnar, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 93–106. [Google Scholar]
- Zhou, J.; Reniers, G. Petri-net Based Modeling and Queuing Analysis for Resource-oriented Cooperation of Emergency Response Actions. Process Saf. Environ. Prot. 2016, 102, 567–576. [Google Scholar] [CrossRef]
- Requeno, J.; Merseguer, J.; Bernardi, S. Performance Analysis of Apache Storm Applications Using Stochastic Petri Nets. In Proceedings of the 2017 IEEE International Conference on Information Reuse and Integration (IRI), San Diego, CA, USA, 4–6 August 2017; pp. 411–418. [Google Scholar] [CrossRef]
- Requeno, J.; Merseguer, J.; Bernardi, S.; Perez-Palacin, D.; Giotis, G.; Papanikolaou, V. Quantitative Analysis of Apache Storm Applications: The NewsAsset Case Study. Inf. Syst. Front. 2019, 21, 67–85. [Google Scholar] [CrossRef]
- Fiuk, M.; Czachórski, T. A Queueing Model and Performance Analysis of UPnP/HTTP Client Server Interactions in Networked Control Systems. In Computer Networks (CN 2019); Communications in Computer and Information Science; Springer International Publishing AG: Cham, Switzerland, 2019; pp. 366–386. [Google Scholar] [CrossRef]
- Zatwarnicki, K.; Płatek, M.; Zatwarnicka, A. A Cluster-Based Quality Aware Web System. In Information Systems Architecture and Technology, Proceedings of the 36th International Conference on Information Systems Architecture and Technology—ISAT 2015—Part II, Karpacz, Poland, 20–22 September 2015; Grzech, A., Borzemski, L., Światek, J., Wilimowska, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 15–24. [Google Scholar]
- Zatwarnicki, K.; Zatwarnicka, A. A Comparison of Request Distribution Strategies Used in One and Two Layer Architectures of Web Cloud Systems. In Computer Networks (CN 2019); Communications in Computer and Information Science; Springer International Publishing AG: Cham, Switzerland, 2019; pp. 178–190. [Google Scholar] [CrossRef]
- Kulesza, R.; Sousa, M.; Araújo, M.; Araújo, C.; Filho, A. Evolution of Web Systems Architectures: A Roadmap. In Special Topics in Multimedia, IoT and Web Technologies; Springer International Publishing: Cham, Switzerland, 2020; pp. 3–21. [Google Scholar] [CrossRef]
- Walid, B.; Kloul, L. Formal Models for Safety and Performance Analysis of a Data Center System. Reliab. Eng. Syst. Saf. 2019, 193, 106643. [Google Scholar] [CrossRef]
- Kounev, S.; Buchmann, A. Performance Modelling of Distributed E-business Applications Using Queuing Petri Nets. In Proceedings of the 2003 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS 2003), Austin, TX, USA, 6–8 March 2003; pp. 143–155. [Google Scholar] [CrossRef]
- Doc, V.; Nguyen, T.B.; Huynh Quyet, T. Formal Transformation from UML Sequence Diagrams to Queueing Petri Nets. In Advancing Technology Industrialization Through Intelligent Software Methodologies, Tools and Techniques; IOS Press: Amsterdam, The Netherlands, 2019; pp. 588–601. [Google Scholar] [CrossRef]
- Krajewska, A. Performance Modeling of Database Systems: A Survey. J. Telecommun. Inf. Technol. 2019, 8, 37–45. [Google Scholar] [CrossRef]
- Menascé, D.A.; Bardhan, S. TDQN: Trace-driven analytic queuing network modeling of computer systems. J. Syst. Softw. 2019, 147, 162–171. [Google Scholar] [CrossRef]
- Pant, A. Design and Investigation of a Web Application Environment With Bounded Response Time. Int. J. Latest Trends Eng. Technol. 2019, 14, 31–33. [Google Scholar] [CrossRef]

| Client Think | Two Classes of | One Class of | Measured | Error for One | Error for Two |
|---|---|---|---|---|---|
| Time [ms] | Clients [ms] | Clients [ms] [4] | [ms] [2] | Class of Clients [%] | Class of Clients [%] |
| 66.66 | 76.46 | 56.23 | 65.12 | 17.41 | 13.65 |
| 33.33 | 110.32 | 76.78 | 85.28 | 29.36 | 9.96 |
| 22.22 | 121.23 | 99.38 | 110.83 | 9.38 | 10.34 |
| 16.67 | 126.59 | 109.76 | 120.94 | 4.68 | 9.25 |
| Sub-FE.FE_CPU | Sub-FE.FE_CPU | BE | Sub-BE.BE_IO | Sub-BE.BE_IO | ||
|---|---|---|---|---|---|---|
| (qplace:queue) | (qplace:depository) | (place) | (qplace:queue) | (qplace:depository) | ||
| BE1 | FE1 | 5.12 | 0.00 | 290.58 | 5.35 | 0.00 |
| BE1 | FE3 | 0.28 | 0.23 | 294.46 | 5.34 | 0.00 |
| BE1 | FE6 | 0.47 | 0.69 | 293.76 | 5.33 | 0.00 |
| BE1 | FE9 | 0.68 | 1.26 | 294.25 | 5.34 | 0.00 |
| BE1 | FE12 | 0.89 | 1.90 | 294.06 | 5.34 | 0.00 |
| 2.5 BE3 | FE1 | 162.69 | 0.00 | 0.00 | 0.67 | 0.35 |
| BE3 | FE3 | 0.49 | 0.39 | 82.27 | 3.47 | 2.05 |
| BE3 | FE6 | 0.50 | 0.74 | 82.14 | 3.48 | 2.03 |
| BE3 | FE9 | 0.69 | 1.14 | 82.25 | 3.47 | 2.05 |
| BE3 | FE12 | 0.90 | 1.91 | 82.20 | 3.48 | 2.04 |
| BE6 | FE1 | 162.41 | 0.00 | 0.00 | 0.86 | 1.25 |
| BE6 | FE3 | 36.04 | 22.19 | 13.47 | 2.78 | 3.03 |
| BE6 | FE6 | 0.63 | 0.90 | 32.58 | 2.79 | 2.99 |
| BE6 | FE9 | 0.74 | 1.36 | 32.59 | 2.40 | 3.04 |
| BE6 | FE12 | 0.92 | 1.96 | 32.37 | 2.79 | 3.02 |
| BE9 | FE1 | 162.45 | 0.00 | 0.00 | 1.22 | 2.23 |
| BE9 | FE3 | 59.90 | 34.71 | 0.06 | 1.97 | 3.26 |
| BE9 | FE6 | 0.83 | 18.36 | 17.19 | 2.72 | 3.99 |
| BE9 | FE9 | 0.81 | 1.48 | 17.03 | 2.72 | 3.99 |
| BE9 | FE12 | 0.96 | 2.03 | 17.11 | 2.72 | 3.97 |
| BE12 | FE1 | 162.28 | 0.00 | 0.00 | 1.61 | 3.38 |
| BE12 | FE3 | 60.35 | 34.44 | 0.03 | 2.04 | 4.08 |
| BE12 | FE6 | 1.10 | 1.51 | 10.27 | 2.79 | 4.95 |
| BE12 | FE9 | 1.98 | 1.59 | 10.45 | 2.79 | 4.96 |
| BE12 | FE12 | 1.00 | 2.09 | 10.39 | 2.79 | 4.95 |
| Sub-FE.FE_CPU | Sub-FE.FE_CPU | Sub-BE.BE_IO | Sub-BE.BE_IO | ||
|---|---|---|---|---|---|
| (qplace:queue) | (qplace:depository) | (qplace:queue) | (qplace:depository) | ||
| BE1 | FE1 | 5.52 | 0.00 | 294.17 | 0.00 |
| BE1 | FE3 | 0.28 | 0.23 | 299.92 | 0.00 |
| BE1 | FE6 | 0.47 | 0.69 | 300.20 | 0.00 |
| BE1 | FE9 | 0.68 | 1.26 | 299.06 | 0.00 |
| BE1 | FE12 | 0.89 | 1.90 | 299.02 | 0.00 |
| BE3 | FE1 | 162.76 | 0.00 | 0.67 | 0.36 |
| BE3 | FE3 | 0.53 | 0.42 | 150.47 | 82.24 |
| BE3 | FE6 | 0.51 | 0.74 | 150.26 | 82.56 |
| BE3 | FE9 | 0.69 | 1.14 | 148.54 | 84.06 |
| BE3 | FE12 | 0.90 | 1.91 | 150.24 | 82.03 |
| BE6 | FE1 | 162.22 | 0.00 | 0.86 | 1.25 |
| BE6 | FE3 | 59.30 | 33.20 | 3.93 | 4.81 |
| BE6 | FE6 | 0.75 | 1.06 | 65.32 | 68.05 |
| BE6 | FE9 | 0.78 | 1.43 | 65.78 | 67.71 |
| BE6 | FE12 | 0.95 | 2.00 | 65.25 | 68.32 |
| BE9 | FE1 | 162.27 | 0.00 | 1.22 | 2.24 |
| BE9 | FE3 | 59.87 | 34.84 | 2.02 | 3.43 |
| BE9 | FE6 | 1.83 | 2.50 | 16.24 | 24.62 |
| BE9 | FE9 | 0.99 | 1.78 | 16.96 | 26.47 |
| BE9 | FE12 | 1.05 | 2.20 | 16.93 | 26.20 |
| BE12 | FE1 | 162.45 | 0.00 | 1.61 | 3.37 |
| BE12 | FE3 | 60.20 | 34.66 | 2.05 | 4.16 |
| BE12 | FE6 | 2.98 | 4.01 | 5.01 | 9.11 |
| BE12 | FE9 | 1.10 | 1.96 | 5.06 | 9.32 |
| BE12 | FE12 | 1.10 | 2.30 | 4.95 | 9.30 |
| BE1 | FE1 | 5.12 | 5.52 | 0.00 | 0.00 | 290.58 | 0.00 | 5.35 | 294.17 | 0.00 | 0.00 |
| BE1 | FE3 | 0.28 | 0.28 | 0.23 | 0.23 | 294.46 | 0.00 | 5.34 | 299.92 | 0.00 | 0.00 |
| BE1 | FE6 | 0.47 | 0.47 | 0.69 | 0.69 | 293.76 | 0.00 | 5.33 | 300.20 | 0.00 | 0.00 |
| BE1 | FE9 | 0.68 | 0.68 | 1.26 | 1.26 | 294.25 | 0.00 | 5.34 | 299.06 | 0.00 | 0.00 |
| BE1 | FE12 | 0.89 | 0.89 | 1.90 | 1.90 | 294.06 | 0.00 | 5.34 | 299.02 | 0.00 | 0.00 |
| BE3 | FE1 | 162.69 | 162.76 | 0.00 | 0.00 | 0.00 | 0.00 | 0.67 | 0.67 | 0.35 | 0.36 |
| BE3 | FE3 | 0.49 | 0.53 | 0.39 | 0.42 | 82.27 | 0.00 | 3.47 | 150.47 | 2.05 | 82.24 |
| BE3 | FE6 | 0.50 | 0.51 | 0.74 | 0.74 | 82.14 | 0.00 | 3.48 | 150.26 | 2.03 | 82.56 |
| BE3 | FE9 | 0.69 | 0.69 | 1.14 | 1.14 | 82.25 | 0.00 | 3.47 | 148.54 | 2.05 | 84.06 |
| BE3 | FE12 | 0.90 | 0.90 | 1.91 | 1.91 | 82.20 | 0.00 | 3.48 | 150.24 | 2.04 | 82.03 |
| BE6 | FE1 | 162.41 | 162.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.86 | 0.86 | 1.25 | 1.25 |
| BE6 | FE3 | 36.04 | 59.30 | 22.19 | 33.20 | 13.47 | 0.00 | 2.78 | 3.93 | 3.03 | 4.81 |
| BE6 | FE6 | 0.63 | 0.75 | 0.90 | 1.06 | 32.58 | 0.00 | 2.79 | 65.32 | 2.99 | 68.05 |
| BE6 | FE9 | 0.74 | 0.78 | 1.36 | 1.43 | 32.59 | 0.00 | 2.78 | 65.78 | 3.04 | 67.71 |
| BE6 | FE12 | 0.92 | 0.95 | 1.96 | 2.00 | 32.37 | 0.00 | 2.79 | 65.25 | 3.02 | 68.32 |
| BE9 | FE1 | 162.45 | 162.27 | 0.00 | 0.00 | 0.00 | 0.00 | 1.22 | 1.22 | 2.23 | 2.24 |
| BE9 | FE3 | 59.90 | 59.87 | 34.71 | 34.84 | 0.06 | 0.00 | 1.97 | 2.02 | 3.26 | 3.43 |
| BE9 | FE6 | 0.83 | 1.83 | 18.36 | 2.50 | 17.19 | 0.00 | 2.72 | 16.24 | 3.99 | 24.62 |
| BE9 | FE9 | 0.81 | 0.99 | 1.48 | 1.78 | 17.26 | 0.00 | 2.72 | 16.96 | 3.99 | 26.47 |
| BE9 | FE12 | 0.96 | 1.05 | 2.03 | 2.20 | 17.11 | 0.00 | 2.72 | 16.93 | 3.97 | 26.20 |
| BE12 | FE1 | 162.28 | 162.45 | 0.00 | 0.00 | 0.00 | 0.00 | 1.61 | 1.61 | 3.38 | 3.37 |
| BE12 | FE3 | 60.35 | 60.20 | 34.44 | 34.66 | 0.03 | 0.00 | 2.04 | 2.05 | 4.08 | 4.16 |
| BE12 | FE6 | 1.10 | 2.98 | 1.51 | 4.01 | 10.27 | 0.00 | 2.79 | 5.01 | 4.95 | 9.11 |
| BE12 | FE9 | 1.98 | 1.10 | 1.59 | 1.96 | 10.45 | 0.00 | 2.79 | 5.06 | 4.96 | 9.32 |
| BE12 | FE12 | 1.00 | 1.10 | 2.09 | 2.30 | 10.39 | 0.00 | 2.79 | 4.95 | 4.95 | 9.30 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rak, T. Modeling Web Client and System Behavior. Information 2020, 11, 337. https://doi.org/10.3390/info11060337
Rak T. Modeling Web Client and System Behavior. Information. 2020; 11(6):337. https://doi.org/10.3390/info11060337
Chicago/Turabian StyleRak, Tomasz. 2020. "Modeling Web Client and System Behavior" Information 11, no. 6: 337. https://doi.org/10.3390/info11060337
APA StyleRak, T. (2020). Modeling Web Client and System Behavior. Information, 11(6), 337. https://doi.org/10.3390/info11060337





