1. Introduction
Gaussian and Laplacian pyramids allow images to be viewed, stored, analyzed, and compressed at different levels of resolution, thus minimizing browsing time, required storage capacity, and required transmission capacity, in addition to facilitating comparisons of images across levels of detail [
1,
2,
3]. Different resolution pyramids play a major role in image and speech recognition in machine learning and deep learning [
4,
5].
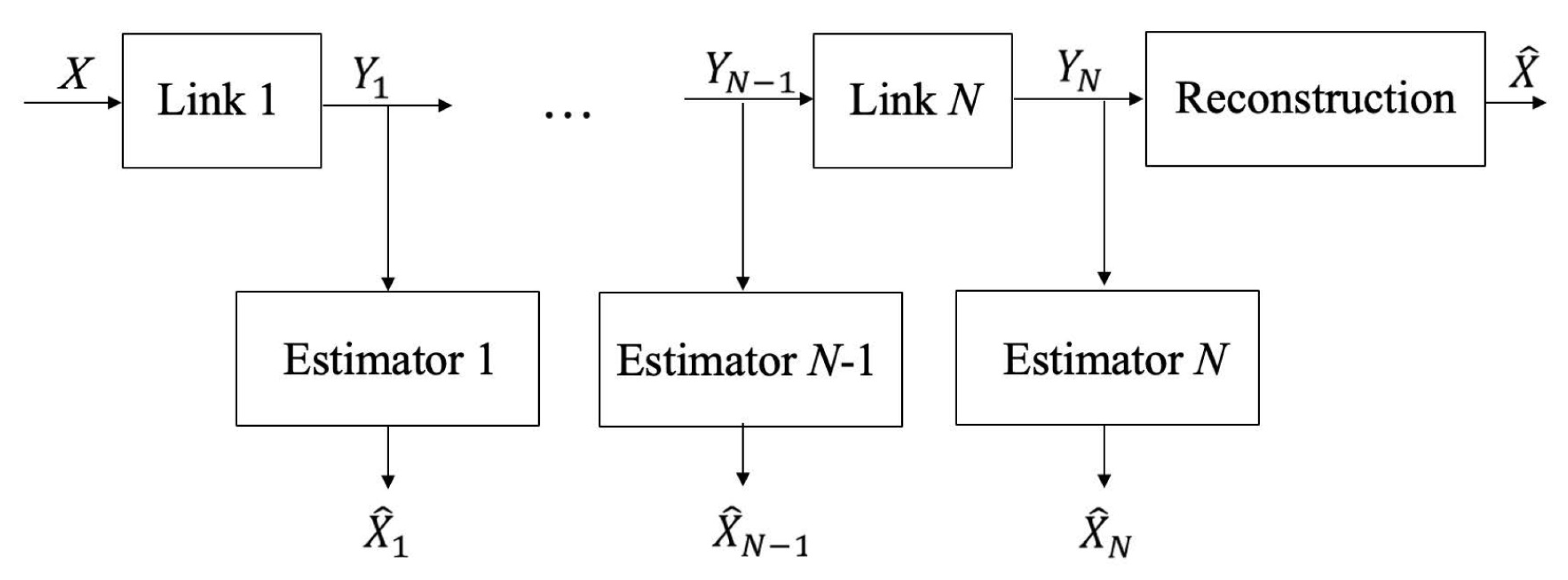
The formation of Gaussian and Laplacian pyramids requires the signal processing steps of filtering/averaging, decimation and interpolation. Interestingly, the filters and the interpolation steps are usually left unspecified, and in applications such as image storage and compression, the performance of the various steps in the Gaussian pyramid is primarily based on mean squared error. The cascade of signal processing steps performed in obtaining a Gaussian pyramid forms a Markov chain, and as such, satisfies the Data Processing Inequality from information theory. Based on this fact, we utilize the quantity entropy rate power from information theory and introduce a new performance indicator, the log ratio of entropy powers, to characterize the loss in mutual information at each signal processing stage in forming the Gaussian pyramid.
In particular, we show that the log of the ratio of entropy powers between two signal processing steps is equivalent to the difference between the differential entropy of the two stages and equal to twice the difference in the mutual information between the two stages. However, in order to calculate the entropy power, we need an expression for the differential entropy, but the accurate computation of the differential entropy can be quite difficult and requires considerable care [
6].
We show that for i.i.d. Gaussian and Laplacian distributions, and note that for logistic, uniform, and triangular distributions, the mean squared estimation error can replace the entropy power in the log ratio of entropy power expression [
7]. As a result, the log ratio of entropy power and the difference in differential entropies and mutual informations can be much more easily calculated.
Note that the mean squared error and the entropy power are only equal when the distribution is Gaussian, and that the entropy power is the smallest variance possible for a random variable with the same differential entropy. However, if the distributions in the log ratio of the entropy powers are the same, then the constant multiplier of the mean squared error in the expressions for entropy power will cancel out and only the mean squared errors are needed in the ratio. We also note that for the Cauchy distribution, which has an undefined variance, the log ratio of entropy powers equals the log ratio of the squared Cauchy distribution parameters.
The concept of entropy power and entropy rate power are reviewed in
Section 2.
Section 3 sets up the basic cascade signal processing problem being analyzed, the well known inequalities for mutual information in the signal processing chain are stated, and the inequalities that follow from the results in
Section 2 are given. The log ratio of entropy powers is developed in
Section 4, explicitly stating its relationship to the changes in mutual information as a signal progresses through the signal processing chain, and wherein a discussion of calculating entropy power and log ratio of entropy powers is presented.
Section 5 provides results using the log ratio of entropy powers to characterize the mutual information loss in bits/pixel for Gaussian and Laplacian image pyramids. In
Section 6 we compare log ratio of entropy powers to a direct calculation of the difference in mutual information.
Section 7 contains a discussion of the results and conclusions.
This paper is an expansion and extension of the conference paper presented in 2019 [
8] with expanded details of the examples and more extensive analyses of the results.
4. Log Ratio of Entropy Powers
We can use the definition of the entropy power in Equation (
3) to express the logarithm of the ratio of two entropy powers in terms of their respective differential entropies as
We can write a conditional version of Equation (
3) as
and from which we can express Equation (
10) in terms of the entropy powers at successive stages in the signal processing chain as
If we add and subtract
to the right hand side of Equation (
12), we then obtain an expression in terms of the difference in mutual information between the two stages as
From the series of inequalities on the entropy power in Equation (
8), we know that both expressions in Equations (
12) and (
13) are greater than or equal to zero.
These results are from [
13] and extend the Data Processing Inequality by providing a new characterization of the information loss between stages in terms of the entropy powers of the two stages. Since differential entropies are difficult to calculate, it would be particularly useful if we could obtain expressions for the entropy power at two stages and then use Equations (
12) and (
13) to find the difference in differential entropy and mutual information between these stages.
More explicitly, we are interested in studying the change in the differential entropy brought on by different signal processing operations by investigating the log ratio of entropy powers. However, in order to calculate the entropy power, we need an expression for the differential entropy! Thus, why do we need the entropy power?
First, entropy power may be easy to calculate in some instances, as we show later. Second, the accurate computation of the differential entropy can be quite difficult and requires considerable care [
6,
14]. Generally, the approach is to estimate the probability density function (pdf) and then use the resulting estimate of the pdf in Equation (
1) and numerically evaluate the integral.
Depending on the method used to estimate the probability density, the operation requires selecting bin widths, a window, or a suitable kernel [
6], all of which must be done iteratively to determine when the estimate is sufficiently accurate. The mutual information is another quantity of interest, as we shall see, and the estimate of mutual information also requires multiple steps and approximations [
14,
15,
16]. These statements are particularly true when the signals are not i.i.d. and have unknown correlation.
In the following we highlight several cases where Equation (
10) holds with equality when the entropy powers are replaced by the corresponding variances. The Gaussian and Laplacian distributions often appear in studies of speech processing and other signal processing applications [
17,
18,
19], so we show that substituting the variances for entropy powers in the log ratio of entropy powers for these distributions satisfies Equations (
10), (
12), and (
13) exactly.
Interestingly, using mean squared errors or variances in Equation (
10) is accurate for many other distributions as well. It is straightforward to show that Equation (
10) holds with equality when the entropy powers are replaced by mean squared error for the logistic, uniform, and triangular distributions as well. Further, the entropy powers can be replaced by the ratio of the squared parameters for the Cauchy distribution.
Therefore, the satisfaction of Equation (
10) with equality occurs not just in one or two special cases. The key points are first that the entropy power is the smallest variance that can be associated with a given differential entropy, so the entropy power is some fraction of the mean squared error for a given differential entropy. Second Equation (
10) utilizes the ratio of two entropy powers, and thus, if the distributions corresponding to the entropy powers in the ratio are the same, the scaling constant (fraction) multiplying the two variances cancels out. So, we are not saying that the mean squared errors equal the entropy powers in any case but for Gaussian distributions.
It is the new quantity, the log ratio of entropy powers that enables the use of the mean squared error to calculate the loss in mutual information at each stage [
13].
6. Comparison to Direct Calculation
Table 1,
Table 2,
Table 3 and
Table 4 also show the difference in mutual information
, where the mutual informations are determined by estimating the probability density functions needed using histograms of the image pixels and then using these results in the standard expression for the mutual information as if the pixels were i.i.d. Since the images certainly have spatial correlations, this is clearly just an approximation.
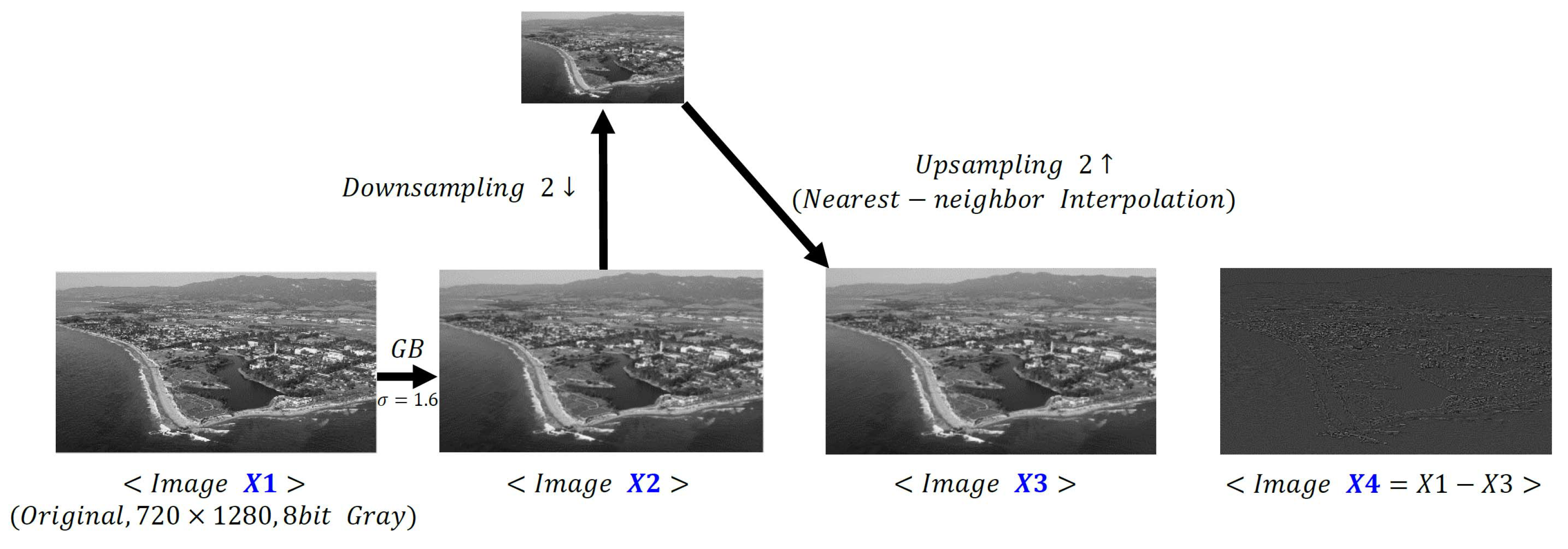
In any event, the quantity is 0.2006, 0.2077, 0.2667, and 0.1462 bits/pixel for the City, News1, News2, and Campus images (720 × 1280 resolution), respectively. Comparing to the loss in mutual information obtained from the expression , we see that the two quantities agree well for the City image and are close for the Campus image, but are significantly different for News1 and News2. It is thus of interest to investigate these differences further.
Specifically, we compare
with
to determine when Equation (
13) is satisfied with equality, viz, when
In
Table 5, we tabulate a normalized comparison between
and
, when normalized by the latter. From
Table 5, we see that for the 720 × 1280 City image, Equation (
16) is satisfied with near equality, less than 1% error, and for the Campus image, the one half log ratio of entropy powers is within 12% of the difference in the mutual information between the two stages. For the 720 × 1280 News1 this discrepancy is 38.3% and for News2 the difference is 24%. These trends are fairly similar across all three resolutions.
Since we know that the one-half the log ratio of entropy powers equals one half the log ratio of mean squared errors when the distributions of the two quantities being compared are the same for i.i.d. Gaussian, Laplacian, Logistic, triangular, and uniform distributions, we are led to investigate the histograms of the four images to analyze these discrepancies. For the Gaussian and Laplacian distributions, we conducted Kolmogorov-Smirnov (K-S) goodness-of-fit tests for the four original images at all three resolutions. The results are shown in
Figure 6,
Figure 7,
Figure 8 and
Figure 9.
The K-S statistic that we use is the distance of the cumulative distribution function from the hypothesized distribution given by
where
is the distribution being tested, after correction for mean and variance, and
is the distribution being hypothesized. For this measure, a smaller value indicates a better match to the hypothesis.
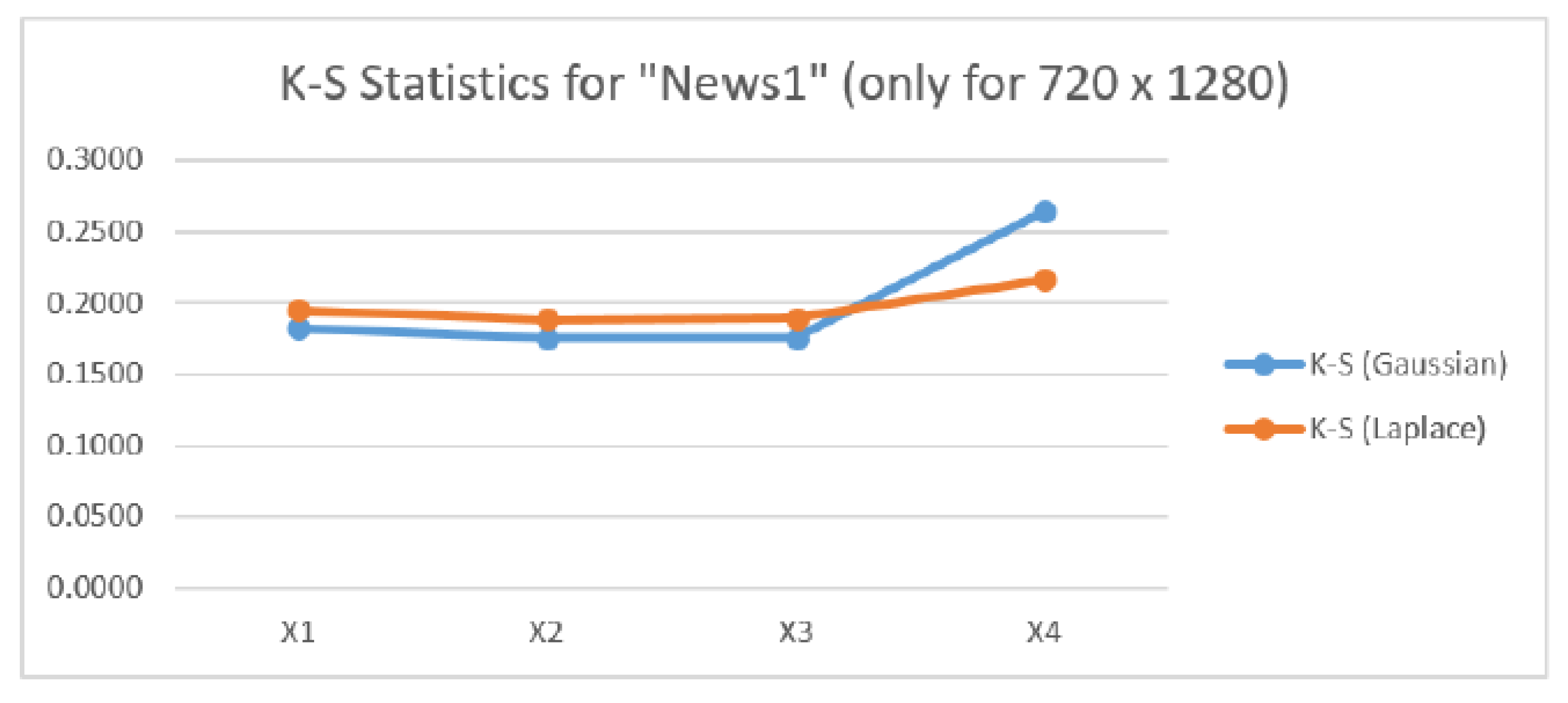
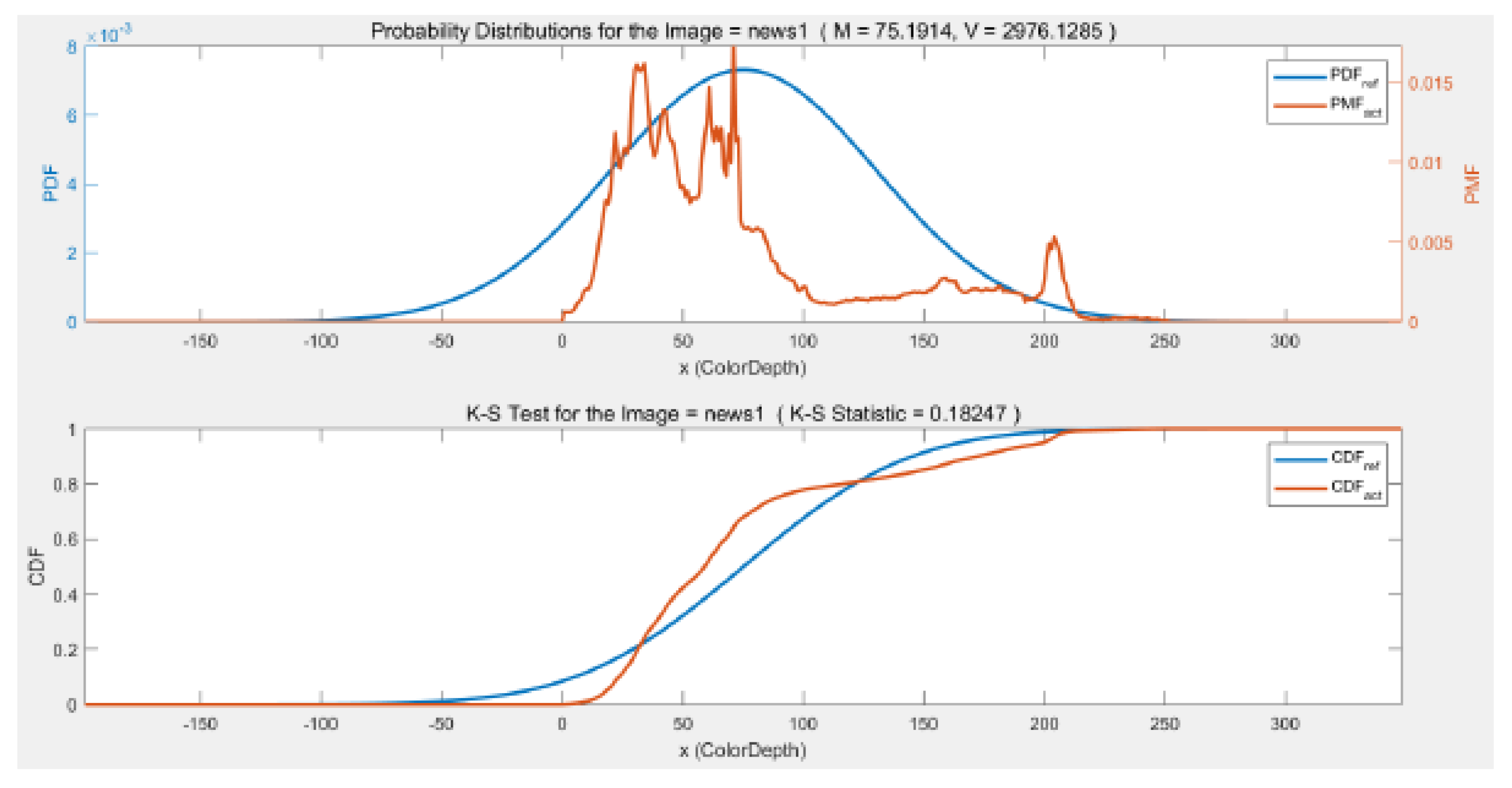
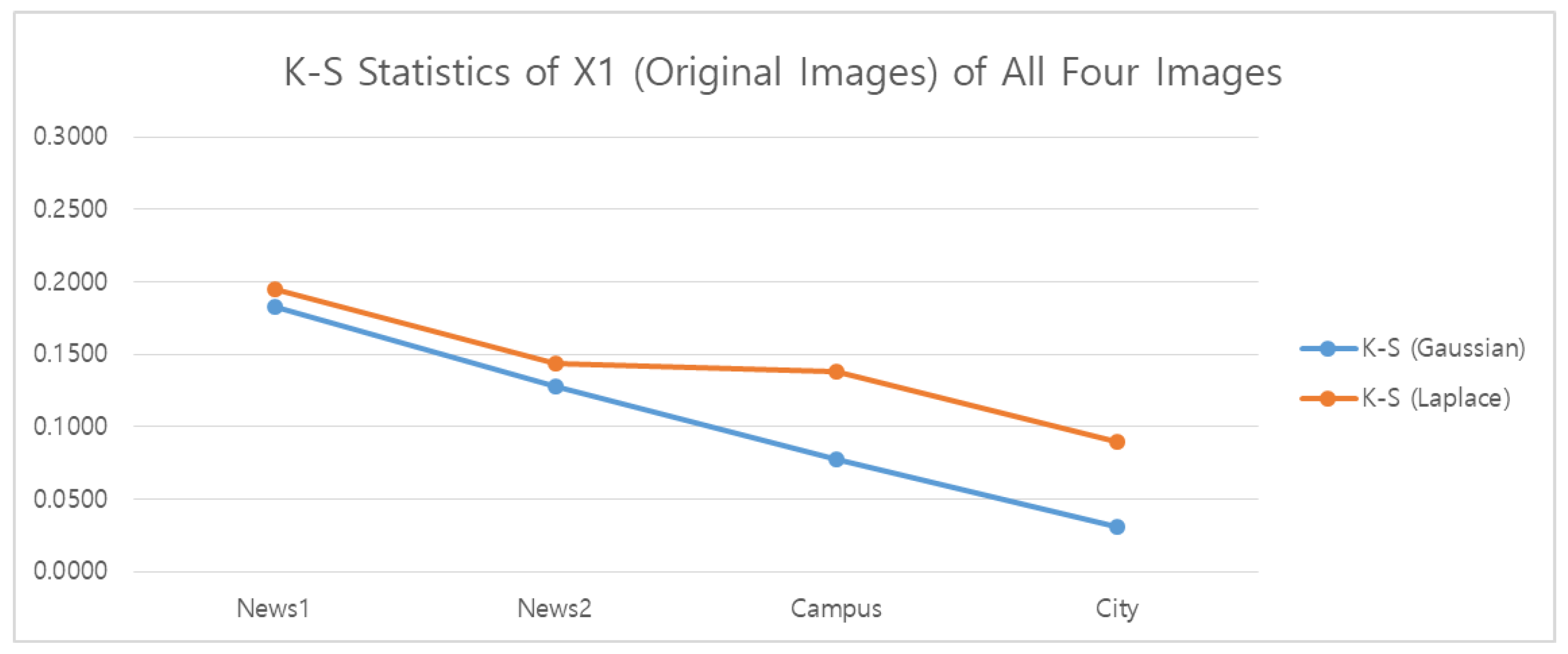
For the News1 image results in
Figure 6, the K-S statistic values are nearly the same for the Gaussian Pyramid for all three resolutions, but for the Laplacian Pyramid difference image the K-S statistic for a Gaussian distribution increases and becomes larger than the K-S value for a Laplacian distribution, suggesting that the difference image is more Laplacian than Gaussian. For the News2 image results in
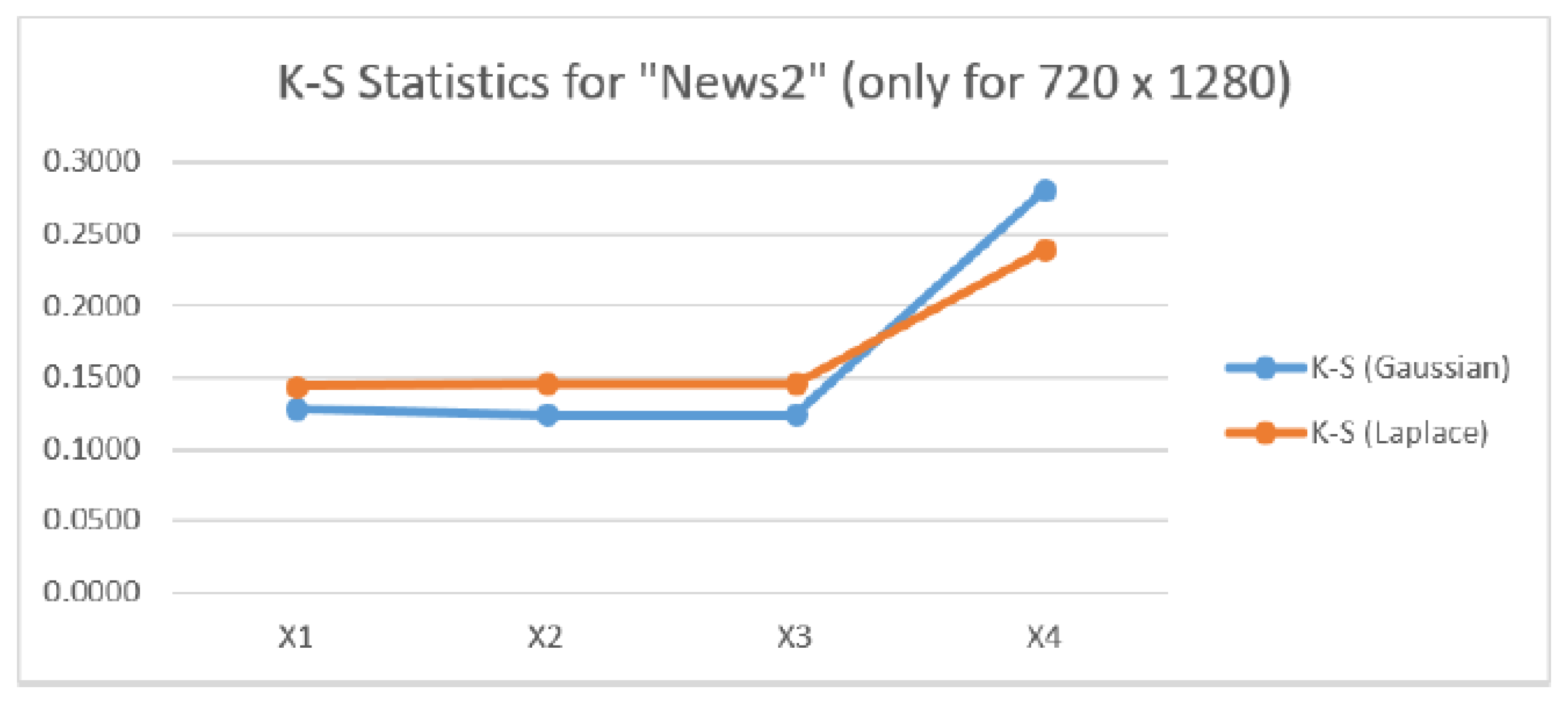
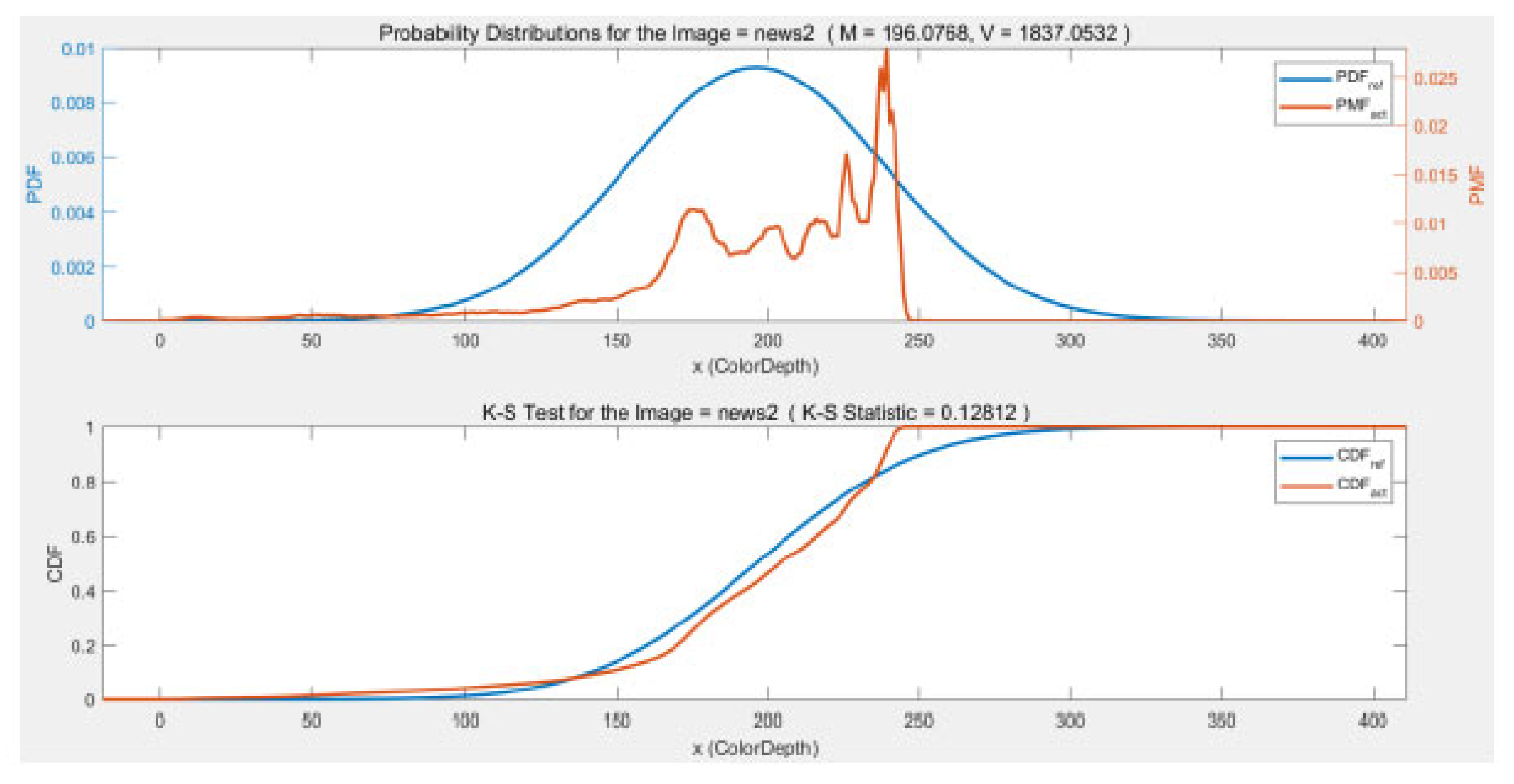
Figure 7, the behavior is similar although the K-S statistic for both the Gaussian and Laplacian distribution increase substantially for the difference image, and that the values of the K-S statistics in
Figure 7 for the Gaussian pyramid are smaller than for News1 but the K-S values are very nearly the same as News1 for the difference image.
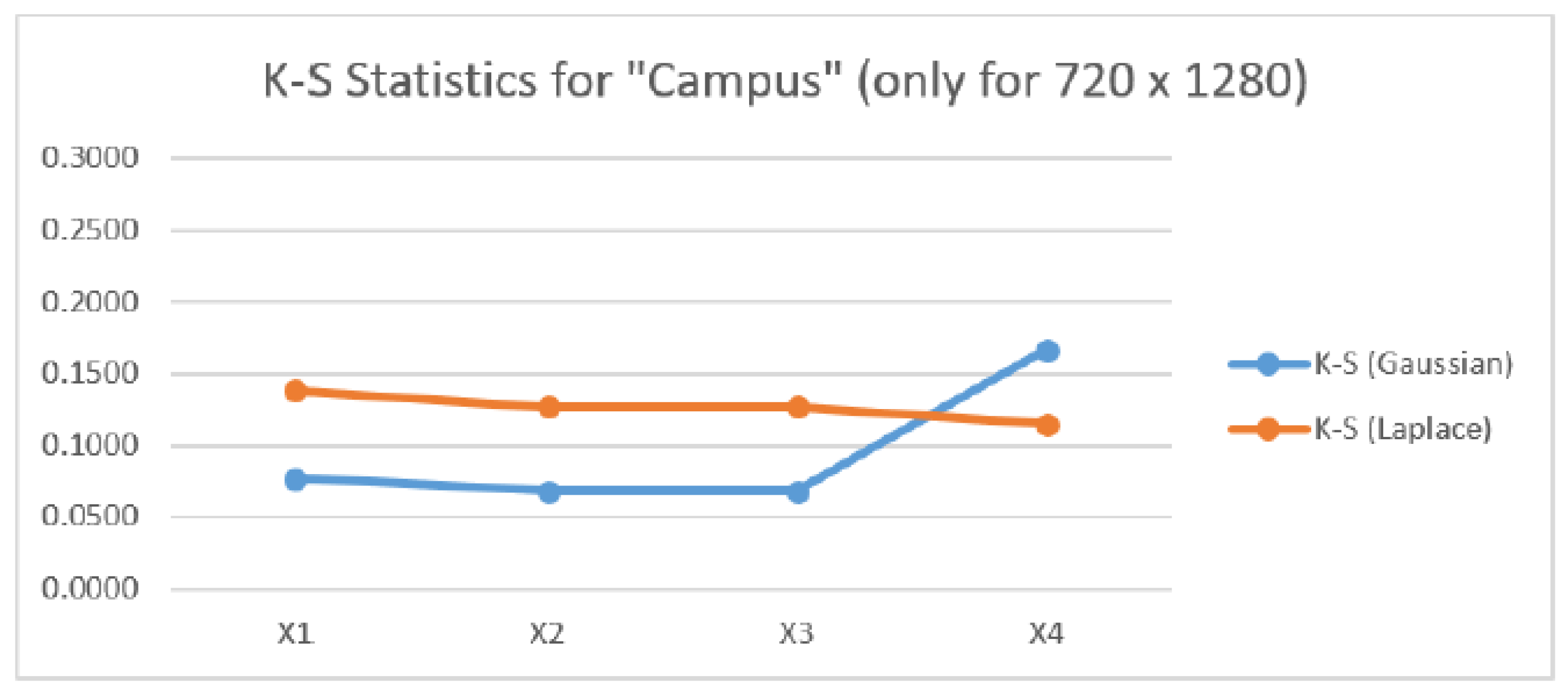
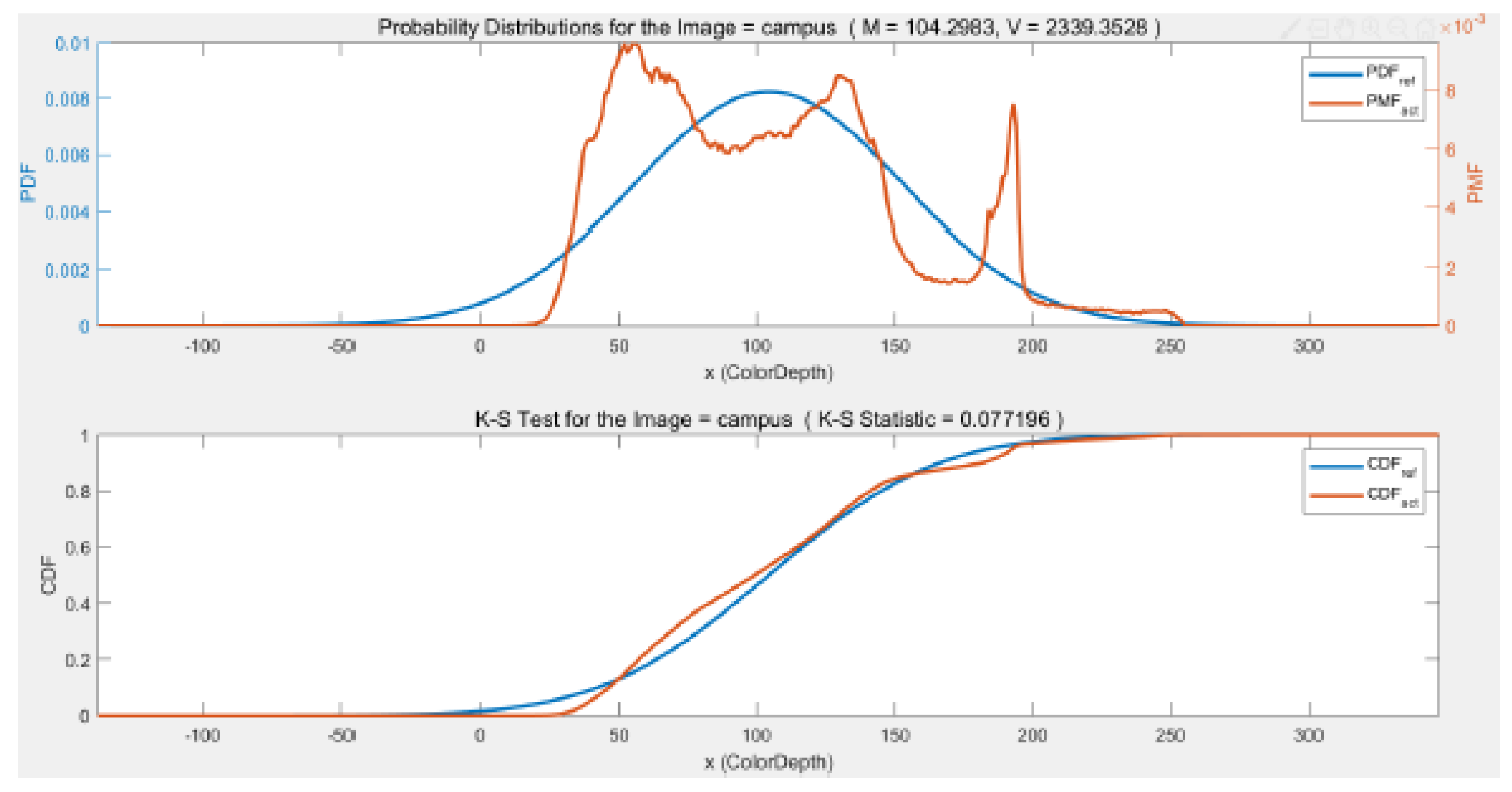
The characteristics of the K-S test values start to change when it comes to the Campus and City images as shown in
Figure 8 and
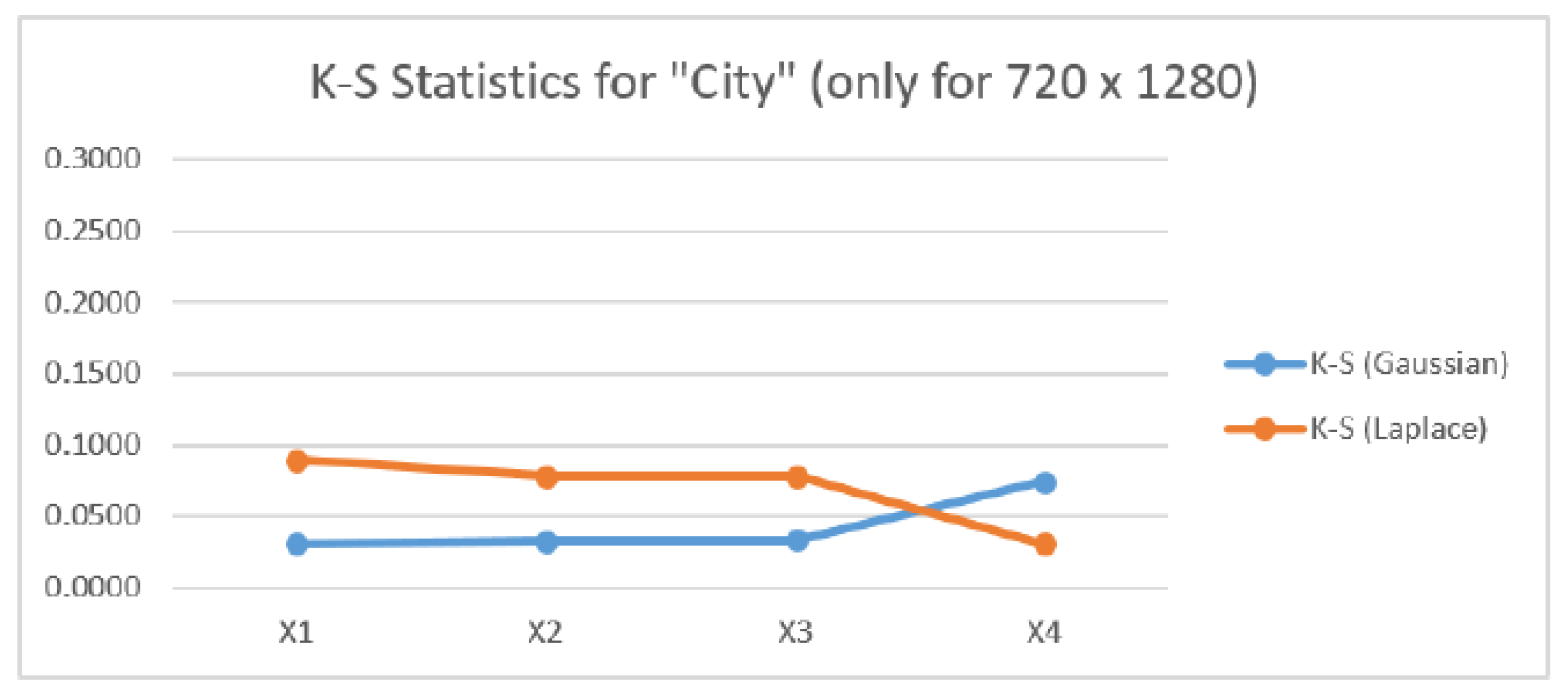
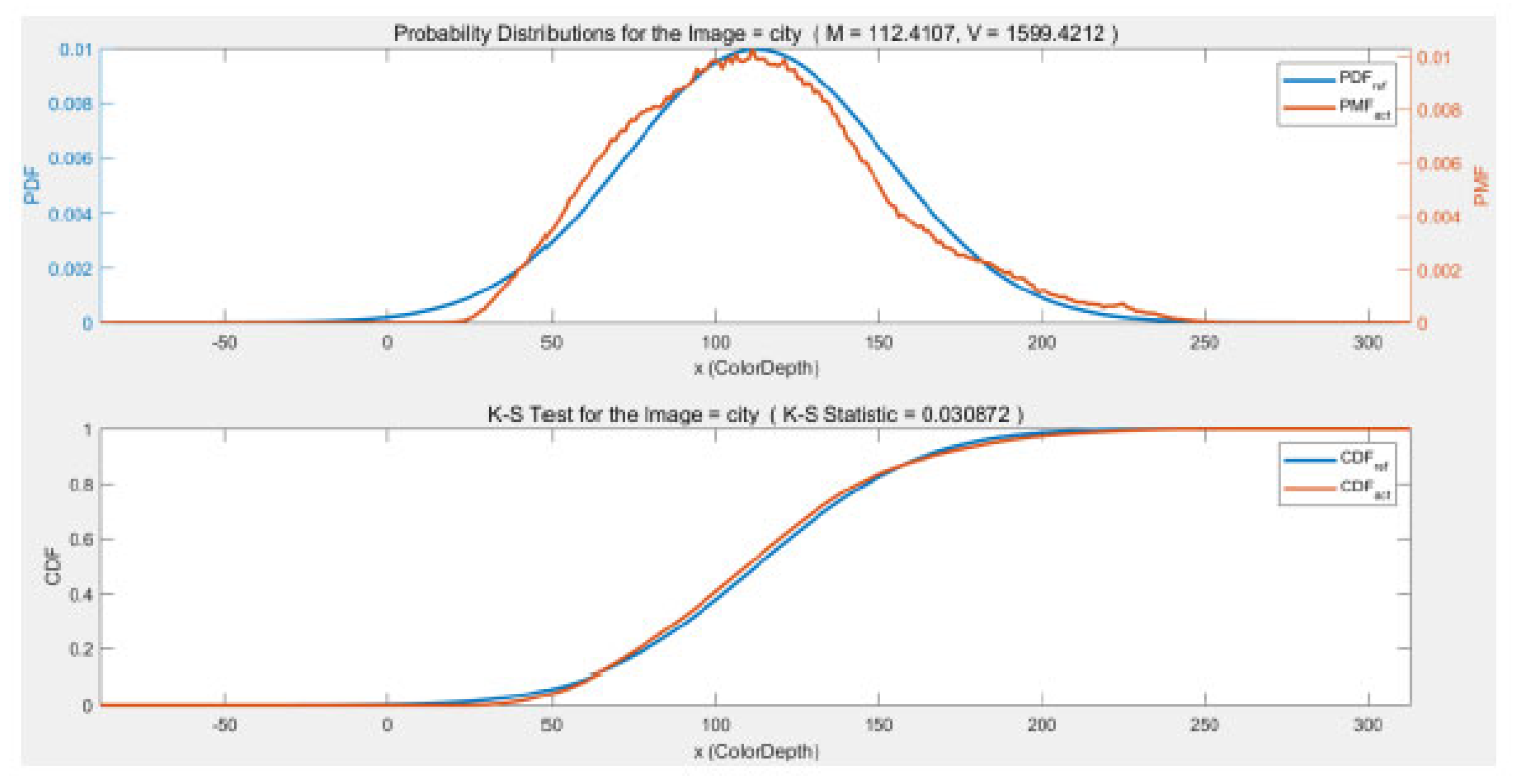
Figure 9. The magnitude of the K-S test statistic drops for the Gaussian distribution for the Campus image and is significantly lower for the Gaussian pyramid resolutions than the Laplacian K-S statistic. Indicating that the Campus image is more Gaussian than Laplacian. For the difference image, the K-S statistic for the Gaussian distribution increases and is larger than the K-S statistic for the Laplacian distribution. For the City image results in
Figure 9, the K-S statistics for both the Gaussian and Laplacian distributions become smaller and the K-S statistic for the Gaussian pyramid images indicates that these images have a Gaussian distribution. For the difference image, again the K-S statistics for the Gaussian and Laplacian distributions change places with the K-S statistic suggesting that the difference image is more Laplacian than Gaussian.
Before applying these Kolmogorov-Smirnov goodness-of-fit test results to the analysis of
Table 5, it is perhaps instructive to show the histograms and cumulative distribution functions of the four original 720 by 1080 resolution images in relation to the Gaussian density and Gaussian cumulative distribution as shown in
Figure 10,
Figure 11,
Figure 12 and
Figure 13, for the four images. Visually it appears evident that News1 and News2 are not Gaussianly-distributed (nor Laplacian for that matter) and that the Campus image, while having multiple peaks in its histogram, has a more concentrated density that News1 and News1. The City image, however, appears remarkably Gaussian, at least visually.
Returning to an analysis of the results shown in
Table 5, we see that for the Gaussian pyramid, the accuracy of the approximation of the change in mutual information of the processing in going from Image
to
is best for the City image, which is as it should be since we know that the expression in Equation (
16) should hold exactly for a Gaussian distributed sequence. The accuracy of the approximation to Equation (
16) is progessively poorer for the Campus, News2, and News1 images in that order. More explicitly, for the Campus image, we see that it tests to be close to Gaussian, and so again the close approximation shown in the table is to be expected. Neither the News1 or News2 images test to be reliably Gaussian or Laplacian and so at least for these two distributions, the relatively poor agreement between the two quantities in the table is as to be expected.
We note that the approximation for the Laplacian pyramid is better in the reverse order to the Gaussian pyramid analyses just presented. These results are investigated further in the next section.
6.1. Laplacian Pyramid Analysis
Table 1 shows results for the difference images in the Laplacian pyramid for the City image. While the results are striking, as noted earlier, the differencing operation means that the Markov chain property and the data processing inequality are no longer satisfied. While the data processing inequality does not hold, Equations (
10), (
14), and (
15) can hold if the distributions in the ratio are the same.
The results in
Table 1 contrast comparing
to
in relation to a comparison between
and
using the quantity
. We see from the table for the City image that the Laplacian difference image formed by subtracting
from
has a loss of mutual information of 2.8 bits/pixel for the largest resolution and a loss of slightly greater than 3 bits/pixel for the smaller images. The same result for the News1 image in
Table 2 shows a loss of about 3.4 bits/pixel for the 720 × 1280 resolution. While one would expect the loss in going from
to the difference image
to entail a significant loss of information, here we have been able to quantify the loss in mutual information using an easily calculated quantity.
As shown in
Table 2 and
Table 4 for the other images studied, News2 and Campus,
reveals an information loss of about 5.1 bits/pixel and 2.9 bits/pixel, respectively, in the Laplacian Pyramid for the 720 × 1280 resolution.
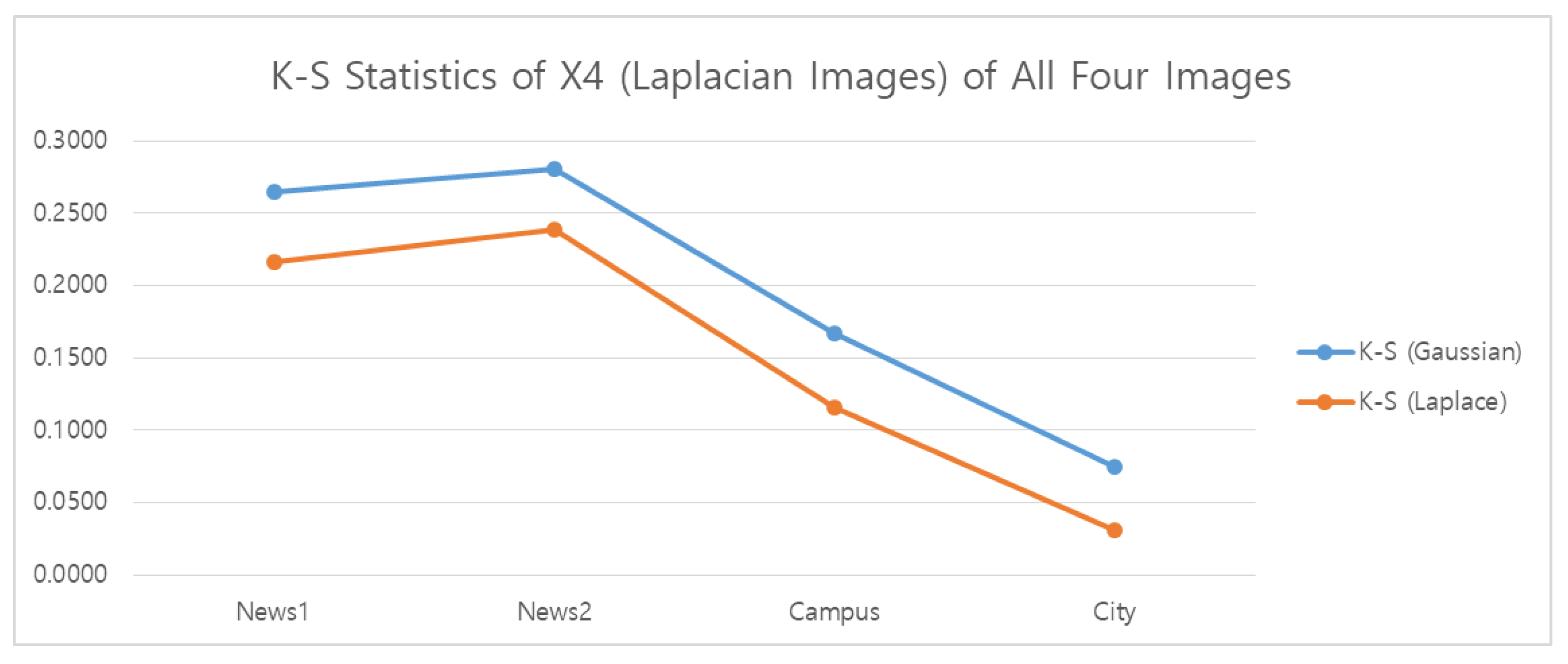
Intriguingly, the approximation accuracy for the Laplacian pyramid shown in
Table 5 is much better for the image News1 than for the other images, and the accuracy of the approximation for the Laplacian pyramid difference image for the City image is the poorest. To analyze this behavior, we consider the Gaussian and Laplacian K-S test results for the four original 720 by 1080 resolution images
in
Figure 14 and compare to the 720 by 1080 resolution Laplacian pyramid difference images
in
Figure 15.
The entropy powers in Equation (
13) can be replaced with the minimum mean squared estimation errors only if the distributions of
and
are the same. An inspection of
Figure 14 and
Figure 15 implies that this is not true. That is, we see from the K-S test results in
Figure 15 that while all of the difference images test to be more Laplacian than Gaussian, the difference image for the City image has the smallest K-S statistic of all the images for the Laplacian distribution hypothesis. At the same time, from
Figure 14, all of the four test images are closer to the Gaussian hypothesis distribution than the Laplacian, and the City image is the closest to a Gaussian distribution of them all. Hence, the poor approximations shown in
Table 5 provided by the log ratio expression for the City image (and also for the News2 and Campus images) can be explained by the differing distributions of
and
.
This analysis does not explain the very positive result shown for the Laplacian pyramid of News1 in
Table 5. We conjecture that this unexpected result, namely that the approximation in
Table 5 for the Laplacian pyramid is much better for the image News1 than for the other images, is the consequence of inherent correlation between the Laplacian pyramid image
for News1 and the original News1 image. We elaborate on this idea as follows. The comparisons in the approximation table, namely
Table 5, are with respect to the difference in mutual information between
and
and the mutual information between
and
. Generally, since
is a difference image, it is expected that the mutual information between
and
should be less than the mutual information between
and
. For the City image the differencing does not enhance the similarities between
and
, whereas for the News1 image the difference enhances the strong edges present. See
Figure 16. From these figures of the difference images, it is evident that all are correlated to some degree with the originals, but the correlation between
and
is considerably larger for the News1 image than for the City image and the other two images.
To further elaborate on the effect of the correlation, if
,
, and
are Gaussian (which for an i.i.d. assumption, they are not), a well known result yields that
which is in fact
. Thus, the fact that
is more correlated with
than
for the City image, makes the denominator of Equation (
18) smaller and the numerator larger, yielding the results shown in
Table 5. Whereas for the News1 image, the differencing enhances the correlation between
and
and thus reduces the numerator in Equation (
18).
A more detailed analysis of the mutual information loss in Laplacian pyramids is left for further study.