The research and development of rolling stock technology has made the running speed of trains continue to increase. At the same time, the requirements for the stability and comfort of the train are becoming more stringent. The lateral damper is one of the key components that affect the running performance of the train. The vibration can be effectively suppressed in the lateral direction of the train, and to ensure riding performance [
1]. In the course of use, the lateral damper will undergo a process of failure from normal to degradation, due to various internal and external factors. Different running states of rolling stock will show different data characteristics. The current maintenance method of lateral dampers is regular maintenance. As the running speed increases, the future development trend will inevitably be to carry out state maintenance to identify the health status of components. The establishment of the relationship between different states and signal data is what is missing from regular to state repair. The key to research is feature extraction and state recognition, and the problem is the identification of early degradation states. There is an urgent need to explore new feature extraction and feature selection methods to more effectively realize the health state recognition of lateral dampers. The faults of high-speed train systems and key components are often expressed in the form of various signals. Using appropriate feature analysis methods, the working status of components can be directly obtained from the signals to achieve the purpose of status recognition and fault diagnosis. Early signal analysis research focused on classic signal analysis methods. Traditional signal processing methods, such as spectrum analysis, Fourier analysis, envelope analysis, correlation analysis, and maximum entropy spectrum analysis, played a huge role in system and component state recognition. Li Tan [
2] adopted principal component analysis (PCA) and multi-fractal analysis method in order to analyze the vibration characteristics of trains during single failure and cross-mixing failure of key components of high-speed trains. Yu Y [
3] adopted empirical mode decomposition (EMD) and adaptive short-time Fourier transform (STFT) diagnosis method to diagnose the faults of railway freight rolling bearings. The results showed that the method could effectively obtain fault information in the time-frequency domain. Zeng Hua et al. [
4] used time-domain statistical methods to calculate the root mean square of the bogie vibration signal and analyzed the frequency response characteristics of the vibration transfer function between each position. Guo-Liang S. [
5] proposed a state estimation method of wavelet packet energy moment that was effective for accurately estimating different faults of high-speed train. When compared with other time domain and frequency domain analysis, the wavelet packet analysis method can effectively eliminate the interference of noise in the fault signal, and it has better sensitivity and stability to features. Therefore, this paper used wavelet packet analysis to extract the features of the fault signal.
Presently, a variety of state recognition methods have been developed in the field of fault state recognition, mainly divided into methods that are based on qualitative empirical knowledge, methods based on analytical models and methods based on data-driven. Lin S. [
6] used principal component analysis (PCA) and rough set-based fault identification method for train door fault identification. The comparison found that, although the PCA method can determine whether a fault has occurred, it cannot perform fault identification. Li Yong [
7] combined Hilbert transform and Berg spectrum estimation method to extract the time-frequency and spectrum characteristics of the fault current signal, and used the binary classification support vector machines as a high-impedance ground fault classifier for the traction network, which can effectively identify the fault type of the traction network, and obtain a high classification accuracy rate. Since the degree of performance degradation is gradual, it cannot be divided into several fixed fault types, so it is unreasonable to use a classifier, such as a support vector machine, to evaluate the degree of performance degradation. References [
8,
9] applied cross correlation analysis to transformer internal fault identification and bearing fault diagnosis, and achieved certain results. When compared with classification methods, such as support vector machines, cross-correlation analysis can effectively extract minor differences between signals, so it is suitable for early degraded signal feature analysis.
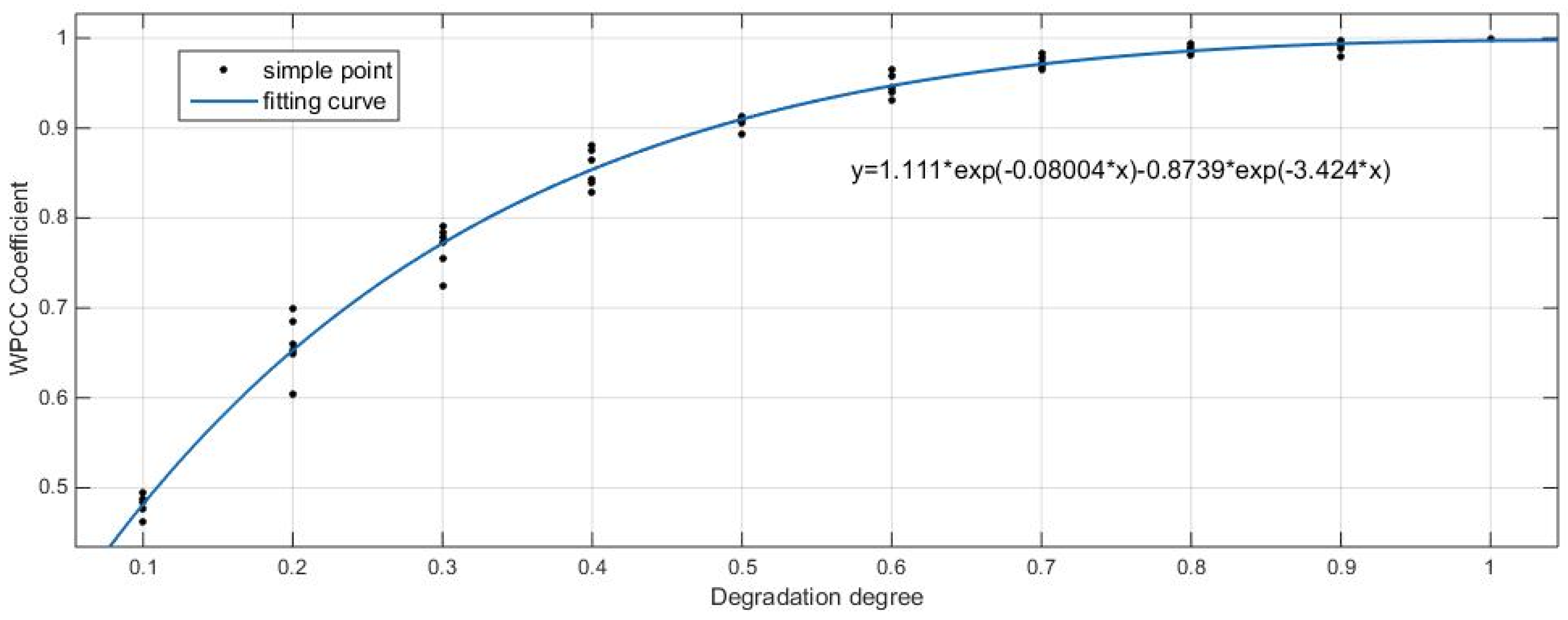
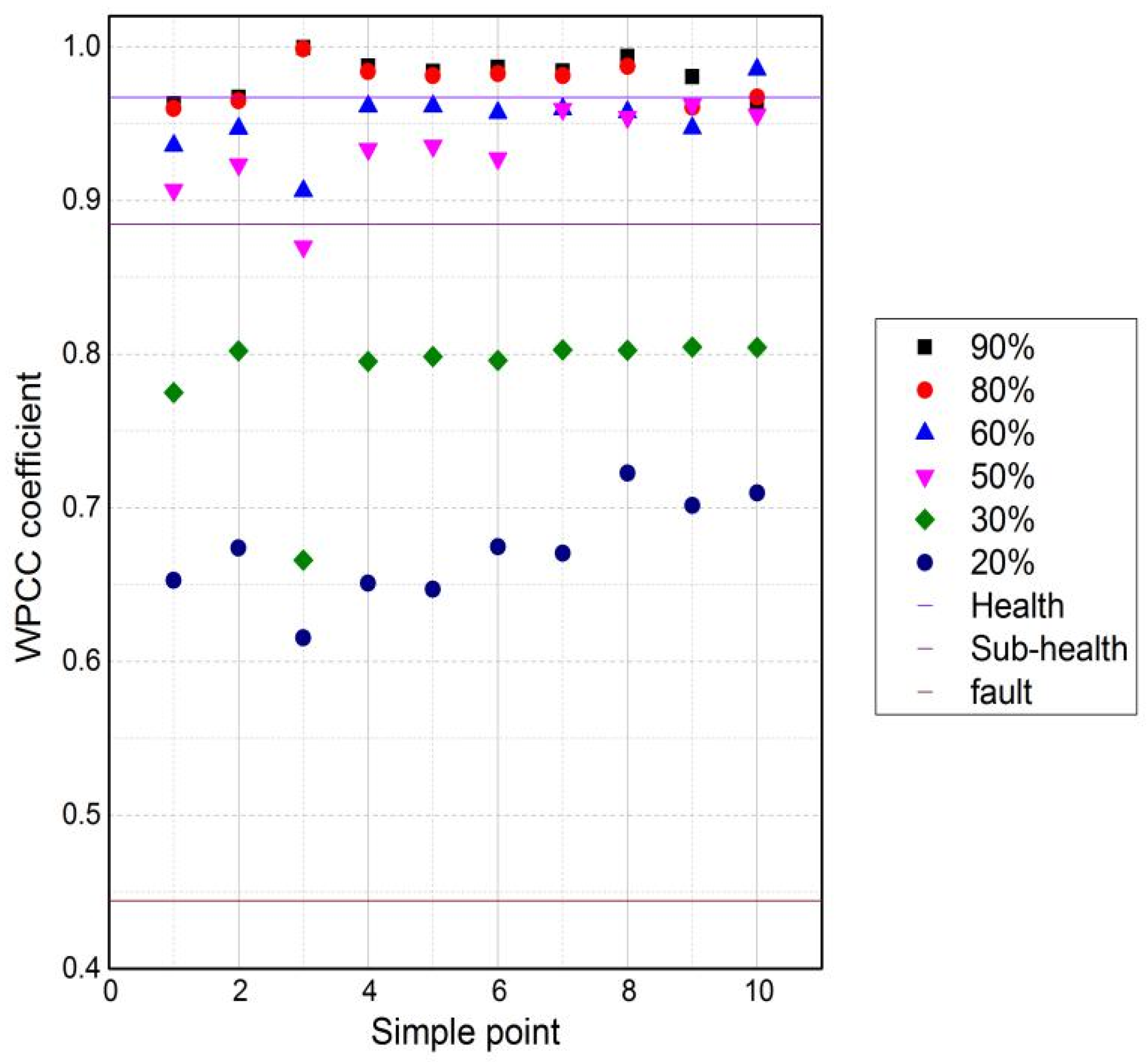
Most of the existing researches on the fault diagnosis of train parts are to identify the failure status of the components. There is no in-depth analysis on the identification of the early degradation of the components. In this paper, a high-speed train lateral damper was used as an example, and a feature analysis method of wavelet packet cross-correlation analysis was proposed in order to identify the early degradation state. It provided a reference for the identification of the degradation status of other components, and introduced new ideas for the early warning calibration of key parts of high-speed trains.