A Social Multi-Agent Cooperation System Based on Planning and Distributed Task Allocation
Abstract
1. Introduction
2. Related Work
- (i)
- Spatially organizing behavior: in this system, the agents interact among themselves to execute a spatial configuration and have minimal interaction with the environment;
- (ii)
- Collective explorations: in this system, the agents focus rather on interacting with the environment than among themselves;
- (iii)
- Cooperative decision making: in this system, the agents interact among themselves as well as with the environment to complete a complicated task.
3. Benchmark Production System
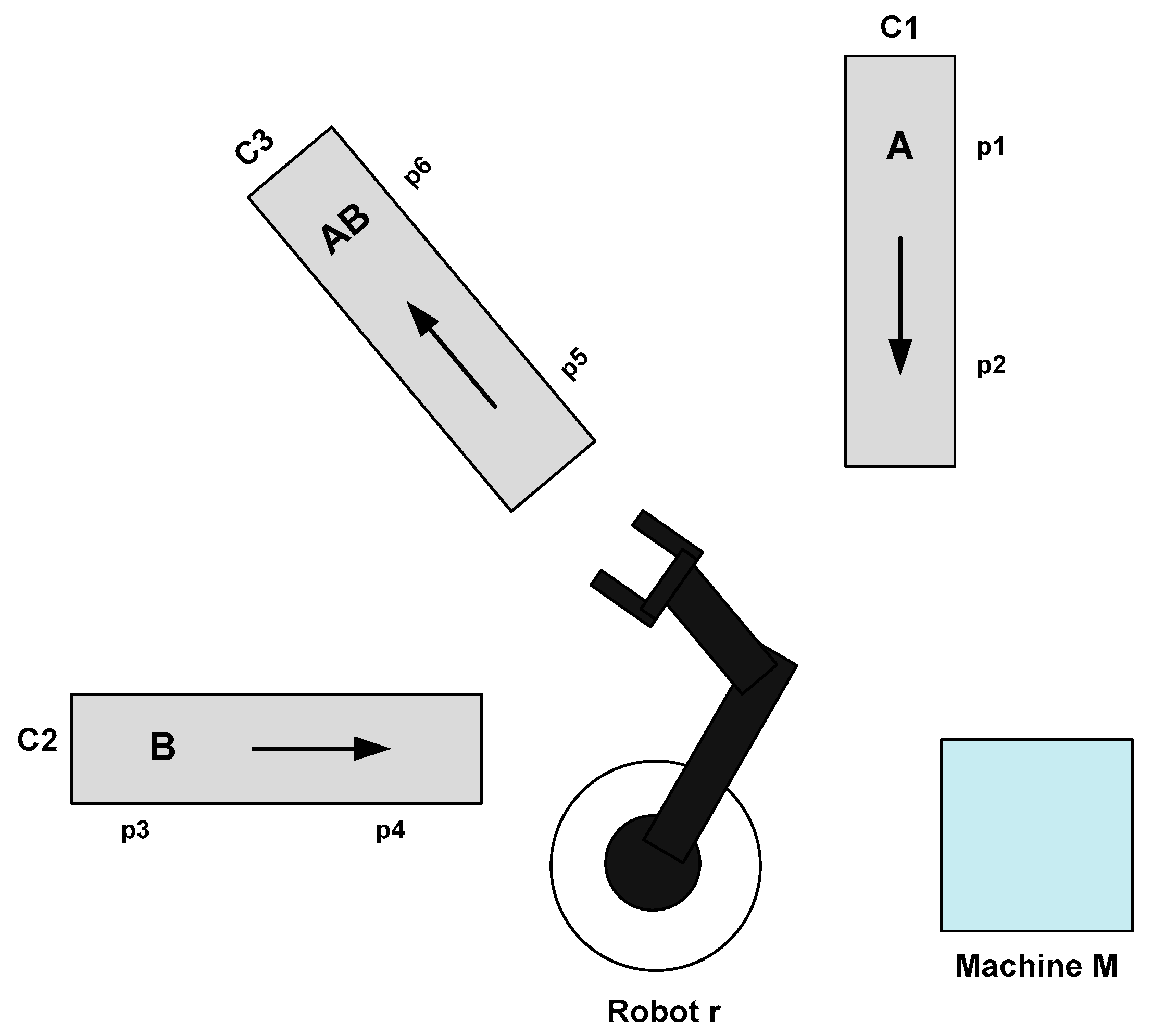
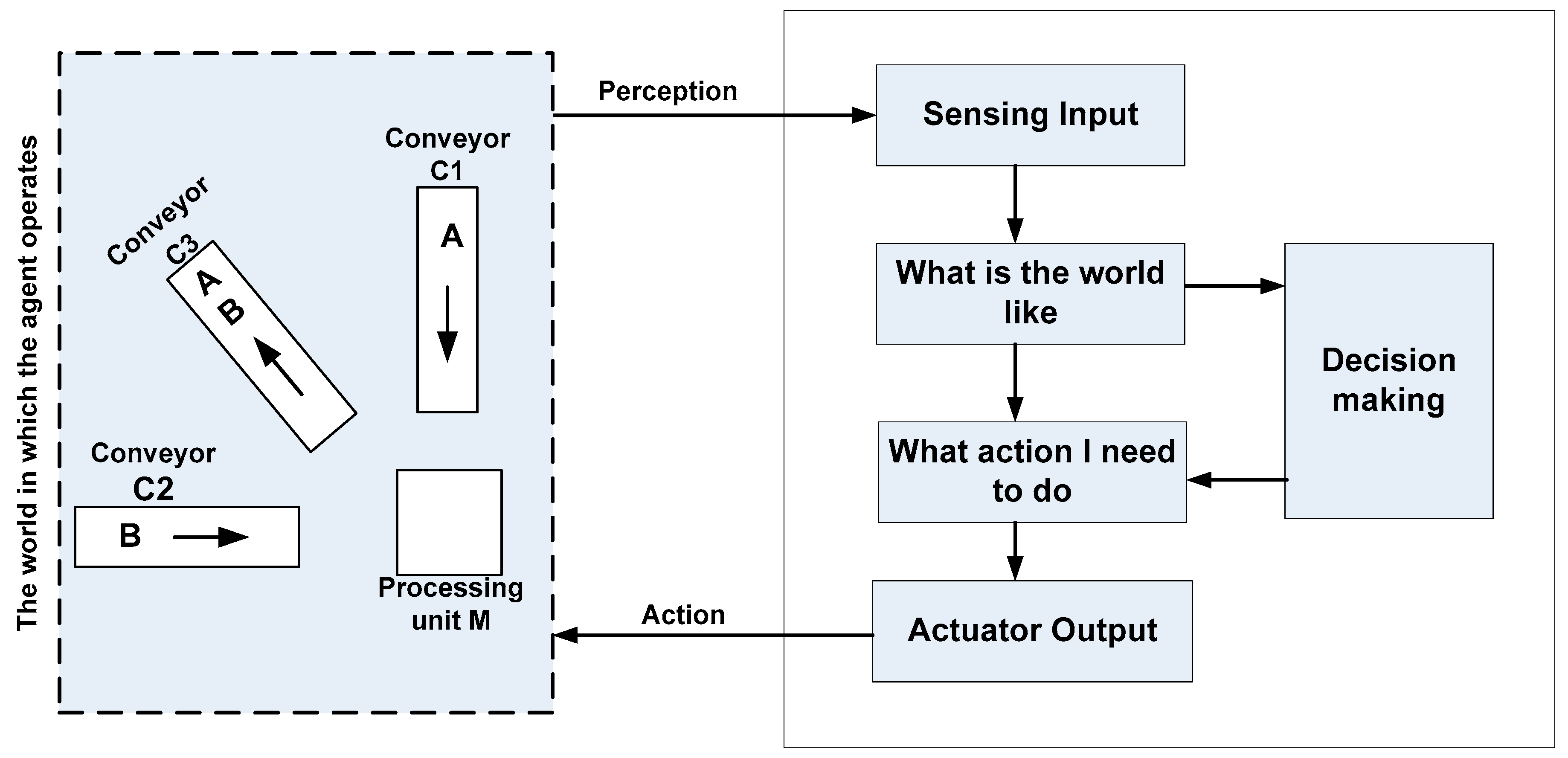
- Running Example
4. The Agent-Based Planning
- The queue, Q, is used to save every arriving event;
- The event, ev, represents any event input;
- The state, Si,j, is an element of the state machine.
| Algorithm 1 GenericBehavior. |
| begin |
| while (Q.length() > 0) do |
| ev ⃪ Q.Head() |
| Si,j ⃪ currentStatei |
| If ev I(Si,j) then |
| For each state Si,k next(Si,j) do |
| 1. Find the plan list that can satisfy Si,k |
| 2. Assess every possible plan’s pre-conditions and retain only those whose pre-conditions are satisfied. |
| 3. For every remaining plan, estimate its required resources. |
| 4. Sort by its priority |
| If execute(Si,k) then |
| currentStatei ⃪ Si,k |
| break |
| end if |
| end for |
| end if |
| end while |
| end. |
- Running Example
- ✓
- The sensor sens1 (respectively sens2) is used to verify if there is a workpiece at the position p1 (respectively the position p2) on the conveyor C1;
- ✓
- The sensor sens3 (respectively sens4) checks for the existence of a workpiece at the position p3 (respectively the position p4) on the conveyor C2;
- ✓
- The sensor sens5 (respectively sens6) verifies if there is a workpiece at the position p5 (respectively the position p6) on the conveyor C3;
- ✓
- The sensor sens7 observes if there is a Type A workpiece at the unit M;
- ✓
- The sensor sens8 enables the checking of if there is a Type B workpiece at the unit M;
- ✓
- The sensor sens9 (respectively sens10) perceives if the conveyor C1 is in its extreme left (respectively right) position;
- ✓
- The sensor sens11 (respectively sens12) determines if the conveyor C2 is in its extreme left (respectively right) position;
- ✓
- The sensor sens13 (respectively sens14) detects if the conveyor C3 is in its extreme left (respectively right) position;
- ✓
- The sensor sens15 (respectively sens16) is used to decide if the robotic agent arm is in its lower (respectively higher) position.
- ✓
- The actuator act1 ensures the movement of the conveyor C1;
- ✓
- The actuator act2 moves the conveyor C2;
- ✓
- The actuator act3 enables the movement of the conveyor C3;
- ✓
- The actuator act4 rotates a robotic agent;
- ✓
- The actuator act5 elevates the robotic agent arm vertically;
- ✓
- The actuator act6 picks up and drops a piece with the robotic agent arm;
- ✓
- The actuator act7 treats the workpiece;
- ✓
- The actuator act8 assemblies two pieces.
- ✓
- Conveyor1_left (respectively Conveyor2_left, Conveyor3_left) means a workpiece of type A (respectively B, AB) is moving to the left of conveyor C1 (respectively C2, C3) from position p1 (respectively p3, p5) to position p2 (respectively p4, p6);
- ✓
- Rotate1_left (respectively Rotate2_left, Rotate3_left) means the robotic agent taking a workpiece of type A (respectively B, AB) is moving to the left from the position p2 (respectively p4, p6) of conveyor C1 (respectively C2, C3) to the processing unit M (respectively the position p2 of conveyor C1);
- ✓
- Rotate1_right (respectively Rotate2_right, Rotate3_right) means the robotic agent taking a workpiece of type A (respectively B, AB) is moving to the right from the processing unit M to the position p2 (respectively p4, p6) of conveyor C1 (respectively C2, C3);
- ✓
- take1 (respectively take2, take3) means the operation of taking a workpiece of type A (respectively B, AB);
- ✓
- load1 (respectively load2, load3) means loading a workpiece of type A (respectively B, AB);
- ✓
- put1 (respectively put2, put3) means the operation of putting a workpiece of type A (respectively B, AB);
- ✓
- process1 (respectively process2) means processing a workpiece of type A (respectively B).
5. Distributed Task Allocation
- -
- a set of planning agent A = {A1, …, An};
- -
- each planning agent Ai has a set of resources Ri = {Ri1, …, Rim};
- -
- a set of tasks to be executed in the multi-planning agent T = {T1, …, Tp};
- -
- each task Tk may require a set of resources {Rk1, …, Rkl}.
5.1. The Principle of Distributed Task Allocation
- ✓
- Initiator: the planning agent that requests help to perform its task;
- ✓
- Participant: the planning agent having the requested resources that receives the announced task and sends back its response.
- ✓
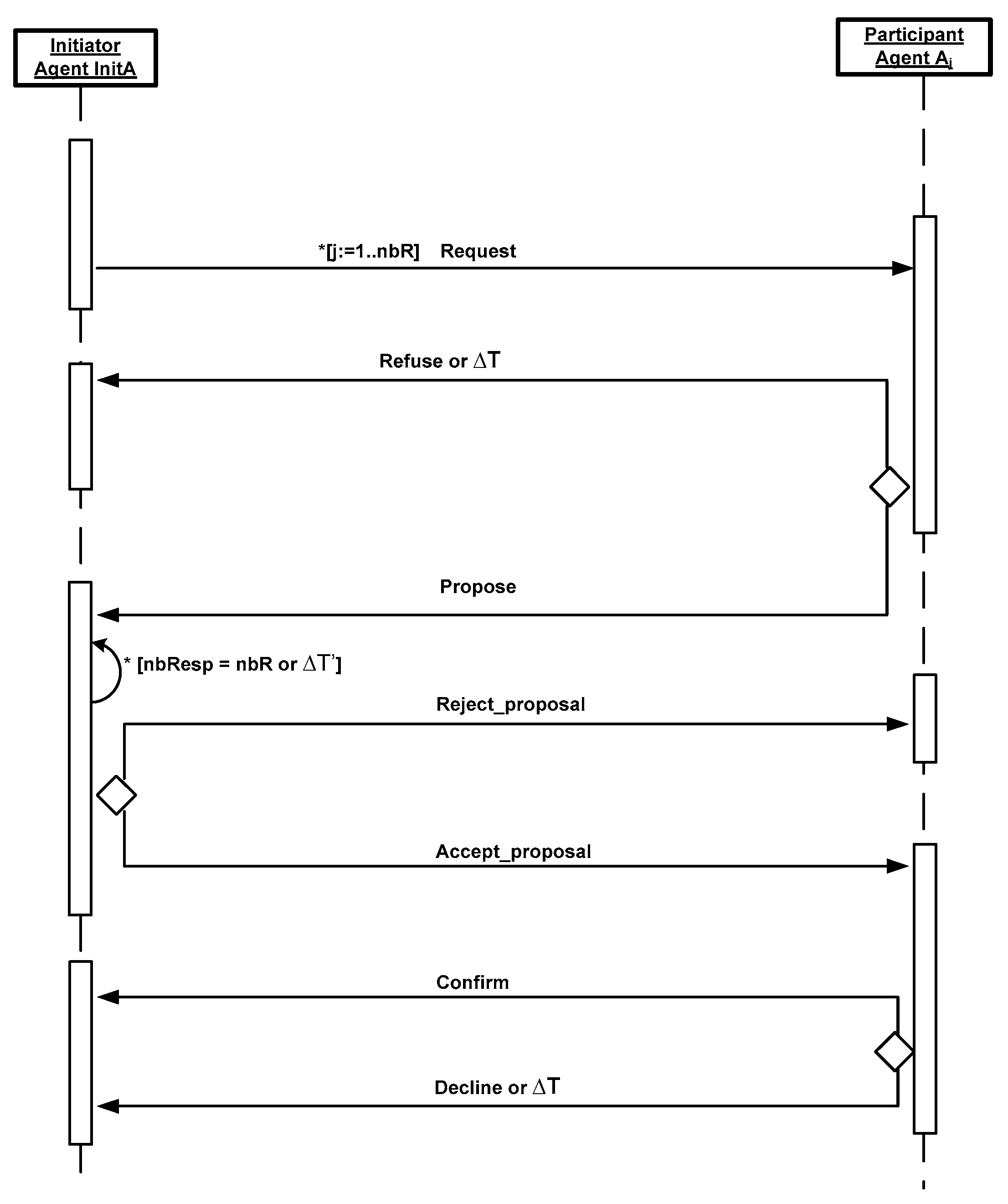
- The initiator agent, denoted as InitA: the planning agent that starts the distributed task allocation process. There are many reasons to apply a distributed task allocation in the whole system such as the fact that the planning agent is unable to execute a task by itself, it is too busy, or it does not have all the necessary resources. Each initiator agent InitA has a list of planning agents. It sends a request to the planning agents: Resource_Announce_Message = ≺AgentID, TaskID, Resource(number)≻, containing the initiator agent identity, the task identity and the number of requested resources.
- ✓
- The planning agent (called the participant agent) receives the message Resource_Announce_Message sent by the initiator agent InitA; it checks the possibility of applying distributed task allocation based on its state. If it is feasible (i.e., the participant agent has the requested resources and is idle), it accepts the collaboration with the initiator agent. If the participant agent is busy, it refuses the request.
- ➢
- If the participant agent Aj is IDLE then it provides data regarding its identity, the types of resources it owns and the executing time, explicitly, Propose_Message = ≺AgentID, Resource, Execute≻.
- ➢
- If the participant agent Aj is BUSY then it sends a negative response containing the following message Refuse_Message = ≺AgentID≻.
- ✓
- After collecting the responses from all the participant agents or the timeout is over, the initiator agent InitA then compares the available resources from these participant agents with the resources required for its task tInitA. This leads to two cases:
- ✓
- Two cases can happen depending on the selected participant agent Aj state
- ➢
- If the selected participant agent Aj is still free, it sends a confirmation message to the initiator agent InitA and its state will be changed to BUSY: Confirm_Message = ≺AgentID≻. Consequently, the distributed task allocation protocol finishes well.
- ➢
- If the selected participant agent Aj becomes busy (which means it receives a notification message from another initiator), it sends a decline message to the initiator agent InitA: Decline_Message = ≺AgentID≻. Therefore, the initiator agent InitA repeats the same steps from the beginning.
5.2. Dynamic Planning Agent Discovery with JADE
5.2.1. Publish a Provided Resource
- ➢
- The agent AID (unique identifier);
- ➢
- A collection of resource descriptions (class ServiceDescription):
- The resource type (e.g., “Resource1”);
- The resource name (e.g., “Resource”);
- The languages, ontologies and interaction protocols that must be known to exploit the service.
5.2.2. Search a Required Resource
- Running Example
- DFAgentDescription template = new DFAgentDescription();ServiceDescription desc = new ServiceDescription();desc.setType(“Resource1”);template.addServices(desc);DFAgentDescription[[] result;try {do{result = DFService.search(myAgent, template);planningAgents = new AID[result.length];for (int i = 0; i < result.length; i++)planningAgents[i] = result[i].getName();}while (result.length <= 0);}catch (FIPAException fe) {fe.printStackTrace();}nbR = planningAgents.length;
5.3. Message Exchanged between Initiator and Planning Agents with JADE
5.3.1. Creating a Message According to FIPA ACL Specification
- Running Example
- // The code below creates a new message with the following content:ACLMessage msg = new ACLMessage(ACLMessage.INFORM); // (1) the performative: INFORM,msg.addReceiver(new AID(“Agent1”, AID.ISLOCALNAME)); // (3) the receiver: Agent1msg.setContent(“I need the help from others”); // (2) the content: requesting help from other agentssend(msg); // sending the message
5.3.2. Receiving a Message with a Matching Method
- Running Example
- The action() method is modified so that the call to myAgent.receive() ignores all messages except those whose performative is PROPOSE:public void action() {MessageTemplate mt = MessageTemplate.MatchPerformative(ACLMessage. PROPOSE);ACLMessage msg = myAgent.receive(mt);if (msg != null) {// REQUEST Message received. Process it...}else {block();}}
5.4. Agent Behavior in JADE
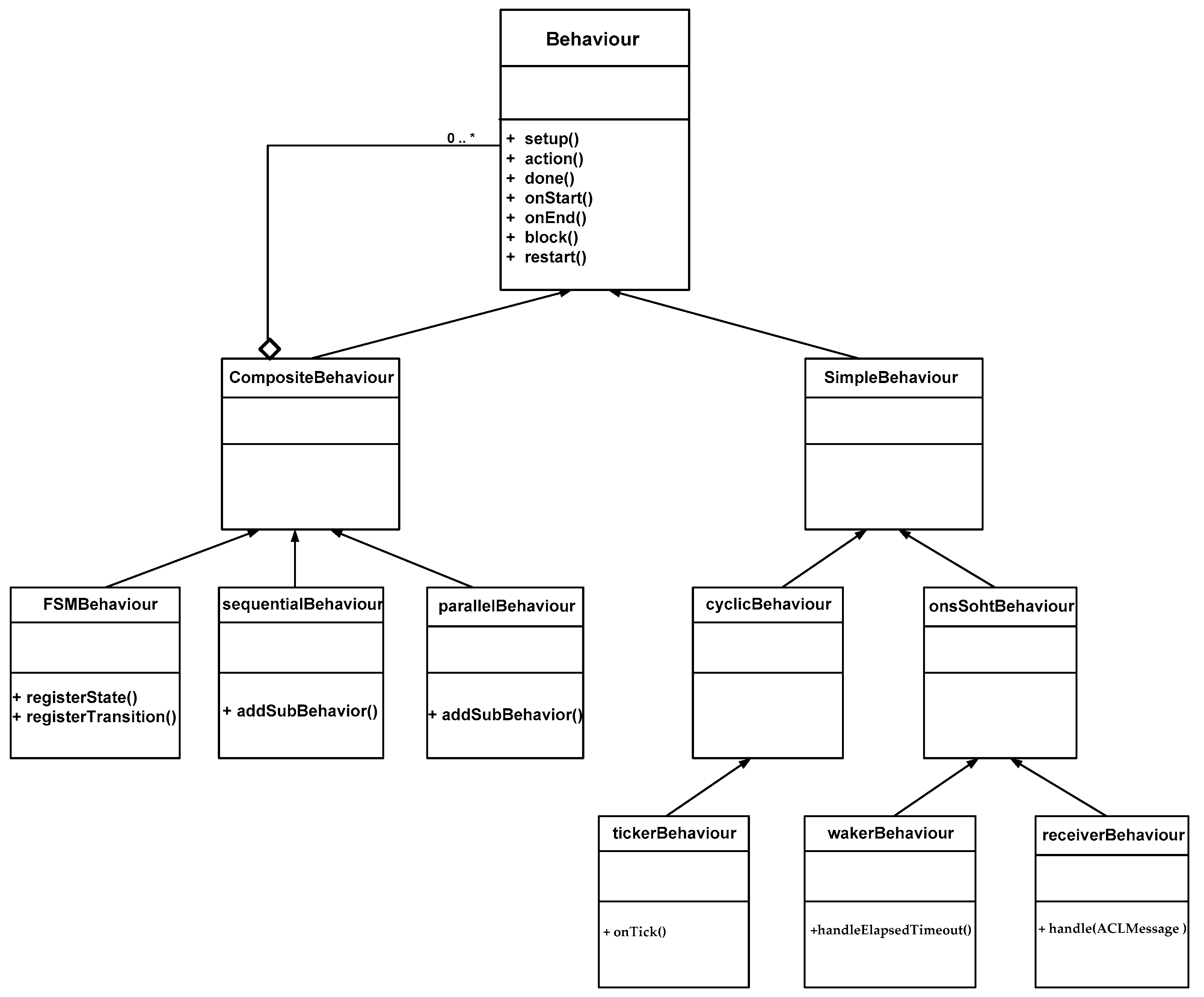
- Behaviour class: it is implemented as an object of a class that extends jade.core.behaviours.Behaviour. The Behaviour class is an abstract class having several abstract methods. The action method defines the operation to be performed when the behavior is in execution. The done method returns a boolean value to indicate whether or not a behavior has completed. The Behaviour class also provides two methods, named onStart and onEnd. These methods can be overridden by user defined subclasses when some actions are to be executed before and after running behavior execution.
- SimpleBehaviour class: it is an abstract class representing simple atomic behaviors (which means it is composed of only one behavior). It can be overridden by user defined subclasses which are OneShotBehaviour and CyclicBehaviour classes.
- OneShotBehaviour class: it represents atomic behaviors that must be executed only once and cannot be blocked. Two subclasses inherit from the OneShotBehaviour class, which are the WakerBehaviour and the TickerBehaviour classes.
- ✓
- The WakerBehaviour class implements a one-shot task that must be executed only once just after a given timeout has elapsed, which is specified in the handleElapsedTimeout method.
- ✓
- The ReceiverBehaviour class, which triggers when a given type of message is received or a timeout expires.
- CyclicBehaviour class: it models atomic behaviors that must be executed forever. Thus, its done method always returns false. The CyclicBehaviour class represents “Cyclic” behaviors that never complete and whose action method executes the same operations each time it is called.
- ✓
- The TickerBehaviour class implements a cyclic task that must be executed recurrently. The periodic actions are determined in the onTick method.
- CompositeBehaviour class: This abstract class models behaviors that are made up of a number of other behaviors (children). Thus, the actual operations performed by executing this behavior are not defined in the behavior itself but inside its children, while the composite behavior only takes care of child scheduling according to a given policy (sequentially for the SequentialBehaviour class, concurrently for the ParallelBehaviour class and as a finite state machine for the FSMBehaviour class).
- ✓
- ParallelBehaviour class: this behavior controls a set of sub-behaviors that execute in parallel. The most important thing is the termination condition; it is possible to specify the termination of ParallelBehaviour when all of its sub-behaviors terminate or any sub-behavior is ended.
- ✓
- SequentialBehaviour class: this behavior is composed of a set of sub-behaviors where each one is executed after the other. The SequentialBehaviour terminates when all its sub-behaviors have terminated.
- ReceiverBehaviour class: a behavior with a timeout that waits until the reception of a message or the elapsing of a given timeout.
- Running Example
- ✓
- A ParallelBehaviour, which is composed of a sub-behavior set. Each sub-behavior is a ReceiverBehaviour class, which means it waits until the reception of a message, an answer from a particular participant agent or a given timeout is elapsed. The termination of this ParallelBehaviour is ensured when all of its sub-behaviors (i.e., ReceiverBehaviour) terminate. The ReceiverBehaviour have 0.5 s as a timeout period.
- ✓
- After that, there is a delay (1 s) before sending a REQUEST to the best answer from a specific participant agent.
- ✓
- The final behavior is a receiver behavior, which waits for an AGREE/REFUSE message from this specific participant agent with a common conversation ID.
- public class Initiator extends Agent{private Initiator myAgent;private int requested;private int resourceType;int bestExecute;ACLMessage message, bestProposal;static protected Random genAleatoire = new Random();protected void setup(){Object[[] args = getArguments();if (args != null && args.length > 0) {resourceType=((Integer)args[0]).intValue();}bestExecute = 1000;bestProposal = null;// number of resources requested: generated rondomrequested=(int) Math.floor(genAleatoire.nextDouble() *10;myAgent=this;// Register the resource offered by the Initiator agent in DFServiceDFAgentDescription dfd = new DFAgentDescription();dfd.setName(getAID());ServiceDescription sd = new ServiceDescription();sd.setType(String.valueOf(resourceType));sd.setName("Resource");dfd.addServices(sd);try {DFService.register(this, dfd);}catch (FIPAException fe) {fe.printStackTrace();}// Add a TickerBehaviour that searches Planning agents every 2 seconds in the DFaddBehaviour(new TickerBehaviour(this, 2000){protected void onTick() {// Update the list of Planning agentsDFAgentDescription template = new DFAgentDescription();ServiceDescription desc = new ServiceDescription();desc.setType(resourceType);template.addServices(desc);DFAgentDescription[[] result;try {do{result = DFService.search(myAgent, template);planningAgents = new AID[result.length];for (int i = 0; i < result.length; i++)planningAgents[i] = result[i].getName();}while (result.length <= 0);}catch (FIPAException fe) {fe.printStackTrace();}nbR= planningAgents.length;}};message = newMsg( ACLMessage.REQUEST );MessageTemplate template = MessageTemplate.and(MessageTemplate.MatchPerformative( ACLMessage.PROPOSE ),MessageTemplate.MatchConversationId( message.getConversationId() ));SequentialBehaviour seq = new SequentialBehaviour();addBehaviour( seq );ParallelBehaviour par = new ParallelBehaviour( ParallelBehaviour.WHEN_ALL );seq.addSubBehaviour( par );for (int i = 0; i < planningAgents.length; i++){message.addReceiver( new AID(planningAgents[i], AID.ISLOCALNAME ));par.addSubBehaviour( new ReceiverBehaviour( this, 500, template){public void handle( ACLMessage message){if (message != null) {int execute = Integer.parseInt( message.getContent());if (execute < bestExecute) {bestExecute = execute;bestProposal = message;}}}});}seq.addSubBehaviour(new DelayBehaviour(this, 1000){public void handleElapsedTimeout(){if (bestProposal != null) {//The best proposal is obtained through bestProposal.getSender()ACLMessage reply = bestProposal.createReply();reply.setPerformative( ACLMessage.ACCEPT );send ( reply );}}});seq.addSubBehaviour( new ReceiverBehaviour( this, 500,MessageTemplate.and(MessageTemplate.MatchConversationId( message.getConversationId()),MessageTemplate.or(MessageTemplate.MatchPerformative( ACLMessage.CONFIRM ),MessageTemplate.MatchPerformative( ACLMessage.REFUSE ))) ){public void handle( ACLMessage message){if (message != null ) {if( message.getPerformative() == ACLMessage. CONFIRM)System.out.println("Distributed Task Allocation is Finished”);else// repeat the same steps in case of failuresetup();}else {//The time is elapsed without response so repeat the same stepssetup();}}});send ( message );}
5.5. The Model Checking of Distributed Task Allocation
- Property 1: Whenever an initiator agent needs to ensure a task but does not have all the necessary resources, the initiator agent informs the participant agentj.
- AG (P1 = > EF P9).
- Property 2: During the negotiation, the initiator agent receives a positive response from the participant agentj or receives a disapproval message.
- EF P1 AND EF (P11 OR P15).
- Property 3: The participant agenti could not receive two different decisions from the initiator agent at the same time (i.e., either the initiator agent accepts or refuses the new distributed allocation).
- NOT EF (P5 AND P6).
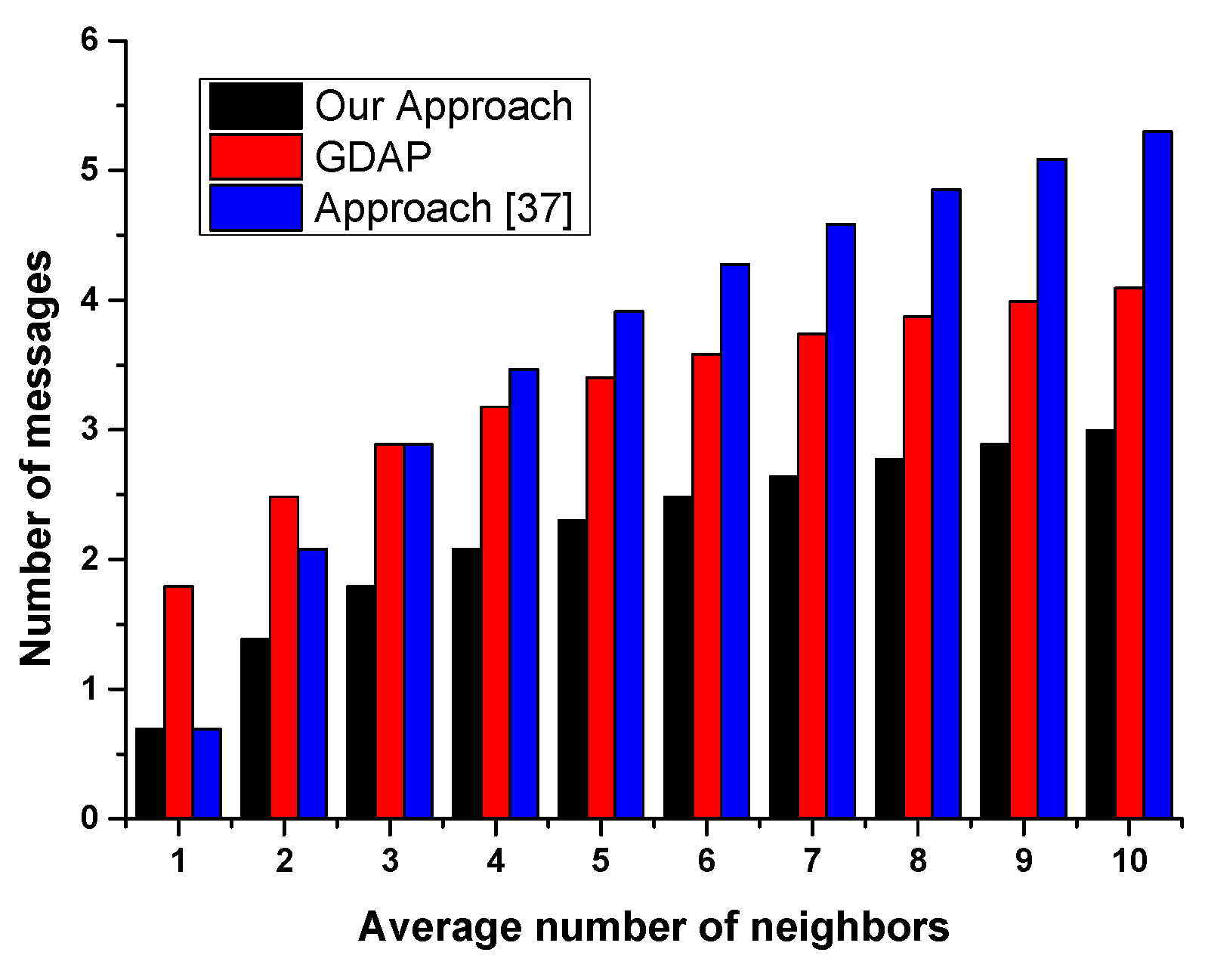
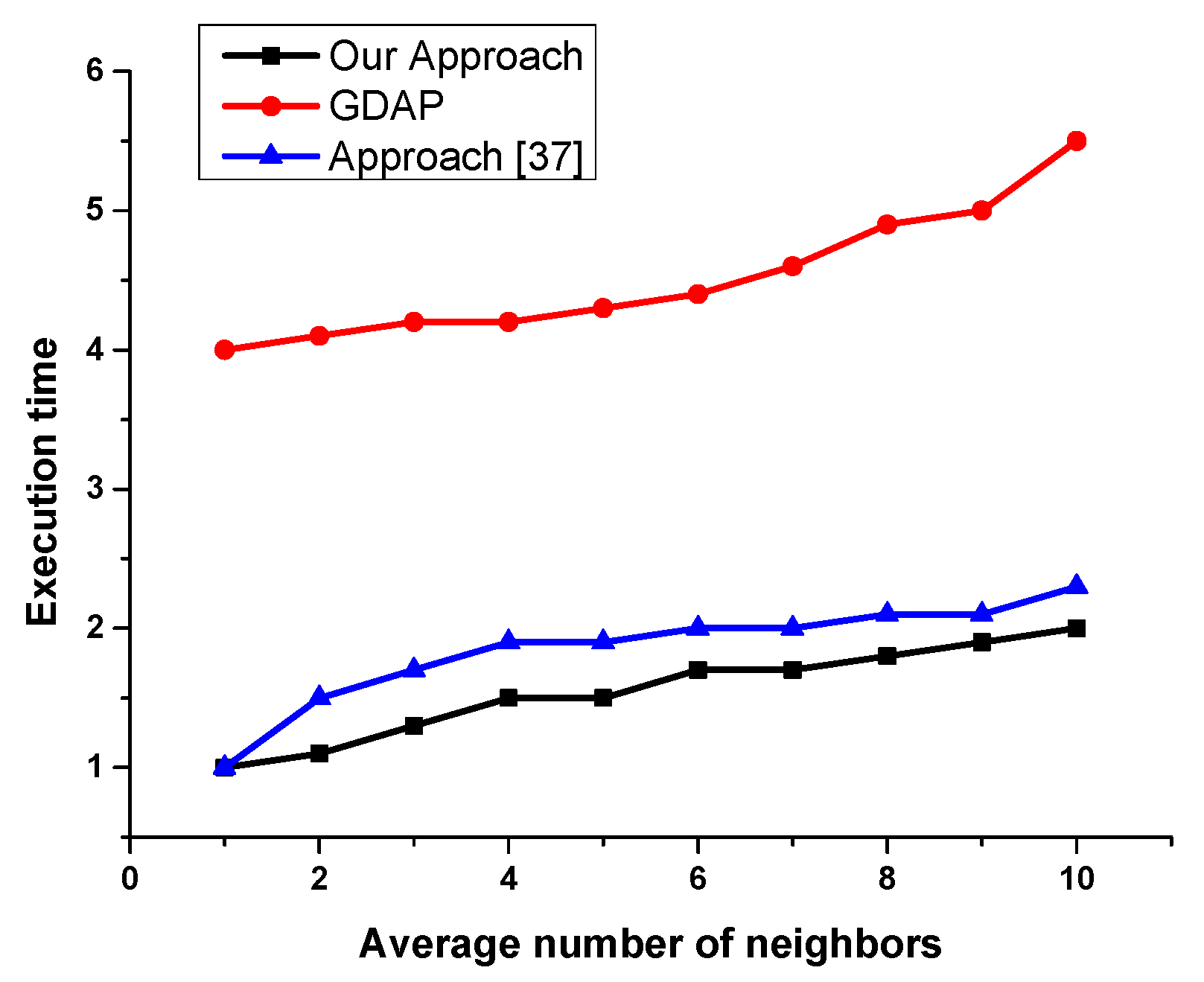
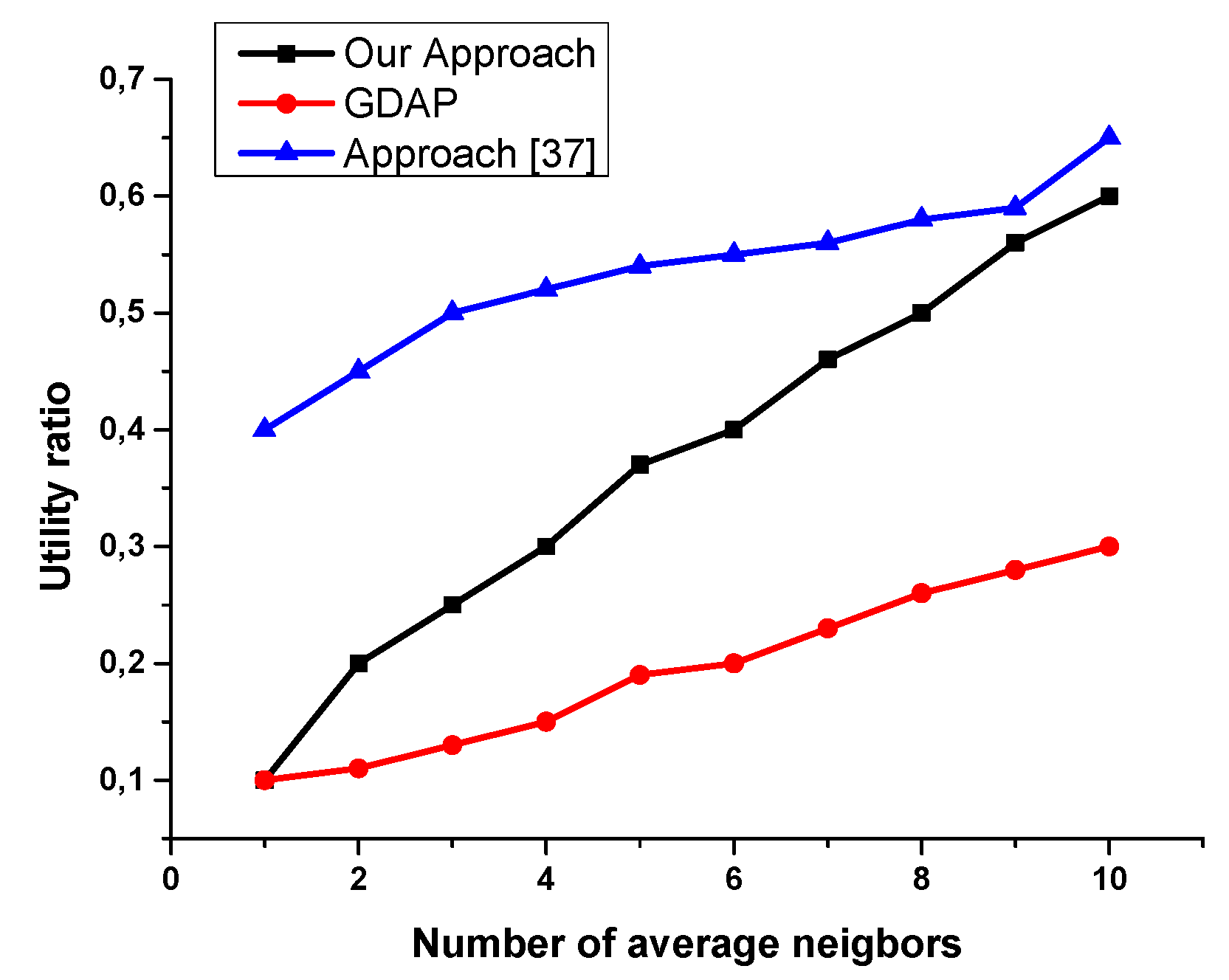
6. Evaluation
- -
- Not all the planning agents having the requested resources are registered in the directory facilitator (some of them are selfish and do not like sharing their resources).
- -
- Even when the initiator agent searches the neighboring agent providing the requested resources (the number is reduced), some of the planning agents refuse to participate in the distributed task allocation for the simple reason that the resource can be used by itself later.
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Aramrattana, M.; Andersson, A.; Reichenberg, F.; Mellegård, N.; Burden, H. Testing cooperative intelligent transport systems in distributed simulators. Transp. Res. Part F Traffic Psychol. Behav. 2019, 65, 206–216. [Google Scholar] [CrossRef]
- Viloria, A.; Rodado, D.; Lezama, O. Recovery of scientific data using Intelligent Distributed Data Warehouse. Procedia Comput. Sci. 2019, 151, 1249–1254. [Google Scholar] [CrossRef]
- Zhen, Z.; Zhu, P.; Xue, Y.; Ji, Y. Distributed intelligent self-organized mission planning of multi-UAV for dynamic targets cooperative search-attack. Chin. J. Aeronaut. 2019, 32, 2706–2716. [Google Scholar] [CrossRef]
- Jacobson, D.; Dickerman, L. Distributed intelligence: A critical piece of the microgrid puzzle. Electr. J. 2019, 32, 10–13. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H. A biologically-inspired distributed fault tolerant flocking control for multi-agent system in presence of uncertain dynamics and unknown disturbance. Eng. Appl. Artif. Intell. 2019, 79, 1–12. [Google Scholar] [CrossRef]
- Briones, A.; Mezquita, Y.; Garzón, J.; Prieto, J.; Corchado, J. Intelligent multi-agent system for water reduction in automotive irrigation processes. Procedia Comput. Sci. 2019, 151, 971–976. [Google Scholar] [CrossRef]
- Kovalenko, I.; Tilbury, D.; Barton, K. The model-based product agent: A control oriented architecture for intelligent products in multi-agent manufacturing systems. Control Eng. Pract. 2019, 86, 105–117. [Google Scholar] [CrossRef]
- Panteleev, M.G. Advanced Iterative Action Planning for Intelligent Real-Time Agents. Procedia Comput. Sci. 2019, 150, 244–252. [Google Scholar] [CrossRef]
- Fu, Q.; Du, L.; Xu, G.; Wu, J.; Yu, P. Consensus control for multi-agent systems with distributed parameter models. Neurocomputing 2018, 308, 58–64. [Google Scholar] [CrossRef]
- Pupkov, K.A.; Fadi, I. Collective Opinion Formation as a Set of Intelligent Agents to Achieve the Goal. Procedia Comput. Sci. 2019, 150, 216–222. [Google Scholar] [CrossRef]
- Ghadimi, P.; Wang, C.; Lim, M.; Heavey, C. Intelligent sustainable supplier selection using multi-agent technology: Theory and application for Industry 4.0 supply chains. Comput. Ind. Eng. 2019, 127, 588–600. [Google Scholar] [CrossRef]
- Salazar, L.; Mayer, F.; Schütz, D.; Heuser, B. Platform Independent Multi-Agent System for Robust Networks of Production Systems. IFAC-PapersOnLine 2018, 51, 1261–1268. [Google Scholar] [CrossRef]
- Komenda, A.; Novák, P.; Pěchouček, M. Domain-independent multi-agent plan repair. J. Netw. Comput. Appl. 2014, 37, 76–88. [Google Scholar] [CrossRef]
- Geanakoplos, J.; Karatzas, I.; Shubik, M.; Sudderth, W. Inflationary equilibrium in a stochastic economy with independent agents. J. Math. Econ. 2014, 52, 1–11. [Google Scholar] [CrossRef]
- Qu, G.; Brown, D.; Li, N. Distributed greedy algorithm for multi-agent task assignment problem with submodular utility functions. Automatica 2019, 105, 206–215. [Google Scholar] [CrossRef]
- Trujillo, M.A.; Becerra, H.M.; Gómez-Gutiérrez, D.; Ruiz-León, J.; Ramírez-Treviño, A. Priority Task-Based Formation Control and Obstacle Avoidance of Holonomic Agents with Continuous Control Inputs. IFAC-PapersOnLine 2018, 51, 216–222. [Google Scholar] [CrossRef]
- Vorobiev, V. Inference algorithm for teams of robots using local interaction. Procedia Comput. Sci. 2018, 123, 507–511. [Google Scholar] [CrossRef]
- An, B.; Liu, G.; Tan, C. Group consensus control for networked multi-agent systems with communication delays. ISA Trans. 2018, 76, 78–87. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Chen, M.; Wang, W. Distributed optimization for multi-agent systems with constraints set and communication time-delay over a directed graph. Inf. Sci. 2018, 438, 1–14. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, G. End to end communication rate-based adaptive fault tolerant control of multi-agent systems under unreliable interconnections. Inf. Sci. 2018, 460–461, 331–345. [Google Scholar] [CrossRef]
- Torreño, A.; Sapena, Ó.; Onaindia, E. FMAP: A platform for the development of distributed multi-agent planning systems. Knowl.-Based Syst. 2018, 145, 166–168. [Google Scholar]
- Tucnik, P.; Nachazel, T.; Cech, P.; Bures, V. Comparative analysis of selected path-planning approaches in large-scale multi-agent-based environments. Expert Syst. Appl. 2018, 113, 415–427. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm Robotics: A Review from the Swarm Engineering Perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Liu, Y.; Song, R.; Bucknall, R.; Zhang, X. Intelligent multi-task allocation and planning for multiple unmanned surface vehicles (USVs) using self-organising maps and fast marching method. Inf. Sci. 2019, 496, 180–197. [Google Scholar] [CrossRef]
- Yao, F.; Li, J.; Chen, Y.; Chu, X.; Zhao, B. Task allocation strategies for cooperative task planning of multi-autonomous satellite constellation. Adv. Space Res. 2019, 63, 1073–1084. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, P.; Du, G.; Li, F. A distributed method for dynamic multi-robot task allocation problems with critical time constraints. Robot. Auton. Syst. 2019, 118, 31–46. [Google Scholar] [CrossRef]
- Mahi, M.; Baykan, O.; Kodaz, H. A new approach based on particle swarm optimization algorithm for solving data allocation problem. Appl. Soft Comput. 2018, 62, 571–578. [Google Scholar] [CrossRef]
- Saxena, K.; Abhyankar, A. Agent based bilateral transactive market for emerging distribution system considering imbalances. Sustain. Energy Grids Netw. 2019, 18, 100203. [Google Scholar] [CrossRef]
- Liang, H.; Kang, F. A novel task optimal allocation approach based on Contract Net Protocol for Agent-oriented UUV swarm system modeling. Optik 2016, 127, 3928–3933. [Google Scholar] [CrossRef]
- Panescu, D.; Pascal, C. Holonic coordination obtained by joining the contract net protocol with constraint satisfaction. Comput. Ind. 2016, 81, 36–46. [Google Scholar] [CrossRef]
- Momen, S. Ant-inspired Decentralized Task Allocation Strategy in Groups of Mobile Agents. Procedia Comput. Sci. 2013, 20, 169–176. [Google Scholar] [CrossRef]
- Shehory, O.; Kraus, S. Methods for task allocation via agent coalition formation. Artif. Intell. 1998, 101, 165–200. [Google Scholar] [CrossRef]
- Hruz, B.; Zhou, M. Modeling and Control of Discrete-Event Dynamic Systems with Petri Nets and Other Tools; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gharbi, A.; Gharsellaoui, H.; Ben Ahmed, S. Multi-Agent control system. In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA), Vienna, Austria, 29–31 August 2014; pp. 117–124. [Google Scholar]
- Homepage of ITS-Tools. Available online: https://lip6.github.io/ITSTools-web (accessed on 8 November 2019).
- Ben Noureddine, D.; Gharbi, A.; Ben Ahmed, S. A Social Multi-Agent Cooperation System based on Planning and Distributed Task Allocation: Real Case Study. In Proceedings of the ICSOFT, Porto, Portugal, 26–28 July 2018; pp. 483–493. [Google Scholar]
- Weerdt, M.; Zhang, Y.; Klos, T. Distributed task allocation in social networks. In Proceedings of the 6th Automous Agents and Multiagent Systems (AAMAS 2007), Honolulu, HI, USA, 14–18 May 2007; pp. 500–507. [Google Scholar]
- Available online: https://drive.google.com/open?id=1SYKk2CyxpAgq6o-n2VqZ7gOuwRPj3qJw (accessed on 10 May 2020).
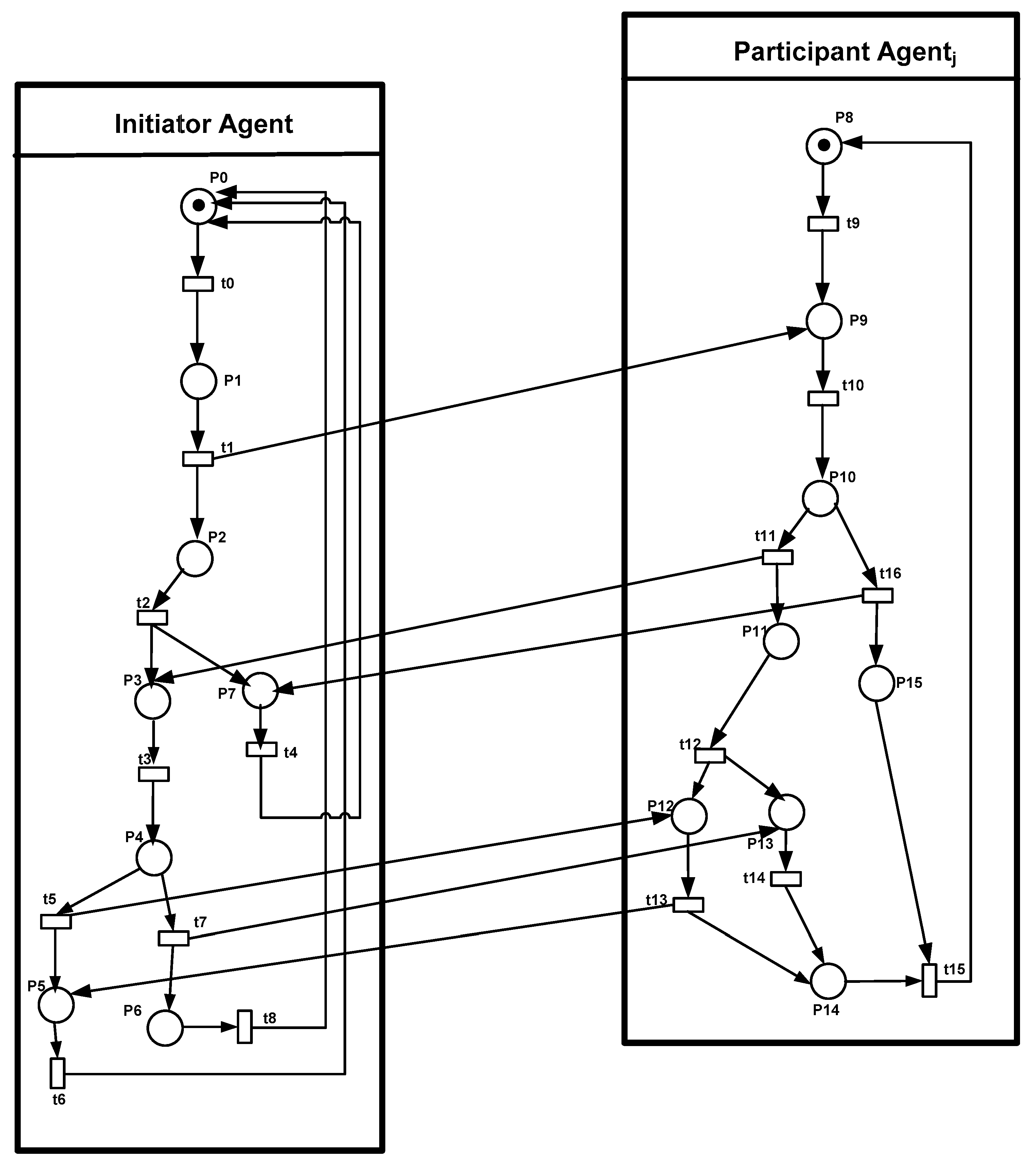
| Transition | Meaning |
|---|---|
| t0 | The initiator agent needs to apply a distributed task allocation |
| t1 | The initiator agent sends a request to a participant agenti |
| t3 | The initiator agent receives a positive answer from the participant agenti |
| t4 | The initiator agent receives a negative answer from the participant agenti |
| t5 | The initiator agent accepts the proposition from the participant agenti to apply the new distributed task allocation |
| t7 | The initiator agent refuses the proposition from the participant agenti to apply the new distributed task allocation |
| t9 | A participant agentj receives the request from the initiator agent for distributed task allocation |
| t10 | The participant agentj receives a disapproval message from the initiator agent |
| t11 | The participant agentj sends a proposition to the initiator agent |
| t12 | The participant agentj receives an approval message from the initiator agent |
| t13 | The participant agentj send a confirmation to the initiator agent |
| t16 | The participant agentj refuses to help the initiator agent |
| Setting | Quantity |
|---|---|
| Number of agents | 10 |
| Average number of neighbors | [1..10] |
| Tasks | 5 |
| Available resources | 6 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharbi, A. A Social Multi-Agent Cooperation System Based on Planning and Distributed Task Allocation. Information 2020, 11, 271. https://doi.org/10.3390/info11050271
Gharbi A. A Social Multi-Agent Cooperation System Based on Planning and Distributed Task Allocation. Information. 2020; 11(5):271. https://doi.org/10.3390/info11050271
Chicago/Turabian StyleGharbi, Atef. 2020. "A Social Multi-Agent Cooperation System Based on Planning and Distributed Task Allocation" Information 11, no. 5: 271. https://doi.org/10.3390/info11050271
APA StyleGharbi, A. (2020). A Social Multi-Agent Cooperation System Based on Planning and Distributed Task Allocation. Information, 11(5), 271. https://doi.org/10.3390/info11050271





