Reliable Estimation of Urban Link Travel Time Using Multi-Sensor Data Fusion
Abstract
1. Introduction
2. Link Travel Time Extraction Algorithms Based on Single-Sensor Traffic Data
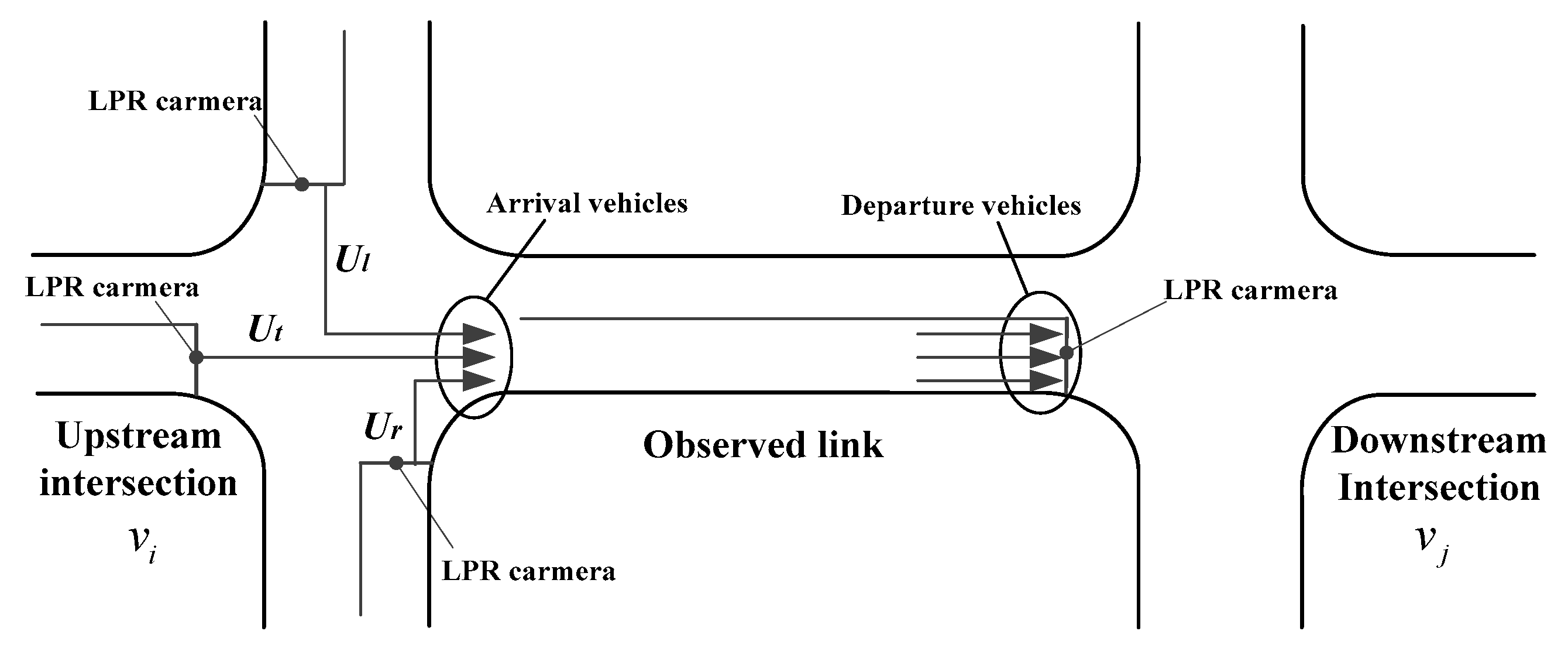
2.1. Travel Time Extraction from License Plate Recognition Data
2.2. Travel Time Extraction from Geomagnetic Detector Data
2.3. Travel Time Extraction from Floating Car Data
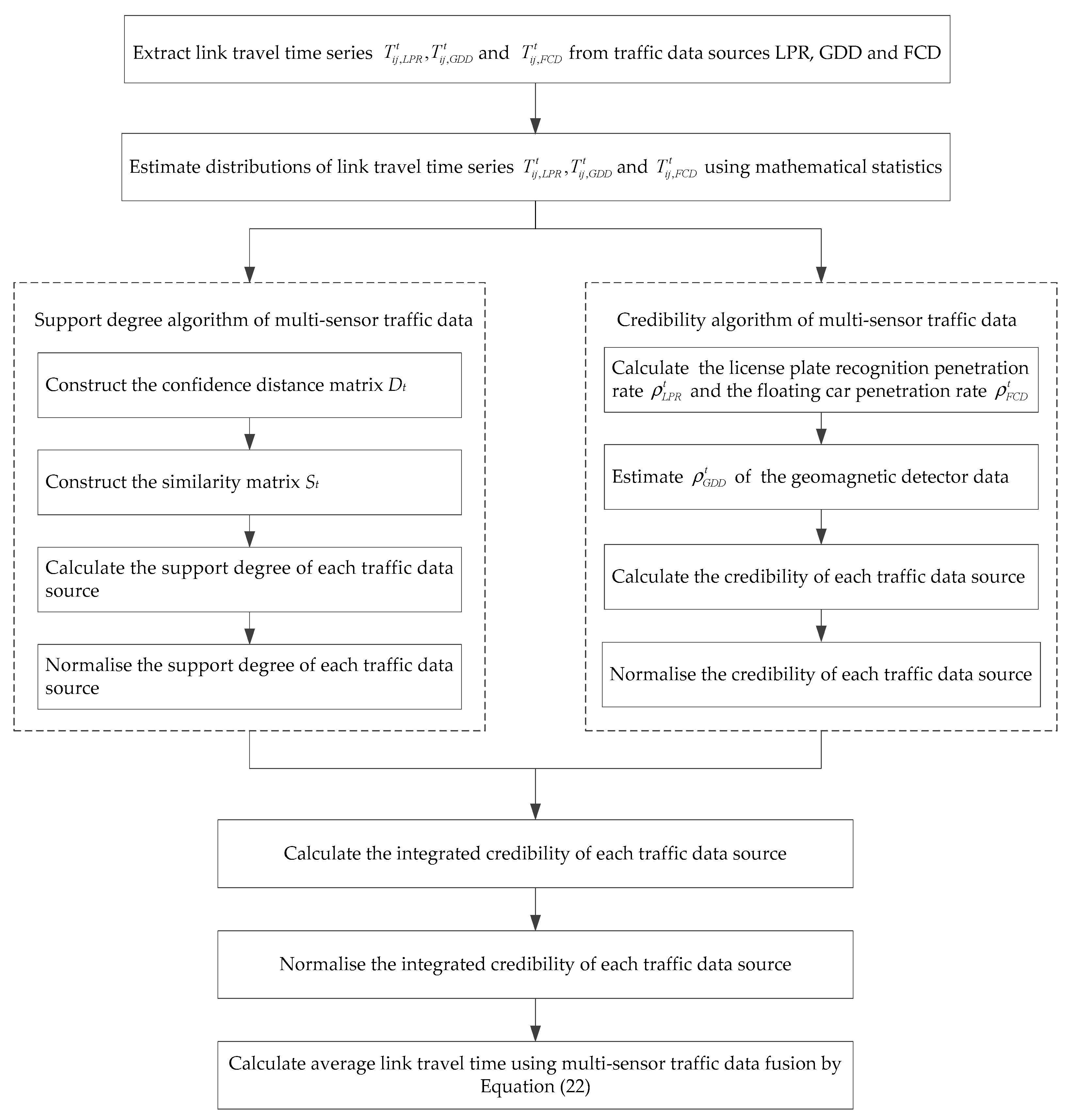
3. Urban Link Travel Time Estimation Method Using Multi-Sensor Data Fusion
3.1. Support Degree Algorithm of Multi-Sensor Traffic Data
3.2. Credibility Algorithm of Multi-Sensor Traffic Data
3.3. Reliable Fusion of Average Link Travel Time
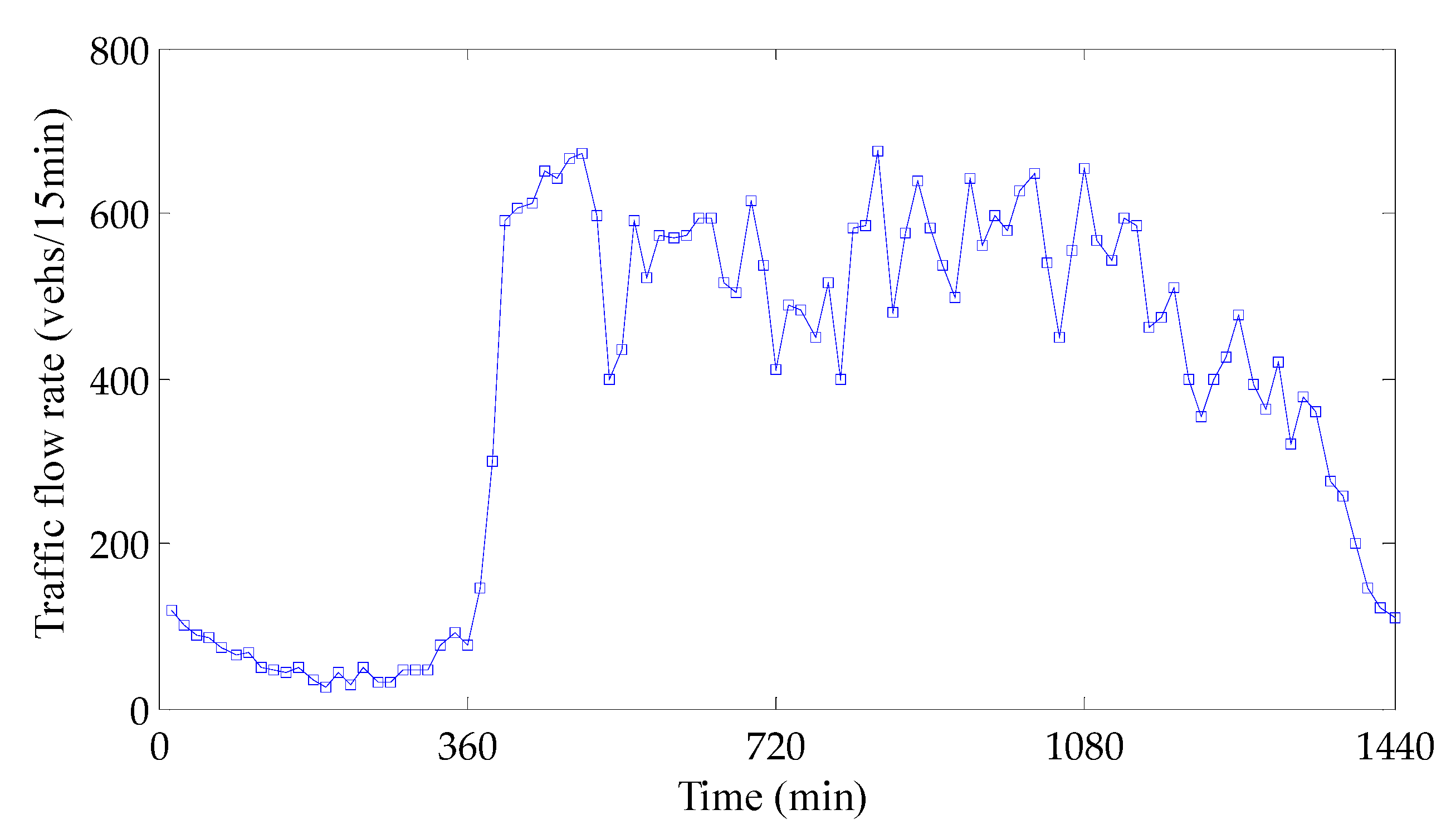
4. Case Study and Results
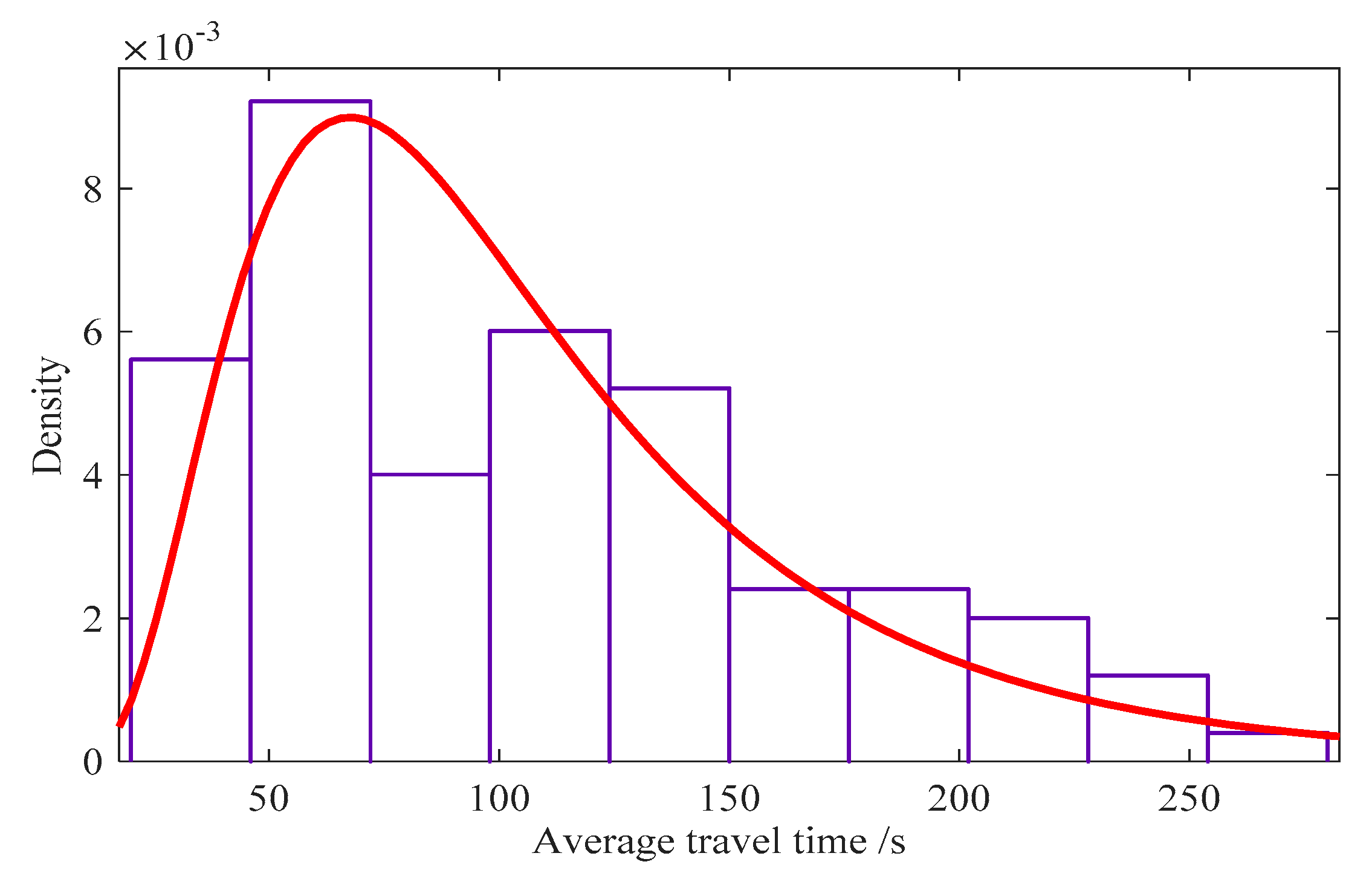
4.1. Distribution Fitting of Average Link Travel Time Series
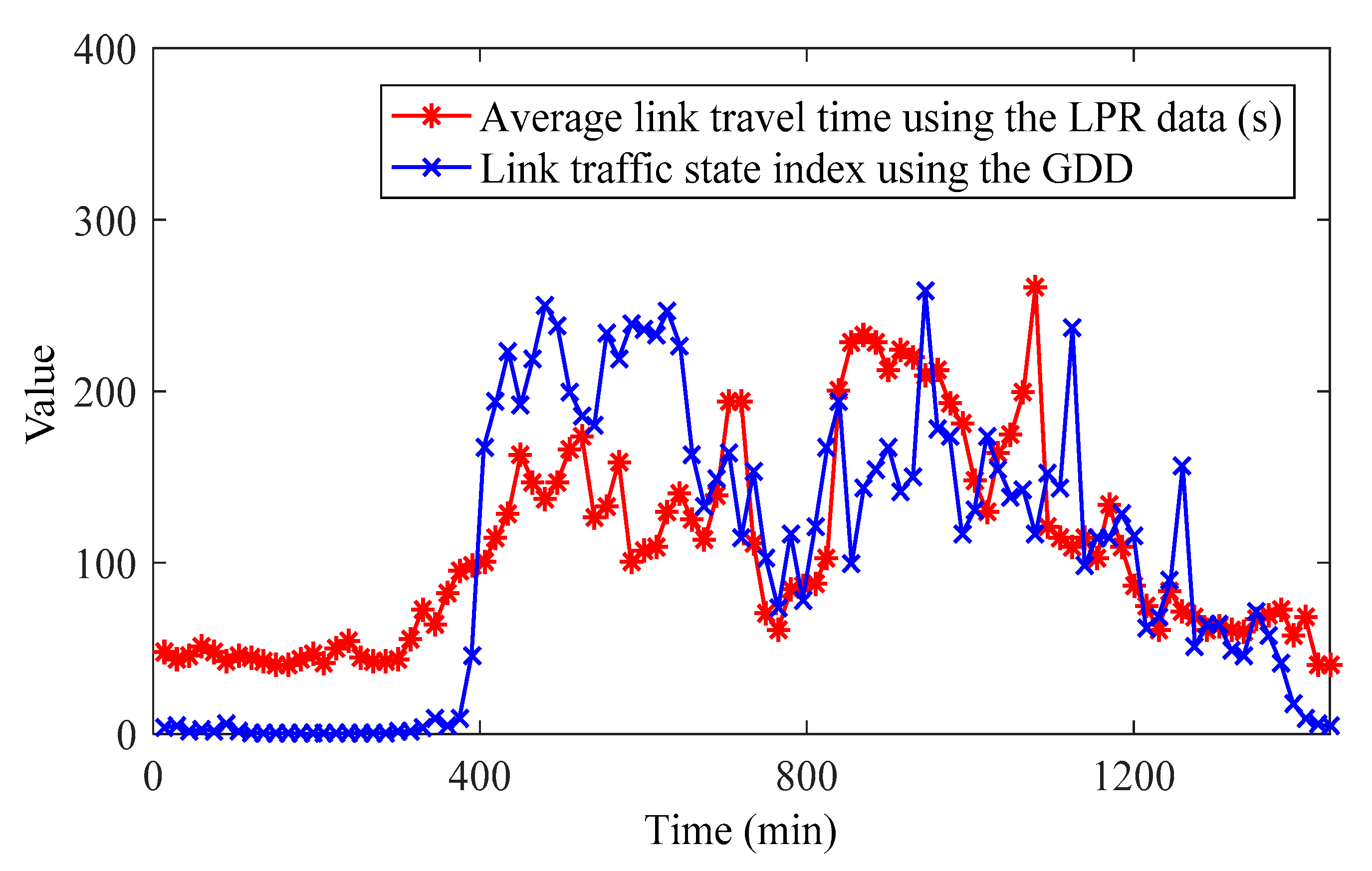
4.2. Analysis of Case Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nie, Q.; Xia, J.; Qian, Z.; An, C.; Cui, Q.; Information, R. Use of Multisensor Data in Reliable Short-Term Travel Time Forecasting for Urban Roads. Transp. Res. Rec. J. Transp. Res. Board 2015, 2526, 61–69. [Google Scholar] [CrossRef]
- Bhaskar, A.; Chung, E.; Dumont, A.-G. Fusing Loop Detector and Probe Vehicle Data to Estimate Travel Time Statistics on Signalized Urban Networks. Comput. Civ. Infrastruct. Eng. 2010, 26, 433–450. [Google Scholar] [CrossRef]
- Yuan, Y.; Van Lint, H.; Van Wageningen-Kessels, F.; Hoogendoorn, S. Network-Wide Traffic State Estimation Using Loop Detector and Floating Car Data. J. Intell. Transp. Syst. 2014, 18, 41–50. [Google Scholar] [CrossRef]
- Zhu, N.; Liu, Y.; Ma, S.; He, Z. Mobile Traffic Sensor Routing in Dynamic Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2273–2285. [Google Scholar] [CrossRef]
- Li, X.; Shu, W.; Li, M.; Huang, H.-Y.; Luo, P.-E.; Wu, M.-Y. Performance Evaluation of Vehicle-Based Mobile Sensor Networks for Traffic Monitoring. IEEE Trans. Veh. Technol. 2008, 58, 1647–1653. [Google Scholar] [CrossRef]
- Shi, C.; Chen, B.; Lam, W.H.; Li, Q. Heterogeneous Data Fusion Method to Estimate Travel Time Distributions in Congested Road Networks. Sensors 2017, 17, 2822. [Google Scholar] [CrossRef]
- Choi, K.; Chung, Y.S. A data fusion algorithm for estimating link travel time. J. Intell. Transp. Syst. Technol. Plan. Oper. 2002, 7, 235–260. [Google Scholar] [CrossRef]
- Tarko, A.; Rouphail, N. Travel time data fusion in ADVANCE. In Proceedings of the Pacific Rim Trans Tech Conference, Seattle, WA, USA, 25–28 July 1993. [Google Scholar]
- El Faouzi, N.-E. Data-driven aggregative schemes for multisource estimation fusion: A road travel time application. Defense Secur. 2004, 5434, 351–359. [Google Scholar] [CrossRef]
- Nantes, A.; Ngoduy, D.; Bhaskar, A.; Miska, M.; Chung, E. Real-time traffic state estimation in urban corridors from heterogeneous data. Transp. Res. Part C Emerg. Technol. 2016, 66, 99–118. [Google Scholar] [CrossRef]
- Mil, S.; Piantanakulchai, M.; Soknath, M.; Mongkut, P. Modified Bayesian data fusion model for travel time estimation considering spurious data and traffic conditions. Appl. Soft Comput. 2018, 72, 65–78. [Google Scholar] [CrossRef]
- El Faouzi, N.; Lefevre, E. Classifiers and distance-based evidential fusion for road travel time estimation. In Proceedings of the Multisensor, Multisource Information Fusion: Architectures, Algorithms, and Applications, Kissimmee, FL, USA, 19–20 April 2006; Volume 6242. [Google Scholar]
- Xia, J.X.; Zhang, W.H.; Ma, D.S. A method to urban road travel time estimation through its data fusion based on DS evidential theory. Appl. Mech. Mater. 2014, 488, 1419–1425. [Google Scholar] [CrossRef]
- Xiao, F. A Novel Evidence Theory and Fuzzy Preference Approach-Based Multi-Sensor Data Fusion Technique for Fault Diagnosis. Sensors 2017, 17, 2504. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y. Generalized evidence theory. Appl. Intell. 2015, 43, 530–543. [Google Scholar] [CrossRef]
- Kolanowski, K.; Świetlicka, A.; Kapela, R.; Pochmara, J.; Rybarczyk, A. Multisensor data fusion using Elman neural networks. Appl. Math. Comput. 2018, 319, 236–244. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, K.; Liao, T. Practical travel time prediction algorithms based on neural network and data fusion for urban expressway. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 4, pp. 1754–1758. [Google Scholar]
- Tak, S.; Kim, S.; Jang, K.; Yeo, H. Real-Time Travel Time Prediction Using Multi-Level k-Nearest Neighbor Algorithm and Data Fusion Method. Comput. Civ. Build. Eng. 2014, 2014, 1861–1868. [Google Scholar] [CrossRef]
- Liu, J.; Li, T.; Xie, P.; Du, S.; Teng, F.; Yang, X. Urban big data fusion based on deep learning: An overview. Inf. Fusion 2020, 53, 123–133. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Y.; Qu, Y.; Yin, H.; Liu, Y.; Sun, H. Travel Time Prediction: Based on Gated Recurrent Unit Method and Data Fusion. IEEE Access 2018, 6, 70463–70472. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.X. Using high-resolution event-based data for traffic modeling and control: An overview. Transp. Res. Part C Emerg. Technol. 2014, 42, 28–43. [Google Scholar] [CrossRef]
- Mo, B.; Li, R.; Zhan, X. Speed profile estimation using license plate recognition data. Transp. Res. Part C Emerg. Technol. 2017, 82, 358–378. [Google Scholar] [CrossRef]
- Zhan, X.; Li, R.; Ukkusuri, S. Lane-based real-time queue length estimation using license plate recognition data. Transp. Res. Part C Emerg. Technol. 2015, 57, 85–102. [Google Scholar] [CrossRef]
- Robinson, S.; Polak, J.W. Overtaking Rule Method for the Cleaning of Matched License-Plate Data. J. Transp. Eng. 2006, 132, 609–617. [Google Scholar] [CrossRef]
- Rothrock, C.A.; Keefer, L.A. Measurement of urban traffic congestion. Highw. Res. Board Bull. 1957, 156, 1–13. [Google Scholar]
- Branston, D. Link capacity functions: A review. Transp. Res. 1976, 10, 223–236. [Google Scholar] [CrossRef]
- Bureau of Public Roads. Traffic Assignment Manual; Department of Commerce: Washington, DC, USA, 1964.
- Jiang, G.; Li, J.; Zhang, C. Modified BPR functions for travel time estimation of urban arterial road segment. J. Southwest Jiaotong Univ. 2010, 45, 124–129. [Google Scholar]
- Rahmani, M.; Koutsopoulos, H.N. Path inference from sparse floating car data for urban networks. Transp. Res. Part C Emerg. Technol. 2013, 30, 41–54. [Google Scholar] [CrossRef]
- Wu, L. Fuzzy distribution fitting for law of traffic accidents based on MATLAB. Math. Pract. Theory 2009, 39, 90–95. [Google Scholar]
- Song, L.; Chen, J.; Shi, J.; Wang, S. Algorithm research of auto-detecting the travel delay information with vehicle license plate automatic recognition. J. Transp. Eng. Inf. 2008, 6, 107–112. [Google Scholar]
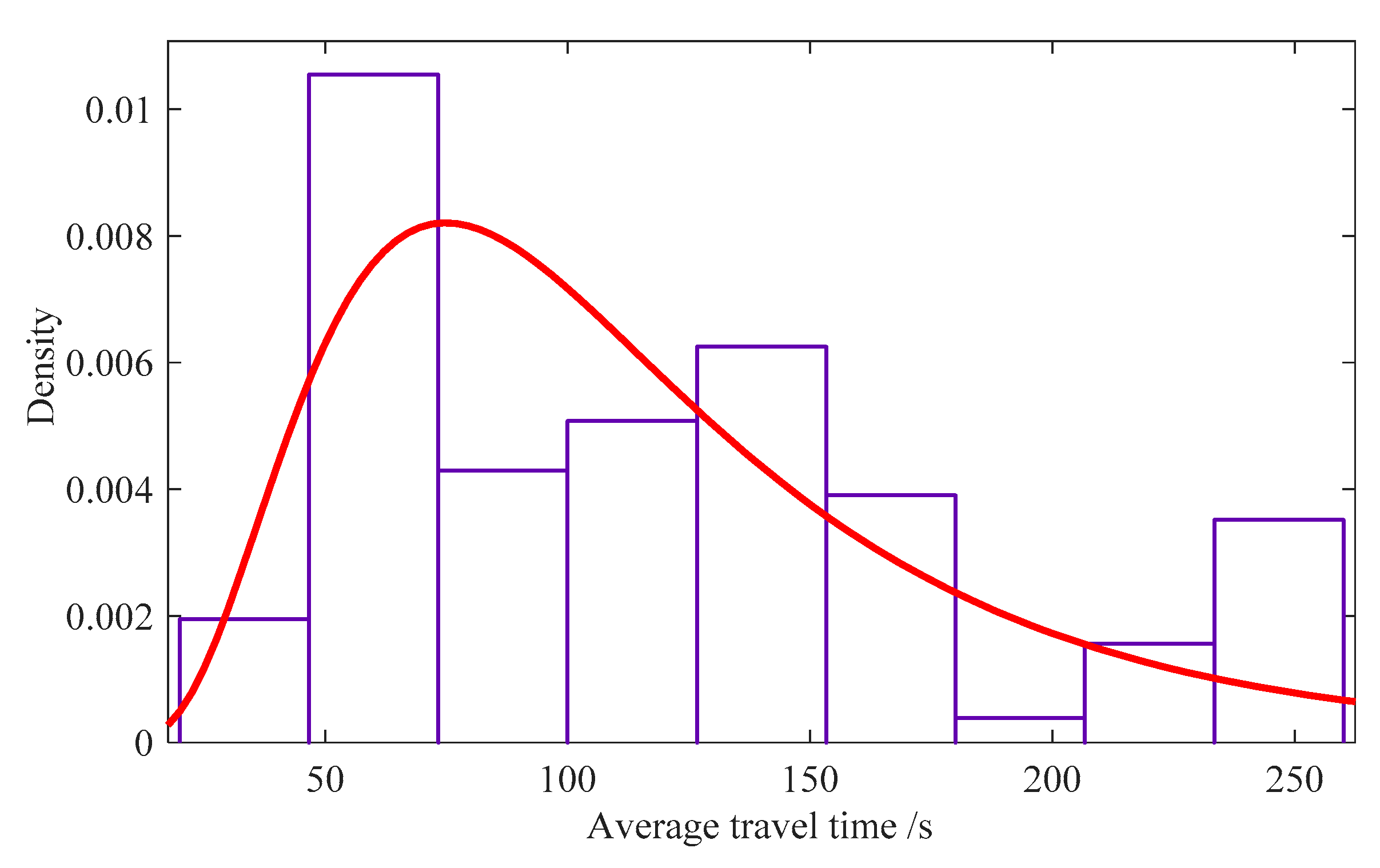
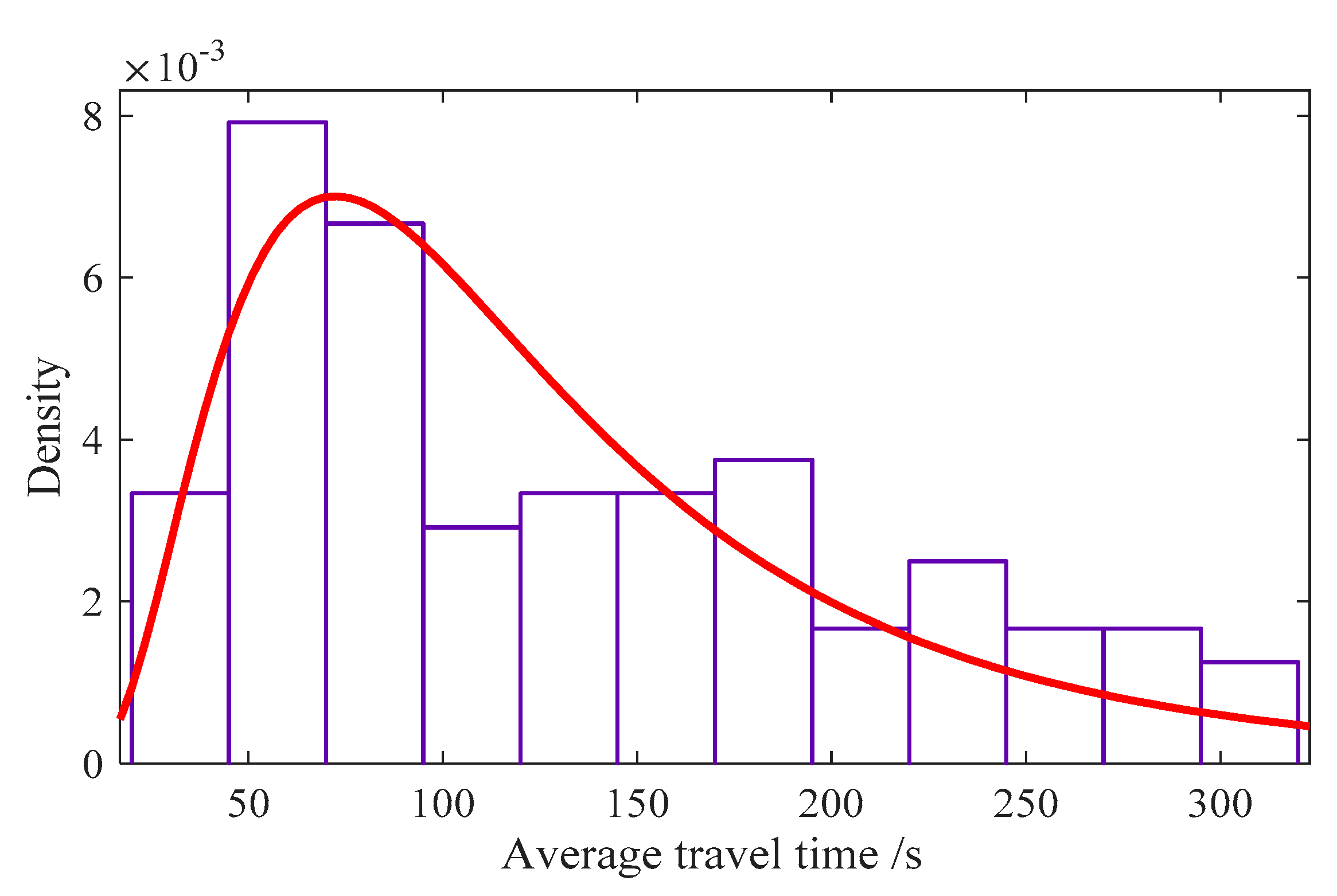

| Traffic Sensor Data | Distribution Parameter | Kolmogorov–Smirnov Test | |||
|---|---|---|---|---|---|
| Mean μα | Standard Deviation δα | Test Statistics | Critical Value at 0.05 Significance Level | Result | |
| LPR | 4.5276 | 0.5612 | 0.0823 | 0.1388 | Accepted |
| GDD | 4.6254 | 0.5561 | 0.1206 | 0.1388 | Accepted |
| FCD | 4.6923 | 0.6410 | 0.0873 | 0.1388 | Accepted |
| Methods | MAPE/% | MAE | RMSE |
|---|---|---|---|
| GDD extraction method | 22.34 | 26.82 | 35.59 |
| FCD extraction method | 27.43 | 31.37 | 44.72 |
| LPR extraction method | 12.31 | 15.43 | 22.72 |
| Weight distribution fusion method | 10.39 | 11.46 | 16.07 |
| The proposed fusion method | 9.34 | 10.43 | 13.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Yang, L. Reliable Estimation of Urban Link Travel Time Using Multi-Sensor Data Fusion. Information 2020, 11, 267. https://doi.org/10.3390/info11050267
Guo Y, Yang L. Reliable Estimation of Urban Link Travel Time Using Multi-Sensor Data Fusion. Information. 2020; 11(5):267. https://doi.org/10.3390/info11050267
Chicago/Turabian StyleGuo, Yajuan, and Licai Yang. 2020. "Reliable Estimation of Urban Link Travel Time Using Multi-Sensor Data Fusion" Information 11, no. 5: 267. https://doi.org/10.3390/info11050267
APA StyleGuo, Y., & Yang, L. (2020). Reliable Estimation of Urban Link Travel Time Using Multi-Sensor Data Fusion. Information, 11(5), 267. https://doi.org/10.3390/info11050267




