1. Introduction
A best-first search algorithm was initially introduced as a method to find the game-theoretic value using a specific technique to progress towards a game tree framework. One of the prominent best-first search algorithms in such a context is the proof number search (PNS) [
1]. PNS utilizes two variables, proof and disproof numbers (
and
for short, respectively), as the search indicators to find the best possible options. The proof number of a node represents the smallest number of leaf nodes that have to be proven in order to prove that it is a win, while the disproof number represents the smallest number of leaf nodes that have to be disproved in order to prove that it is a loss, thus representing the difficulty in proving a node [
2]. A node is then chosen to provide the best possible choice (called the most proving node (MPN)) and subsequently expanded for further search [
3,
4,
5].
Finding a game-theoretic value has shown to be fruitful when employing PNS [
6]. However, several drawbacks observed from its implementation include the usage of a large amount of memory space, overly long solutions, and the see-saw effect (The see-saw effect is observed when the search goes back and forth between several sub-trees, preventing it from progressing to a deeper branch) [
3,
4]. An improvement of PNS that aims to reduce the usage of computation resources is the depth-first proof number (df-pn) search [
7], which turns PNS from a best-first search algorithm into a depth-first search by introducing iterative deepening. The df-pn expands less on the interior node and reduces the number of proof numbers and disproof numbers that have to be recomputed.
The Monte Carlo tree search (MCTS) is another prevalent best-first search algorithm that has been employed to solve games. First, proposed by [
8], the MCTS framework consists of four steps: (1) selection, (2) expansion, (3) simulation, and (4) backpropagation. The algorithm starts with selecting the next action based on a stored value (selection). When it encounters a state that cannot be found in the tree, it expands the node (expansion). The node expansion is based on multiple, randomly simulated games (simulation or playout). The value is then stored and backpropagated to the root of the tree, where the algorithm continues to repeat the steps until the desired outcome is reached (backpropagation). MCTS utilizes simulation to gain information from unexplored nodes, and this was expanded by the introduction of upper confidence bound applied to trees (UCT) by [
9]. A new best-first search algorithm derived from MCTS and UCT was then introduced by [
10]. The algorithm’s goal was to overcome the difficulty found in building heuristic knowledge for a non-terminal game state by employing stochastic simulations. Determining a game-playing strategy is effective when using multiple simulations. Its usage has become well known, especially in the field of Go, and in part led to the AlphaGo’s wins against top grandmasters [
11].
Although it has been proven that MCTS converges to minimax when evaluating the available moves [
12], MCTS converges only in so-called “Monte Carlo Perfect” games [
13]. By leveraging both strengths of PNS and MCTS, an improved game solver’s quality is expected. An early example of such a combination is the Monte Carlo proof number search (MCPNS) [
14]. The work proposed the best-first search algorithm by employing its MIN/SUM rules to backpropagate information coming from the simulation, while gaining access to node information based on its Monte Carlo infused proof number, called the Monte Carlo proof number (
). The MCPNS provides a better degree of flexibility while retaining its reliability. However, the drawback is that its MIN/SUM rules compute results from integer numbers, while the statistical results from the MCTS counterparts produce a real number, thus leading to a loss of information from the simulation (Such information loss is related to the minimization of accuracy in the floating-point arithmetic, where it deals with complicated formulae that suffer from substantial errors due to round-off (called numerical stability). This problem can be addressed by adopting extended precision or logarithm transform, where such information becomes numerically stable and can compute to full double precision. Hence, we would direct interested readers to [
15] for further reading.
To conform to the requirement of processing real numbers derived from statistical probability, the probability-based proof number search (PPNS) [
16] is used, which solves positions in a simulated balanced and unbalanced tree [
16]. It applies the idea of “searching with probabilities” first suggested by [
17] to draw better results from real numbers produced by Monte Carlo simulation in the playout step.
PPNS is proposed to address the need for processing real numbers that are derived from statistical information that of the product of Monte Carlo simulation. PPNS is independently developed but utilizes similar principles as product propagation (PP) [
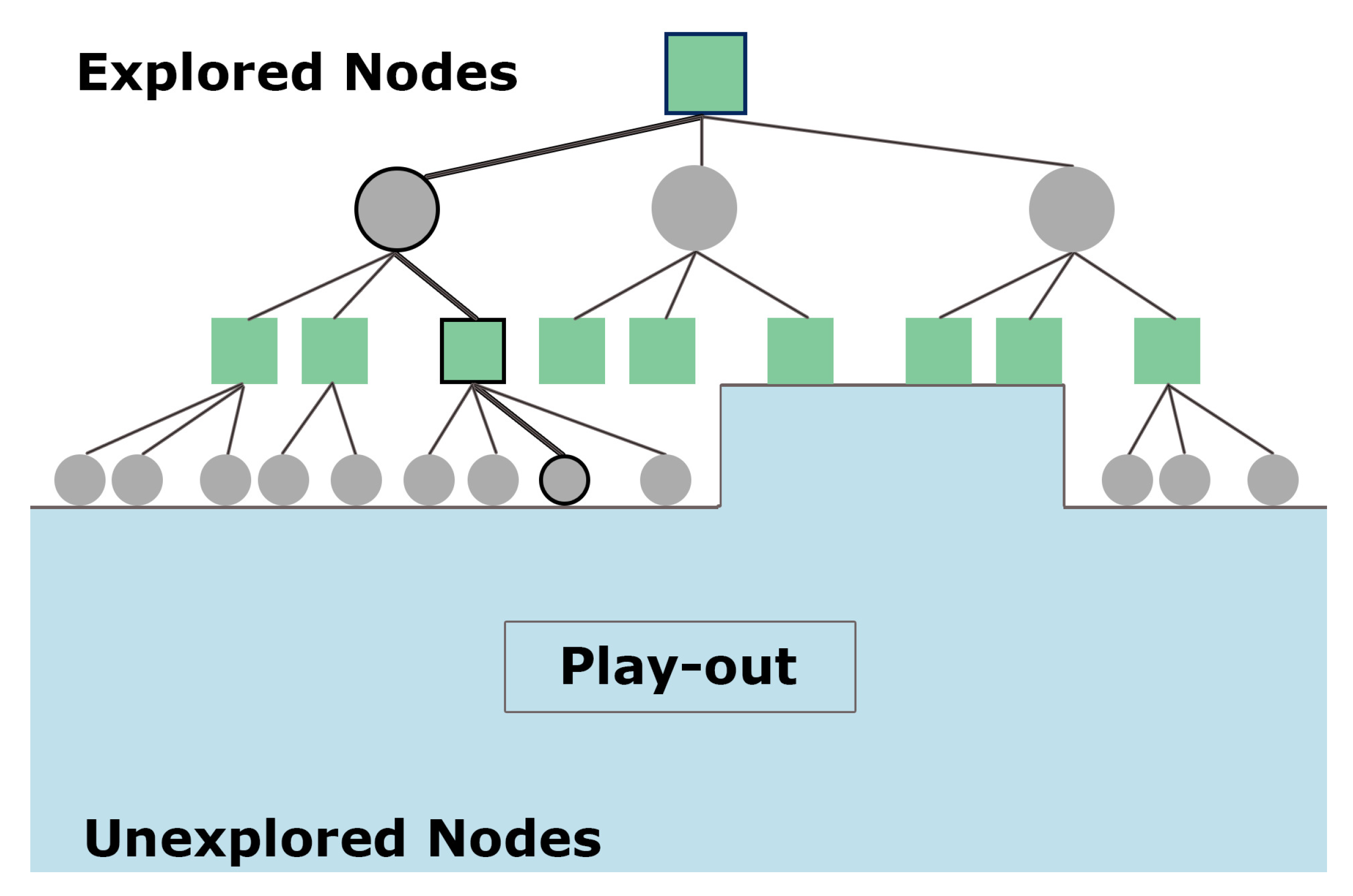
18]. The main difference between PPNS and PNS is that the PPNS indicator is derived from both explored and unexplored areas of the tree to obtain information on the most proving node (MPN) (
Figure 1), whereas PNS utilizes only the information from the explored area of the tree [
19].
Nevertheless, the quality of PPNS as a solver in an unbalanced and balanced game tree, especially in a real game environment, is limited. Connect Four and Othello are two-player perfect information games, which have distinct features for application of the PPNS. Connect Four can be won between 13-ply and 42-ply, as well as by sudden death moves, thus making its game tree highly varied, and its structure unbalanced. Meanwhile, Othello is a well-balanced game that requires a sequential decision to end the game and offers fairness to both sides of the players [
20,
21], thus making it a good candidate for a real game with a balanced game tree. Connect Four is characterized as
P-Space, while Othello is
P-space complete [
1]. All of these traits make these two games suitable for use as testbeds to characterize the nature of PPNS as well as its distinction from other game solvers. Therefore, the contribution of this study is twofold. Firstly, this study intends to determine the characteristics that make the performance of PPNS optimal in solving game positions. Secondly, such performance of the PPNS is demonstrated by adopting it in real two-player, zero-sum, perfect information games such as Othello and Connect Four.
5. Discussion
This study conducted experiments on two distinct games, Connect Four and Othello, which adopted to examine the quality of PPNS. These games represent the real case of unbalanced and balanced game tree structures. In addition, two related algorithms, PNS and MCPNS, were similarly applied to these games for comparison purposes. Based on such a setting, the experiments were conducted in twofold.
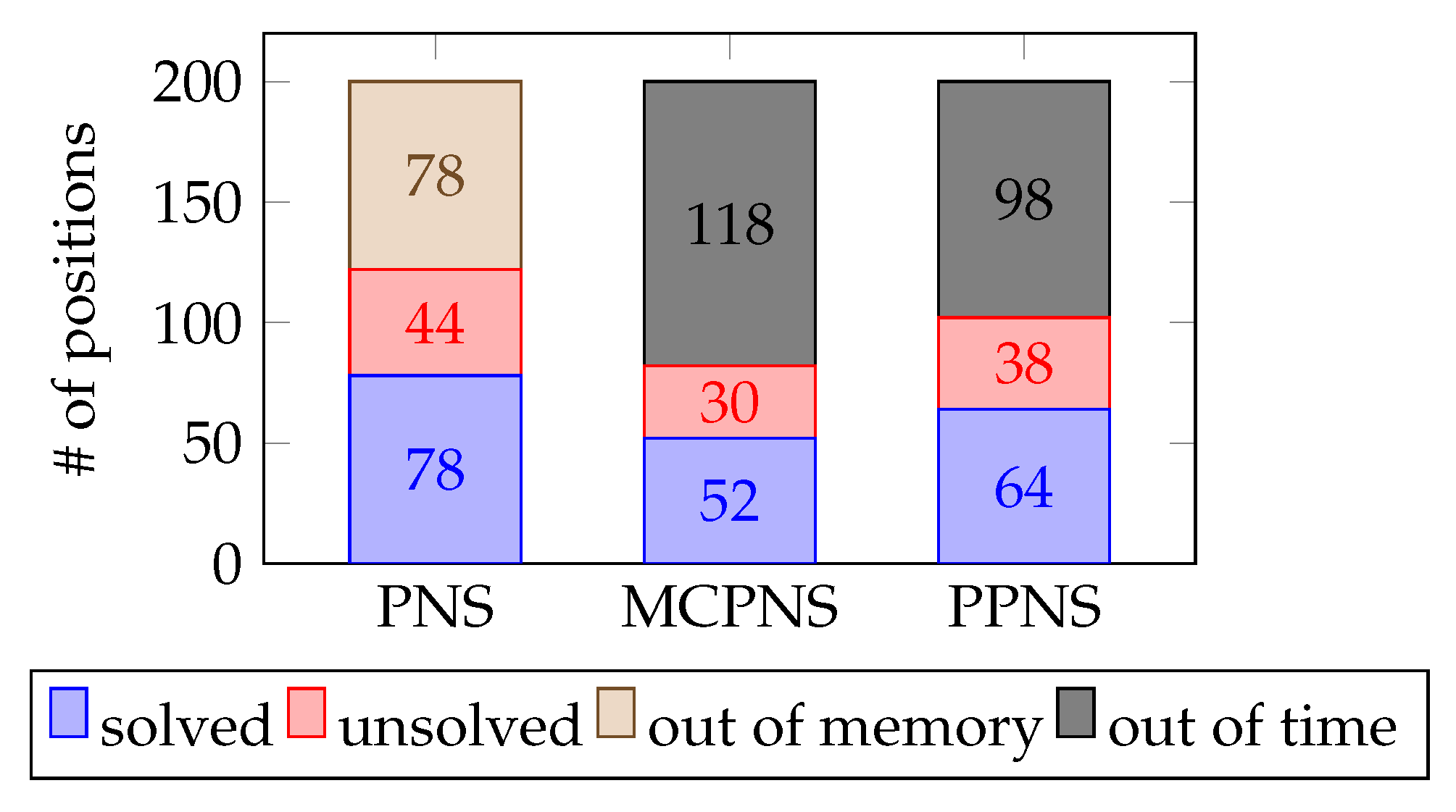
In the first experiment, among the three algorithms applied to Connect Four, PPNS showed that there are positions where it performs suboptimally. It visits more nodes than PNS before solving the positions (against the idea of PPNS combining information of the visited node and the probability of unexplored nodes). Upon further analysis, the prolonged search problem was identified, which caused the PPNS to underperform. The compared algorithms (PNS and MCPNS) uses the integer-based backpropagation technique, while PPNS use real numbers—thus making the precision of floating-point affect PPNS performance. Thus, the PPN of a node went through product operations, where errors on precision arose.
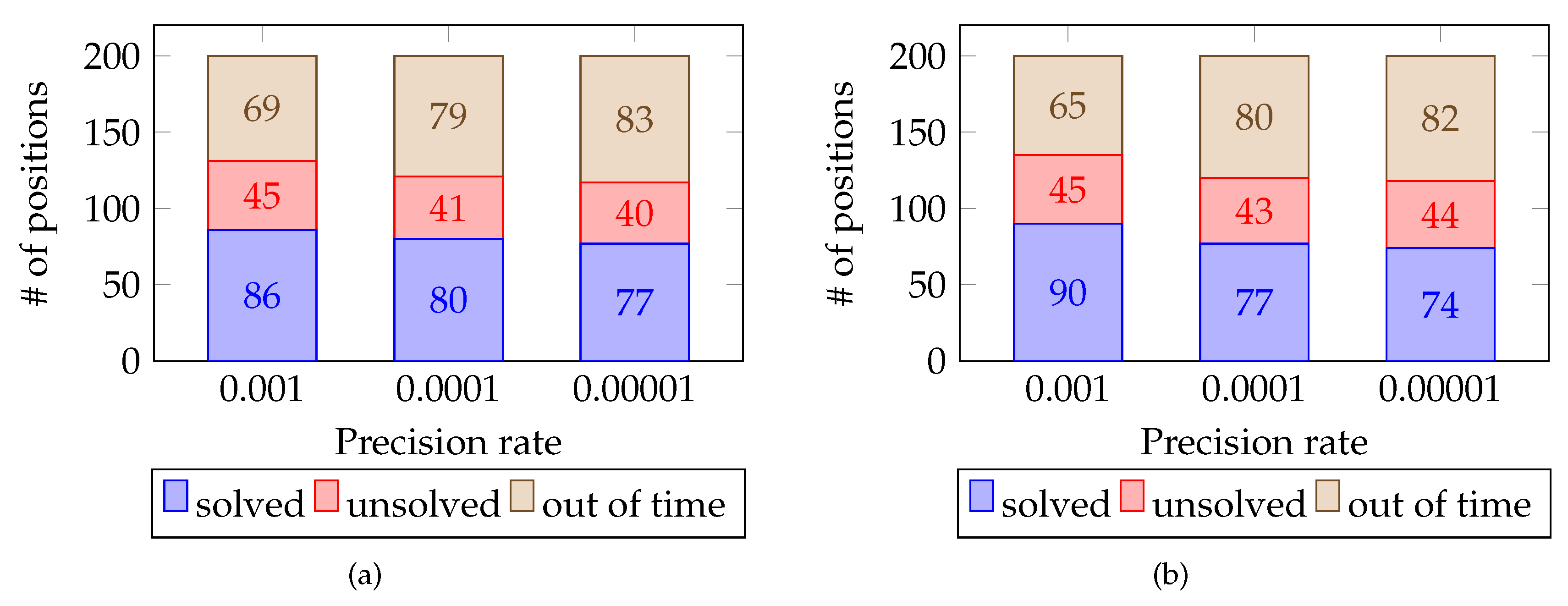
A precision rate () parameter is introduced to the PPNS algorithm to negate the precision problem. Experiments with various configurations show that the addition of the value increases the performance of PPNS without affecting its accuracy result. It was found that the closer the value is to , the better the PPNS performance. However, a value lower than will worsen the PPNS performance. The results from the experiments demonstrate that PPNS with a value reduces the amount of explored nodes needed to solve a position by up to 57%. This situation implies that even a small amount of explored nodes allowed information from an unexplored area to be exploited and combined to reach the desired goal.
Another experiment was also performed while considering the different stages of the Othello game (opening, mid-opening, and middle stages). It was observed that an increasing amount of information allowed for more positions to be solved. PPNS utilizes information from both explored and unexplored nodes, resulting in a drastically better performance compared to the other two algorithms, and highlighting the importance of information from the explored nodes.
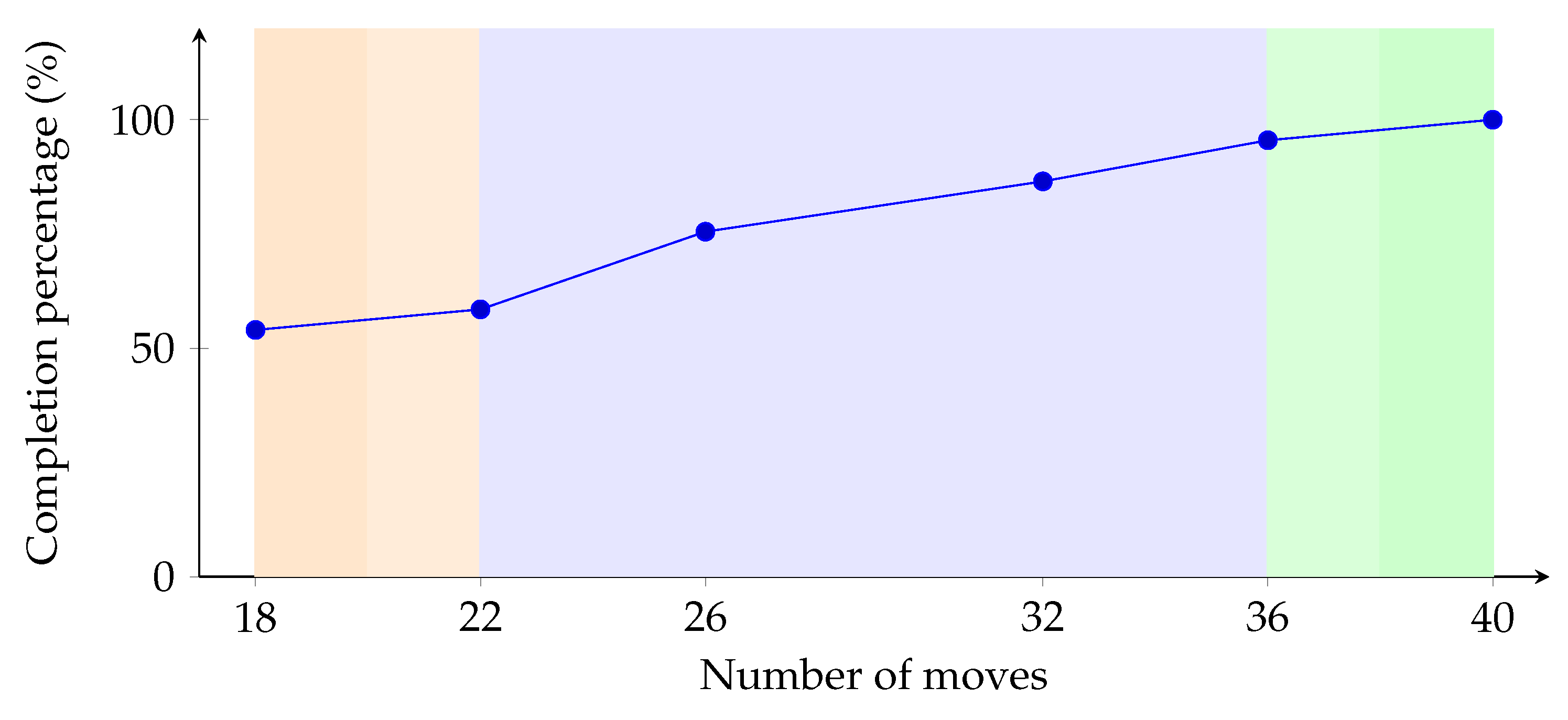
The experiment was expanded to observe the behavior of PPNS into more specific stages of Othello. The result from additional stages of Othello’s positions serves as an indication of the PPNS behavior. In the opening and mid-opening stages, the player mobility (and branching factor of the search tree) is limited, and the possible search space is enormous. As such, statistical information from the unexplored nodes during these stages was crucial for selecting the most proving node (MPN), which either leads to better mobility or just thinning out the number of choices (a sharp increase in the PPNS completion percentage).
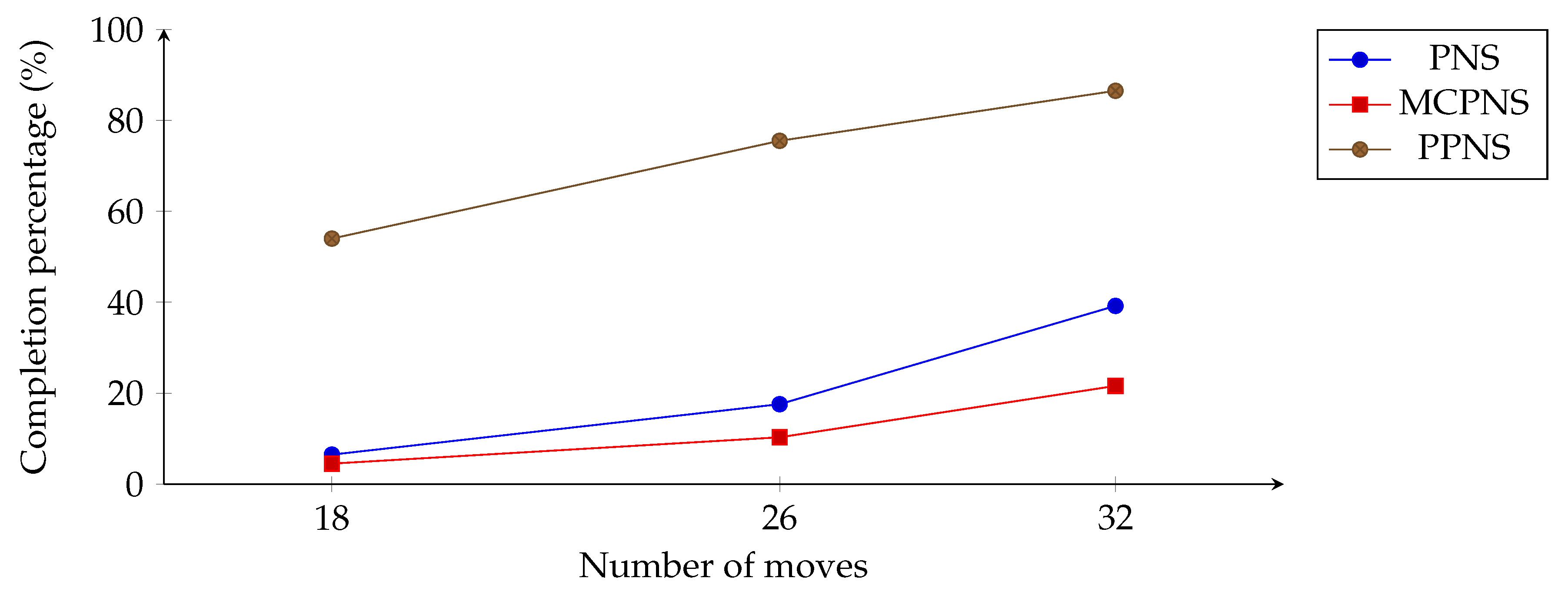
Compared to PNS and MCPNS, such an increase appears in the later stage (middle) when more information becomes available. This situation showed that PPNS was able to obtain such information earlier. For the middle to end game stages, the PPNS degree of completion slowly increases to 100% completion when approaching the end game. In this stage, players’ mobility is again limited because the board is getting filled with player disks, and the search space becomes small. In this stage, information from the explored nodes becomes more prominent since its information is more readily available. As such, information from unexplored nodes becomes prominent and highly critical for PPNS and lies between the opening and middle stages of the Othello game.
Current insight suggested from the two experiments leads to a hypothesis that PPNS is suitable for a game that requires a long look-ahead strategy. PPNS has been introduced to solve two different tree structures (an unbalanced tree in Connect Four and a balanced tree in Othello), where PPNS demonstrates better performance than the other related algorithms. PPNS application to Connect Four showed that the quality of the available information is critical compared to the quantity of the information, where a small amount of explored nodes, combined with the appropriate statistical information (or rather the precision of said information) of the unexplored nodes, can vastly improve the performance of the solver. Furthermore, the PPNS application to Othello demonstrates the importance of considering the appropriate “moment” to take advantage of the information from both the explored and unexplored nodes to solve more positions faster and earlier.
Author Contributions
Conceptualization, A.P.; methodology, A.P.; software, A.P.; validation, A.P., M.N.A.K. and H.I.; formal analysis, A.P.; investigation, A.P.; resources, M.N.A.K. and H.I.; data curation, M.N.A.K. and H.I.; writing—original draft preparation, A.P.; writing—review and editing, M.N.A.K. and H.I.; visualization, M.N.A.K. and H.I.; supervision, M.N.A.K. and H.I.; project administration, M.N.A.K. and H.I.; funding acquisition, M.N.A.K. and H.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by a grant from the Japan Society for the Promotion of Science, within the framework of the Grant for fundamental research.
Conflicts of Interest
The authors declare that there is no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Allis, L.V.; van der Meulen, M.; Van Den Herik, H.J. Proof-number search. Artif. Intell. 1994, 66, 91–124. [Google Scholar] [CrossRef]
- Khalid, M.N.A.; Yusof, U.K.; Iida, H.; Ishitobi, T. Critical Position Identification in Games and Its Application to Speculative Play. In Proceedings of the International Conference on Agents and Artificial Intelligence, Lisbon, Portugal, 10–12 January 2015; SCITEPRESS—Science and Technology Publications, Lda: Setubal, Portugal, 2015; Volume 2, pp. 38–45. [Google Scholar] [CrossRef]
- Kishimoto, A.; Winands, M.H.; Müller, M.; Saito, J.T. Game-tree search using proof numbers: The first twenty years. Icga J. 2012, 35, 131–156. [Google Scholar] [CrossRef]
- Ishitobi, T.; Plaat, A.; Iida, H.; van den Herik, J. Reducing the Seesaw Effect with Deep Proof-Number Search. In Advances in Computer Games; Plaat, A., van den Herik, J., Kosters, W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 185–197. [Google Scholar]
- Primanita, A.; Iida, H. Nature of Probability-based Proof Number Search. In Proceedings of the Sriwijaya International Conference of Information Technology and Its Applications (SICONIAN), Palembang, Indonesia, 16 November 2019. [Google Scholar]
- Van Den Herik, H.J.; Winands, M.H. Proof-number search and its variants. In Oppositional Concepts in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 91–118. [Google Scholar]
- Nagai, A. Df-pn Algorithm for Searching AND/OR Trees and Its Applications. Ph.D. Thesis, Department of Information Science, University of Tokyo, Tokyo, Japan, 2002. [Google Scholar]
- Coulom, R. Efficient selectivity and backup operators in Monte Carlo tree search. In International Conference on Computers and Games; Springer: Berlin/Heidelberg, Germany, 2006; pp. 72–83. [Google Scholar]
- Kocsis, L.; Szepesvári, C. Bandit based Monte Carlo Planning. In ECML-06. Number 4212 in LNCS; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar]
- Chaslot, G.M.J.B.; Winands, M.H.M.; Herik, H.J.V.D.; Uiterwijk, J.W.H.M.; Bouzy, B. Progressive strategies for Monte Carlo tree search. New Math. Nat. Comput. 2008, 4, 343–357. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef] [PubMed]
- Bouzy, B.; Tutorial, C. Old-fashioned computer go vs monte-carlo go. In Proceedings of the IEEE Symposium on Computational Intelligence in Games (CIG), Honolulu, HI, USA, 1–5 April 2007. [Google Scholar]
- Althöfer, I. On board-filling games with random-turn order and Monte Carlo perfectness. In Advances in Computer Games; Springer: Berlin/Heidelberg, Germany, 2011; pp. 258–269. [Google Scholar]
- Saito, J.T.; Chaslot, G.; Uiterwijk, J.W.; Van Den Herik, H.J. Monte Carlo proof-number search for computer Go. In International Conference on Computers and Games; Springer: Berlin/Heidelberg, Germany, 2006; pp. 50–61. [Google Scholar]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; SIAM: Philadelphia, PA, USA, 2002; Volume 80. [Google Scholar]
- Song, Z.; Iida, H.; Van Den Herik, H.J. Probability based Proof Number Search. In Proceedings of the 11th International Conference on Agents and Artificial Intelligence, Prague, Czech Republic, 19–21 February 2019. [Google Scholar]
- Palay, A.J. Searching with Probabilities; Technical Report; Carnegie-Mellon Univ Pittsburgh PA Dept of Computer Science: Pittsburgh, PA, USA, 1983. [Google Scholar]
- Saffidine, A.; Cazenave, T. Developments on product propagation. In International Conference on Computers and Games; Springer: Berlin/Heidelberg, Germany, 2013; pp. 100–109. [Google Scholar]
- Stern, D.; Herbrich, R.; Graepel, T. Learning to solve game trees. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 839–846. [Google Scholar]
- Van Eck, N.J.; van Wezel, M. Application of reinforcement learning to the game of Othello. Comput. Oper. Res. 2008, 35, 1999–2017. [Google Scholar] [CrossRef]
- Buro, M. The evolution of strong Othello programs. In Entertainment Computing; Springer: Berlin/Heidelberg, Germany, 2003; pp. 81–88. [Google Scholar]
- Edelkamp, S.; Kissmann, P. On the complexity of BDDs for state space search: A case study in Connect Four. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]
- Maby, E.; Perrin, M.; Bertrand, O.; Sanchez, G.; Mattout, J. BCI could make old two-player games even more fun: A proof of concept with “Connect Four”. Adv. Hum. Comput. Interact. 2012, 2012, 124728. [Google Scholar] [CrossRef]
- Allis, V. A Knowledge-Based Approach of Connect-Four-the Game is Solved: White Wins. Master’s Thesis, Vrije Universiteit, Amsterdam, The Netherlands, 1988. [Google Scholar]
- Van Den Herik, H.J.; Uiterwijk, J.W.; Van Rijswijck, J. Games solved: Now and in the future. Artif. Intell. 2002, 134, 277–311. [Google Scholar] [CrossRef]
- Lazard, I. Othello Strategy Guide. 1993. Available online: http://radagast.se/othello/Help/strategy.html (accessed on 18 October 2019).
Figure 1.
Explored and unexplored nodes in a MIN/SUM game tree framework. Green squares signify MIN nodes and gray circles signify SUM nodes. Nodes with black outline signify the most proving node.
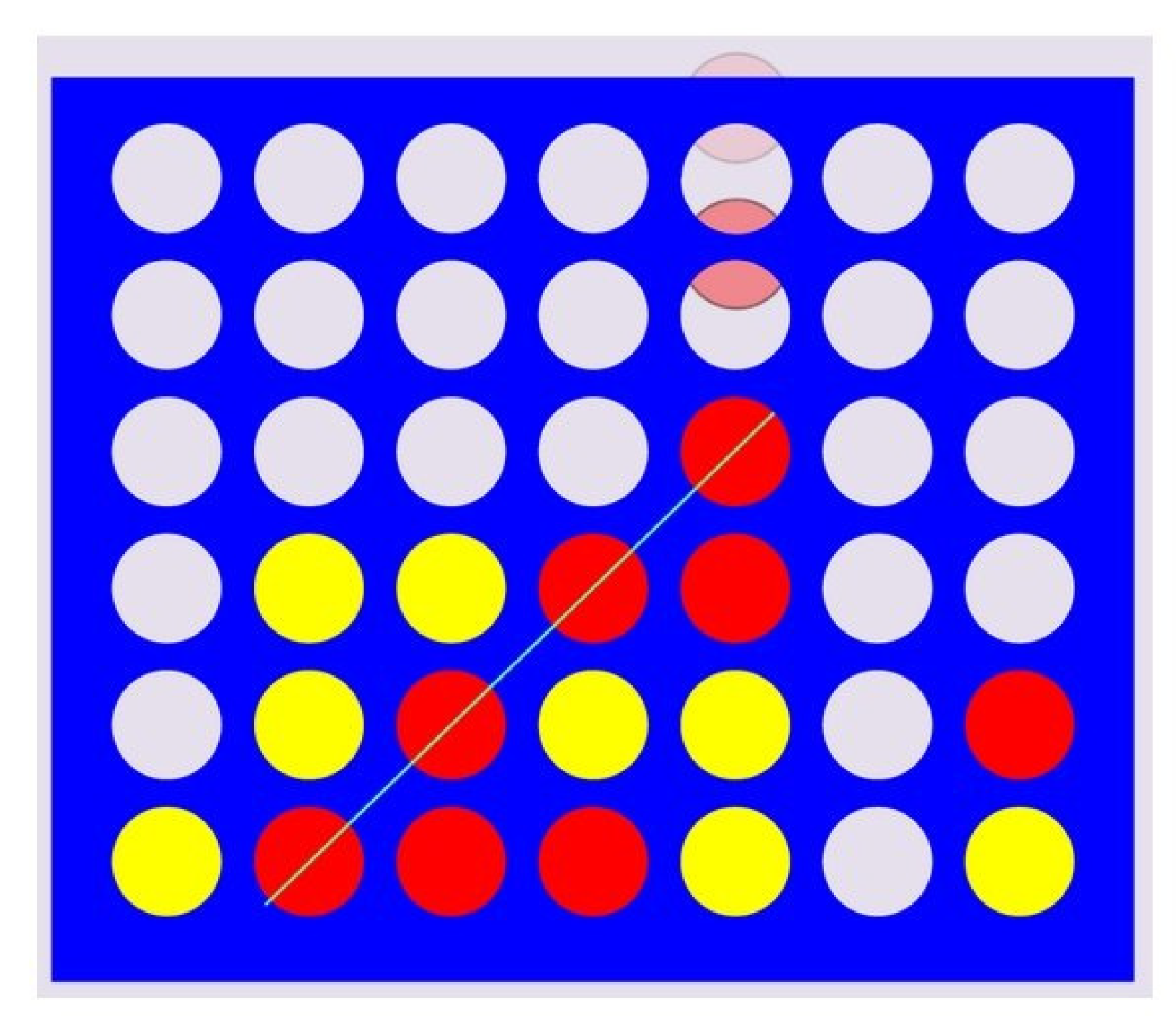
Figure 2.
Illustration of Connect Four with a
board (adopted from [
23]).
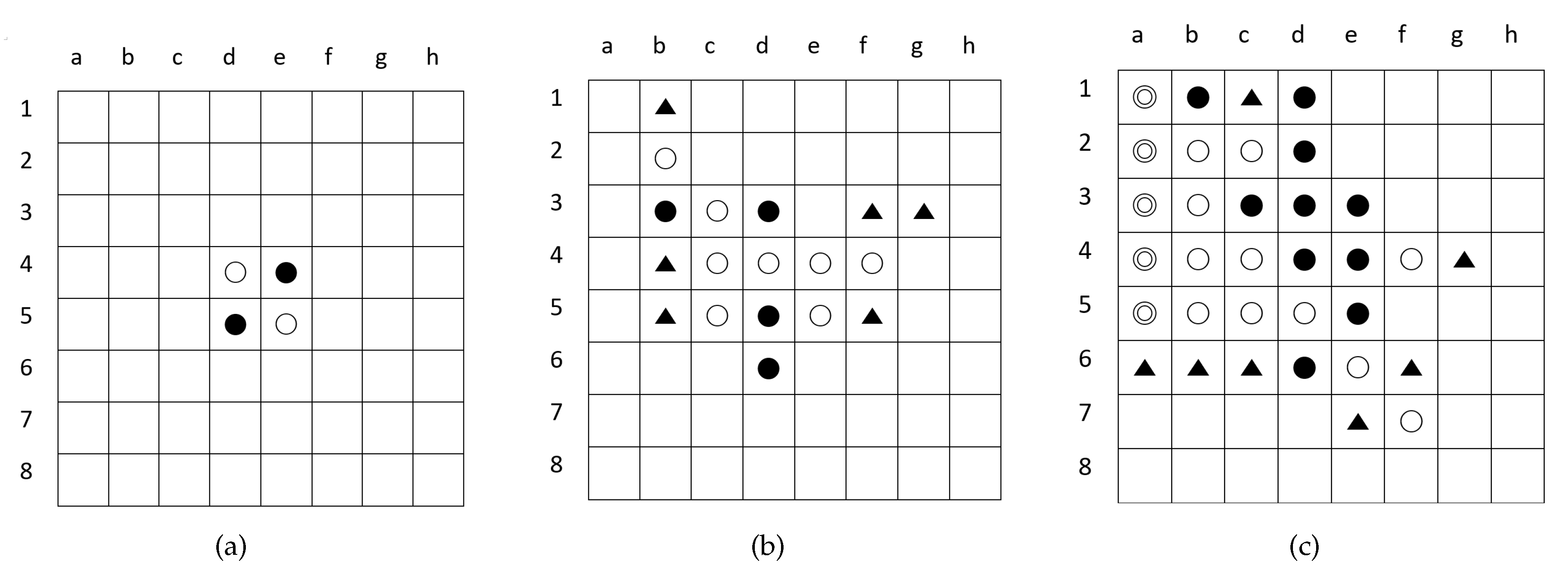
Figure 3.
Illustration of Othello with an board. (a) initial position; (b) After eight moves, black is to play. The triangle marked the black player’s mobility of six (six move options); (c) After 22 moves, black is to play. The triangle marked the black player’s mobility of seven (seven position options), and the white disks with marked inner circles are the stable disks (cannot be captured by the black player).
Figure 4.
Number of Connect Four positions solved, unsolved, and out of bounds by proof number search (PNS), Monte Carlo proof number search (MCPNS), and probability-based proof number search (PPNS).
Figure 5.
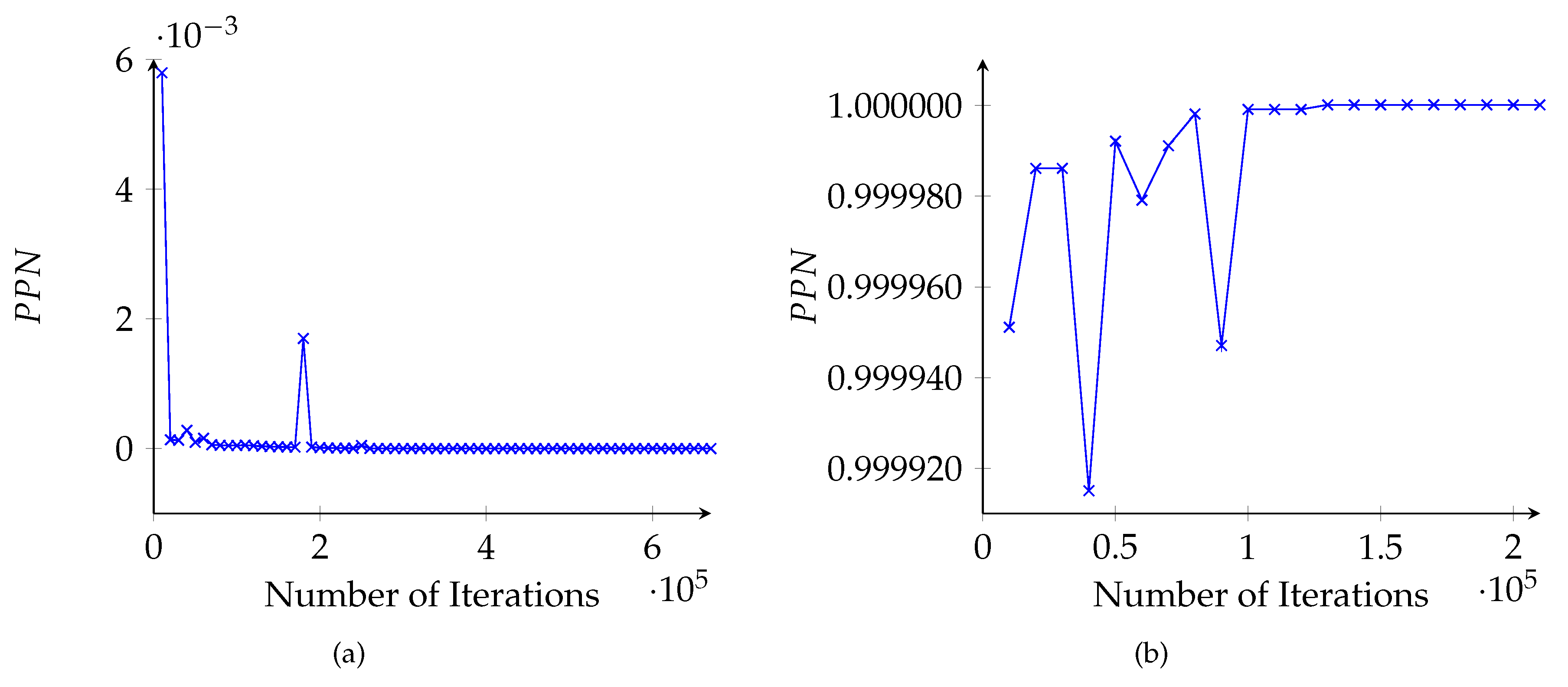
Probability-based proof number (PPN) value of the root of two different positions for PPNS. (a) an example position with a time difference of 322.345 s; (b) an example position with a time difference of 77.802 s.
Figure 6.
Number of positions solved, unsolved, and out of bounds by PPNS. (a) , (b) .
Figure 7.
The completion percentage of PNS, MCPNS, and PPNS for different numbers of moves.
Figure 8.
The completion percentage of PPNS in different stages of Othello. The left-most area colored in orange represents the opening stage of Othello, the middle area (blue) represents the middle game of Othello, and the right-most green area represents the end game of Othello.
Table 1.
Average time and node for each PPNS configurations.
| | Average Time(s) * | Average Node ** |
|---|
| 0.01 | no precision | 251.180925 | 2,004,052.895 |
| 0.01 | 0.001 | 183.256315 | 1,323,718.975 |
| 0.01 | 0.0001 | 214.63364 | 1,582,187.985 |
| 0.01 | 0.00001 | 226.707205 | 1,667,750.875 |
| 0.001 | 0.001 | 174.90736 | 1,269,587.96 |
| 0.001 | 0.0001 | 217.987025 | 1,614,710.08 |
| 0.001 | 0.00001 | 229.07937 | 1,638,641.2 |
Table 2.
Experimental result of different algorithms applied to Othello positions.
| Moves | Algorithm | Solved | Unsolved | Out | Completion * (%) |
|---|
| 18 | PPNS | 52 | 56 | 92 | 54.00 |
| PNS | 12 | 1 | 187 | 6.50 |
| MCPNS | 5 | 4 | 191 | 4.50 |
| 26 | PPNS | 63 | 88 | 49 | 75.50 |
| PNS | 19 | 16 | 165 | 17.50 |
| MCPNS | 10 | 10 | 180 | 10.00 |
| 32 | PPNS | 82 | 91 | 27 | 86.50 |
| PNS | 39 | 39 | 122 | 39.00 |
| MCPNS | 6 | 37 | 157 | 21.50 |
Table 3.
Additional experiment result of applying PPNS to different stages of Othello positions.
| Moves | Solved | Unsolved | Out | Completion * (%) |
|---|
| 18 | 52 | 56 | 92 | 54.00 |
| 22 | 60 | 57 | 83 | 58.50 |
| 26 | 63 | 88 | 49 | 75.50 |
| 32 | 82 | 91 | 27 | 86.50 |
| 36 | 97 | 94 | 8 | 95.50 |
| 40 | 83 | 117 | 0 | 100.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).