Measuring Language Distance of Isolated European Languages

Abstract

Phylogenetics is a sub-field of historical linguistics whose aim is to classify a group of languages by considering their distances within a rooted tree that stands for their historical evolution. A few European languages do not belong to the Indo-European family or are otherwise isolated in the European rooted tree. Although it is not possible to establish phylogenetic links using basic strategies, it is possible to calculate the distances between these isolated languages and the rest using simple corpus-based techniques and natural language processing methods. The objective of this article is to select some isolated languages and measure the distance between them and from the other European languages, so as to shed light on the linguistic distances and proximities of these controversial languages without considering phylogenetic issues. The experiments were carried out with 40 European languages including six languages that are isolated in their corresponding families: Albanian, Armenian, Basque, Georgian, Greek, and Hungarian.

1. Introduction

The aim of computational linguistic phylogenetics is to estimate evolutionary histories of languages, which are usually represented in the form of a tree where the root stands for the common ancestor of its daughter languages, which are the leaves [1]. The most used technique to elaborate phylogenetic trees is known as lexicostatistics, consisting of comparing and classifying languages on the basis of a pre-defined set of concepts and their corresponding words in the languages to be classified. The lexicostatistic method, developed by Morris Swadesh in the 1950s [2], requires defining a standard list of concepts, determine whether the corresponding words are written in similar form (whether they are cognate or not), compute the ratio of cognates shared by each pair of languages giving rise to a similarity matrix, and generate a graphic (usually a tree) on the basis of this matrix [3]. Such a strategy had a strong impact on phylogenetics and historical linguistics.

Lexicostatistic methods typically depend on lists of words that are cognates and for some languages this resource might not be available. Besides, this method is designed to compare languages that already have a high degree of relatedness since they share a large number of cognates, but it is not well suited for comparing languages that have already been separated for a long time. This is the case of isolated languages. In Europe, even though most languages belong to a single-language family, namely Indo-European, there is one isolate language, Basque, and other few languages belonging to non-Indo-European language families, e.g., Georgian (Caucasian Kartvelian) and Finnish, Estonian, and Hungarian (Uralic or Finno-Ugric). In addition, a few languages can be identified as Indo-European, although they cannot be assigned to any larger group: Greek, Armenian, and Albanian. These three are the only “living” isolated branches of the Indo-European language family. By contrast, most languages belong to quite large Indo-European language groups such as Germanic, Latin, Celtic, or Slavic [4].

The objective of this article is to calculate the linguistic distance between these isolated languages and the rest using corpus-based techniques and natural language processing methods. More precisely, we measure the distance between each isolated language and the other European languages, so as to create a similarity matrix of distances and proximities of these controversial languages without considering phylogenetic and diachronic relations. We calculate the distance between languages from a purely synchronic perspective.

From a methodological point of view, we do not use the lexicometric strategy based on a list of concepts and cognates, but we adopt corpus-based methods that have given such good results in other fields, namely language identification and authorship detection.

Our hypothesis is that it is possible to find similarity patterns between isolated languages and other European languages by using corpus-based measures of language distance. We believe that, if different measures and strategies coincide in returning the same pattern of approximation, then we can conclude that there is a possibility of closeness between languages that in principle do not have an evident relationship according to typological studies. The experiments confirmed a quite evident relationship between Basque and Georgian. By contrast, concerning Albanian, Armenian, and Hungarian, we did not find any evidence of approximation to other European languages or between them.

The article is organized as follow. Related work is introduced in Section 2. Then, in Section 3, we describe some strategies to measure language distance. Section 4 explains the experiments we carried out with a set of forty European languages, six of them being isolated in terms of linguistic family, and discusses the results. Section 5 presents the final conclusions.

2. Related Work

In the last few decades, the distance between languages has been defined and measured by making use of various methods and strategies. Most compare word lists to look for phylogenetic relationships, while a few approaches, based on corpus, search for similarities from a synchronic point of view.

2.1. Phylogenetics and Lexicostatistics

Computational linguistic phylogenetics aims at automatically building a rooted tree representing how a set of related languages evolve across time [5]. As mentioned above, the most popular strategy to build this phylogenetic tree is the use of lexicostatistics, which is a method within the field of historical linguistics that compare languages by the means of lists of lexical cognates they share or not [5,6,7,8,9,10]. In other very related research, the objective is not to distinguish cognates from non-cognates by just computing the Levenshtein distance between words of an open cross-lingual list so as to find the average of all pairwise distances in the list [11]. In dialectometry, stylometry, or second-language learning, similar methods are used to measure the linguistic distance [12].

A quite different strategy relies on traditional supervised machine learning techniques. The annotated dataset contains different types of linguistic features (also called characters) representing typological information [1,13]. Features are not only lexical, but can also be phonological or even syntactic features. An interesting dataset for training these models was described by Carling et al. [14]

2.2. Corpus-Based Approaches

Other approaches to language distance do not rely on lists of words/cognates, but on large corpora, both cross-lingual or parallel [15,16,17]. These approaches are based on models mainly built with n-grams of words or characters and languages are thus compared by making use of distributional similarity [15,16,17]. The work reported by Asgari and Mofrad [15] compared 50 languages from different families on the basis of a parallel corpus compiled from the Bible Translations Project [18].

In previous work, we applied perplexity-based methods to measure language distance using character n-grams from monolingual corpora [19]. The strategy was inspired by another earlier work to discriminate among closely related languages [20]. We also applied perplexity-based methods to other tasks such as measuring the intralinguistic distance between historical periods of the same language [21]. In fact, those approaches are very close to those used in more traditional tasks such as language detection, variety discrimination [20,22], or authorship attribution [23]. Notice that, in the last shared task organized in PAN at CLEF 2019 for authorship profiling and bot detection [23], most participants used traditional machine learning approaches, mainly Support Vector Machines (SVM), while only few participants approached the task with deep learning methods, including the new neural-based transformers. The evaluation carried out in that shared task showed that classical machine learning techniques (SVM, Random Forest, and Linear Regression), provided with the appropriate linguistic features, achieved the best results among all participants. This tendency is also found in other related tasks such as discriminating between similar languages and varieties. In the last VarDial Evaluation Campaign [24], as in previous years, systems based on neural networks did not reach competitive scores.

3. The Methods

Our strategies to measure language distance relies on different traditional techniques used in language detection and authorship attribution, which have given excellent results in their respective fields. We make use of two types of techniques: clustering performed with state-of-the-art algorithms in authorship attribution and a new method which consists of averaging the results of several distance metrics applied to pairs of language models.

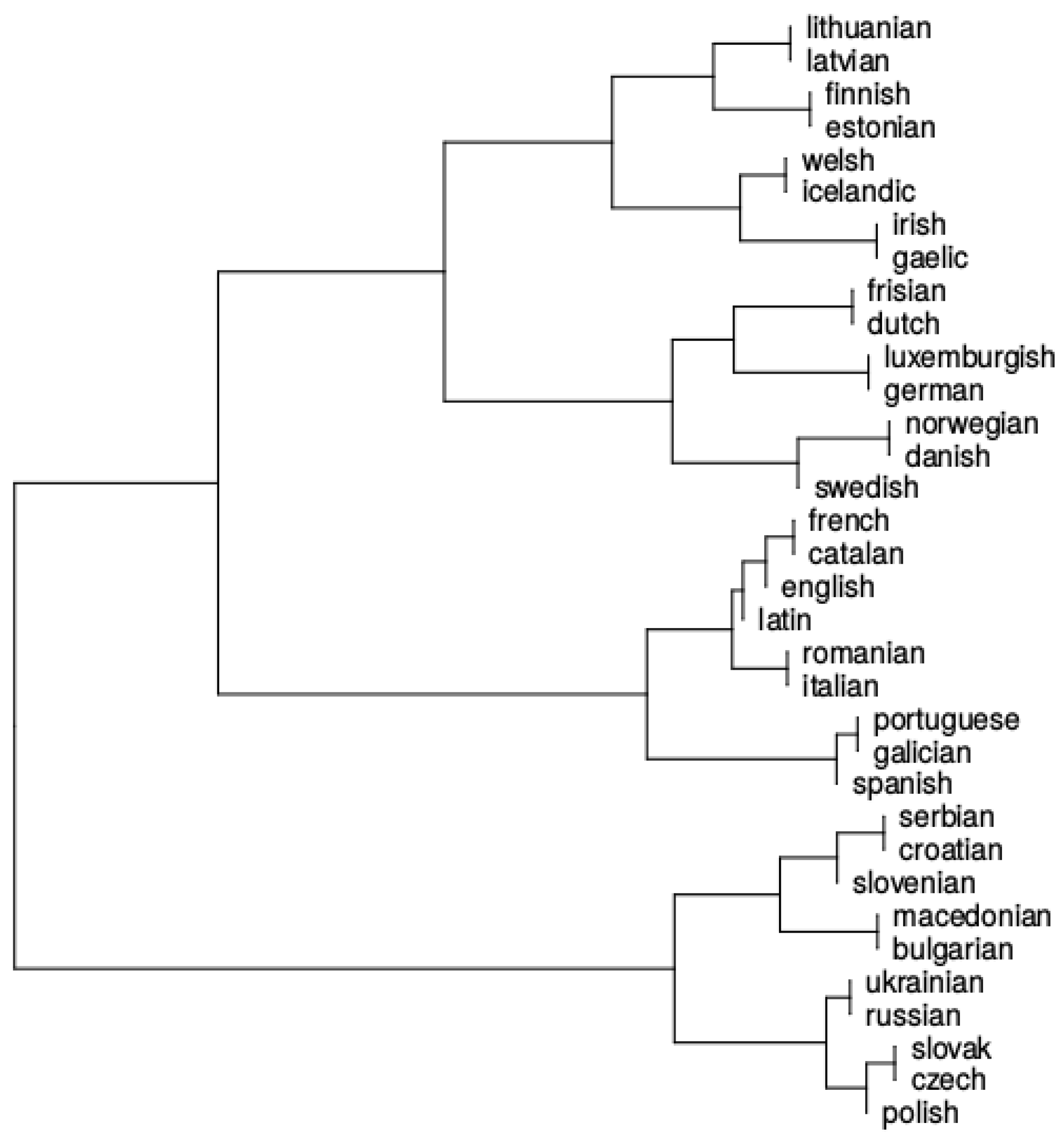
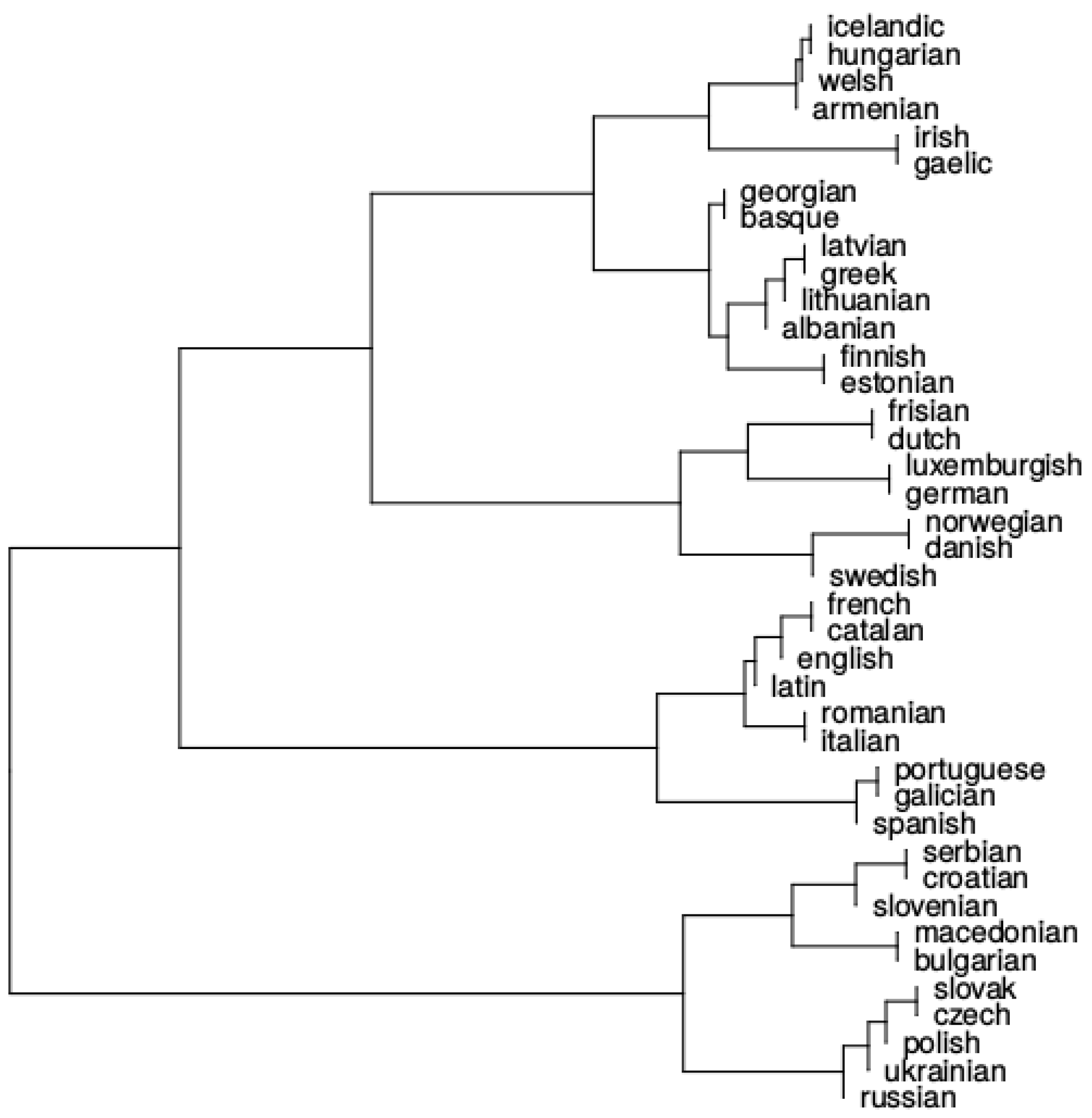
3.1. Language Clustering

Clustering analysis allows the languages to be grouped on the basis of n-gram similarities. The resulting clusters of individual languages are displayed in a dendrogram. We used an agglomerative clustering method very popular in authorship attribution and stylometric studies [25] based on the Delta measure [26] and Ward linkage method [27].

Delta measure normalizes frequencies by means of z-score to reduce the influence of very frequent words. For $f_i\left(D\right)$ being the frequency of n-gram i in document D, ${\mu }_i$ the mean frequency of the n-gram in the corpus, and ${\sigma }_i$ its standard deviation, then z-score is defined as follows:

$$z\left(f_i\left(D\right)\right)=(f_i\left(D\right)-{\mu }_i)/{\sigma }_i$$

(1)

Given the normalized document vectors, the Burrows’s Delta is just the Manhattan distance by using normalized frequencies with z-scores. Given documents $D_1$ and $D_2$, distance Delta $\Delta$ is computed as follows:

$$\Delta =\sum _{i=1}^n|z\left(f_i\left(D_1\right)\right)-z\left(f_i\left(D_2\right)\right)|$$

(2)

The lower the is Delta value, the higher is the similarity between the textual items compared. An attempt to improve the Burrows’s Delta is Eder’s Delta [28], which reduces the z-score weight of less-frequent words by considering a ranking factor. In experiments on authorship attribution reported by Calvo Tello [29], this last version outperformed the older versions of Delta as well as other distance/similarity measures. In our experiments, we applied specific configurations of this clustering methodology to language family detection including isolated languages.

The Ward linkage Method analyzes the variance of clusters instead of measuring the distance directly. Good performance of Ward’s method has been proven in many applications within the field of quantitative linguistics, authorship attribution, corpus linguistics, and related disciplines [30].

It is important to note here that our objective is not to find phylogenetic and family relations but to find distances and proximities with regard to these controversial isolated languages from a purely synchronic perspective. Thus, clustering is just another strategy to search for distances and similarities between different languages. We use well-known language families to verify that, given a specific configuration, clusters make sense and thus it is possible to find reliable similarities between unknown language pairs.

3.2. Language Distance Measures

In the second strategy, we explore other types of linguistic measures including those reported by Gamallo et al. [19]. We expand and extend the ones described in that work by proposing the following four measures: Perplexity, Kullback–Leibler divergence, Rank-Based distance, and Distance Metrics Mean. Notice that they were not originally designed to serve the purpose of measuring language distance as they were typically employed in other NLP tasks such as language detection or information retrieval. It is important to note that Perplexity, Kullback–Leibler, and Rank are asymmetric distances, i.e. divergences. We also propose a new measure consisting of the average of the scores obtained from the four measures after standardization.

Unlike the clustering strategy described above, the objective is not to make clusters of languages, but to compare pairs of language models. Given a specific language, the final result is a ranked list of 39 languages ordered by the value of the language distance.

3.2.1. Perplexity

Perplexity is a measure aimed at evaluating the quality of language models. It consists of measuring how well a language model predicts a given sample or test. More formally, perplexity is the inverse of the cross entropy of a given test. We use it to compare two languages, namely the proposed probability model of the source language (S) and the empirical distributions of the test language (T). The perplexity PP of T given the language model S is defined by the following equation:

$$PP(S,T)=2^{-{\sum }_{i}T\left(ng{r}_i\right)lo{g}_{2}S\left(ng{r}_i\right)}$$

(3)

where $ng{r}_i$ is a n-gram shared by both T and S. Equation (3) can be used to set the divergence between two different languages. The lower is the perplexity of T given S, the lower is the distance between the two compared languages. Languages may be modeled with n-grams of either words or characters.

3.2.2. Kullback–Leibler

Kullback–Leibler divergence [31] measures how much two distributions differ. Thus, we can use it to measure to what extent one probability distribution (for instance, the language model of the source language) is different from a reference probability distribution (e.g., the language model of the target language). Álvaro Iriarte et al. [32] described an experiment with Kullback–Leibler divergence to measure the distance between texts written by women with regard to men, and also texts written by academics versus non-academics. The Kullback–Leibler divergence KL of the distributions S and T of the source and target languages, respectively, is defined as follows:

$$KL(S,T)=\sum _{i}S\left(ng{r}_i\right)log\frac{S\left(ng{r}_i\right)}{T\left(ng{r}_i\right)}$$

(4)

Equation (4) allows computing how far the T distribution is from the S distribution, taking into account the probabilities of the n-grams (of words or characters) in each compared language.

3.2.3. Rank-Based

The Rank-Based distance between two languages relies on ranked lists. It takes the most frequent n-grams of each language list and computes a rank-order algorithm based on the “out-of-place” concept [33]. More formally, given the ranked lists $Ran{k}_S$ and $Ran{k}_T$ of the source and target languages, respectively, the rank-based distance, R, is computed as follows:

$$R(S,T)=\sum _{\begin{array}{c}i=1\\ ng{r}_i\in Ran{k}_S\end{array}}^K\left|\right(Ran{k}_S\left(ng{r}_i\right)-Ran{k}_T\left(ng{r}_i\right)|$$

(5)

where K stands for the number of the most frequent n-grams in each language, $Ran{k}_S\left(ng{r}_i\right)$ is the rank of a specific n-gram, $ng{r}_i$, in the source language, and $Ran{k}_T\left(ng{r}_i\right)$ is the rank of the same n-gram in the target.

3.2.4. Distance Metrics Mean

Distance Metric Mean between two languages, noted $DistMean$, is the average of five similarity/distance measures, namely Cosine, Manhattan, Canberra, Dice, and Euclidean:

$$\begin{array}{c}DistMean(S,T)=\hfill \\ \hfill \frac{1}{5}(Cosine(S,T)+Manhattan(S,T)+Camberra(S,T)+Dice(S,T)+Euclidean(S,T))\end{array}$$

(6)

These are coefficients typically used for clustering techniques, but we use them not for clustering, but for comparing language pairs. The mean of these five coefficients can be seen as a new robust distance measure. We consider that the five distance/similarity measures represent the most used set of metrics in textual and document similarity.

The five measures, $Cosine$, $Manhattan$, $Camberra$, $Dice$, and $Euclidean$ are computed as follows:

$$Cosine(S,T)=1-\frac{{\displaystyle \sum _{i}S\left(ng{r}_i\right)T\left(ng{r}_i\right)}}{\sqrt{{\sum }_{i}S{\left(ng{r}_i\right)}^2}\sqrt{{\sum }_{i}T{\left(ng{r}_i\right)}^2}}$$

(7)

$$Manhattan(S,T)={\displaystyle \sum _i|S\left(ng{r}_i\right)-T\left(ng{r}_i\right)|}$$

(8)

$$Canberra(S,T)={\displaystyle \sum _i\frac{|S\left(ng{r}_i\right)-T\left(ng{r}_i\right)|}{|S\left(ng{r}_i\right)|+|T\left(ng{r}_i\right)|}}$$

(9)

$$Dice(S,T)=1-\frac{{\displaystyle 2*\sum _{i}Min(S\left(ng{r}_i\right),T\left(ng{r}_i\right))}}{{\sum }_{i}S\left(ng{r}_i\right)+{\sum }_{i}T\left(ng{r}_i\right)}$$

(10)

$$Euclidean(S,T)={\displaystyle \sqrt{{\sum }_i{(S\left(ng{r}_i\right)-T\left(ng{r}_i\right))}^2}}$$

(11)

Given that Cosine and Dice are similarity measures, we need to subtract the value from 1 to make them distances, similar to the other three measures.

It is important to note that we have not implemented the Delta measure because, although we use Manhattan distance, frequencies of n-grams were not normalized with z-score.

3.2.5. Average Language Distance

Average Language Distance (ALD) consists of both standardizing and averaging the scores obtained from the results of the four distance measures: $PP$, $KL$, R, and $DistMean$. The average of the four measures minimizes some of the disadvantages and problems of applying each of them individually.

It should be clear that, to carry out the clustering strategy, we used third party software: Stylo, a R package for clustering analysis [28]. However, for the second strategy comparing language models, we implemented all the measures with PERL, and the software is available at GitHub  (https://github.com/gamallo/LanguageDistance). To implement the $KL$ measure, we made use of the PERL module Math::KullbackLeibler::Discrete (https://github.com/ambs/Math-KullbackLeibler-Discrete).

4. Experiments

The objective of the experiments was to discover which languages are closest to the six so-called isolated languages, namely Albanian, Armenian, Basque, Georgian, Greek, and Hungarian. The experiments also tried to discover if there is any relationship between them. We placed Hungarian as isolated and not Estonian and Finnish because the latter two are already clearly classified in the Finno-Permic sub-family of Uralic; however, Hungarian is more isolated as it is the only Uralic (Finno-Ugric) European language that is not Finno-Permic. The experiments consisted of applying both the clustering method and ALD measure to a set of forty European languages belonging to several families (Latin, Germanic, Slavic, Celtic, and Finno-Permic), as well as the six isolated languages.

4.1. The Corpus

As the experiments consisted of comparing forty different languages, we searched comparable corpora containing multilingual texts belonging to similar domains and genres. We used a part of the comparable corpus built for the experiments reported in [19] with the aid of the WebBootCat tool applied on Wikipedia (WebBootCat is available at https://the.sketchengine.co.uk). For each language, we compiled a corpus of $\sim 50k$ tokens.

4.2. Development and Configuration

To set the best configuration of the clustering algorithm, in the development phase, we prepared a subset of the 40 languages containing only those that can be classified in one of the known European families. In this way, we eliminated the six isolated languages, being left 34 languages. Figure 1 shows the dendrogram obtained with Delta-Eder distance, 3-grams of characters, 1000 most frequent words per language, and hierarchical clustering carried out with Ward’s method [34]. There are only three errors of classification: English is situated with the Latin languages (probably because almost 50% of the lexicon is of Latin origin through French), and Icelandic with the Celtics; in addition, the two Baltic languages are not included in the Slavic group (even though this might not be a mistake since the common ancestry of Baltic and Slavic languages has long been disputed). Despite this, these are the best results we have obtained after testing several configurations (with different n-grams and distance measures). Therefore, we used that clustering configuration to group all the languages, including the isolated ones.

The clustering algorithm was executed with Stylo, a R package for clustering analysis of documents [28].

Concerning ALD, we followed the main configuration reported in Gamallo et al. [19] for $PP$ and R, where the main characteristic is the use of 7-grams of characters with a smoothing technique based on linear interpolation. This technique, which is not used by Stylo in the clustering process described above, allows taking advantage of all n-grams smaller than 7. The same configuration was also applied to $KL$ and $DistMean$. Besides, all languages were converted to the Latin script and transliterated to a shared spelling as in [19].

Table 1. Languages most similar to one representative of each of the well-known European families: Germanic (ger), Slavic (sla), Latin (lat), Celtic (cel), and Finno-Permic (fin) using ALD measure. The test was performed with ALD on 7-grams and linear interpolation.

Rank	Danish (Ger)	Croatian (Sla)	Latin (Lat)	Irish (Cel)	Finnish (Fin)
1	norwegian 0.00	serbian 0.00	french 0.25	gaelic 0.01	estonian 0.05
2	swedish 0.23	slovenian 0.22	portuguese 0.32	welsh 0.70
3	english 0.48	macedonian 0.26	italian 0.37
4	french 0.48	bulgarian 0.29	spanish 0.37
5	german 0.51	basque 0.45	galician 0.41
6	luxemburgish 0.55	georgian 0.47	english 0.42
7	frisian 0.71	russian 0.57	catalan 0.44
8	dutch 0.73	czech 0.58	romanian 0.45
9	icelandic 0.76	ukrainian 0.61
10		slovak 0.63
11		polish 0.66
12		latvian 0.70

shows a development experiment using ALD on 7-grams and linear interpolation. For each well-known family, one representative language was selected. Then, its top N most similar languages were ranked. According to the results we obtained, only four errors were generated (italic + bold in the table). The number of errors is lower than if we take into account only the results of one of the four measures. Therefore, it seems to be as robust a technique as the clustering process described above.

Unlike most lexicostatistic approaches, which are supervised techniques relying on aligned multilingual word lists, our corpus-based strategy is totally unsupervised. Thus, classification errors are expected. Asgari and Mofrad [15] proposed a related corpus-based work whose objective was to apply hierarchical clustering to fifty languages by using divergence of joint distance distribution on a Bible parallel corpora [18]. Some of the resulting clusters of the reported experiments were counter-intuitive. For instance, Norwegian and Hebrew, belonging to two different language families (Indo-European and Semitic), were wrongly grouped together. The clustering algorithm also separated in different clusters the two main languages of the Finno-Permian family: Estonian was clustered with Arabic and Korean, while Finish was grouped with Icelandic, an Indo-European language. In addition, Latin was grouped with Greek instead of with Italian, Portuguese, or Spanish (Latin family). Therefore, and due to the difficulty of the task, it is expected to find some error in the classification proposed by our algorithms.

4.3. Results

Figure 2 shows the dendrogram resulting of applying the clustering algorithm to the forty languages using the same configuration as in Figure 1. On the one hand, Albanian and Greek are rather oddly placed within the group of Baltic languages and, on the other hand, Hungarian and Armenian appear grouped together with Welsh and Icelandic, which seems more as a catch-all. Basque and Georgian are put together and are located close to the heterogeneous groups containing the rest of isolated languages.

Table 2. Top 10 most similar languages to the six isolated targeted languages using ALD measure. To simplify, we just put the two first decimal places of ALD.

Rank	Albanian	Armenian	Basque	Georgian	Greek	Hungarian
1	czech 0.11	basque 0.14	georgian 0.03	basque 0.02	latvian 0.09	albanian 0.06
2	lithuanian 0.11	latvian 0.17	czech 0.07	russian 0.06	basque 0.10	frisian 0.47
3	portuguese 0.22	dutch 0.21	macedonian 0.10	bulgarian 0.07	swedish 0.15	french 0.52
4	catalan 0.24	polish 0.22	albanian 0.12	czech 0.10	czech 0.18	polish 0.52
5	french 0.25	czech 0.22	portuguese 0.13	macedonian 0.11	albanian 0.19	macedonian 0.52
6	bulgarian 0.26	frisian 0.23	russian 0.14	serbian 0.15	russian 0.22	danish 0.52
7	basque 0.27	swedish 0.23	bulgarian 0.15	latvian 0.16	french 0.23	basque 0.53
8	spanish 0.27	danish 0.24	greek 0.17	lithuanian 0.19	bulgarian 0.26	finnish 0.53
9	russian 0.28	croatian 0.25	spanish 0.18	albanian 0.20	georgian 0.30	portuguese 0.53
10	dutch 0.33	finnish 0.26	croatian 0.20	greek 0.22	spanish 0.31	norwegian 0.54

shows the results of applying ALD measure to the six isolated languages. Each column depicts the top 10 most similar languages to each one of the six under study. In general, the six isolated languages follow a different pattern of behavior than that shown in the clustering process. With the ALD scores, all six languages seem to be related in the same way to the three large Indo-European families: Slavic, Romance, and Germanic. Besides, the same languages tend to appear on all six lists, e.g., Czech, Bulgarian, Portuguese, Spanish, Basque, Dutch, and a few others. However, it is important to emphasize that there are at least two patterns that also have emerged in the previous clustering experiment: Albanian and Greek are close to Baltic languages, and Basque and Georgian are again very close to each other.

4.4. Discussion

From the results obtained in the two experiments, it is not easy to draw clear conclusions in relation to the six languages analysed. In particular, nothing clear seems to derive from the distances related to Armenian, Greek, Albanian, and Hungarian. There is a vague closeness between Albanian and Greek, but perhaps it is simply because Greek is the largest minority language of Albania and first largest foreign language in this country. It is also noteworthy that Hungarian does not show any connections to Estonian and Finnish. Even though traditional historical linguistics situates Hungarian as a member of the Uralic/Finno-Ugric family, it seems that this language is very far from the Finno-Permic sub-family (Estonian and Finnish).

As for the relationship between Basque and Georgian, there seems to be more regularity, as it is a relationship that is maintained regardless of the methodology used. Unlike Greek and Albanian, they are two languages far apart in space. Basque is a non-Indo-European language spoken in Navarre and Basque Country (both in Northern Kingdom of Spain), and in southwest of French Republic, while Georgian belongs to the non-Indo-European Kartvelian family (also known as Ibero-Caucasian), which is spreading through the Southern Caucasus. In historical linguistics, there are works that defend Caucasian–Basque connection on the basis of comparative-historical and typological approaches [35]. By contrast, other authors claim that the link between these languages remains unproven, or is even firmly rejected [36]. It should be noted that, in another work based on a computational phylogenetic strategy [14], the Basque language is also very close to the Georgian family in the dendrogram resulting from their analysis.

However, it is important to note that the results obtained with the two strategies (clustering and ALD distance) are not completely reliable since, with the same strategy and several different configurations, we can also obtain different results. For instance, Georgian and Basque are not always so closely related when we use other less accurate configurations (according to the development experiments).

Finally, and taking into account a suggestion made by one of the reviewers of the article, we can use our method to verify the so-called Balkan Sprachbund or (Balkan language area) [37], which states that several Balkan languages share linguistic features (e.g., grammar, syntax, and to a lesser extent vocabulary and phonology) independently of their origin. Thus, according to this hypothesis, Greek, Albanian, Romanian, Serbian, Macedonian, Bulgarian, or Croatian should be close languages. However, our data do not show much evidence for it. The reason might be that our method is more sensitive to the lexical and vocabulary level than to the grammatical and syntactic level, and it seems that the lexical level is less important in Balkan Sprachbund as unrelated Balkan languages share little vocabulary, whereas their grammars may have very extensive similarities.

5. Conclusions

In this article, we propose complementary corpus-based strategies to calculate the distances between languages, namely a clustering method and a set of distances based on comparing probability models. These strategies were applied to discover some kind of relatedness between isolated languages and the rest using simple corpus-based techniques and natural language processing methods. These strategies were used in the search for relationships between isolated European languages and other languages belonging to recognized families.

This type of study, along with other work in computational linguistic phylogenetics, can be very useful to open new avenues of research in historical linguistics or to support controversial hypotheses that have not yet been agreed upon by the community of researchers.

In future work, we will explore new techniques that allow us to separate the linguistic levels (e.g., phonological, morphological, lexical, and syntactic) into different language models. We will also analyze the influence of normalization/transliteration on the results by comparing transliterated with no transliterated models. Furthermore, since our goal is not to find a common ancestor, we will make use of non-hierarchical clustering strategies.