A Multi-Task Framework for Action Prediction
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
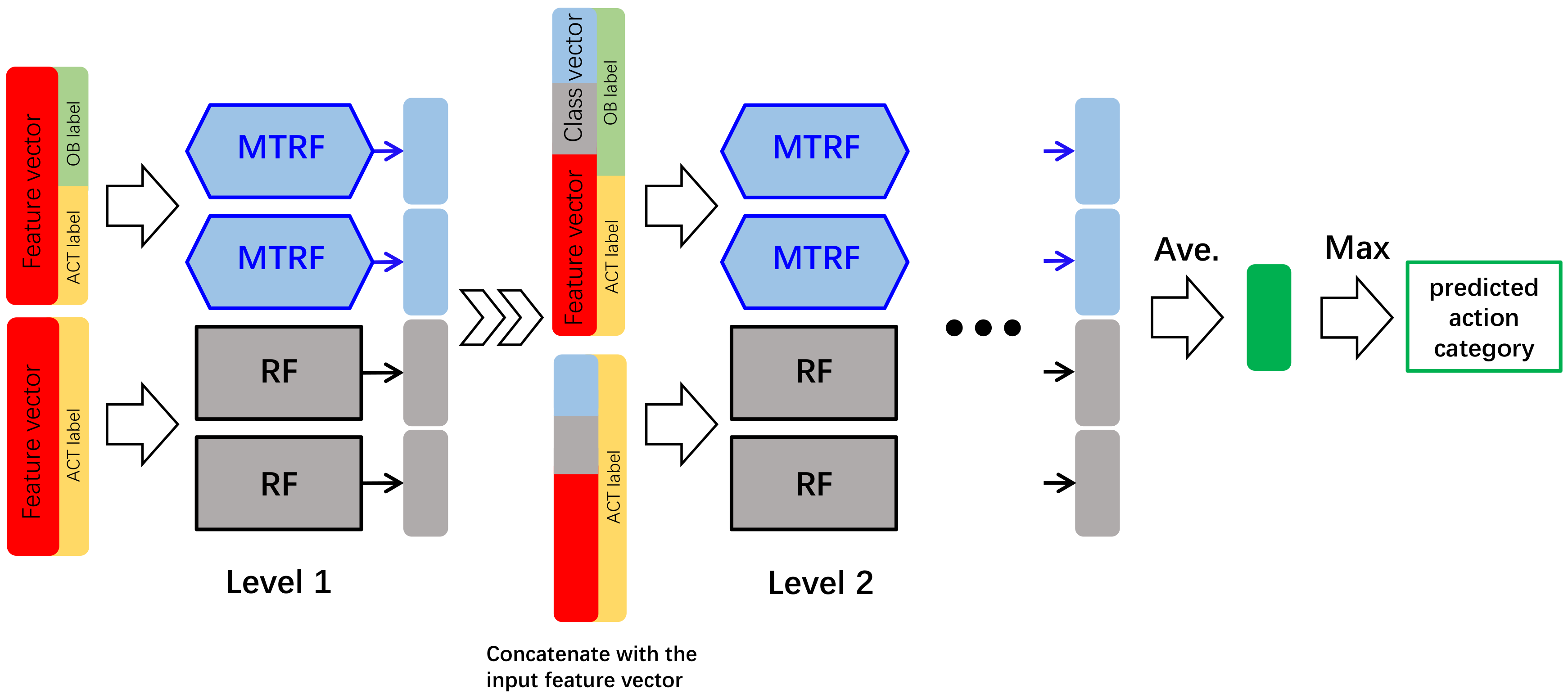
3.1. Multi-Task Deep Forest
3.2. Random Forest
3.3. Multi-Task Random Forest
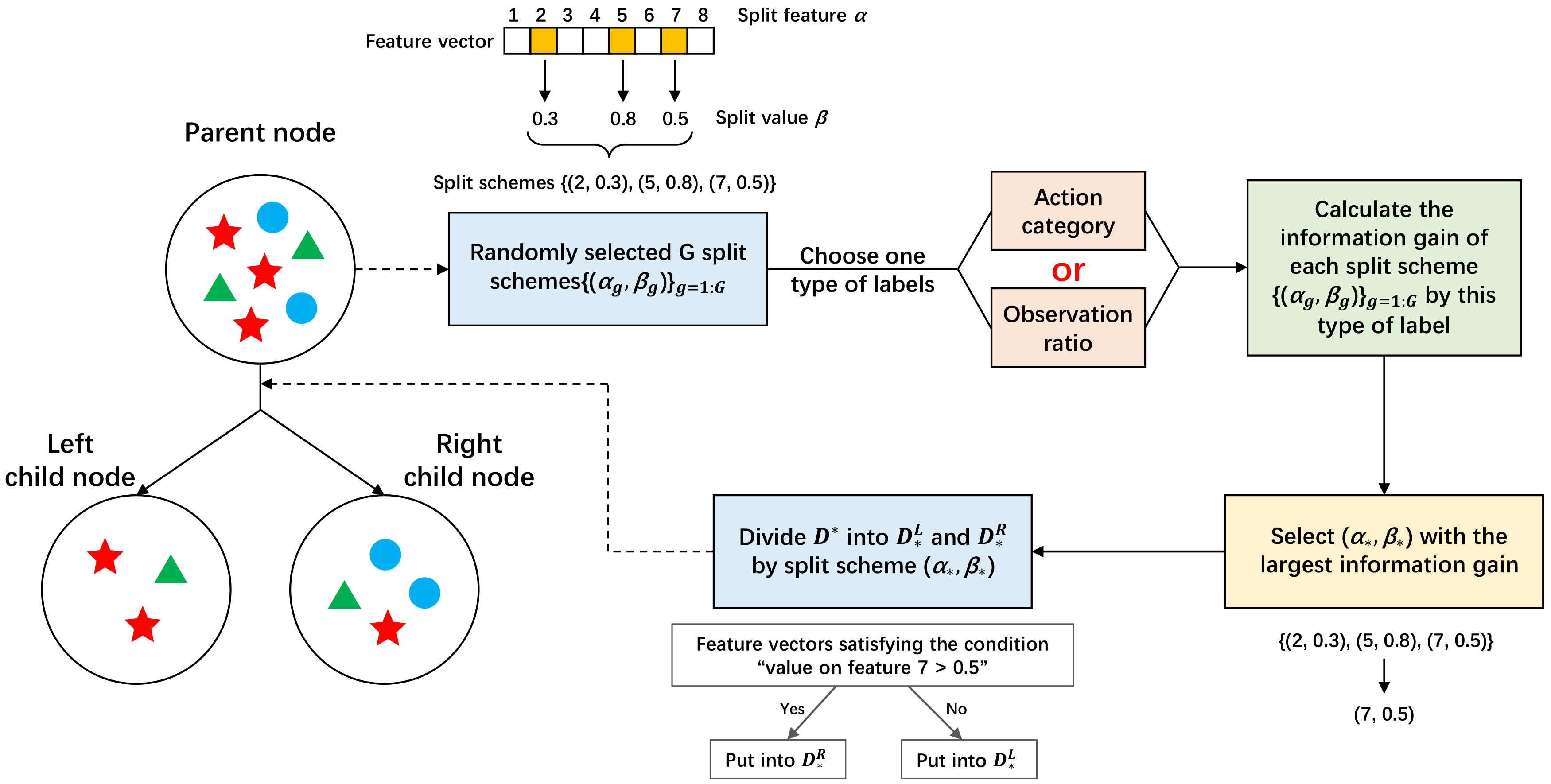
3.3.1. Construction of a Multi-task Decision Tree
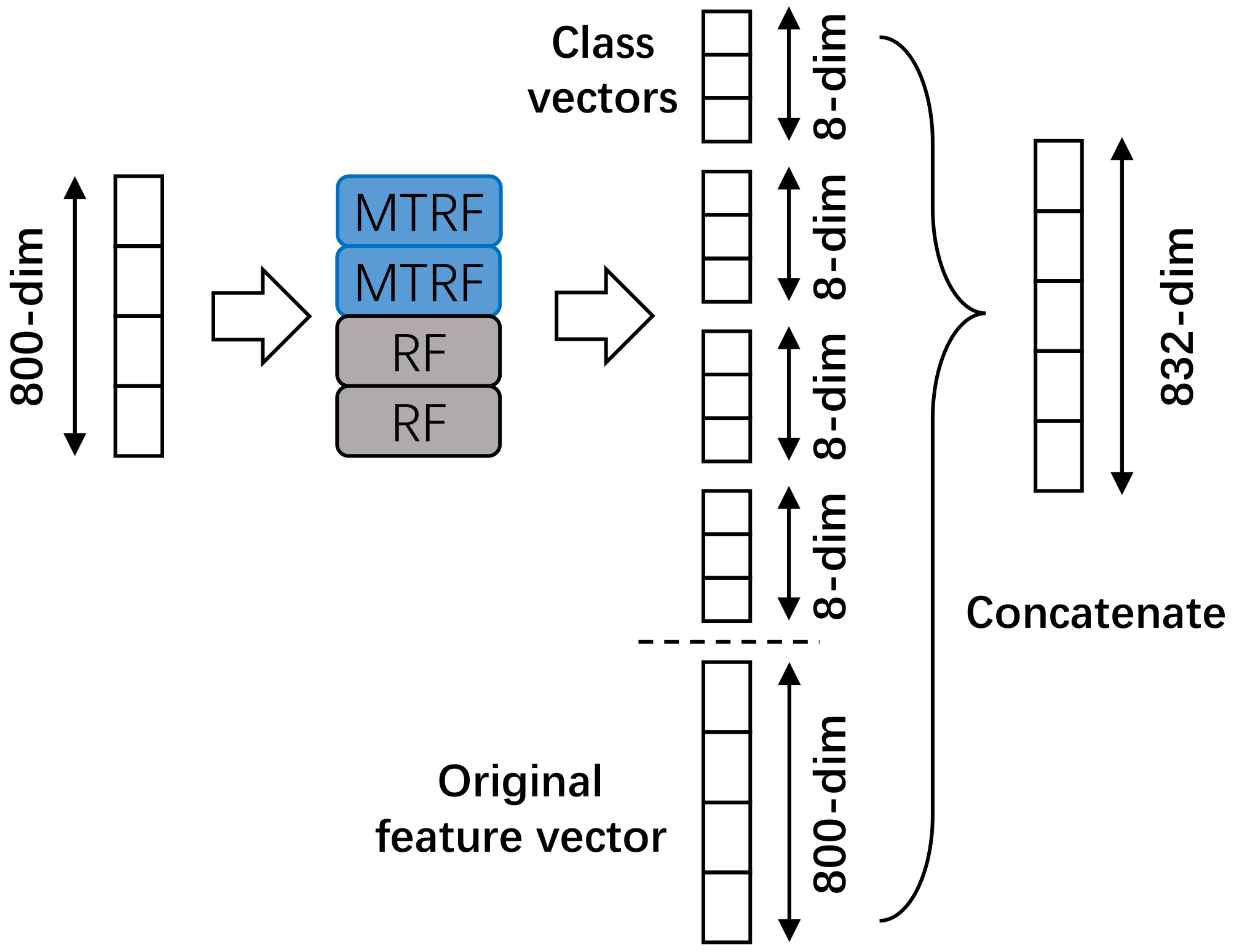
3.3.2. Class Vector of a Multi-Task Random Forest
| Algorithm 1 Construction of a multi-task decision tree |
| Input: a training set // |
| Output: a node sequence S |
| 1: create a node sequence S storing settled nodes and a pending node sequence Q containing unsettled nodes; |
| 2: create the root node as (1,1,0,D’) and put it into Q; |
| 3: // the total number of generated nodes |
| 4: while Q is not do |
| 5: take out the first node (,l,f,) of Q; |
| 6: if l is equal to the preset maximum depth or samples in belong to the same categories on both action category label and observation ratio label then |
| 7: // the current node is a leaf node |
| 8: put the current node into S; |
| 9: else |
| 10: // the current node is an intermediate node need to be split |
| 11: randomly select G split schemes , and each scheme splits samples in into two subsets and ; |
| 12: generate a random value and compare it with a predefined parameter ; |
| 13: if or samples in belong to the same categories on observation ratio label then |
| 14: //evaluate each split scheme in terms of action labels of samples in |
| 15: for g is 1 to G do |
| 16: calculate the information gain GainAction according to Equation 2 |
| 17: end for |
| 18: choose the best split scheme according to Equation 3, and the dataset is divided into subsets and ; |
| 19: else |
| 20: //evaluate each split scheme in terms of observation ratio labels of samples in |
| 21: for g is 1 to G do |
| 22: calculate the information gain GainRatio according to Equation 5 |
| 23: end for |
| 24: choose the best split scheme according to Equation 6, and the dataset is divided into subsets and ; |
| 25: end if |
| 26: //put the current node into S |
| 27: //put the left child node into Q |
| 28: //put the right child node into Q |
| 29: end if |
| 30: |
| 31: end while |
| 32: return S |
4. Experiments
4.1. Datasets and Experimental Setup
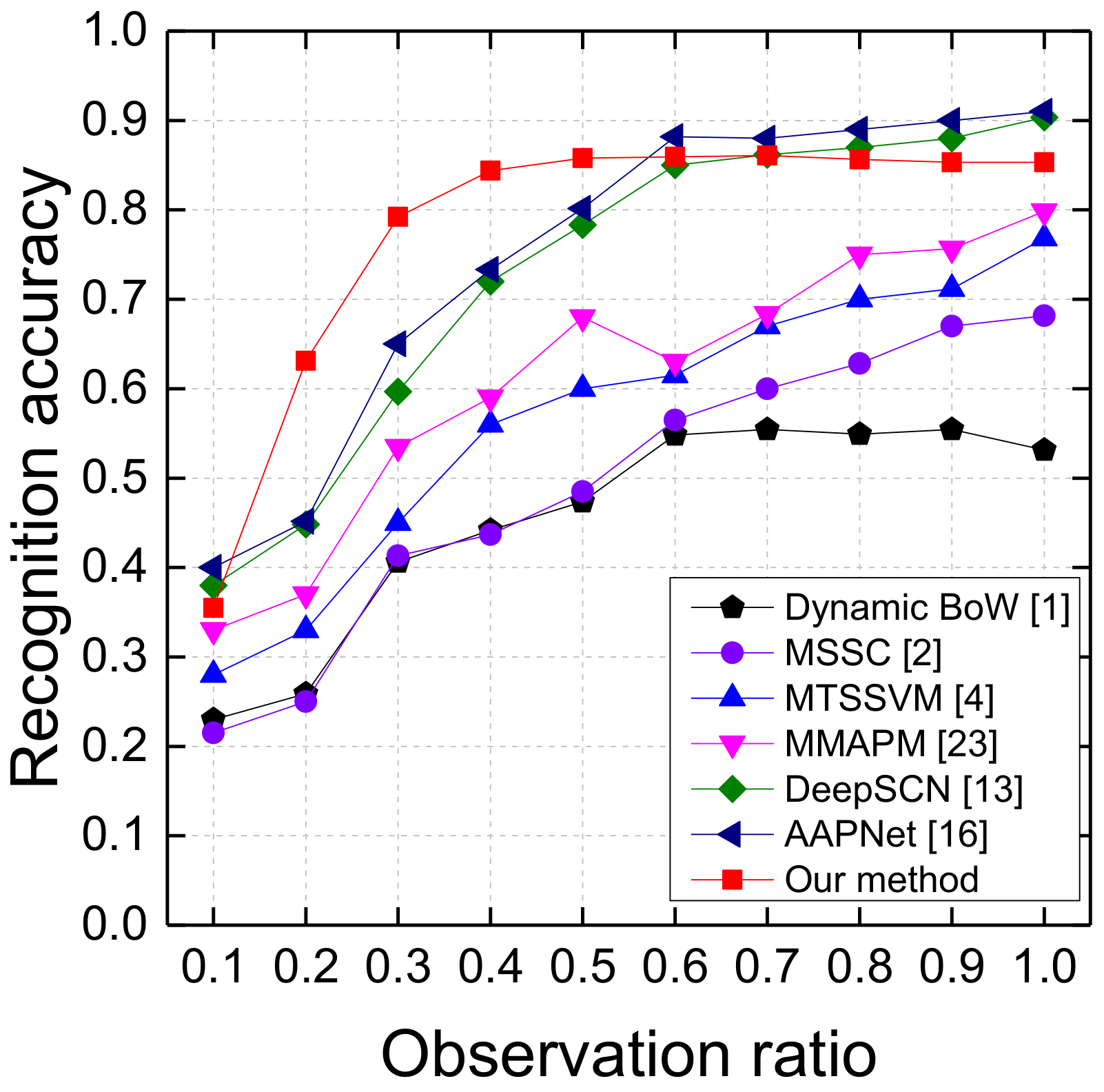
4.2. Experimental Results
4.2.1. Comparison between MTDF and gcForest
4.2.2. Results on the UT-I #1 and UT-I #2 Datasets
4.2.3. Results on the BIT Dataset
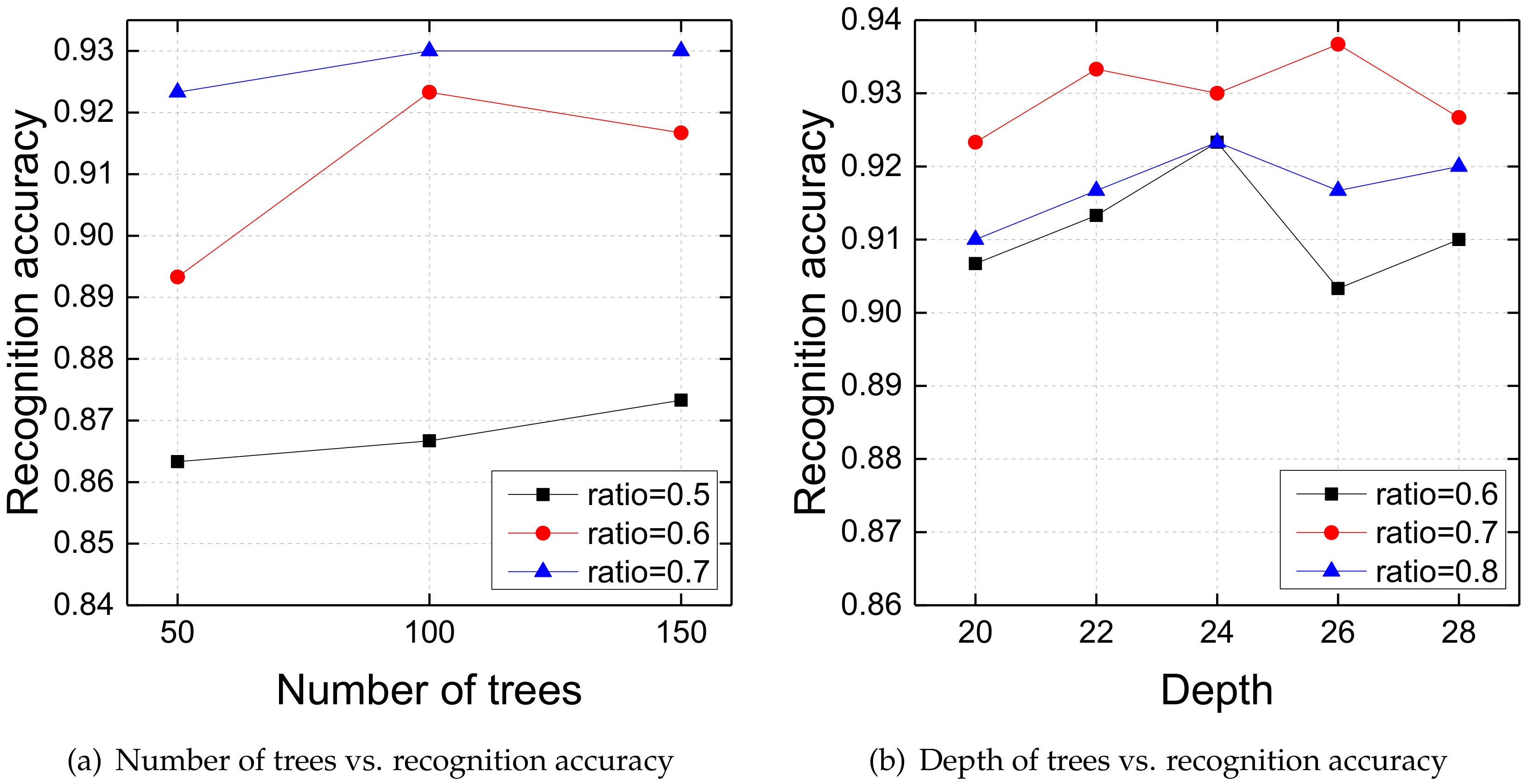
4.3. Effects of Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MTDF | Multi-Task Deep Forest |
| MTRF | Multi-Task Random Forests |
| RF | Random Forest |
References
- Ryoo, M.S. Human activity prediction: Early recognition of ongoing activities from streaming videos. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 7 November 2011; pp. 1036–1043. [Google Scholar]
- Yu, C.; Barrett, D.; Barbu, A.; Narayanaswamy, S.; Song, W. Recognize Human Activities from Partially Observed Videos. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2658–2665. [Google Scholar]
- Lan, T.; Chen, T.C.; Savarese, S. A Hierarchical Representation for Future Action Prediction. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 689–704. [Google Scholar]
- Yu, K.; Kit, D.; Yun, F. A Discriminative Model with Multiple Temporal Scales for Action Prediction. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 596–611. [Google Scholar]
- Laptev, I. On Space-Time Interest Points. Int. J. Comput. Vis. 2005, 64, 107–123. [Google Scholar] [CrossRef]
- Wang, H.; Schmid, C. Action Recognition with Improved Trajectories. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 11 September 2014; pp. 3551–3558. [Google Scholar]
- Liu, C.; Wu, X.; Jia, Y. A hierarchical video description for complex activity understanding. Int. J. Comput. Vis. 2016, 118, 240–255. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Feng, J. Deep Forest: Towards An Alternative to Deep Neural Networks. In Proceedings of the International Joint Conferences on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3553–3559. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, H.; Yang, W.; Yuan, C.; Ling, H.; Hu, W. Human activity prediction using temporally-weighted generalized time warping. Neurocomputing 2017, 225, 139–147. [Google Scholar] [CrossRef]
- Feng, Z.; Torre, F.D.L. Generalized Time Warping for Multi-modal Alignment of Human Motion. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3551–3558. [Google Scholar]
- Ma, S.; Sigal, L.; Sclaroff, S. Learning Activity Progression in LSTMs for Activity Detection and Early Detection. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 26 June 2016; pp. 1942–1950. [Google Scholar]
- Kong, Y.; Tao, Z.; Yun, F. Deep Sequential Context Networks for Action Prediction. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1473–1481. [Google Scholar]
- Singh, G.; Saha, S.; Sapienza, M.; Torr, P.; Cuzzolin, F. Online Real-time Multiple Spatiotemporal Action Localisation and Prediction. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3637–3646. [Google Scholar]
- Wang, D.; Yuan, Y.; Wang, Q. Early Action Prediction with Generative Adversarial Networks. IEEE Access 2019, 7, 35795–35804. [Google Scholar] [CrossRef]
- Kong, Y.; Tao, Z.; Fu, Y. Adversarial Action Prediction Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018. 1-1. Available online: https://ieeexplore.ieee.org/abstract/document/8543243 (accessed on 10 March 2020).
- Liu, J.; Shahroudy, A.; Gang, W.; Duan, L.Y.; Kot, A.C. SSNet: Scale Selection Network for Online 3D Action Prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 12–18 July 2018; pp. 8349–8358. [Google Scholar]
- Schydlo, P.; Rakovic, M.; Jamone, L.; Santos-Victor, J. Anticipation in Human-Robot Cooperation: A Recurrent Neural Network Approach for Multiple Action Sequences Prediction. In Proceedings of the IEEE International Conference on Robotics and Automation, Guangzhou, China, 17–19 November 2018; pp. 1–6. [Google Scholar]
- Liu, F.T.; Kai, M.T.; Yu, Y.; Zhou, Z.H. Spectrum of Variable-Random Trees. J. Artif. Intell. Res. 2008, 32, 355–384. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Boot-Strap. Chapman & Hall 1993, 57, 1–436. [Google Scholar]
- Ryoo, M.S.; Aggarwal, J.K. UT-Interaction Dataset, ICPR contest on Semantic Description of Human Activities (SDHA). 2010. Available online: http://cvrc.ece.utexas.edu/SDHA2010/Human_Interaction.html (accessed on 10 March 2020).
- Kong, Y.; Jia, Y.; Fu, Y. Learning human interaction by interactive phrases. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Kong, Y.; Fu, Y. Max-Margin Action Prediction Machine. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1844–1858. [Google Scholar] [CrossRef]

| Observation ratio | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| UT-I #1 | gcForest | 19.33% | 33.67% | 60.00% | 78.00% | 86.33% | 91.67% | 92.00% | 91.67% | 91.00% | 90.67% |
| MTDF | 20.00% | 33.67% | 60.33% | 81.33% | 86.67% | 92.33% | 93.00% | 92.33% | 91.67% | 91.67% | |
| UT-I #2 | gcForest | 16.67% | 32.33% | 51.33% | 68.00% | 83.33% | 90.67% | 93.67% | 93.33% | 92.00% | 92.00% |
| MTDF | 16.67% | 36.33% | 52.67% | 69.67% | 83.00% | 91.67% | 95.33% | 94.67% | 91.67% | 91.67% | |
| BIT | gcForest | 36.72% | 60.94% | 77.50% | 83.44% | 85.63% | 85.00% | 84.69% | 84.38% | 84.06% | 84.06% |
| MTDF | 35.47% | 63.13% | 79.22% | 84.38% | 85.78% | 85.94% | 86.09% | 85.63% | 85.31% | 85.31% | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Liu, C.; Yan, Z.; Shi, X. A Multi-Task Framework for Action Prediction. Information 2020, 11, 158. https://doi.org/10.3390/info11030158
Yu T, Liu C, Yan Z, Shi X. A Multi-Task Framework for Action Prediction. Information. 2020; 11(3):158. https://doi.org/10.3390/info11030158
Chicago/Turabian StyleYu, Tianyu, Cuiwei Liu, Zhuo Yan, and Xiangbin Shi. 2020. "A Multi-Task Framework for Action Prediction" Information 11, no. 3: 158. https://doi.org/10.3390/info11030158
APA StyleYu, T., Liu, C., Yan, Z., & Shi, X. (2020). A Multi-Task Framework for Action Prediction. Information, 11(3), 158. https://doi.org/10.3390/info11030158




