A Ranking-Based Hashing Algorithm Based on the Distributed Spark Platform
Abstract
1. Introduction
2. Related Work
3. Basic Knowledge
4. Distributed Ranking-Based Hashing Algorithm
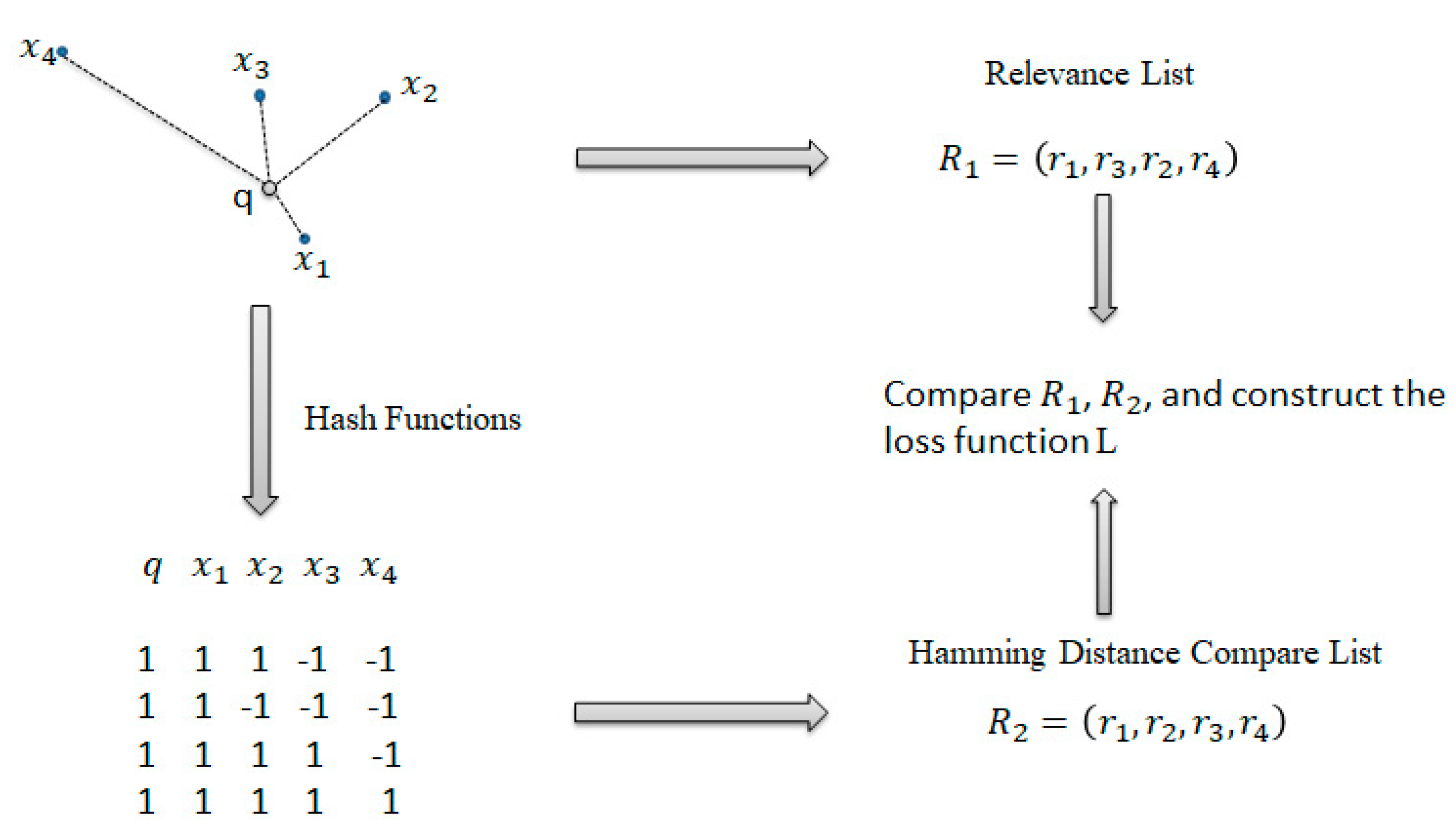
4.1. Overall Description of the Algorithm
- In the distributed Spark environment, all the data in the datasets are mapped to different averaged working nodes. The Euclidean distances between the query points in the query set and all the data points in the datasets in each working node are calculated, and then the distance is ranked. The actual ranking of each point is obtained.
- Similarly, the query points and all the data points are converted into binary codes on each working node, and the Hamming distance is calculated to obtain the ranking in the Hamming space.
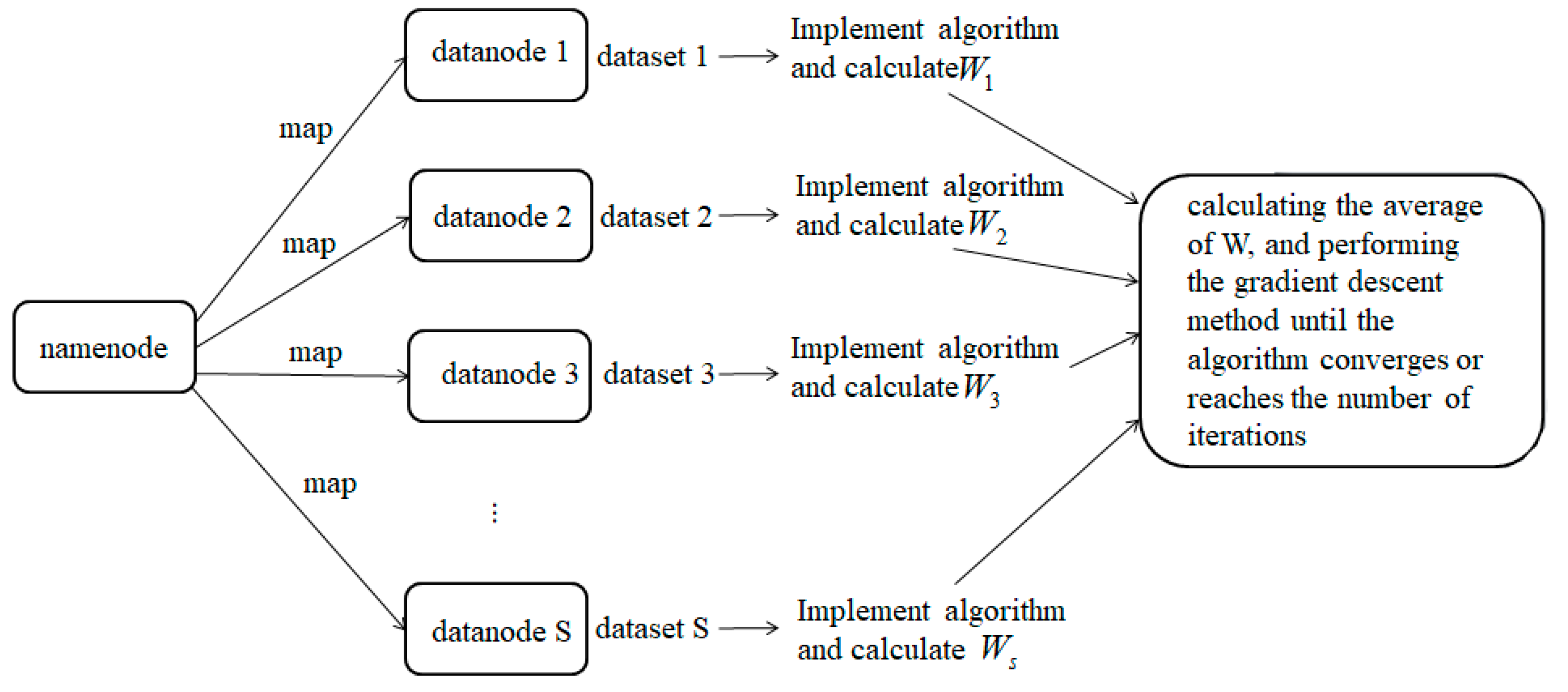
- According to the loss function, minimize the inconsistency of the data points in the two spaces is minimized. The data transformation matrix on each working node is calculated, and then all the nodes are summed and the average values are calculated using the gradient descent method until the algorithm converges or the number of iterations is reached.
4.2. The Details of the Algorithm
5. Experiments
5.1. Experimental Platform Construction
5.2. Experimental Datasets
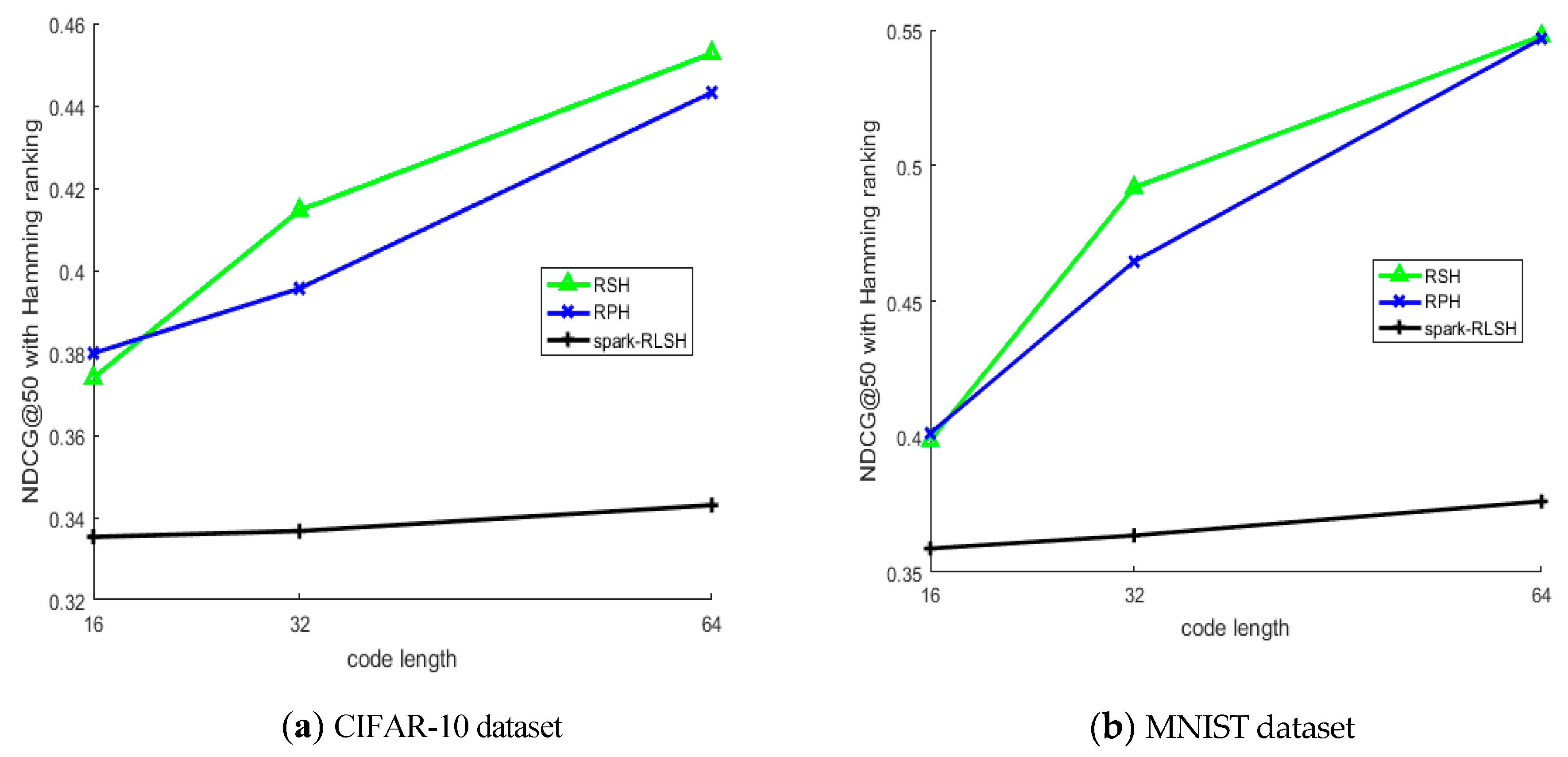
5.3. Experimental Result
6. Conclusion
- Improvements in the ranking formula. After converting the data points into binary codes, all the data needs to be ranked according to Hamming distance, and then the ranking list can be constructed. This requires comparison between every two points, so that the time complexity of the designed ranking algorithm is too high, which can seriously affect the training efficiency. Later, we can consider redesigning the ranking formula to run the algorithm model with the lowest cost.
- The gradient descent method is implemented as a whole on the distributed platform. This paper considers the complexity of the algorithm in the ranking process. Each working node runs the algorithm model and implements the gradient descent method independently. Although this method can reduce the training time of the model effectively, there is no overall calculation gradient, and there is a certain training error. In the future, the overall comparison of the Hamming distance between the query set and the dataset can be considered, which can improve the accuracy of the search and reduce the training time simultaneously.
Author Contributions
Funding
Conflicts of Interest
References
- Indyk, P. Nearest Neighbors in High-Dimensional Spaces. Discrete Math. Its Appl. 2004, 20042571. [Google Scholar]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An Optimal Algorithm for Approximate Nearest Neighbor Searching. J. ACM 1998, 45, 91–923. [Google Scholar] [CrossRef]
- Guttman, A. R-trees: A Dynamic Index Structure for Spatial Searching. In ACM SIGMOD International Conference on Management of Data; SIGMOD: New York, NY, USA, 1984; pp. 47–57. [Google Scholar]
- Bentley, J.L. K-d trees for semidynamic point sets. Annu. Symp. 1990, 187–197. [Google Scholar]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V. Locality-sensitive hashing scheme based on p-stable distributions. Annu. Symp. 2004, 253–262. [Google Scholar]
- Wangb, J.; Zhang, T.; Song, J.; Sebe, N.; Shen, H.T. A Survey on Learning to Hash. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 769–790. [Google Scholar] [CrossRef] [PubMed]
- Kulis, B.; Grauman, K. Kernelized Locality-Sensitive Hashing. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1092–1104. [Google Scholar] [CrossRef] [PubMed]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral Hashing. Available online: https://people.csail.mit.edu/torralba/publications/spectralhashing.pdf (accessed on 7 March 2020).
- Zhang, D.; Wang, J.; Cai, D.; Lu, J. Self-taught hashing for fast similarity search. In Proceedings of the 33rd international ACM SIGIR conference, New York, NY, USA, 19 July 2010; pp. 18–25. [Google Scholar]
- Fu, H.; Kong, X.; Lu, J. Large-scale image retrieval based on boosting iterative quantization hashing with query-adaptive reranking. Neurocomputing 2013, 122, 480–489. [Google Scholar] [CrossRef]
- Wu, G.; Han, J.; Guo, Y.; Liu, L.; Ding, G.; Ni, Q.; Shao, L. Unsupervised Deep Video Hashing via Balanced Code for Large-Scale Video Retrieval. IEEE Trans. Image Process. 2018, 28, 1993–2007. [Google Scholar] [CrossRef] [PubMed]
- Lin, R.-S.; Ross, D.A.; Yagnik, J. SPEC Hashing: Similarity Preserving Algorithm for Entropy-Based Coding; In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA2010; pp. 848–854. [Google Scholar]
- Norouzi, M.; Blei, D.M. Minimal Loss Hashing for Compact Binary Codes; In Proceedings of the International Machine Learning Society (IMLS), 28 June–2 July 2011; pp. 353–360. [Google Scholar]
- Liu, W.; Wang, J.; Ji, R.; Jiang, Y.-G.; Chang, S.-F. Supervised hashing with kernels. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2074–2081. [Google Scholar]
- Shen, F.; Shen, C.; Liu, W.; Shen, H.T. Supervised Discrete Hashing. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 37–45. [Google Scholar]
- Yao, T.; Kong, X.; Fu, H.; Tian, Q. Discrete Semantic Alignment Hashing for Cross-Media Retrieval. IEEE Trans. Cybern. 2019, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Strecha, C.; Bronstein, A.M.; Bronstein, M.M.; Fua, P. LDAHash: Improved Matching with Smaller Descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 66–78. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Shen, C.; Wu, J. Optimizing Ranking Measures for Compact Binary Code Learning. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Volume 8691, pp. 613–627. [Google Scholar]
- Wang, J.; Wangb, J.; Yu, N.; Li, S. Order preserving hashing for approximate nearest neighbor search. In Proceedings of the 21st ACM international conference on Multimedia—MM’13, Nara, Japan, 21 October 2013; pp. 133–142. [Google Scholar]
- Ji, T.; Liu, X.; Deng, C.; Huang, L.; Lang, B. Query-Adaptive Hash Code Ranking for Fast Nearest Neighbor Search. In Proceedings of the ACM International Conference on Interactive Experiences for TV and Online Video—TVX’16; Association for Computing Machinery (ACM), Newcastle, UK, 3 November 2014; pp. 1005–1008. [Google Scholar]
- Song, D.; Liu, W.; Ji, R.; Meyer, D.; Smith, J.R. Top Rank Supervised Binary Coding for Visual Search. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1922–1930. [Google Scholar]
- Song, D.; Liu, W.; Meyer, D.; Tao, D.; Ji, R.D.A.M. Rank Preserving Hashing for Rapid Image Search. In Proceedings of the 2015 Data Compression Conference. In Proceedings of the Institute of Electrical and Electronics Engineers (IEEE), Snowbird, UT, USA, 7–9 April 2015; pp. 353–362. [Google Scholar]
- Jiang, Y.-G.; Wang, J.; Xue, X.; Chang, S.-F. Query-Adaptive Image Search with Hash Codes. IEEE Trans. Multimedia 2012, 15, 442–453. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Heung-Yeung, S. QsRank:Query-sensitive Hash Code Ranking for Efficient ε-nighbor Search. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Li, X.; Lin, G.; Shen, C.; Hengel, A.V.D.; Dick, A. Learning Hash Functions Using Column Generation. arXiv 2013, arXiv:1303.0339. [Google Scholar]
- Norouzi, M.; Fleet, D.J.; Salakhutdinov, R. Hamming Distance Metric Learning. In Proceedings of the Twenty-sixth Conference on Neural Information Processing Systems, Lake Tahoe, NA, USA, 3–8 December 2012. [Google Scholar]
- Wang, J.; Liu, W.; Sun, A.X.; Jiang, Y.-G. Learning Hash Codes with Listwise Supervision. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 2–3 June 2013; pp. 3032–3039. [Google Scholar]
- Wang, Q.; Zhang, Z.; Si, L. Ranking Preserving Hashing for Fast Similiarity Search. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 27 June 2015. [Google Scholar]
- Yao, T.; Long, F.; Mei, T.; Rui, Y. Deep Semantic Preserving and Ranking-based Hashing for Image Retrieval. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 9 July 2016. [Google Scholar]
- Liu, L.; Shao, L.; Shen, F.; Yu, M. Discretely Coding Semantic Rank Orders for Supervised Image Hashing. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5140–5149. [Google Scholar]
| Software Environment | Configuration |
|---|---|
| Operation System | Ubuntu 14.04 |
| Hadoop | Hadoop 2.7.6 |
| Spark | Spark 2.3.0 |
| Java | jdk-8u172 |
| Python | Python 3.5.2 |
| 16 bit | 32 bit | 64 bit | |
|---|---|---|---|
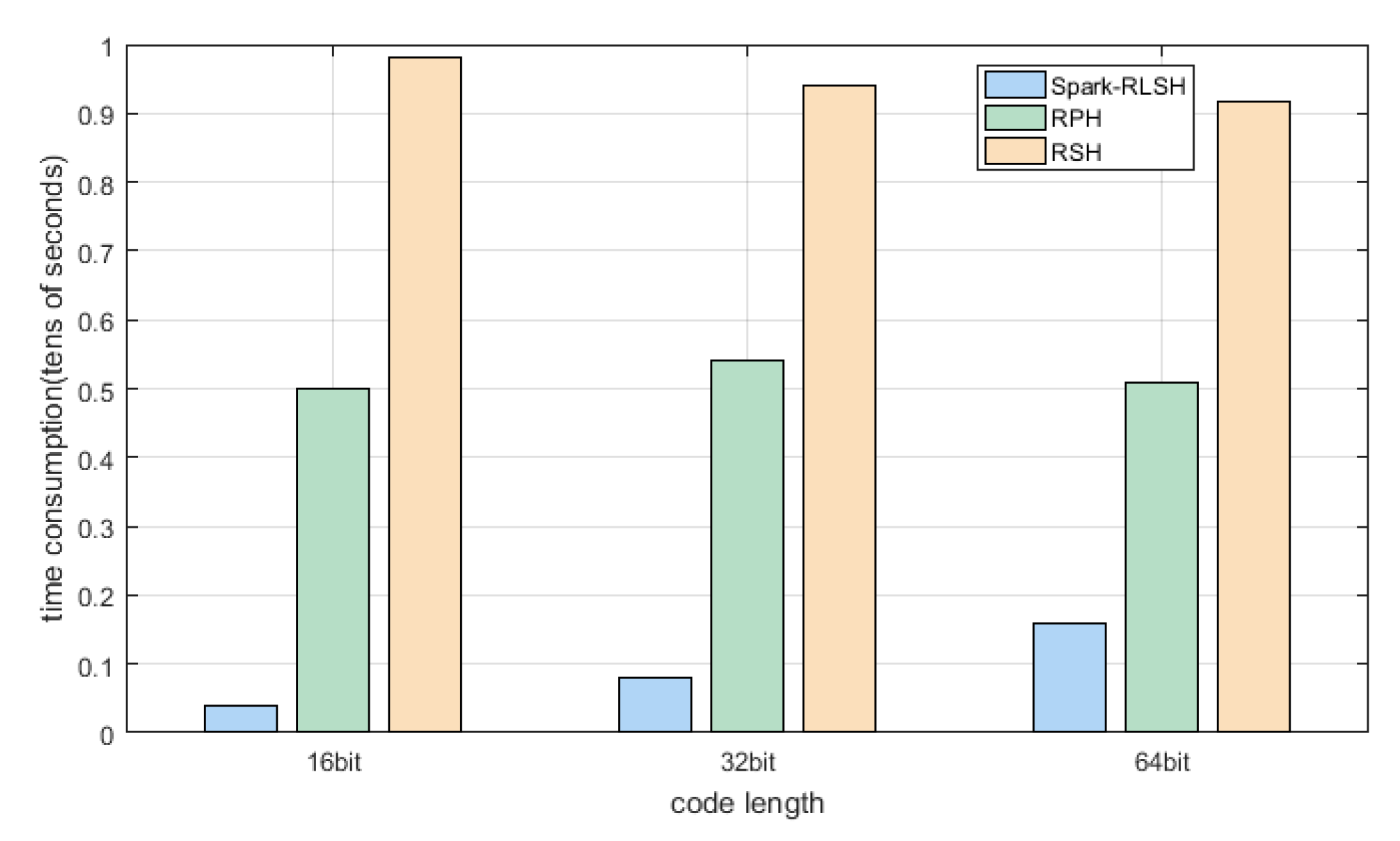
| RPH | 5000.68 | 5420.92 | 5087.96 |
| RSH | 9803.62 | 9388.89 | 9162.93 |
| RLSH | 26478.66 | 51835.27 | 104892.85 |
| Spark-RLSH | 395.77 | 796.71 | 1602.98 |
| 16 bit | 32 bit | 64 bit | |
|---|---|---|---|
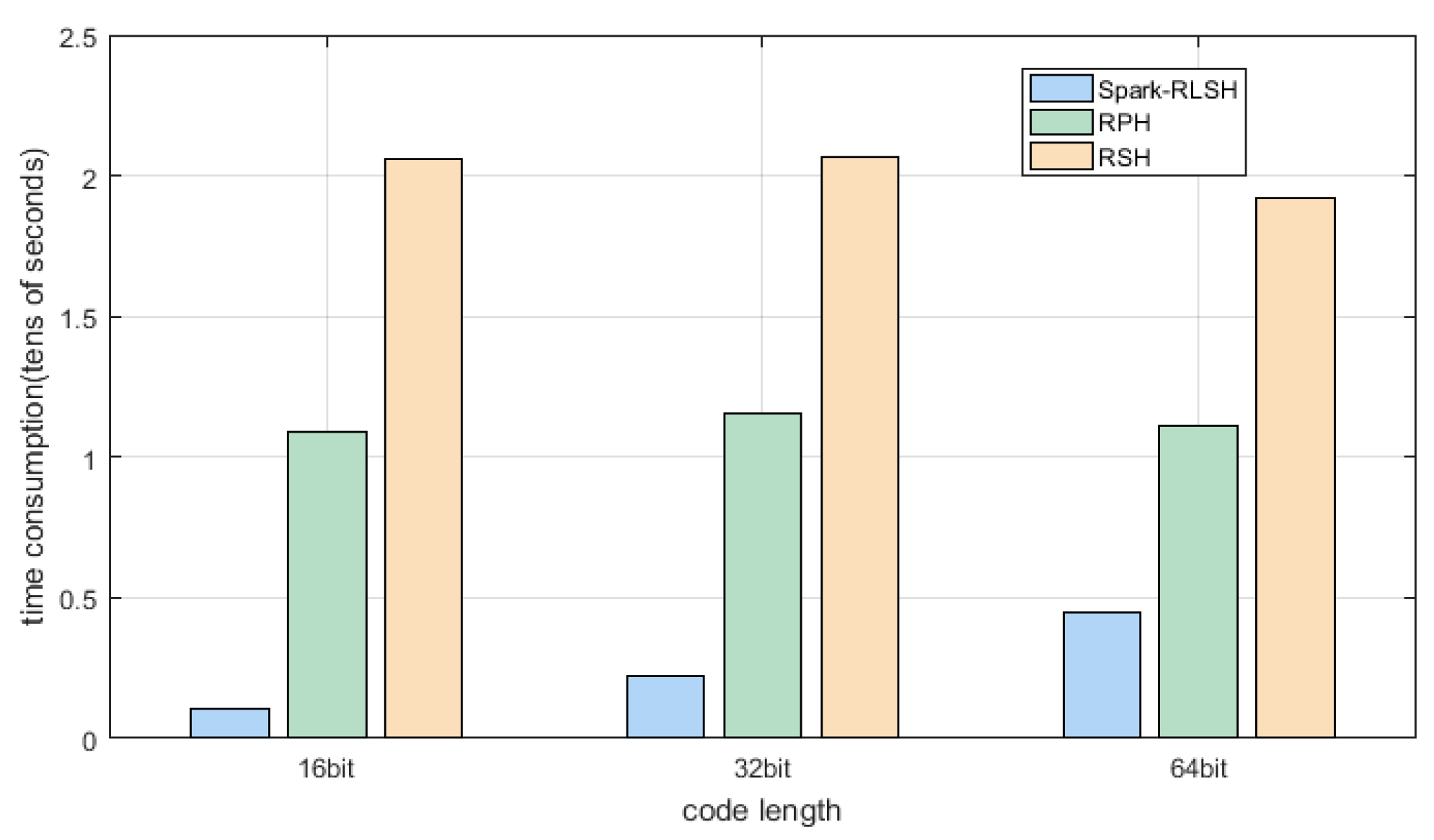
| RPH | 10889.39 | 11542.78 | 11095.41 |
| RSH | 20577.43 | 20629.58 | 19171.19 |
| RLSH | 46302.18 | 93483.59 | 191638.21 |
| Spark-RLSH | 1073.69 | 2204.01 | 4495.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, A.; Qian, J.; Chen, H.; Dong, Y. A Ranking-Based Hashing Algorithm Based on the Distributed Spark Platform. Information 2020, 11, 148. https://doi.org/10.3390/info11030148
Yang A, Qian J, Chen H, Dong Y. A Ranking-Based Hashing Algorithm Based on the Distributed Spark Platform. Information. 2020; 11(3):148. https://doi.org/10.3390/info11030148
Chicago/Turabian StyleYang, Anbang, Jiangbo Qian, Huahui Chen, and Yihong Dong. 2020. "A Ranking-Based Hashing Algorithm Based on the Distributed Spark Platform" Information 11, no. 3: 148. https://doi.org/10.3390/info11030148
APA StyleYang, A., Qian, J., Chen, H., & Dong, Y. (2020). A Ranking-Based Hashing Algorithm Based on the Distributed Spark Platform. Information, 11(3), 148. https://doi.org/10.3390/info11030148




