Abstract
DouDiZhu, a multiplayer game with incomplete information, is the most popular card game in China. Although there are many DouDiZhu card games in the world, the specific characteristics of classical DouDiZhu card games are a harmonious combination of player numbers, player characters (landlords and peasants), deck numbers, and scoring systems. However, research on the complexity and attractiveness of DouDiZhu has not established. Therefore, in this paper, artificial intelligence (AI) players of different levels of DouDiZhu game were constructed for research, self-game simulation was conducted for DouDiZhu AI players, and game refinement measures were used to evaluate and identify the best Settings of the game. The results show that classical DouDiZhu provides the most complex game setup for all types of DouDiZhu AI players, while also clarifying its popularity.
1. Introduction
Games predate human culture [1]. With the emergence of games, human culture gradually began to take shape. On one level, games reflect different aspects of human cultures. Humans create games and, at the same time, learn from games. Many research efforts have been directed towards investigating reasons for the game’s excitement, from rules alteration to game setting. With the development of digital game technology, various games gradually formed, which are getting more sophisticated in either the types or rules, attracting more players, and initiating new research interests. Most games tend to go towards the sophistication direction that harmoniously address fairness, entertainment, and challenge [2]. Various types of fun games and serious games have been explored from different aspects, which bring us closer to the nature of real entertainment perceived in mind. Nevertheless, it is still unclear how the engagement of a game would affect the multi-player game in terms of the number of players, playing hands, and cooperation mode.
Confrontational games are focusing on a single specialized player (Go, Chess, Mahjong, Olympic track and field events), and also cooperation games that need teamwork (Bridge, Diablo 3, Olympic games except for track and field events). It has been known that creating confrontation is the fundamental means of a game, whether it is between players or between players and rules, where the goal is to give users timely feedback on wins and losses [3]. Game theory explains how and why cooperation emerged [4]. An essential condition for cooperation is that both sides will reciprocate, where cooperation can happen when both are equally profitable. However, how cooperation would affect a game is not well understand. Games could simulate reality. Hence, it is interesting to observe cooperation in games when taking game benefits, such as engagement, into consideration.
Card games have a long history of their form being easy to simulate, and the rules are relatively simple, while it is capable of explaining the sophistication of the game structure. Moreover, card games are popular with all ages. In this study, we consider using a shedding-type card game, called DouDiZhu, in which the primary purpose is to empty one’s hand of all cards before all other players (https://en.wikipedia.org/wiki/List_of_shedding-type_games). DouDiZhu is used as the benchmark to explore how settings changing in multi-player games would affect the engagement of players. Among all the settings, we further studied the importance of cooperation in the gameplay.
DouDiZhu [5], one of the most popular game in China, also known as ‘Fighting Landlord’, ‘2 against 1’. It has a massive amount of users and generally regarded as the most sought-after card game in China (Figure 1). The DouDiZhu’s mobile application was downloaded 1.13 billion times in 2017 alone (http://youxiputao.com/articles/13003/). The classic DouDiZhu game involves three players, two of whom, called “the peasants”, need to cooperate against one another, called “the landlord”. The game is short, usually lasted around one to three minutes. This situation allowed people to play the game anytime and anywhere. The peasants win if any of their hands are played first; otherwise, the landlord wins. The profits or losses in the game are shared between the peasants while the landlord carries himself alone, which means the game is a zero-sum game satisfying the Nash Equilibrium. As in most card games, the starting hand of DouDiZhu can primarily affect the outcome of the game. The rules of DouDiZhu are not complicated; however, the two essential aspects of winning the game required strategies and skills.

Figure 1.
A screenshot of the Happy DouDiZhu game.
The conventional wisdom is that a good game should have both strategic challenges and player skills, but there should also be an element of chance (or rather, uncertainty). This study attempts to explore the optimal parameter setting of DouDiZhu, and analyze the game from the perspective of game progression through the game refinement theory [6].
Analysis of the rules of DouDiZhu is conducted where its respective game length and branching factor is found. Then, a simulation experiment is conducted by changing the setting of the game in several variants of the game. The bidding session to be a landlord is also skipped for simplicity. After that, the optimal setting of DouDiZhu is adopted as the benchmark to consider game cooperation issues. Mainly, the investigation of this study is concerned with the following questions:
- Can the DouDiZhu game be considered a good game? As an incomplete information dynamic card game, how well sophisticated is the game for different level players?
- What would happen if the settings of DouDiZhu changes? Does the game have the most enjoyable settings already? How does cooperation affect engagement among these types of card games?
- There are many card games similar to DouDiZhu with different hand settings. Moreover, there are also other well-refined card and board games in China. Cooperation is their most distinct missing feature. Is cooperation the essential factor that makes DouDiZhu game becoming so popular and exciting with only about 30 years’ development?
2. Related Works
2.1. Multi-Player Card Games and Cooperation
The history of card games can be traced back to the records of ancient China from the past millennia. The earliest card game originated from the Tang dynasty and is known as “leaf game”, which is believed to be the ancestor of Poker, character cards and Mahjong.
Since Billing started the study on Poker since 1995 [7], scholar interest had been spurred towards incomplete information games since it is similar to a real-world environment. Only parts of the information during the game can be observed by the participants, which requires dealing with uncertainty, managing risks, opponent model, fraud, reliability of information, and other problems. Such a situation is the main difference between Poker and chess, which gradually becomes a new trend in the field of computer games.
Card games can be played in thousands of ways around the world. Many scholars have studied theories related to Poker and Bridge, focusing on artificial intelligence (AI) solutions. Billing et al. proposed a theory of optimal strategy to address the two-player limited betting problem in Texas hold’em [8]. Although the opponent’s information was not taken into account, the agents of the Texas Hold’em card game were realized by using such strategy and still showed a high-performance level. Zinkevich et al. proposed another virtual regret concept that uses regret minimization to solve large-scale Texas Hold’em gaming problems [9].
Studies about Bridge cards can be traced back to the 1960s. According to the different schools of thought, the main strategy developed in the computer Bridge is either derived from the human player or search-based computing technique. Initially proposed in [10], different suit combinations are considered as independent sub-problems is a common way to reduce the search space to automate Bridge play. A study of search algorithms in an incomplete information game had been conducted where the problems of incomplete information in expert texts were analyzed [11]. An optimal defense model of incomplete information games was proposed based on general assumptions.
In addition to Bridge, other card games also found with the cooperation aspects, such as Préférence (Central Europe), which also has dynamic cooperation for players at the setting of two-on-one. However, according to the rules of the game (https://en.wikipedia.org/wiki/Préférence), the gains and losses of two sides are not in well within the Nash-equilibrium.
Game theory has been a method to study the interaction among incentive structures in a mathematical way, considering the predictive and actual behavior of individuals in a game and studies their optimal strategies [12]. A Nash equilibrium is a list of strategies in a game, where each player has their own and no one player can get a better payoff when switching to another available strategy while the remaining players conform to the specified strategies in the list [13]. Evolution of cooperation, a study of organized two-round repeated prisoner’s dilemma competitions, found that the winners of both rounds were the most straightforward strategy, “tit-for-tat”. They found that the relationship of humans in real society would eventually result in cooperation [4].
Experiments were conducted and found that human players were more cooperative when they received higher returns than strictly rational allowed [14]. The orthodox concept of reason is inherently flawed and inadequate to explain social interaction. An experiment conducted by [15] showed that the cooperative goal structure could lead the participants to invest more effort than the competitive goal structure. Based on the analysis of 14 cooperative games, [16] proposed a new cooperative model and cooperative performance indicator (CPM). In the context of cooperative goal structure, a stronger commitment to the in-game goal is elicited when playing with friends compared to playing with strangers. In contrast, either playing with friends or strangers, in the context of competitive goal structure, present no differences in dedication to the in-game goal.
This study explores multiplayer card games that take cooperative settings into account; therefore, DouDiZhu is selected as the primary research object in this study. As a kind of shedding-card game, DouDiZhu has plenty of similar variations all over the world, such as Winner (China), Tien Len (Vietnam), Killer (Hawaii), Daifugo (Japan), etc. A discussion on these varieties is conducted in the latter part of this paper (Section 5).
2.2. DouDiZhu
Invented in China’s Hubei province around the 1990s, the name DouDiZhu comes from the land reform movement in the early days of the founding of the People’s Republic of China, which is a typical incomplete information game for the Chinese people. Formerly known as the champion (known as “paodekuai”), it was renamed as DouDiZhu in 1995. The DouDiZhu game was recognized as an athletic event in China, General Administration of Sport of China, (http://www.sport.gov.cn), which was officiated on 3rd September 2016 by the Chess and Card Sports Department of the General Administration of Sport of China, held the national two-in-one chess and card championship.
Due to the distinctive Chinese characteristics of DouDiZhu, most domestic studies focus on the historical reasons for the popularity of DouDiZhu in China, as seen in [17,18]. Many books about the techniques of the DouDiZhu game are also being published, mainly derived from the author’s experience [19]. As the field of AI is conquering more and more games, researchers have now begun to study the aspects of DouDiZhu AI. Reference [20] analyzed the characteristics of the DouDiZhu game, and it holds that the DouDiZhu game is a two-person zero-sum game. On the premise that computer players know the information of opponents’ hand cards, an AI engine of the DouDiZhu game system was designed by using an efficient search mechanism, historical inspiration, transposition table, iterative deepening, and other search techniques. By analyzing the reasoning and learning of the dynamic fuzzy logic, the game of “three-against-one” applied and the learning function of the game system was realized theoretically [21].
In the previous study, a performance comparison between the cheating Upper Confidence bounds applied to Trees (UCT) agent against a determined UCT agent has been conducted, which called Mini DouDiZhu [22]. By studying the performance of the precise algorithms in the simplified version of DouDiZhu, they presented evidence that the advantages of cheating are lesser than obtaining hidden information and overcoming the inherent disadvantages of determined one. Nevertheless, narrowing the gap effectively between complete and incomplete information games has small consequences for the AI agent’s strength. Solving the fairness issue in the compound DouDiZhu competition is addressed through the concept of equal hand quality [23]. There are two kinds of methods: (1) classifying the two hands according to the mean and standard deviation of Landlord players’ scores in-game data, and (2) classifying the two hands according to the probability distribution of Landlord players’ scores and dimensional reduction is applied in each stage. Better classification impact has been justified from the probability distribution compared to the statistical method. Monte Carlo Tree search (MCTS) was employed for training its agents by self-playing and successfully achieved a human level [24].
To this end, more and more scholars have begun to pay attention to this field, mostly focusing on the development of the game from technical or historical point-of-view. To the best of our knowledge, this study is the first attempt to rationalize the popularity of DouDiZhu from the perspective of game processes and settings. Therefore, this study proposes a method to measure how the DouDiZhu game becomes refined or sophisticated, in which different settings are checked to determine the most suitable setting.
3. Methodology and Assessment Method
In this section, we illustrate how the game process from the perspective of game information is utilized to formulate the theory of game refinement measure. Assessment methodology being used to analyze the DouDiZhu game is proposed based on the theory.
3.1. Game Refinement Theory
Game refinement (GR) theory proposes a logistical model of game information progress to quantify and evaluate the sophistication of different kinds of games [6]. It also provides a different perspective to understand better the design and direction of optimizing a game [25]. In the current context, the game information progress can be defined in twofold. One is the speed or score rate of the game, while the other one is the game’s information progress, which focused on the result, indicating the outcome certainty of the game. If we consider the information process in the human brain, which can be measured as in the physics, taking Newton’s second law into comparison, we could get the game acceleration, which we denote as value [26].
The value is derived from the average scores (denoted as ) over the average times of attempts (denoted as ). Game information certainty is a function of time t corresponds to the average number of possible moves and game length in board games and card games, respectively, where and [6,27]. In the continuous movement, games such as sports and video games can employ a game progress model to find the measure of game refinement. Different types of popular games had been analyzed, which is summarized in Table 1.

Table 1.
Measure () of game refinement for some popular games [28].
The values observed from the previous study, representing the acceleration of the game process, where popular games converge to a sophistication “zone” between the value of to . This sophistication zone represents the balance region for a good game where the uncertainty of the game is appropriate to make the game enjoyable and entertaining. indicates the outcome of the game becomes certain, requiring skill to be exciting or the game become boring. Conversely, corresponds to the outcome of the game being too uncertain, which dependent on the chance to be enjoyable or the game becomes frustrating. Therefore, concerning the interpretation of value, a sophisticated game is a game that balances between chance and skill where players are expected to experience an appropriate enjoyment, entertainment, and challenge.
3.2. Assessment Methods Employed for DouDiZhu
If we take the game as the process that keeps getting information about the game outcome, when the uncertainty of game outcome is finally eliminated, the game is over. The information process model can be seen from the Figure 2.
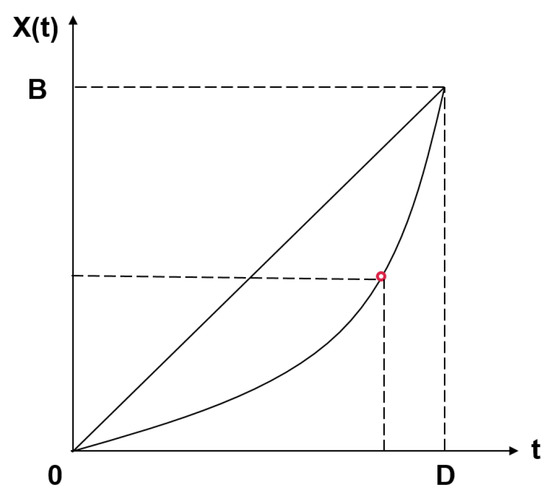
Figure 2.
Game information process: certainty of outcome.
From the player’s point-of-view, with increases of the obtained information, the more predictable the game outcome becomes when approaching the end. As such, the outcome of game information or certainty can be approximated as a linear function of time t, denoted as in (1).
The variable n is a constant parameter based on the skill differences among the players of the game. Let D be the total moves of the game. Assume and , noting that , . Hence, determining the rate of outcome uncertainty of the game is ensured, which is directly proportional to (Equqtion (2)).
The accelerated velocity of the solved uncertainty along the game process can be achieved by deriving (2) twice. Assuming the game lasts until (in DouDiZhu, one of the players plays out all his hands), (3) is obtained.
The measurement () of game refinement for DouDiZhu is given in (4), where could reflect some attractive characteristic of the DouDiZhu, where B stands for the average number of possible moves at each hand and D stands for the average game length.
4. Simulation and Data Collection
Usually, DouDiZhu is played in four stages, as shown in Figure 3. The simulation experiment is conducted by utilizing a simulation program (namely as DouDiZhu AI) with a fixed strategy. Such a strategy is similar to the strategy used by the best human best player, which involves calculating the numerical setting of each card category [29]. The parameter settings used in this study are the number of players (two types of players: landlord and peasants, where only one landlord is present, and peasant can be more than one) and their card distribution. The simulation was run 10,000 times for each of the game settings. The average possible options (B) and the average game length (D) were calculated, which then analyzed using the measure.
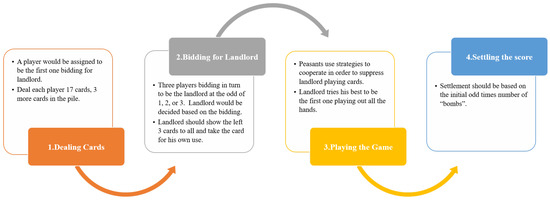
Figure 3.
Stages of classical DouDiZhu.
The experiments were conducted as follows. Firstly, the simulation is first set up to accommodate different settings, annotations of the experiment, and strategy adoption, which considering three different DouDiZhu AI levels (weak, fair, and strong) to simulate the presence of cooperation among the players. Secondly, the simulation experiment is conducted on Classical DouDiZhu, which then compared with different DouDiZhu AI levels. Thirdly, another simulation experiment is conducted on known variants of the DouDiZhu in China to highlight the impact of the cooperation in the Classical DouDiZhu game.
4.1. Simulation Setups
In this study, no bidding phase is conducted where the landlord assignment is random. Fifty-four cards are split randomly among three players in the classical DouDiZhu, where the cards number is (20, 17, 17), where the one with 20 cards corresponds to the landlord, which is denoted as (L, , ). From one side, the landlord (L) is fighting on his/her own. On the other side, peasant 1 () and peasant 2 () cooperate against L. The game is won by the side that first plays out all the card hands.
There are two categories of gameplay, initiative play or passive play. After dealing with the cards, the landlord will play the first card or combination (initiative play). Alternatively, , can play a bigger-force card to follow the last player’s cards one by one (passive play). If they do not have bigger cards or decided to skip, it is called a pass. When pass is chosen by two players consecutively, the round will end. Then, the third player can initiate play with any card and begin the next round. For instance, play card in turns as , , , , , , , , which then will start a new round and initiate the card plays. The game ends when any one of the three players has played all the cards.
In this study, the game length (D) of DouDiZhu is the number of the total moves of the three players. Assuming the number of game players as n, number of landlord as l, number of the peasants as p, hands allocation will be shown as , a game setting will be denoted as . In the case of classical DouDiZhu, a setting denoted as . The average number of possible moves at each hand (B) is counted as follows:
- When a player begins a game phase, the number of possible conventional combinations on the player’s hand is the estimation for the number of options. For example, ’s deck is “2221K999888633”, can play a card with the possible options of 3, 6, 8, 9, k, 1, 2. Thus, a total of seven cards; possible options can play two cards is 33 88 99 22, a total of four cards; and so on until the possible option can play ten cards is “8889992233”, this is just one card. Adding all the options together, , the total for .
- When a player plays a phase passively, the number of choices is limited to the last played card of the same type. For example, plays “66633”, L’s remaining card is “22”, so L’s option is only to “pass”, which is just a single option; deck is “21kkkjj8876544”, can play “kkk44”, “kk88”, “jjj88”, “JJJKK”, and “pass”; thus, totaling to 7.
Notation: peasants need to cooperate, sometimes they will choose “pass” even when they have cards to play. Sometimes they do not want to split bigger-force combinations; thus, they may also “pass” anytime when they passively play cards.
The implementation of the DouDiZhu AI program involves dealing cards and playing cards during which cooperation between peasants should work as intelligent as possible. For functional convenience, different card categories are provided with a different numeric value according to the game rules (see further in [30]).
The adopted optimal strategy for the simulation experiments is according to the strategy mentioned by the practical technique books of DouDiZhu [19], which corresponds to the strong DouDiZhu AI level. For initiative play, the DouDiZhu AI will prioritize playing a sequence of planes, wings, lines, triples, pairs, and singletons. However, smaller cards are used when playing against an opponent or of the same class. Passive play is one of the alternative strategies that use smaller cards. The landlord is unscrupulous. At all costs, the peasant plays a bigger card than the landlord. Finally, when the card force is less than the lower bound, the first peasant plays more cards than the second peasant to ensure the success of both. The algorithm 1 describes the optimal core strategy.
| Algorithm 1 Optimal simulation strategy for DouDiZhu. |
|
The simulation uses three levels of DouDiZhu AI: strong, fair and weak. The strong DouDiZhu AI always follows the above strategy. For the fair DouDiZhu AI, peasants cooperate, and peasants always choose for any card, while landlords can play as long as they have a larger card. For the weak DouDiZhu AI, all three players played bigger cards or passed at random.
4.2. Experiment on The Classical DouDiZhu
The classic Doudizhu is the most popular version in China, played by three players. Valid cards include a single card, pair card, straight card, triple card, double-wing card, plane card, bomb card, rocket card, and 300 cards, which can also be played by kickers (see Table 2).

Table 2.
Categories of cards.
DouDiZhu game has a unique score system. The basic score is set as 3 points in this study, where the score is doubled when the player played a bomb or rocket (https://en.wikipedia.org/wiki/Dou_dizhu). For example, the landlord obtains a total of 24 points while the peasant loses 12 points if there are three bombs, and the landlord wins the game. The conducted simulation considers a fair level of DouDiZhu AI, which corresponds to an average level of a human player (Table 3).

Table 3.
Measures of game refinement for classical DouDiZhu.
In a real gameplay situation, however, emotion tends to overtake human players where changes in decision and strategies are expected in corresponds to their experiences and preferences; thus, producing an unexpected outcome. Hence, simulating such a situation is crucial through the consideration of the computer peasants’ cooperation. Additionally, DouDiZhu has millions of players which composed of novice to master level of players. In this simulation experiment, weak DouDiZhu AI represents a novice with little skills and intentions to cooperate, while fair AI represents an average human level with a weak cooperation strategy. A strong DouDiZhu AI stands for a specific kind of professional players with tournament-level performance.
Since cooperation and competition are important aspects of the game, the expected fairness of the game setting can be determined based on the average score for each set. Table 4 provide different settings of the landlord and peasants with their respective possible scores. The scores are collected using DouDiZhu AI with the optimal strategy that prioritizes the best sense of cooperation. As a zero-sum game, the peasants’ score and the landlord’s score should be the same from the perspective of fairness.

Table 4.
Possible scores of landlord and peasant with different card distribution settings.
The result indicates that setting is relatively fair based on their respective winning rate. However, observing the score setting of , it is perceived to be less fair for the peasants’ side, which implies that it is hard for the landlord to win equivalent scores. Interestingly, for and , while also perceived to be less fair to the peasant side, actually implies the opposite where one of the peasants tend to win at the cost of another. This setting implies that one of the peasants, while co-operating with another, played selfishly; thus, promoting less cooperation.
The simulation results performed with different settings through different DouDiZhu AI levels are given in Table 5 which suggests that both weak DouDiZhu AI with little cooperation and fair DouDiZhu AI with lower-level cooperation show almost the same performance quality. However, when it comes to the strong DouDiZhu AI with optimal cooperation strategy, value dropped radically.

Table 5.
The results of simulation performed using different DouDiZhu artificial intelligences (AIs) for various game settings.
Numbers of hands also affect the experience of a card game. The setting of is found to be the most sophisticated one for novice and average players, while the setting of is ideally exciting and challenging for professional players. It might reveal that for a typical case, we should play as the setting of ; however, in the tournament, it should adjust the hands to the more significant disparity.
Different levels of the players also affect the possible outcome and attractiveness of the game [31]. By analyzing the performance of the classic game setting , a possible score of different DouDiZhu AI levels was collected and summarized in Table 6. While achieving a fairest winning ratio, weak DouDiZhu AI has no cooperation which implies they fought among themselves. Comparing the strong DouDiZhu AI with fair DouDiZhu AI, it could be observed that strong DouDiZhu AI with a high level of cooperation can also maintain balanced benefits of two sides (landlord versus peasants).

Table 6.
Possible score using different DouDiZhu AIs in the game setting .
In multiplayer cooperative games, cooperative strategies can keep DouDiZhu relatively fair, which may have a significant impact on game complexity. When the cooperative strategy is prioritized, the measurement drops, meaning that the game is challenging for most players. In other words, when considering a strong cooperative strategy, the game is less fun for the novice. Summarizing the results from Table 5 and Table 6, it can be conjectured that DouDiZhu is profoundly refined with both luck and skill under such mode of cooperation.
4.3. Comparison with the Variants of DouDiZhu Game in China
The rules of DouDiZhu has not changed much, although its development is about 30 years. Still, its popularity showed that if the game changes, it will do so for the better. Table 7 provides the variants of the DouDiZhu game analyzed in this section.

Table 7.
Versions of DouDiZhu games.
When two players, initial hands will be 17–25 cards for both players such as (20,20); when three players, initial hands will be (18,18,18); when four players, get rid of two jokers, initial hands will be (13,13,13,13); more people will deal two decks of card in this way.
For two-player DouDiZhu, while the rules are similar to the classic DouDiZhu, one player plays as the peasant while the other plays as the landlord. At first, each player is randomly dealt with 17 hand cards. After the bidding, the landlord will have three additional cards. As such, a total of 17 cards will be unknown during the game. On the other hand, the rules for the four-player DouDiZhu are similar to the classic DouDiZhu but utilize two decks of cards. Instead of two versus one, DouDiZhu of four players are three versus one (a single player is the landlord while the remaining players are peasants). At first, each player is dealt with 25 hand cards. After the bidding, the landlord will have eight more cards.
The simulation experiment in this section utilizes similar rules as the classical DouDiZhu to simulate other versions of the DouDiZhu game considered for this study. The first simulations were conducted for the versions of two-players and four-players setting with fair level DouDiZhu AI. The simulation result is given in Table 8.

Table 8.
Measures of game refinement for two variants of DouDiZhu.
According to the theory, a sophisticated game is a game that harmoniously balances challenge and skill as they changed over time [6]. Since the sophisticated zone of game refinement value for most popular games has been verified to be , it was found that the measure is different in the traditional settings. The data might imply that the two-player DouDiZhu game ( = 0.142) is more likely based on chance, while the four-player DouDiZhu ( = 0.0649) with too many cards to play is complicated, more likely boring.
The two-player DouDiZhu is too easy to finish, making its value higher than the sophistication zone. The four-player DouDiZhu, on the other hand, is not equivalently fair for every player, and too challenging for the landlord to compete and for peasants to cooperate; thus, the value is lower than the GR zone. This distinction of the player number probably offered a numerical interpretation of the popularity of the classic DouDiZhu game in China (three-player setting).
Table 9 provides the possible scores of landlord and peasants in different settings. The scores are collected using DouDiZhu AI with the optimal strategy that prioritizes the best sense of cooperation. As a zero-sum game, the peasants’ score and the landlord’s score should be the same from the perspective of fairness. Table 9 indicates that the settings is relatively fair based on their respective winning rate. However, it can be observed from the score that the settings and are perceived to be less fair for the landlord side, which implies that it is hard for the landlord to achieve equivalent scores. These findings further justify that the four-players setting sacrifices both the expected enjoyment and fairness of the game.

Table 9.
Possible scores of landlord and peasant in different game settings.
The simulation results performed with different settings through different DouDiZhu AI levels are given in Table 10. Similar to the experiment for the classical DouDiZhu, Table 10 implies that both weak DouDiZhu AI with little cooperation had almost similar performance quality to the fair DouDiZhu AI with lower-level cooperation (except for strong DouDiZhu AI). Additional insights also can be observed from the distribution of the cards between the landlord and the peasants. Increases in the number of cards the landlord have, the lower the value. This situation implies that the game is more challenging since the landlord has more hands at the start of the game. With more cards on hand, the landlord has to deal with more combinations and strategies (high branching factors). Peasants also have to deal with higher risks that the landlord might have a higher chance of getting high-value card categories. Such a situation demands the landlord to play out all the cards skillfully. Thus, more cards are nonequivalent to being advantageous in the DouDiZhu game.

Table 10.
The results of simulation performed using different DouDiZhu AIs for various game settings.
The most popular activity in this game is the “pass”. Peasants can choose “pass” even when they have bigger cards to play to let their teammates win. Hence, based on the simulation strategy, the frequency of “pass” in a game could be taken as a parameter to estimate the cooperation between peasants. Table 11 shows that peasants with weak DouDiZhu AI represent human novice, with no intention of cooperating, passes less than a fair DouDiZhu AI representing average players with a weak level of cooperation skills. In other words, after the novices get some sense of cooperation, they begin to reserve cards and choose to deliberately “pass” to let more cards to be played by their teammate. It can be inferred that the existence of cooperation increases the engagement of the game. By having an awareness of cooperation in playing this game, they become more cautious at every step.

Table 11.
Pass frequency of different level DouDiZhu AIs: comparing classical DoudiZhu and four-player DouDiZhu settings.
5. Comparative Study and Discussion
In this section, a comparison between different card games similar to DouDiZhu is conducted where different variations of similar popular card games from other countries were analyzed relative to the DouDiZhu game and cooperation factor from the perspective of measure.
5.1. Other Popular Shedding-Type Card Games
Analysis of different DouDiZhu and similar games all over the world is conducted to test if DouDiZhu has the most advantages among them. In general, they have similar rules. However, they are quite different in the card categories and their cooperation aspects. To understand the difference of all the card games mentioned, their main categories are summarized in Table 12.

Table 12.
Popular shedding-type card games from different regions.
- Winner shared similarity to the DouDiZhu. The main differences between Winner and classic DouDiZhu are found in two aspects. Firstly, the number of players where Winner can play at least by two players and usually not more than eight, using two decks of cards when more than four players (https://en.wikipedia.org/wiki/Winner_(card_game)). Secondly, each player of Winner fights on their own. Winner plays out all the hands, while other players continued until there is just one player and they score by ranks of sequence to play out cards. Thirdly, hands in Winner have a different weight of the suit, where spades are biggest followed by hearts, clubs, and diamonds. Suit discrimination gives Winner a lot of card combination possibilities.
- Daifug (Grand Millionaire) or Daihinmin (Grand Pauper) is a Japanese card game played by three or more players using standard 52 Cards. The goal of the game is to get rid of all hands as quickly as possible. The method is to gradually play a stronger card than the previous player’s card. The major characteristic of Daifugō is that Daifugō only has the category where straight works with the same color and with more than three consecutive cards.
- Big two is popular among the southern Asia and East-southern Asia, commonly played by four players. Valid card combinations is the primary differences between Big Two and DouDiZhu. Big Two can play flushes, while DouDiZhu does not care about the suit. In Big Two, the straight can only consist of exactly five cards, while DouDiZhu’s straight can consist of five to 12 cards.
- Tin Ln, also known as Vietnamese cards, Thirteen, “Bomb", is a Vietnamese shedding-type card game devised in Southern China and Vietnam. Tien Lên has many variants. The rules are similar to Big Two with no boom and the game starts with spade 3.
- Killer is a variant from Tien Lên which is famous among Hawaii district. It is an updated version of Tien Lên, with a complicated bomb category.
Theoretically, the characteristics of local games can reflect humans’ culture from a side profile. The results of simulation using DouDiZhu AI performed on these DouDiZhu and similar card games are shown in Table 13 while finding their game refinement values. It can be inferred that the Chinese, overall, tend to explore the unknowns by playing games with more stochastic elements, which prefer “entertainment”. Likewise, it can also be conjectured that the Japanese are likely to challenge their limits by conquering more difficult games, which prefer “accomplishment”. More importantly, the results of Table 13 suggest that popular similar to DouDiZhu card games over the world were outside of the GR zone. We believe that the existence of cooperation is the most important distinction in DouDiZhu compared to other card games that make it situated in the most sophisticated zone of the GR measure.

Table 13.
DouDiZhu similar card games over the world.
5.2. Why DouDiZhu Is the Most Popular Card Game in China?
An early psychological study by Csikszentmihalyi had pointed out that flow is the state of deep enjoyment of people [32]. Human getting fully engaged and immersed in a game may be caused by the games’ mechanism, which contains a clear purpose, instant feedback, and the feeling of control. Based on the results, it was found that DouDiZhu provides players with an exciting play experience and perceived to be fair in a particular setting while promoting engagement and cooperation in its play mechanism. Additionally, the DouDiZhu game has a similar sophistication level compared to other popular games in China, which is justified by being the highest sought after the game just next to Mahjong online (Figure 4). Hence, revisited the question “why foes DouDizhu have the highest number of users among all the card and chess games?”, several reasons were found based on the simulation experiments conducted in this study.
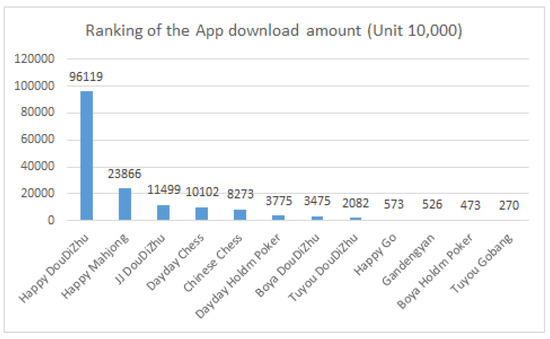
Figure 4.
Download ranking adopted from the web article from http://www.youxiputao.com/articles/13003/.
Firstly, it is reasonable to justify the reason for DouDiZhu’s popularity relative to the Mahjong, Chinese chess, and Go games. According to the value (Table 14), these games were well-refined to have a level of sophistication similar to DouDiZhu. However, the differences were based on their respective game length and rival mode. The game length alone may not be meaningful in this context since different game mechanisms, adopted by each game, may affect it differently. For example, short game length of the Mahjong and DouDiZhu typically associated with stochastic and chance-based gameplay [33]. However, their rival mode may hint on the importance of balancing cooperation and competition. For example, it is typical for Mahjong to be played individually or cooperatively. While the former may be right most of the time, the latter could potentially make the game more interesting. Explicit cooperation through the role of the peasants in DouDiZhu makes the game superior to Mahjong, although the game length is shorter than Mahjong. Hence, it can be speculated that with some level of cooperation, the more exciting the game becomes to the players as the shorter the duration of the game.

Table 14.
Comparison of some well-refined board and card games in China (ordered by decreasing value).
Secondly, compared to Chess and Go, the DouDiZhu is an incomplete information game that usually has more complicated solutions. In Mahjong, players have complete information about their situation but not their opponents. However, in DouDiZhu, for the peasants, they have both incomplete information of the rival’s and their own. This situation adds more uncertainty to the game and makes this game unique. Hence, there is a high degree of confidence DouDiZhu is situated in the zone of the game sophistication, where attractiveness and fun of the game strongly affected by the degree of cooperation.
Finally, Figure 5 showed various board and card games and possible score opportunities in continuous sports games, which depicted by the game length (D) versus the average branching factors (B). It can be observed from the figure that DouDiZhu, both three-players, and four-players versions, were located close to the “zone” of sophisticated game. DouDiZhu also provides the best setting concerning the aspects highlighted in the Flow theory [32], where the game incorporated a level of sophistication that includes instant feedback and much uncertainty as well as fun.
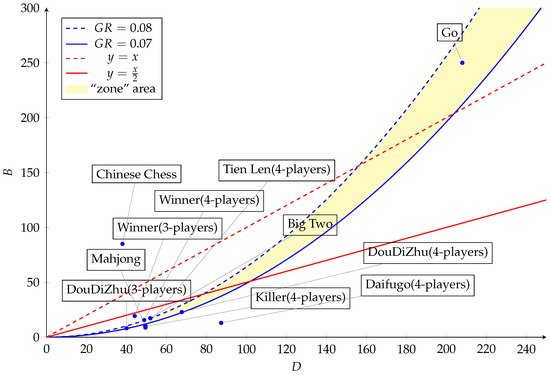
Figure 5.
The depiction of game refinement values of the well-refined games mentioned in the study.
In essence, DouDiZhu is a unique game that emphasizes both competition and cooperation. The occurrence of cooperation in the game is affected by two factors: the number of players and their respective roles (landlord vs. peasants) and the game mechanisms which allow players to cooperate or compete against one another based on the usage of “pass”. These factors encourage cooperation between peasants while balances the expected competition between the landlord and the peasants, which provide insights into the nature of the DouDiZhu game as well as being sophisticated enough to be an attractive multiplayer game. Hence, such a setting is not surprising when the DouDizhu is nominated as the most popular card game in China within less than 30 years of development.
6. Concluding Remarks
This study had tested different aspects of the Chinese most popular card game, DouDiZhu. Simulation results indicate that the multi-person incomplete-information games like DouDiZhu, having both cooperated behavior and competitive behavior, follow the principle of a seesaw game. The preliminary simulation results revealed that three-player DouDiZhu is perfectly refined with sophistication, entertainment, and fairness on the measurement of game refinement at the value of 0.0715.
It was found that the number of cards effectively influences the player’s experience. A small disparity is needed for novice and fair level players, while significant disparity is reasonable for a professional level. The most sophisticated game setting for DouDiZhu is found as . Lastly, we compared DouDiZhu with a similar version over the world and other well-refined card and board games in China, where the DouDiZhu is numerically found to be the most exciting game. A cooperation strategy is required to balance the expected game fairness among the players, which is measured using the scoring system.
Nevertheless, the DouDiZhu game was somewhat simplified in terms of its score system compared to a real-world DouDiZhu game scenario. Further study can be conducted to investigate how different scoring mechanism will affect the sophistication of the game. Additionally, it can be hypothesized that the player’s characteristics could hugely affect the game result. Our simulation just tests one specific type of strong players. Future studies can focus on the various characteristic of players to determine the influence of such characters on the game outcome.
Author Contributions
Conceptualization, methodology, software, validation, investigation, formal analysis and writing—original draft preparation is contributed by Y.G., W.L., Y.X. and H.I.; Data curation, supervision, project administration, validation, visualization, resources, funding acquisition, and writing—review and editing is contributed by M.N.A.K. and H.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by a grant from the Japan Society for the Promotion of Science, within the framework of the grant for fundamental research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huizinga, J. Homo ludens, a study of the play-element in culture. Am. Sociol. Rev. 1980, 16, 274. [Google Scholar]
- Iida, H. Where Is a Line between Work and Play? Available online: https://dspace.jaist.ac.jp/dspace/handle/10119/15366 (accessed on 28 February 2020).
- McGonigal, J. Reality Is Broken: Why Games Make Us Better and How They Can Change the World; The Penguin Press: New York, NY, USA, 2011. [Google Scholar]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Wikimedia. Dou Dizhu. Available online: https://en.wikipedia.org/wiki/Dou_dizhu (accessed on 28 February 2020).
- Iida, H.; Takahara, K.; Nagashima, J.; Kajihara, Y.; Hashimoto, T. An Application of Game-Refinement Theory to Mah Jong. In Proceedings of the International Conference on Entertainment Computing, Eindhoven, Netherlands, 1–3 September 2004. [Google Scholar]
- Billings, D. Computer Poker. Available online: https://era.library.ualberta.ca/items/a92e1a72-bf40-4ae8-b3fb-eb34723367be (accessed on 2 March 2020).
- Billings, D.; Burch, N.; Davidson, A.; Holte, R.C.; Schaeffer, J.; Schauenberg, T.; Szafron, D. Approximating Game-Theoretic Optimal Strategies for Full-scale Poker. In Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003. [Google Scholar]
- Zinkevich, M.; Johanson, M.; Bowling, M.; Piccione, C. Regret minimization in games with incomplete information. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, CA, USA, 3–8 December 2007; pp. 1729–1736. [Google Scholar]
- Berlin, D.L.S. SPAN: Integrating Problem-Solving Tactics. Available online: https://pdfs.semanticscholar.org/0231/e118c916157c87396dc67da55e9b5597c242.pdf (accessed on 28 February 2020).
- Frank, I.; Basin, D. Search in Games with Incomplete Information: A Case Study Using Bridge Card Play. Available online: https://core.ac.uk/download/pdf/82412244.pdf (accessed on 28 February 2020).
- Myerson, R.B. Game Theory. Available online: https://www.hup.harvard.edu/catalog.php?isbn=9780674341166 (accessed on 28 February 2020).
- Dixit, A.K.; Skeath, S. Games of Strategy: Fourth International Student Edition; WW Norton & Company: New York, NY, USA, 2015. [Google Scholar]
- Colman, A.M. Cooperation, psychological game theory, and limitations of rationality in social interaction. Behav. Brain Sci. 2003, 26, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Hsieh, G. The influence of competition, cooperation, and player relationship in a motor performance centered computer game. Comput. Hum. Behav. 2012, 28, 2100–2106. [Google Scholar] [CrossRef]
- Seif El-Nasr, M.; Aghabeigi, B.; Milam, D.; Erfani, M.; Lameman, B.; Maygoli, H.; Mah, S. Understanding and evaluating cooperative games. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Atlanta, GA, USA, 12–15 April 2010; pp. 253–262. [Google Scholar]
- Cai, X. Why Do Chinese People Like Playing “Doudizhu”? Available online: http://36.112.18.13/article/detail.aspx?id=37015580 (accessed on 2 March 2020).
- Hu, C. A Brief Analysis of the Phenomenon of “Doudizhu”. Available online: http://www.cnki.com.cn/Article/CJFD2000-QYWH200008040.htm (accessed on 2 March 2020).
- Weimin, K. Poker Guide: Tips for “DouDiZhu”. Available online: https://book.douban.com/subject/4814771/ (accessed on 2 March 2020).
- Lin, J. The Application of Game Tree Searching Technology in Card Online Game. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10560-2010042531.htm (accessed on 2 March 2020).
- Liu, X. Research and its Application On Dynamic Fuzzy Relational Learning Algorithm. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10285-1011032182.htm (accessed on 2 March 2020).
- Whitehouse, D.; Powley, E.J.; Cowling, P.I. Determinization and information set Monte Carlo Tree Search for the card game Dou Di Zhu. In Proceedings of the 2011 IEEE Conference on Computational Intelligence and Games (CIG’11), Seoul, South Korea, 31 August–3 September 2011; pp. 87–94. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zheng, L.; Zhang, Z.; Ding, M.; Meng, K.; Li, S. Research on Hand Discrimination for Doudizhu Game. In Proceedings of the 4th International Conference on Education, Management, Arts, Economics and Social Science (ICEMAESS 2017), Sanya, China, 11–12 November 2017. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, K.; Du, B.; Chen, H.; Fang, H. DeltaDou: Expert-level doudizhu AI through self-play. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1265–1271. [Google Scholar]
- Panumate, C.; Xiong, S.; Iida, H. An Approach to Quantifying Pokemon’s Entertainment Impact with Focus on Battle. In Proceedings of the 2015 3rd International Conference on Applied Computing and Information Technology/2nd International Conference on Computational Science and Intelligence, Okayama, Japan, 12–16 July 2015; pp. 60–66. [Google Scholar]
- Xiong, S.; Tiwary, P.P.; Iida, H. Solving the sophistication-population paradox of game refinement theory. In Proceedings of the 15th International Conference on Entertainment Computing, Vienna, Austria, 28–30 September 2016; pp. 266–271. [Google Scholar]
- Sutiono, A.P.; Purwarianti, A.; Iida, H. A mathematical model of game refinement. In Proceedings of the International Conference on Intelligent Technologies for Interactive Entertainment, Chicago, IL, USA, 9–11 July 2014; pp. 148–151. [Google Scholar]
- Xiong, S.; Zuo, L.; Iida, H. Quantifying engagement of electronic sports game. Adv. Soc. Behav. Sci. 2014, 5, 37–42. [Google Scholar]
- Dian, S. Fight All over the World Invincible Hand. Dou Landlord Transcendent Skill. Available online: https://item.jd.com/11240301550.html (accessed on 2 March 2020).
- Gao, Y.; Li, W.; Khalid, M.N.A.; Iida, H. Quantifying attractiveness of incomplete-information multi-player game: Case study using DouDiZhu. In Computational Science and Technology; Alfred, R., Lim, Y., Haviluddin, H., On, C., Eds.; Springer: Kota Kinabalu, Malaysia, 2020; pp. 301–310. [Google Scholar]
- Xiong, S.; Li, W.; Xinting, M.; Iida, H. Mafia Game Setting Research using Game Refinement Measurement. Available online: https://www.researchgate.net/profile/Hiroyuki_Iida3/publication/321822554_Mafia_Game_Setting_Research_using_Game_Refinement_Measurement/links/5a331c48458515afb63c599e/Mafia-Game-Setting-Research-using-Game-Refinement-Measurement.pdf (accessed on 28 February 2020).
- Csikszentmihalyi, M. Beyond Boredom and Anxiety. Available online: https://psycnet.apa.org/record/2000-12701-000 (accessed on 2 March 2020).
- Yicong, W.; Aung, H.P.P.; Khalid, M.N.A.; Iida, H. Evolution of Games Towards The Discovery of Noble Uncertainty. In Proceedings of the 2019 International Conference on Advanced Information Technologies (ICAIT), Yangon, Myanmar, 6–7 November 2019; pp. 72–77. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).