A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach
Abstract
1. Introduction
1.1. Control Engineering Learning Involving the Ball and Beam Process
1.1.1. Related Works Associated with the Ball and Beam Modeling and Simulation
1.1.2. Related Works Associated with the Construction of the Ball and Beam Plant
2. Ball and Beam Process Description and Modelling
2.1. The Ball and Beam Apparatus
2.2. Physical Modeling
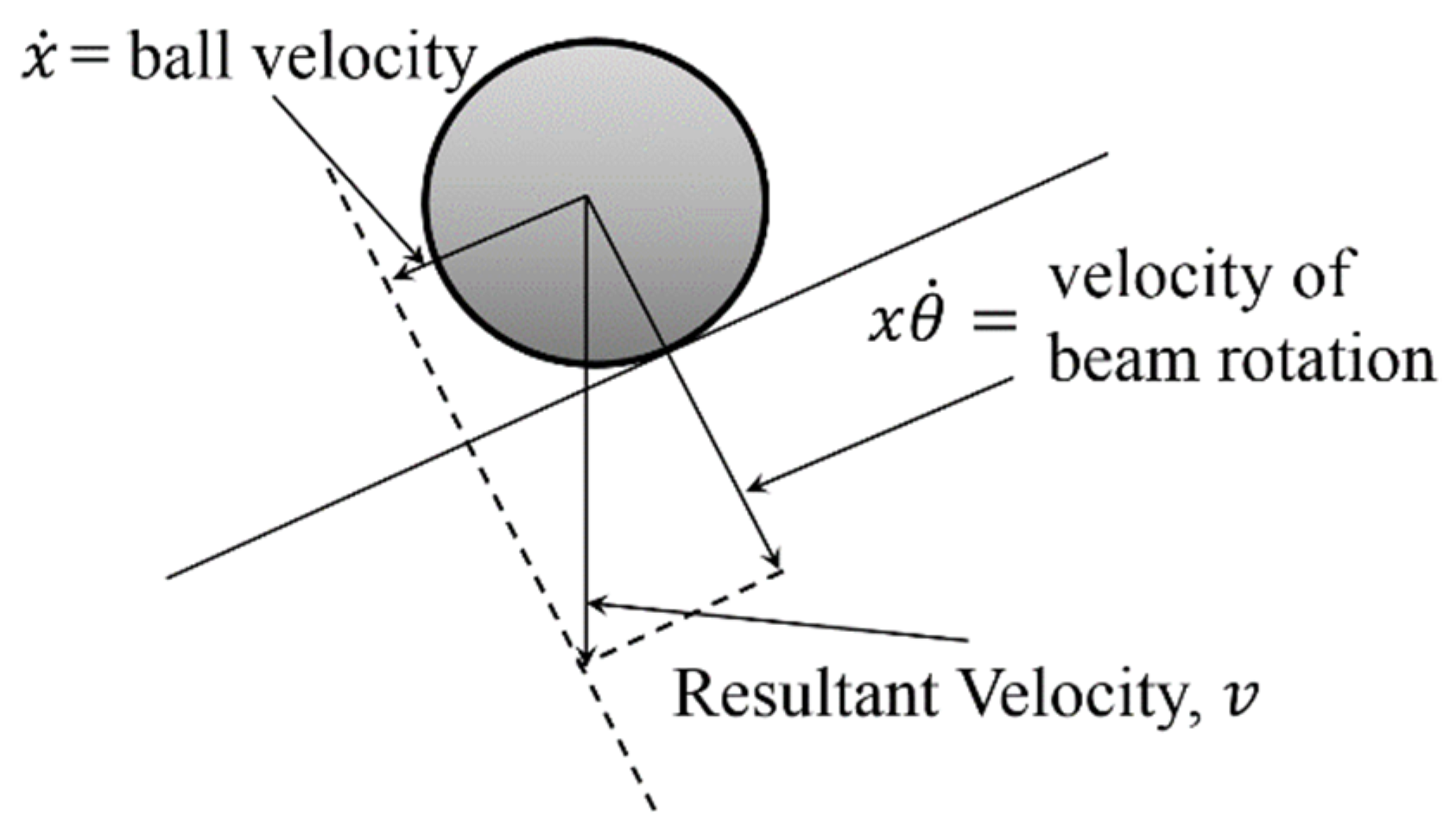
2.2.1. Simplified Model
2.2.2. Full Model
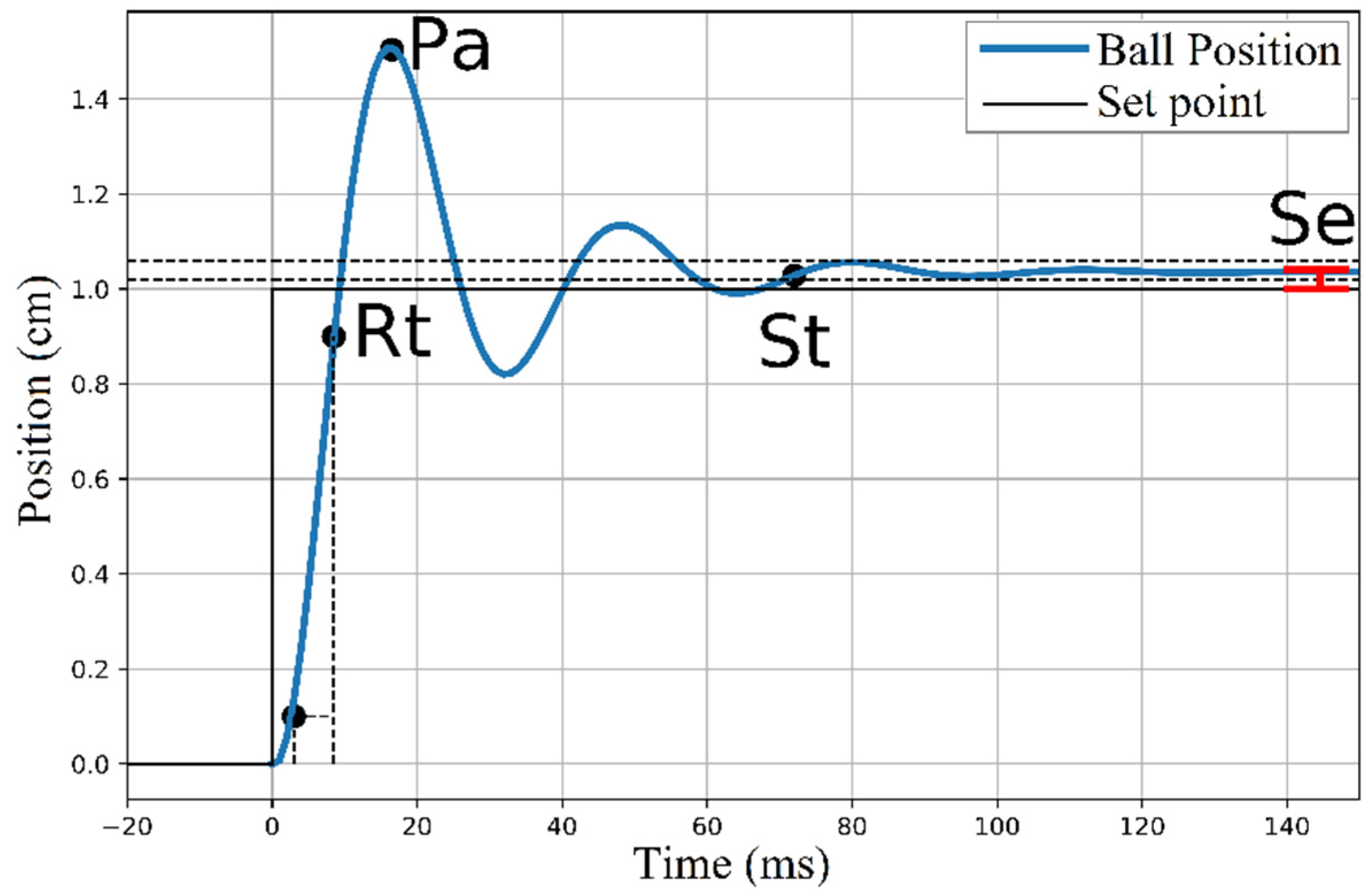
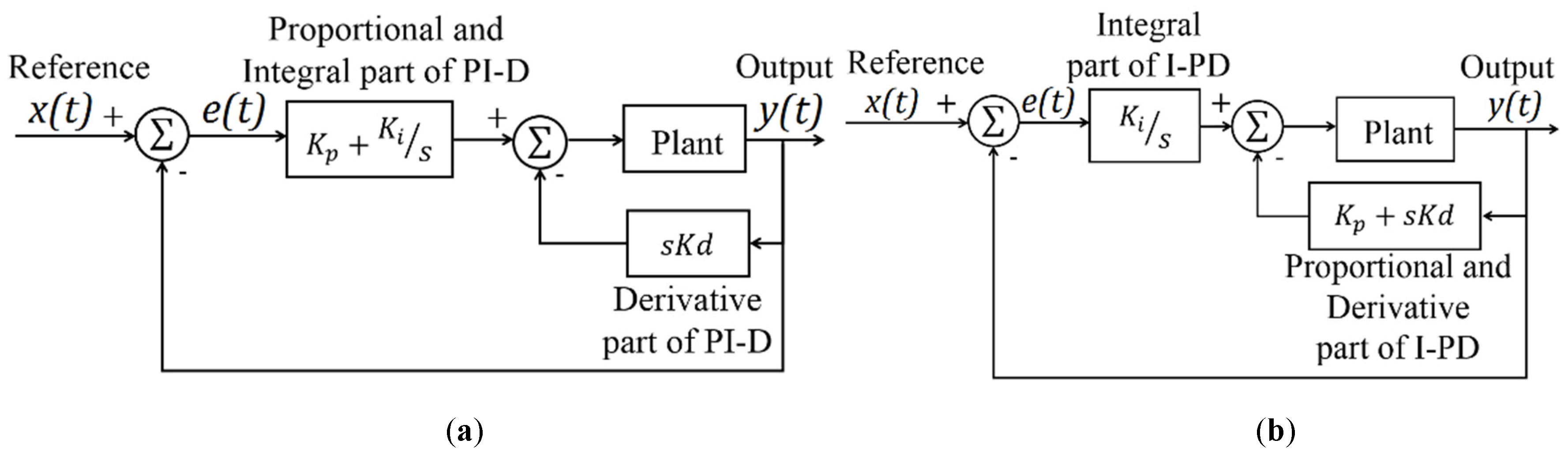
3. PID Control and Performance Measures
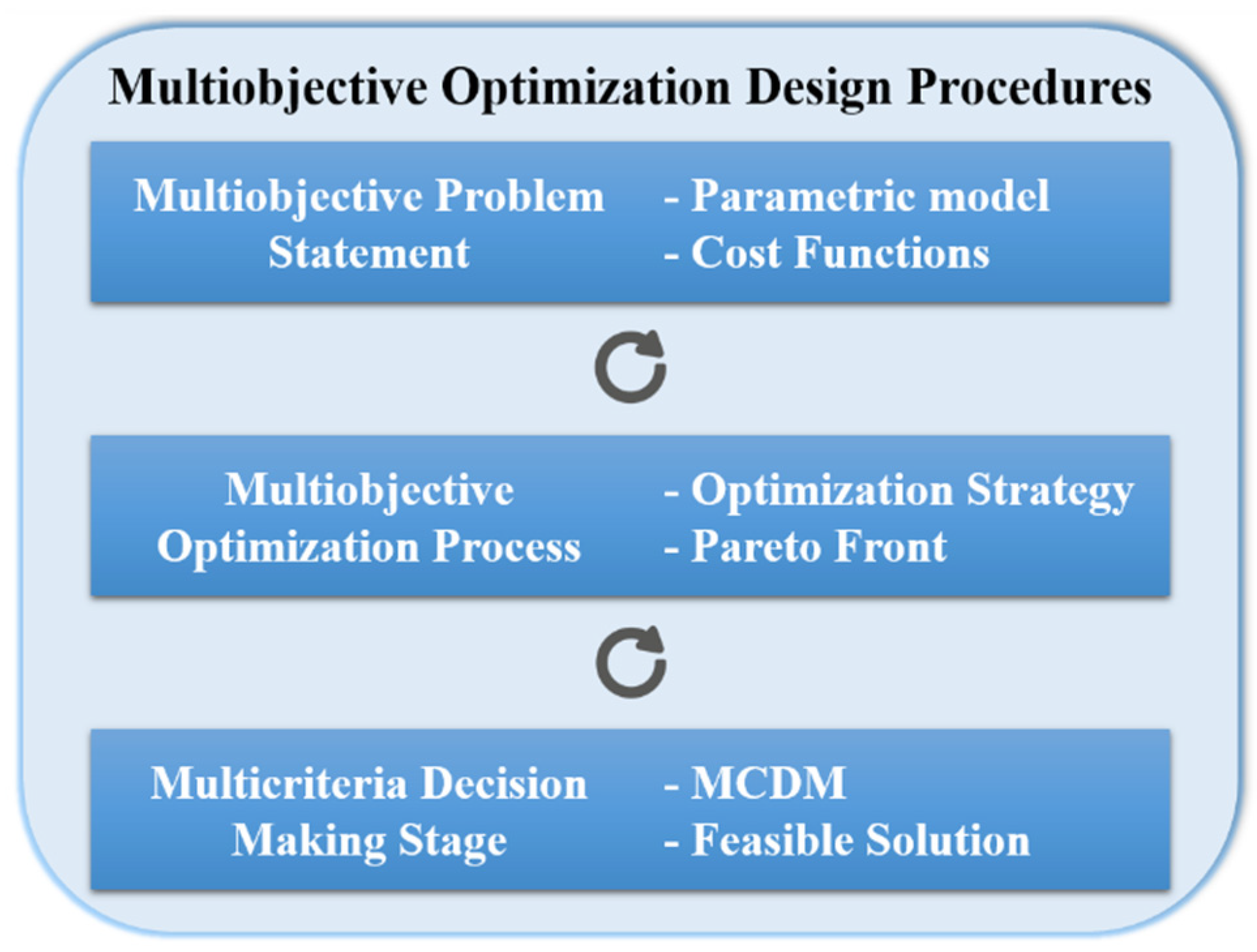
4. Multiobjective Optimization Applied to Control Engineering
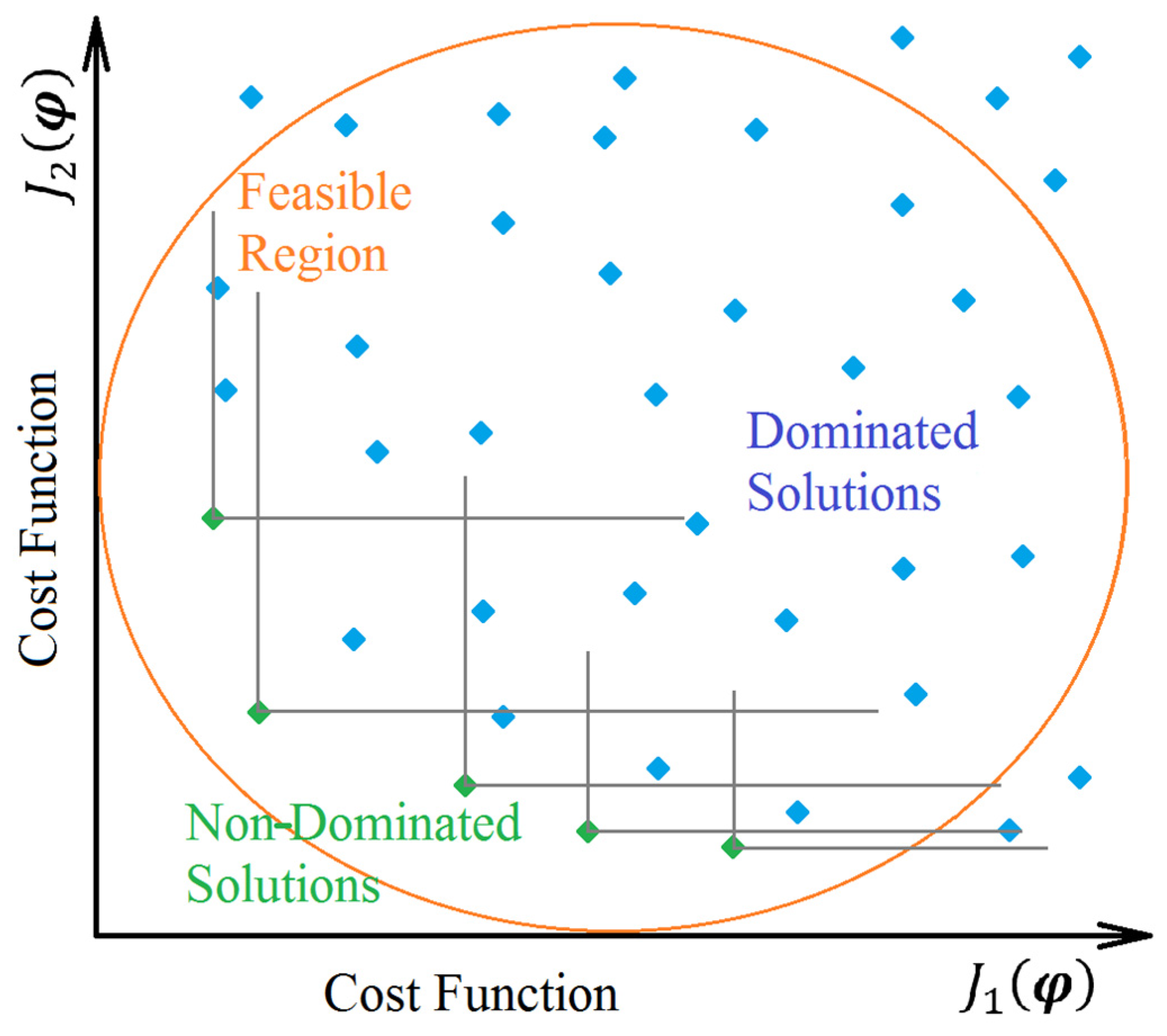
4.1. Multiobjective Problem Statement
4.2. Multiobjective Optimization Process
4.3. Multicriteria Decision Making
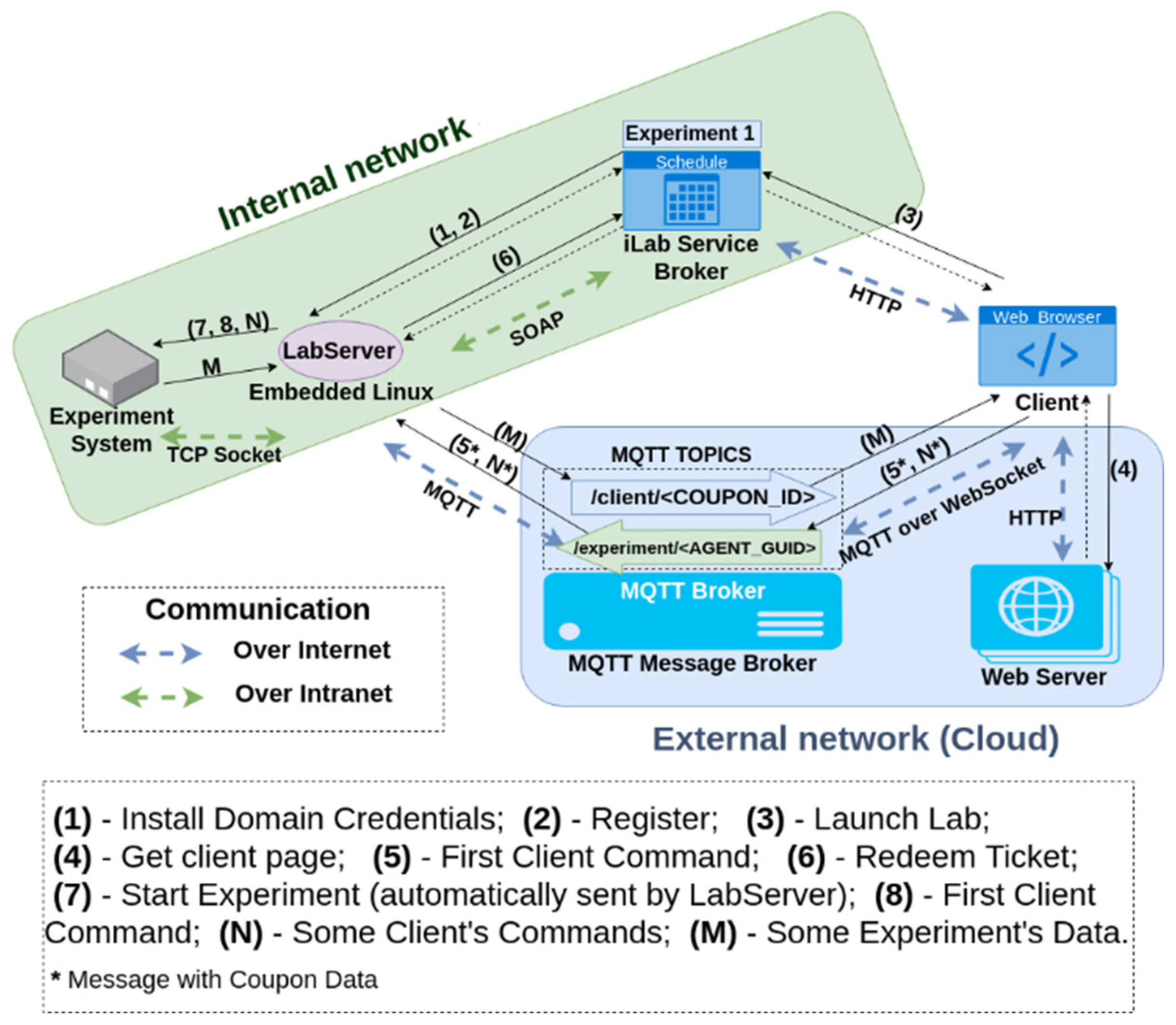
5. Remote Experiment Description
5.1. Experiment Structure
5.2. Experimental Procedures
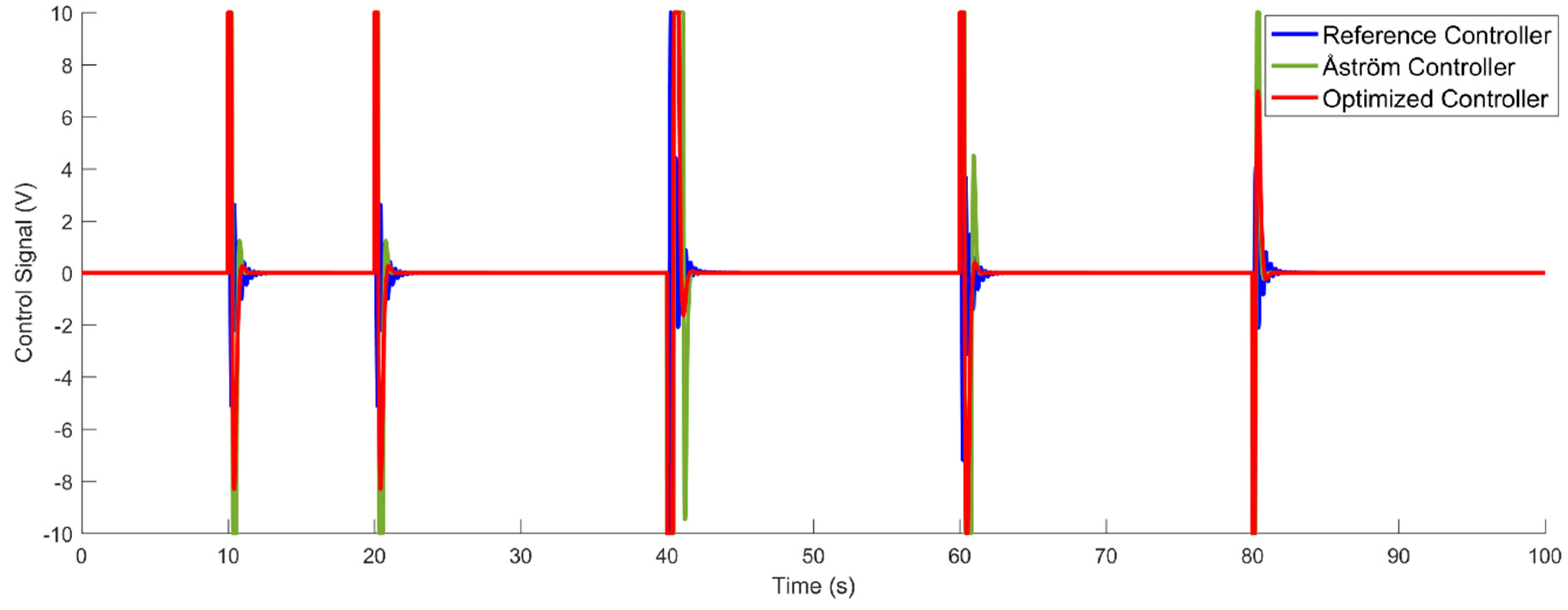
6. Results and Discussion
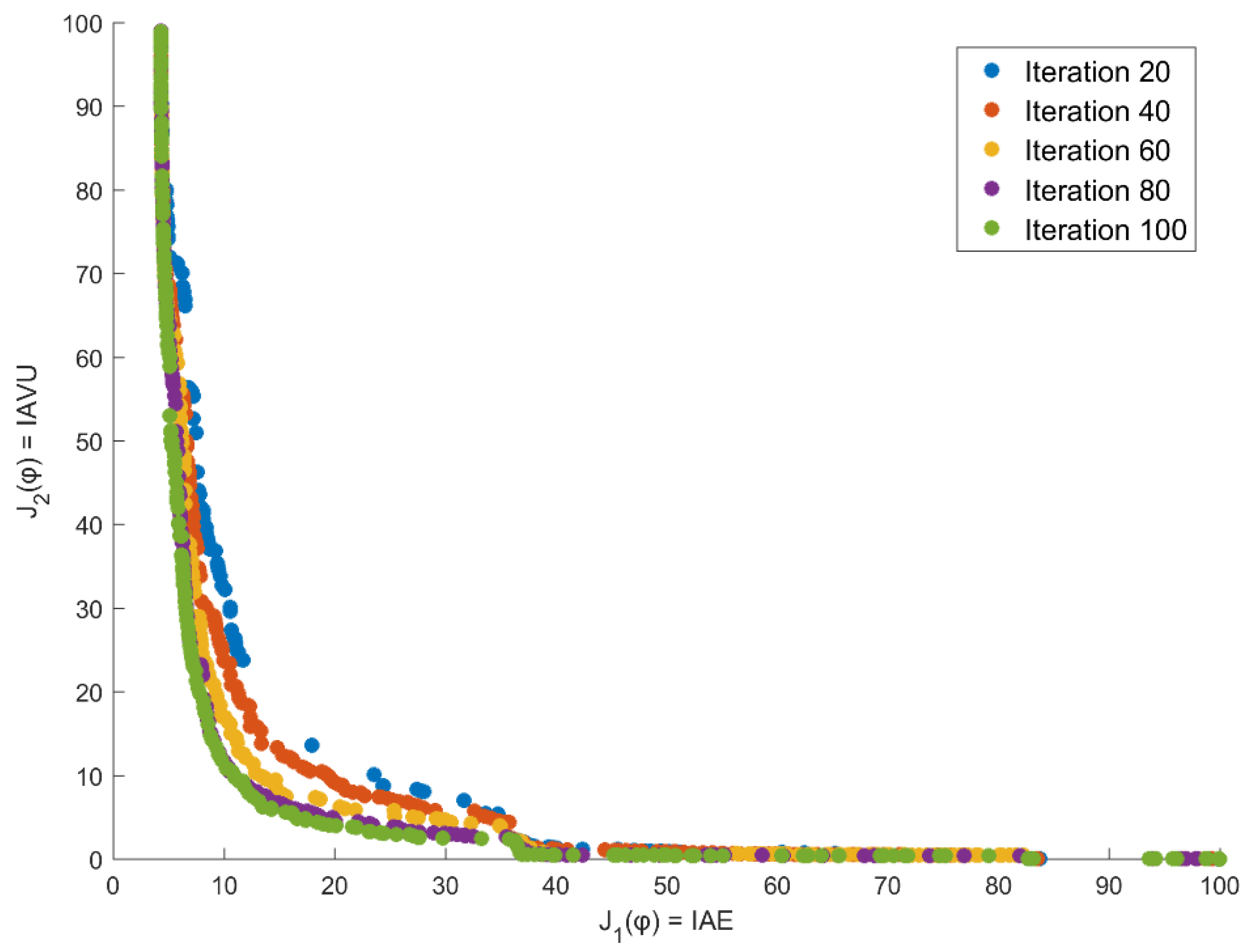
6.1. Multiobjective Optimization Procedures
6.1.1. Problem Definition
6.1.2. Multiobjective Optimization through NSGA-II
| Algorithm 1 NSGA-II procedures |
| 1: Initialize the population |
| 2: Evaluate the objective functions for the individuals |
| 3: Rank the individual based on non-dominated sorting |
| 4: Calculate the crowding distance |
| 5: While (Stopping Criteria is not satisfied) |
| 6: Select the individuals by using a binary tournament for the mating pool |
| 7: Apply the genetic operators, crossover, and mutation, to the mating pool |
| 8: Evaluate the objective functions of the offspring population |
| 9: Combine the offspring population with the current generation |
| 10: Rank the individual based on non-dominated sorting |
| 11: Calculate the crowding distance |
| 12: Select better solutions until complete the size of the population |
| 13: End While |
| 14: Output the non-dominated solutions |
6.1.3. Multicriteria Decision Making Strategy
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: Upper Saddle River, NJ, USA, 2010; ISBN 9780136156734. [Google Scholar]
- Hernández-Guzmán, V.M.; Silva-Ortigoza, R. Automatic Control with Experiments; Advanced Textbooks in Control and Signal Processing; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-319-75803-9. [Google Scholar] [CrossRef]
- Gan, B.; Menkhoff, T.; Smith, R. Enhancing students’ learning process through interactive digital media: New opportunities for collaborative learning. Comput. Hum. Behav. 2015, 51, 652–663. [Google Scholar] [CrossRef]
- Roberto, J.; Peña, Q.; Oliveira, J.; Leonel, M.; Henrique, L.; Rodrigues, N. Active Methodologies in Education of Electronic Instrumentation Using Virtual Instrumentation Platform Based on Labview and Elvis II. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Islas Canarias, Spain, 17–20 April 2018; pp. 1696–1705. [Google Scholar]
- Maskeliunas, R.; Damaševičius, R.; Lethin, C.; Paulauskas, A.; Esposito, A.; Catena, M.; Aschettino, V. Serious game iDO: Towards better education in dementia care. Information 2019, 10, 355. [Google Scholar] [CrossRef]
- Araujo, V.; Mendez, D.; Gonzalez, A. A Novel Approach to Working Memory Training Based on Robotics and AI. Information 2019, 10, 350. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Chan, C.L. Remote hardware controlled experiment virtual laboratory for undergraduate teaching in power electronics. Educ. Sci. 2019, 9, 222. [Google Scholar] [CrossRef]
- Selmer, A.; Kraft, M.; Moros, R.; Colton, C.K. Weblabs in Chemical Engineering Education. Educ. Chem. Eng. 2007, 2, 38–45. [Google Scholar] [CrossRef]
- Oliveira, O.N., Jr. Research Landscape in Brazil: Challenges and Opportunities. J. Phys. Chem. 2016, 120, 5273–5276. [Google Scholar] [CrossRef][Green Version]
- Zheng, P.; Wang, H.; Sang, Z.; Zhong, R.Y.; Liu, Y.; Liu, C.; Mubarok, K. Smart manufacturing systems for Industry 4.0: Conceptual framework, scenarios, and future perspectives. Front. Mech. Eng. 2018, 13, 137–150. [Google Scholar] [CrossRef]
- Raz, A.K.; Blasch, E.; Cruise, R.; Natarajan, S. Enabling Autonomy in Command and Control Via Game-Theoretic Models and Machine Learning with a Systems Perspective. AIAA Scitech Forum 2019. [Google Scholar] [CrossRef]
- Carreras Guzman, N.H.; Mezovari, A.G. Design of IoT-based Cyber—Physical Systems: A Driverless Bulldozer Prototype. Information 2019, 10, 343. [Google Scholar] [CrossRef]
- De Torre, L.; Guinaldo, M.; Heradio, R.; Dormido, S. The Ball and Beam System: A Case Study of Virtual and Remote Lab Enhancement With Moodle. IEEE Trans. Ind. Inform. 2015, 11, 934–945. [Google Scholar] [CrossRef]
- Hauser, J.; Sastry, S.; Kokotović, P. Nonlinear control via approximate input-output linearization: The ball and beam example. IEEE Trans. Automat. Control 1992, 37, 392–398. [Google Scholar] [CrossRef]
- Chang, B.C.; Kwtany, H.; Hu, S.-S. An Application of Robust Feedback Linearization to a Ball and Beam Control Problem. In Proceedings of the IEEE International Conference on Control Applications, Trieste, Italy, 4 September 1998; pp. 694–698. [Google Scholar]
- Lo, J.; Kuo, Y. Decoupled Fuzzy Sliding-Mode Control. IEEE Trans. Fuzzy Syst. 1998, 6, 426–435. [Google Scholar]
- Ali, T.; Adeel, M.; Malik, S.A.; Amir, M. Stability Control of Ball and Beam System Using Heuristic Computation Based PI-D and PI-PD Controller. Tech. J. Univ. Eng. Technol. 2019, 24, 21–29. [Google Scholar]
- Ding, M.; Liu, B.; Wang, L. Position control for ball and beam system based on active disturbance rejection control. Syst. Sci. Control Eng. 2019, 7, 97–108. [Google Scholar] [CrossRef]
- Almutairi, N.B.; Zribi, M. On the sliding mode control of a Ball on a Beam system. Nonlinear Dyn. 2010, 59, 221–238. [Google Scholar] [CrossRef]
- Keshmiri, M.; Jahromi, A.F.; Mohebbi, A.; Amoozgar, M.H.; Xie, W. Modeling and control of ball and beam system using model based and non-model based control approaches. Int. J. Smart Sens. Intell. Syst. 2012, 5, 14–35. [Google Scholar] [CrossRef]
- Chang, Y.; Chan, W.; Chang, C.T.-S. Fuzzy Model-Based Adaptive Dynamic Surface Control for Ball and Beam System. IEEE Trans. Ind. Electron. 2013, 60, 2251–2263. [Google Scholar] [CrossRef]
- Osinski, C.; La, A.; Silveira, R. Control of Ball and Beam System Using Fuzzy PID Controller. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 12–14 November 2018; IEEE: New York, NY, USA; pp. 875–880.
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Shah, M.; Ali, R.; Malik, F.M. Control of Ball and Beam with LQR Control Scheme using Flatness Based Approach. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; IEEE: New York, NY, USA; pp. 1–5. [Google Scholar]
- Tecquipment Academia. Ball and beam apparatus. In CE106: User manual; Tecquipment: Nottingham, UK, 1993; p. 132. [Google Scholar]
- Khalore, A.G. Relay Approach for tuning of PID controller. Int. J. Comput. Technol. Appl. 2012, 3, 1237–1242. [Google Scholar]
- Åström, K.J. PID controllers: Theory, Design and Tuning; Instrument society of America: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Sain, D. PID, I-PD and PD-PI controller design for the ball and beam system: A comparative study. Int. J. Control Theory Appl. 2016, 9, 9–14. [Google Scholar]
- Åström, K.; Hägglund, T. Advanced PID Control; ISA—Instrumentation Systems and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1989; ISBN 0-201-15767-5. [Google Scholar]
- Kagami, R.M.; Reynoso-Meza, G.; Santos, E.A.P.; Freire, R.Z. Control of a Refrigeration System Benchmark Problem: An Approach based on COR Metaheuristic Algorithm and TOPSIS Method. IFAC-PapersOnLine 2019, 52, 85–90. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Venkata Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Tangherloni, A.; Rundo, L.; Nobile, M.S. Proactive Particles in Swarm Optimization: A Settings-Free Algorithm for Real-Parameter Single Objective Optimization Problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 1940–1946. [Google Scholar] [CrossRef]
- Rueda, J.; Erlich, I. Hybrid Population Based MVMO for Solving CEC 2018 Test Bed of Single-Objective Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Fan, Z.; Fang, Y.; Li, W.; Yuan, Y.; Wang, Z.; Bian, X. LSHADE44 with an Improved ϵ Constraint-Handling Method for Solving Constrained Single-Objective Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: New York, NY, USA; pp. 1–8. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Wu, C.; Lei, L. Hunting optimization: An new framework for single objective optimization problems. IEEE Access 2019, 7, 31305–31320. [Google Scholar] [CrossRef]
- Azlan, N.A.; Yahya, N.M. Modified Adaptive Bats Sonar Algorithm with Doppler Effect Mechanism for Solving Single Objective Unconstrained Optimization Problems. In Proceedings of the 2019 IEEE 15th International Colloquium on Signal Processing & Its Applications (CSPA), Penang, Malaysia, 8–9 March 2019; pp. 27–30. [Google Scholar] [CrossRef]
- Feliot, P.; Bect, J.; Vazquez, E. A Bayesian approach to constrained single- and multi-objective optimization. J. Glob. Optim. 2017, 67, 97–133. [Google Scholar] [CrossRef]
- Han, H.; Lu, W.; Zhang, L.; Qiao, J. Adaptive gradient multiobjective particle swarm optimization. IEEE Trans. Cybern. 2017, 48, 3067–3079. [Google Scholar] [CrossRef]
- Azwan, A.; Razak, A.; Jusof, M.F.M.; Nasir, A.N.K.; Ahmad, M.A. A multiobjective simulated Kalman filter optimization algorithm. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 23–26. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, H.; Cui, Z.; Chen, J. Hybrid multi-objective cuckoo search with dynamical local search. Memetic Comput. 2018, 10, 199–208. [Google Scholar] [CrossRef]
- Antunes, C.H.; Alves, M.J.; Clímaco, J. Multiobjective Linear and Integer Programming; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-28744-7. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Garcia-Nieto, S.; Sanchis, J.; Blasco, F.X. Controller tuning by means of multi-objective optimization algorithms: A global tuning framework. IEEE Trans. Control Syst. Technol. 2013, 21, 445–458. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 1998; Volume 12, ISBN 978-1-4613-7544-9. [Google Scholar] [CrossRef]
- Ojha, M.; Singh, K.P.; Chakraborty, P.; Verma, S. A review of multi-objective optimisation and decision making using evolutionary algorithms. Int. J. Bio-Inspired Comput. 2019, 14, 69–84. [Google Scholar] [CrossRef]
- Coello, C.C.A.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Genetic and Evolutionary Computation Series; Springer: Boston, MA, USA, 2007; Volume 139, ISBN 978-0-387-33254-3. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Blasco Ferragud, X.; Sanchis Saez, J.; Herrero Durá, J.M. Controller Tuning with Evolutionary Multiobjective Optimization; Intelligent Systems, Control and Automation: Science and Engineering; Springer International Publishing: Cham, Switzerland, 2017; Volume 85, ISBN 978-3-319-41299-3. [Google Scholar] [CrossRef]
- Yano, H. Interactive Multi-Objective Decision Making under Uncertainty; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498763547. [Google Scholar]
- Ljung, L. System Identification: Theory for the User; PTR Prentice-Hall: Hemel Hempstead, UK, 1987; ISBN 0138816409. [Google Scholar]
- Reynoso-Meza, G. Controller Tuning by Means of Evolutionary Multiobjective Optimization: A Holistic Multiobjective Optimization Design Procedure; Universitat Politècnica de València: Valencia, Spain, 2014. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J. Normal-Boundary Intersection: An Alternate Method for Generating Pareto Optimal Points in Multicriteria Optimization. Nasa Contract. Rep. 1996. [Google Scholar] [CrossRef]
- Messac, A.; Mattson, C.A. Generating well-distributed sets of pareto points for engineering design using physical programming. Optim. Eng. 2002, 3, 431–450. [Google Scholar] [CrossRef]
- Messac, A.; Ismail-Yahaya, A.; Mattson, C.A. The normalized normal constraint method for generating the Pareto frontier. Struct. Multidiscip. Optim. 2003, 25, 86–98. [Google Scholar] [CrossRef]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huo, J.; Liu, L. An improved multi-objective artificial bee colony optimization algorithm with regulation operators. Information 2017, 8, 18. [Google Scholar] [CrossRef]
- Yu, X.; Estevez, C. Adaptive multiswarm comprehensive learning particle swarm optimization. Information 2018, 9, 173. [Google Scholar] [CrossRef]
- Thomson, W. Cooperative Models of Bargaining. In Handbook of Game Theory with Economic Applications; Aumann, R.J., Hart, S., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; Volume 2, pp. 1237–1284. [Google Scholar]
- Harward, V.J.; del Alamo, J.A.; Lerman, S.R.; Bailey, P.H.; Carpenter, J.; DeLong, K.; Felknor, C.; Hardison, J.; Harrison, B.; Jabbour, I.; et al. The iLab Shared Architecture: A Web Services Infrastructure to Build Communities of Internet Accessible Laboratories. Proc. IEEE 2008, 96, 931–950. [Google Scholar] [CrossRef]
- Uhlmann, T.S.; Lima, H.D.; Luppi, A.L.; Mendes, L.A. ELSA-SP-Through-The-Cloud Subscribe-Publish Scheme for Interactive Remote Experimentation under iLab Shared Architecture and Its Application to an Educational PID Control Plant. In Proceedings of the 2019 5th Experiment at International Conference, exp.at 2019, Funchal, Portugal, 12–14 June 2019; pp. 58–62. [Google Scholar] [CrossRef]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; Imperial College Press: London, UK, 2009; ISBN 9781848162426. [Google Scholar]
- Esmaeili, M.; Shayeghi, H.; Aryanpour, H.; Nooshyar, M. Design of new controller for load frequency control of isolated microgrid considering system uncertainties. Int. J. Power Energy Convers. 2018, 9, 285. [Google Scholar] [CrossRef]
- Yegireddy, N.K.; Panda, S.; Papinaidu, T.; Yadav, K.P.K. Multi-objective non dominated sorting genetic algorithm-II optimized PID controller for automatic voltage regulator systems. J. Intell. Fuzzy Syst. 2018, 35, 4971–4975. [Google Scholar] [CrossRef]
- Deng, T.; Lin, C.; Luo, J.; Chen, B. NSGA-II multi-objectives optimization algorithm for energy management control of hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1023–1034. [Google Scholar] [CrossRef]







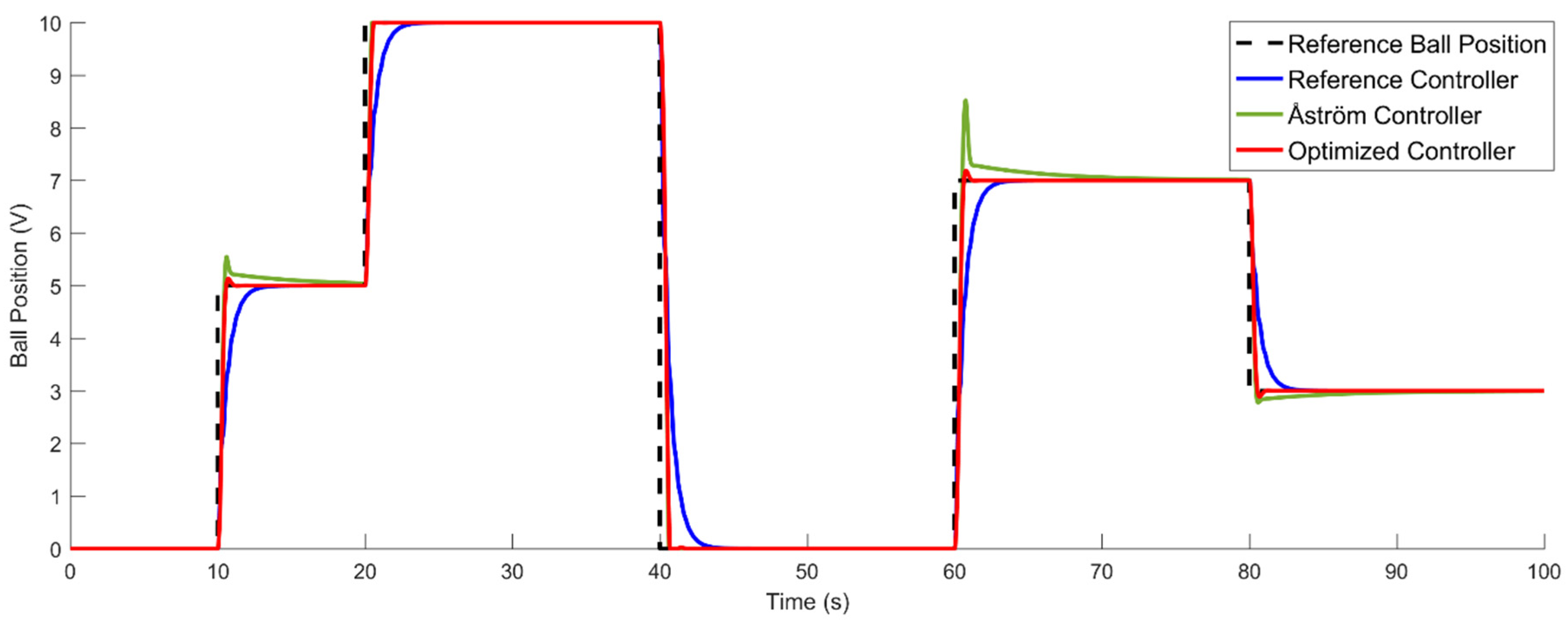
| Model | |||
|---|---|---|---|
| Reference Controller | 0.5 | 0.8 | 8 | 8 | 1931.2 | 240.4 |
| Optimized Controller | 50 | 11.3588 | 40.6189 | 0.1376 | 1064.7 | 191.9 |
| Åström Controller | 21.8814 | 0.1757 | 0.1402 | - | 1952.0 | 233.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kagami, R.M.; da Costa, G.K.; Uhlmann, T.S.; Mendes, L.A.; Freire, R.Z. A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach. Information 2020, 11, 132. https://doi.org/10.3390/info11030132
Kagami RM, da Costa GK, Uhlmann TS, Mendes LA, Freire RZ. A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach. Information. 2020; 11(3):132. https://doi.org/10.3390/info11030132
Chicago/Turabian StyleKagami, Ricardo Massao, Guinther Kovalski da Costa, Thiago Schaedler Uhlmann, Luciano Antônio Mendes, and Roberto Zanetti Freire. 2020. "A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach" Information 11, no. 3: 132. https://doi.org/10.3390/info11030132
APA StyleKagami, R. M., da Costa, G. K., Uhlmann, T. S., Mendes, L. A., & Freire, R. Z. (2020). A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach. Information, 11(3), 132. https://doi.org/10.3390/info11030132





