Similarity Analysis of Learning Interests among Majors Using Complex Networks

Abstract

At present, multi-specialization cross integration is the new trend for high-level personnel training and scientific and technological innovation. A similarity analysis of learning interests among specializations based on book borrowing behavior is proposed in this paper. Students of different majors that borrow the same book can be regarded as a way of measuring similar learning interests among majors. Considering the borrowing data of 75 majors, 14,600 undergraduates, and 280,000 books at the Northwest Normal University (NWNU), as an example, this study classified readers into majors depending on similarity among students. A complex network of similar learning interests among specializations was constructed using group behavior data. The characteristics of learning interests were revealed among majors through a network topology analysis, importance of network nodes, and calculation of the similarity among different majors by the Louvain algorithm. The study concluded that the major co-occurrence network was characterized as scale-free and small-world; most majors had mutual communication and an infiltrating relationship, and the 75 majors of NWNU may form six major interest groups. The conclusions of the study were related to the development of majors of the university, and a match between major learning communities was based on the borrowing interest in a similar network to reflect the relationship between the characteristics and internal operating rules of a major.

1. Introduction

Cross-integration can enhance the fusion of knowledge across disciplines and the interactions between different majors, eventually facilitating the development of majors. Through the study of college students’ interest in learning, we can understand their enthusiasm, direction, and scope of interest in learning. From the perspective of the type of books borrowed, different students may borrow the same book, which can reflect the students’ interest in learning, knowledge structure, and value orientation. Therefore, quantitatively analyzing the relationship among major learning interests is a key issue in the development of cross-integration across majors. Systematically analyzing the complex relationships among majors can uncover the similarities and interaction mechanisms of learning interests among different majors. This has important theoretical and practical significance for the study of inter-major relationships and managing undergraduate major decision-making.

The relationships between academic disciplines were intensively studied using both citations and co-authorship analyses of published academic papers. For each meta-analysis, Cecile, Janssens, and Gwinn extracted co-citations from randomly selected “known” articles from the Web of Science database, counted their frequencies, and screened all articles with a score above a selection threshold [1]. Karunan attempted to investigate the interdisciplinarity at the level of published articles [2]. Their paper investigated the interdisciplinarity of scientific fields based on graphing the collaboration between researchers. A new measure for interdisciplinarity was proposed that took into account graph content and structure [3]. These studies were conducted using citations and co-authors of published academic papers. Few studies addressed students’ interest in learning based on group interest.

Book borrowing data can better reflect an undergraduate’s interest in learning. Extensive accumulation of book borrowing data provides an excellent dataset for related research based on book borrowing behavior. Zhifeng applied an h-index to library borrowing data and analyzed the data [4]. Xingang et al. performed a descriptive statistical analysis of historical data on book borrowing [5]. Fei et al. employed a dataset from Peking University Library to construct a user lending behavior network to analyze user behavior [6]. Tian and Sha analyzed book corner borrowing based on sequential pattern mining [7,8]. Shuqing and Xia used book lending behavior to build a reader-based binary network to research personalized recommendations of books [9]. Husheng and others constructed a network of personalized recommendations based on weighted lending [10]. Ke et al. applied the theory of complex networks to study the library borrowing network of colleges and universities, and they proposed the implementation of personalized recommendation services [11]. Nannan and others constructed a borrowing binary network to study book borrowing data [12]. Xiang et al. analyzed book borrowing based on the complex network theory of books [13]. Xiaowei and others developed a co-occurrence network to explore the relationship among books in different disciplines [14]. Most of these studies analyzed borrowing patterns, user characteristics, and network attributes from the perspective of readers, or they discussed book recommendation algorithms and service issues from the perspective of books. Few scholars directly used book borrowing behavior data to study the relationship among majors.

The American cognitive psychologist Brunner once noted that “the best stimulus for learning is the interest in the materials studied” and emphasized the important role of interest in learning activities. Hidi and Anderson divided interest into personal interest and social interest based on the structural characteristics of interest [15]. Personal interest refers to the positive, biased, and selective attitudes and emotions generated by individuals for specific things, activities, and people. Social interest (group interest) refers to the general interest of members of society in a certain field or the general needs of members of society in a certain field of society. Group interest may develop into relatively long-lasting individual interest in certain conditions [16]. Current research on individual interests is described below.

Yanhui and others started with a library of reader’s borrowing records, generated frequency statistics, and performed cluster analysis of the classification number of the reader’s borrowing records; then, a reading interest ontology model based on the obtained borrowing interest categories was developed [17]. Maojie et al. proposed the IWSR rumor propagation model based on individual interest degree differences and rumor mechanisms. The influences of rumor transmission factors in different network topologies on a Watts and Strogatz (WS) small-world network and Barabási and Albert (BA) scale-free network were obtained [18]. Jianmin and others combined a user’s individual and related interests into the user’s extended interest for Weibo recommendations [19]. Xiufen and others performed an analysis and generated a thermal network model of a special book shelf mode considering the borrower’s shared interest characteristics; they constructed a thermal data library that allowed users to borrow a book based on an analysis of thermal book lending laws, heat storage time, book lending intervals, and other shared interest characteristics [20]. Shuqing and others enhanced the recognition ability of a user’s personalized interest characteristics via user access times [9]. Jian et al. applied an updated algorithm combining a progressive forgetting strategy and a sliding window to establish a lexicon of reader interests, a multi-feature database, and an index library, and they realized a personalized recommendation method for library books based on interest characteristics [21]. Zhoufeng et al. proposed a scoring model to convert the number of book borrowing events and borrowing time into readers’ interest to realize book recommendations based on an implicit semantic model [22]. Yuan analyzed the relationship between library user emotions, user satisfaction, and loyalty from the aspects of user value information needs, psychological characteristics, and borrowing interest [23]. Zhijun introduced a data mining method, collected book borrowing information based on data mining analyses, and evaluated the interest and needs of teachers and students [24]. Research on group interest is detailed below.

Hailing et al. constructed a portrait of a group of user interests based on a concept lattice, which revealed the behavioral needs of different groups of users and explored the potential behavior rules, providing a reference to offer personalized service to different groups of users in college libraries [25]. This research provides some innovative research ideas and methods from data on book borrowing behavior. Few studies addressed students’ interest in learning based on group interest.

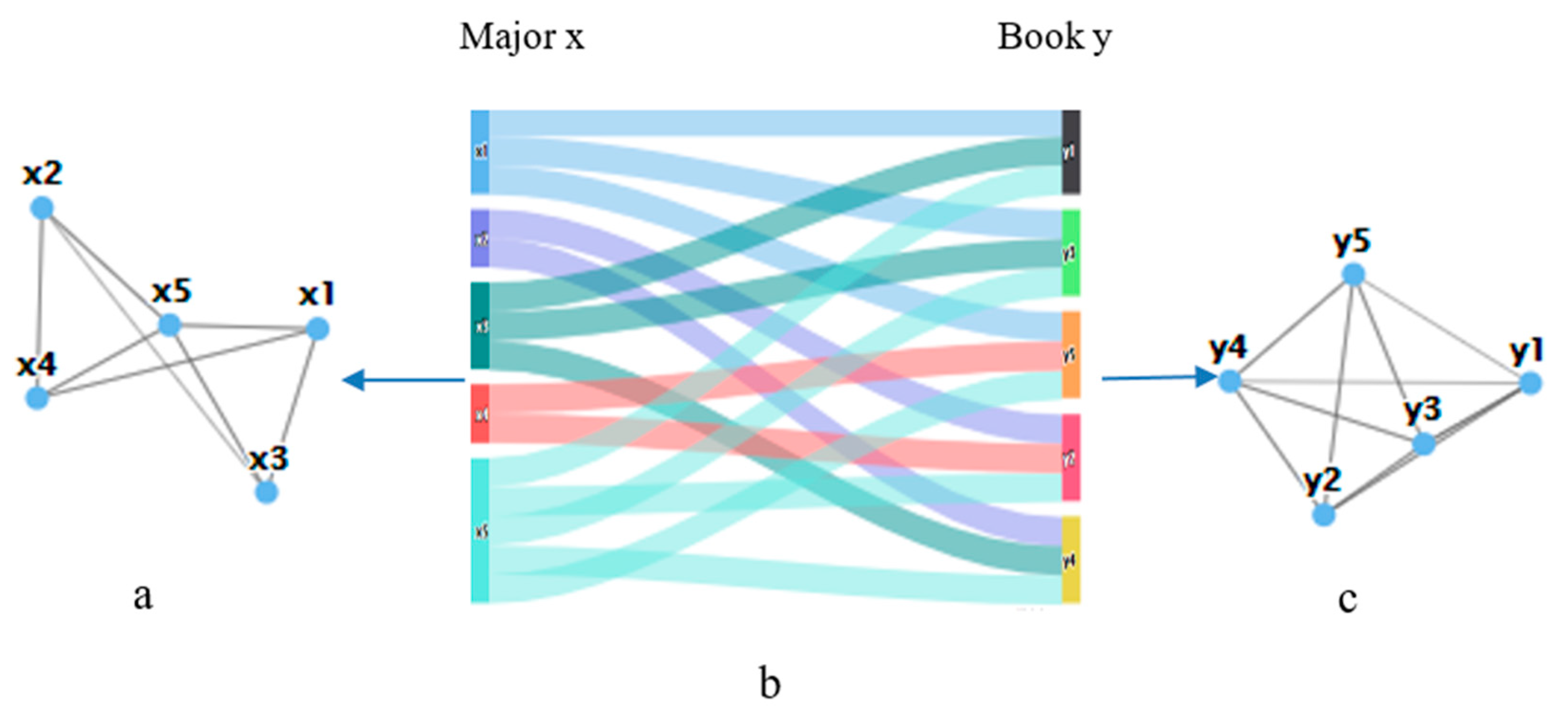
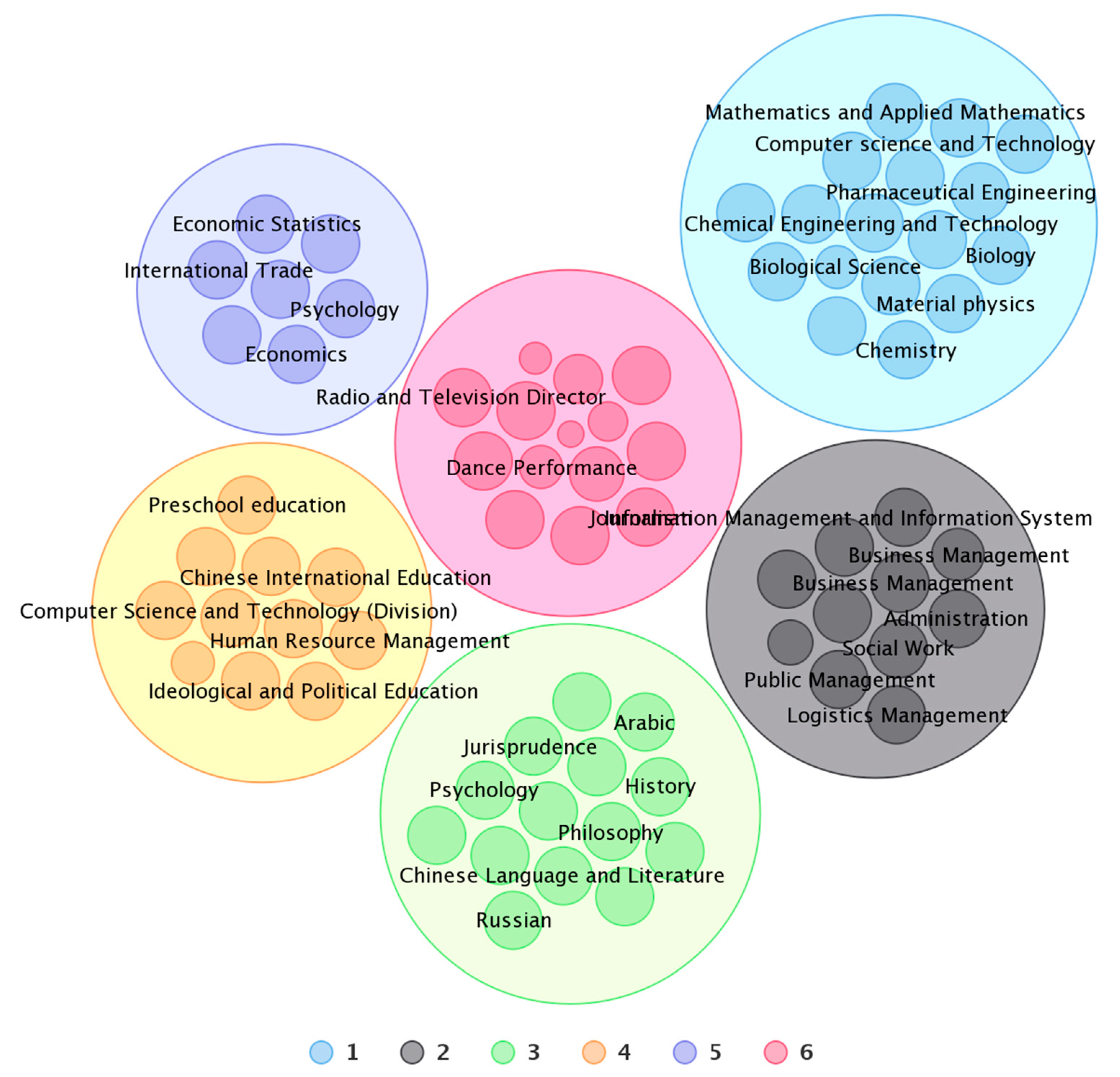
Therefore, this paper follows the research of current scholars, and, based on students borrowing books, more attention is paid to studying the relationship of learning interests among students of different majors. We strived to understand the interaction between majors and the similarity among group learning interests in the development of undergraduate majors. Based on the theory and method of a complex network, students from different majors that borrowed the same book could help us learn the similar relationships of interest among the majors. Considering 75 majors at Northwest Normal University (NWNU; a typical college) and 280,000 books used to generate borrowing data as an example, a network of major interest learning groups was constructed. By analyzing the topological characteristics of the complex network, the interaction rules and operational mechanisms of the professions for the group borrowing behavior were explored. Python was used to calculate the various eigenvalues, and charts were drawn with the help of Excel. This analysis provides a new idea for the study of interest relationship similarities among majors. Relevant research conclusions can serve as the basis for making decisions in the development planning of majors, such as training in top majors and new major applications.

2. Data and Major Learning Interest Similarity Network Construction

2.1. Data Sources

To study the relationship of group learning interest among various professions based on book borrowing behavior, data from a total of 287,674 books were collected from NWNU library from August 2015 to 2018 via data cleaning. Fiction books were the most borrowed type of book; to remove this influence, data from 282,727 valid borrowing records for 14,600 students were employed in this study after eliminating missing data, invalid data, and borrowing novels (our inclusion of books was based on the classification of Chinese Library Book Classification; novels refer to book classification I). Through a major statistical analysis of 14,600 students, a total of 75 majors, which encompasses all majors offered by NWNU, were evaluated. Using data collection and collation, student information, major information, and book borrowing information required for this study were obtained. Student information included student number, name, gender, college, major, and class, as shown in

Table 1. Student information form. ID—identifier.

Student ID	Name	Gender	College	Major	Class
22030311	Xiao Z.	Male	Business College	Accounting	2015
31010203	Dong W.	Female	Academy of Marxism	Ideological and Political Education	2016
33010249	Ming L.	Female	Law College	Law	2017

This table has a total of 14,600 articles.

(partial sample data). Major information included major number, major name, college name, and other information, as shown in

Table 2. Major information form.

Major ID	Major Name	College Name
01	Accounting	Business College
02	Ideological and political education	Academy of Marxism
75	Law	Law College

This table has a total of 75 articles.

(partial sample data). Book borrowing information included student number, name, borrow time, return time, name of the book, and book classification number for borrowing books, as shown in

Table 3. Book lending information table.

Student ID	Borrow Time	Return Time	Borrow Book Name	Classification Number 1
22030311	20160428 19:45:31	20160507 18:26:05	Accounting Computerization	F232/T862
31010203	20170626 17:39:17	20170823 16:56:13	Legal Methodology	D90-03/Y860
33010249	20150917 10:41:32	20151014 12:12:30	Criminal Procedure Law	D925.2/C580
22020142	20171101 19:50:14	20180108 16:48:34	Wuthering Heights. English-Chinese Bilingual Version	H319.4:I/B936-3=1
55010409	20180316 12:58:12	20180429 15:05:56	Design Sketch. 2 Version	J214/Z089:2

¹ Classification number used the Chinese Library Book Classification. This table has a total of 282,727 articles.

(partial sample data).

2.2. Major Learning Interest Similarity Network Construction

In university book lending, students borrow a large number of books, each student belongs to a certain major, and the behavior of borrowing the same book by different major students is regarded as a similar relationship among majors. According to this relationship, students can be assigned to individual majors, and a binary network composed of professions and books can be obtained, which can be represented by a bipartite graph. The bipartite graph contains two types of nodes. The first node, which is referred to as a major node, is the major of the student who borrows a book. The second node is the book that belongs to the collection, which is referred to as a book node. If a borrowing relationship between the major node and the book node exists, the two nodes are connected by a line to form an edge. In the picture set, G = (V,E), the vertex set V represents two non-intersecting, non-empty subsets X and Y, where X represents the reader major set and Y represents the book collection. The two endpoints i and j of each edge $e=(i,j)$ in the edge set E belong to X and Y, respectively, where E means that the reader from major $i$ borrowed book $j$. The graph G is referred to as a bipartite graph, and Figure 1a is projected from Figure 1b. As shown in the figure, major x1 and major x3 simultaneously borrowed book y1. Thus, a common learning interest exists between x1 and x3, i.e., a connection exists between the two majors. Figure 1c is obtained from the projection of Figure 1b. As shown in the figure, both book y1 and book y2 were borrowed by major x1; thus, a connection exists between y1 and y2. Generally, a binary structure is often projected onto set X or set Y to form two different unit graphs to study a binary network. The figure is configured to provide an example of X; for $G=(X,E,Y)$, X is set if two vertices are connected to a vertex of set Y. In the corresponding unit diagram, the two vertices have a relationship, and the edges are connected. The projection process is shown in Figure 1.

This paper assumed that a larger number of people who share the same book and a larger number of persons who belong to the profession denote more similar interests between two majors. A similar common borrowing interest often reflects potential knowledge that can be characterized, such as the degree of relevance for each major or the knowledge structure of readers from different majors. Therefore, to study the relationship interests among different professions, a book lending network was projected by major collections with major nodes. Figure 1b shows the relationship of different majors x borrowing books y. This paper projects Figure 1b into Figure 1a, i.e., different majors x borrowed the same books y, as if a link existed between two different majors, primarily based on the model in Figure 1a, to build a similar network of group learning interests among majors.

Table 4. Major and corresponding major data sheet.

ID	Major 1	Major 2	Common Borrowing Times
1	Information and Computing Science	Mathematics and Applied Mathematics	6050
2	Translation	English	5171
3	Mathematics and Applied Mathematics	Physics	4810
4	History	Chinese Language and Literature	3483
5	History	English	2910
6	Ideological and Political Education	History	2719
7	Computer Science and Technology	Software Engineering	2456
8	Mathematics and Applied Mathematics	English	2368

This table has a total of 2558 articles.

displays the original data table that corresponds to major and profession, which indicated the number of books borrowed between major 1 and major 2.

According to the data in Table 4, this paper used a chord diagram to draw a network of major interest learning groups.

In Figure 2, the inter-major group learning interest similarity network, the node represents the major; a greater proportion of nodes denotes a larger number of books that the library borrows, as well as a greater similarity of the books with other majors’ interests. The color of the nodes was used to distinguish different majors. The connected edges between nodes represent the relationship similarity between different majors. The width and color of the edges indicate the degree of similarity between the majors. Wider and darker edges signify a more similar interest between the majors, i.e., the two majors simultaneously borrowed books.

Based on the network similarity of group learning interest, a network attribute analysis, including node degree, node strength, shortest path length, and aggregation coefficient, was firstly used to analyze the interest relationship among the majors. Secondly, using the PageRank [26] algorithm and Pearson correlation coefficient method, important nodes were found by searching for important nodes in the network. Lastly, the Louvain [27] algorithm was used to classify the community, and the major learning interest group in the network was determined.

3. Characteristics of Network Similarity Learning among Majors

In recent years, many concepts and methods were proposed to characterize the statistical characteristics of complex network structures. Topological characteristics of complex networks are used to statistically measure the complexity of networks to reveal their performance [28]. Commonly employed statistics include network attributes, such as degree and degree distribution, node strength, shortest path length, aggregation coefficient, and community partitioning, to characterize the topological characteristics of a network. This enables us to explore the relationship among different professions and the internal relationships among different professions, and it provides a theoretical basis for the rational planning of book resources and decision-making in major development.

3.1. Node Degree and Degree Analysis

Degree is one of the most important and fundamental concepts for describing the nature of independent nodes in complex networks. In the inter-major group learning interest similarity network, the degree indicates the number of majors that are similar to a major learning interest, which is referred to as the degree of the major node.

Table 5. Values of major node degrees.

Major Name	Degree	Major Name	Degree
Choreography	2	-	-
Calligraphy	25	Preschool Education	73
Sports Training	47	English	74
Biological Sciences	54	History	74
Pedagogy	56	Mathematics and Applied Mathematics	74
Public Management	58	Physics	74
Material Physics	59	Labor and Social Security	74
Hotel Management	59	Chinese International Education	74
Business Administration	63	Chinese Language and Literature	74

lists the values of the degree of each major node.

In the case of group borrowing, regardless of the difference in the number of people in each major, from the analysis of the degree of major nodes, most of the major nodes had higher degrees, including Chinese language and literature, Chinese international education, physics, mathematics, and applied mathematics. The degree of professionalism in English and history was 74. This is because students of these majors have a wide range of learning interests, and reading involves multiple majors, while individual majors such as dance and calligraphy were relatively low, with degrees of two and 25, respectively. This finding shows that most majors were closely related and the major similarity was high. Only some majors were at the edge.

From the global distribution analysis of the major node degree, the degree of the major node can be defined. For a simple graph without a self-loop and a heavy edge, the degree of the node is the number of other nodes that are directly connected to the node. The average of the degrees of all professions in the major group interest learning network is referred to as the average degree of the group learning interest network in the majors, which is recorded as $<k>$. The specific calculation for the average majors’ learning interest similarity is shown in Equation (1).

$$<k>=\frac{1}{N}{\displaystyle \sum _{i,j=1}^N{k}_i}.$$

(1)

Figure 3 shows the distribution degree of different major nodes, which obeys the logarithmic distribution of $y=11.829\ln (x)+27.462$. The distribution concluded that the degree of difference of different major nodes was relatively small, i.e., a common learning interest existed between most majors and other majors. The results showed that the average degree $<k>$ of group learning interest in similar networks among majors was 67.316; 60 majors had a major node degree greater than $<k>$, and only 15 majors had a major node degree less than $<k>$. The number of majors with a larger specialty degree was greater than that with a smaller specialty degree in the network, and the connection condition (degree number) between two major nodes had a serious uneven distribution. Therefore, the similarity network of group learning interest among majors could be characterized as a preference attachment model [29]. In the future, we should strengthen major construction and constantly promote cross-integration of all disciplines.

3.2. Node Strength Analysis

The most prominent feature of weighted networks is the heterogeneity of the strength values of connected edges. This heterogeneity characterizes the difference in the interaction among components in the system, which comprises the important statistical characteristics of a complex system and explains the nonlinear behavior of self-organization [30]. In weighted networks, the degree $k_i$ of nodes can be naturally extended to the strength $s_i$ of nodes, and it is defined as follows:

$$si={\displaystyle {\sum }_{j\in N_i}{\omega }_{ij}}.$$

(2)

In this formula, $s_i$ is the node strength of node $i$, node $j$ is the adjacent node of node $i$, $N_i$ is the set of adjacent nodes of node $i$, and ${\omega }_{ij}$ is the edge weight of node $i$ and node $j$.

In the network of group learning interest similarity among majors, the node strength indicates the degree of learning interest similarity between a major and other majors, i.e., the number of the same books borrowed by the two majors. A greater strength denotes a higher degree of learning interest similarity between the major and other majors, and establishing a strong connection becomes easier. Figure 4 shows a statistical diagram of the strength of each major node, which indicates that there was a large number of nodes with low strength and a small number of nodes with high strength in the network. Thus, the strengths of major nodes had distinct, non-uniform characteristics. Chinese language and literature, history, English, mathematics, and applied mathematics had a higher node intensity, which indicated a greater similarity of learning interest between these majors and other majors. On the other hand, dance, calligraphy, sports training, and other majors had a lower node intensity, indicating that the connection between these majors and other majors was relatively sparse, i.e., the similarity of learning interest was relatively low.

Figure 5 displays a cumulative probability distribution diagram of the intensity of learning interest similarity network nodes in a semilogarithmic coordinate system. In this paper, the nonlinear least-squares method was used to fit the major data. The intensity of each major node followed a lognormal distribution; the expression of the cumulative probability distribution of intensity was $P(s)=-0.015\ln (s)+0.0646$, and the goodness of fit was 0.9751. The goodness of fit refers to how well the regression line fits the observations. The statistic that measures the goodness of fit is the determination coefficient, also known as R². The maximum value of R² is 1. The closer the value R² is to 1, the better the fit of the regression line is to the observed value.

The lognormal distribution [14] means that the logarithm of a random variable obeys a normal distribution, i.e., the random variable obeys a lognormal distribution, which is a distribution form between the power law and normal distributions. Two selection mechanisms—preferential and random—exist in the evolution of inter-group learning interest similarity networks. The evolution of a major interest group similarity network may be affected by many factors. For example, book borrowing by different major readers is a random and disorderly behavior. Most borrowers tended to borrow basic books from their majors. In the major network of interest learning groups, the major node strength was subject to a lognormal distribution. Single logarithmic coordinates were used. In further research, double logarithmic coordinates may be considered.

The relationship between the node degree and intensity of the similarity of network learning interest groups (refer to Figure 6) is depicted to explore the relationship between the edge weight and the topological structure. When these two aspects are irrelevant, the average intensity $s(k)$ of a node with degree $k$ linearly increases with $k$. As shown in Figure 6, the degree of a node is related to the intensity of major interest learning groups in the network. The relationship between the two aspects can be characterized by the exponential function $s(k)=1.116e^{0.1218k}$, which indicates that the side with a larger weight tends to be connected with the major with a larger node degree, i.e., the relationship among the professions that have established extensive contact with other professions is also strong.

3.3. Aggregation Analysis

In the inter-disciplinary group learning interest similarity network, the clustering coefficient c_i indicates the possibility that a major neighbor remains a neighbor to other neighbors, i.e., the similarity of learning interest among major A, major B, and major C is higher. Thus, the similarity of learning interest between major B and major C is also higher. In the unprivileged network, Watts and Strogatz proposed that the local clustering coefficient of the node reflects the group nature between the node and its immediate neighbor. In general, a higher similarity among neighbors signifies a closer relationship and a higher clustering coefficient [31]. This definition does not take into account that neighbor nodes in a weighted network are more important than other nodes. To solve this problem, Barrat et al. [32] defined the weighted clustering coefficient of node $i$ as

$$C_{\omega }(i)=\frac{1}{s_i(k_i-1)}{\displaystyle \sum _{i,j,k}\frac{{\omega }_{ij}+{\omega }_{jk}}{2}{\alpha }_{ij}{\alpha }_{jk}{\alpha }_{ki}},$$

(3)

where $C_{\omega }(i)$ is the weighted clustering coefficient of the major interest group similarity network, $s_i$ is the strength of node $i$, $k_i$ is the degree of node $i$, ${\omega }_{ij}$ and ${\omega }_{jk}$ and are the K-edge weights of nodes $i$ and $j$ and nodes $j$ and $k$, respectively, and ${\alpha }_{ij}$, ${\alpha }_{jk}$ and ${\alpha }_{ki}$ are the relationships among nodes $i$, $j$, and $k$. When all nodes are 1, all three nodes have connected edges, which can form a triangle. The average weighted clustering coefficient $<C_{\omega }>$, which takes into account the network topology and weight distribution information, can be used to reflect the clustering degree of weighted networks.

The cluster coefficients $C(i)\in [0.4574,1]$ and $<C>=0.4748$ and the weighted cluster coefficients $C_{\omega }(i)\in [0.9148,1]$ and $<C_{\omega }>=0.9583$ from similar networks of group learning interests among majors were calculated. $<C>$ and $<C_{\omega }>$ can be obtained from the results, which showed that the topology aggregation of the network was primarily formed by edges with high weights. Figure 7 shows the changes in the node degrees and clustering coefficients in unweighted networks and weighted networks. The degree of node was negatively correlated with the clustering coefficient, which indicates that the community learning interests in different groups formed a hierarchical network. This negative correlation indicates that a smaller number of clusters that are combined results in larger and sparser clusters. This feature is shared by many complex networks. However, in weighted networks, this feature is not distinct, as, even when the degree of node is large, the corresponding clustering coefficient remains large.

As revealed by the average weighted clustering coefficient, the degree of aggregation of major interest group similarity networks was extremely high, which indicated a great probability of a relationship between other professions that have a relationship with a certain profession. For example, mathematics and applied mathematics and physics majors had similar learning interests, and physics and chemistry majors had similar interests. Thus, mathematics and applied mathematics and chemistry majors had similar interests. The majors can be divided into different clusters according to the degree of similarity of learning interests. The majors in the same cluster often complemented each other and developed together, and the similarity of different professions among different clusters was lower. In general, a close connection existed between majors in the network of interests in the community, which indicated that the degree of association among the majors was high, the major construction was reasonable, and the readers had rich knowledge structures. Since the average shortest path length of the network was 1 and had a large aggregation coefficient, the network had small-world network characteristics.

4. Analysis of the Interest Range of Majors Based on the Importance of Nodes

Social networks gradually form due to the migration of people’s lives to networks. These networks carry a vast amount of complex information and are gradually attracting the attention of scholars in related fields. In the network, as the location of the node is different from that of other nodes, the role and influence of each node in the network also differ. An important node in the social network, i.e., the hub of the social network, can substantially affect the network functions and structure. Evaluating and quantifying the importance of nodes in the network of interest learning among majors and discovering the range of interests of various majors in the network are fundamental issues in the field of network research. This research has significance in the development of disciplines, book recommendations, and rational planning and decision-making in major development.

Many methods for evaluating the importance of network nodes exist. This paper used the PageRank [26] ranking algorithm and major node strength, weighted intermediate center degree, weighted proximity center degree, and ranking index of each major to conduct a Pearson correlation analysis.

The core idea of PageRank is described as follows: if a web page is linked by many other web pages, this webpage is more important, i.e., the PageRank value is higher. In the major group community learning interest similarity network, if a major is linked to many other major institutes that are connected to the description, then this major has a wide range of learning interests, is involved in many fields, and exhibits a greater similarity of interest in learning with other majors.

Table 6. Ranking results of indicators (top 10).

Rank	Major	Weight	Major	WIC 1	Major	WAC 2	Major	Harmonic	Major	Page Rank
1	History	42517	Chinese International Education	42.04	History	0.98	History	0.993	Chinese International Education	0.015
2	English	42013	Geographic information science	40.35	English	0.98	English	0.993	History	0.0146
3	Mathematics and Applied Mathematics	41617	labor and Social Security	8.924	Mathematics and Applied Mathematics	0.98	Mathematics and Applied Mathematics	0.993	English	0.0143
4	Physics	29949	History	8.92	Physics	0.98	Physics	0.993	Mathematics and Applied Mathematics	0.0143
5	Chemistry	25359	Mathematics and Applied Mathematics	8.92	Chinese International Education	0.98	Chinese International Education	0.993	Physics	0.0143
6	Chinese language and literature	24381	Physics	8.92	Ideological and political education	0.98	Ideological and Political Education	0.987	Chinese Language and Literature	0.0143
7	Accounting	22334	English	8.92	Chinese language and literature	0.97	Chinese language and literature	0.987	Ideological and political education	0.0143
8	Ideological and political education	20403	Business management	6.76	Preschool education	0.97	Preschool education	0.987	Preschool education	0.0141
9	Computer Science and Technology	19172	Translation	6.76	Business management	0.97	Business management	0.987	Business management	0.0141
10	Finance	17651	Computer Science and Technology	6.76	Computer Science and Technology	0.97	Computer Science and Technology	0.987	Computer Science and Technology	0.0141

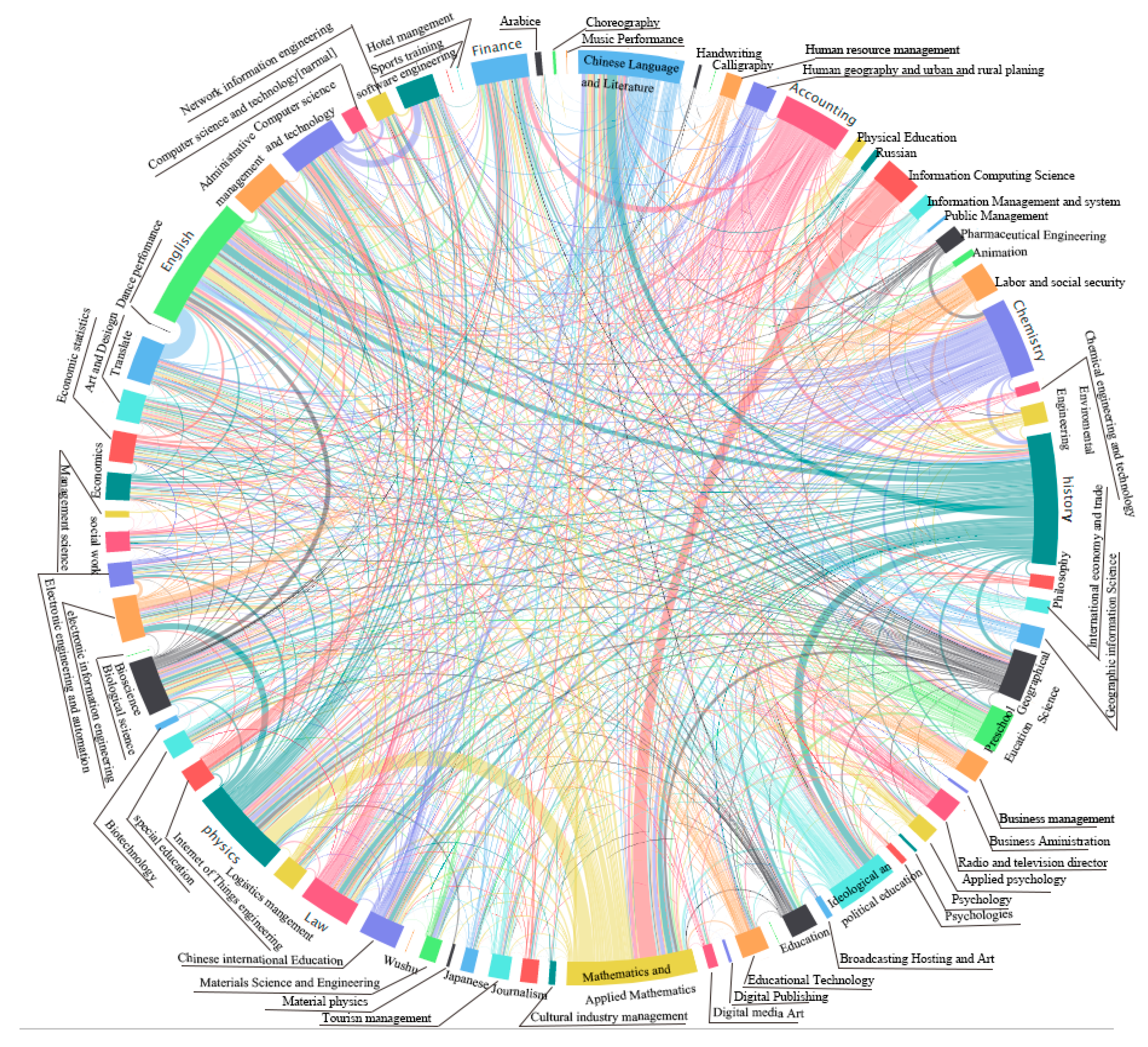
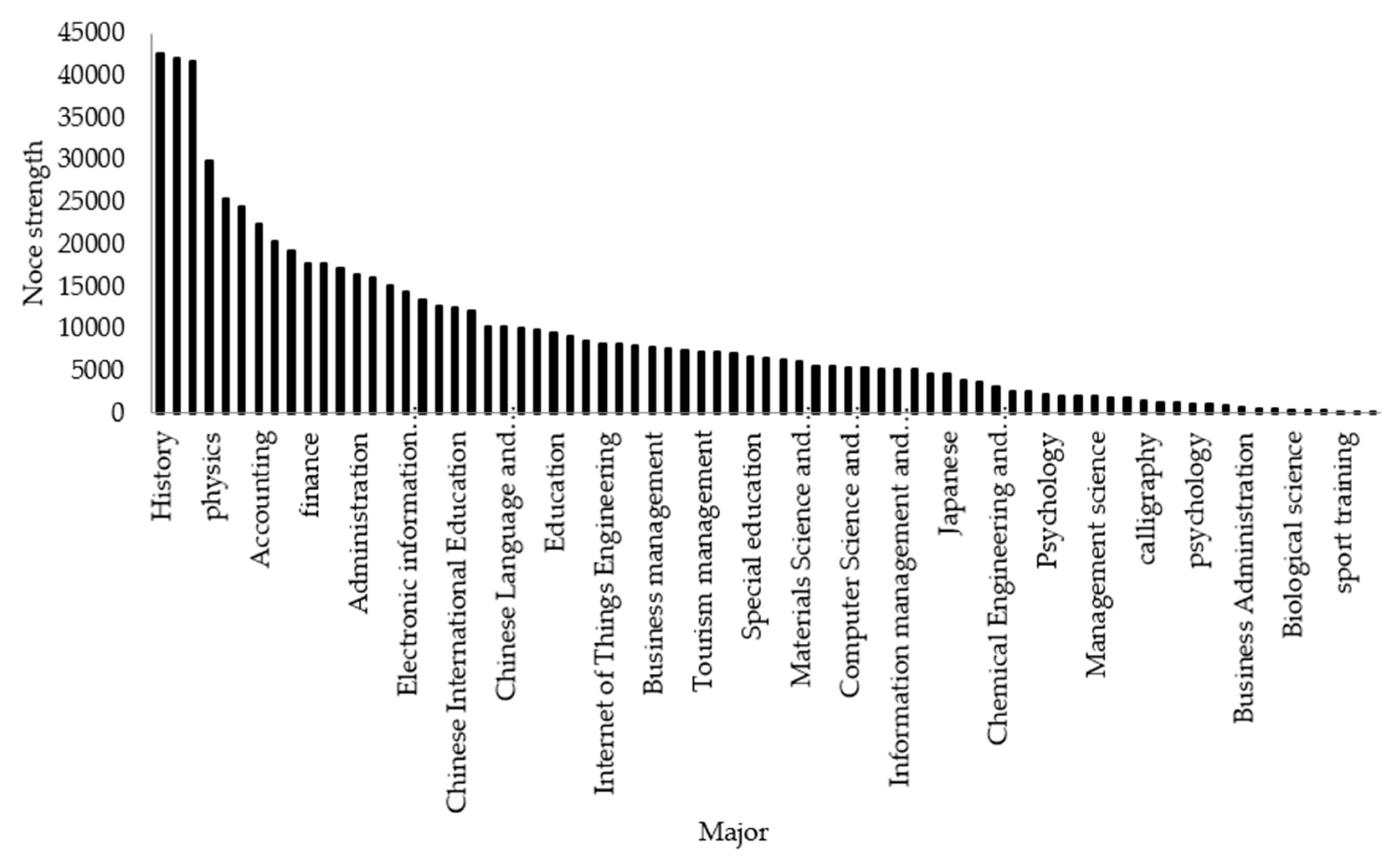
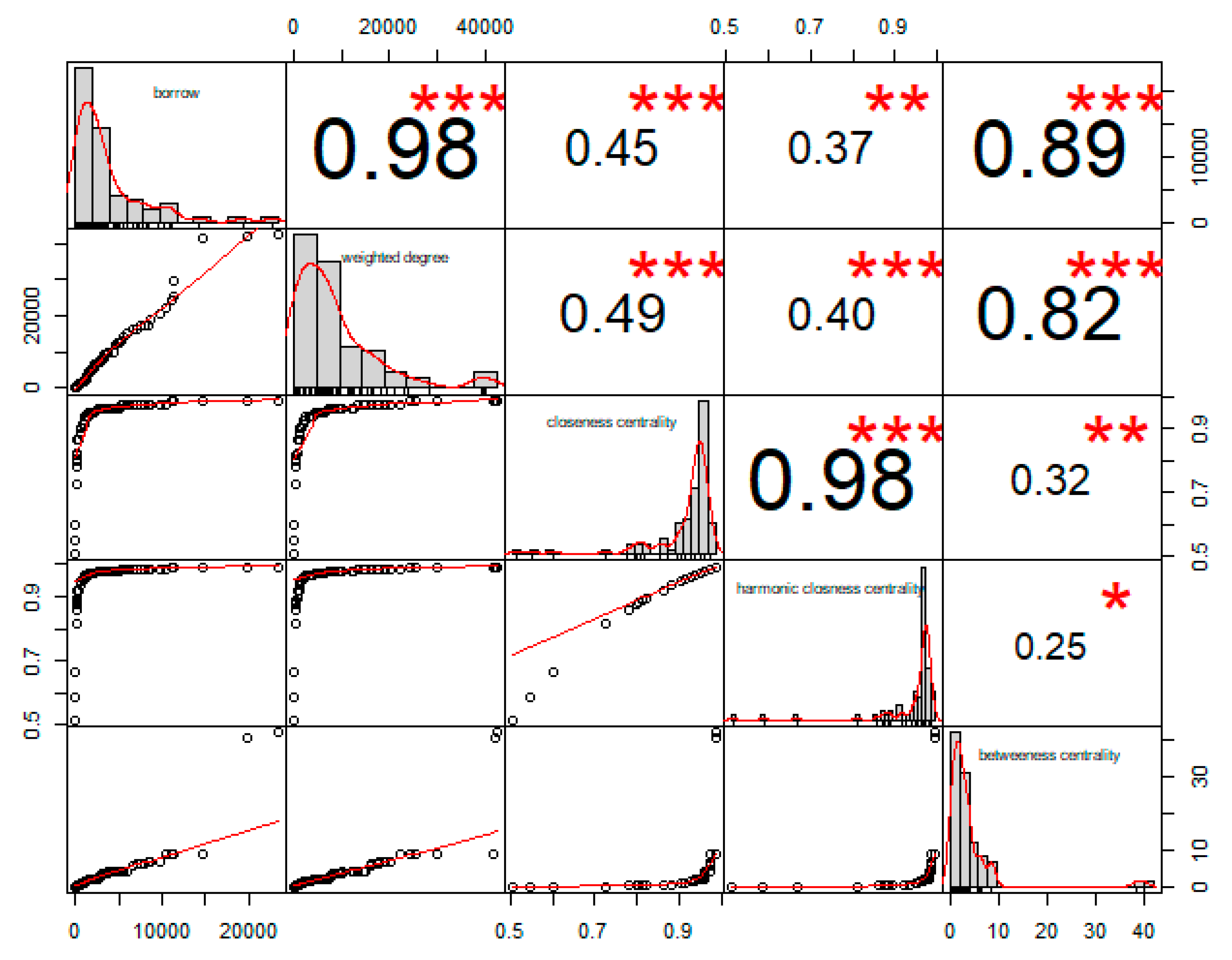
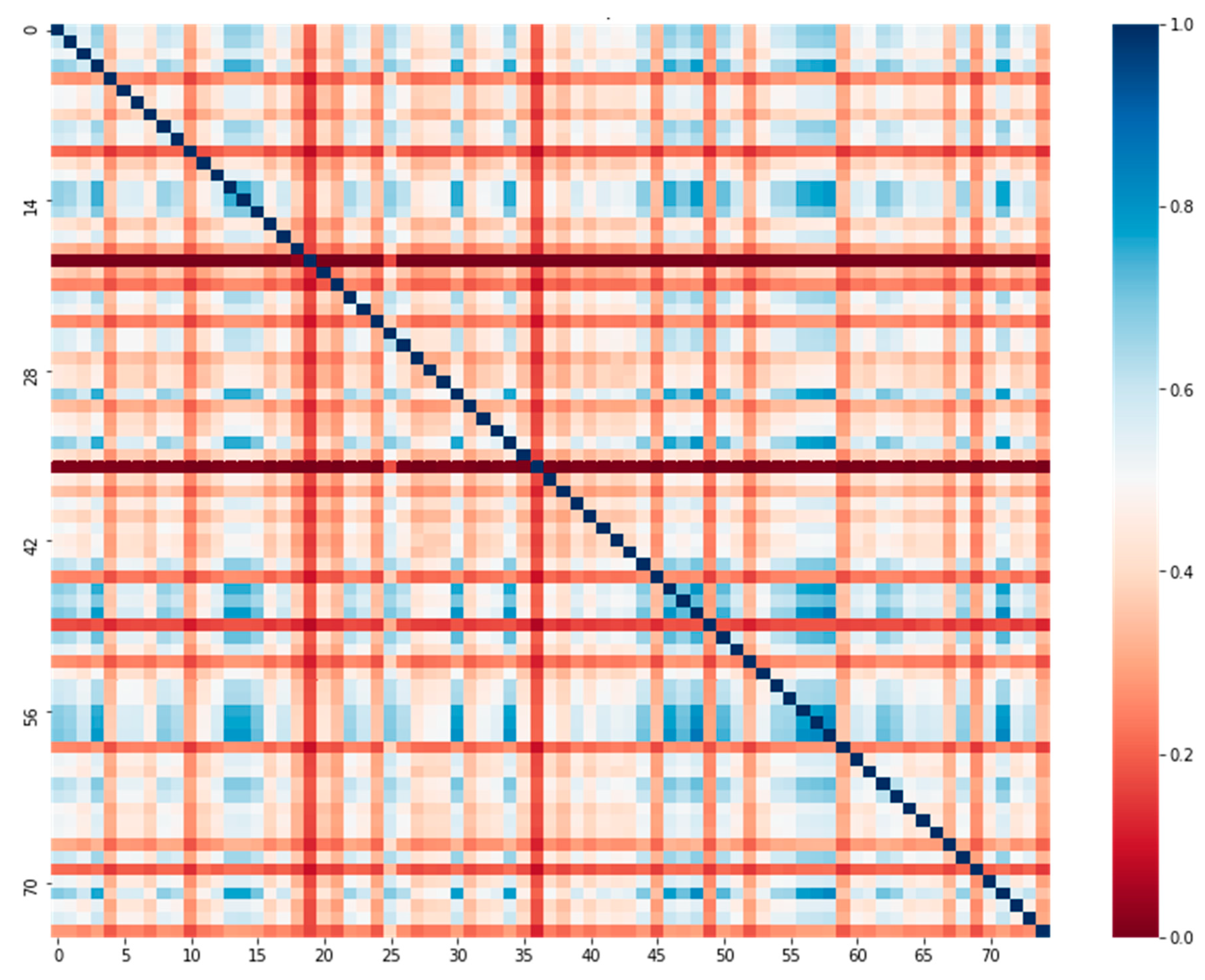
¹ WIC: weighted intermediate centrality; ² WAC: weighted approach centrality.

lists the top 10 majors in each indicator. The results of PageRank indicated that the PageRank values of Chinese international education, history, mathematics and applied mathematics, English, physics, and other majors were higher, which indicated that these majors had a wide range of interest in the entire network. Pearson correlation analyses of each major node strength, weighted intermediate center degree, harmonic centrality, weighted close centrality, and ranking of borrowing were performed for each major, and the correlation coefficient matrix was obtained, as shown in Figure 8. History, English, mathematics and applied mathematics, Chinese international education, Chinese language and literature, and other majors had the widest range of interest in this network, which was equivalent to that of PageRank. All p-values were substantially smaller than 0.05, which indicated that the evaluation results of the five indicators were highly significant. A higher occurrence major borrowed books better enabled establishing contact with other majors, i.e., the group’s interest in learning was higher. As the “power” in the major interest learning group network becomes more extensive and greater, the ability to control the knowledge flow becomes stronger, and it becomes easier to promote knowledge exchange between other majors.

Therefore, in the major group interest learning network, most majors had a wide range of interest in learning. Removing any node would have a greater impact on the transmission of the network. Dance, calligraphy, and sports training were marginal majors in the network. At the edge of the study, the range of interest in learning was small, which may be affected by many factors. In the future major development process, NWNU can develop these important majors as first-class majors for the school and simultaneously pay attention to the construction of marginal majors (i.e., dance, calligraphy, and sports training).

5. Interest Community Formation

5.1. Similarity of Interest in Group Learning among Majors

Interest-based similarity calculations can fully exploit user interests and hobbies, which is consistent with the original intention of people who tend to find like-minded friends [33]. A similar interest in group learning was observed among different professions, i.e., an “adjacent” relationship existed among groups. In some traditional methods of calculating interest similarity, such as cosine similarity and modified cosine similarity, learning occurs for students of various majors. The interest vector was fully calculated.

In this study, the cosine similarity method [34] was used to measure the similarity degree of group learning interest among different majors, as shown in Equation (4).

$$sim(x,y)=\cos (\overrightarrow{x},\overrightarrow{y})=\frac{\overrightarrow{x}\times \overrightarrow{y}}{\left|\overrightarrow{x}\right|\times \left|\overrightarrow{y}\right|}.$$

(4)

In this paper, students’ knowledge interests and preferences (all books were learning interest vectors) were represented by an n-dimensional vector, and the assignment of each component in the vector was used to express the learning interests of students of different majors. If students preferred certain knowledge, the corresponding component was assigned to 1. If users did not prefer certain knowledge, the corresponding component was assigned to 0. The cosine angle between vectors was used to measure the similarity degree of students’ learning interest of different majors. The similarity degree of learning interest of different majors was calculated by the cosine similarity degree. A thermodynamic diagram of learning interest similarity of different majors is drawn in Figure 9.

In Figure 9, the cosine value was normalized, and a heat map was used to indicate the degree of similarity in learning interests between different majors. The horizontal and vertical coordinates represent different majors, and majors are indicated by serial numbers.

Table 7. Table of serial numbers of each discipline in the thermodynamic diagram.

ID	Major	ID	Major	ID	Major	ID	Major	ID	Major
1	Arabic	16	Management Science	31	Education	46	Biology	61	Internet of Things Engineering
2	Broadcasting Hosting and Art	17	Radio and Television Director	32	Finance	47	Biological Science	62	Logistics Management
3	Materials Science and Engineering	18	International Trade	33	Economic Statistics	48	Calligraphy	63	Psychology
4	Material Physics	19	Chinese International Education	34	Economics	49	Calligraphy Art	64	Psychology Class
5	Geographic Science	20	Chinese Literature	35	Hotel Management	50	Mathematics and Applied Mathematics	65	Journalism
6	Geographic Information Science	21	Administration	36	Labor and Social Security	51	Digital publishing	66	Information Management and Information System
7	Electrical Engineering and Automation	22	Chemistry	37	History	52	Digital Media Art	67	Information and Computing Science
8	Electronic Information Engineering	23	Chemical Engineering and Technology	38	Tourism Management	53	Ideological and Political Education	68	Preschool Education
9	Animation	24	Environmental Engineering	39	Art and Design	54	Special Education	69	Music Performance
10	Russian	25	Accounting	40	Human Resource Management	55	Physical Education	70	English
11	Law	26	Computer Science and Technology Teacher	41	Human Geography and Urban and Rural Planning	56	Cultural Industry Management	71	Applied Psychology
12	Translation	27	Network and Information Security	42	Japanese	57	Martial Arts and National Traditional Sports	72	Sport Training
13	Business Management	28	Computer Science and Technology	43	Software Engineering	58	Dance Performance	73	Philosophy
14	Business Administration	29	Educational Technology	44	Social Work	59	Dance	74	Pharmaceutical Engineering
15	Public Management	30	Education	45	Biotechnology	60	Physics	75	Chinese Language and Literature

presents specific serial numbers corresponding to majors.

5.2. Major Group Learning Interest Similarity Community

Numerous studies explored the community structure in a social network, and the process of mining the community structure according to the network characteristics involved community discovery [35]. The definition of community in different research fields is extensive and diverse. Generally, the nodes in the same community are closely related, and the similarity of learning interest is high; however, when the similarity of learning interest between two different communities is low, the connection is loose. An investigation of the modules and functions in the similarity network of interests in group learning among majors is important to understand the topological structure of a network and the group learning relationship among majors.

Many kinds of community discovery algorithms exist. Based on the similarity of learning interest among different specialties, this paper used the Louvain algorithm [27] to analyze the similarity network of learning interest among specialties. This algorithm is based on a multilevel optimization of modularity. The advantages of the algorithm are that it is fast and accurate, and it is considered to be one of the community discovery algorithms with the best performance. The Louvain algorithm divided the network into six communities; the results are shown in Figure 10.

As shown in Figure 10, the majors were divided into six major communities. The first type of community mainly consisted of a group of science and engineering majors in chemistry, physics, mathematics and applied mathematics, and computer science and technology. The second type of community was a group of students who were primarily engaged in management-related departments, such as information management and information systems, business administration, tourism management, and management science. The third type of community was a group of students who mainly focused on liberal arts, such as Chinese language and literature, English, philosophy, and geography. The fourth type of community was a group of students primarily related to education, such as preschool education, education, psychology, and applied psychology. The fifth type was a group of students who were mainly engaged in economics, statistics, international trade, and other related majors. The sixth category was a group of students mainly in journalism, animation, dance performances, and art and design studies. This is consistent with the principle behind the creation of journal-based disciplines [36], i.e., the majors are grouped according to similarity of interest, the interest similarity within the group is high, and the interest similarity between groups is low. These divisions indicated that the students in the major groups had a high degree of similar interest in learning, the major groups in the same community showed a high degree of interest in learning, and the major groups were in the same theme. The similarity of learning interests was high, and the links were more closely related. Knowledge learning in majors was highly correlated, and the subject characteristics of different major student communities were more distinct.

6. Conclusions and Prospects

This study considered library students’ borrowing data from a typical college as the research object and used a complex network analysis method to learn the topical characteristics, node importance, and community division of a similarity network from an interdisciplinary group. The relationship between majors and interest similarities in the “affinity network” was investigated as follows:

(1)

From the perspective of network topology characteristics, the degree of connection among major nodes of major group interest learning networks had a substantially uneven distribution and was characterized as a scale-free network. The major node strength obeyed a lognormal distribution and core major and marginal expertise. The network had a small average shortest path length and a large clustering coefficient. With the characteristics of a small-world network, the information exchange between most majors was relatively smooth and did not need to pass the intermediary of “professionals can get information, and major groups have strong cohesiveness”. This statement fully reflects the similarity of group learning interests among majors and the interdisciplinary integration of majors. However, a few majors also needed to be integrated at the marginal position. Among the large groups, majors formed a synergistic development effect.

(2)

From the point of view of node importance, most majors were more active, and their control ability was relatively large, which was at the core of a network. Majors were more dependent on other majors when transmitting information.

(3)

A user’s borrowing behavior was analyzed from a microscopic point of view. The research objects comprised different majors in the major interest group similarity network, which helped to explain the internal relationship between majors and the extensive range of majors.

(4)

This paper was based on the relevant indicators and methods of complex theory to explore the network of interest learning among majors. The investigated networks consisted of a weighted network and an unprivileged network. After comparing the two networks, the weighted network was compared with the powerless. The network was more convincing and accurate, which provided empirical materials for the empirical evaluation of weighted networks and the study of group learning interests.

Based on this research, future work will focus on the following:

We acknowledge that spectral characteristics are also important and informative, but they are beyond the scope of this study. They may be explored in future studies.

Book borrowing data from colleges of different backgrounds can be compared to reveal the common characteristics of major relationships in different institutions.

In future research, we will improve the community discovery algorithm and further divide the community.