Abstract
Current research on computer-aided diagnosis (CAD) of liver cancer is based on traditional feature engineering methods, which have several drawbacks including redundant features and high computational cost. Recent deep learning models overcome these problems by implicitly capturing intricate structures from large-scale medical image data. However, they are still affected by network hyperparameters and topology. Hence, the state of the art in this area can be further optimized by integrating bio-inspired concepts into deep learning models. This work proposes a novel bio-inspired deep learning approach for optimizing predictive results of liver cancer. This approach contributes to the literature in two ways. Firstly, a novel hybrid segmentation algorithm is proposed to extract liver lesions from computed tomography (CT) images using SegNet network, UNet network, and artificial bee colony optimization (ABC), namely, SegNet-UNet-ABC. This algorithm uses the SegNet for separating liver from the abdominal CT scan, then the UNet is used to extract lesions from the liver. In parallel, the ABC algorithm is hybridized with each network to tune its hyperparameters, as they highly affect the segmentation performance. Secondly, a hybrid algorithm of the LeNet-5 model and ABC algorithm, namely, LeNet-5/ABC, is proposed as feature extractor and classifier of liver lesions. The LeNet-5/ABC algorithm uses the ABC to select the optimal topology for constructing the LeNet-5 network, as network structure affects learning time and classification accuracy. For assessing performance of the two proposed algorithms, comparisons have been made to the state-of-the-art algorithms on liver lesion segmentation and classification. The results reveal that the SegNet-UNet-ABC is superior to other compared algorithms regarding Jaccard index, Dice index, correlation coefficient, and convergence time. Moreover, the LeNet-5/ABC algorithm outperforms other algorithms regarding specificity, F1-score, accuracy, and computational time.
1. Introduction
Liver cancer is among the most common causes of death worldwide []. In order to raise opportunities for survival by supplying optimal treatments, detecting the presence of liver cancer early is of significant importance. At the current time, biopsy is considered golden standard to detect cancer, although it is uncomfortable, invasive, and does not always represent a viable option, depending on the tumor location []. Noninvasive diagnosis of liver lesions could be evaluated by using medical imaging modalities. Computed tomography (CT) is among the most commonly used modalities for detecting, diagnosing, and following up the status of liver lesions, specifically metastases []. The images are acquired before and after intravenous injection of a contrast agent with optimal detection of lesions in the portal phase (60–80 s post injection) images. However, current radiological practice is to visually inspect the image of the liver. Visual inspection for an enormous number of medical images can be tedious and time consuming. This task requires the radiologist to search through a three-dimensional CT scan which may include hundreds of slices and multiple lesions, causing human bias and mistakes [].
For this reason, computer-aided diagnosis (CAD) through computer vision and machine learning [,,,] has been developed to assist doctors in decision-making through facilitating the interpretation of liver CT scans [,,,,,,]. However, little work has been conducted on liver cancer diagnosis using CT images. Moreover, most of the proposed solutions in the literature are based on manually crafted features [,,,,,,]. Different visual descriptors have been tested, including texture [,,,], shape [], and a combination of them []. The grey level co-occurrence matrix (GLCM) features [,,,], wavelet coefficient statistics [], and first-order statistics [,] have been used frequently for texture and shape description, while support vector machine (SVM) [,,] and artificial neural networks (ANNs) [,] have been used in the classification stage.
Despite the success of these methods, it is usually challenging to design handcrafted features that are optimal for a specific classification task. Furthermore, these methods cannot present discriminative hierarchical feature representations from image data effectively. In recent years, the importance of representation learning in liver cancer diagnosis has been emphasized instead of feature engineering [,]. Deep learning [,,] is one type of representational learning technique that can learn abstract mid-level and high-level features from image data. One advantage of deep learning is that it can learn extremely complex patterns. Deep learning algorithms, especially convolutional neural networks (CNNs), use "hidden layers" between inputs and outputs in order to model intermediary representations of image data that other algorithms cannot easily learn. Hence, they can generate high-level feature representations directly from raw medical images.
CNNs [,], which are biologically inspired networks, have led to significant contributions in medical image analysis tasks, including organ segmentation [], texture analysis [], and disease classification []. Several studies have also emphasized that CNNs achieve promising performance in cancer detection and diagnosis [,,]. However, the accuracy of segmenting and classifying tumors using CNN models depends on the network hyperparameters and topology, which also have an impact on the overall performance of the CAD system. Since these parameters affect performance directly, algorithms that take inspiration from natural phenomena [,,,,,,] can be integrated with deep learning models to select optimal hyperparameters by searching the solution space in a global manner.
Particle swarm optimization (PSO) [], artificial bee colony optimization (ABC) [], differential evolution (DE) [], harmony search (HS) [], gravitational search (GS) [], grey wolf optimization (GWO) [], antlion optimization (ALO) [], and ant colony optimization (ACO) [] are a few of the popular algorithms of this class. Other works have demonstrated that each of these algorithms can be considered an effective solver of complex optimization problems in the medical domain [,]. The ABC optimization algorithm as an instance represents a prominent candidate among effective optimization algorithms. It is inspired by the intelligent foraging behavior of honey bees and is able to share information [].
Contrary to state-of-the-art systems which are based on using feature engineering methods, or hybrids of feature engineering and deep learning algorithms, this work presents a fully bio-inspired deep learning approach for liver cancer diagnosis using CT images. The effect of hybridizing multiple deep learning models with ABC bio-inspired optimization is investigated in the segmentation, feature extraction, and classification of liver lesions. The main contributions of the paper include the following:
- An extensive survey is introduced to discuss current state-of-the-art methods for diagnosing both other cancers and liver cancer. Also, recent applications of bio-inspired methods in the optimization of medical domain problems are reviewed.
- A novel hybrid segmentation algorithm, namely, SegNet-UNet-ABC, is proposed for extracting liver lesions from CT images using the SegNet network [], the UNet network [], and ABC. In this algorithm, the SegNet network is used for extracting liver from the abdominal CT scan, while the UNet network is used to extract lesions from the liver. In parallel, the components of ABC bio-inspired optimization are integrated with each deep learning network to adjust its hyperparameters, as they highly affect the segmentation performance []. These parameters include the learning rate, minibatch size, momentum, maximum epochs, shuffle, and regularization. Hence, this hybridization can provide near-optimal segmentation results in comparison to state-of-the-art algorithms for liver lesion segmentation.
- Furthermore, to investigate the efficiency of the ABC algorithm in optimizing segmentation of liver lesions appearing on CT images when it is used as a hybrid with SegNet and UNet architectures, extensive comparisons are made to other bio-inspired optimization algorithms, including GWO, ALO, and ACO. Therefore, this work compares the performance of the proposed SegNet-UNet-ABC algorithm with that obtained by hybridization of SegNet-UNet with GWO (SegNet-UNet-GWO), SegNet-UNet with ALO (SegNet-UNet-ALO), and SegNet-UNet with ACO (SegNet-UNet-ACO). A detailed performance comparison is reported.
- Moreover, a hybrid algorithm of the LeNet-5 deep learning model [] and the ABC algorithm, namely, LeNet-5/ABC, is proposed as a feature extractor and classifier of liver lesions. The reason for this hybridization is that the hyperparameters mainly determine the layer architecture, i.e., the size of resulting feature map, in the feature extraction step of the LeNet-5 network, which affects the learning time and classification accuracy. Therefore, the ABC algorithm is used to determine the optimal topology for constructing the LeNet-5 model by selecting the best values of kernel size, padding, stride, and number of filters applied at each convolution and pooling layer. This, in turn, can optimize the classification part in the LeNet-5 model by reducing classification error and minimizing the probability of being trapped in local optima.
2. Related Work
By reviewing the state of the art of cancer diagnosis using image modalities, we find that the contributions can generally be divided into feature-engineering-based CAD methods and deep-learning-based CAD methods. Hence, this section presents an overview on utilizing these methods in diagnosing cancers, including liver cancer. Furthermore, this section sheds light on using bio-inspired methods in optimizing medical diagnosis.
2.1. Feature Engineering Methods for Diagnosis of Cancers Generally and Liver Cancer Specifically
For feature engineering approaches, several studies have been introduced to diagnose either other cancers or liver cancer. In [], a texture descriptor was introduced for representing rich texture features through the integration of multiscale Gabor filters with local binary pattern histograms for the classification of lung tissue. In [], the authors introduced a CAD system for thyroid cancer using internal and external characteristics, where geometric and textural features were extracted. Further, multilayer perceptron was utilized for classifying internal characteristics, whereas SVM was utilized for classifying external characteristics.
As for liver cancer diagnosis, many studies have proposed feature engineering methods embedded into CAD systems by using CT scan images [,,,,], as illustrated in Table 1. In the segmentation phase, the region growing algorithm and fuzzy C-means (FCM) are popular algorithms that have been frequently employed for either liver or lesion segmentation [,]. For feature extraction, the majority of liver CAD systems have used statistical features for describing texture and shape [,,,], including GLCM features; wavelet coefficient statistics; and statistical measures of mean, skewness, variance, standard deviation, and kurtosis. In this context, feature extraction has played a crucial role in the liver CAD system as it heavily affects overall performance. In the classification phase, conventional linear and nonlinear machine learning algorithms have been used, including probabilistic neural networks [,], SVM [,], and binary logistic regression [].

Table 1.
Review on feature engineering methods utilized in liver cancer diagnosis from computed tomography (CT) images.
2.2. Deep Learning Methods for Diagnosis of Cancers Generally and Liver Cancer Specifically
Recently, applications of the deep learning have emerged generally in medical image analysis using a variety of image modalities. Segmentation, feature extraction, and classification are the three most basic tasks that deep learning algorithms have been investigated in. For instance, these algorithms have been widely investigated with different anatomical structures (organs or body locations) for medical image analysis, including breast [], prostate [], heart/cardiac [], carotid [], thyroid [], intravascular [], fetus [], lymph node [], spine [], bone [], muscle [], tongue [], and more. Different kinds of deep networks have been adopted to do these tasks.
For state-of-the-art systems using deep learning approaches in the diagnosis of cancers [,,], including liver cancer [,,,], demonstrated in Table 2, the majority of works have applied CNN models to learn from the image modalities and hierarchical abstract representations, followed by a softmax layer or other linear classifier (such as SVM) that is used to provide one or more probabilities or class labels. To date, the majority of these works have neglected the effect of network hyperparameters on overall performance. Until now, few solutions have been introduced to optimize the performance of segmentation, feature extraction, and classification using ordinary deep learning architectures [].

Table 2.
The current state-of-the-art deep learning approaches for diagnosing cancers, including liver cancer.
2.3. Bio-Inspired Optimization in Medical Diagnosis
As with most neural networks, deep learning architectures are susceptible to problems such as lack of hyperparameter tuning, multiple local optima, and increased computational time. To avoid these problems, optimization of the network topology and hyperparameters has become a crucial task. The bio-inspired optimization algorithms are broadly utilized in general optimization problems in the medical domain, as demonstrated in Table 3 [,,,,,,], including ultrasonic echo estimation [], selecting cancer progression pathway genes [], microarray cancer classification [], classification of DNA microarrays [], retinal blood vessel localization [], bioinformatics data dimension reduction for solving classification problems [], and diabetes disease diagnosis []. However, these algorithms have been rarely used to optimize the results of segmentation, feature extraction, and classification obtained using a CNN. Therefore, this work investigates the effect of hybridizing multiple deep learning networks with bio-inspired optimization on the segmentation, feature extraction, and classification of liver lesions from CT images.

Table 3.
Recent state-of-the-art bio-inspired optimization approaches utilized in medical diagnosis.
3. Materials and Methods
A brief explanation is given in this section on materials and methods employed in current work including the dataset, performance measures, CNN, bio-inspired ABC algorithm, and the proposed approach.
3.1. Datasets of Liver CT Images
The approach proposed in this work was tested using two publicly available datasets. Firstly, we used the dataset tested in [,], namely, LiTS, which comprises 131 CT scan images along with their ground truths (clinical annotation). The LiTS dataset also includes a set of 70 CT images for testing purposes, but this does not have any accompanying annotations. Hence, only the 131 annotated CT images were considered in this work. Secondly, we used the Liver CT dataset that was tested in [], namely, Radiopaedia. This dataset is a complex one which includes abdominal CT images for the liver taken from more than 105 patients. Furthermore, more than 150 slices for each patient are included. The images are all available in JPEG format, obtained from a DICOM file of dimension 630 × 630 and bit depth of 24 bits.
3.2. Performance Measures
For confirming adequacy of liver lesion segmentation by the proposed hybrid algorithm and also to compare it to the state-of-the-art algorithms, this work implements a quantitative analysis using three indices: the Jaccard index [,], Dice coefficient [,,,], and correlation coefficient [,]. Furthermore, convergence time [] is another criterion used to evaluate the quality of segmentation using hybrid methods.
Jaccard index: This similarity index is a popular measure used for binary data as given below, where represents the area of overlapping, is a binary image, and is a ground truth image.
Dice Index: This coefficient is utilized to measure segmentation performance. The value of the Dice coefficient describes the percentage of pixels in the predicted image which exactly match the ground truth. This measure is computed by Equation (2).
Correlation coefficient: This measure is used to compute similarity of segmented image to ground truth, in terms of their respective pixels’ intensity. This coefficient is defined by Equation (3), where the indices and represent the locations of pixels in liver CT image.
Convergence time: The convergence time of each hybrid segmentation algorithm is expressed as the time taken by the algorithm versus the false alarm rate (FAR), computed by Equation (4).
On the other side, three measures were used as validation metrics for testing performance of proposed LeNet-5/ABC liver cancer classification algorithm.
Specificity: The specificity represents the true negative rate that is given using Equation (5) [].
F1-score: This measure expresses the harmonic average of both precision and recall [], which is computed by Equation (6).
Accuracy: The accuracy is expressed as the probability of obtaining a true prediction [], which can be computed using Equation (7).
Computational time (in seconds): This is used for assessing quality of classification obtained by each classifier.
3.3. Convolutional Neural Networks
To demonstrate how the CNNs work [,,,,,,,,,], it is required to understand the architecture of the basic ANNs, which represent human-brain-inspired architectures widely utilized in machine learning. ANN comprises three basic layers: the first is input one, the middle is hidden, and the final is output layer. The set of characteristics which represents the class that the ANN has to learn is received by the input layer. Further, input data processing is performed by the hidden layer through recognizing patterns to give identical or approximate value for the class that has to be recognized by the output layer. As depicted in Figure 1 [], this process is expressed as feed-forward. If the output is not matched to the correct class, a back-propagation process is performed by the ANN for adjusting the connection weights of the corresponding hidden layers according to the calculated error, allowing correct class recognition based on repetitive learning iterations.
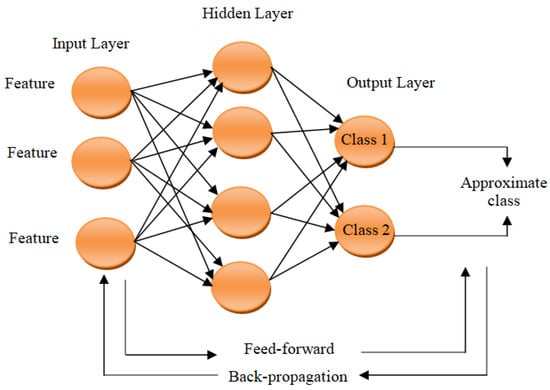
Figure 1.
Conventional artificial neural network (ANN) architecture.
A recent alternative to ANN for big data, including images, is CNN. The basic difference between CNNs and ANNs is the convolution and pooling layers adopted in the former to extract image characteristics more effectively using fewer dimensions. A CNN passes a given image through its layers and outputs the decision class. The network may comprise tens or hundreds of layers, where each layer learns to detect different feature kinds. Each training image is subjected to filters at different resolutions, then the output of every convolved image is given as input to subsequent layer. The basic architecture of CNNs is depicted in Figure 2 and includes the following layers.
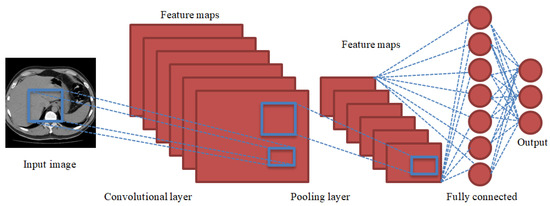
Figure 2.
Basic architecture of a CNN showing its convolutional, pooling, fully connected, and output layers. The given image is passed through these layers to predict the decision class.
3.3.1. Convolutional Layer
The convolution represents particular kind of linear operation, in which the image matrix is subjected to a kernel. Figure 3 presents an instance on convolutions, e.g., a filter application to the given image. Figure 3a presents the matrix of image that will be filtered, the kernel or filter is presented in Figure 3b, and the convolution result is presented in Figure 3c. The filter depicted in Figure 3b successively reads from the left to right, besides to, top to bottom, where all pixels in the area of kernel action are within the gray area of the matrix shown in Figure 3a. Subsequent to this operation, pixel value 16 in the array of Figure 3a becomes 17 in the matrix of Figure 3c due to the convolution. This operation is computed as follows: .
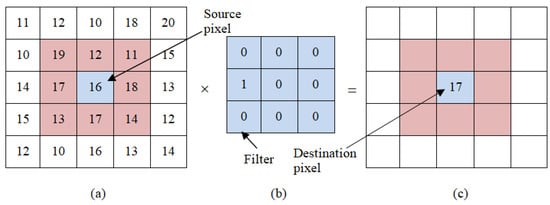
Figure 3.
Convolution operation of the CNN.
3.3.2. Rectified Linear Unit Layer
Rectified linear unit, referred as ReLU, comes after the convolution layers where feature maps are fed to nonlinear activation functions. Accordingly, the whole neural network becomes able to approximate nonlinear functions []. The activation function generally represents a simple ReLU, defined as in Equation (8). The ReLU function swaps all negative states with zeros. At the same time, feeding the resulting feature maps to the activation function generates new tensors, termed as feature maps. Figure 4 demonstrates an example of ReLU operation.
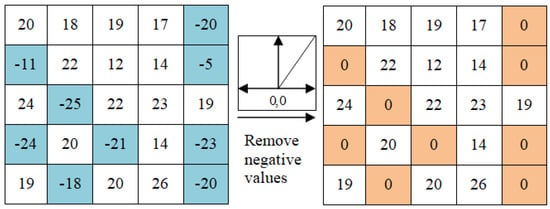
Figure 4.
The rectified linear unit operation, which changes all negative states of feature maps into zeros.
3.3.3. Pooling Layer
The pooling layers aim at reducing the parameter number of big image data. To this end, each feature map generated through feeding the data to single or multiple convolutional layers is then pooled within a pooling layer. The pooling operations obtain small grid segment as input and generate singular number for every segment. This is known as subsampling or downsampling, in which dimensionality of every map is minimized while retaining important information. There are different types of spatial pooling, comprising (1) max-pooling; (2) average-pooling; and (3) sum-pooling. Max-pooling obtains the largest value of the considered rectified feature map. Obtaining the average of elements in the feature map is referred as average pooling, while taking their sum is named sum-pooling. Figure 5 demonstrates the max-pooling operation used in this work with different filters and stride values. The stride refers to number of shifts in pixels over the input image matrix. When the stride value is 1, filters are shifted one pixel at a time. When the value is 2, filters are shifted two pixels at a time, and so on.
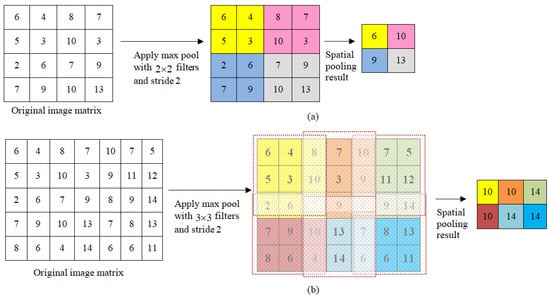
Figure 5.
Max-pooling with different filters and stride values: (a) max-pooling with filters and stride of 2, and (b) max-pooling with filters and stride of 2.
3.3.4. Fully Connected Layer
Fully connected layer (FCL) represents the decision layer in a CNN. The softmax function is utilized to compress the outputs of every neuron to be between 0 and 1. It acts similarly to sigmoid function. The FCL divides every output as if the total output sum is equal to one. The produced output represents the categorical probability distribution. The FCL computes a probability that a class is true, as follows, where denotes the input vector to the output layer. If the number of output units is equal to ten, then there will be ten elements in . indexes the units of outputs, so that .
3.4. Artificial Bee Colony Optimization
In ABC [,,,,,,] meta-heuristics, artificial bees of the colony cooperate to find optimal solutions to the optimization problem. One important feature of ABC is it being inspired by nature, exactly, by honey bees’ behavior seeking a good-quality food source. The essential components of ABC which are modeled after bees’ foraging process are demonstrated as follows: (1) food source, which refers to a feasible solution for the optimization problem; (2) fitness value, which represents food source quality and is expressed as single quantity associating to objective function for the feasible solution; and (3) the bee agents, which represent a group of computational agents. For the algorithm of ABC, the colony is divided equally into three kinds of honey bees: employed bees, onlooker bees, and scout bees. The solution within the search space encompasses parameter set that represents food source location. The count of employed bees equals to the count of food sources, where one employed bee is specified for one food source. Basic steps of ABC optimization are illustrated below.
3.4.1. Initialization
The ABC algorithm begins with the random choice of a food source corresponding to a potential solution. Equation (10) is used to produce initial solutions for employed bees, where represents the dimension for the food source’s employed bee; and denote the lower and upper bounds of the parameter, respectively; is a random number that falls in . is the food source number, i.e., the swarm size, while refers to the dimensionality of the problem considered for optimization. Resetting of abandonment counter (AC) is also done for every employed bee in the initialization phase.
3.4.2. Employed Bees Phase
For every employed bee, a new solution is immediately produced in this phase. Firstly, the employed bee solution is copied to the candidate new solution ( = ). Then, Equation (11) is used to update the solution parameters:
where the parameter is randomly selected to be updated and the coefficient is obtained as unity in the basic ABC algorithm. Such process is done through randomly choosing a candidate in the neighborhood of the candidate. Also, is a random number falling in the interval , indicates the count of employed bees, and represents the dimensionality of the problem considered for optimization. After locating a candidate solution and computing the objective function value, the fitness values for candidate solutions and employed bees’ solutions are computed as shown below:
where indicates fitness value for candidate solution and represents the objective function value for the employed bee. Subsequently, if the resulting fitness value of an updated solution is superior to that of the present solution, then the present solution is replaced by the candidate solution, while the AC of an employed bee is readjusted to zero; otherwise, the abandonment counter is immediately increased by 1.
3.4.3. Onlooker Bees Phase
To enhance the solution, every onlooker bee chooses an employed bee. In this context, the Roulette wheel is utilized to compute the selection probability for the employed bee as follows:
where symbolizes the selection probability of the employed bee. Accordingly, the solution of the chosen employed bee is optimized by the onlooker bee, according to Equation (11). If the resulting fitness value for the new solution, located by onlooker bee, is superior to that by the employed bee, then the latter replaces the onlooker bee and the AC of an employed bee is immediately readjusted to zero; otherwise, the abandonment counter is incremented by 1.
3.4.4. Scout Bee Phase
A predefined limit is used in this phase to check the AC of every employed bee. Any employed bee that fails to optimize the solution prior to limit is met, will be considered a scout bee. Thereafter, the solution of the scout bee is produced using Equation (10) and the AC is immediately reset. Accordingly, the scout bee is considered an employed bee. Hence, scout bees also prevent the employed bees from stagnating.
3.5. The Proposed Approach
A new methodology for liver cancer diagnosis using CT images is proposed in this section. Instead of using the conventional feature engineering methods which are designed to be suitable for specific medical pattern recognition problems, the approach proposed in this work is a fully deep learning one. However, the more complex a deep learning method is, the more computational time it demands in order to perform at an acceptable pace. To overcome this problem, in this work we investigate the effect of hybridizing multiple deep learning networks with bio-inspired algorithms to optimize the segmentation, feature extraction, and classification of liver lesions. The proposed liver cancer diagnosis approach is demonstrated in Figure 6 and includes three stages. The first stage is preprocessing of liver CT images. A proposed hybrid algorithm is used in the second stage to segment liver lesions from the CT images, based on the SegNet network, UNet network, and ABC algorithm. In the third stage, a proposed hybrid LeNet-5/ABC algorithm is used as a feature extractor and classifier of the liver lesions into benign and malignant.
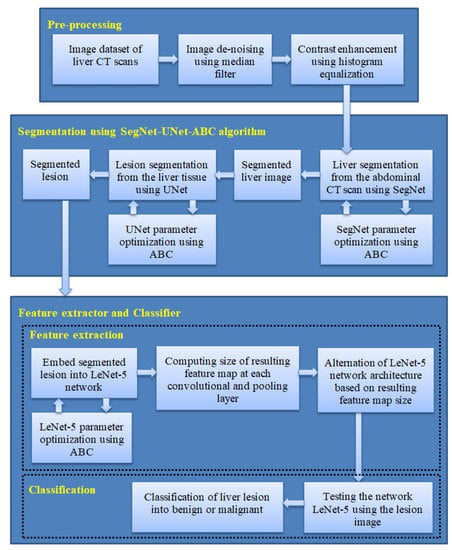
Figure 6.
Proposed approach for liver cancer diagnosis, including (1) preprocessing, (2) liver lesion segmentation using the SegNet-UNet-ABC algorithm, and (3) feature extraction and classification of liver lesions using the LeNet-5/ABC algorithm.
3.5.1. Preprocessing of CT Images
In this phase, the liver CT image is firstly converted into grayscale then resized to a size of as the SegNet network receives inputs of this size. The noise is removed using a median filter, whereas contrast is enhanced by histogram equalization. Then grayscale image of the liver is smoothed, enhanced, and denoised by a median filter algorithm of window size. The filter runs over every element of the CT image and replaces every pixel by the median value of its neighborhood pixels located in the square neighborhood surrounding the evaluated pixel. Equation (14) demonstrates using the histogram equalization for modifying the dynamic range of each intensity value and increasing CT contrast without an effect on structure of information included therein. is the cumulative distribution function of unique pixel value , and represents the grey level number used for an image of size . Figure 7 shows preprocessing results on some CT slices.
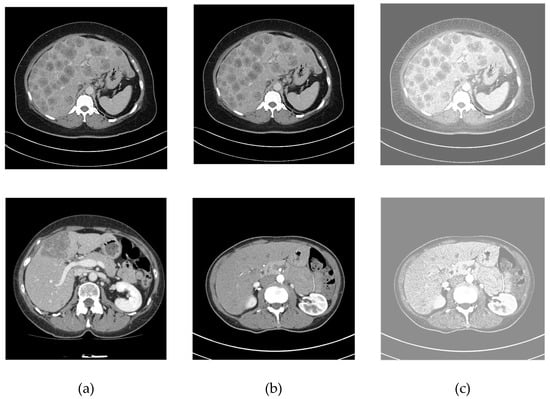
Figure 7.
Preprocessing results of different cases: (a) original image, (b) median filtering result, and (c) histogram equalization result.
3.5.2. The Proposed Hybrid SegNet-UNet-ABC Algorithm for Liver Tumor Segmentation
CNN has different architectures for segmentation, feature extraction, and classification problems. SegNet and UNet have recently been used for semantic segmentation purposes. However, the network hyperparameters have a direct effect on the segmentation accuracy. This requires the optimization of hyperparameters in order to obtain near-optimal segmentation results. Hence, hyperparameter selection through recent effective optimization algorithms is necessary. These algorithms can search the solution space efficiently in a global way. For optimizing liver lesion segmentation from CT images, we propose a hybrid algorithm, namely, SegNet-UNet-ABC, which integrates SegNet and UNet deep learning architectures with ABC optimization for segmenting livers from abdominal CT images and lesions from liver tissue. The proposed hybrid segmentation algorithm is depicted in Figure 8 and includes the following:
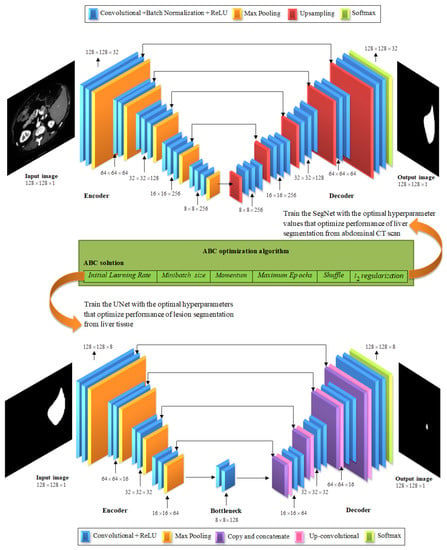
Figure 8.
The proposed SegNet-UNet-ABC algorithm for segmenting liver lesions from CT images, which comprises three steps: (1) liver segmentation from the abdominal CT image using the SegNet network, (2) lesion segmentation from the liver tissue using the UNet network, and (3) optimization of segmentation performance of the SegNet and UNet architectures using the ABC algorithm.
A. Liver segmentation from the abdominal CT image using the SegNet network.
The abdominal CT scan includes other organs in addition to the liver. Therefore, liver extraction is a critical task to achieve accurate cancer diagnosis. In this work, the CNN is used to accomplish this task, wherein the SegNet architecture is employed. This architecture has shown robustness in pixel-wise semantic segmentation tasks []. The SegNet network encompasses an encoder–decoder architectural engine that is ended at a pixel-wise classification layer, as shown in Figure 8.
The encoder section of the SegNet architecture comprises a repeating group of layers. Each group is constituted of some convolutional layers that are followed by a layer of max-pooling. This portion reveals the first 13 convolutional layers in the VGG16 [] architecture. The role of the convolutional layer is to produce the required number of feature maps through the convolution process of input by a filter bank. Thereafter, resulting feature maps are patch normalized []. Next, the ReLU process, namely, the pixel-wise operation, is implemented, where the output represents . In this context, a max-pooling layer is used to perform downsampling by 2 through defining a window with size and using a stride value of 2. The max-pooling is crucial for the SegNet to fulfill translational invariance. However, it exhibits loss of the boundary details, which is unfavorable in the segmentation process. To overcome this issue, the boundary information is sorted within feature maps of the encoder before implementing the max-pooling process. Practically, the index of the pixel with the maximum value is kept within the feature maps of every pooling window.
For the decoder section of the SegNet architecture, the layers are organized in parallel to the encoder but in reverse order. The memorized max-pooling locations are firstly used to upsample the input maps and to present a sparse feature map. The convolutions are then used to produce a dense feature map using the filter banks of the decoder. In the same manner as the encoder section, the batch normalization is implemented after the convolution operation. At the final layer of the decoder, the pixel information is fed into the output layer using the Softmax activation function. The predicted segmentation is achieved through classification of every pixel to a corresponding class.
B. Lesion segmentation from the liver tissue using the UNet network.
This step is crucial to extracting lesions from liver tissue to be analyzed later. For this purpose, the UNet architecture is used. The UNet architecture has demonstrated good results when applied to biomedical images []. As depicted in Figure 8, the input layer receives the liver image in the form . Furthermore, the UNet architecture comprises three parts. The downsampling path is the first part, in which we can find two convolutional layers which are followed by a max-pooling layer of window size and a stride value of 2. The input liver image is convolved twice using a filter of size followed by a ReLU activation function. Padding value is retained the same because the output image will have the same size as the input image. The filter number in the convolution layer of the first group is set to eight and continues doubling until reaching the fifth layer group.
Thereafter, an upsampling path is followed where the feature maps of each group are halved []. In this regard, the UNet architecture uses a concatenation layer to concatenate the features from both the previous layer and the downsampling layer, which has the same number of filters as the current layer group. Following this, there are two layers with a convolutional filter of , followed by a ReLU activation function. This group of layers is repeated starting from group six to group nine. The output layer is the tenth, which is a convolutional one with filter [] and has eight feature channels. To sum up, 27 layers [] are involved in this architecture (18 convolutional + ReLU, 4 pooling, 4 up-convolutional, and 1 softmax layer).
C. Optimization of segmentation performance using the ABC algorithm.
Solution vectors are firstly generated by the ABC algorithm. Each generated vector comprises all possible values of hyperparameters to be optimized. These values are then employed as training parameters during training process of SegNet network. The fitness value for each hyperparameter vector produced by the ABC is evaluated using Equation (15). This is implemented by computing the contour matching score () between the predicted image and ground truth image . Accordingly, the optimal solution for liver segmentation from the abdominal CT scan will be the one that increases the F1-score, precision, and recall. The three weights , , and were used to define the F1-score, precision, and recall, respectively.
The precision and recall are computed as follows, while F1-score is computed by Equation (6).
As demonstrated in Algorithm 1, the optimal hyperparameters for liver segmentation are computed using Algorithm 2. The best solution is returned by Algorithm 2 when the termination criterion is satisfied (), which is achieved when the number of iterations reaches the threshold value. Thereafter, the resulting solution is passed to Algorithm 1, where training is implemented afresh using the produced hyperparameter values, the SegNet deep learning architecture, and the training set (), as shown in Steps 6 and 7. After that, the trained SegNet network is tested using the testing set () to validate the liver segmentation performance, as shown in Step 8.
The previous steps are done for the UNet network as demonstrated in lines 10 to 19 of Algorithm 1, where the resulting set of segmented liver images is divided to training () and testing (). The training set of UNet () is then divided to training () and validation (). Thereafter, the , , and UNet structure are sent as functional parameters of Algorithm 2 of the ABC, which computes the hyperparameters that optimize lesion segmentation using UNet. The resulting optimized parameters are embedded into the UNet network. Then, the network is trained using the original training set () and tested on (), as demonstrated in Steps 17 and 18 of Algorithm 1. Figure 9 demonstrates the liver segmentation results using SegNet and the UNet predictions of liver lesions. The optimized hyperparameter values selected by the ABC algorithm for segmentation using the SegNet and UNet networks, are shown in Table 4.
| Algorithm 1: The proposed hybrid SegNet-UNet-ABC for liver lesion segmentation. |
| Inputs: training set of abdominal CT images. |
| testing set of abdominal CT images. |
| Output: Optimized performance of liver lesion segmentation from CT scan image. |
|
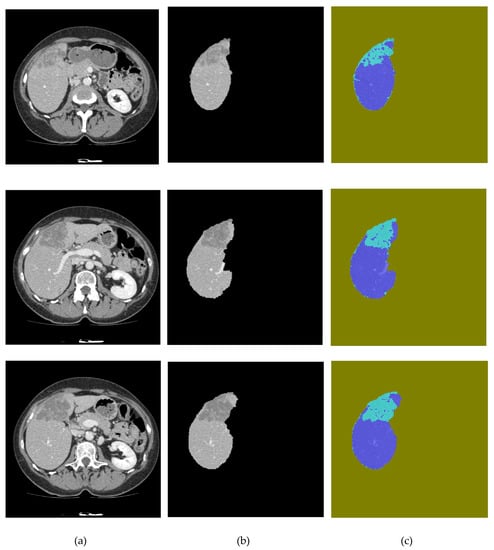
Figure 9.
Segmentation results: (a) original image, (b) liver segmentation using SegNet, and (c) UNet predictions of liver lesions.

Table 4.
The optimized hyperparameters for segmenting livers and liver lesions using SegNet and UNet, respectively.
| Algorithm 2: The ABC algorithm for selecting the optimal hyperparameter values that optimize the performance of segmentation using the deep network. |
| Inputs: the food source number. |
| the limit or maximum number of trials for abandoning a source. |
| the maximum cycle number. |
| training set. |
| validation set. |
| Deep learning architecture (SegNet, UNet, or LeNet-5). |
| Output: Optimal hyperparameters optimizing segmentation performance using the deep network. |
|
3.5.3. The Proposed Hybrid LeNet-5/ABC Algorithm as Feature Extractor and Classifier of Liver Lesions
One advantage of the CNN is that it can operate directly on the raw data without extraction of data characteristics. This is due to the feature extraction step embedded inside. When constructing CNN architecture, the hyperparameters including convolutional kernel size, number of filters, padding, and stride can affect the network performance as they determine structure of layers, comprising size of resulting feature map at the layer level. Contrarily, the pretrained deep learning networks such as LeNet-5 and AlexNet use static predefined hyperparameters to extract features from images. In LeNet-5 as an example, all convolutional kernels are set to size 5, while in the AlexNet architecture, the sizes of kernels are 11, 5, and 3. Hence, to get optimal feature extraction results using CNN, hyperparameter setting has to be appropriately done. However, there are no standard rules for optimizing CNN hyperparameters that influence the feature extraction process. This has depended mostly on the designer’s intuition [,].
Contrary to the ordinary work on CNNs as feature extractors, the ABC optimization algorithm is proposed in this work for tuning the hyperparameters of feature extraction step; this is hypothesized to optimize the predictive results of liver lesion classification, as depicted in the optimized LeNet-5 of Figure 10. The steps of the hybrid LeNet-5/ABC algorithm are shown in Algorithm 3, in which the ABC is used for optimizing the ordinary LeNet-5 topology, which is considered to be the first architecture for CNNs. The ABC algorithm generates an initial population with potential solutions for LeNet-5 construction, where each solution vector comprises the kernel size, stride, and padding, in addition to the number of filters at each convolution and pooling layer, as presented in Step 3 of Algorithm 3. These parameters are supposed to be the solutions for employed bees. The classification error computed at the LeNet-5 classification step is used for evaluating the classification quality of liver lesions, which is used for representing the fitness of solutions computed by ABC, as demonstrated in Step 30 of Algorithm 2. In other words, the fitness value of the hyperparameter vector generated by Algorithm 2 is computed using the following cost function that determines the new solution generated in each iteration step.
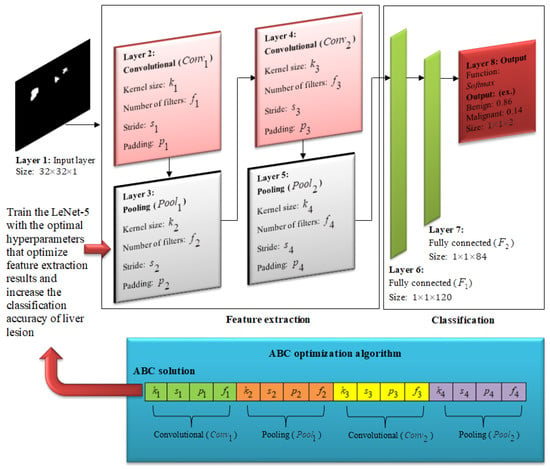
Figure 10.
Optimization model of the LeNet-5 network structure, in which the ABC algorithm determines an optimal topology for constructing LeNet-5 by selecting optimal values for kernel size, padding, stride, and number of filters applied at each convolution and pooling layer. Then the LeNet-5 network is trained with the resulting values to optimize the feature extraction step and increase classification accuracy of liver lesions.
Thereafter, the onlooker bees choose the solutions which return higher fitness values, update these solutions, and compute the fitness values of their solutions once again. Such process is repeated till the termination criterion of Algorithm 2 is met, . Solutions which cannot optimize the fitness value through a certain time period are considered as abandoned, while new solutions are generated using the scout bees. Further, the LeNet-5 architecture of the CNN is trained using the new optimized hyperparameter values of each convolution and pooling layer. Since size of input layer in the LeNet-5 architecture is , the segmented lesion image is resized using MATLAB from to . Then, the 2D kernels of LeNet-5 are exploited to extract the local information of liver lesions. On the other side, setting the hyperparameters using the ABC algorithm will influence the feature map size resulting at each subsequent layer of the feature extraction step in the CNN. Thus, the feature map size is computed at each layer using Equation (20), as demonstrated in Step 6 of Algorithm 3.
Here, denotes output layer size, is input layer size, represents the padding value, is the stride value, and denotes kernel size. In the proposed algorithm, the neuron numbers of the fully connected layer equal 120 and 84, while the neuron number at output layer was set to 2, which indicates the number of liver lesion classes, i.e., malignant and benign.
The LeNet-5 network is then constructed according to the new topology, as demonstrated in Step 8 of Algorithm 3. Accordingly, the new LeNet-5 architecture is trained using the original training set and tested on , as shown in Steps 9 and 10 of Algorithm 3. Table 5 presents the optimal hyperparameter set selected by the ABC algorithm to construct the LeNet-5 architecture. From the table, the best values of convolutional kernels are , , , and , respectively, for the first convolutional layer (), first pooling layer (), second convolutional layer (), and second pooling layer (). The best stride values are also , , , and , while the best padding values are , , , and , respectively, for , , , and . The new sizes of feature maps are , , , , respectively, at the same layers.
| Algorithm 3: The proposed hybrid LeNet-5/ABC for liver lesion classification. |
| Inputs: training set of CT images after segmenting the liver using SegNet. |
| testing set of CT images after segmenting the liver using SegNet. |
| Output: Optimal topology of the LeNet-5 network which optimizes the predictive results of liver lesion classification. |
|

Table 5.
The optimal values selected by the ABC algorithm to construct the LeNet-5 topology.
4. Experimental Results
This section clarifies a performance evaluation of the segmentation and classification algorithms proposed in this work. Results and discussion along with comparisons to the other work are demonstrated as follows.
4.1. Experimental Setup
In this work, each dataset was split into a 7:3 ratio []; hence, 70% of each was allocated as a training set and 30% was allocated for testing. The original training set was split further to create a validation set: training (35%) and validation (35%). The validation set was used to tune the hyperparameters. More specifically, a model was trained with various hyperparameters on the reduced training set (i.e., the full training set minus the validation set), and the values that performed best on the validation set were returned by the bio-inspired algorithm. Once the bio-inspired algorithm selected the best-performing parameters on the validation set, the best model was trained on the full training set (including the validation set), and this gave the final model. Eventually, the final model was evaluated on the test set to get an estimate of the performance measures and report results. The results reported in this paper were taken using a testing set.
4.2. Results and Discussion
For validating the proposed approach for liver cancer diagnosis, this section tests its main phases, which include lesion segmentation from the CT images using the proposed SegNet-UNet-ABC algorithm, and lesion classification using the proposed hybrid LeNet-5/ABC algorithm. Furthermore, comparisons to the previously published approaches for liver cancer diagnosis are made.
4.2.1. Validation of the Liver Lesion Segmentation Algorithm
To test the efficiency of the proposed SegNet-UNet-ABC algorithm in liver tumor segmentation, this study compares its performance to that of two recent segmentation methods that have been proposed in the literature in this regard. The first method was proposed in [], which is a hybrid of watershed algorithm (WA), neutrosophic sets (NS), besides to fast fuzzy c-mean-based clustering (FFCM). The authors tested their method, named NS-WS-FFCM, using the Radiopaedia dataset. The obtained results were 92.88%, 86.84%, and 91.66%, respectively, for Jaccard index, Dice index, and correlation coefficient. On the other side, the second compared method was introduced in [] and utilizes cascaded CNNs optimized using GA to perform liver lesion segmentation using the LiTS dataset. The authors reported that their deep learning method achieved 0.9557 in terms of Dice score. For comparison purposes, Table 6 demonstrates the results of liver lesion segmentation obtained in this work using the proposed SegNet-UNet-ABC method, over the Radiopaedia and LiTS datasets.

Table 6.
The application results of the SegNet-UNet-ABC algorithm for liver lesion segmentation.
The results demonstrate that the application of proposed SegNet-UNet-ABC algorithm over the Radiopaedia dataset achieved 0.96, 0.968, and 0.962 in terms of the Jaccard index, Dice index, and correlation coefficient, respectively, while it achieved 0.964, 0.97, and 0.958, respectively, for the three measures when it was tested on the LiTS dataset. It is obvious that the proposed method outperformed the NS-WS-FFCM method and the other method when each of them was applied to one of the datasets tested in this work. These results are due to the robustness of the SegNet and UNet in segmenting liver parenchyma and liver lesions from the CT images, respectively, which perform well in the case of absent clear edges, the definite shape of the liver parenchyma, in addition to the near connection between the liver tissue and the adjacent organs, as illustrated in the cases in Figure 9. In addition, the ABC bio-inspired optimization algorithm optimized the segmentation results of the liver parenchyma and liver lesions by selecting the best hyperparameters for SegNet and UNet which achieved the highest fitness in each step of segmentation.
To investigate the effect of the ABC algorithm on optimizing liver lesion segmentation from CT images when it is used as a hybrid with the SegNet and UNet architectures, some comparisons were made to other bio-inspired optimization algorithms: grey wolf optimization (GWO) [], antlion optimization (ALO) [], and ant colony optimization (ACO) []. Therefore, in this work we compare the performance of SegNet-UNet-ABC algorithm with that obtained by hybridization of SegNet-UNet with each one of these three other bio-inspired algorithms. Figure 11 presents comparisons of the segmentation performance using SegNet-UNet-ABC, SegNet-UNet-GWO, SegNet-UNet-ALO, and SegNet-UNet-ACO, over the datasets (a) Radiobaedia and (b) LiTS. From the figure, the proposed hybrid SegNet-UNet-ABC outperformed the other hybrid segmentation algorithms in terms of liver lesion segmentation according to the Jaccard index, Dice index, and correlation coefficient.
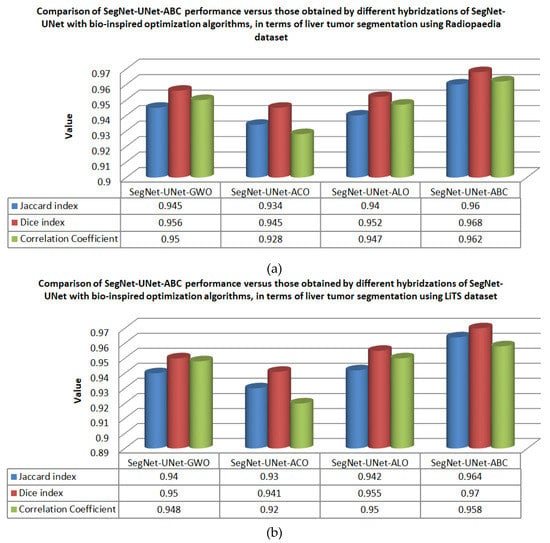
Figure 11.
Comparisons of the segmentation performance using SegNet-UNet-ABC, SegNet-UNet-GWO, SegNet-UNet-ALO, and SegNet-UNet-ACO, over the datasets (a) Radiopaedia and (b) LiTS.
Furthermore, the convergence time of the proposed SegNet-UNet-ABC algorithm was computed and then compared to those of SegNet-UNet-GWO, SegNet-UNet-ALO, and SegNet-UNet-ACO. Figure 12 presents the time taken by all hybrid algorithms to segment the lesions from CT images using the Radiopaedia and LiTS datasets, respectively. As depicted in Figure 12, when following the proposed SegNet-UNet-ABC algorithm across the two datasets, we can see that it obtained lower convergence time than the other compared algorithms. Hence, it is superior to SegNet-UNet-GWO, SegNet-UNet-ALO, and SegNet-UNet-ACO in terms of convergence time, Jaccard index, Dice index, and correlation coefficient. Table 7 demonstrates the parameter list that achieved the best segmentation results for each bio-inspired optimization algorithm.
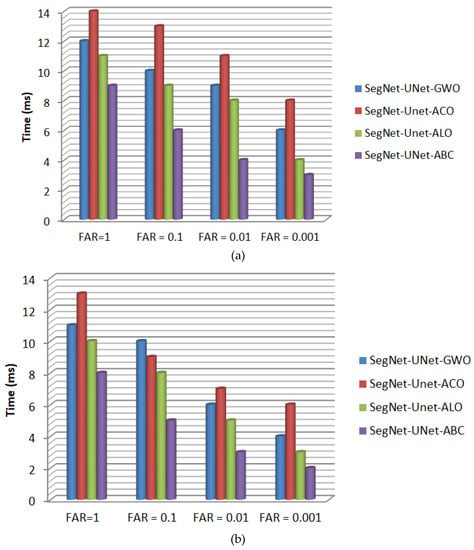
Figure 12.
The convergence times obtained by all hybrid algorithms to segment liver lesions from the CT images using (a) the Radiopaedia dataset and (b) the LiTS dataset.

Table 7.
The parameter lists which achieved the best segmentation results for each bio-inspired algorithm.
These results verify that the ABC is the most successful bio-inspired algorithm among those examined when it is used to tune the hyperparameters of SegNet and UNet. High flexibility, broad applicability, population of solutions, capability for handling an objective cost, capability to effectively explore the local solutions, ease of implementation, and robustness properties played a crucial role in optimizing the segmentation of liver and lesions. This result agrees with [], where the ABC algorithm showed high ability to tune CNN hyperparameters when it was used to optimize hand gesture recognition performance.
4.2.2. Validation of the LeNet-5/ABC Algorithm
For validating performance of proposed LeNet-5/ABC algorithm as a feature extractor and classifier of liver cancer, we compared the solution results obtained by it against two other algorithms used in the literature for the same purpose, which are the single CNN [] and traditional feature-based SVM []. In the first compared algorithm, the single CNN was employed as a feature extractor and classifier of liver cancer. In the second compared algorithm, a 114-dimensional feature vector was extracted from CT images including gray level statistics, GLCM features, and Gabor features, then principal component analysis (PCA) was used to reduce the feature space into a 25-dimensional vector.
For comparison, the number of runs used for validating each algorithm was set to 10. The three algorithms were validated using the two datasets, LiTS and Radiopaedia. The total averages of specificity, F1-score, and classification accuracy at each run of LeNet-5/ABC are presented in Figure 13. The same averages were likewise computed at each run of the single CNN algorithm and traditional feature-based SVM, as demonstrated in Figure 14 and Figure 15, respectively. The overall averages at all runs of each algorithm were also computed to give a clear view of the optimization occurring across the three algorithms.
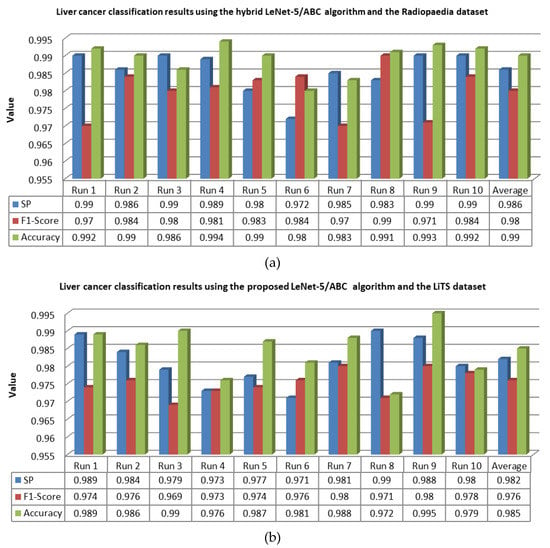
Figure 13.
Classification results of liver lesions obtained over 10 runs of the proposed LeNet-5/ABC algorithm, in terms of specificity (SP), F1-score, and accuracy. Results are demonstrated using the (a) Radiopaedia dataset and (b) LiTS dataset.
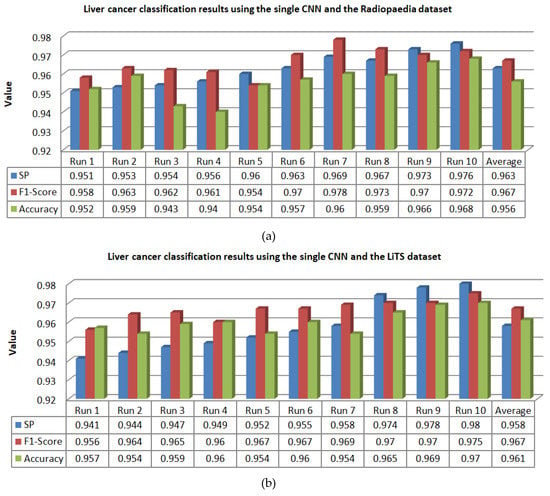
Figure 14.
Classification results of liver lesions obtained using the single CNN algorithm, in terms of specificity (SP), F1-score, and accuracy. Results are demonstrated using the (a) Radiopaedia dataset and (b) LiTS dataset.
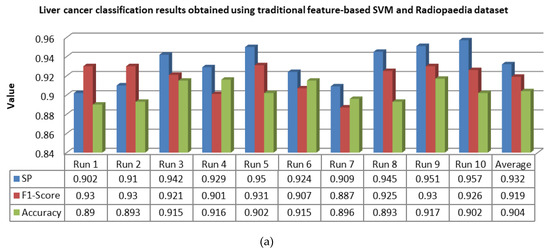
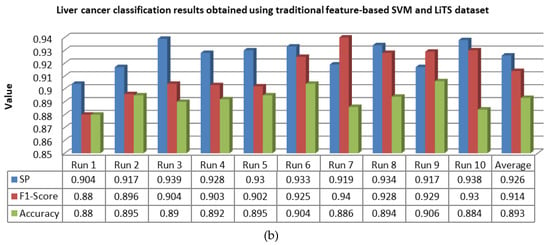
Figure 15.
Classification results of liver lesions obtained using the traditional feature-based SVM, in terms of specificity (SP), F1-score, and accuracy, using the (a) Radiopaedia dataset and (b) LiTS dataset.
For 10 runs of the LeNet-5/ABC algorithm, it is obvious from Figure 13 that the overall averages of specificity, F1-score, and accuracy were 0.986, 0.98, and 0.99, respectively, over the Radiopaedia dataset, whereas they were 0.982, 0.976, and 0.985, respectively, over the LiTS dataset. By following the 10 runs of the single CNN algorithm, it is evident that the averages were 0.963, 0.967, and 0.956 over the Radiopaedia dataset, while they were 0.958, 967, and 0.961 over the LiTS dataset. Eventually, the averages of specificity, F1-score, and accuracy obtained through 10 runs of traditional feature-based SVM were 0.932, 0.919, and 0.904 over the Radiopaedia dataset, whereas they were 0.926, 0.914, and 0.893 over the LiTS dataset.
As computational time is a necessary measure to evaluate the quality of classification, Figure 16 presents a comparison of the computational time (in seconds) required to test each CT image in the LiTS and Radiopaedia sets using LeNet-5/ABC, single CNN, and traditional feature-based SVM. For the two datasets, it is vivid that LeNet-5/ABC achieved the lowest computational time (4 s) in comparison to the two other algorithms. Therefore, LeNet-5/ABC outperforms them regarding specificity, F1-score, accuracy, and computational time.
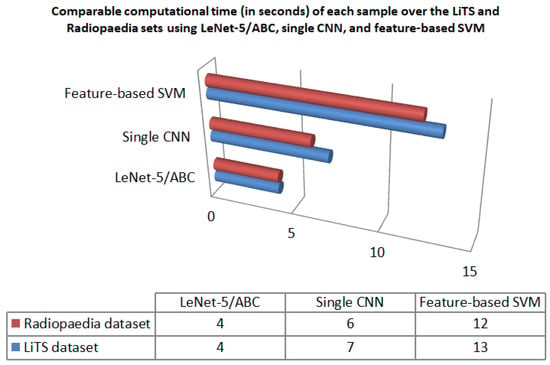
Figure 16.
The computational time (in seconds) required by each CT image over the LiTS and Radiopaedia sets using LeNet-5/ABC, single CNN, and feature-based SVM.
4.2.3. Comparisons to Other Work
To investigate the effectiveness of the overall proposed approach for liver cancer diagnosis, a comparison between it and the most recent works was made. Table 8 [,,,] demonstrates the comparison, which includes the following: (1) dataset used; (2) the approach which comprises segmentation method, feature extraction, and classification algorithm; and (3) the performance measures used. As can be observed, the majority of segmentation methods proposed in the literature [,] depend on region-based and clustering approaches, which check the low contrast between the liver and the surrounding tissues and organs. However, the noise of CT images, together with the large difference in liver shapes of patients, makes the state-of-the-art algorithms for liver segmentation incapable of giving optimal results. For instance, in comparison to current work, the two segmentation algorithms proposed in [] achieved lower performance regarding Dice index and . The results reported for Dice index are 0.8602 and 0.8803, while those reported for are 0.8771 and 0.8556.

Table 8.
Comparison to other works on liver cancer diagnosis using CT images.
On the other side, classification of liver cancer depends on traditional feature-based SVM, ANN, and CNN, and hybrid approaches [,]. For instance, 0.880 was reported in [] as the classification accuracy obtained on the Radiopaedia dataset, which is lower than the accuracies reported in the current work. In [], 92.4% was reported in terms of specificity, which is lower than the specificity results achieved using the proposed approach. In [], the authors attained their results using two datasets: training and testing. The results reported using the testing set were 98.38%, 95%, and 97.72% for accuracy, Jaccard index, and specificity, respectively, while the results reported using the training set (samples seen by the system) were 99.38%, 98.18%, and 99.09%, respectively, for the same measures. Therefore, the results reported in the current work using the testing set (samples unseen by the system) outperform those reported in [] in terms of accuracy, Jaccard index, and specificity. Hence, it is evident from Table 8 that the proposed hybrid bio-inspired deep learning approach outperforms state-of-the-art contributions that have used the same and different CT datasets in terms of accuracy, Jaccard index, Dice index, specificity, and .
The main thought to justify why the proposed hybrid model performs better than the other works is that the deep learning networks achieve robust performance in terms of liver lesion segmentation and classification when they are hybridized with the ABC bio-inspired optimization algorithm. This hybridization helped to increase the segmentation performance by minimizing over-segmentation. It also helped to handle the indeterminacy and uncertainty in CT images in a more effective way. Furthermore, it improved the classification performance of the LeNet-5 network by providing an optimal topology of the network and reducing over-fitting and the probability of being trapped in local optima. This eventually achieved high classification accuracy that led to better diagnostic results. Likewise, this reduced the computational time needed by the deep learning algorithms either to segment the liver lesions from the CT image or to classify the lesions into the corresponding cancer types.
5. Conclusions
This work proposed a new approach for liver cancer diagnosis from CT images, based on the hybridization of different deep learning models with the ABC bio-inspired optimization algorithm. Firstly, a novel hybrid segmentation algorithm was proposed for extracting liver lesions from CT images using SegNet, UNet, and ABC, named SegNet-UNet-ABC. The ABC algorithm was used in this regard to tune the hyperparameters of the SegNet and UNet deep learning architectures, in such a way as to optimize the performance of liver lesion segmentation. Secondly, a proposed hybrid LeNet-5/ABC algorithm was introduced; this uses the LeNet-5 architecture of CNN as a feature extractor and classifier in a different way to other works on liver cancer diagnosis which employ the traditional feature-based classification methods. Furthermore, the ABC algorithm was used to select the optimal topology for constructing the LeNet-5 network, with the aim to improve the predictive results of liver cancer diagnosis. Two publicly available datasets, namely, Radiopaedia and LiTS, were tested. To investigate the efficacy of the proposed SegNet-UNet-ABC algorithm in liver lesion segmentation from CT images, this work firstly compared its performance to that of two other segmentation methods from the state-of-the-art. The results demonstrate that the SegNet-UNet-ABC algorithm outperformed the two other algorithms when it was applied to the two datasets. The results obtained using the Radiopaedia dataset were 0.96, 0.968, and 0.962, while those obtained using the LiTS dataset were 0.964, 0.97, and 0.958 for Jaccard index, Dice index, and correlation coefficient, respectively. Furthermore, extensive comparisons were made to investigate the efficiency of the ABC algorithm in selecting hyperparameters that improve segmentation accuracy when used in combination with the SegNet and UNet architectures. The other bio-inspired optimization algorithms used in the comparison were GWO, ALO, and ACO. Hence, this work compared performance of SegNet-UNet-ABC algorithm to that of SegNet-UNet-GWO, SegNet-UNet-ALO, and SegNet-UNet-ACO. The results demonstrate that the SegNet-UNet-ABC algorithm outperformed the other algorithms regarding Jaccard index, Dice index, correlation coefficient, and convergence time. Moreover, the hybridization of deep learning networks with the ABC bio-inspired concept provides optimal hyperparameters which minimize over-segmentation and overcome indeterminacy and uncertainty in CT images in a more effective way. Further, validation of the hybrid LeNet-5/ABC algorithm was done by comparing the solution results obtained by it to those obtained by two other algorithms used in the literature for feature extraction and classification of liver cancer: the single CNN and traditional feature-based SVM. Results obtained across 10 runs of each algorithm revealed optimization in overall averages of specificity, F1-score, and accuracy, in favor of the LeNet-5/ABC algorithm. The optimization ratios obtained over the Radiopaedia dataset were 2.3%, 1.3%, and 3.4%, respectively, for the aforementioned algorithms, while the ratios were 2.4%, 1.3%, and 2.4%, respectively, for the same algorithms, over the LiTS dataset. Moreover, the LeNet-5/ABC algorithm is superior than other algorithms in terms of computational time. For future work on liver cancer diagnosis, multiple modalities such as ultrasound and CT images are intended to be fused as a multimodal diagnostic approach including deep learning. This approach is hypothesized to increase diagnosis confidence through the merits of deep multimodal fusion of medical images.
Acknowledgments
This research was funded by the Deanship of Scientific Research at Princess Nourah Bint Abdulrahman University through the Fast-track Research Funding Program.
Conflicts of Interest
The author declares no conflict of interest.
References
- WHO. The World Health Report—World Health Organization; WHO: Geneva, Switzerland, 2014. [Google Scholar]
- Smith, R.A.; Cokkinides, V.; Brooks, D.; Saslow, D.; Brawley, O.W. Cancer Screening in the United States, 2010: A Review of Current American Cancer Society Guidelines and Issues in Cancer Screening. CA A Cancer J. Clin. 2010, 60, 99–119. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-C.; Chen, H.-H.; Chang, Y.-C.; Yang, M.-Y.; Lo, C.-M.; Ko, W.-C.; Lee, Y.-F.; Liu, K.-L.; Chang, R.-F. Computer-aided diagnosis of liver tumors on computed tomography images. Comput. Methods Programs Biomed. 2017, 145, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Ben-Cohen, A.; Klang, E.; Kerpel, A.; Konen, E.; Amitai, M.M.; Greenspan, H. Fully convolutional network and sparsity-based dictionary learning for liver lesion detection in CT examinations. Neurocomputing 2018, 275, 1585–1594. [Google Scholar] [CrossRef]
- Arribas, J.I.; Calhoun, V.D.; Adali, T. Automatic Bayesian Classification of Healthy Controls, Bipolar Disorder, and Schizophrenia Using Intrinsic Connectivity Maps From fMRI Data. IEEE Trans. Biomed. Eng. 2010, 57, 2850–2860. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; He, J.; Man, Y.; Arribas, J. Neural network fusion strategies for identifying breast masses. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004. [Google Scholar]
- Santos-Mayo, L.; San-Jose-Revuelta, L.M.; Arribas, J.I. A Computer-Aided Diagnosis System With EEG Based on the P3b Wave During an Auditory Odd-Ball Task in Schizophrenia. IEEE Trans. Biomed. Eng. 2017, 64, 395–407. [Google Scholar] [CrossRef]
- Wolfers, T.; Buitelaar, J.K.; Beckmann, C.F.; Franke, B.; Marquand, A.F. From estimating activation locality to predicting disorder: A review of pattern recognition for neuroimaging-based psychiatric diagnostics. Neurosci. Biobehav. Rev. 2015, 57, 328–349. [Google Scholar] [CrossRef]
- Sayed, G.I.; Hassanien, A.E.; Schaefer, G. An Automated Computer-aided Diagnosis System for Abdominal CT Liver Images. Procedia Comput. Sci. 2016, 90, 68–73. [Google Scholar] [CrossRef]
- Chen, Y.; Yue, X.; Fujita, H.; Fu, S. Three-way decision support for diagnosis on focal liver lesions. Knowl.-Based Syst. 2017, 127, 85–99. [Google Scholar] [CrossRef]
- Gunasundari, S.; Janakiraman, S.; Meenambal, S. Multiswarm heterogeneous binary PSO using win-win approach for improved feature selection in liver and kidney disease diagnosis. Comput. Med Imaging Graph. 2018, 70, 135–154. [Google Scholar] [CrossRef]
- Kumar, S.; Moni, R.; Rajeesh, J. An automatic computer-aided diagnosis system for liver tumours on computed tomography images. Comput. Electr. Eng. 2013, 39, 1516–1526. [Google Scholar] [CrossRef]
- Jiang, H.; Zheng, R.; Yi, D.; Zhao, D. A Novel Multiinstance Learning Approach for Liver Cancer Recognition on Abdominal CT Images Based on CPSO-SVM and IO. Comput. Math. Methods Med. 2013, 2013, 434969. [Google Scholar] [CrossRef] [PubMed]
- Ting, F.F.; Tan, Y.J.; Sim, K.S. Convolutional neural network improvement for breast cancer classification. Expert Syst. Appl. 2019, 120, 103–115. [Google Scholar] [CrossRef]
- Das, A.; Acharya, U.R.; Panda, S.S.; Sabut, S. Deep learning based liver cancer detection using watershed transform and Gaussian mixture model techniques. Cogn. Syst. Res. 2019, 54, 165–175. [Google Scholar] [CrossRef]
- Fu, Y.; Aldrich, C. Flotation froth image recognition with convolutional neural networks. Miner. Eng. 2019, 132, 183–190. [Google Scholar] [CrossRef]
- Traore, B.B.; Kamsu-Foguem, B.; Tangara, F. Deep convolution neural network for image recognition. Ecol. Inform. 2018, 48, 257–268. [Google Scholar] [CrossRef]
- Fang, L.; Jin, Y.; Huang, L.; Guo, S.; Zhao, G.; Chen, X. Iterative fusion convolutional neural networks for classification of optical coherence tomography images. J. Vis. Commun. Image Represent. 2019, 59, 327–333. [Google Scholar] [CrossRef]
- Ferreira, M.V.D.S.; Filho, A.O.D.C.; Sousa, A.D.D.; Silva, A.C.; Gattass, M. Convolutional neural network and texture descriptor-based automatic detection and diagnosis of glaucoma. Expert Syst. Appl. 2018, 110, 250–263. [Google Scholar] [CrossRef]
- Nanda, N.; Kakkar, P.; Nagpal, S. Computer-Aided Segmentation of Liver Lesions in CT Scans Using Cascaded Convolutional Neural Networks and Genetically Optimised Classifier. Arab. J. Sci. Eng. 2019, 44, 4049–4062. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Anaraki, A.K.; Ayati, M.; Kazemi, F. Magnetic resonance imaging-based brain tumor grades classification and grading via convolutional neural networks and genetic algorithms. Biocybern. Biomed. Eng. 2019, 39, 63–74. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Yang, F.; Yu, D.; Dong, D.; Yang, C.; Zang, Y.; Tian, J. Multi-crop Convolutional Neural Networks for lung nodule malignancy suspiciousness classification. Pattern Recognit. 2017, 61, 663–673. [Google Scholar] [CrossRef]
- Ghoniem, R.M.; Shaalan, K. FCSR—Fuzzy Continuous Speech Recognition Approach for Identifying Laryngeal Pathologies Using New Weighted Spectrum Features. In Advances in Intelligent Systems and Computing, Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2017, Cairo, Egypt, 9–11 September 2017; Springer: Cham, Germany, 2017; pp. 384–395. [Google Scholar]
- Bansal, J.C.; Gopal, A.; Nagar, A.K. Stability analysis of Artificial Bee Colony optimization algorithm. Swarm Evol. Comput. 2018, 41, 9–19. [Google Scholar] [CrossRef]
- Maione, G.; Punzi, A.; Li, K. A comparative study on differential evolution with other heuristic methods for continuous optimization. In Proceedings of the 21st Mediterranean Conference on Control and Automation, Chania, Greece, 25–28 June 2013. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mostafa, A.; Houssein, E.H.; Houseni, M.; Hassanien, A.E.; Hefny, H. Evaluating Swarm Optimization Algorithms for Segmentation of Liver Images. In Advances in Soft Computing and Machine Learning in Image Processing Studies in Computational Intelligence; Springer: Cham, Germany, 2017; pp. 41–62. [Google Scholar]
- Decerle, J.; Grunder, O.; Hassani, A.H.E.; Barakat, O. A hybrid memetic-ant colony optimization algorithm for the home health care problem with time window, synchronization and working time balancing. Swarm Evol. Comput. 2019, 46, 171–183. [Google Scholar] [CrossRef]
- Garro, B.A.; Rodríguez, K.; Vázquez, R.A. Classification of DNA microarrays using artificial neural networks and ABC algorithm. Appl. Soft Comput. 2016, 38, 548–560. [Google Scholar] [CrossRef]
- Qi, A.-L.; Zhang, G.-M.; Dong, M.; Ma, H.-W.; Harvey, D.M. An artificial bee colony optimization based matching pursuit approach for ultrasonic echo estimation. Ultrasonics 2018, 88, 1–8. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Chung, H.; Shin, K.-S. Genetic algorithm-optimized multi-channel convolutional neural network for stock market prediction. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Lee, W.-Y.; Park, S.-M.; Sim, K.-B. Optimal hyperparameter tuning of convolutional neural networks based on the parameter-setting-free harmony search algorithm. Optik 2018, 172, 359–367. [Google Scholar] [CrossRef]
- Song, Y.; Cai, W.; Zhou, Y.; Feng, D.D. Feature-Based Image Patch Approximation for Lung Tissue Classification. IEEE Trans. Med Imaging 2013, 32, 797–808. [Google Scholar] [CrossRef] [PubMed]
- Nugroho, H.A.; Frannita, E.L.; Ardiyanto, I.; Choridah, L. Computer aided diagnosis for thyroid cancer system based on internal and external characteristics. J. King Saud Univ. Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Bian, C.; Lee, R.; Chou, Y.-H.; Cheng, J.-Z. Boundary Regularized Convolutional Neural Network for Layer Parsing of Breast Anatomy in Automated Whole Breast Ultrasound. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2017, Quebec City, QC, Canada, 11–13 September 2017; pp. 259–266. [Google Scholar]
- Azizi, S.; Imani, F.; Zhuang, B.; Tahmasebi, A.; Kwak, J.T.; Xu, S.; Uniyal, N.; Turkbey, B.; Choyke, P.; Pinto, P.; et al. Ultrasound-Based Detection of Prostate Cancer Using Automatic Feature Selection with Deep Belief Networks. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer: Cham, Germany; pp. 70–77.
- Pereira, F.; Bueno, A.; Rodriguez, A.; Perrin, D.; Marx, G.; Cardinale, M.; Salgo, I.; Nido, P.D. Automated detection of coarctation of aorta in neonates from two-dimensional echocardiograms. J. Med. Imaging 2017, 4, 014502. [Google Scholar] [CrossRef] [PubMed]
- Lekadir, K.; Galimzianova, A.; Betriu, A.; Vila, M.D.M.; Igual, L.; Rubin, D.L.; Fernandez, E.; Radeva, P.; Napel, S. A Convolutional Neural Network for Automatic Characterization of Plaque Composition in Carotid Ultrasound. IEEE J. Biomed. Health Inform. 2017, 21, 48–55. [Google Scholar] [CrossRef]
- Ma, J.; Wu, F.; Jiang, T.; Zhu, J.; Kong, D. Cascade convolutional neural networks for automatic detection of thyroid nodules in ultrasound images. Med. Phys. 2017, 44, 1678–1691. [Google Scholar] [CrossRef]
- Smistad, E.; Løvstakken, L. Vessel Detection in Ultrasound Images Using Deep Convolutional Neural Networks. In Deep Learning and Data Labeling for Medical Applications Lecture Notes in Computer Science; Springer: Cham, Germany, 2016; pp. 30–38. [Google Scholar]
- Yaqub, M.; Kelly, B.; Papageorghiou, A.T.; Noble, J.A. A Deep Learning Solution for Automatic Fetal Neurosonographic Diagnostic Plane Verification Using Clinical Standard Constraints. Ultrasound Med. Biol. 2017, 43, 2925–2933. [Google Scholar] [CrossRef]
- Zhang, Y.; Ying, M.T.C.; Yang, L.; Ahuja, A.T.; Chen, D.Z. Coarse-to-Fine Stacked Fully Convolutional Nets for lymph node segmentation in ultrasound images. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016. [Google Scholar]
- Hetherington, J.; Lessoway, V.; Gunka, V.; Abolmaesumi, P.; Rohling, R. SLIDE: Automatic spine level identification system using a deep convolutional neural network. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1189–1198. [Google Scholar] [CrossRef]
- Hareendranathan, A.R.; Zonoobi, D.; Mabee, M.; Cobzas, D.; Punithakumar, K.; Noga, M.; Jaremko, J.L. Toward automatic diagnosis of hip dysplasia from 2D ultrasound. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017. [Google Scholar]
- Burlina, P.; Billings, S.; Joshi, N.; Albayda, J. Automated diagnosis of myositis from muscle ultrasound: Exploring the use of machine learning and deep learning methods. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Xu, K.; Roussel, P.; Csapó, T.G.; Denby, B. Convolutional neural network-based automatic classification of midsagittal tongue gestural targets using B-mode ultrasound images. J. Acoust. Soc. Am. 2017, 141, EL531–EL537. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiang, Z.; Xie, F.; Zhang, H.; Ma, Y.; Shi, H.; Zhao, Y. Feature extraction from histopathological images based on nucleus-guided convolutional neural network for breast lesion classification. Pattern Recognit. 2017, 71, 14–25. [Google Scholar] [CrossRef]
- Xie, H.; Yang, D.; Sun, N.; Chen, Z.; Zhang, Y. Automated pulmonary nodule detection in CT images using deep convolutional neural networks. Pattern Recognit. 2019, 85, 109–119. [Google Scholar] [CrossRef]
- Wu, K.; Chen, X.; Ding, M. Deep learning based classification of focal liver lesions with contrast-enhanced ultrasound. Optik 2014, 125, 4057–4063. [Google Scholar] [CrossRef]
- Takao, S.; Kondo, S.; Ueno, J.; Kondo, T. Deep multi-layered GMDH-type neural network using revised heuristic self-organization and its application to medical image diagnosis of liver cancer. Artif. Life Robot. 2017, 23, 48–59. [Google Scholar] [CrossRef]
- Romero, F.P.; Diler, A.; Bisson-Gregoire, G.; Turcotte, S.; Lapointe, R.; Vandenbroucke-Menu, F.; Tang, A.; Kadoury, S. End-To-End Discriminative Deep Network For Liver Lesion Classification. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019. [Google Scholar]
- Chitradevi, D.; Prabha, S. Analysis of brain sub regions using optimization techniques and deep learning method in Alzheimer disease. Appl. Soft Comput. 2019, 86, 105857. [Google Scholar] [CrossRef]
- Agarwalla, P.; Mukhopadhyay, S. Bi-stage hierarchical selection of pathway genes for cancer progression using a swarm based computational approach. Appl. Soft Comput. 2018, 62, 230–250. [Google Scholar] [CrossRef]
- Motieghader, H.; Najafi, A.; Sadeghi, B.; Masoudi-Nejad, A. A hybrid gene selection algorithm for microarray cancer classification using genetic algorithm and learning automata. Inform. Med. Unlocked 2017, 9, 246–254. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Emary, E.; Zawbaa, H.M. Retinal blood vessel localization approach based on bee colony swarm optimization, fuzzy c-means and pattern search. J. Vis. Commun. Image Represent. 2015, 31, 186–196. [Google Scholar] [CrossRef]
- Prasartvit, T.; Banharnsakun, A.; Kaewkamnerdpong, B.; Achalakul, T. Reducing bioinformatics data dimension with ABC-kNN. Neurocomputing 2013, 116, 367–381. [Google Scholar] [CrossRef]
- Beloufa, F.; Chikh, M. Design of fuzzy classifier for diabetes disease using Modified Artificial Bee Colony algorithm. Comput. Methods Programs Biomed. 2013, 112, 92–103. [Google Scholar] [CrossRef]
- Kakkar, P.; Nagpal, S.; Nanda, N. Automatic Liver Segmentation in CT Images Using Improvised Techniques. In Proceedings of the Smart Health Lecture Notes in Computer Science, Shenzhen, China, 1–2 July 2018; pp. 41–52. [Google Scholar]
- Anter, A.M.; Hassenian, A.E. CT liver tumor segmentation hybrid approach using neutrosophic sets, fast fuzzy c-means and adaptive watershed algorithm. Artif. Intell. Med. 2019, 97, 105–117. [Google Scholar] [CrossRef]
- Ghoniem, R.M.; Algarni, A.D.; Shaalan, K. Multi-Modal Emotion Aware System Based on Fusion of Speech and Brain Information. Information 2019, 10, 239. [Google Scholar] [CrossRef]
- Ghoniem, R.M.; Alhelwa, N.; Shaalan, K. A Novel Hybrid Genetic-Whale Optimization Model for Ontology Learning from Arabic Text. Algorithms 2019, 12, 182. [Google Scholar] [CrossRef]
- Ghoniem, R.M. Deep Genetic Algorithm-Based Voice Pathology Diagnostic System. In Lecture Notes in Computer Science; Proceedings of the Natural Language Processing and Information Systems, Salford, UK, 26–28 June 2019; Springer: Cham, Germany, 2019; pp. 220–233. [Google Scholar]
- Ronneberger, O. Invited Talk: U-Net Convolutional Networks for Biomedical Image Segmentation. In Informatik aktuell Bildverarbeitung für die Medizin 2017; Springer: Berlin/Heidelberg, Germany, 2017; p. 3. [Google Scholar]
- Lee, W.-Y.; Ko, K.-E.; Geem, Z.-W.; Sim, K.-B. Method that determining the Hyperparameter of CNN using HS algorithm. J. Korean Inst. Intell. Syst. 2017, 27, 22–28. [Google Scholar] [CrossRef]
- Ozcan, T.; Basturk, A. Transfer learning-based convolutional neural networks with heuristic optimization for hand gesture recognition. Neural Comput. Appl. 2019, 31, 8955–8970. [Google Scholar] [CrossRef]
- Li, J.; Wu, Y.; Shen, N.; Zhang, J.; Chen, E.; Sun, J.; Deng, Z.; Zhang, Y. A fully automatic computer-aided diagnosis system for hepatocellular carcinoma using convolutional neural networks. Biocybern. Biomed. Eng. 2019. [Google Scholar] [CrossRef]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing 2018, 321, 321–331. [Google Scholar] [CrossRef]
- Anter, A.M.; Ali, M. Feature selection strategy based on hybrid crow search optimization algorithm integrated with chaos theory and fuzzy c-means algorithm for medical diagnosis problems. Soft Comput. 2019. [Google Scholar] [CrossRef]
- Doğantekin, A.; Özyurt, F.; Avcı, E.; Koç, M. A novel approach for liver image classification: PH-C-ELM. Measurement 2019, 137, 332–338. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).