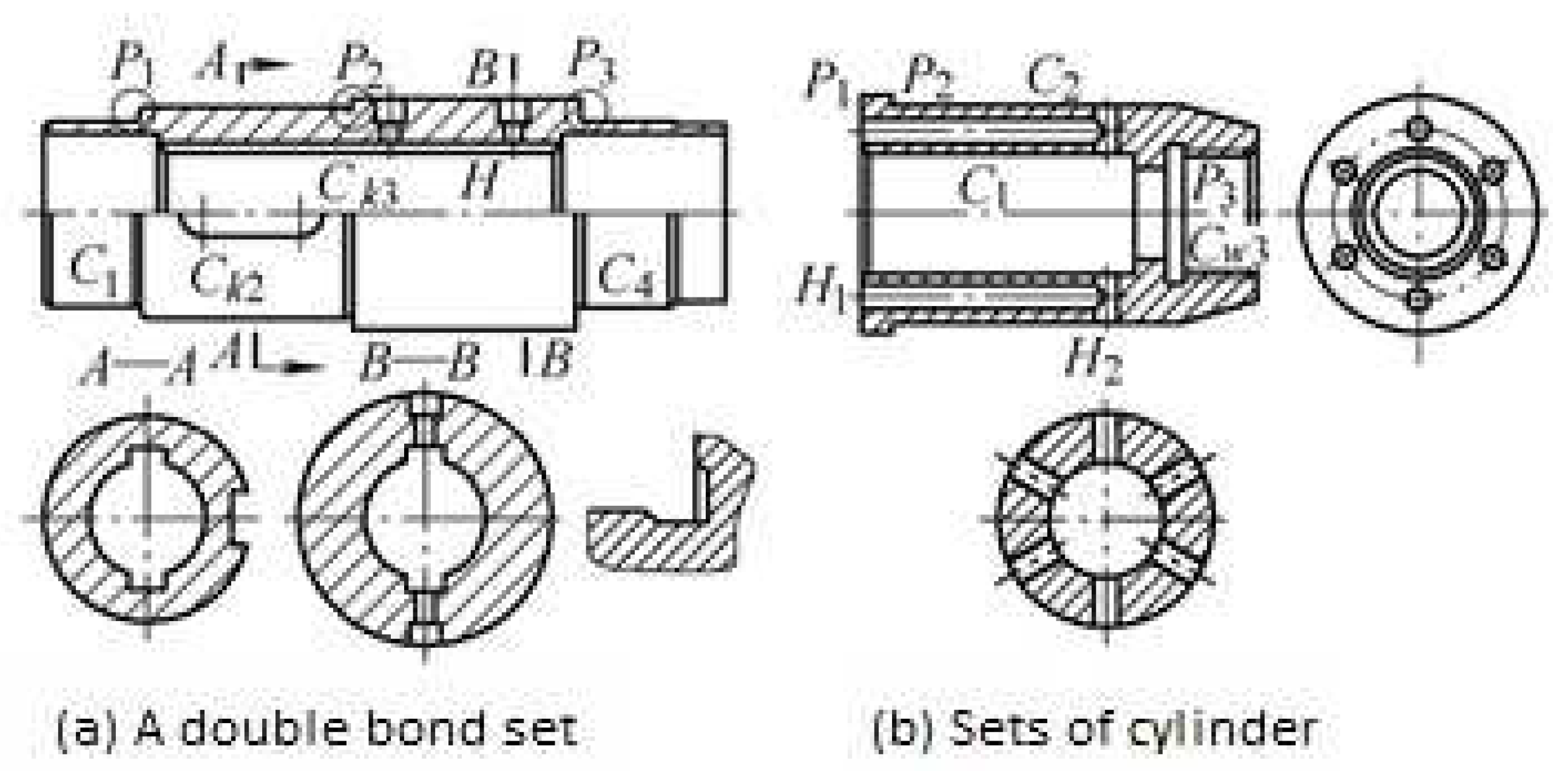
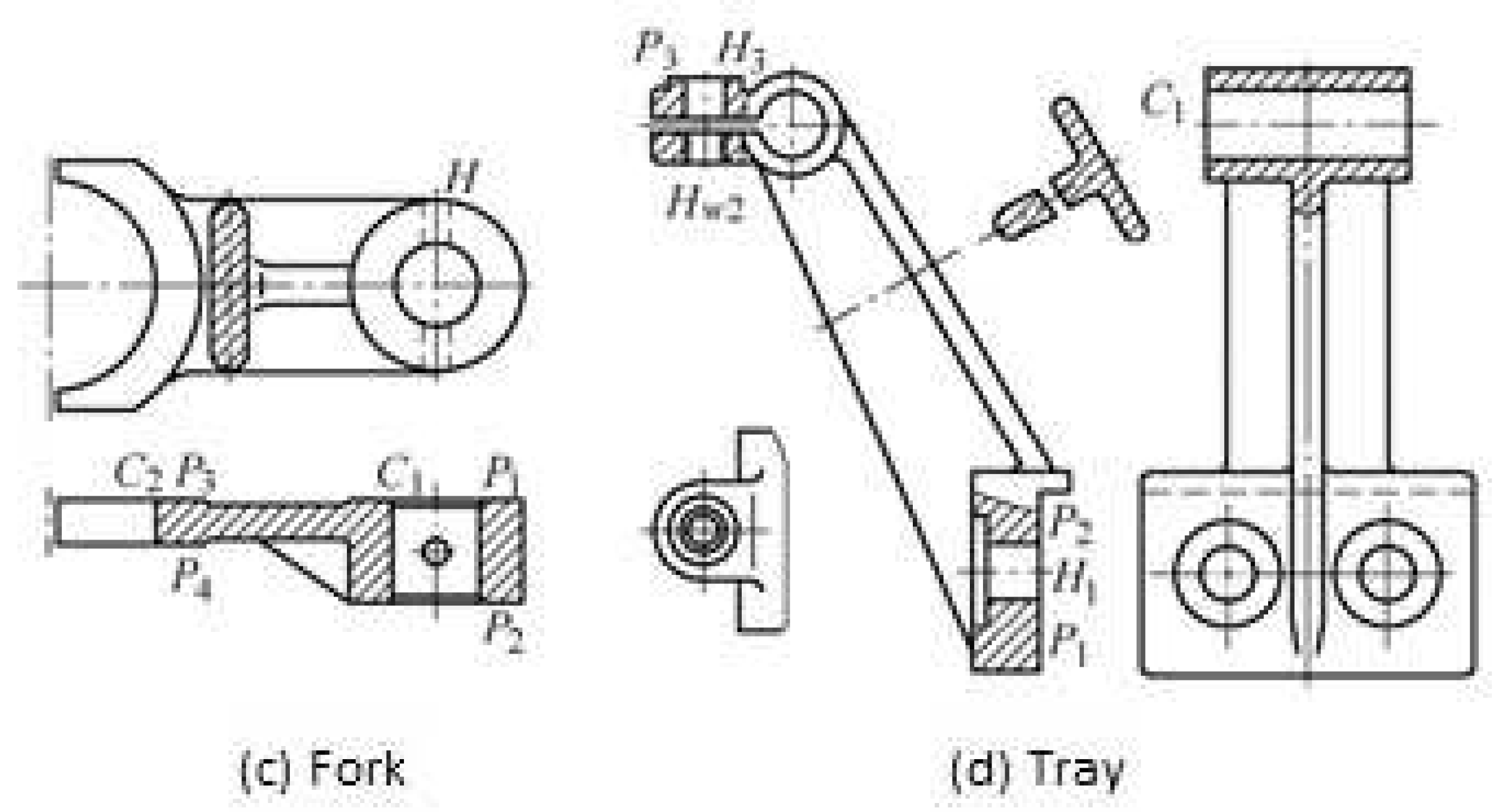
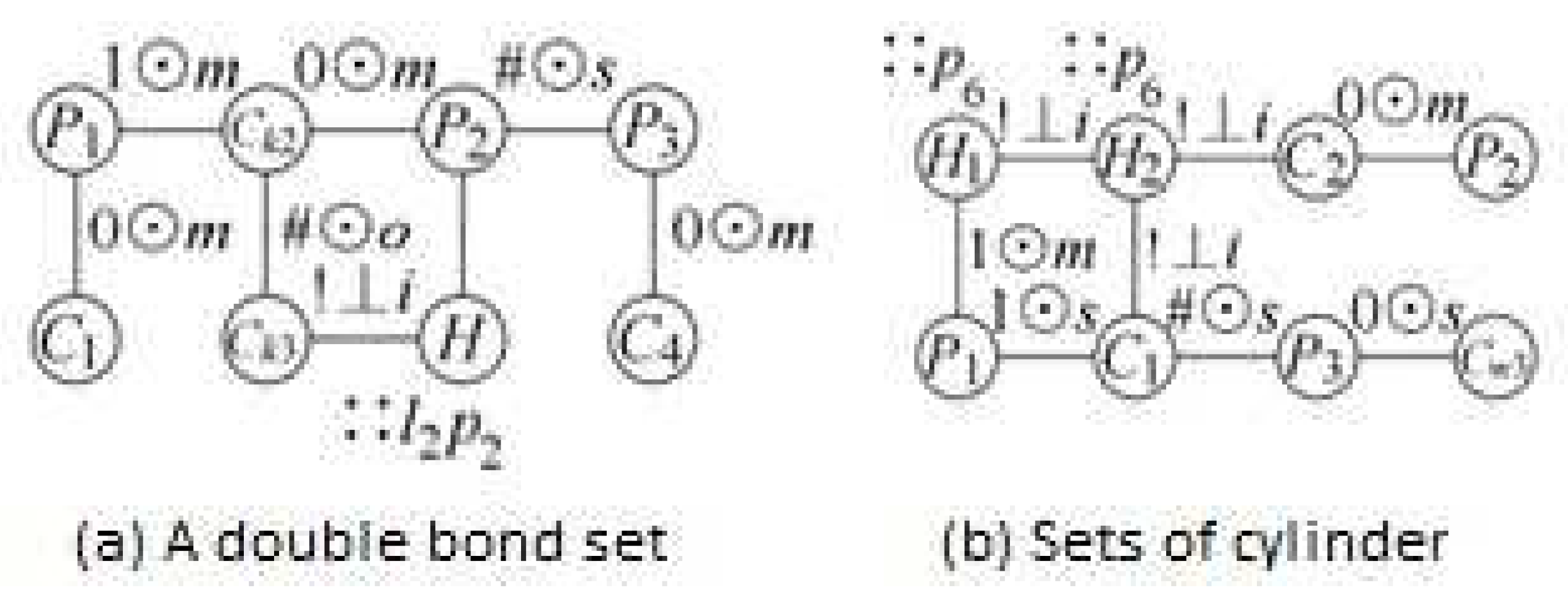
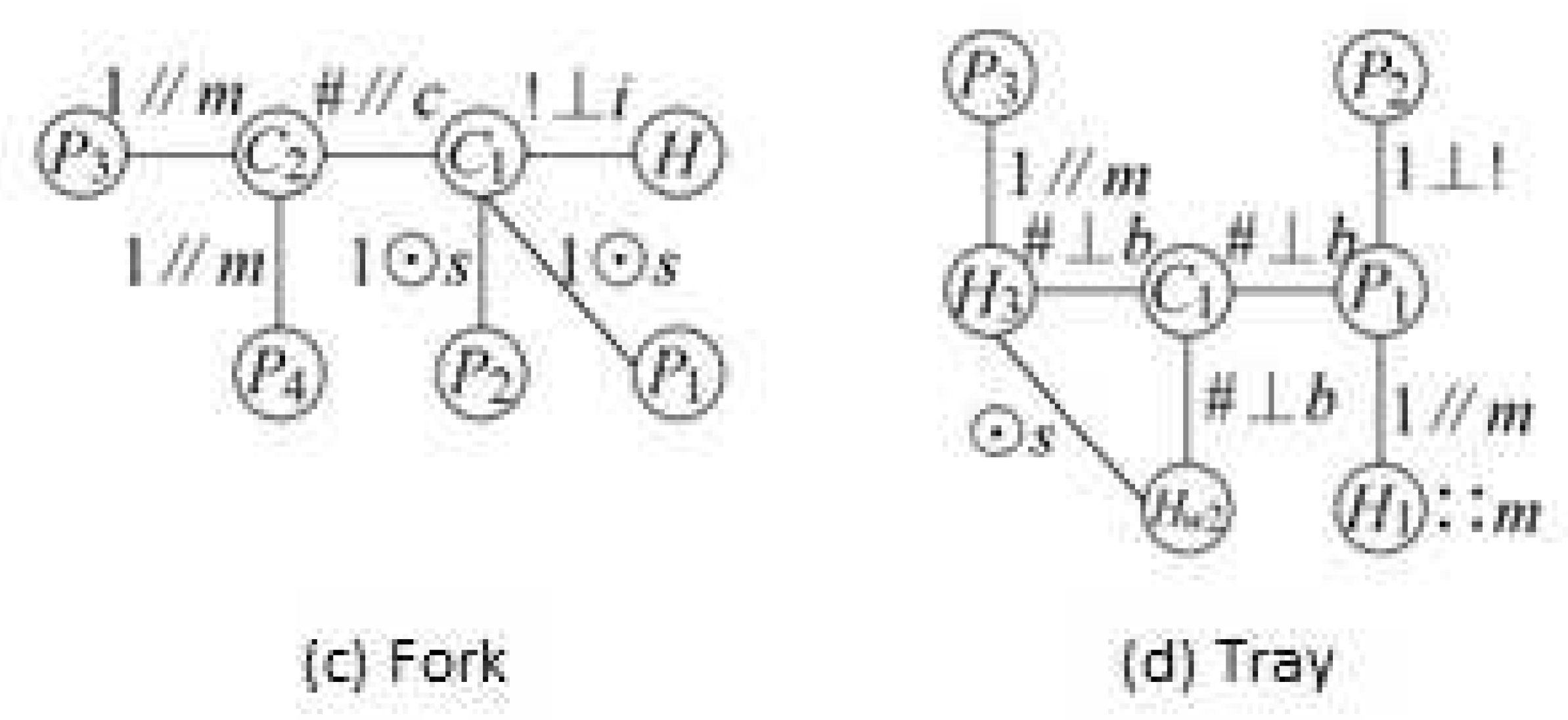
3.2. Weighted Concept Lattice Based on Decision Formal Context
Due to space limitations, we assume that readers are familiar with the basic concepts of formal concept analysis [
8].
A formal context can be depicted visually in a tabular form with crosses (or 1) representing the pairs
. For example, consider the cross table in
Table 3.
The cross table in
Table 3 depicts a formal context in which object 1 has attributes
a and
c, object 2 has attribute
a, etc.
Let be a formal context. A set pair of , is a formal concept if and only and , where are common attributes set of all the objects in X and common objects set of all attributes in B, respectively. The set of all formal concepts in is expressed as . Partial order ⪯ of super-concept and sub-concept in constitutes the concept lattice of .
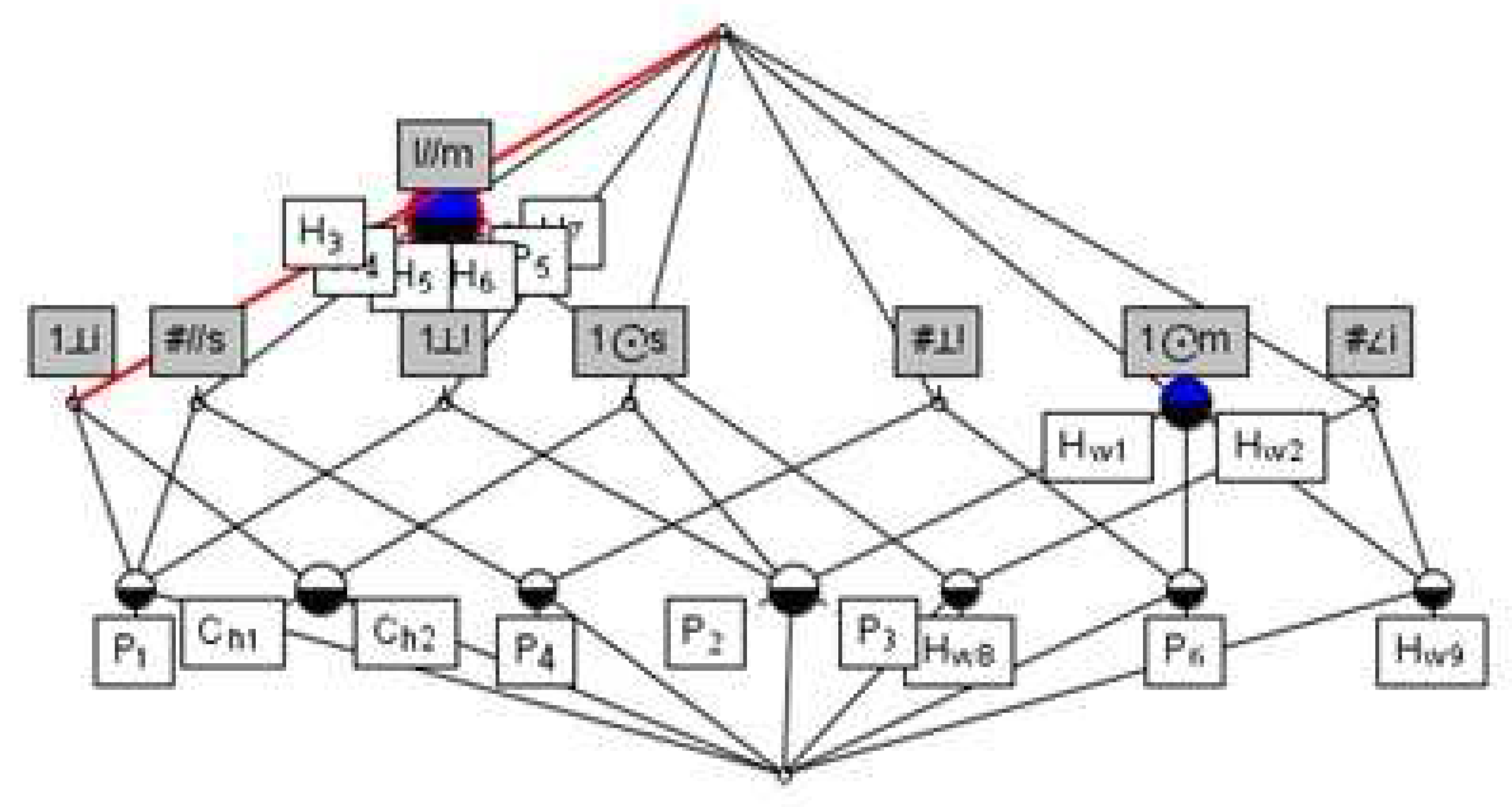
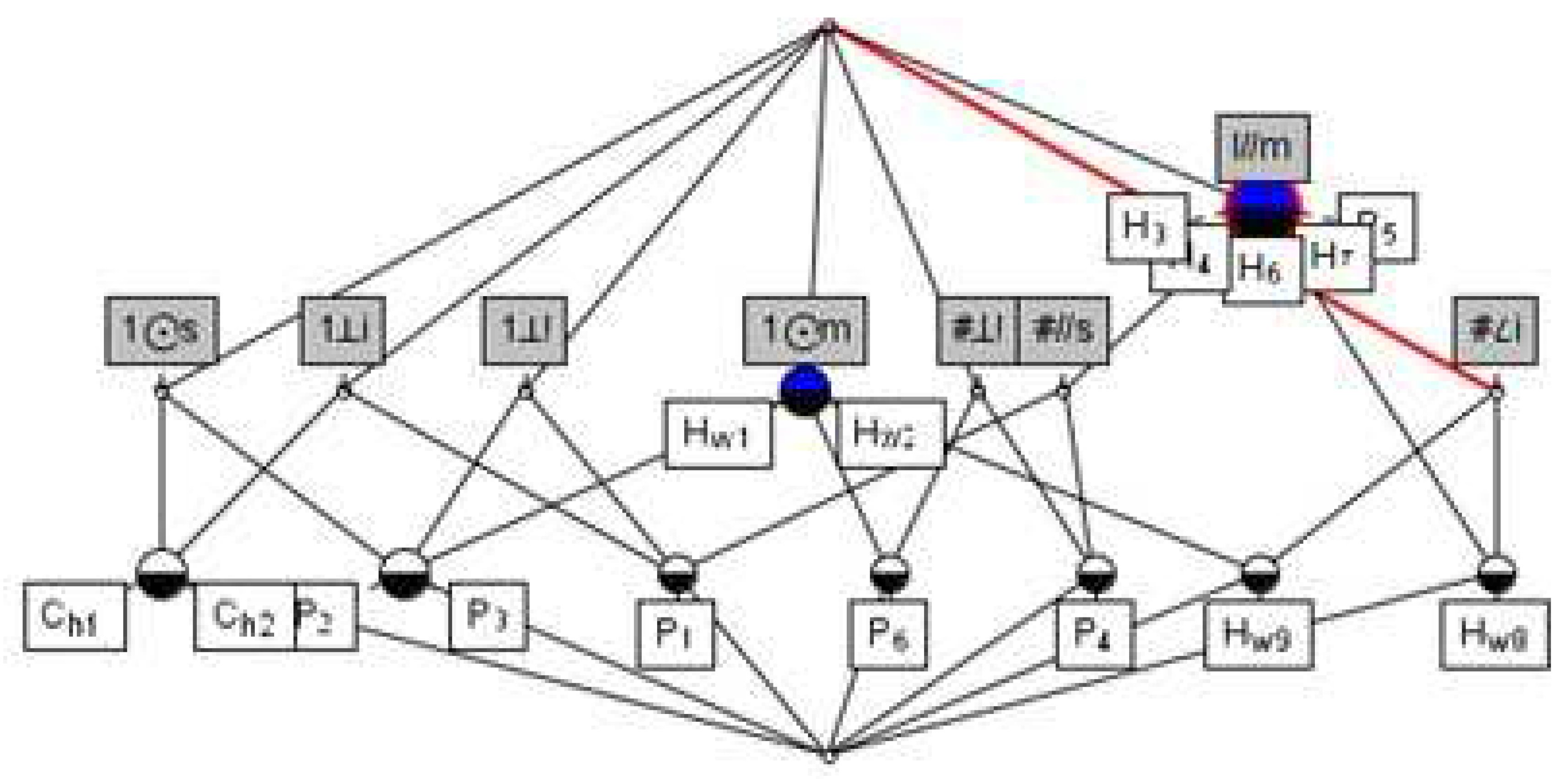
Figure 7 is the formal concept lattice of the formal context shown in
Table 2.
The formal context is the basis of formal concept analysis. Its main objective is to form concepts and concept lattice: The concept is unity of the extension and intension. In essence, the concept lattice describes the link between objects and attributes, indicating generalization relations between concepts, The corresponding Hasse diagram is achieved for data visualization. The traditional concept lattice is based on a simple binary context. In practical application, the data are large and complex. Thus, we must extend it. Belohlávek et al. studied the concept lattice in fuzzy and uncertain data [
26,
27]. The critical part of concept lattice (called core concepts or important concepts) is an important part of the parts structure. As a user is usually interested in some certain attribute characteristics, according to his/her preference and requirement, the researchers establish a new concept lattice structure with the weight
to identify importance of intentions: weighted concept lattice [
10].
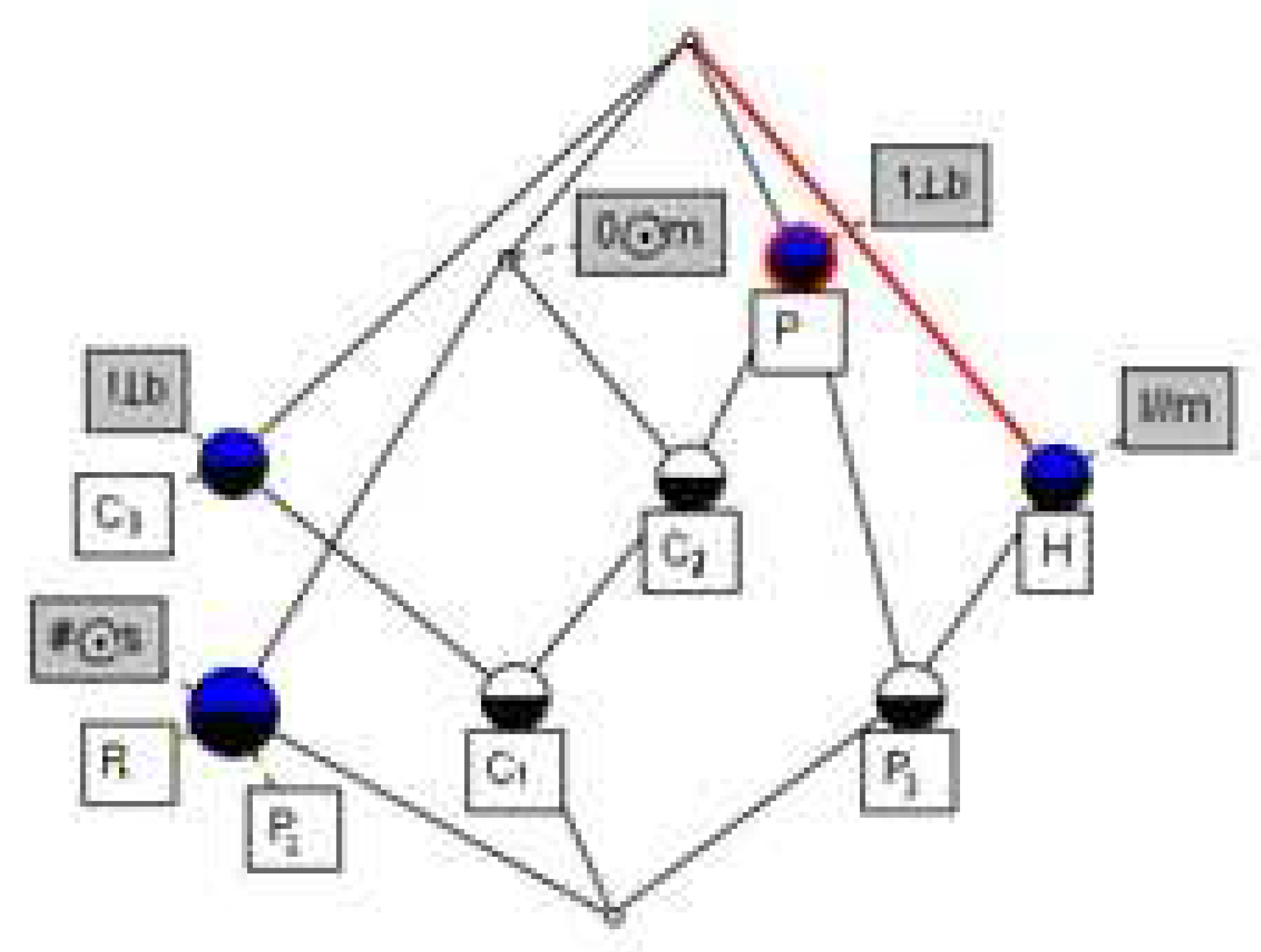
Example 1. Table 4 is a formal context. Its object set U, attribute set A, and I describe the value set of attribute in A that U has. Table 5 is the weight table of a single attribute intent. (,0.6) and (,0.6) are the weighted formal concept formed by the above formal context and single attribute intent weight table. All such formal concepts constitute the weighted concept lattice.
Let be a formal context and a set of attributes is denoted by . are the weights of attributes, where denotes the importance of the attribute . is known as a weighted formal concept on ) if is a formal concept and is the weight of the attribute set . A and B are the extent, the intent of weighted formal concepts, respectively. Its super-concept and sub-concept are the same as the general concept lattice.
Given a value , we can obtain a part of the formal concept , can be seen as a set of important formal concepts.
Definition 1. [28] Let be a formal context, . is called an attribute set x in B for is called an object set of attribute a for . Definition 2. [9] A decision formal context is defined as a quintuple , where and are two formal contexts in which their attribute sets are disjoint. A and D are called condition and decision attribute sets, respectively. Definition 3. In a decision formal context , if and and are called the indiscernibility relation determined by the condition and decision attribute, respectively), then is denoted as the equivalence class of object x on B. is the equivalence class of object x on D.
Definition 4. Let X be a subset of U, .
(1)The lower approximation of X with respect to B is the set of all objects, which can be for certain classified as X with respect to B and it is denoted by . That is, .
(2)The upper approximation of X with respect to B is the set of all objects, which can be possibly classified as X with respect to B and it is denoted by . That is, .
Definition 5. Let be a decision formal context. If , then we say is consistent.
Definition 6. In , the lower approximation on the condition attribute B of the decision attribute is . The positive domain of B at the decision-making objective is defined as indicates that there are r decision-making objectives.
Theorem 1. Let be consistent, .
Proof. If , then, for any , we have . Since is consistent, it follows that . Then, there exists such that .
If , then, for and , it is clear that . We have . Consequently, . □
Theorem 2. If be consistent, then a is a core(No-remove attributes).
Proof. It follows immediately from Theorem 1. □
Definition 7. For a decision formal context , let be a formal concept of F. The importance of the decision-making objective δ with ) is defined as follows: It is obvious that .
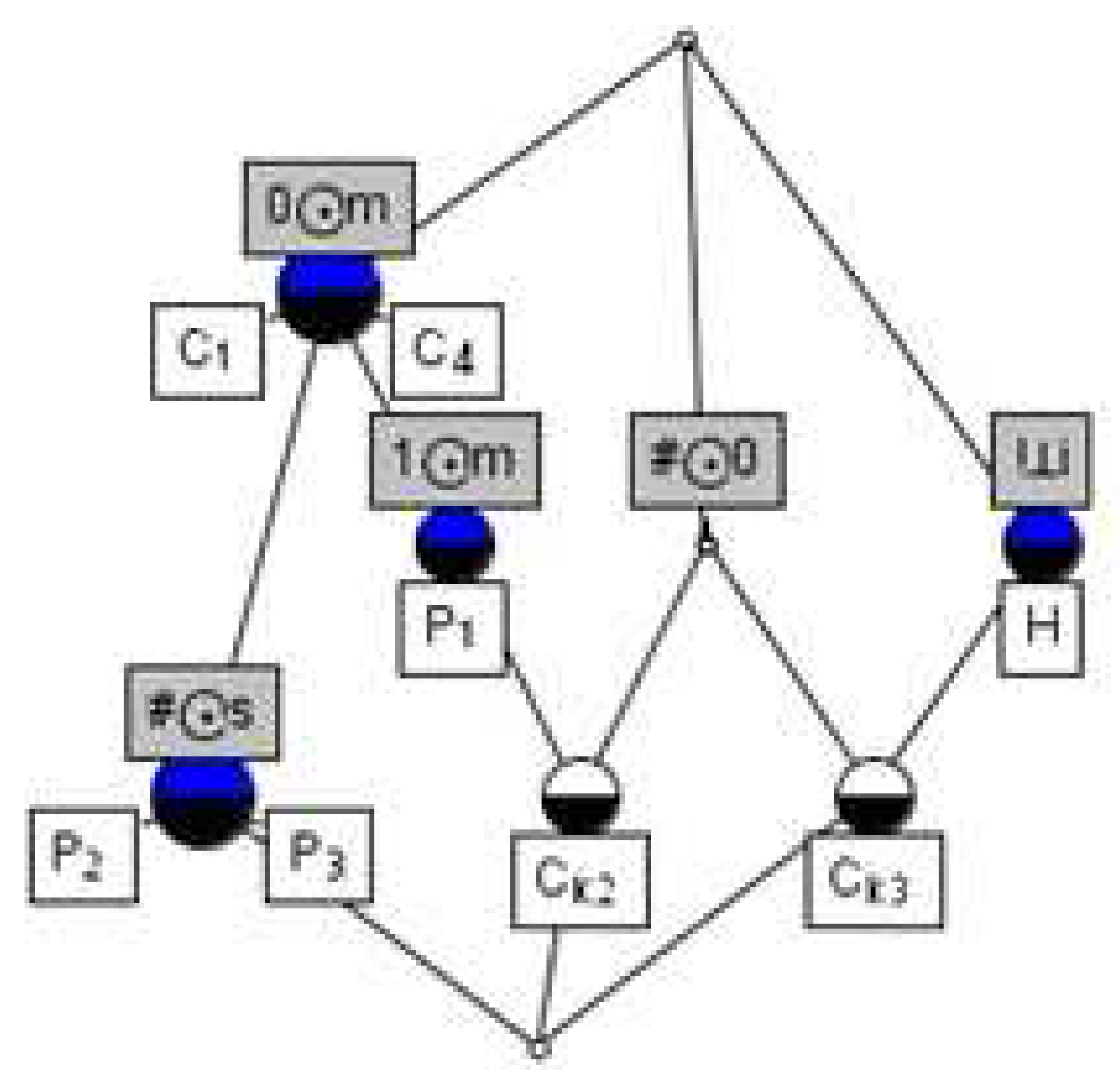
Example 2. A formal context of part as Table 6, and . Its formal concept lattice is shown as Figure 8. Computing the importance of concepts: .
In the decision formal context, cohesion of the equivalence classes determined by the condition attributes and decision attributes indicates that the condition attributes impact decision-making, namely the importance of attributes. Next, we will compare attributes of the concept to study the cohesion of the concept to objects (functional surfaces).
The similarity of attributes
and
can naturally be assessed by the similarity of their corresponding extents, i.e., similarity of
and
. That is, the similarity measure between attributes
and
is given by
In our experiments, we use the following functions for
on the decision formal context
:
, where is the lower approximation of in the decision attribute D. In particular,
(1) If and , then ;
(2) If , then . It produces a computing formula for the general formal context.
Note that is the number of objects that belong to both and classes divided by the number of all attributes that belong to or .
Definition 8. Cohesion for a formal concept on the decision formal context is defined as the following: Theorem 3. The satisfies:
(1) ;
(2) For a formal concept , if and , then .
(3) For a formal concept , if , and , then .
Proof. (1) Obviously, ; therefore, the conclusion holds.
(2) In fact, for , there exist only two cases , hence, .
(3) Since , it follows from Definition 8 that . Thus, . □
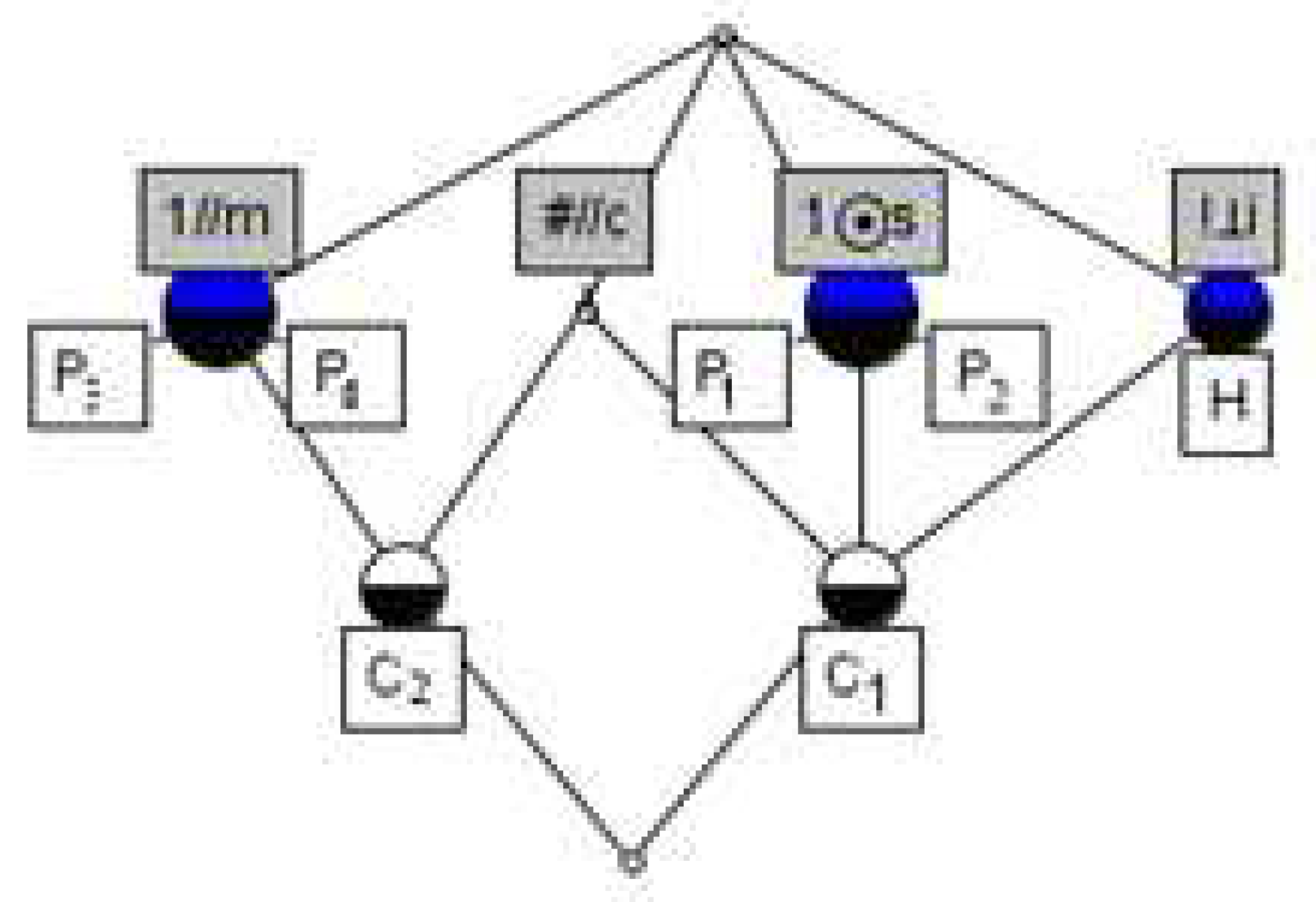
Example 3. Table 7 is a decision formal context, where is the object set, is the condition attribute set. is the decision attribute set. , , , . , , , , , , .
A simple approach to measure the cohesion
for a formal concept
is the following if
:
Definition 9. Let be a decision formal context. is a triple on . If is a formal concept, or is the weight of attribute set B and . is called the weighted concept of . The set consisting of all of these concepts is the weighted concept lattice of .
Its formal concept lattice is as
Figure 9. Here, the black is an important concept.