A Matrix Approach for Analyzing Signal Flow Graph
Abstract
1. Introduction
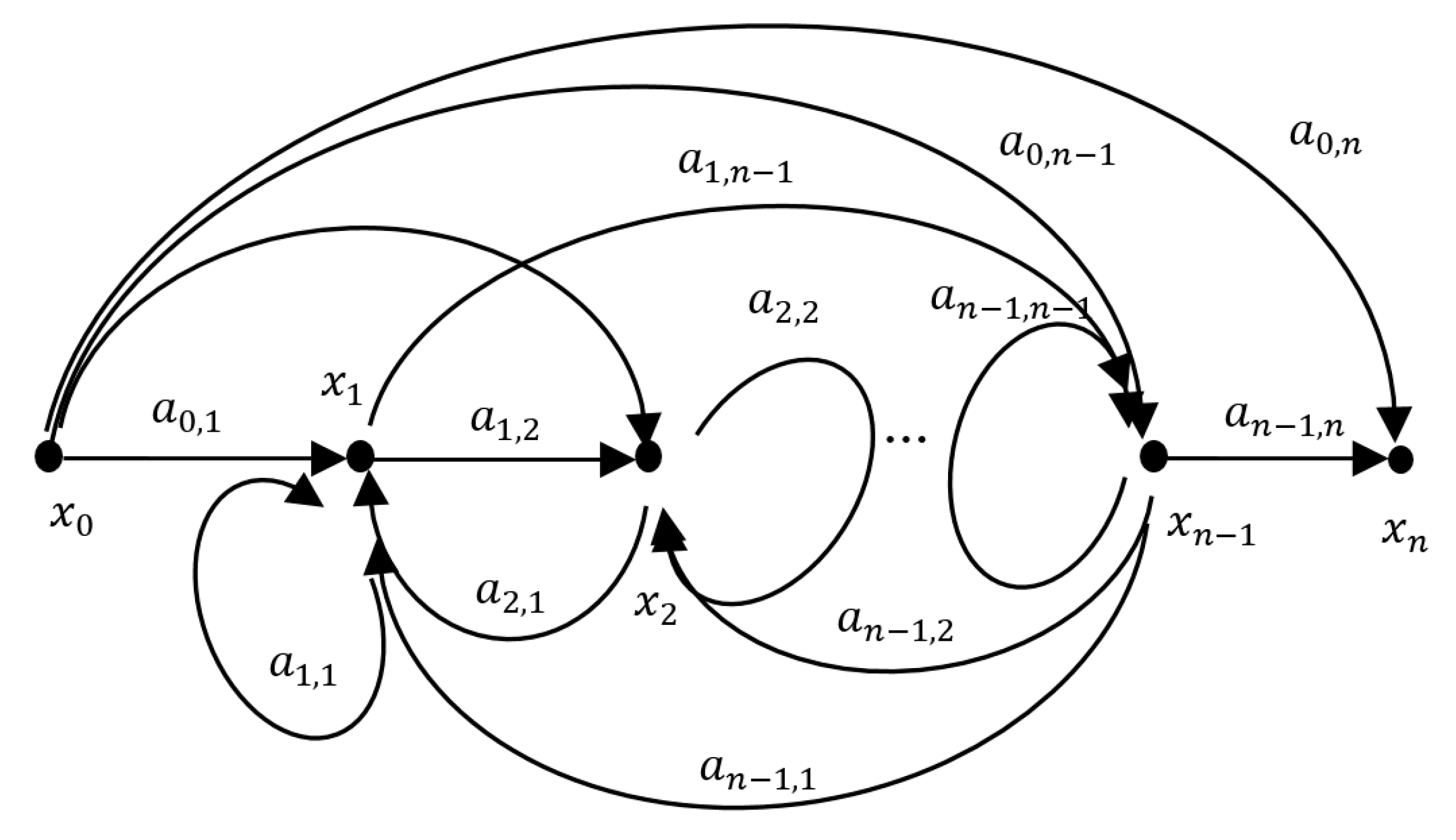
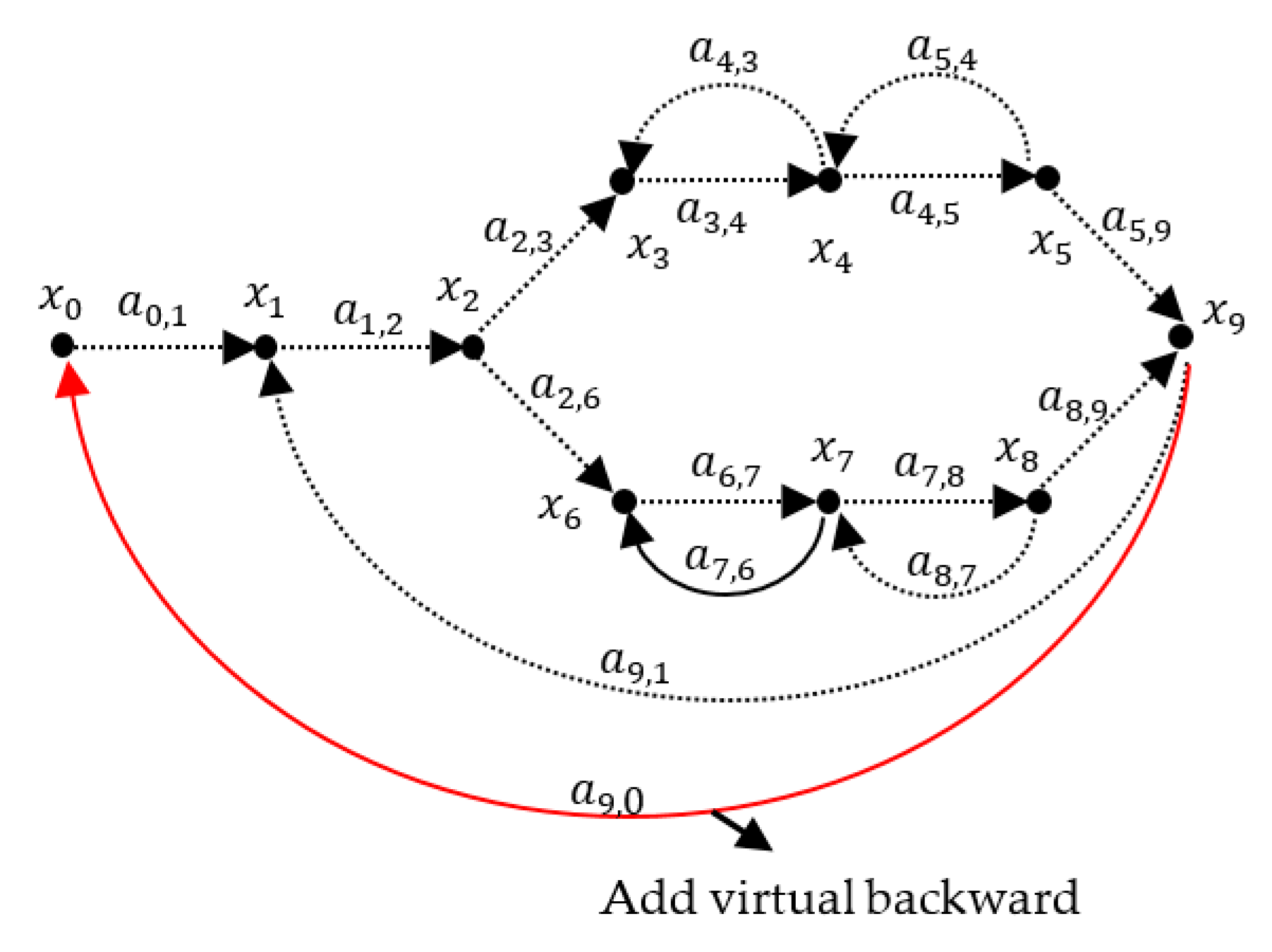
2. Transfer Matrix Method
3. Mason’s Gain Formula
- is the input-node variable
- is the output-node variable
- is the transfer function between and
- is the determinant of the graph
- is path gain of the kth forward path between and
- the cofactor value of Δ for the kth forward path, with the loops touching the kth forward path removed
- is loop gain of each closed loop in the system
- is product of the loop gains of any two non-touching loops
- is product of the loop gains of any three pairwise non-touching loops
| Algorithm 1. Transfer matrix method’s workflow |
| Pseudocode: |
| Requirement: |
| (1) transfer function with output node and input node |
| (2) loop group gain with nodes from to |
| Input: |
| adjacent metric |
| If Requirement == transfer function: |
| Input.append(0, j); |
| else if Requirement == loop group gain: |
| Input.append(i, k); |
| Output: required result |
| augmented matrix |
| If Requirement == Transfer function: |
| transfer function given in Equation (4) |
| return |
| If Requirement == loop group gain (given node:, and ) |
| forward path= given in Section 4 |
| loop group grain= |
| return |
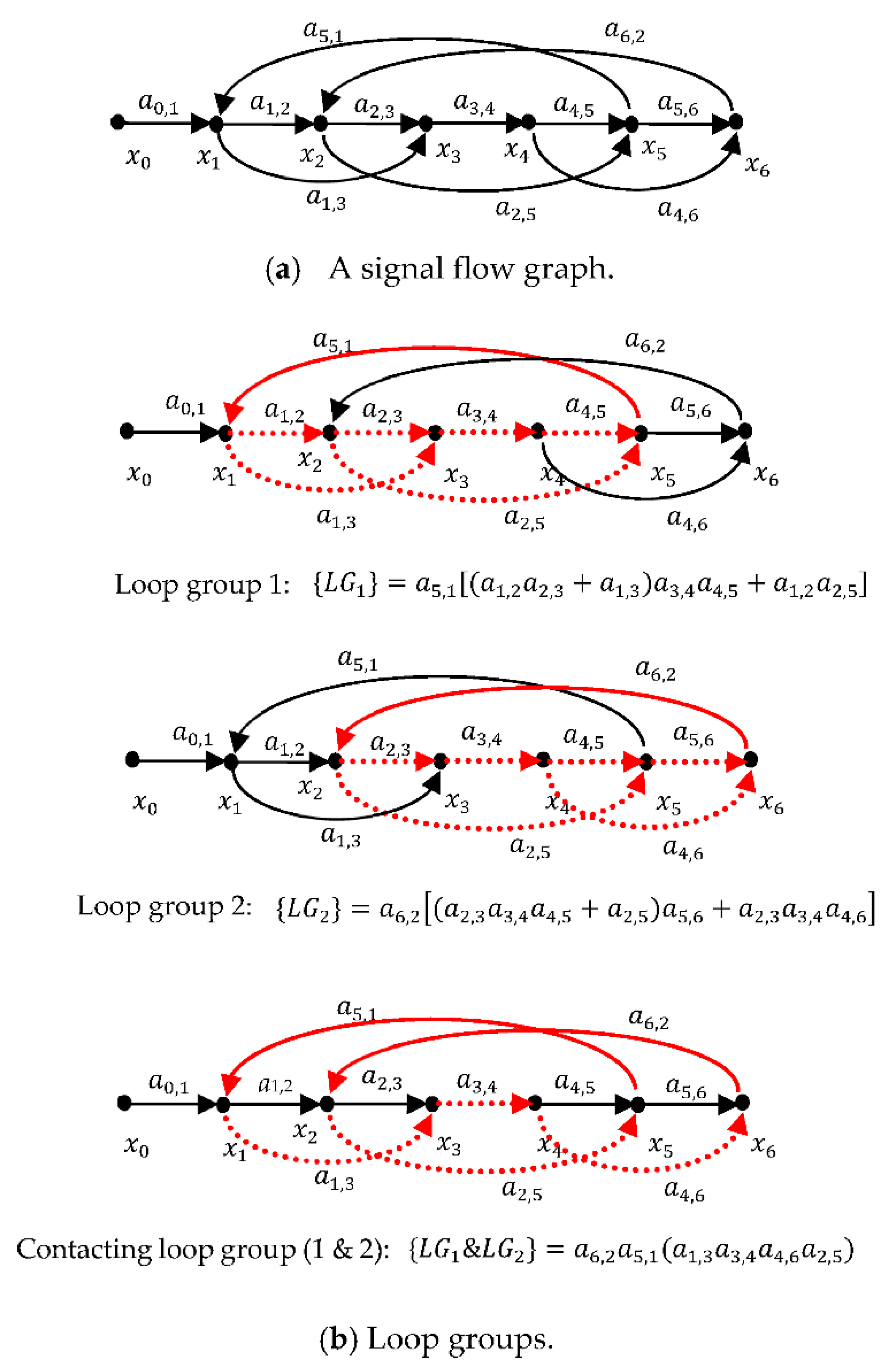
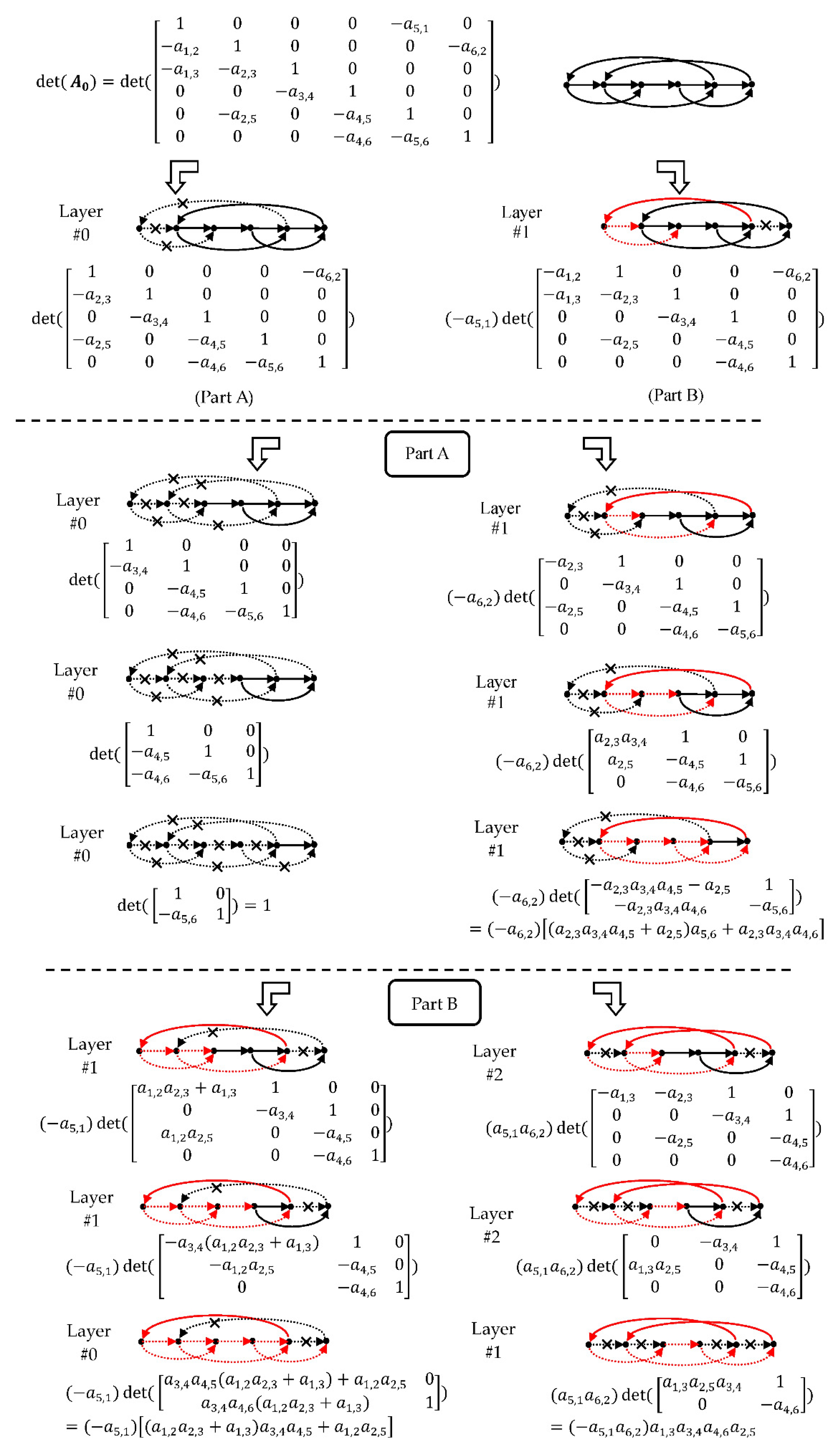
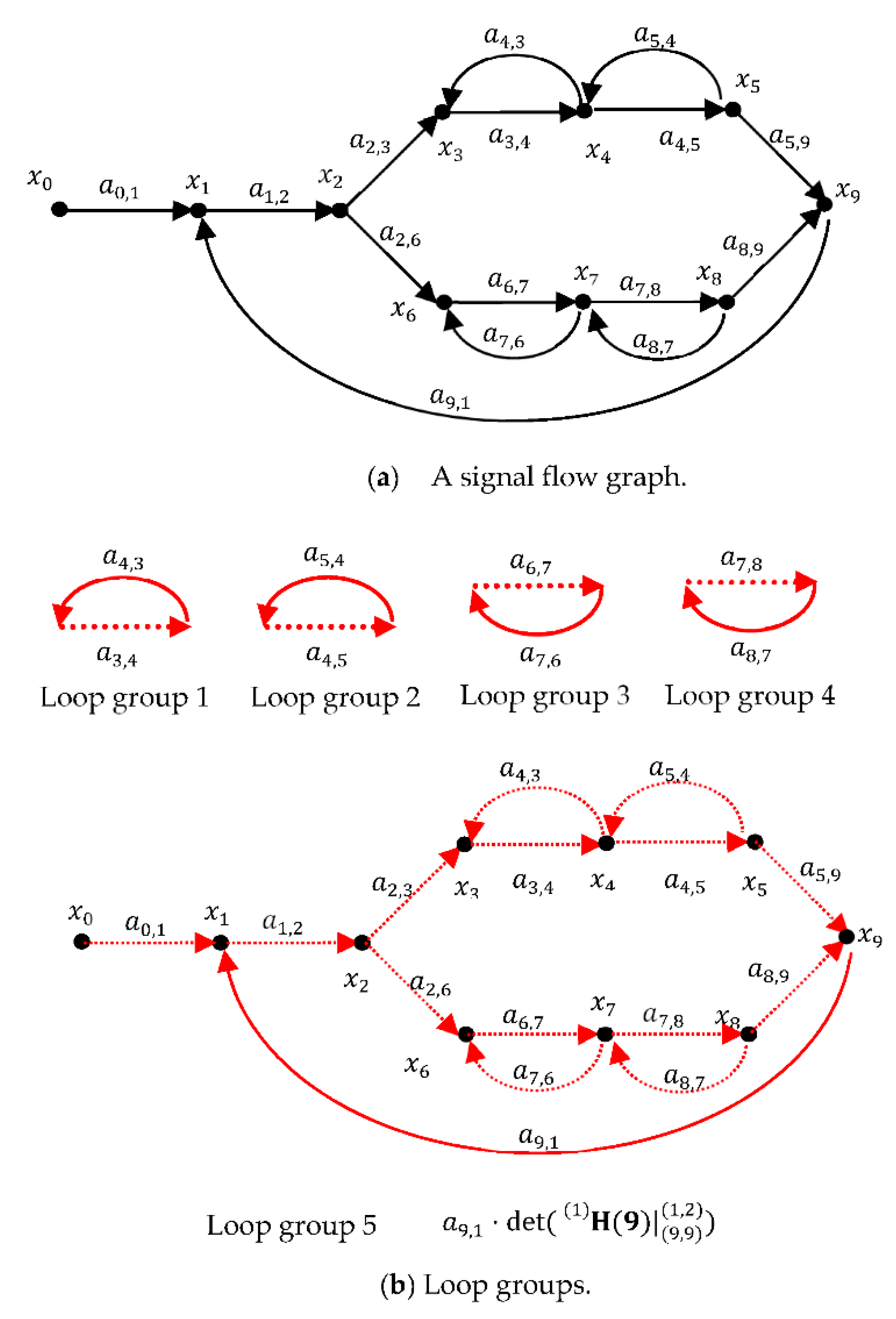
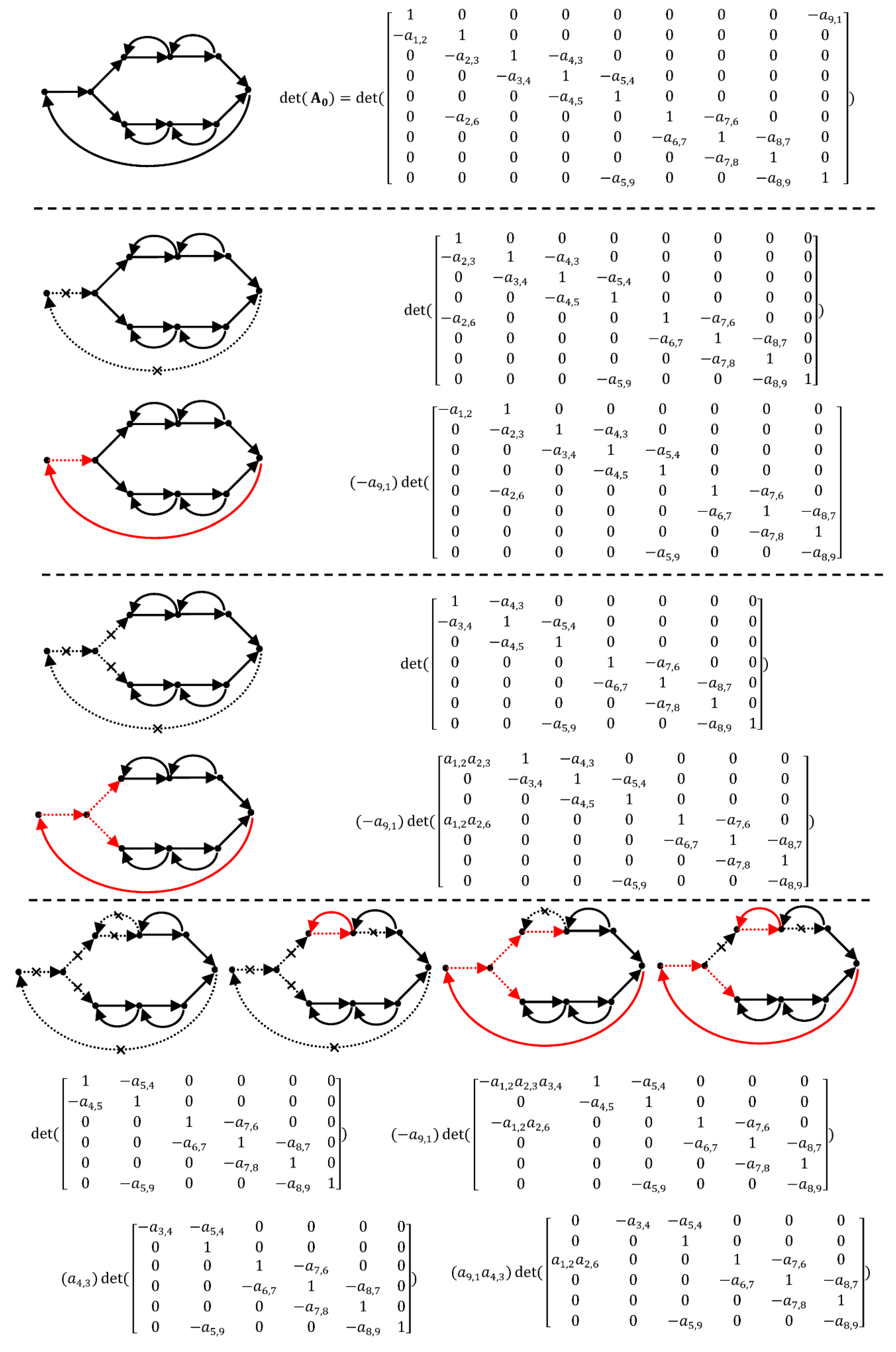
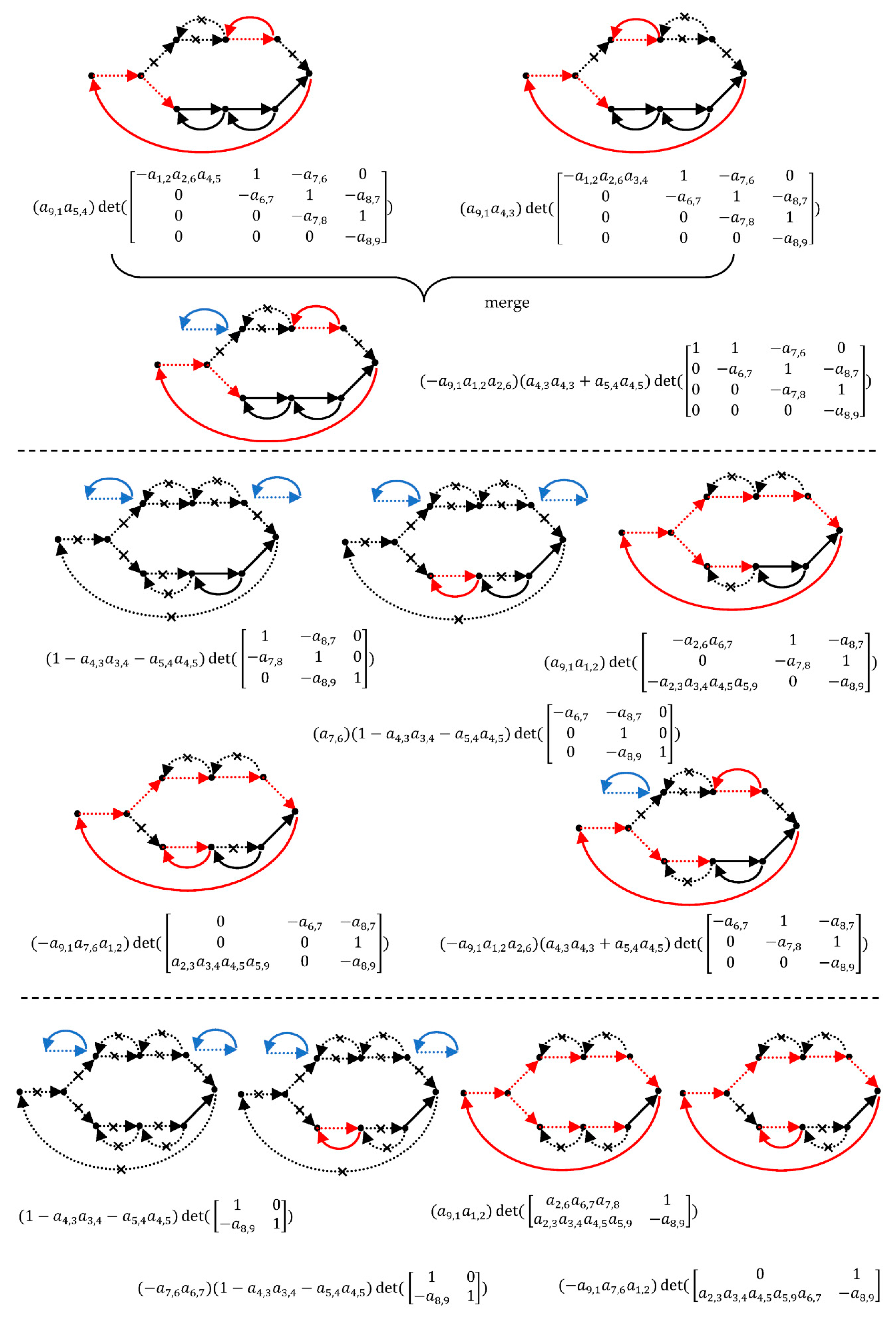
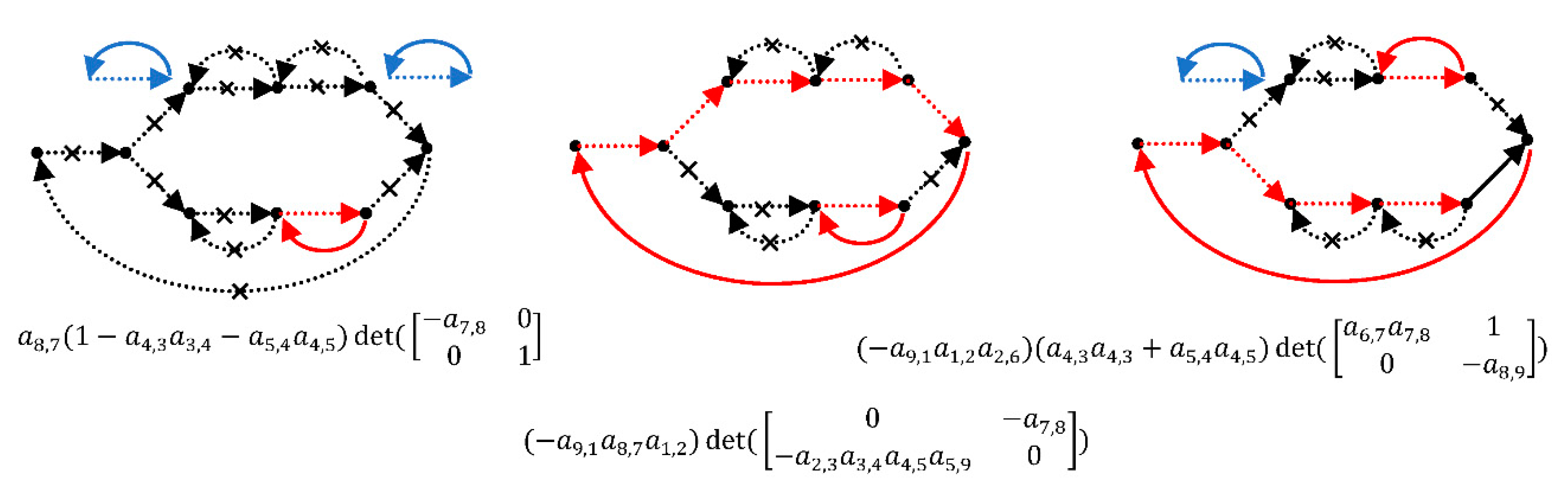
4. Graph Decomposition
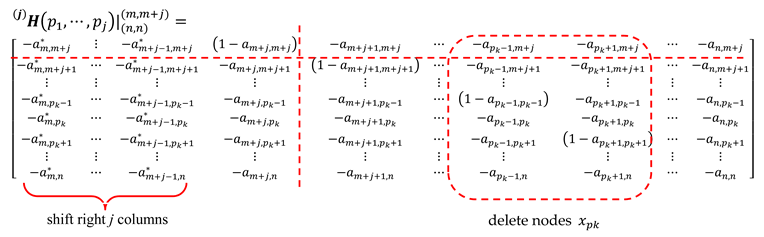
5. Forward Path Gain
6. Transfer Function
7. Complexity Analysis
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gepreel, K.A.; Higazy, M.; Mahdy, A.M.S. Optimal control, signal flow graph, and system electronic circuit realization for nonlinear Anopheles mosquito model. Int. J. Mod. Phys. C 2020, 31, 2050130. [Google Scholar] [CrossRef]
- Moschytz, G.S. An introduction to signal-flow graph theory. In Analog Circuit Theory and Filter Design in the Digital World; Springer: Cham, Switzerland, 2019; pp. 85–100. [Google Scholar]
- Abbasi, M.; Afifi, A.; Pahlavani, M.R.A. Ripple base signal flow graph modelling of DC–DC switching converters. IET Power Electron. 2019, 12, 1274–1284. [Google Scholar] [CrossRef]
- Schmid, H.; Huber, A. Analysis of switched-capacitor circuits using driving-point signal-flow graphs. Analog. Integr. Circuits Signal Process. 2018, 96, 495–507. [Google Scholar] [CrossRef]
- Appikonda, M.; Dhanalakshmi, K.; Krishna, P.S.V. Signal Flow Graph Model and Feed-Forward Control for a High Voltage Gain Dual Input Boost DC-DC Converter. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020) IEEE, Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Rasim, F.R.; Sattler, S.M. Analysis of Electronic Circuits with the Signal Flow Graph Method. Circuits Syst. 2017, 8, 261–274. [Google Scholar] [CrossRef][Green Version]
- Mahdy, A.M.S.; Mohamed, M.S.; Gepreel, K.A.; AL-Amiri, A.; Higazy, M. Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model. Chaos Solitons Fractals 2020, 141, 110308. [Google Scholar] [CrossRef]
- Brtnik, B. Comparison of the Methods of Graphical Solution of Symbolic Sensitivity. In Proceedings of the 2019 29th International Conference Radioelektronika (RADIOELEKTRONIKA) IEEE, Pardubice, Czech Republic, 16–18 April 2019; pp. 1–5. [Google Scholar]
- Asenova, I.; Balik, F. Symbolic sensitivity analysis enhanced by nullor model and modified Coates flow graph. In Pathological Elements in Analog Circuit Design; Springer: Cham, Switzerland, 2018; pp. 149–176. [Google Scholar]
- Kono, H.; Omura, I. Study of parasitic oscillation of a multi-chip SiC MOSFET circuit based on a signal flow graph model by TCAD simulation. Solid-State Electron. 2020. [Google Scholar] [CrossRef]
- Mason, S.J. Feedback theory-some properties of signal flow graphs. Proc. IRE 1953, 41, 1144–1156. [Google Scholar] [CrossRef]
- Mason, S.J. Feedback theory: Further properties of signal flow graphs. Proc. IRE 1956, 44, 920–926. [Google Scholar] [CrossRef]
- Prasad, V.C. On Boolean techniques for non touching loops of signal flow graphs. Circuits Syst. Signal Process. 2013, 32, 1443–1453. [Google Scholar] [CrossRef]
- Prasad, V.C. Simplification of signal flow graphs. Circuits Syst. Signal Process. 2013, 30, 673–682. [Google Scholar] [CrossRef]
- Prasad, V.C. Compact form of Mason’s gain formula for signal flow graphs. Int. J. Electr. Eng. Educ. 2010, 47, 393–403. [Google Scholar] [CrossRef]
- Coates, C. Flow-graph solutions of linear algebraic equations. IRE Trans. Circuit Theory 1959, 6, 170–187. [Google Scholar] [CrossRef]
- Desoer, C.A. The optimum formula for the gain of a flow graph or a simple derivation of Coates’ formula. Proc. IRE 1960, 48, 883–889. [Google Scholar] [CrossRef]
- Dorf, R.C. (Ed.) The Electrical Engineering Handbook-Six Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jeng, S.L.; Lue, B.H.; Chieng, W.H. Transfer matrix method for deriving transfer functions of LTI systems. In Proceedings of the Sixth International Conference on Electronics and Information Engineering, International Society for Optics and Photonics, Dalian, China, 26–27 September 2015; Volume 9794, p. 979439. [Google Scholar]
- Lu, H.; Wu, C.; Bao, S. An Improved Algorithm based on Shannon-Happ Formula for Calculating Transfer Function from Signal Flow Graph and Its Visualization. arXiv 2009, arXiv:0906.556. [Google Scholar]
- Beillahi, S.M.; Siddique, U.; Tahar, S. On the Formalization of Signal-Flow-Graphs in HOL; Technical Report; ECE Department, Concordia University: Montreal, QC, Canada, 2014. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, S.-L.; Roy, R.; Chieng, W.-H. A Matrix Approach for Analyzing Signal Flow Graph. Information 2020, 11, 562. https://doi.org/10.3390/info11120562
Jeng S-L, Roy R, Chieng W-H. A Matrix Approach for Analyzing Signal Flow Graph. Information. 2020; 11(12):562. https://doi.org/10.3390/info11120562
Chicago/Turabian StyleJeng, Shyr-Long, Rohit Roy, and Wei-Hua Chieng. 2020. "A Matrix Approach for Analyzing Signal Flow Graph" Information 11, no. 12: 562. https://doi.org/10.3390/info11120562
APA StyleJeng, S.-L., Roy, R., & Chieng, W.-H. (2020). A Matrix Approach for Analyzing Signal Flow Graph. Information, 11(12), 562. https://doi.org/10.3390/info11120562




