Community Detection Based on a Preferential Decision Model
Abstract
1. Introduction
1.1. Basic Idea
1.2. Contributions
- Higher accuracy. By comparing classic and latest algorithm experiments in the complex network, the CDPD algorithm has an accurate community partition on the real-world network and the synthetic network. In addition, the discovered communities are relatively close to the real communities.
- Stability. The randomness has been greatly reduced by introducing the preferential decision mechanism and the past memory similarity.
- Scalability. Although the iterative process based on dynamic relationships is complicated, CDPD only needs to consider the characteristics of neighboring nodes, which results in low time complexity of . The values of t and k are usually small. Therefore, the CDPD algorithm can be applied to large-scale networks.
- Free parameters. Instead of relying on prior knowledge and parameter setting methods, the CDPD method does not require parameter settings, and the communities are automatically discovered based on the local topology of the network.
2. Related Work
3. Community Detection Based on Preferential Decision
3.1. Basic Formula Principle and Concepts
3.2. Preferential Decision Model Based on Dynamic Iteration
3.3. Community Detection Based on the Preferential Decision Algorithm
| Algorithm 1 CDPD |
Input:
|
3.4. Complexity Analysis
4. Experiment
4.1. Comparing Algorithms
4.2. Data Description
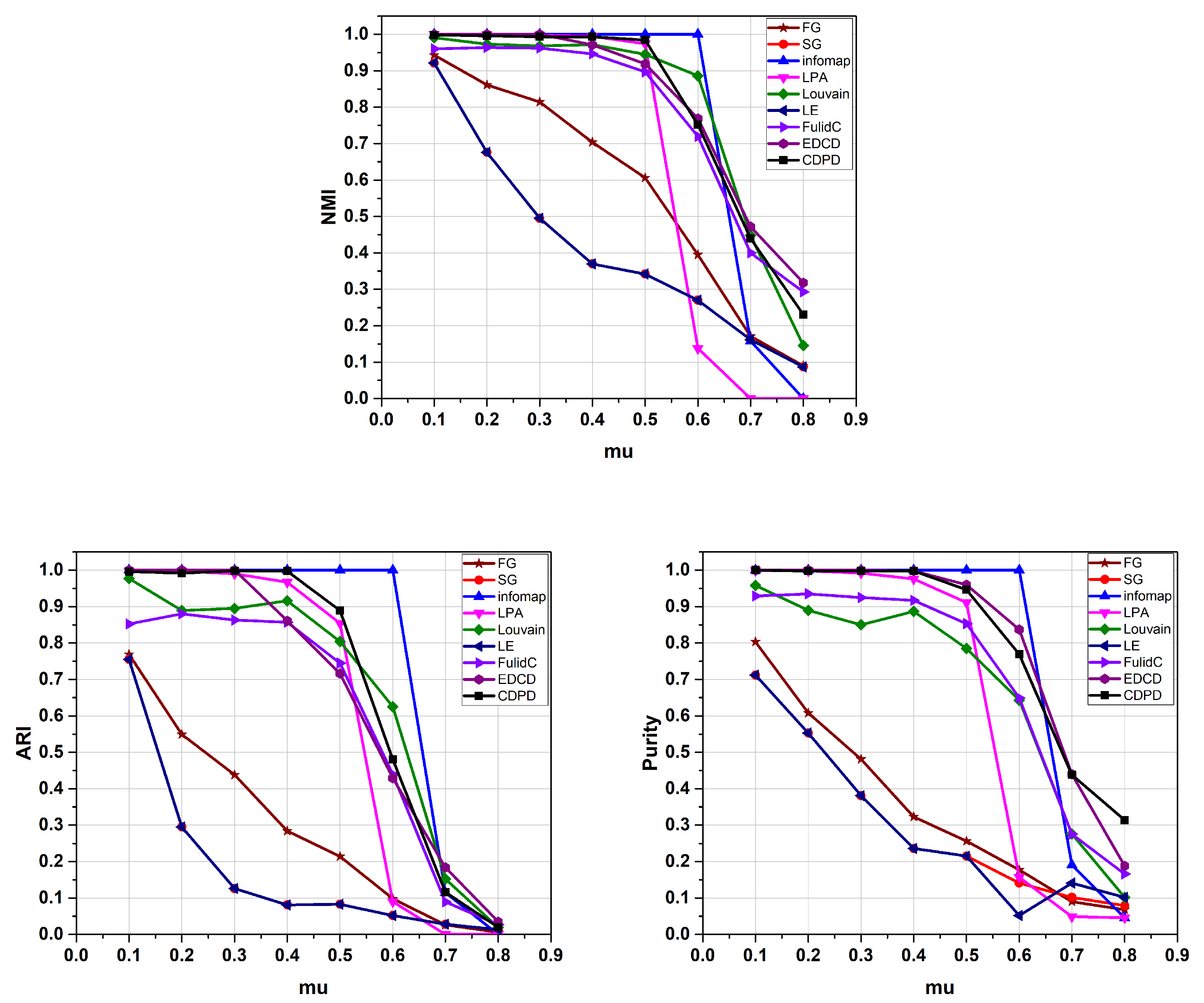
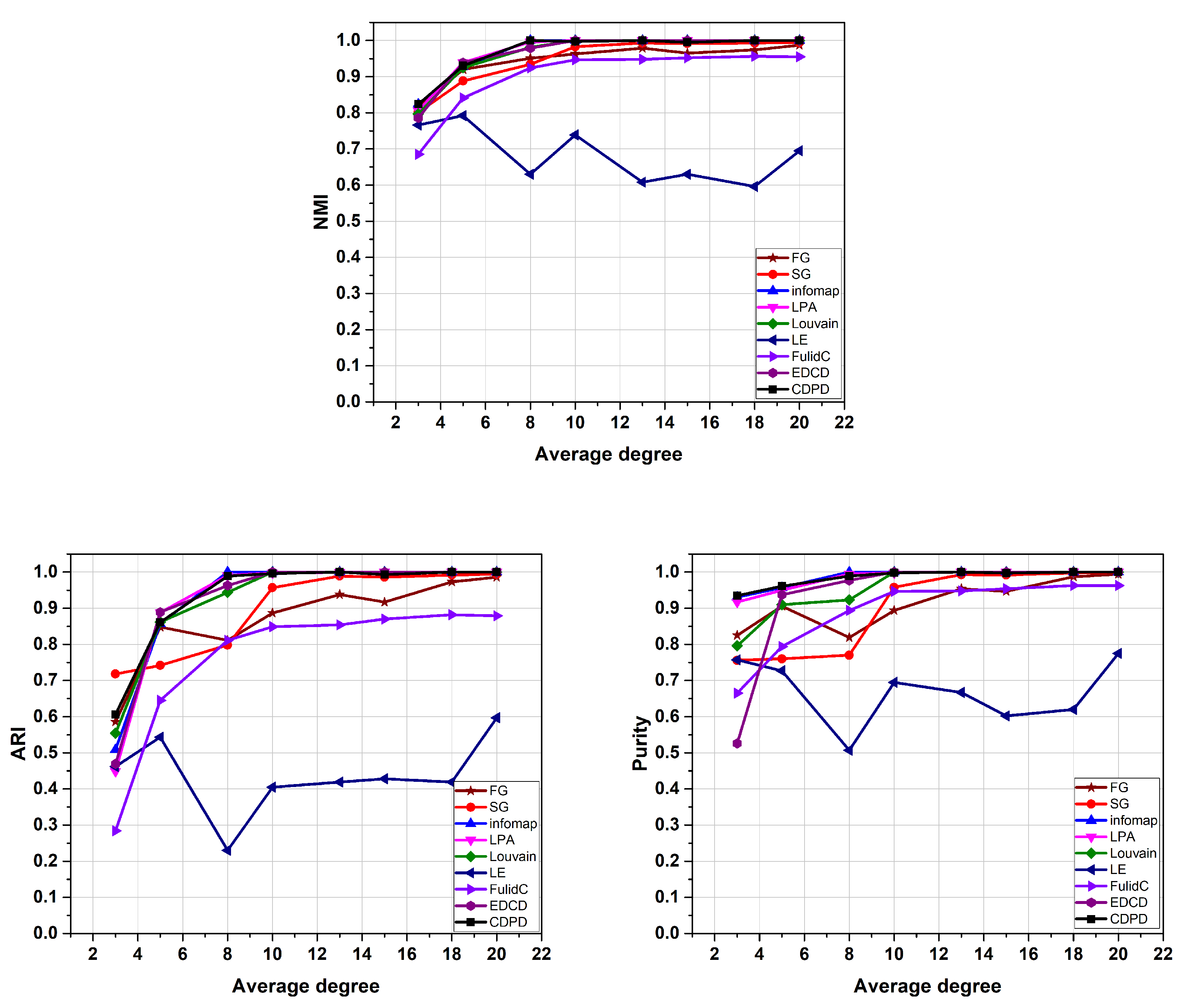
4.2.1. Synthetic Networks
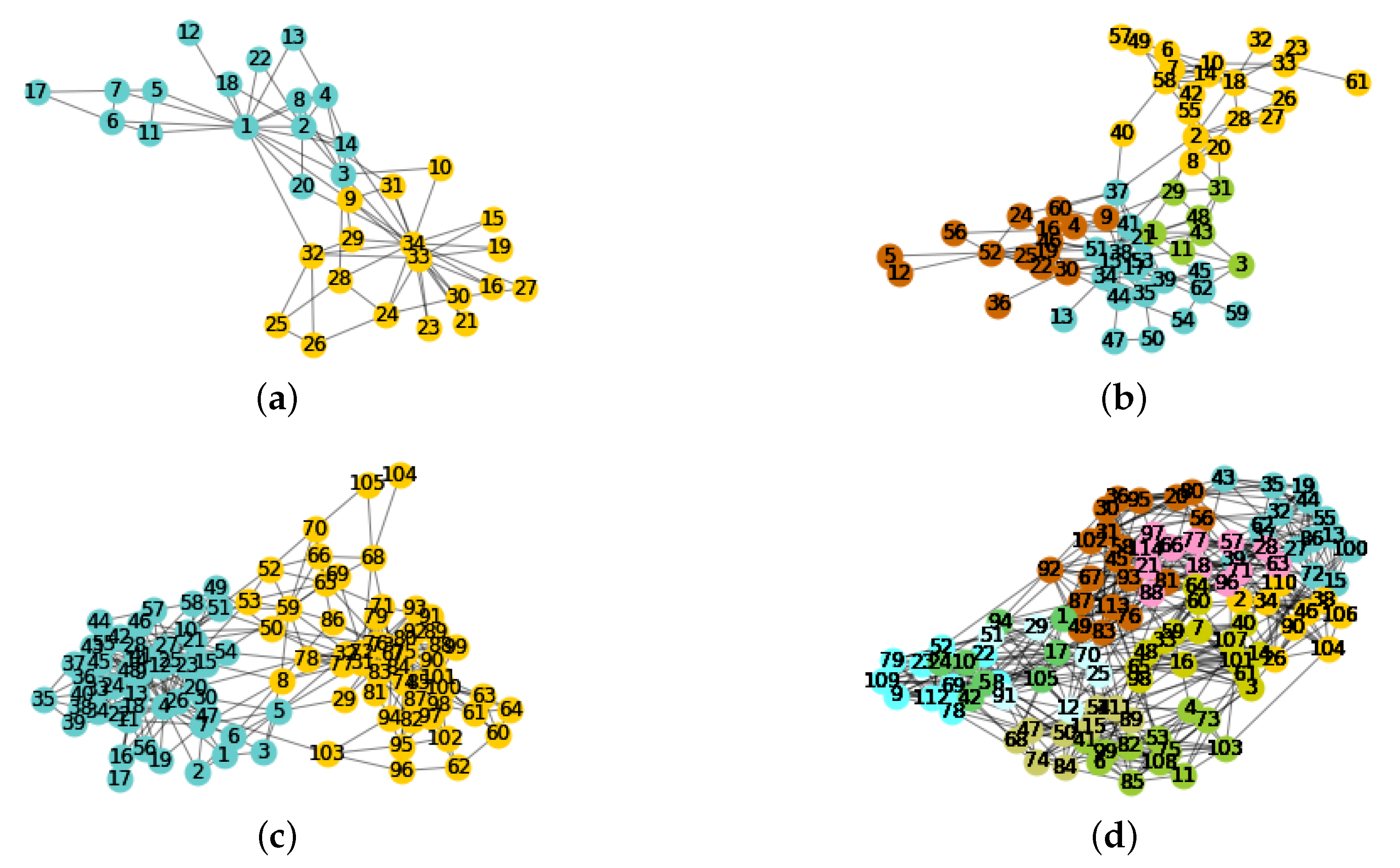
4.2.2. Real-World Networks
4.3. Evaluation Metrics
4.4. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oger, R.; Yerson, B.M. Game theory: Analysis of conflict. Long Range Plan. 1992, 25, 130. [Google Scholar]
- Basu, S.; Maulik, U. Community detection based on strong Nash stable graph partition. Soc. Netw. Anal. Min. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Fortunato, S.; Barthelemy, M. Resolution limit in community detection. Mob. Netw. Appl. 2007, 104, 36–41. [Google Scholar] [CrossRef] [PubMed]
- IEEE Transactions on Emerging Topics in Computational Intelligence; Publishing House: New York, NY, USA, 2018; Volume 2, pp. 214–223.
- Li, H.J.; Daniels, J.J. Social significance of community structure: Statistical view. Phys. Rev. E 2015, 91, 012801. [Google Scholar] [CrossRef] [PubMed]
- Bu, Z.; Li, H.J.; Zhang, C.; Cao, J.; Li, A.; Shi, Y. Graph K-means based on Leader Identification, Dynamic Game and Opinion Dynamics. IEEE Trans. Knowl. Data Eng. 2019. [Google Scholar] [CrossRef]
- Li, H.J.; Bu, Z.; Wang, Z.; Cao, J. Dynamical clustering in electronic commerce systems via optimization and leadership expansion. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Khan, B.S.; Niazi, M.A. Network Community Detection: A Review and Visual Survey. arXiv 2017, arXiv:1708.00977. [Google Scholar]
- Jonnalagadda, A.; Kuppusamy, L. A survey on game theoretic models for community detection in social networks. Soc. Netw. Anal. Min. 2016, 6, 83. [Google Scholar] [CrossRef]
- Qi, X.; Tang, W.; Wu, Y.; Guo, G.; Fuller, E.; Zhang, C.Q. Optimal local community detection in social networks based on density drop of subgraphs. Pattern Recognit. Lett. 2014, 36, 46–53. [Google Scholar] [CrossRef]
- Badie, R.; Aleahmad, A.; Asadpour, M.; Rahgozar, M. An efficient agent-based algorithm for overlapping community detection using nodes closeness. Phys. Stat. Mech. Appl. 2013, 392, 129–140. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Guimera, R.; SalesPardo, M.; Amaral, L.A. Modularity from fluctuations in random graphs and complex networks. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2004, 70, 025101. [Google Scholar] [CrossRef]
- Jordi, D.; Alex, A. Community Detection in Complex Networks Using Extremal Optimization. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2005, 72, 027104. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Li, H.-J.; Wang, Q.; Liu, S.; Hu, J. Exploring the trust management mechanism in self-organizing complex network based on game theory. Phys. Stat. Mech. Appl. 2019, 123514. [Google Scholar] [CrossRef]
- Cao, J.; Bu, Z.; Wang, Y.; Yang, H.; Jiang, J.; Li, H.-J. Detecting Prosumer-Community Groups in Smart Grids From the Multiagent Perspective. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–13. [Google Scholar] [CrossRef]
- Narayanam, R.; Narahari, Y. A game theory inspired, decentralized, local information based algorithm for community detection in social graphs. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 1072–1075. [Google Scholar]
- Cao, L.; Li, X.; Han, L. Detecting community structure of networks using evolutionary coordination games. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 2533–2536. [Google Scholar]
- Alvari, H.; Hajibagheri, A.; Sukthankar, G. Community detection in dynamic social networks: A game-theoretic approach. In Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Beijing China, 17–20 August 2014; pp. 101–107. [Google Scholar]
- Pons, P.; Latapy, M. Computing Communities in Large Networks Using Random Walks. J. Graph Algorithms Appl. 2006, 10, 191–218. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2007, 76, 036106. [Google Scholar] [CrossRef]
- Hosseini, R.; Azmi, R. Memory-based label propagation algorithm for community detection in social networks. In Proceedings of the International Symposium on Artificial Intelligence and Signal Processing, Mashhad, Iran, 3–5 March 2015; pp. 256–260. [Google Scholar]
- Cordasco, G.; Gargano, L. Community Detection via Semi-Synchronous Label Propagation Algorithms. In Proceedings of the 2010 IEEE International Workshop on: Business Applications of Social Network Analysis (BASNA), Bangalore, India, 5 December 2010; pp. 1–8. [Google Scholar]
- Zhang, X.; Kun, R.; Jing, S.; Chen, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Mob. Phys. Lett. 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Khadivi, A.; Rad, A.A.; Hasler, M. Community detection enhancement in networks using proper weighting and partial synchronization. In Proceedings of the IEEE International Symposium on Circuits and System, Florence, Italy, 27–30 May 2018; pp. 3777–3780. [Google Scholar]
- Shao, J.; Han, Z.; Yang, Q.; Zhou, T. Community Detection based on Distance Dynamics. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 8–9 August 2015; pp. 1075–1084. [Google Scholar]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2004, 70, 066111. [Google Scholar] [CrossRef] [PubMed]
- Reichardt, J.; Bornholdt, S. Statistical mechanics of community detection. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2006, 74, 016110. [Google Scholar] [CrossRef] [PubMed]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of community hierarchies in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, 10008. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2006, 74, 036104. [Google Scholar] [CrossRef]
- Parés, F.; Gasulla, D.G.; Vilalta, A.; Moreno, J.; Ayguadé, E.; Labarta, J.; Cortés, U.; Suzumura, T. Fluid Communities: A Competitive, Scalable and Diverse Community Detection Algorithm. In Proceedings of the Complex Networks and Their Applications VI, Lyon, France, 29 November–1 December 2017; pp. 229–240. [Google Scholar]
- Chen, X.; Li, J. Community detection in complex networks using edge-deleting with restrictions. Phys. Stat. Mech. Appl. 2019, 519, 181–194. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2008, 78, 046110. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster Ensembles—A Knowledge Reuse Framework for Combining Multiple Partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Rand, W.M. Objective Criteria for the Evaluation of Clustering Methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Ying, Z.; Karypis, G. Criterion Functions for Document Clustering: Experiments and Analysis. 2002. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.16.6872 (accessed on 16 January 2020).
- Vinh, N.X.; Epps, J.; Bailey, J. Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Lawrence, H.; Phipp, A. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar]

| Symbol | Definition |
|---|---|
| The number of nodes | |
| The number of edges | |
| The i-th memory tag of the node u | |
| The neighborhood of node u | |
| The Jaccard similarity coefficient of node u and node v | |
| The contact strength of node u and node v | |
| The past memory similarity of node u and node v | |
| The preferential decision degree of node u for node v | |
| Node u determines the probability of selecting node v |
| Algorithm | Basic Principle | Time Complexity |
|---|---|---|
| FG | Modularity optimization | |
| SG | Spin configuration | |
| Infomap | Random walk | |
| LPA | Label propagation | |
| Louvain | Separate division | |
| LE | Eigenvectors of matrices | |
| FluidC | Fluids interacting in an environment | |
| EDCD | Edge deletion | |
| CDPD | Preferential decision |
| Dataset | k | maxk | mu | minc | maxc | |
|---|---|---|---|---|---|---|
| 1st | 1000 | 15 | 38 | 0.1–0.8 | 10 | 50 |
| 2nd | 1000 | 3–20 | 0.1 | 10 | 50 |
| Datasets | k | Clustering Coefficient | Average Path Length | |||
|---|---|---|---|---|---|---|
| Karate | 34 | 78 | 4.588 | 2 | 0.588 | 2.408 |
| Dolphins | 62 | 159 | 5.129 | 2 | 0.303 | 3.357 |
| Football | 115 | 613 | 10.611 | 12 | 0.403 | 2.508 |
| Polbooks | 105 | 441 | 8.4 | 3 | 0.48 | 3.097 |
| Citeseer | 2114 | 7396 | 3.52 | 6 | 0.24 | 9.32 |
| Zachary | Dolphins | Polbooks | Football | Citeseer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NMI | ARI | Pur. | NMI | ARI | Pur. | NMI | ARI | Pur. | NMI | ARI | Pur. | NMI | ARI | Pur. | |
| FG | 0.707 | 0.68 | 0.971 | 0.652 | 0.493 | 0.984 | 0.531 | 0.638 | 0.838 | 0.757 | 0.474 | 0.583 | 0.362 | 0.198 | 0.705 |
| SG | 0.703 | 0.526 | 0.994 | 0.638 | 0.369 | 0.999 | 0.511 | 0.51 | 0.851 | 0.906 | 0.846 | 0.897 | 0.28 | 0.16 | 0.62 |
| Infomap | 0.711 | 0.702 | 0.971 | 0.611 | 0.352 | 0.991 | 0.503 | 0.536 | 0.848 | 0.92 | 0.897 | 0.922 | 0.397 | 0.033 | 0.777 |
| LPA | 0.664 | 0.642 | 0.913 | 0.679 | 0.556 | 0.978 | 0.556 | 0.652 | 0.845 | 0.878 | 0.756 | 0.846 | 0.388 | 0.071 | 0.776 |
| Louvain | 0.618 | 0.462 | 0.971 | 0.568 | 0.343 | 0.968 | 0.513 | 0.549 | 0.848 | 0.891 | 0.807 | 0.87 | 0.352 | 0.159 | 0.698 |
| LE | 0.715 | 0.512 | 1 | 0.497 | 0.283 | 0.952 | 0.525 | 0.547 | 0.848 | 0.703 | 0.464 | 0.626 | 0.341 | 0.176 | 0.666 |
| FluidC | 0.642 | 0.594 | 0.76 | 0.631 | 0.628 | 0.886 | 0.496 | 0.532 | 0.751 | 0.885 | 0.79 | 0.866 | 0.239 | 0.197 | 0.482 |
| EDCD | 0.896 | 0.88 | 0.968 | 0.37 | 0.13 | 0.387 | 0.52 | 0.56 | 0.790 | 0.92 | 0.896 | 0.921 | 0.435 | 0.13 | 0.243 |
| CDPD | 0.897 | 0.902 | 1 | 0.72 | 0.69 | 0.984 | 0.586 | 0.69 | 0.924 | 0.92 | 0.85 | 0.922 | 0.398 | 0.198 | 0.492 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, J.; Lu, B.; Wang, B.; Hu, J.; Wang, K.; Pan, X.; Dong, Q.; Aklilu, D. Community Detection Based on a Preferential Decision Model. Information 2020, 11, 53. https://doi.org/10.3390/info11010053
Sheng J, Lu B, Wang B, Hu J, Wang K, Pan X, Dong Q, Aklilu D. Community Detection Based on a Preferential Decision Model. Information. 2020; 11(1):53. https://doi.org/10.3390/info11010053
Chicago/Turabian StyleSheng, Jinfang, Ben Lu, Bin Wang, Jie Hu, Kai Wang, Xiaoxia Pan, Qiangqiang Dong, and Dawit Aklilu. 2020. "Community Detection Based on a Preferential Decision Model" Information 11, no. 1: 53. https://doi.org/10.3390/info11010053
APA StyleSheng, J., Lu, B., Wang, B., Hu, J., Wang, K., Pan, X., Dong, Q., & Aklilu, D. (2020). Community Detection Based on a Preferential Decision Model. Information, 11(1), 53. https://doi.org/10.3390/info11010053





