Punctuation and Parallel Corpus Based Word Embedding Model for Low-Resource Languages
Abstract
1. Introduction
2. Related Works
2.1. Word Embeddings for Low-Resource Languages
2.2. Applications of Punctuations in Natual Language Processing
2.3. GIZA++ Word Alignment
2.4. Word-Pair Co-Occurrence Matrix
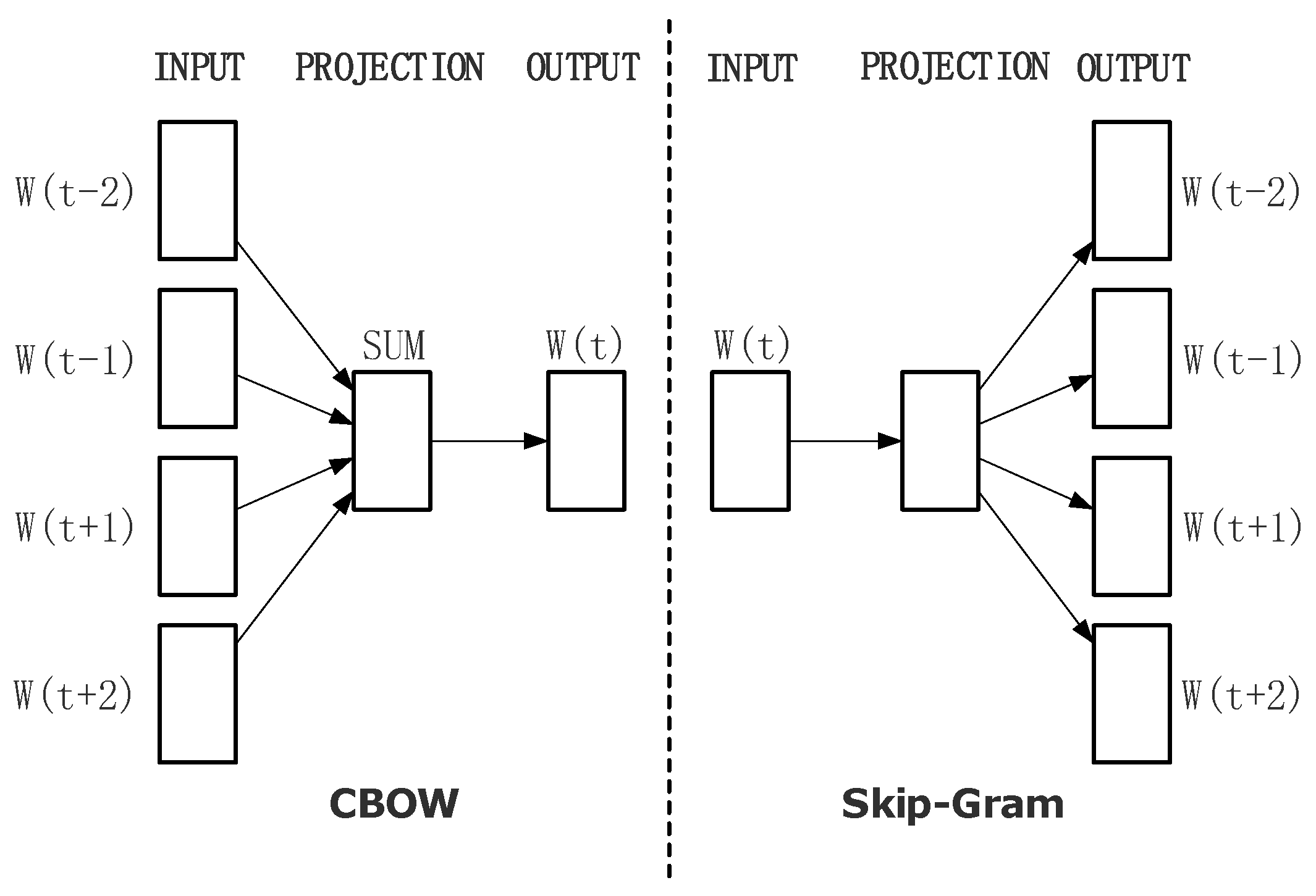
2.5. Neural Network Word Embedding Models
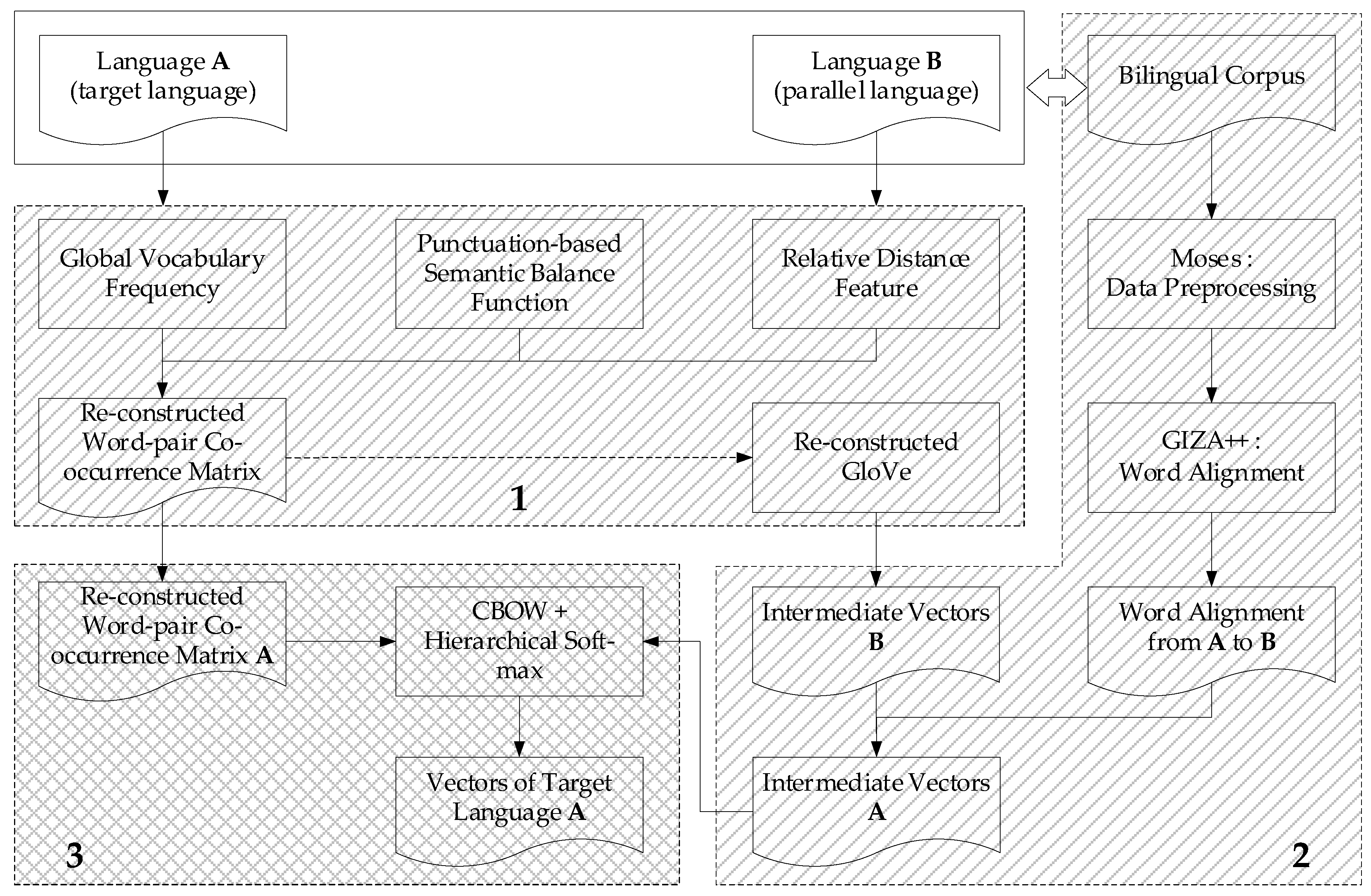
3. Word Embedding Model Based on SOP and Parallel Corpus
- Construct the global word-pair co-occurrence matrix. We integrate with the global vocabulary frequency information, the punctuation-based semantic balance function, and relative distance feature to generate the global word-pair co-occurrence matrix. We also adjust the GloVe model with this re-constructed matrix, and use the optimized model to generate the intermediate vectors in the next stage.
- Generate the bi-lingual based intermediate word embedding. We obtain the word alignment probability from bilingual parallel corpus trained with Moses and GIZA++, and get the intermediate vectors of language B trained with the reconstructed model mentioned in Stage 1. Then we combine the alignment probability with the intermediate vectors B to figure out the intermediate vectors A.
- Refactor the word embedding model. We refer to Word2vec and build the final word embedding model, which combined with the word-pair co-occurrence matrix generated from Stage 1 and the intermediate vectors A from Stage 2. Finally, calculating the word vectors of target language A by using this model.
3.1. Construct the Global Word-Pair Co-Occurrence Matrix
3.2. Generate the Bi-Lingual Based Intermediate Word Embedding
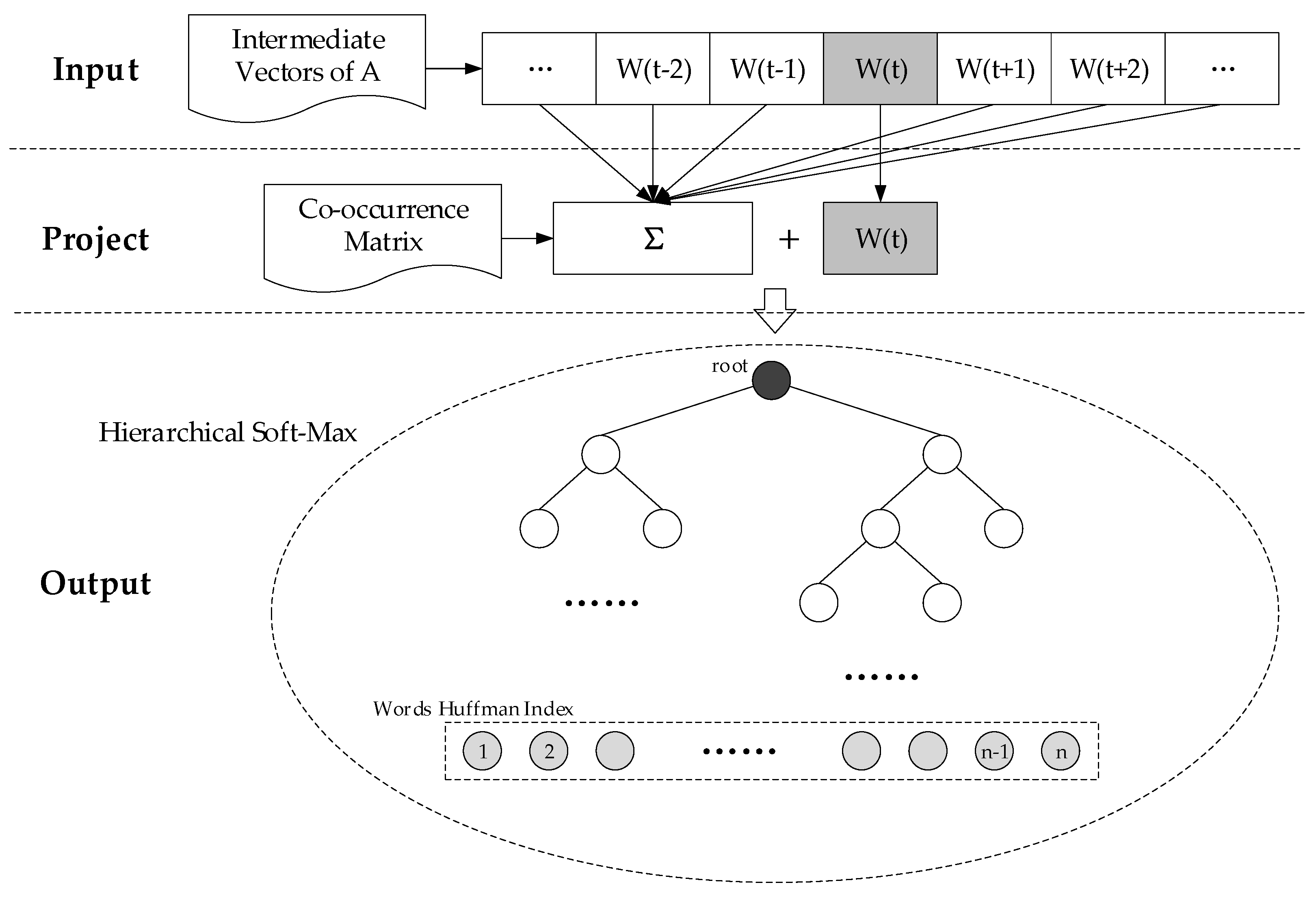
3.3. Refactor the Word Embedding Model
4. Experiments and Results
4.1. Corpus, Model and Parameter Settings
4.2. Evaluation Tasks
4.3. Results
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Sahlgren, M. The Word-Space Model: Using Distributional Analysis to Represent Syntagmatic and Paradigmatic Relations between Words in High-Dimensional Vector Spaces. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2006. [Google Scholar]
- Turney, P.D.; Pantel, P. From frequency to meaning: Vector space models of semantics. J. Artif. Intell. Res. 2010, 37, 141–188. [Google Scholar] [CrossRef]
- Mnih, A.; Hinton, G.E. A scalable hierarchical distributed language model. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; pp. 1081–1088. [Google Scholar]
- Deerwester, S.; Dumais, S.T.; Furnas, G.W.; Landauer, T.K.; Harshman, R. Indexing by latent semantic analysis. J. Am. Soc. Inf. Sci. 1990, 41, 391–407. [Google Scholar] [CrossRef]
- Bullinaria, J.A.; Levy, J.P. Extracting semantic representations from word-pair co-occurrence statistics: A computational study. Behav. Res. Methods 2007, 39, 510–526. [Google Scholar] [CrossRef] [PubMed]
- RRitter, A.; Etzioni, O. A latent dirichlet allocation method for selectional preferences. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, Uppsala, Sweden, 11–16 July 2010. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Jauvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Stateline, NV, USA, 5–10 December 2013. [Google Scholar]
- Cotterell, R.; Schütze, H. Morphological word-embeddings. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, CO, USA, 31 May–5 June 2015. [Google Scholar]
- Levy, O.; Goldberg, Y. Dependency-based word embeddings. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, Baltimore, MD, USA, 22–27 June 2014. [Google Scholar]
- Xu, C.; Bai, Y.; Bian, J.; Gao, B.; Wang, G.; Liu, X.; Liu, T.-Y. Rc-net: A general framework for incorporating knowledge into word representations. In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014. [Google Scholar]
- Liu, Q.; Jiang, H.; Wei, S.; Ling, Z.-H.; Hu, Y. Learning semantic word embeddings based on ordinal knowledge constraints. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015. [Google Scholar]
- Peters, M.E.; Neumann, M.; Iyyer, M.; Gardner, M.; Clark, C.; Lee, K.; Zettlemoyer, L. Deep contextualized word representations. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; pp. 2227–2237. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training. Available online: https://www.cs.ubc.ca/~amuham01/LING530/papers/radford2018improving.pdf (accessed on 28 December 2019).
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Lample, G.; Conneau, A. Cross-lingual Language Model Pretraining. Available online: https://arxiv.org/pdf/1901.07291.pdf (accessed on 28 December 2019).
- Jiang, C.; Yu, H.F.; Hsieh, C.J.; Chang, K.W. Learning Word Embeddings for Low-Resource Languages by PU Learning. Available online: https://arxiv.org/pdf/1805.03366.pdf (accessed on 28 December 2019).
- Bel-Enguix, G.; Gómez-Adorno, H.; Reyes-Magaña, J.; Sierra, G. Wan2vec: Embeddings learned on word association norms. Semant. Web. 2019, 10, 991–1006. [Google Scholar] [CrossRef]
- Artetxe, M.; Labaka, G.; Agirre, E. A Robust Self-Learning Method for Fully Unsupervised Cross-Lingual Mappings of Word Embeddings. Available online: https://arxiv.org/pdf/1805.06297.pdf (accessed on 28 December 2019).
- Tilk, O.; Alumäe, T. Bidirectional Recurrent Neural Network with Attention Mechanism for Punctuation Restoration. In Proceedings of the Interspeech, San Francisco, CA, USA, 8–12 September 2016; pp. 3047–3051. [Google Scholar]
- Spitkovsky, V.I.; Alshawi, H.; Jurafsky, D. Punctuation: Making a point in unsupervised dependency parsing. In Proceedings of the Fifteenth Conference on Computational Natural Language Learning, Association for Computational Linguistics, Portland, OR, USA, 23–24 June 2011. [Google Scholar]
- Farooq, U.; Mansoor, H.; Nongaillard, A.; Ouzrout, Y.; Qadir, M.A. Negation Handling in Sentiment Analysis at Sentence Level. J. Comput. 2017, 12, 470–478. [Google Scholar] [CrossRef]
- Koto, F.; Adriani, M. A comparative study on twitter sentiment analysis: Which features are good? In Proceedings of the 20th International Conference on Applications of Natural Language to Information Systems, NLDB 2015, Passau, Germany, 17–19 June 2015; pp. 453–457. [Google Scholar]
- Gao, Q.; Vogel, S. Parallel implementations of word alignment tool. In Proceedings of the Software Engineering, Testing, and Quality Assurance for Natural Language Processing, Columbus, OH, USA, 19–20 June 2008; pp. 49–57. [Google Scholar]
- Gutmann, M.U.; Hyvärinen, A. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics. J. Mach. Learn. Res. 2012, 13, 307–361. [Google Scholar]
- Che, W.; Li, Z.; Liu, T. Ltp: A Chinese language technology platform. In Proceedings of the 23rd International Conference on Computational Linguistics: Demonstrations, Beijing, China, 23–27 August 2010. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. Available online: https://arxiv.org/pdf/1301.3781.pdf (accessed on 28 December 2019).
- Rubenstein, H.; Goodenough, J.B. Contextual correlates of synonymy. Commun. Acm 1965, 8, 627–633. [Google Scholar] [CrossRef]
- Miller, G.A.; Charles, W.G. Contextual correlates of semantic similarity. Lang. Cogn. Processes 1991, 6, 1–28. [Google Scholar] [CrossRef]
- Finkelstein, R.L. Placing search in context: The concept revisited. Acm Trans. Inf. Syst. 2002, 20, 116–131. [Google Scholar] [CrossRef]
- Huang, E.H.; Socher, R.; Manning, C.D.; Ng, A.Y. Improving word representations via global context and multiple word prototypes. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics, Jeju Island, Korea, 8–14 July 2012. [Google Scholar]
- Luong, T.; Socher, R.; Manning, C. Better word representations with recursive neural networks for morphology. In Proceedings of the Seventeenth Conference on Computational Natural Language Learning, Sofia, Bulgaria, 8–9 August 2013. [Google Scholar]
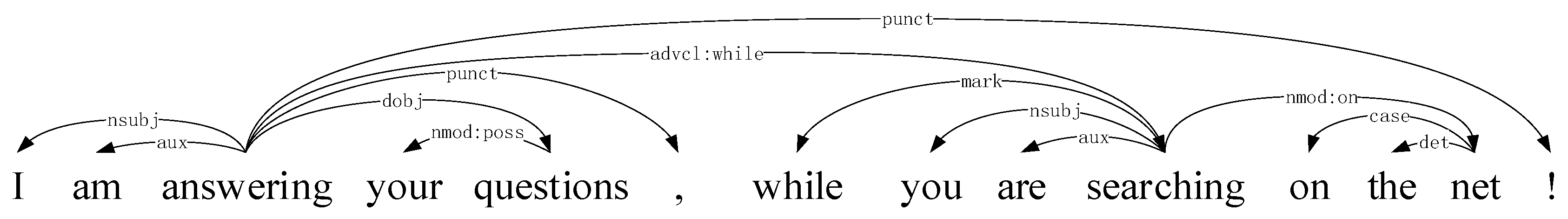
| Number | Proportion | |||||||
|---|---|---|---|---|---|---|---|---|
| Word | 455,725 | |||||||
| N-SOP | . | ! | ? | 8760 | 1.92% | |||
| 7159 | 652 | 949 | ||||||
| SOP | , | : | ; | ‘ | “ | 54,774 | 98.45% | 12.02% |
| 35,073 | 339 | 5906 | 3295 | 10,161 | ||||
| Total Sentence | 9240 | |||||||
| Sentence with SOP | 8133 | 88.02% | ||||||
| Data Set | WS353 | MC | RG | SCWS | RW |
|---|---|---|---|---|---|
| Word Pairs | 353 | 30 | 65 | 2003 | 2034 |
| Subjects | 38 | 51 | |||
| Human Judgements | 10 | 10 | 10 |
| Models | Win-Size | Accuracy (%) | |||||
|---|---|---|---|---|---|---|---|
| Min-Count 0 | Min-Count 5 | ||||||
| Semantic | Syntactic | Total | Semantic | Syntactic | Total | ||
| GloVe | 5 | 4.12 | 4.13 | 4.12 | 12.82 | 7.19 | 8.29 |
| G+SOP+Distance | 3.92 | 4.41 | 4.06 | 13.25 | 7.10 | 8.30 | |
| Word2vec | 5.38 | 20.37 | 14.49 | 15.02 | 21.94 | 20.59 | |
| W+SOP+Distance | 5.64 | 20.08 | 14.75 | 13.97 | 22.29 | 20.67 | |
| W+SOP+Distance+Align | 6.47 | 21.09 | 15.03 | 15.66 | 22.67 | 21.30 | |
| GloVe | 8 | 4.71 | 5.73 | 5.33 | 14.68 | 9.23 | 10.30 |
| G+SOP+Distance | 4.43 | 6.02 | 5.40 | 14.22 | 9.62 | 10.52 | |
| Word2vec | 5.98 | 18.31 | 13.48 | 14.81 | 19.47 | 18.56 | |
| W+SOP+Distance | 6.58 | 18.29 | 13.70 | 15.07 | 20.61 | 19.53 | |
| W+SOP+Distance+Align | 6.65 | 19.17 | 14.27 | 15.49 | 21.12 | 20.02 | |
| GloVe | 10 | 5.13 | 5.48 | 5.34 | 16.42 | 9.53 | 10.87 |
| G+SOP+Distance | 4.86 | 5.78 | 5.42 | 14.94 | 10.30 | 11.20 | |
| Word2vec | 6.76 | 17.24 | 13.13 | 16.38 | 18.13 | 17.79 | |
| W+SOP+Distance | 6.10 | 18.28 | 13.51 | 15.83 | 19.02 | 18.40 | |
| W+SOP+Distance+Align | 6.35 | 18.20 | 13.56 | 14.05 | 20.10 | 18.92 | |
| Models | WS353 | MC | RG | SCWS | RW |
|---|---|---|---|---|---|
| GloVe | 0.305479 | 0.5839 | 0.413497 | 0.512328 | 0.248499 |
| G+SOP+Distance | 0.303055 | 0.584324 | 0.395285 | 0.513127 | 0.252304 |
| Word2vec | 0.366863 | 0.377726 | 0.27572 | 0.563772 | 0.3066 |
| W+SOP+Distance | 0.397485 | 0.489595 | 0.326235 | 0.560381 | 0.272034 |
| W+SOP+Distance+Align | 0.417886 | 0.578809 | 0.397712 | 0.568058 | 0.316167 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Li, X.; Yang, Y.-T. Punctuation and Parallel Corpus Based Word Embedding Model for Low-Resource Languages. Information 2020, 11, 24. https://doi.org/10.3390/info11010024
Yuan Y, Li X, Yang Y-T. Punctuation and Parallel Corpus Based Word Embedding Model for Low-Resource Languages. Information. 2020; 11(1):24. https://doi.org/10.3390/info11010024
Chicago/Turabian StyleYuan, Yang, Xiao Li, and Ya-Ting Yang. 2020. "Punctuation and Parallel Corpus Based Word Embedding Model for Low-Resource Languages" Information 11, no. 1: 24. https://doi.org/10.3390/info11010024
APA StyleYuan, Y., Li, X., & Yang, Y.-T. (2020). Punctuation and Parallel Corpus Based Word Embedding Model for Low-Resource Languages. Information, 11(1), 24. https://doi.org/10.3390/info11010024





