Waveform Optimization of Compressed Sensing Radar without Signal Recovery
Abstract
1. Introduction
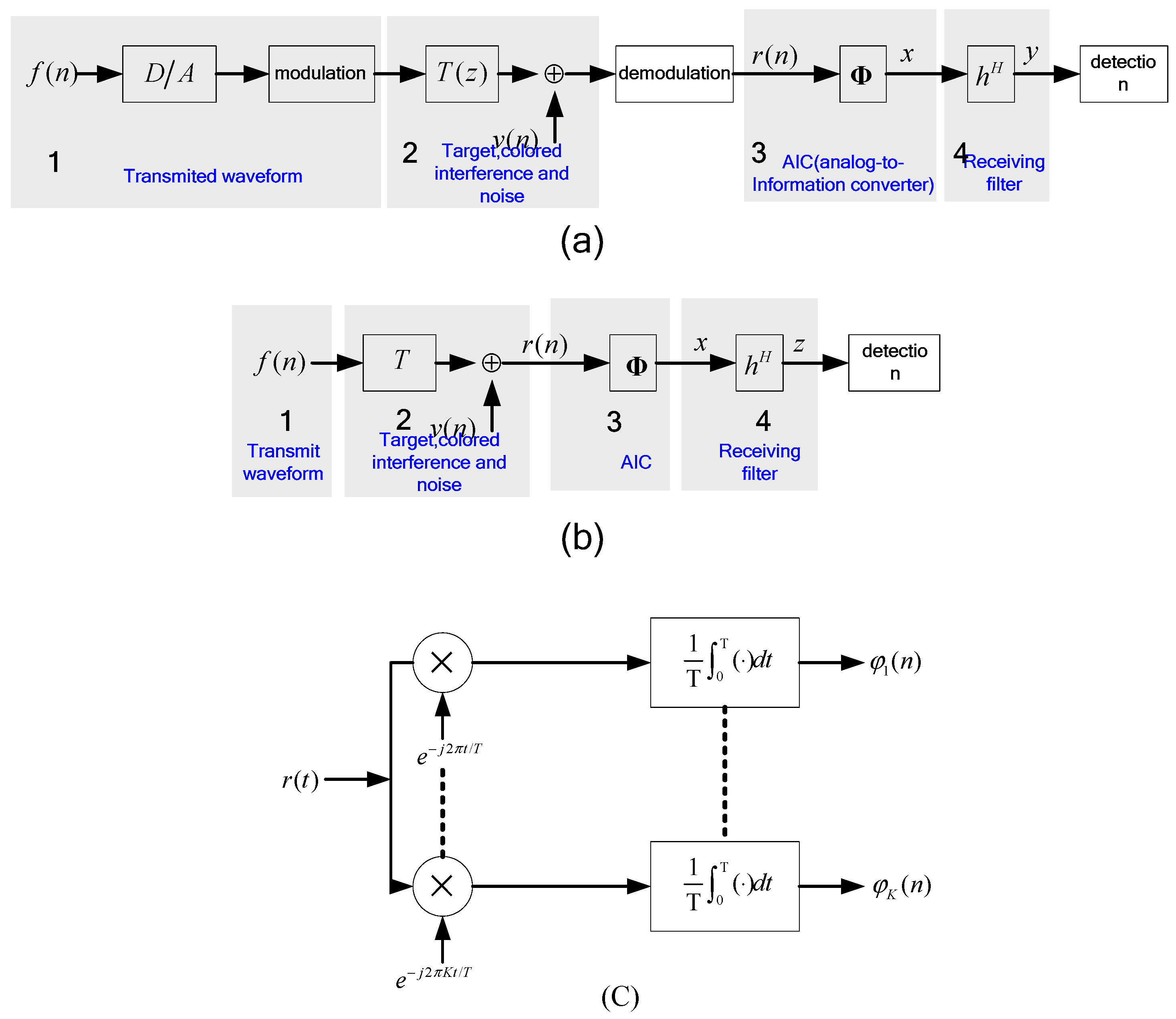
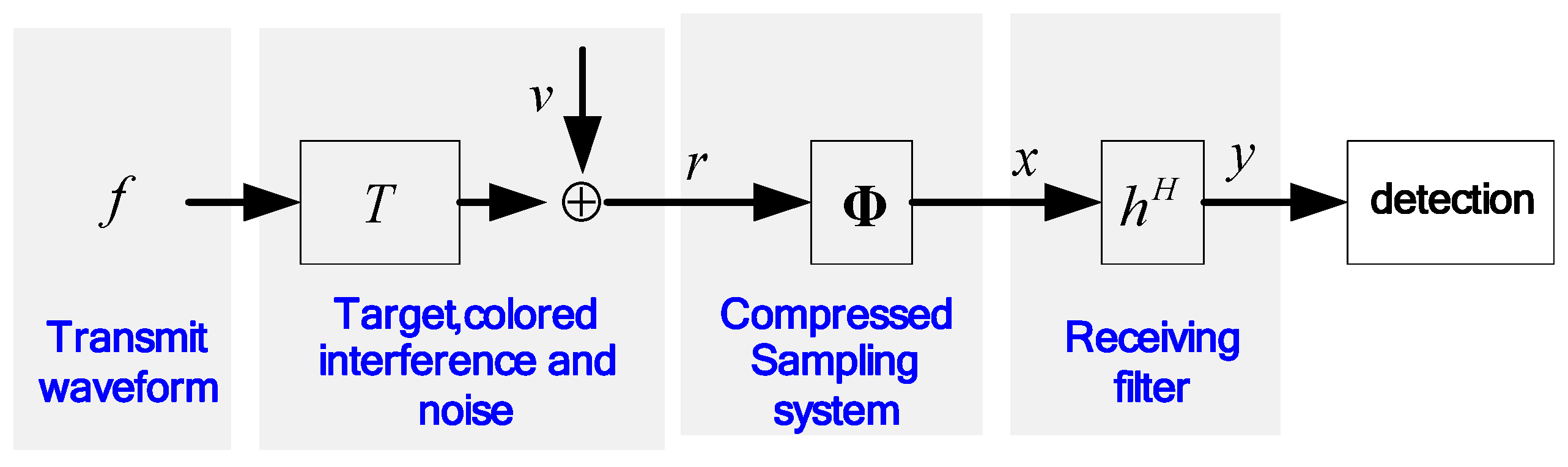
2. Problem Formulation
3. Optimizing Methods for Deterministic Target Impulse Response
4. Iterative Method with Random Target Impulse Response
- (1)
- Compute
- (2)
- Use the resulting to update h via (27).
- (3)
- Calculate
- (4)
- Use the principal component of to update f via (29).
- (5)
- .
- (6)
- The SINR subject to the power constraint via (13), then repeat until convergence. When SINR basically does not change much, (f, h) can be considered to converge. We can also set the number of iterations according to the accuracy requirements.
5. Numerical Results
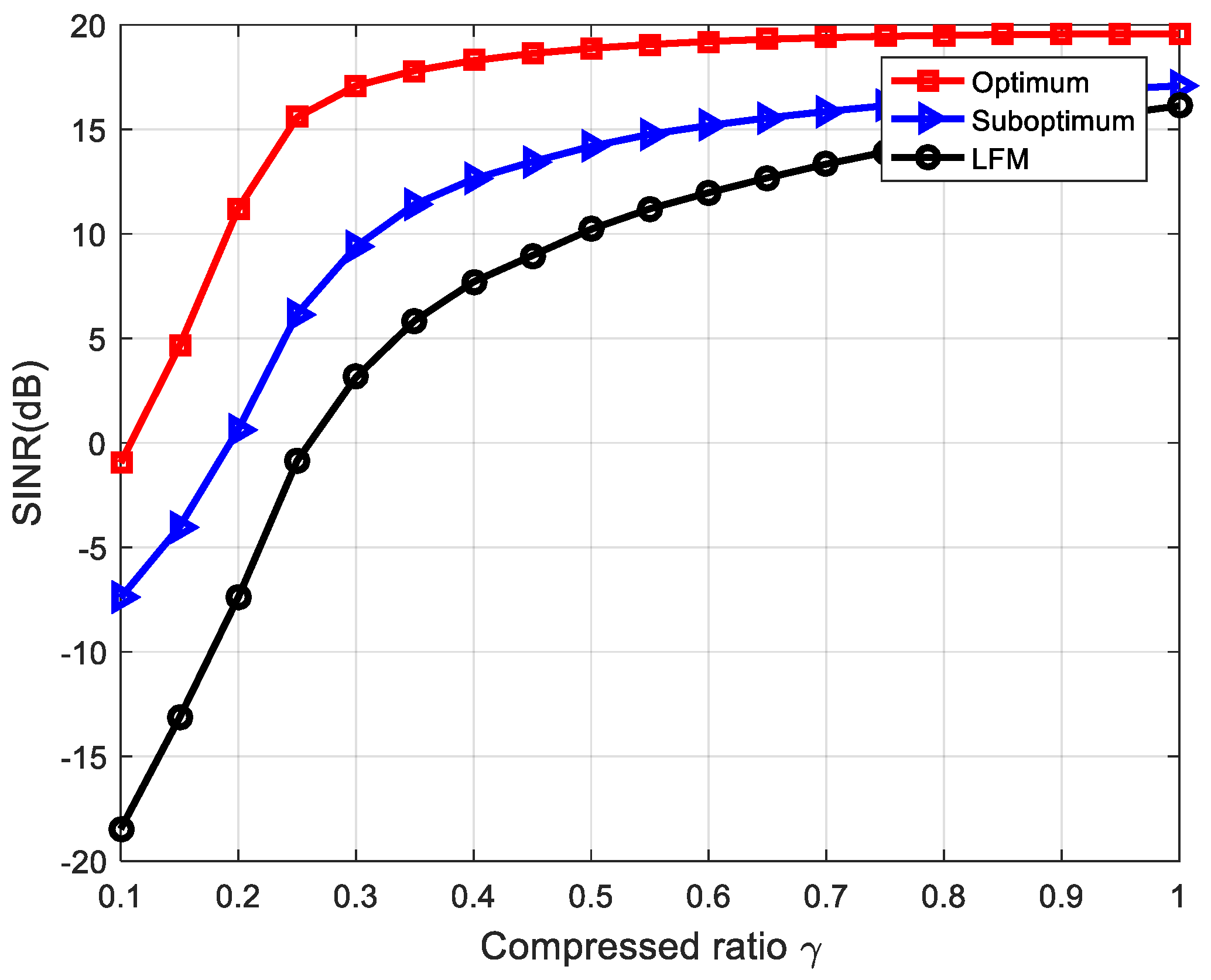
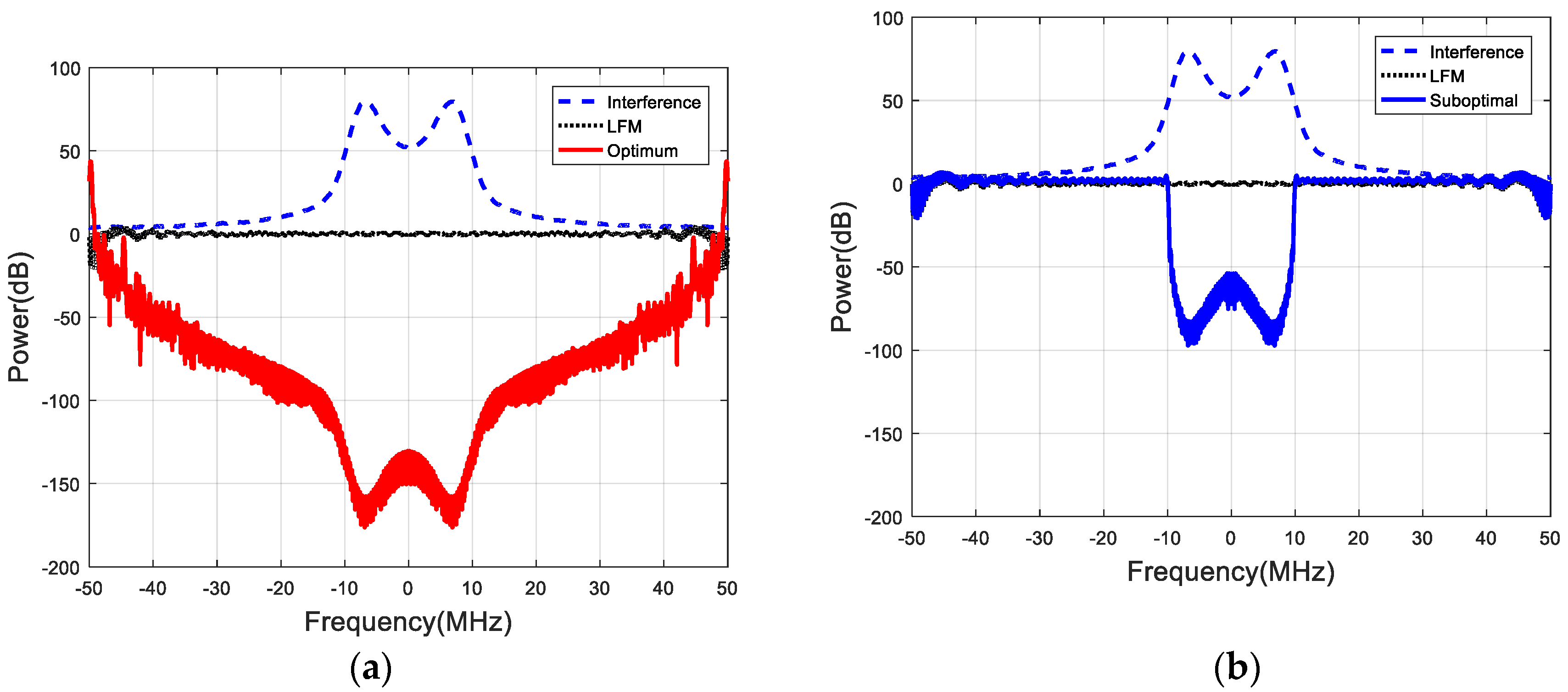
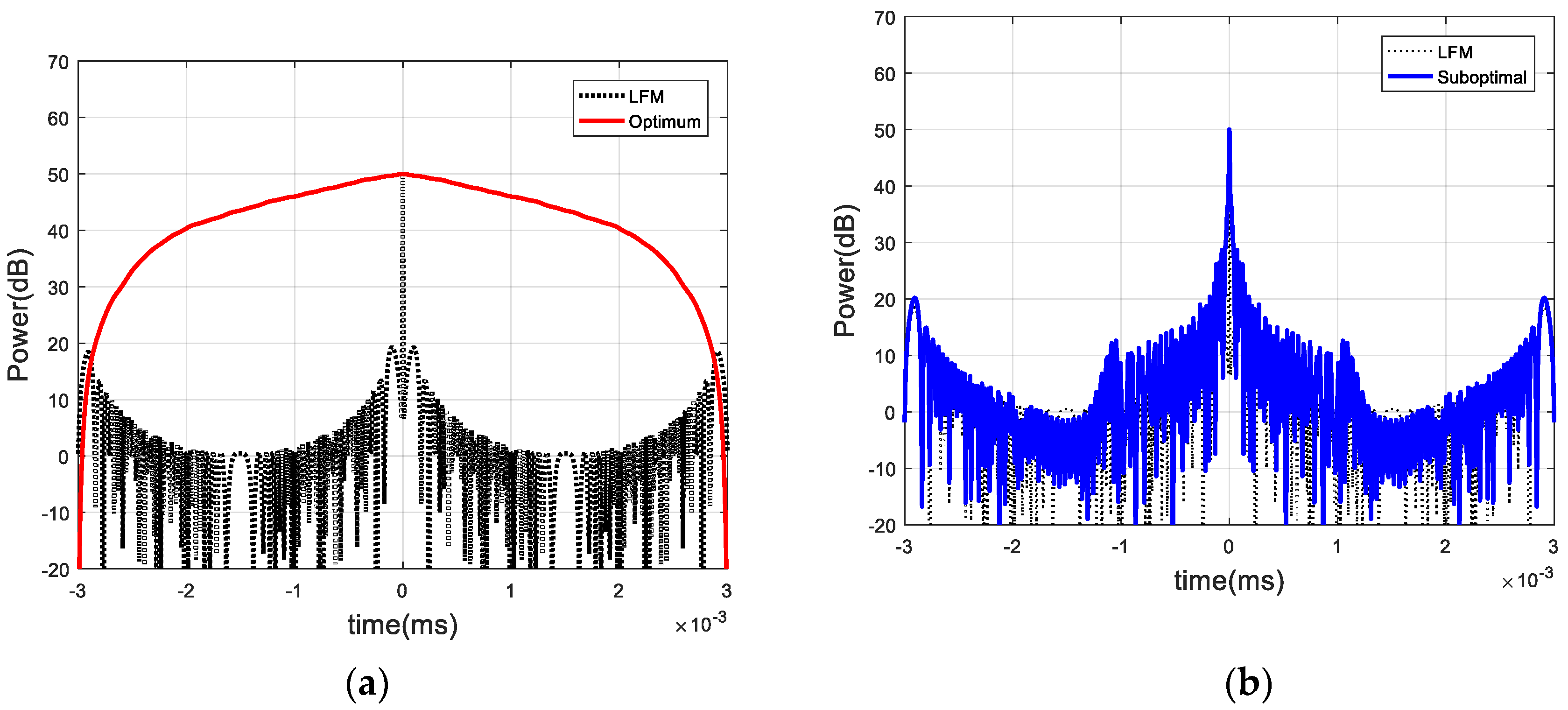
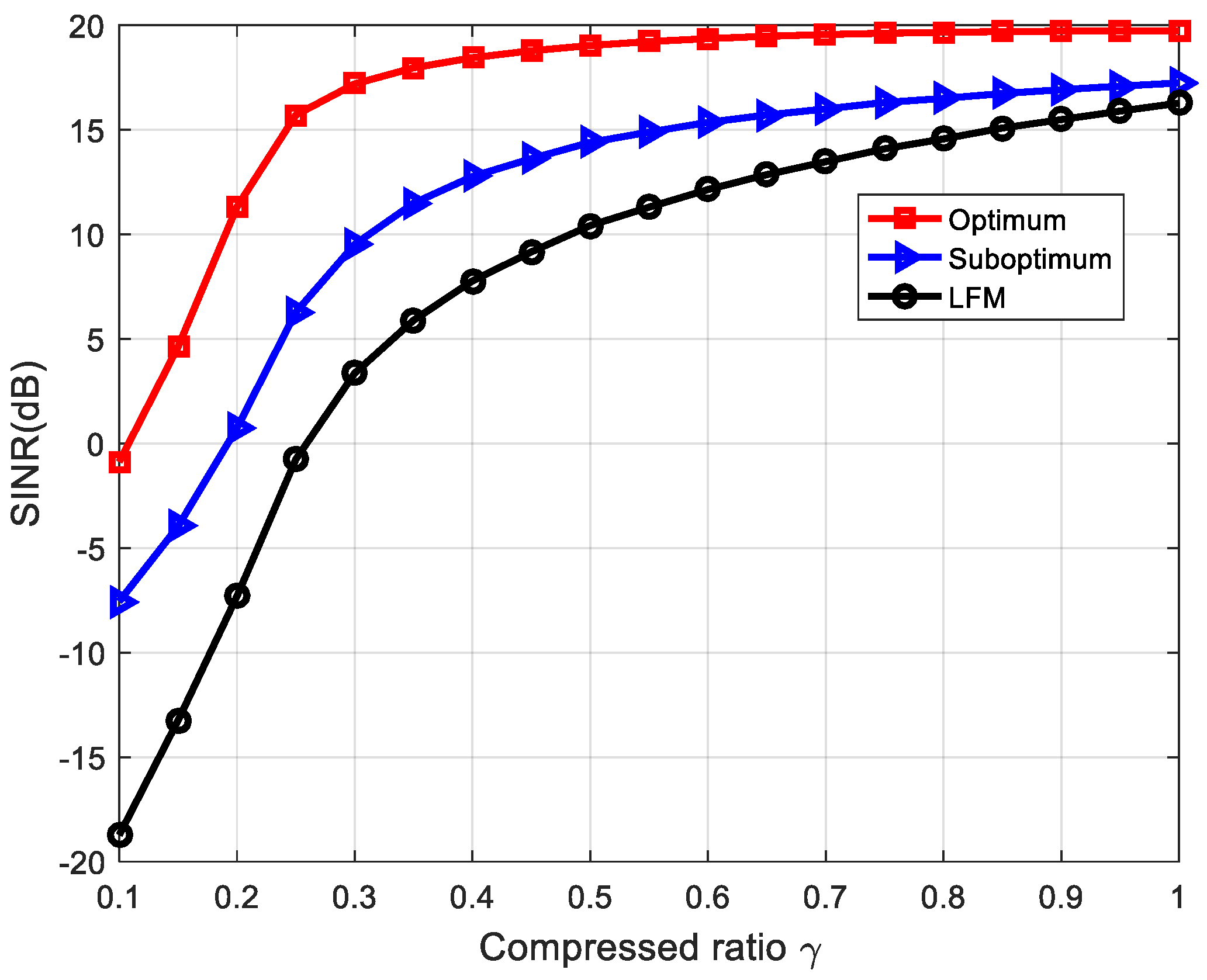
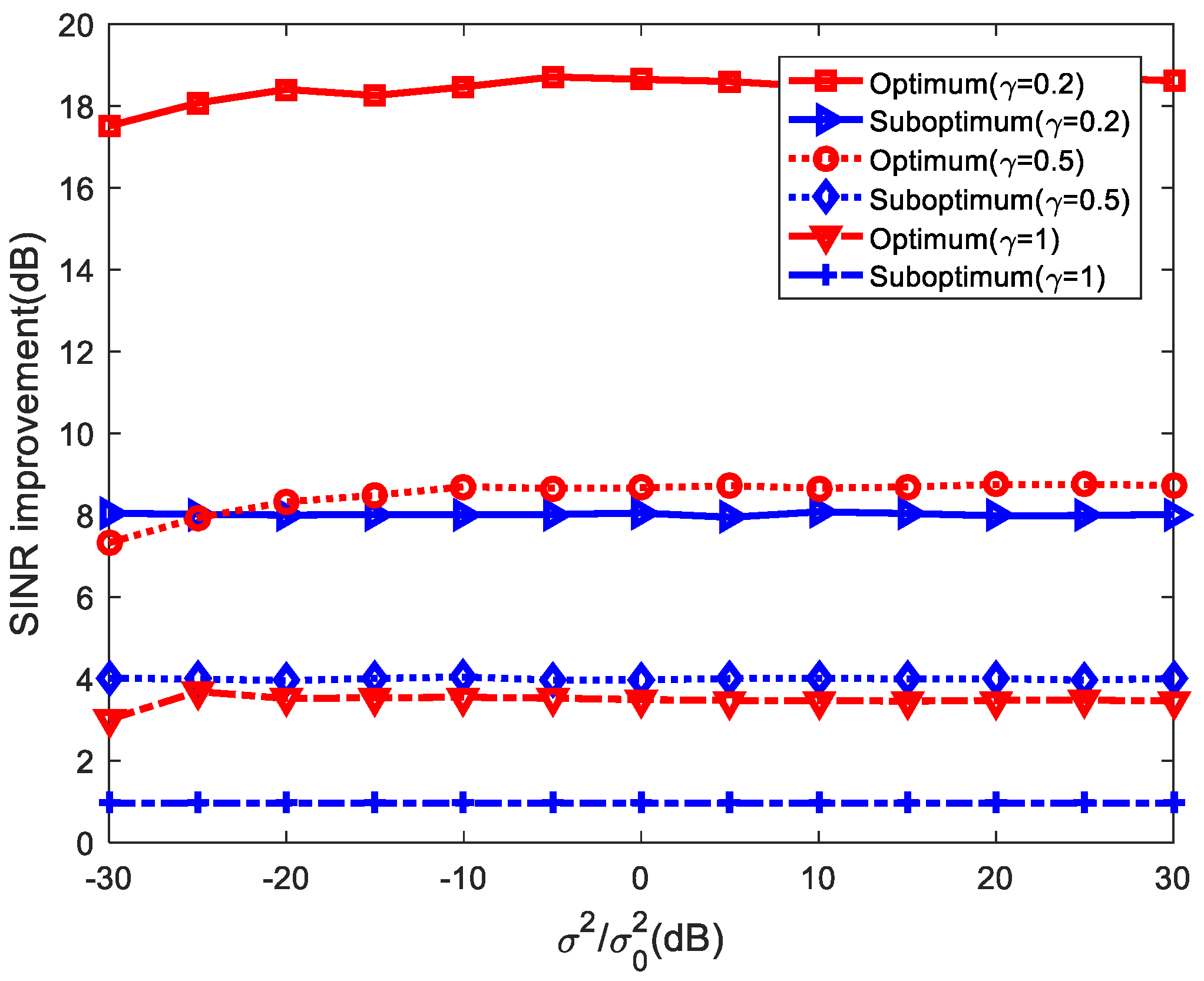
5.1. Deterministic Target Impulse Response
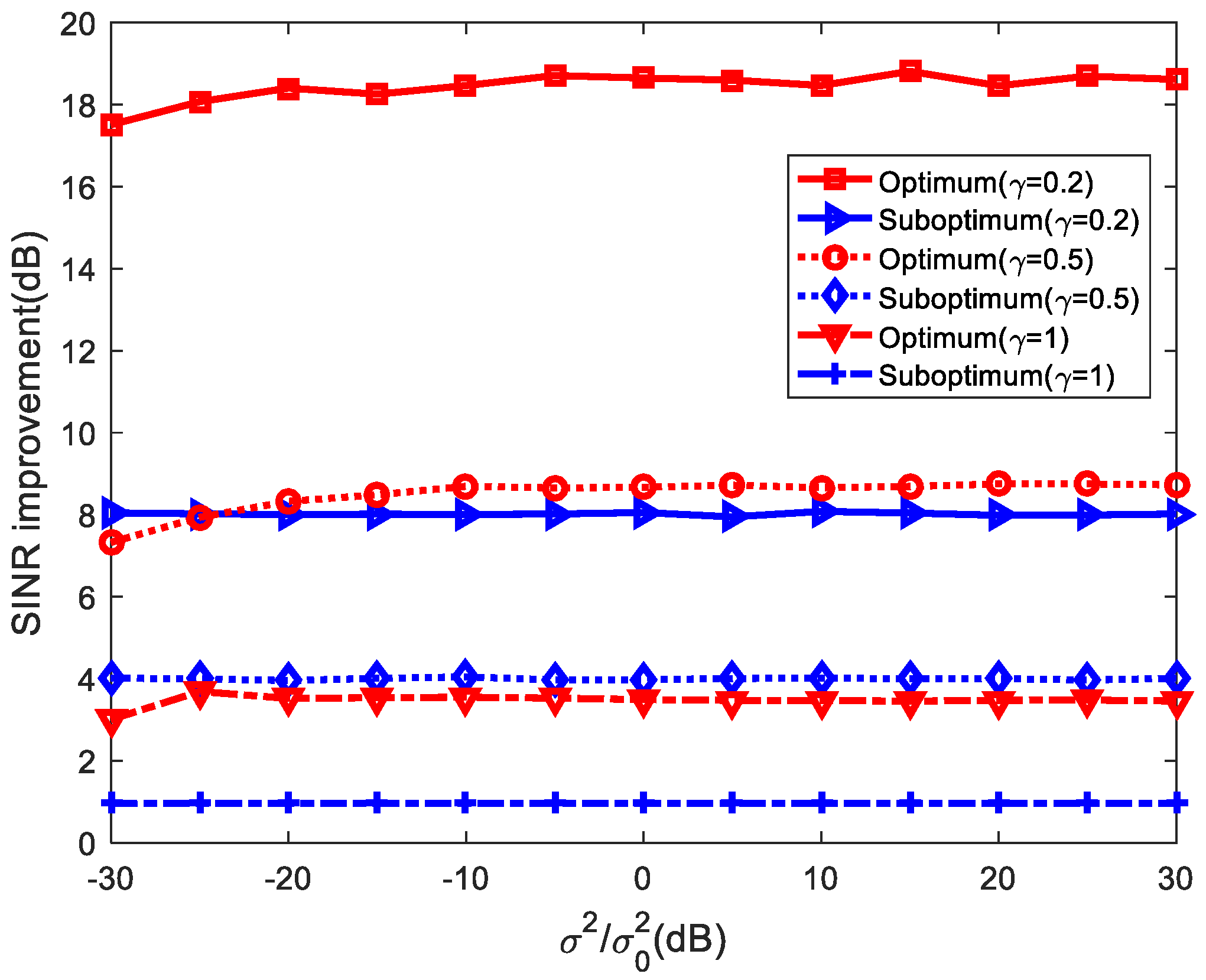
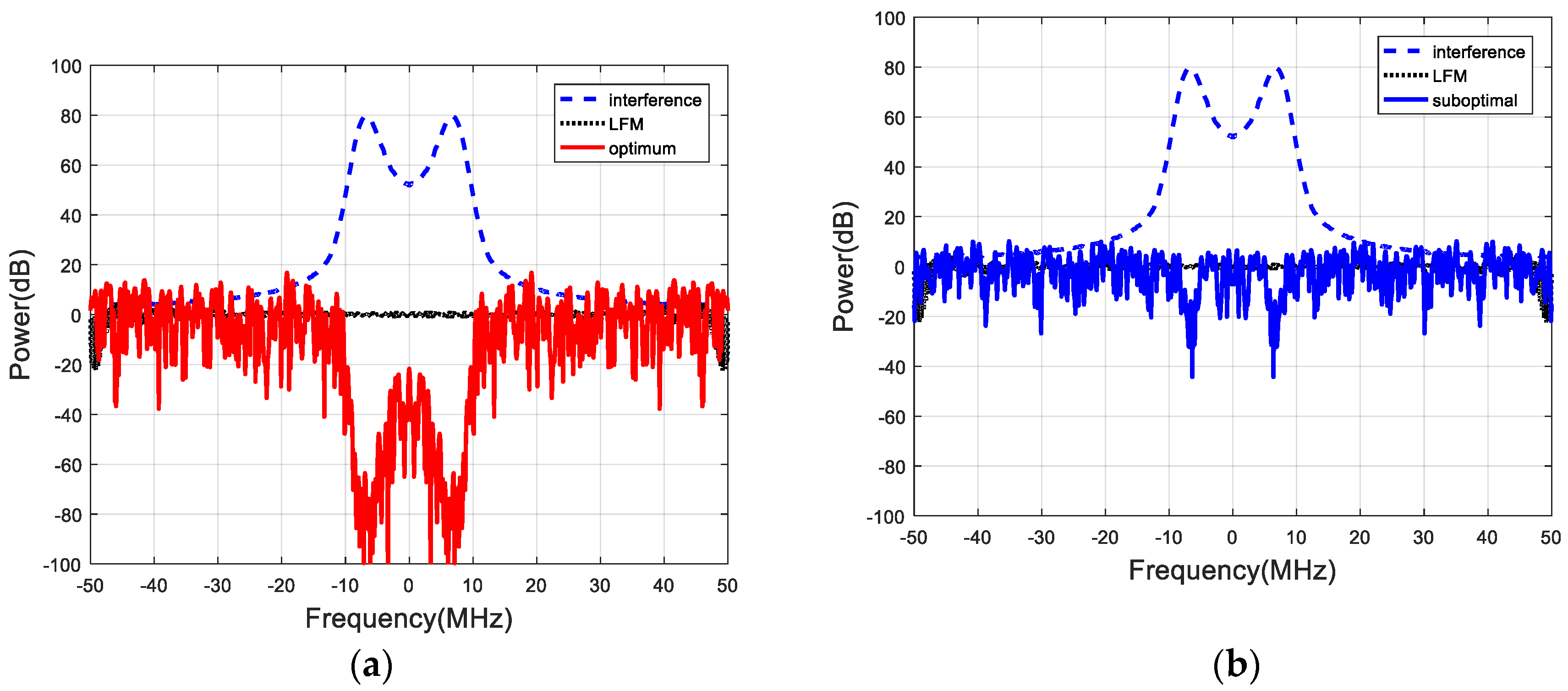
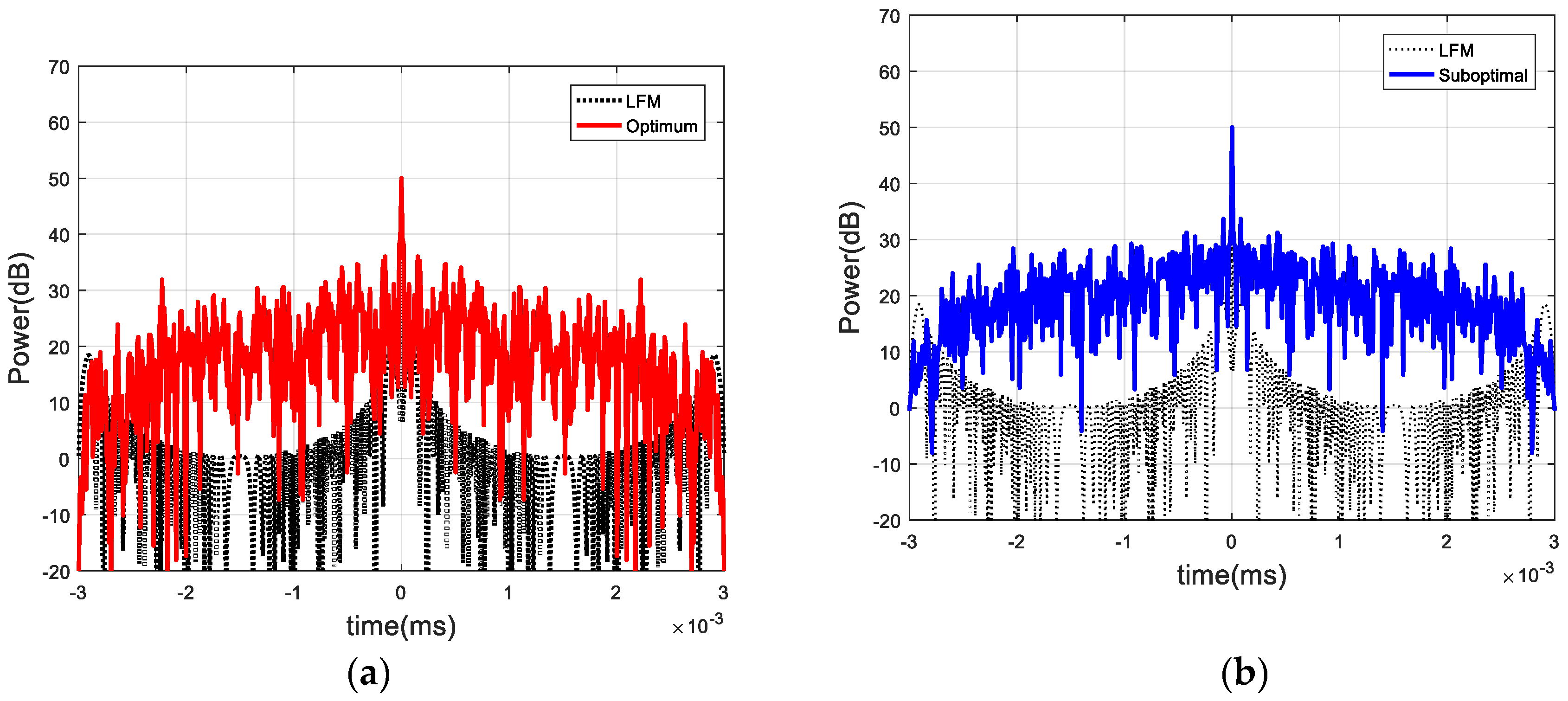
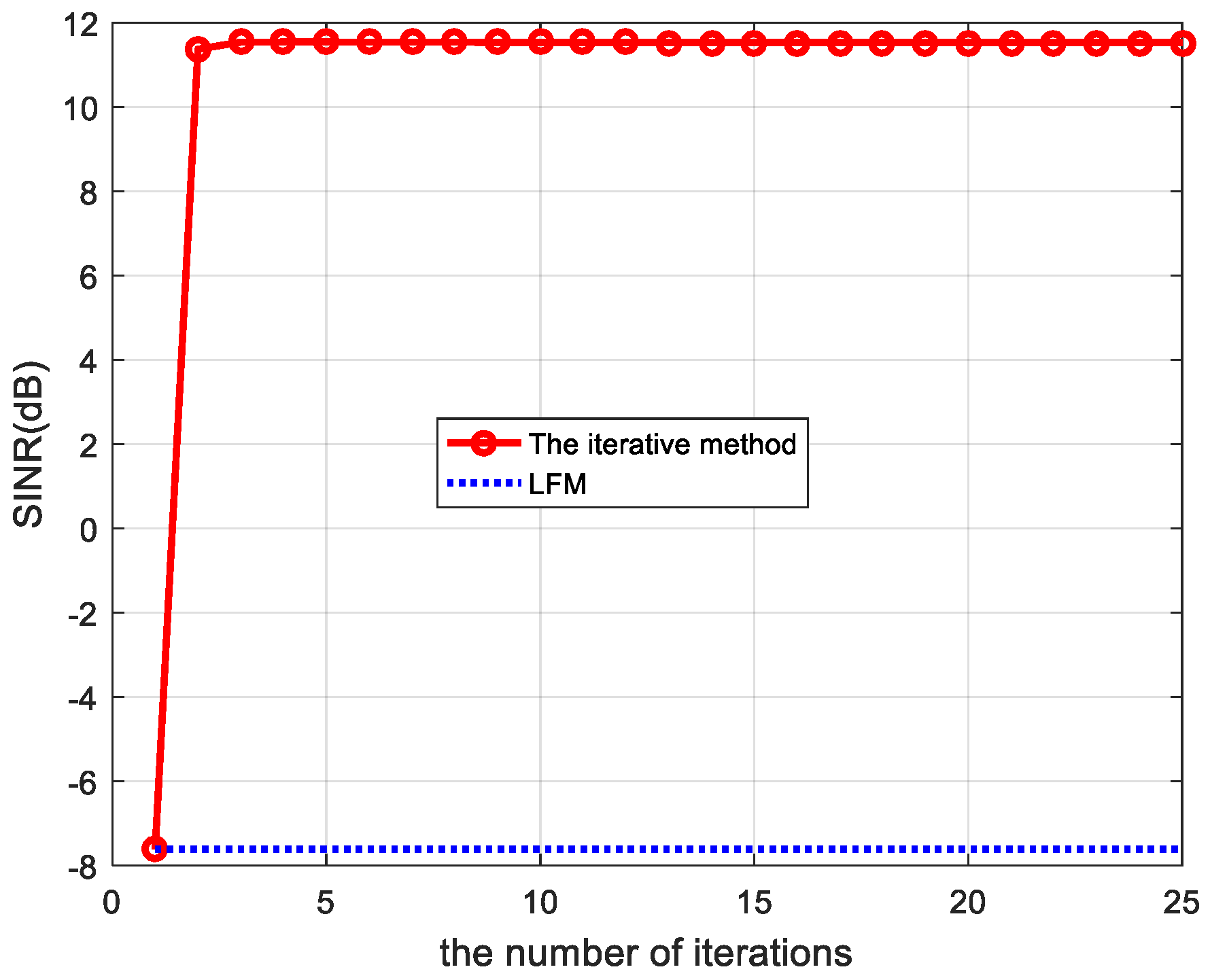
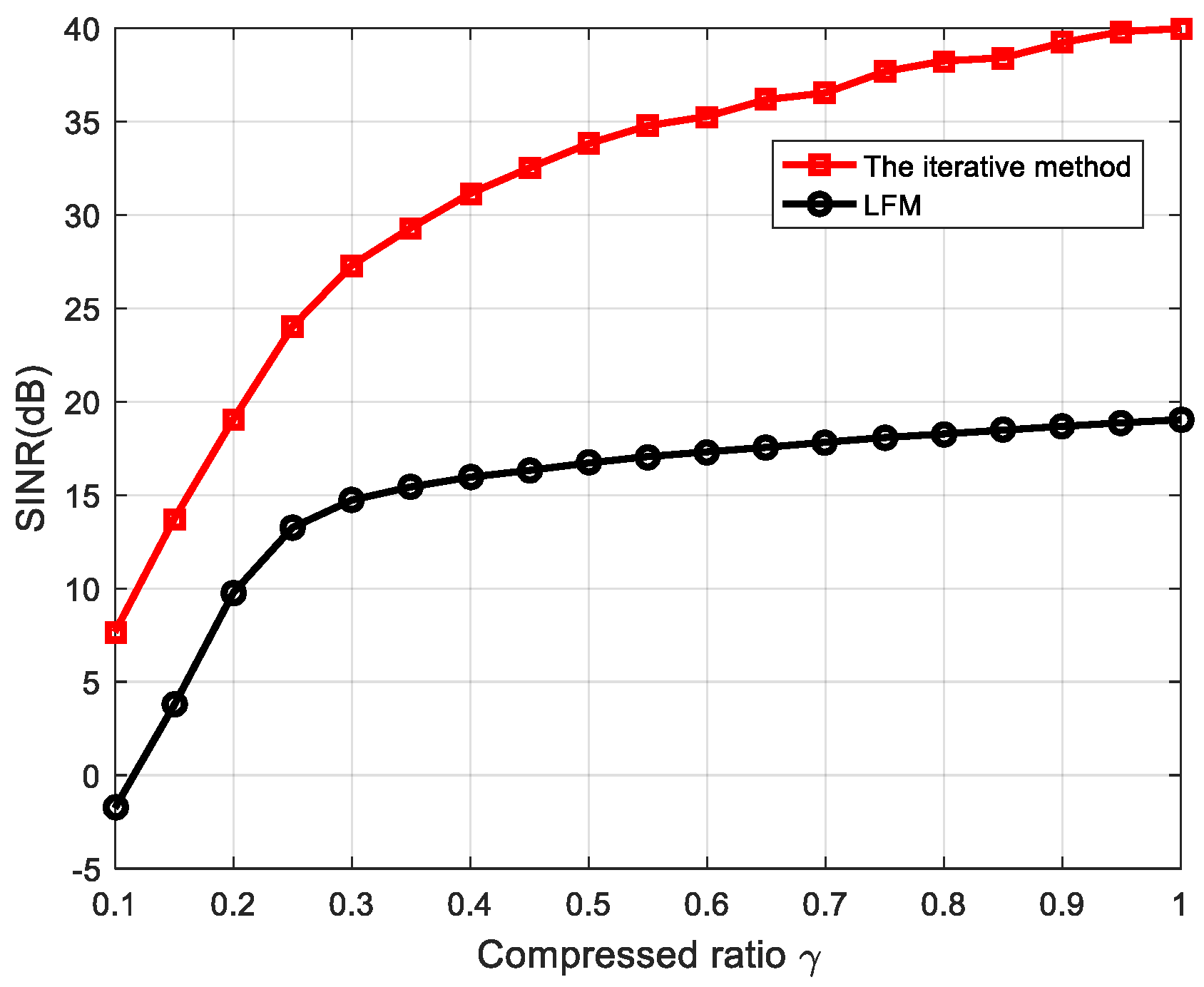
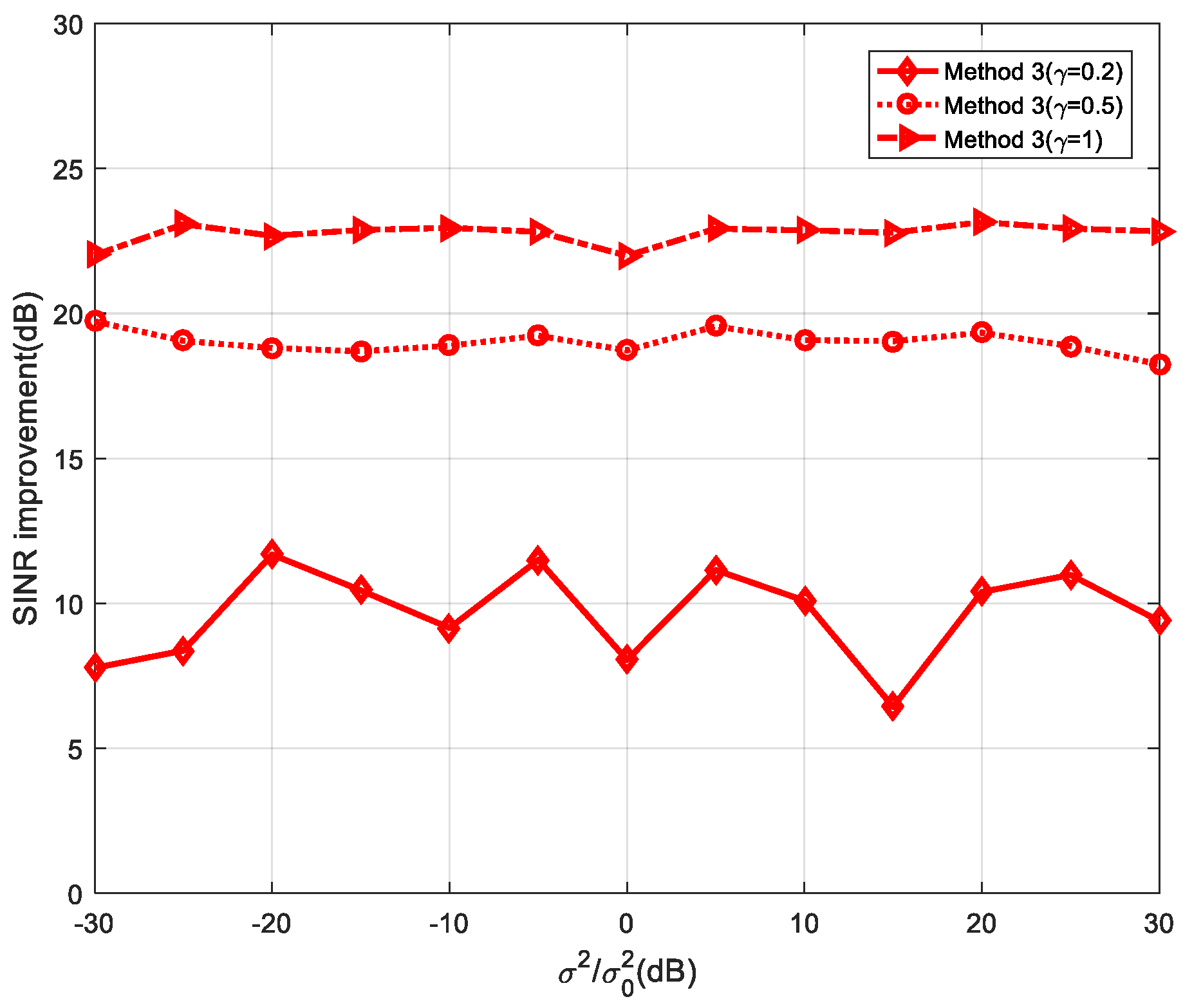
5.2. Random Target Impulse Response
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aubry, A.; Carotenuto, V.; Maio, A.D.; Farina, A.; Pallotta, L. Optimization theory-based radar waveform design for spectrally dense environments. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 14–25. [Google Scholar] [CrossRef]
- Garren, D.A.; Odom, A.C.; Osborn, M.K.; Goldstein, J.S.; Pillai, S.U.; Guerci, J.R. Full-polarization matched-illumination for target detection and identification. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 824–837. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Foglia, G.; Piezzo, M. Intrapulse radar-embedded communications via multiobjective optimization. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2960–2974. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Herman, M.; Strohmer, T. Compressed sensing radar. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 1509–1512. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. Compressed sensing in MIMO radar. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 41–44. [Google Scholar]
- Baraniuk, R.; Steeghs, P. Compressive Radar Imaging. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 128–133. [Google Scholar]
- Herman, M.A.; Strohmer, T. High-Resolution Radar via Compressed Sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Zhang, G. Adaptive Compressed Sensing Radar Oriented Toward Cognitive Detection in Dynamic Sparse Target Scene. IEEE Trans. Signal Process. 2012, 60, 1718–1729. [Google Scholar] [CrossRef]
- Davenport, M.A.; Boufounos, P.T.; Wakin, M.B.; Baraniuk, R.G. Signal Processing with Compressive Measurements. IEEE J. Sel. Top. Signal Process. 2010, 4, 445–460. [Google Scholar] [CrossRef]
- Wang, Z.; Arce, G.R.; Sadler, B.M. Subspace compressive detection for sparse signals. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3873–3876. [Google Scholar]
- Ahmed, K.; Kothuri, S.; Patwary, M.; Abdel-Maguid, M. Subspace compressive GLRT detector for airborne MIMO Radar. In Proceedings of the 2010 16th Asia-Pacific Conference on Communications (APCC), Auckland, New Zealand, 31 October–3 November 2010; pp. 302–306. [Google Scholar]
- Subotic, N.S.; Thelen, B.; Cooper, K.; Buller, W.; Parker, J.; Browning, J.; Beyer, H. Distributed RADAR waveform design based on compressive sensing considerations. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice Hall signal processing series; Prentice-Hall PTR: Englewood Cliffs, NJ, USA, 1998; ISBN 978-0-13-345711-7. [Google Scholar]
- Mishra, K.V.; Shoshan, E.; Namer, M.; Meltsin, M.; Cohen, D.; Madmoni, R.; Dror, S.; Ifraimov, R.; Eldar, Y.C. Cognitive sub-Nyquist hardware prototype of a collocated MIMO radar. In Proceedings of the 2016 4th International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Aachen, Germany, 19–22 September 2016; pp. 56–60. [Google Scholar]
- Karbasi, S.M.; Aubry, A.; De Maio, A.; Bastani, M.H. Robust Transmit Code and Receive Filter Design for Extended Targets in Clutter. IEEE Trans. Signal Process. 2015, 63, 1965–1976. [Google Scholar] [CrossRef]
- Berger, C.R.; Zhou, S.; Willett, P. Signal extraction using compressed sensing for passive radar with OFDM signals. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–6. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. MIMO Radar Waveform Optimization with Prior Information of the Extended Target and Clutter. IEEE Trans. Signal Process. 2009, 57, 3533–3544. [Google Scholar] [CrossRef]
- Cheng, X.; Aubry, A.; Ciuonzo, D.; De Maio, A.; Wang, X. Robust Waveform and Filter Bank Design of Polarimetric Radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 370–384. [Google Scholar] [CrossRef]
- Romero, R.A.; Bae, J.; Goodman, N.A. Theory and Application of SNR and Mutual Information Matched Illumination Waveforms. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 912–927. [Google Scholar] [CrossRef]
- Bergin, J.S.; Techau, P.M.; Carlos, J.E.D.; Guerci, J.R. Radar waveform optimization for colored noise mitigation. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 149–154. [Google Scholar]
- Pillai, S.U.; Oh, H.S.; Youla, D.C.; Guerci, J.R. Optimal transmit-receiver design in the presence of signal-dependent interference and channel noise. IEEE Trans. Inf. Theory 2000, 46, 577–584. [Google Scholar] [CrossRef]
- Li, J.; Guerci, J.R.; Xu, L. Signal Waveform’s Optimal-under-Restriction Design for Active Sensing. IEEE Signal Process. Lett. 2006, 13, 565–568. [Google Scholar] [CrossRef]
- Foutz, J.; Spanias, A.; Banavar, M.K. Narrowband Direction of Arrival Estimation for Antenna Arrays. Synth. Lect. Antennas 2008, 3, 1–76. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. On the Statistical Invariance for Adaptive Radar Detection in Partially Homogeneous Disturbance Plus Structured Interference. IEEE Trans. Signal Process. 2017, 65, 1222–1234. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid Convergence Rate in Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- De Maio, A.; Pallotta, L.; Li, J.; Stoica, P. Loading Factor Estimation Under Affine Constraints on the Covariance Eigenvalues with Application to Radar Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1269–1283. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Pallotta, L. A Geometric Approach to Covariance Matrix Estimation and its Applications to Radar Problems. IEEE Trans. Signal Process. 2018, 66, 907–922. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Sun, Y. Waveform Optimization of Compressed Sensing Radar without Signal Recovery. Information 2019, 10, 271. https://doi.org/10.3390/info10090271
Wang Q, Sun Y. Waveform Optimization of Compressed Sensing Radar without Signal Recovery. Information. 2019; 10(9):271. https://doi.org/10.3390/info10090271
Chicago/Turabian StyleWang, Quanhui, and Ying Sun. 2019. "Waveform Optimization of Compressed Sensing Radar without Signal Recovery" Information 10, no. 9: 271. https://doi.org/10.3390/info10090271
APA StyleWang, Q., & Sun, Y. (2019). Waveform Optimization of Compressed Sensing Radar without Signal Recovery. Information, 10(9), 271. https://doi.org/10.3390/info10090271



