Analysis of Usability for the Dice CAPTCHA
Abstract
1. Introduction
- A traditional statistical analysis as in [2] makes preliminary assumptions on the data. By contrast, the association rule mining does not need any initial assumption on the data, and is able to capture dependences of multiple user’s factors on the Dice CAPTCHA solution time.
- The set of the adopted user’s features is different from the set in [2]. It includes age, education level, Internet use, device type on which Dice CAPTCHA is solved and number of attempts for obtaining a correct solution. Gender is omitted since it has no influence in both association rule mining and artificial neural network analysis.
2. Related Work
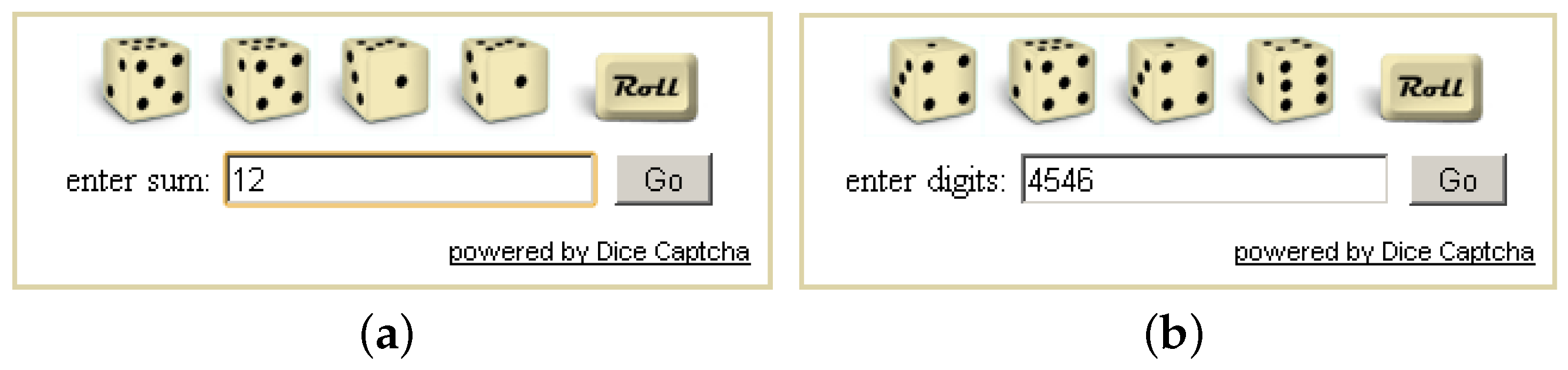
3. The Dice CAPTCHA
4. Materials and Methods
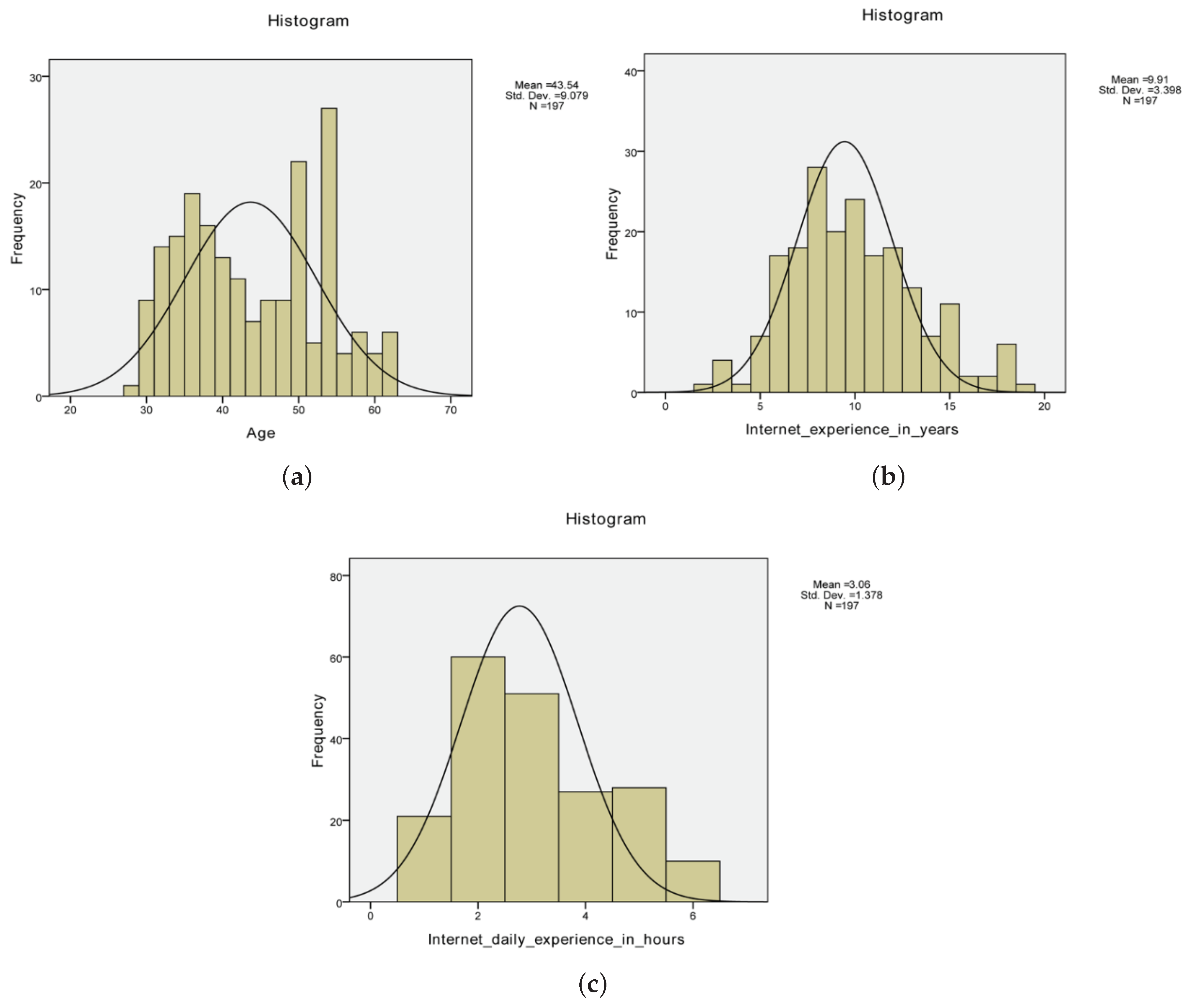
4.1. Participants
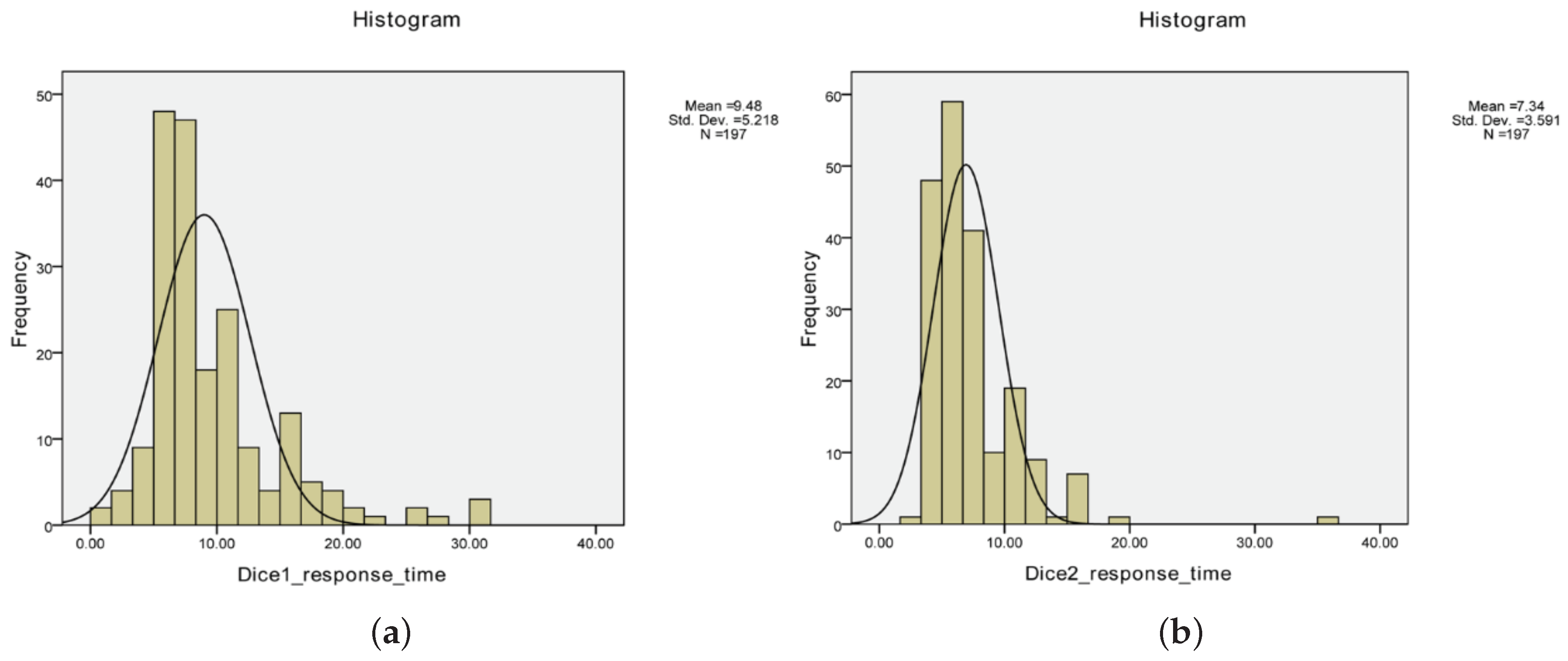
4.2. Materials
4.3. Methods
4.3.1. Modeling Features Dependence by Association Rule Mining
- support
- confidence
- lift
- conviction
- FP-tree creation
- Extraction of the frequent itemsets by FP-tree traversal
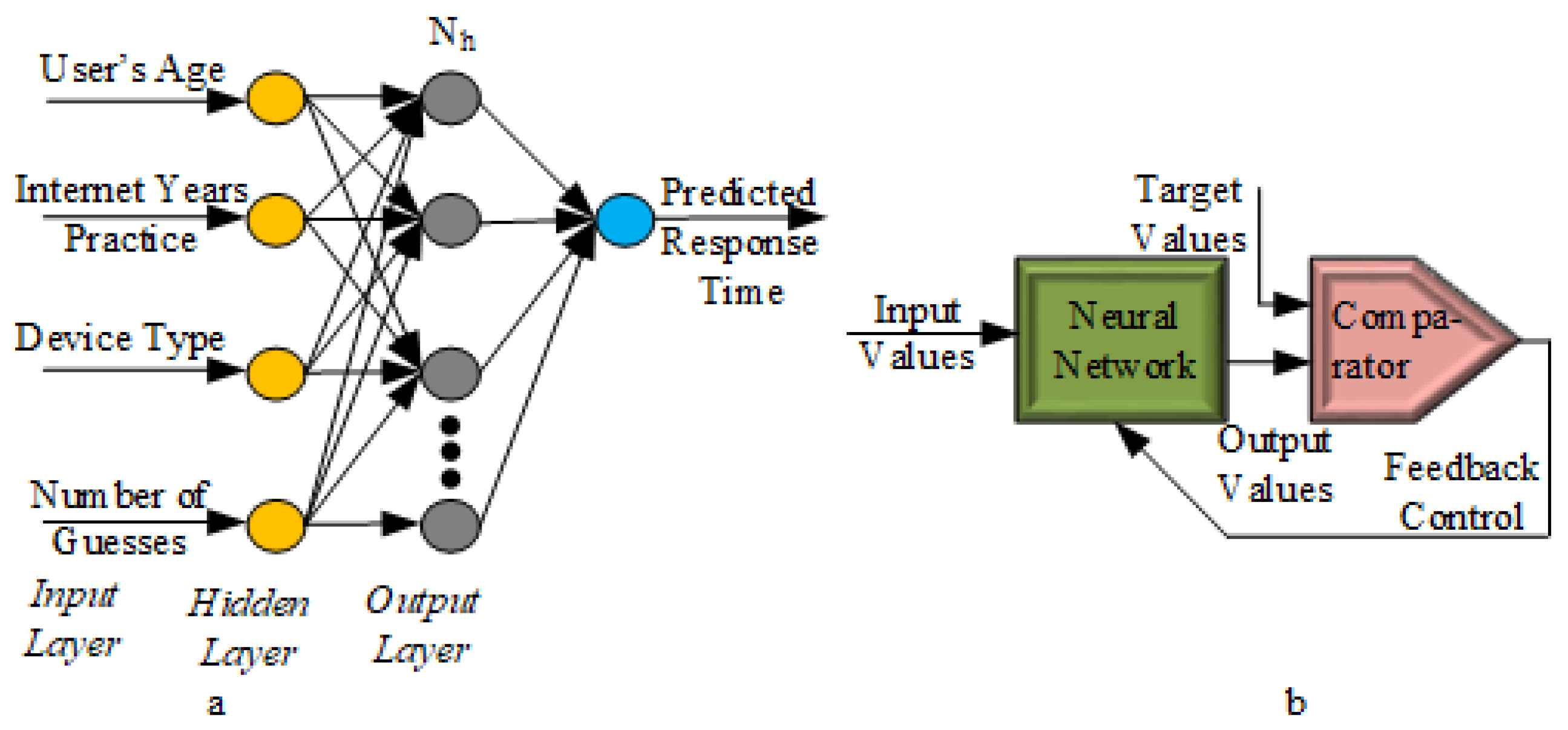
4.3.2. Modeling Features Dependence by Artificial Neural Network
5. Results
5.1. Association Rule Mining Results
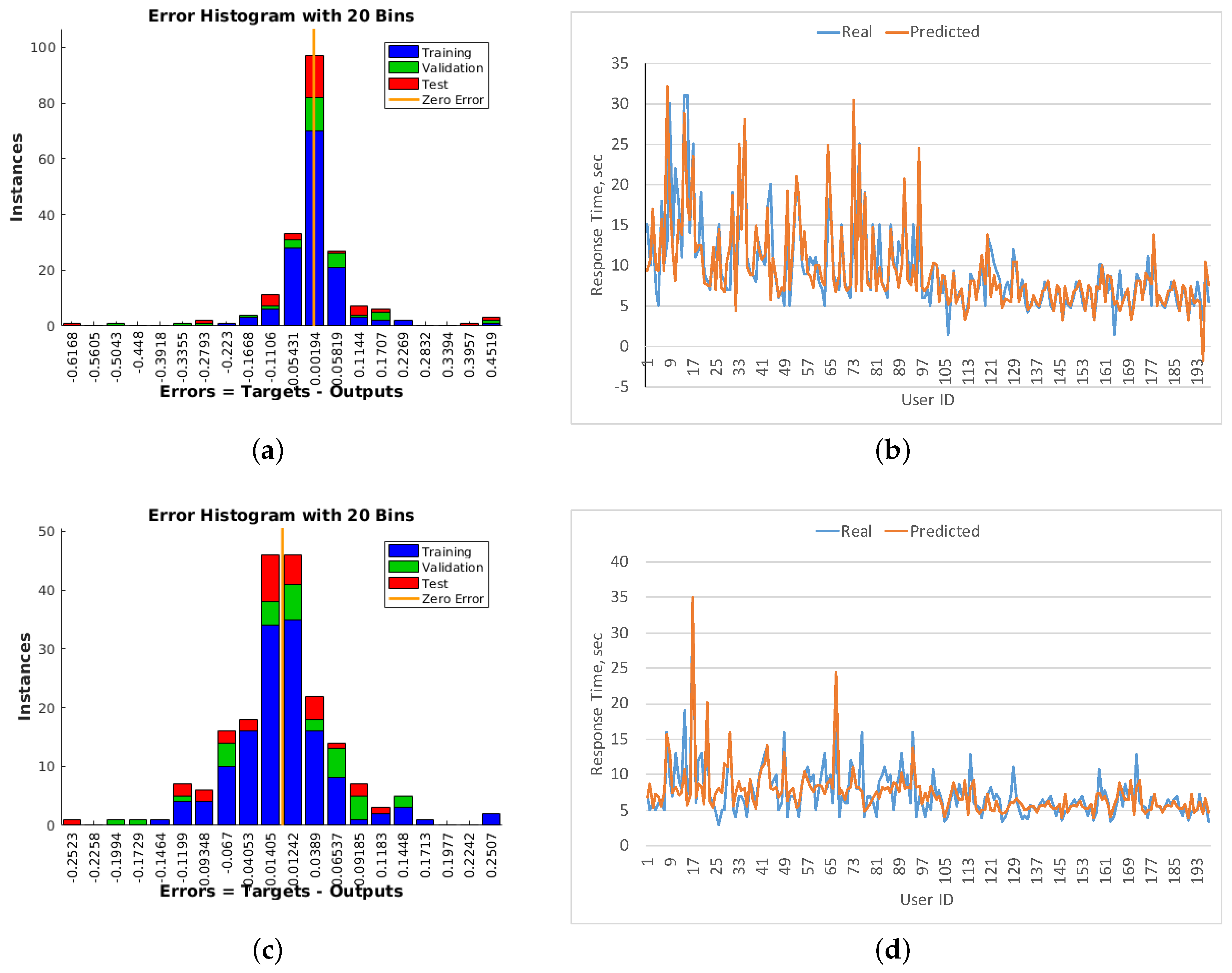
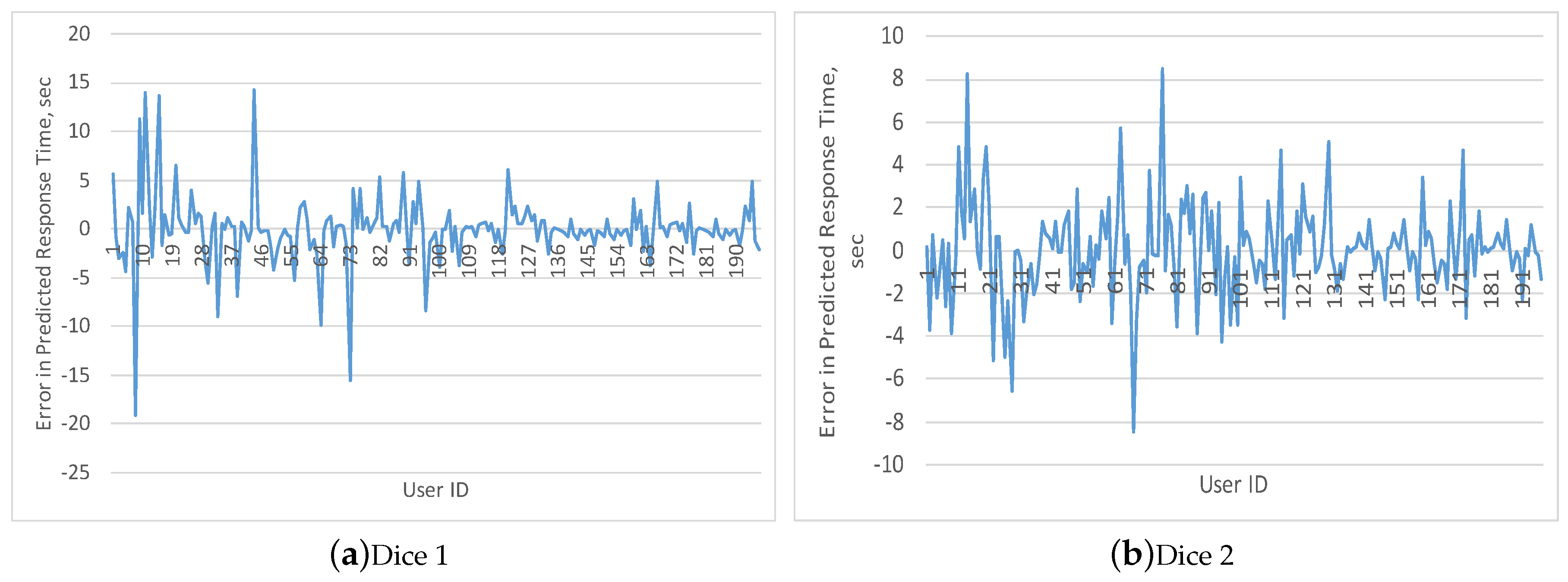
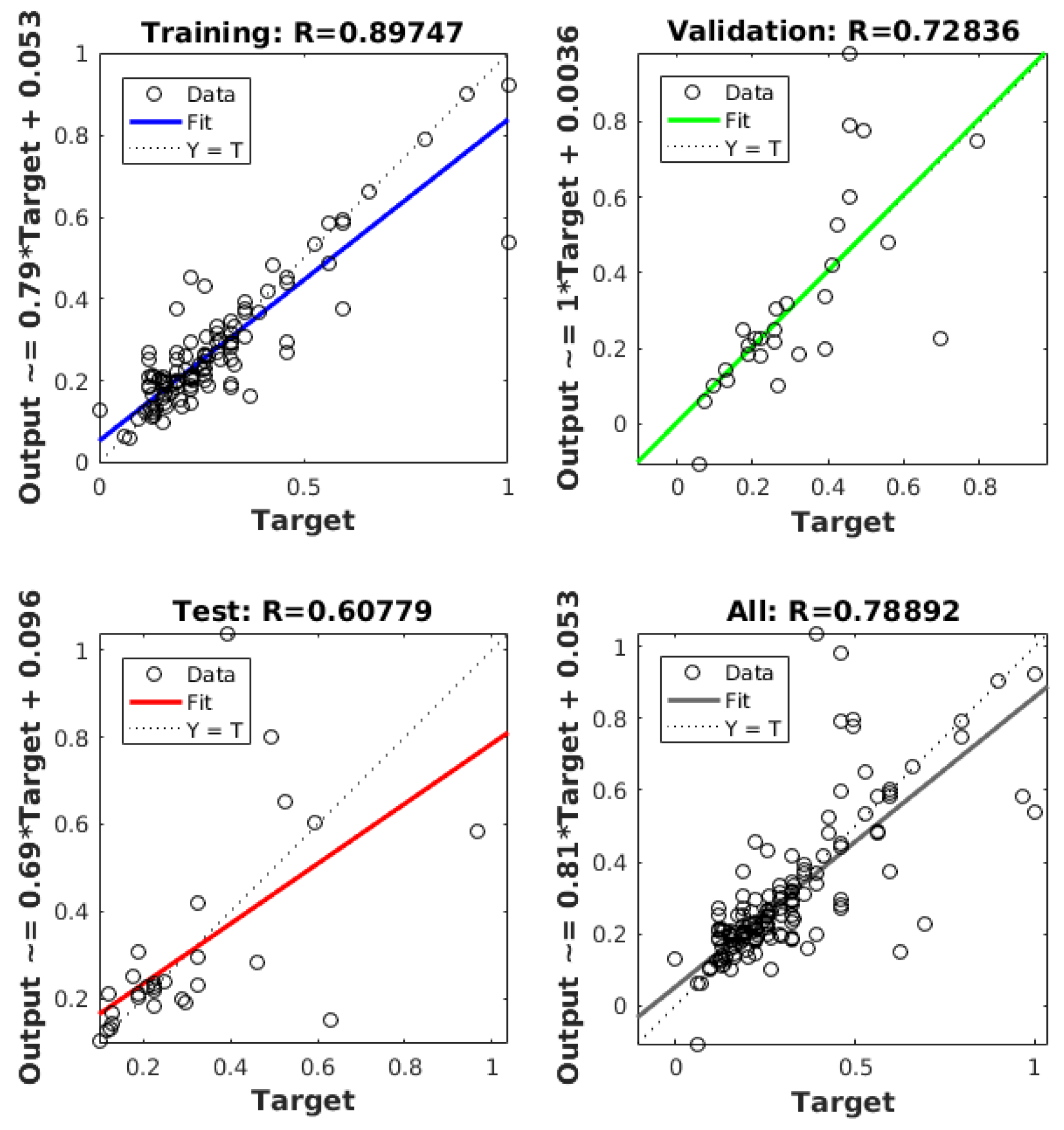
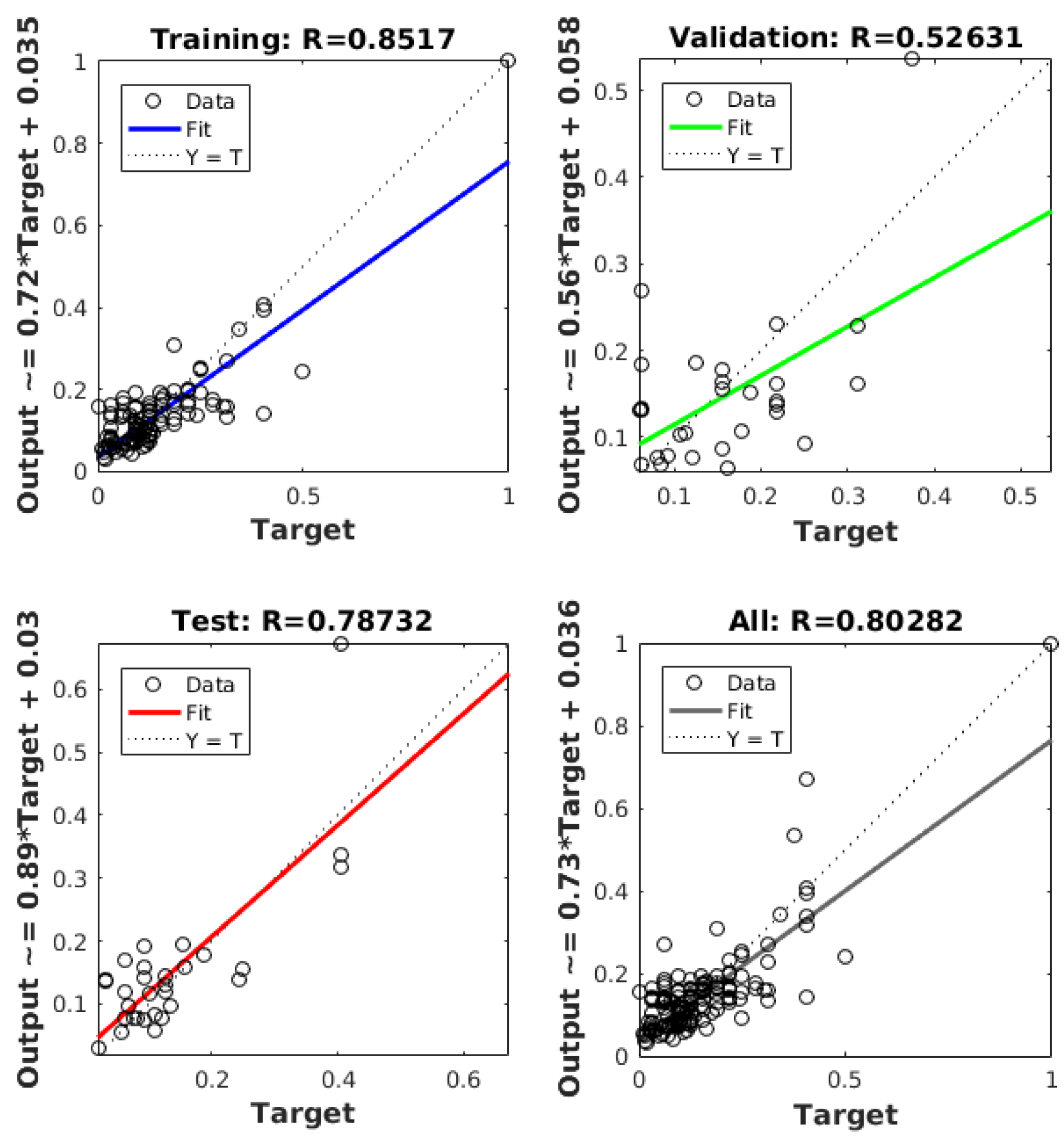
5.2. Artificial Neural Network Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ye, G.; Tang, Z.; Fang, D.; Zhu, Z.; Feng, Y.; Xu, P.; Chen, X.; Wang, Z. Yet Another Text Captcha Solver: A Generative Adversarial Network Based Approach. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, Toronto, ON, Canada, 15–19 October 2018; pp. 332–348. [Google Scholar]
- Brodić, D.; Amelio, A.; Draganov, I.R. Statistical Analysis of Dice CAPTCHA Usability. arXiv 2017, arXiv:1706.10177. [Google Scholar]
- Von Ahn, L.; Blum, M.; Hopper, N.; Langford, J. CAPTCHA: Using hard AI problems for security. In Advances in Cryptology—EUROCRYPT 2003, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; Biham, E., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2656, pp. 294–311. [Google Scholar]
- Brodić, D.; Amelio, A.; Draganov, I.R.; Janković, R. Exploring the Usability of the Dice CAPTCHA by Advanced Statistical Analysis. In Artificial Intelligence: Methodology, Systems, and Applications, Proceedings of the 18th International Conference AIMSA 2018, Varna, Bulgaria, 12–14 September 2018; Agre, G., van Genabith, J., Declerck, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11089, pp. 152–162. [Google Scholar]
- Amelio, A.; Janković, R.; Tanikić, D.; Draganov, I.R. Predicting the Usability of the Dice CAPTCHA via Artificial Neural Network. In Digital Libraries: Supporting Open Science, Proceedings of the 15th Italian Research Conference on Digital Libraries, Pisa, Italy, 31 January–1 February 2019; Manghi, P., Candela, L., Silvello, G., Eds.; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 988, pp. 44–58. [Google Scholar]
- Singh, V.P.; Pal, P. Survey of different types of CAPTCHA. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 2242–2245. [Google Scholar]
- Fidas, C.A.; Voyiatzis, A.G.; Avouris, N.M. On the necessity of user-friendly CAPTCHA. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Vancouver, BC, Canada, 7–12 May 2011; pp. 2623–2626. [Google Scholar]
- Yan, J.; El Ahmad, A.S. Usability of CAPTCHAs or usability issues in CAPTCHA design. In Proceedings of the 4th Symposium on Usable Privacy and Security, Pittsburgh, PA, USA, 23–25 July 2008; pp. 44–52. [Google Scholar]
- Beheshti, S.M.R.S.; Liatsis, P. CAPTCHA Usability and Performance, How to Measure the Usability Level of Human Interactive Applications Quantitatively and Qualitatively? In Proceedings of the International Conference on Developments of E-Systems Engineering (DeSE), Duai, UAE, 13–14 December 2015; pp. 131–136. [Google Scholar]
- Mohamed, M.; Gao, S.; Sachdeva, N.; Saxena, N.; Zhang, C.; Kumaraguru, P.; Van Oorschot, P.C. On the security and usability of dynamic cognitive game CAPTCHAs. J. Comput. Secur. 2017, 25, 205–230. [Google Scholar] [CrossRef]
- Conti, M.; Guarisco, C.; Spolaor, R. CAPTCHaStar! A Novel CAPTCHA Based on Interactive Shape Discovery. In Applied Cryptography and Network Security, Proceedings of the International Conference on Applied Cryptography and Network Security, Guildford, UK, 19–22 June 2016; Manulis, M., Sadeghi, A.-R., Schneider, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9696, pp. 611–628. [Google Scholar]
- Bursztein, E.; Bethard, S.; Fabry, C.; Mitchell, J.C.; Jurafsky, D. How Good Are Humans at Solving CAPTCHAs? A Large Scale Evaluation. In Proceedings of the 2010 IEEE Symposium on Security and Privacy, Berkeley/Oakland, CA, USA, 16–19 May 2010; pp. 399–413. [Google Scholar]
- Brodić, D.; Amelio, A.; Janković, R. Exploring the influence of CAPTCHA types to the users response time by statistical analysis. Multimed. Tools Appl. 2017, 77, 12293–12329. [Google Scholar] [CrossRef]
- Wilkins, J. Strong CAPTCHA guidelines v1.2 Retrieved Nov. Available online: http://www.123seminarsonly.com/Seminar-Reports/008/47584359-captcha.pdf (accessed on 25 June 2019).
- Sullivan, D.G. Data Mining V: Preparing the Data; Boston University: Boston, MA, USA, 2013. [Google Scholar]
- Bradley, P.S.; Mangasarian, O.L.; Street, W.N. Clustering via Concave Minimization. In Advances in Neural Information Processing Systems, Proceedings of the Conference on Neural Information Processing Systems, Princeton, NJ, USA, 1–7 December 1996; ACM: New York, NY, USA, 1996; pp. 368–374. [Google Scholar]
- Tan, P.-N.; Steinbach, M.; Kumar, V. Introduction to Data Mining, 1st ed.; Addison–Wesley Longman Publishing Co.: Boston, MA, USA, 2005. [Google Scholar]
- Tanikić, D.; Marinković, V.; Manić, M.; Devedžić, G.; Randelović, S. Application of response surface methodology and fuzzy logic based system for determining cutting temperature. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 435–445. [Google Scholar] [CrossRef][Green Version]
- LeCun, Y. A Theoretical Framework for Back-Propagation. In Proceedings of the Connectionist Models Summer School, Pittsburgh, PA, USA, 17–26 June 1988; pp. 21–28. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- SPSS Tutorials: Pearson Correlation. Available online: https://libguides.library.kent.edu/SPSS/PearsonCorr (accessed on 25 June 2019).
- Iantovics, B.; Corina, R.; Muaz, N. MetrIntPair—A novel accurate metric for the comparison of two cooperative multiagent systems intelligence based on paired intelligence measurements. Int. J. Intell. Syst. 2018, 33, 463–486. [Google Scholar] [CrossRef]
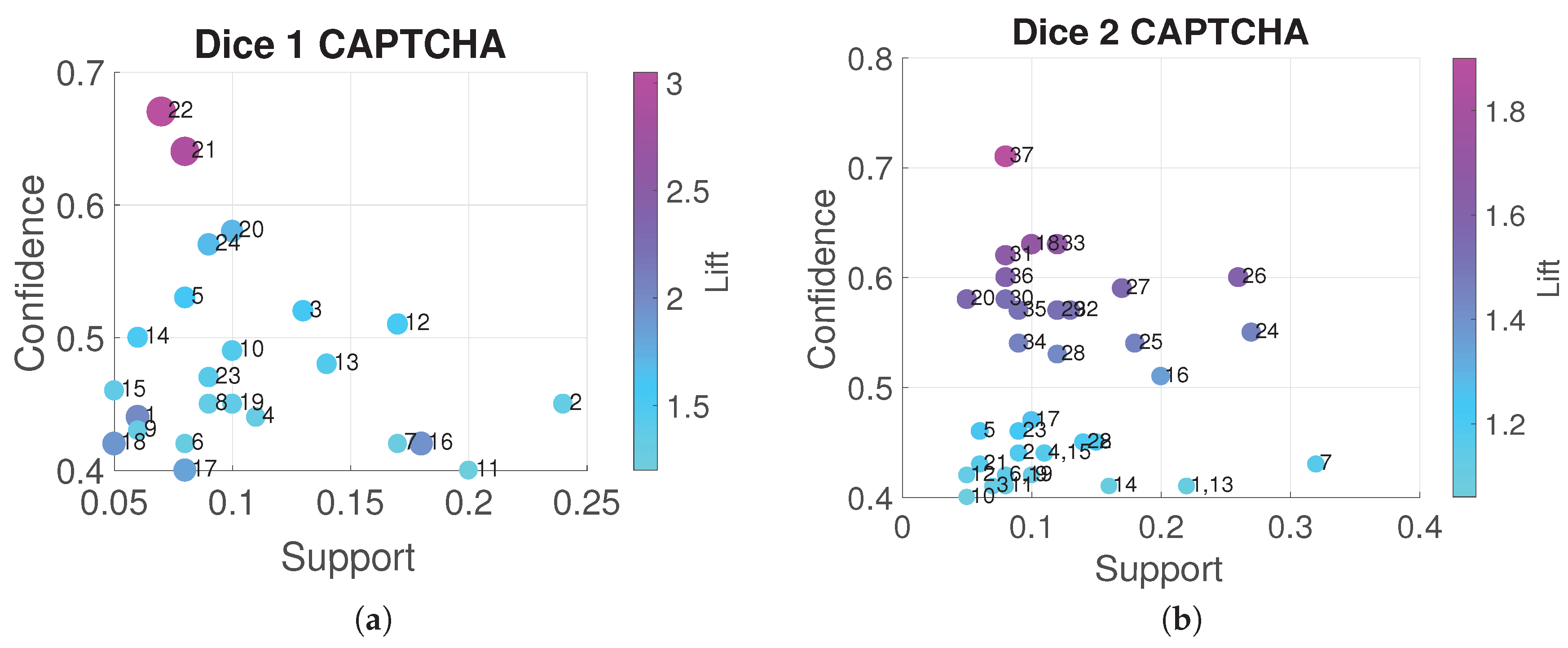
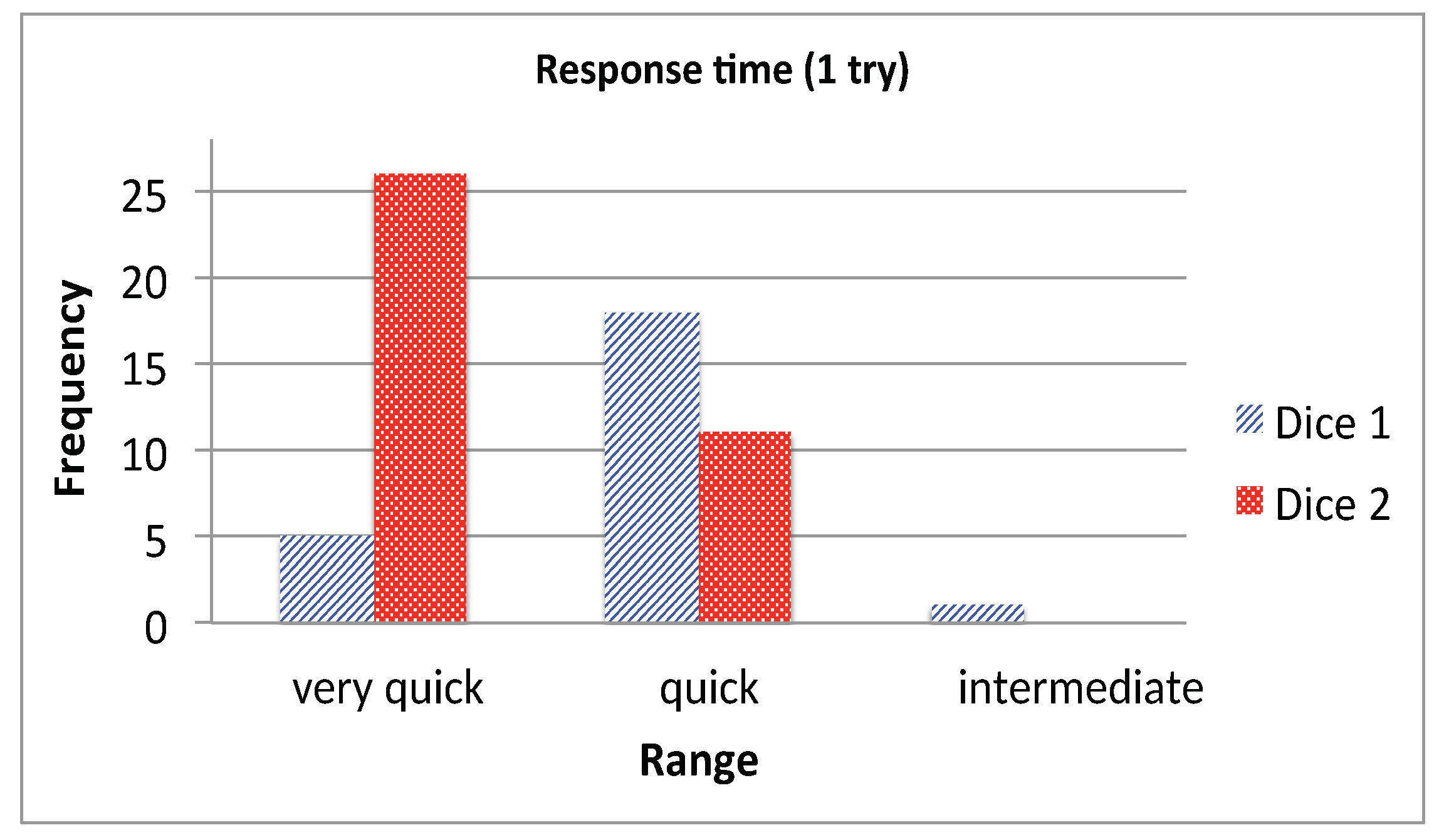
| Id. | Ant. | Cons. | S | C | L | |
|---|---|---|---|---|---|---|
| 1 | > 35, Tablet, High Int. experience | Interm. | 0.06 | 0.44 | 1.99 | 1.40 |
| 2 | Middle Int. experience | Quick | 0.24 | 0.45 | 1.34 | 1.21 |
| 3 | Middle Int. experience, Middle Int. daily usage | Quick | 0.13 | 0.52 | 1.55 | 1.39 |
| 4 | < 35 | Quick | 0.11 | 0.44 | 1.31 | 1.19 |
| 5 | Middle Int. experience, < 35 | Quick | 0.08 | 0.53 | 1.60 | 1.43 |
| 6 | Tablet, < 35 | Quick | 0.08 | 0.42 | 1.26 | 1.15 |
| 7 | > 35, Middle Int. experience | Quick | 0.17 | 0.42 | 1.25 | 1.14 |
| 8 | Middle Int. experience, Low Int. daily usage | Quick | 0.09 | 0.45 | 1.34 | 1.21 |
| 9 | > 35, Middle Int. experience, Low Int. daily usage | Quick | 0.06 | 0.43 | 1.29 | 1.17 |
| 10 | > 35, Middle Int. experience, Middle Int. daily usage | Quick | 0.10 | 0.49 | 1.45 | 1.30 |
| 11 | Laptop | Quick | 0.20 | 0.40 | 1.20 | 1.11 |
| 12 | Middle Int. experience, Laptop | Quick | 0.17 | 0.51 | 1.54 | 1.37 |
| 13 | > 35, Middle Int. experience, Laptop | Quick | 0.14 | 0.48 | 1.44 | 1.28 |
| 14 | Middle Int. experience, Laptop, Low Int. daily usage | Quick | 0.06 | 0.50 | 1.49 | 1.33 |
| 15 | > 35, Middle Int. experience, Laptop, Low Int. daily usage | Quick | 0.05 | 0.46 | 1.37 | 1.23 |
| 16 | > 35, Laptop | Very quick | 0.18 | 0.42 | 1.94 | 1.36 |
| 17 | > 35, Laptop, Low Int. daily usage | Very quick | 0.08 | 0.40 | 1.83 | 1.30 |
| 18 | > 35, Middle Int. experience, Laptop, Low Int. daily usage | Very quick | 0.05 | 0.42 | 1.91 | 1.34 |
| 19 | Laptop, Middle Int. daily usage | Quick | 0.10 | 0.45 | 1.36 | 1.22 |
| 20 | Middle Int. experience, Laptop, Middle Int. daily usage | Quick | 0.10 | 0.58 | 1.72 | 1.57 |
| 21 | Laptop, High Int. experience | Very quick | 0.08 | 0.64 | 2.93 | 2.17 |
| 22 | > 35, Laptop, High Int. experience | Very quick | 0.07 | 0.67 | 3.05 | 2.34 |
| 23 | > 35, Laptop, Middle Int. daily usage | Quick | 0.09 | 0.47 | 1.41 | 1.26 |
| 24 | > 35, Middle Int. experience, Laptop, Middle Int. daily usage | Quick | 0.09 | 0.57 | 1.69 | 1.53 |
| Id. | Ant. | Cons. | S | C | L | |
|---|---|---|---|---|---|---|
| 1 | Middle Int. experience | Quick | 0.22 | 0.41 | 1.11 | 1.07 |
| 2 | Middle Int. experience, Tablet | Quick | 0.09 | 0.44 | 1.18 | 1.12 |
| 3 | Tablet, Middle Int. daily usage | Quick | 0.07 | 0.41 | 1.11 | 1.07 |
| 4 | < 35 | Quick | 0.11 | 0.44 | 1.19 | 1.12 |
| 5 | Middle Int. experience, < 35 | Quick | 0.06 | 0.46 | 1.25 | 1.17 |
| 6 | Tablet, < 35 | Quick | 0.08 | 0.42 | 1.14 | 1.09 |
| 7 | > 35 | Very quick | 0.32 | 0.43 | 1.16 | 1.10 |
| 8 | > 35, Low Int. daily usage | Very quick | 0.15 | 0.45 | 1.21 | 1.14 |
| 9 | > 35, High Int. experience | Very quick | 0.10 | 0.42 | 1.11 | 1.07 |
| 10 | Low Int. daily usage, High Int. experience | Very quick | 0.05 | 0.40 | 1.06 | 1.04 |
| 11 | > 35, Middle Int. experience, Middle Int. daily usage | Quick | 0.08 | 0.41 | 1.11 | 1.07 |
| 12 | > 35, Tablet, Middle Int. daily usage | Quick | 0.05 | 0.42 | 1.12 | 1.08 |
| 13 | Middle Int. experience | Very quick | 0.22 | 0.41 | 1.09 | 1.06 |
| 14 | Middle Int. daily usage | Very quick | 0.16 | 0.41 | 1.09 | 1.06 |
| 15 | Middle Int. experience, Middle Int. daily usage | Very quick | 0.11 | 0.44 | 1.16 | 1.11 |
| 16 | > 35, Middle Int. experience | Very quick | 0.20 | 0.51 | 1.35 | 1.26 |
| 17 | Middle Int. experience, Low Int. daily usage | Very quick | 0.10 | 0.47 | 1.26 | 1.19 |
| 18 | > 35, Middle Int. experience, Low Int. daily usage | Very quick | 0.10 | 0.63 | 1.69 | 1.70 |
| 19 | High Int. daily usage | Quick | 0.08 | 0.42 | 1.14 | 1.09 |
| 20 | Middle Int. experience, High Int. daily usage | Quick | 0.05 | 0.58 | 1.56 | 1.49 |
| 21 | Tablet, High Int. daily usage | Quick | 0.06 | 0.43 | 1.16 | 1.10 |
| 22 | > 35, Middle Int. daily usage | Very quick | 0.14 | 0.45 | 1.20 | 1.14 |
| 23 | > 35, Middle Int. experience, Middle Int. daily usage | Very quick | 0.09 | 0.46 | 1.23 | 1.16 |
| 24 | Laptop | Very quick | 0.27 | 0.55 | 1.45 | 1.38 |
| 25 | Middle Int. experience, Laptop | Very quick | 0.18 | 0.54 | 1.45 | 1.37 |
| 26 | > 35, Laptop | Very quick | 0.26 | 0.60 | 1.60 | 1.56 |
| 27 | > 35, Middle Int. experience, Laptop | Very quick | 0.17 | 0.59 | 1.56 | 1.51 |
| 28 | Laptop, Low Int. daily usage | Very quick | 0.12 | 0.53 | 1.42 | 1.34 |
| 29 | > 35, Laptop, Low Int. daily usage | Very quick | 0.12 | 0.57 | 1.53 | 1.47 |
| 30 | Middle Int. experience, Laptop, Low Int. daily usage | Very quick | 0.08 | 0.58 | 1.53 | 1.47 |
| 31 | > 35, Middle Int. experience, Laptop, Low Int. daily usage | Very quick | 0.08 | 0.62 | 1.66 | 1.66 |
| 32 | Laptop, Middle Int. daily usage | Very quick | 0.13 | 0.57 | 1.51 | 1.44 |
| 33 | > 35, Laptop, Middle Int. daily usage | Very quick | 0.12 | 0.63 | 1.68 | 1.69 |
| 34 | Middle Int. experience, Laptop, Middle Int. daily usage | Very quick | 0.09 | 0.54 | 1.45 | 1.37 |
| 35 | > 35, Middle Int. experience, Laptop, Middle Int. daily usage | Very quick | 0.09 | 0.57 | 1.51 | 1.44 |
| 36 | Laptop, High Int. experience | Very quick | 0.08 | 0.60 | 1.60 | 1.56 |
| 37 | > 35, Laptop, High Int. experience | Very quick | 0.08 | 0.71 | 1.90 | 2.18 |
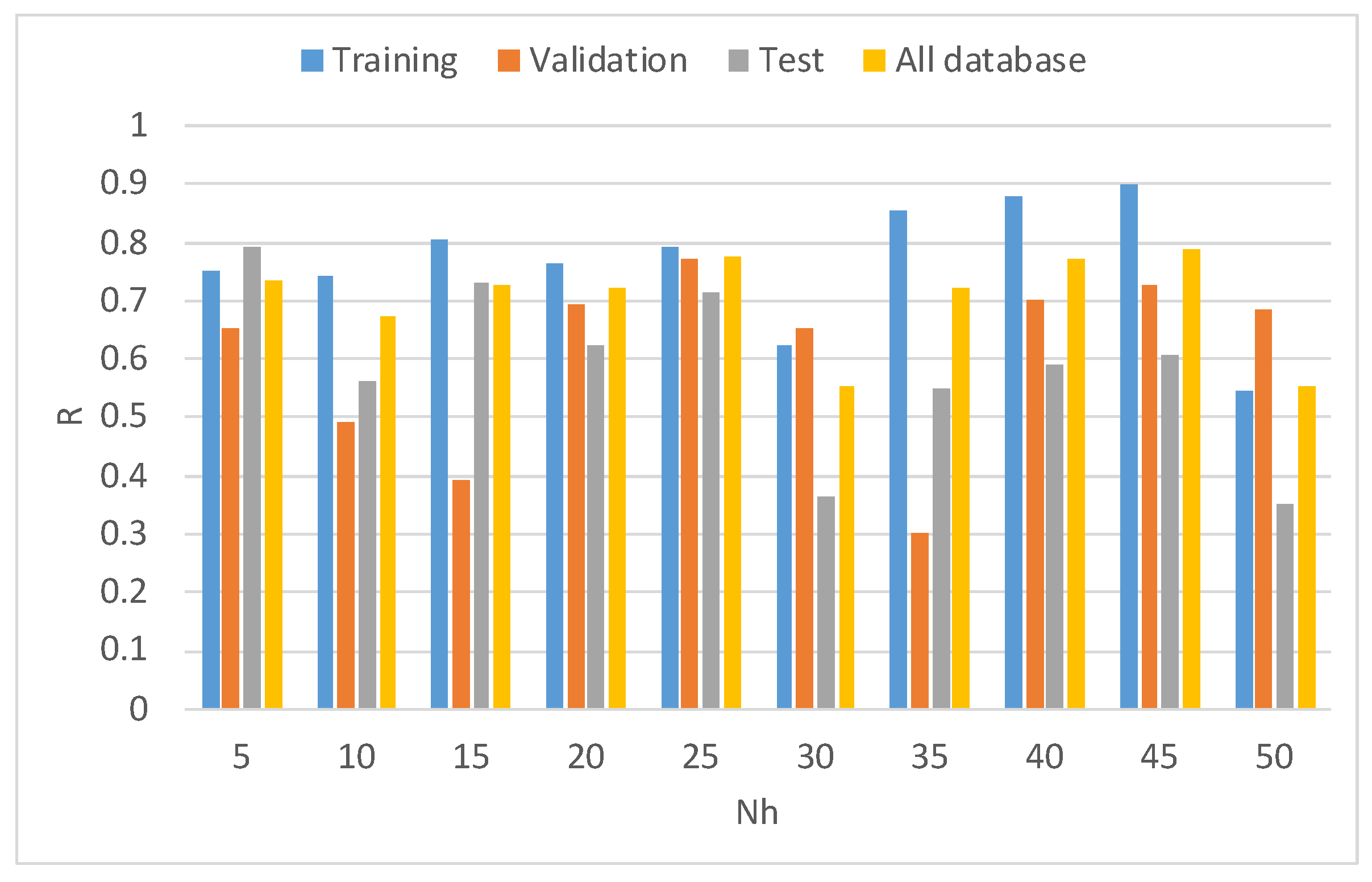
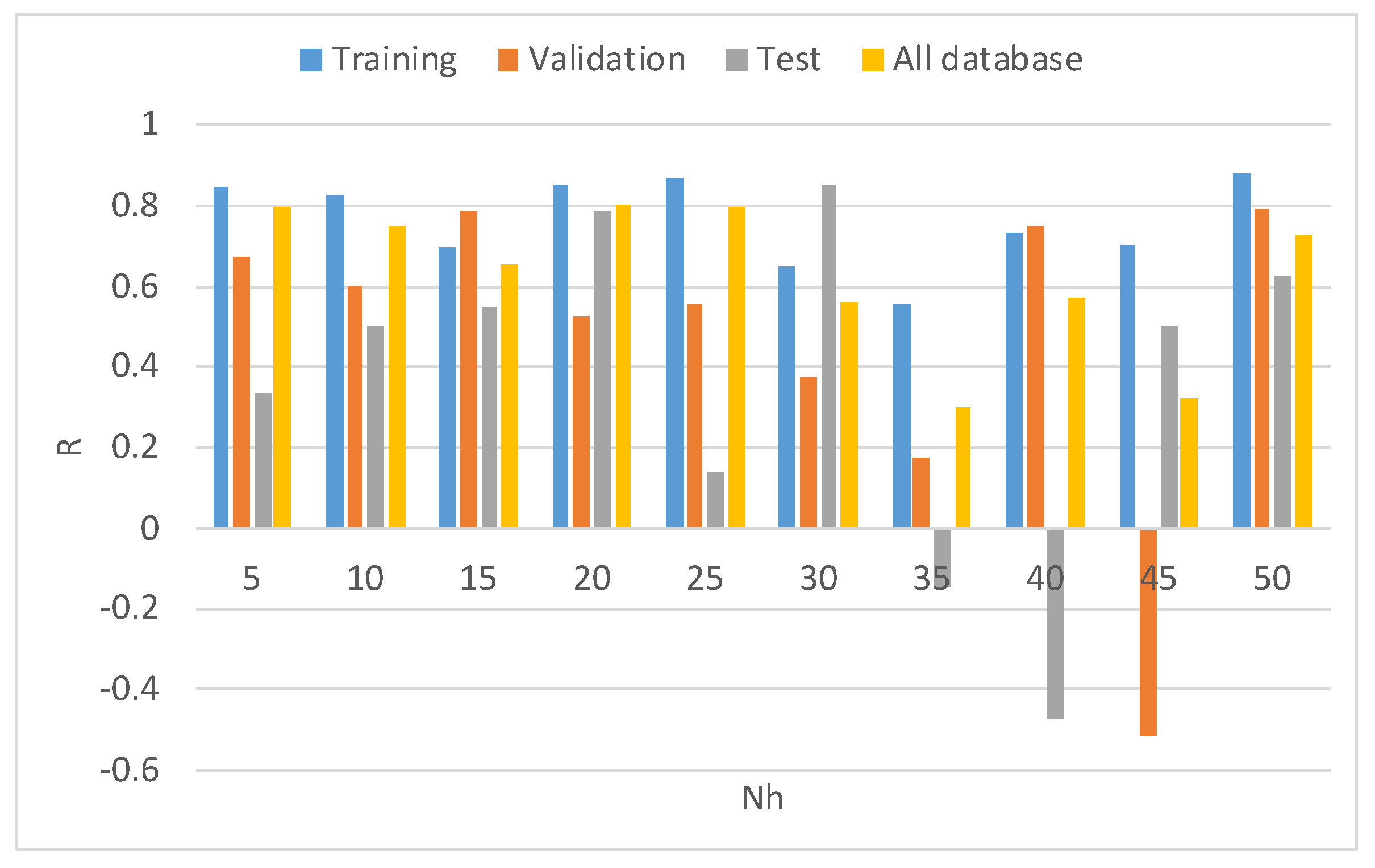
| R | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Dice 1 | 0.733 | 0.675 | 0.728 | 0.724 | 0.777 | 0.553 | 0.723 | 0.774 | 0.789 | 0.553 |
| Dice 2 | 0.796 | 0.752 | 0.657 | 0.803 | 0.795 | 0.560 | 0.300 | 0.569 | 0.321 | 0.726 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amelio, A.; Draganov, I.R.; Janković, R.; Tanikić, D. Analysis of Usability for the Dice CAPTCHA. Information 2019, 10, 221. https://doi.org/10.3390/info10070221
Amelio A, Draganov IR, Janković R, Tanikić D. Analysis of Usability for the Dice CAPTCHA. Information. 2019; 10(7):221. https://doi.org/10.3390/info10070221
Chicago/Turabian StyleAmelio, Alessia, Ivo Rumenov Draganov, Radmila Janković, and Dejan Tanikić. 2019. "Analysis of Usability for the Dice CAPTCHA" Information 10, no. 7: 221. https://doi.org/10.3390/info10070221
APA StyleAmelio, A., Draganov, I. R., Janković, R., & Tanikić, D. (2019). Analysis of Usability for the Dice CAPTCHA. Information, 10(7), 221. https://doi.org/10.3390/info10070221





