Comparative Performance Evaluation of an Accuracy-Enhancing Lyapunov Solver †
Abstract
1. Introduction
- is either M or , for a matrix M.
- is the residual matrix obtained when the unknown matrix X is replaced by M in an equation. For instance, for Equation (1), .
- Matrix M is (upper) quasi-triangular if it is block (upper) triangular with diagonal blocks of order 1 or 2.
- Matrix M is in a real Schur form if it is upper quasi-triangular and any diagonal block has complex conjugate eigenvalues.
- Matrix is in Hessenberg form if it has zeros under the first subdiagonal, i.e., .
- Matrix pair is in a generalized real Schur form, also named real Schur-triangular form, if M is in a real Schur form and N is upper triangular.
- Frobenius norm of a matrix is , where , are the singular values of M. If , , where , , are the eigenvalues of M.
- rcond: estimated reciprocal condition number.
- : relative machine precision, , in double precision format (IEEE 754 standard).
2. Results
2.1. Benchmark Examples
| list_n | for TLEX 4.1 – TLEX 4.3; | list_n for TLEX 4.4; |
| list_r | for TLEX 4.1; | |
| list_s | for TLEX 4.1 and TLEX 4.2; | |
| list_l | for CTLEX 4.2 | list_l for DTLEX 4.2; |
| list_t | for TLEX 4.3 | list_t for TLEX 4.4; |
2.2. Performance Analysis Issues
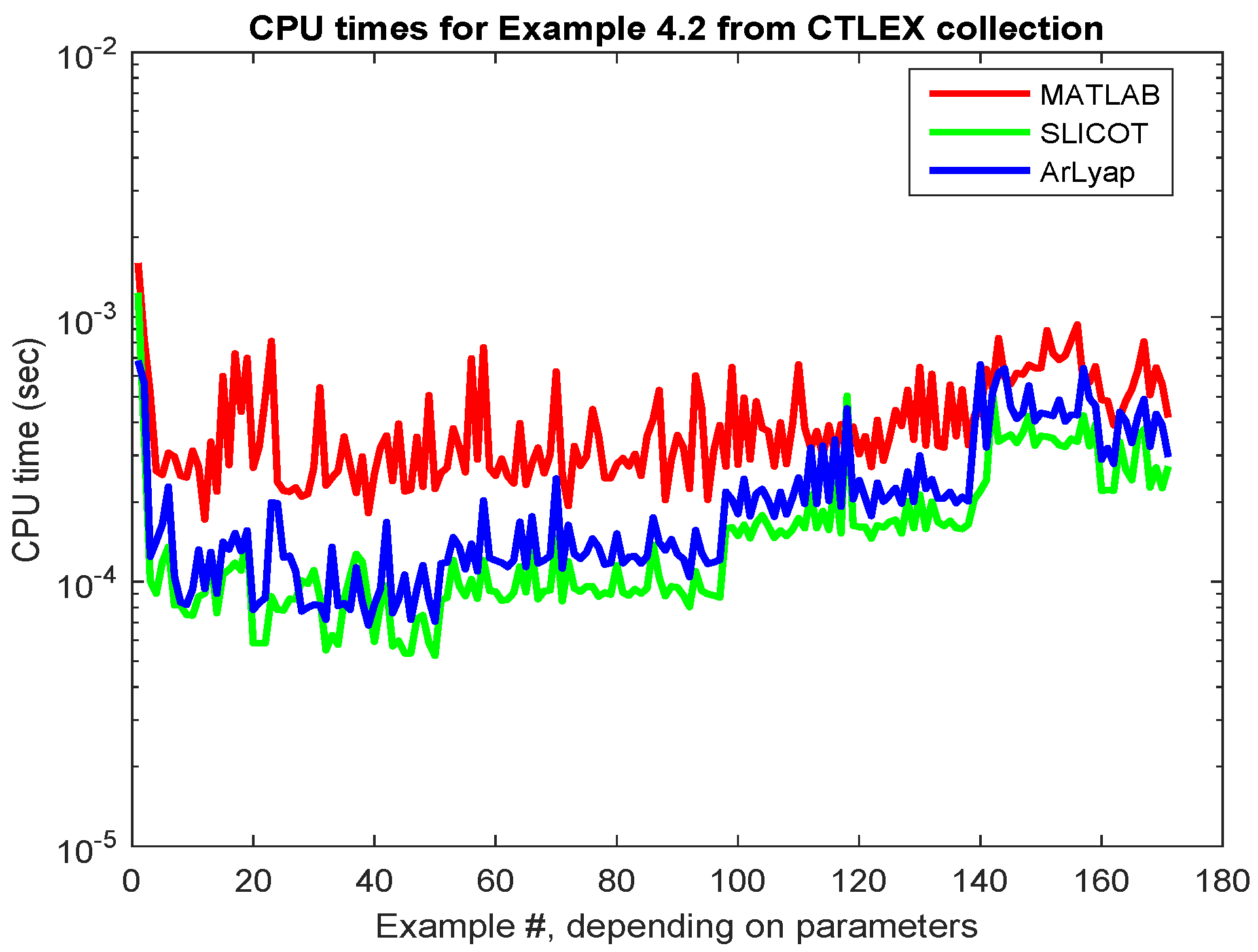
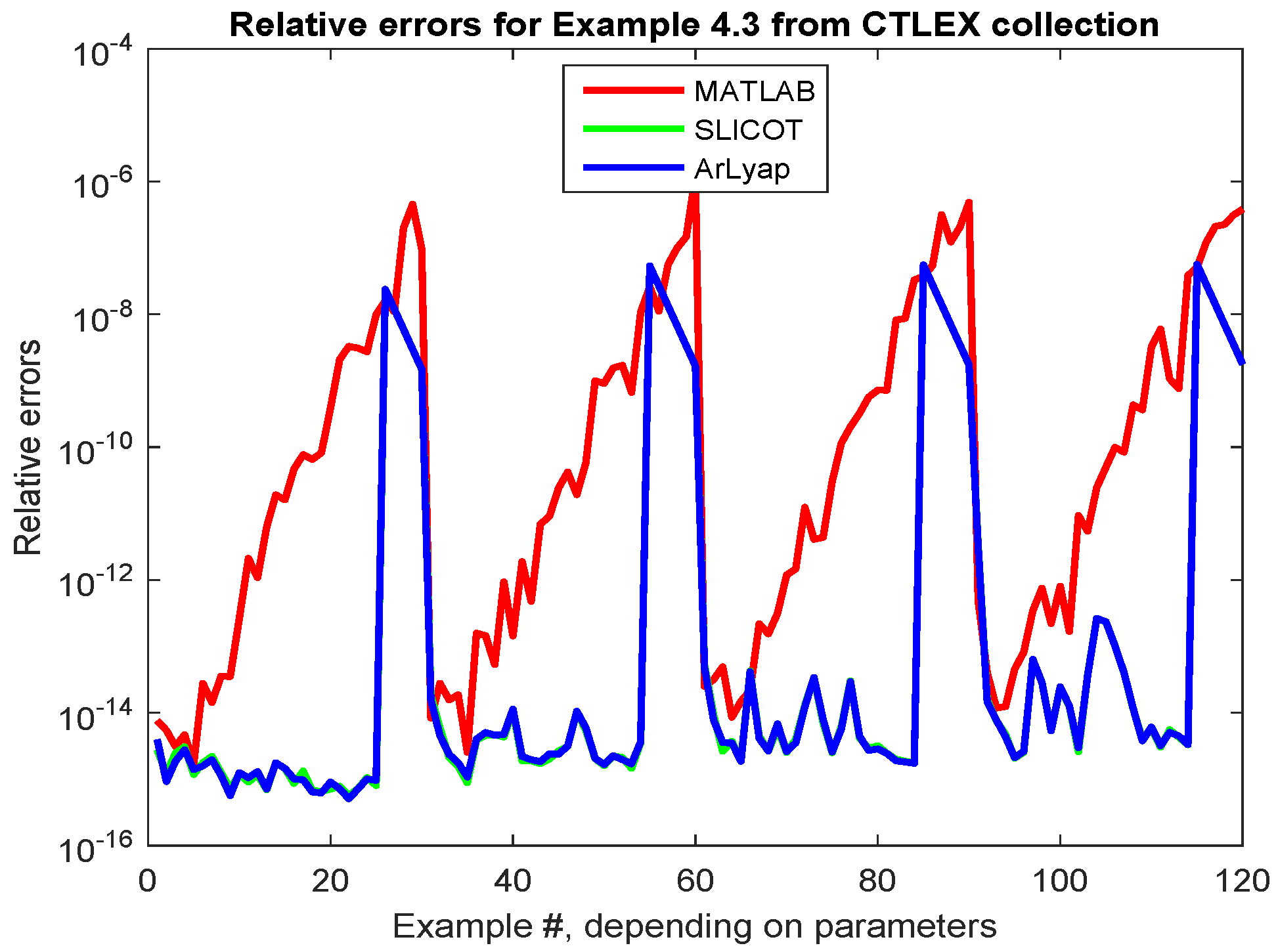
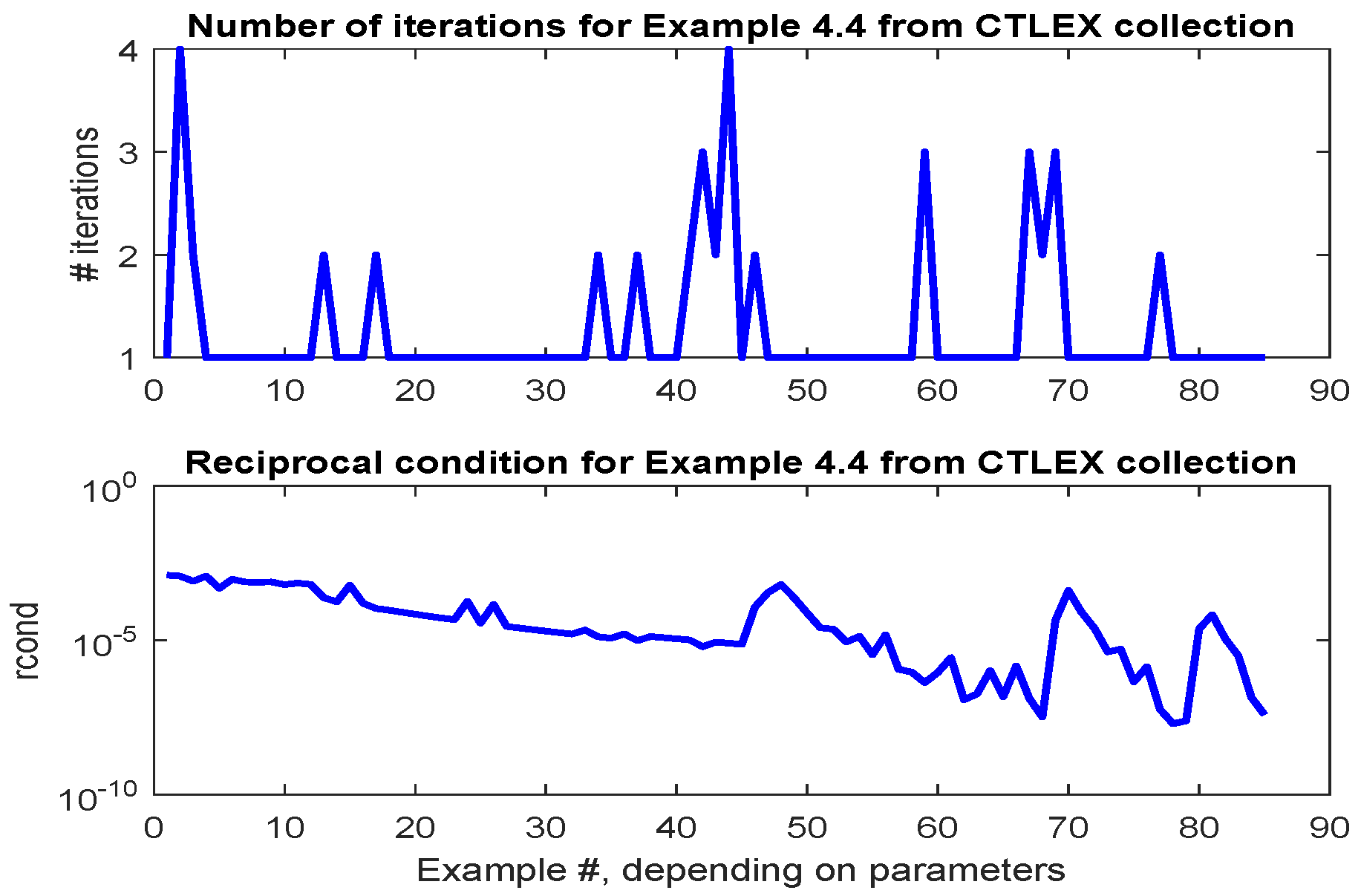
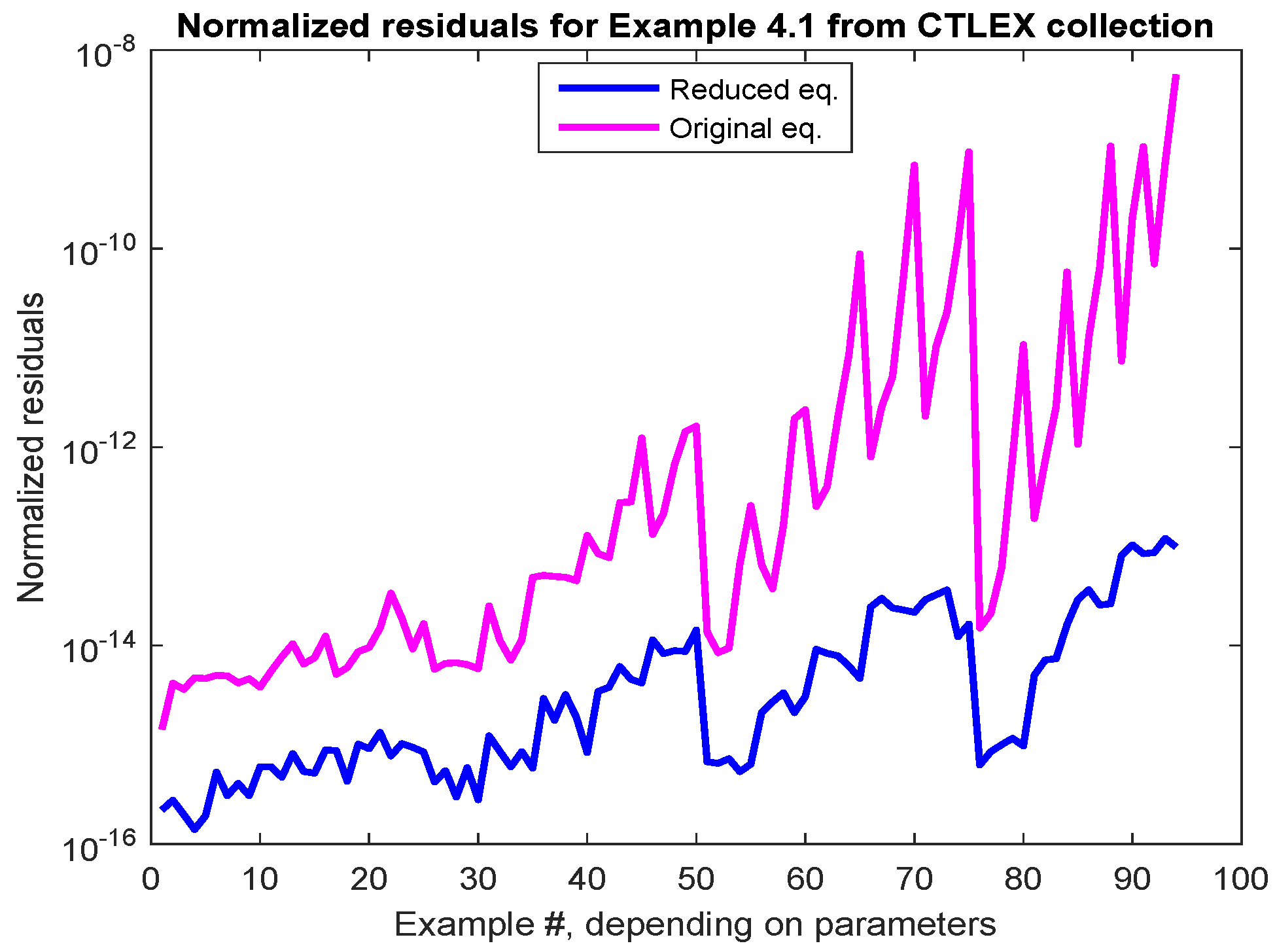
2.3. Continuous-Time Lyapunov Equations
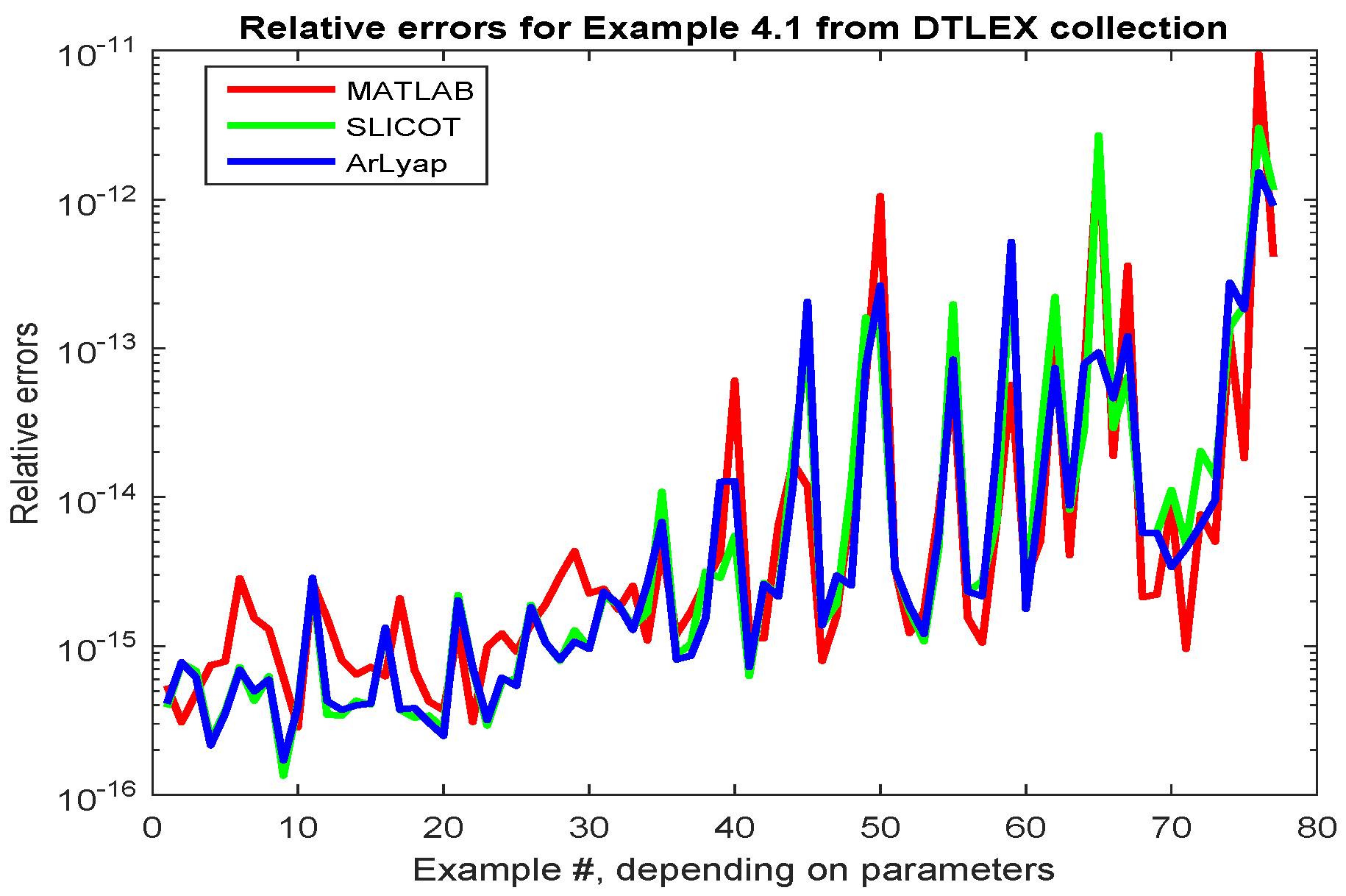
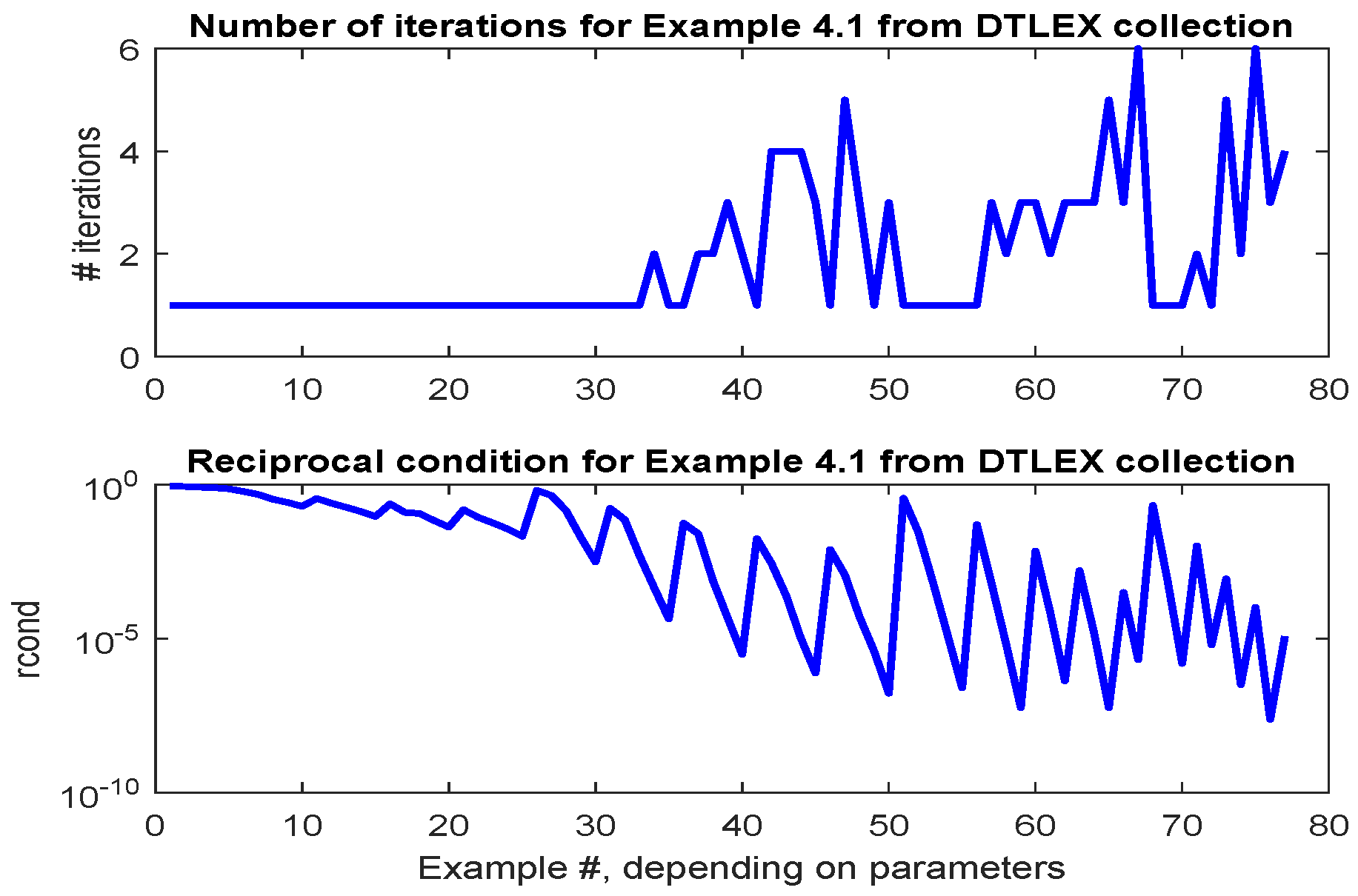
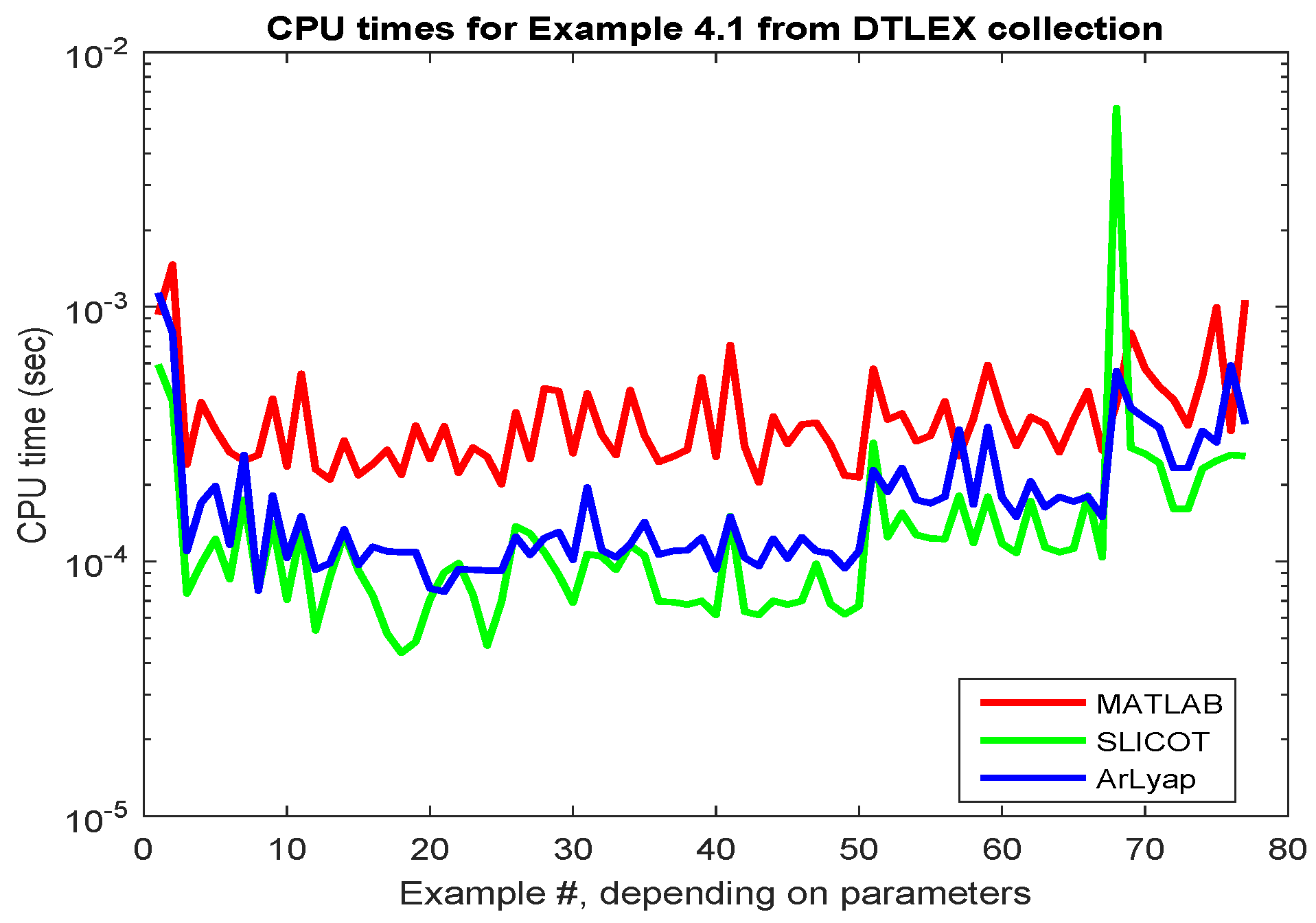
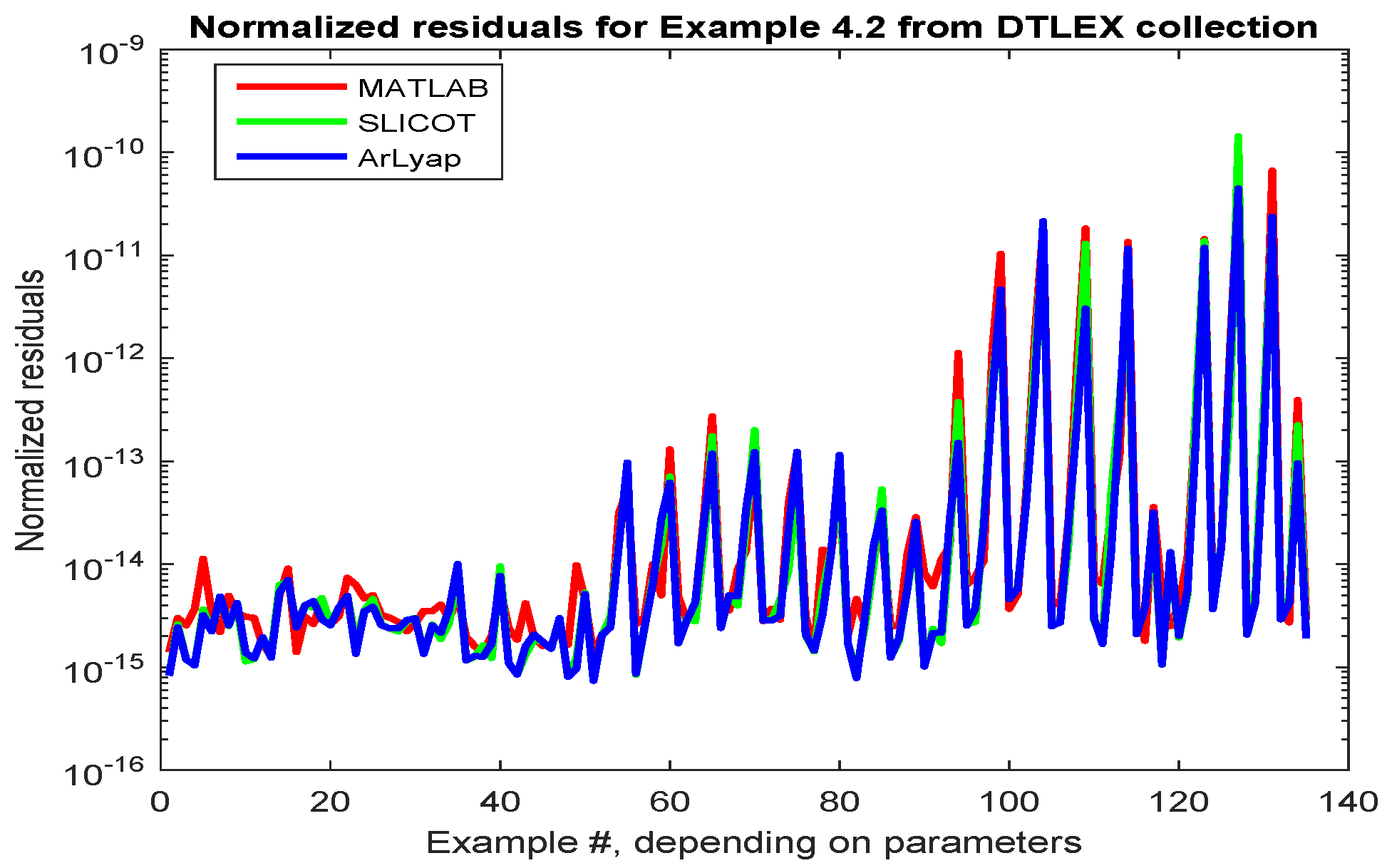
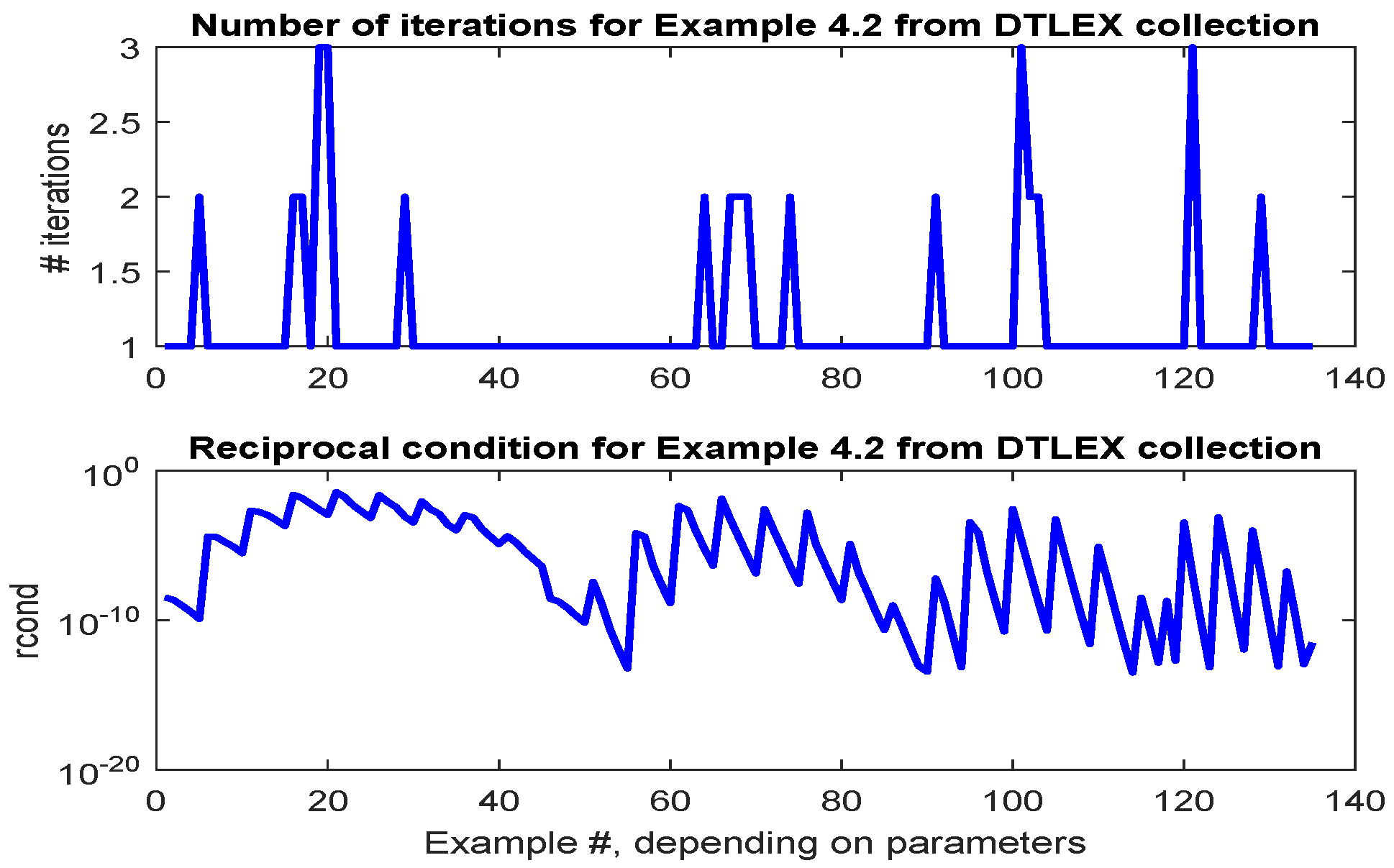
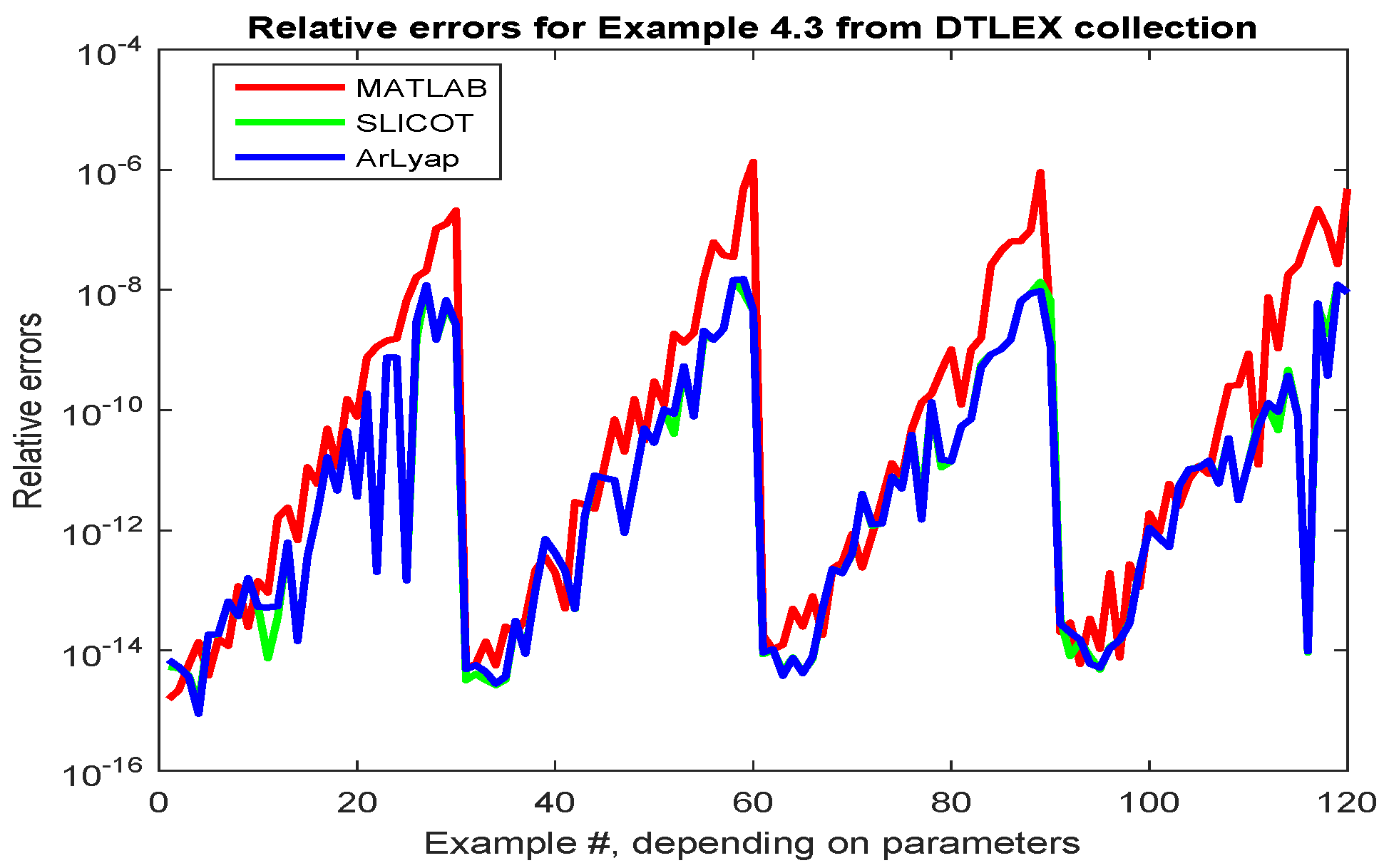
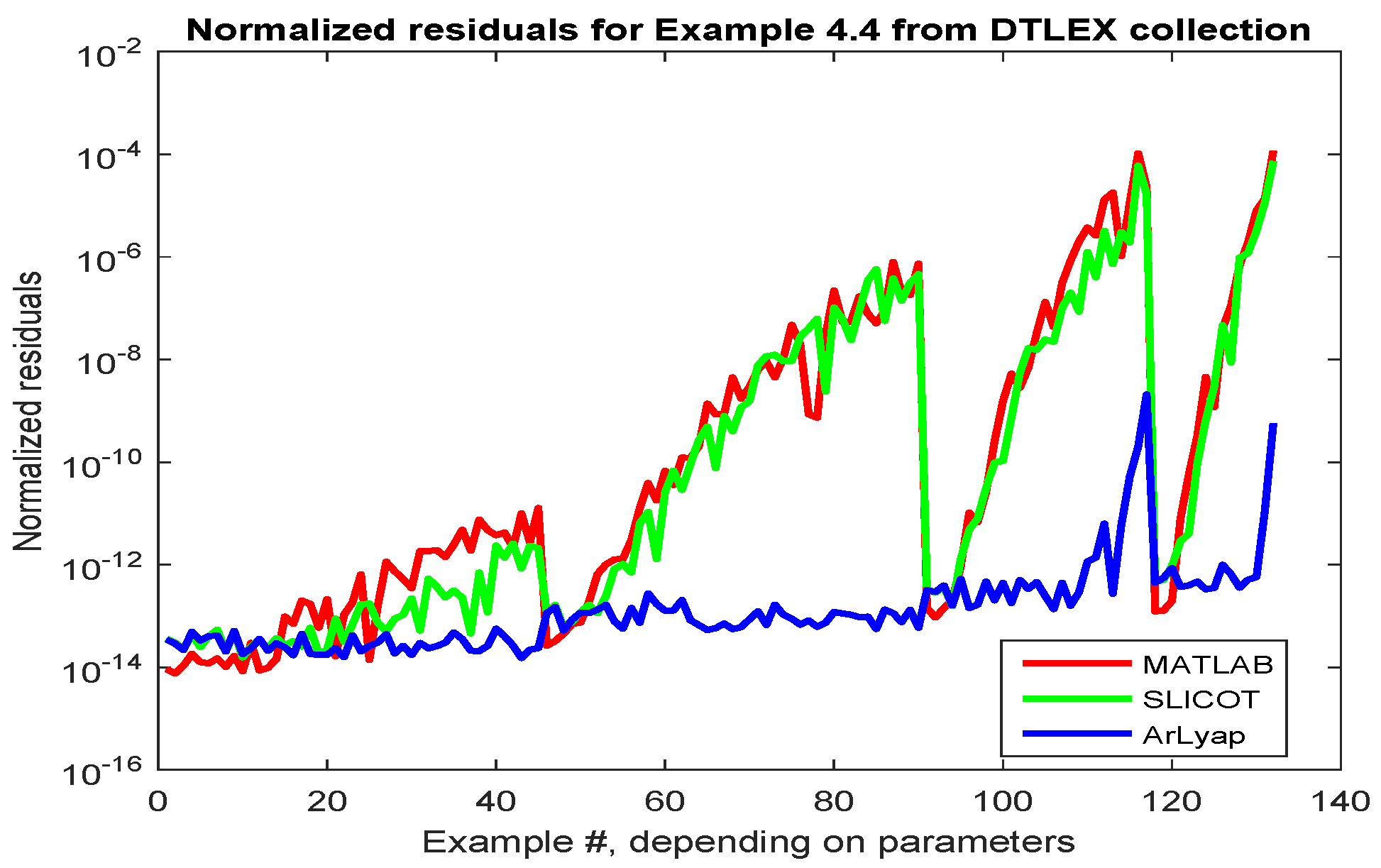
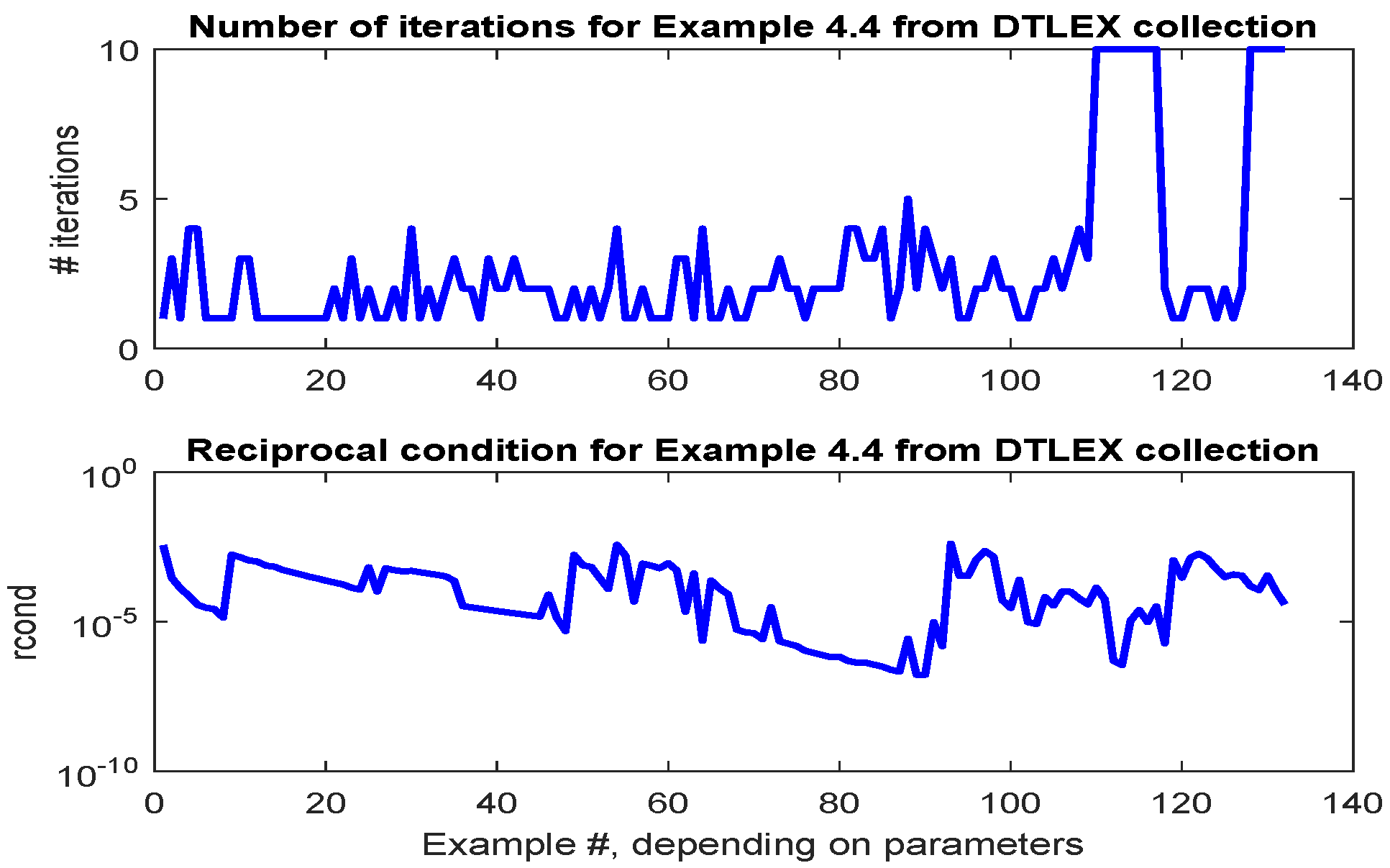
2.4. Discrete-Time Lyapunov Equations
3. Discussion
4. Materials and Methods
4.1. Conceptual Algorithm Description
4.2. New Algorithm
| Algorithm 1 Algorithm ArLyap: Accuracy-enhancing Lyapunov solver |
| Input: The matrices A, E, and Y, and an integer ; optionally, initial and a tolerance . Ensure: The solution of Equations (4) or (5).
|
4.3. Computational Modules for Improving Efficiency
- 1.
- Compute , with H an upper Hessenberg matrix and X a symmetric matrix. This is a special symmetric “rank 2k operation” (a specialized version of the BLAS 3 routine syr2k), needed, e.g., for solving standard continuous-time reduced Lyapunov Equation (18), with .
- 2.
- Compute , with H an upper Hessenberg matrix and X a symmetric matrix. This operation is necessary for solving standard or generalized discrete-time reduced Lyapunov Equation (19). Let , , and denote the diagonal, upper and lower triangles of X, respectively, and define two, upper and lower, respectively, triangular matricesSinceit follows thatAbove, , , , and are again upper Hessenberg matrices. Therefore, all four formulas above are special cases of symmetric rank 2k operations, where both matrices involved are in upper Hessenberg form. Note that one could define, e.g.,but then the matrix would be a full matrix, hence more computational effort would be needed to evaluate .
- 3.
- Compute , with H and G upper Hessenberg matrices. This module is called by the module 2.
- 4.
- Compute , with E an upper triangular matrix and X a symmetric matrix. This operation is needed for solving generalized discrete-time reduced Lyapunov Equation (19), and it can be performed using the formulas:Note that , , , and are all upper triangular matrices. Hence, each of these four formulas involve a special symmetric rank 2k operation on an upper triangular pair. This module needs the product of two upper triangular matrices, expressed as , or , or , or , with U and E upper triangular, and L lower triangular. This is easily done internally using BLAS 2 function trmv in a loop with n cycles.
- 5.
- Compute , with E and U upper triangular matrices. This module is called by the module 4.
- 6.
- Computewith H an upper Hessenberg matrix and X a symmetric matrix, given either the upper triangle U or the lower triangle L of X. This module is needed for computing the relative residual for standard continuous-time reduced Lyapunov equations, since it allows to evaluate the Frobenius norm of this matrix product (which is a term of that equation). Using , or , where and are strictly upper and lower triangular, respectively, the module evaluates the product using BLAS 2 trmv function and other routines. Clearly, both and are upper Hessenberg, but the results of this module are full matrices. Using Equation (24), the function of the module 1 becomes . However, this formula should only be used when relative residual is needed, and hence P should be computed.
- 7.
- Computewith H an upper Hessenberg matrix, X a symmetric matrix, and E an upper triangular matrix. This operation is needed for solving generalized continuous-time reduced Lyapunov Equation (18). Using Equation (23), it follows thatwhere , and . Note that , , , and are all upper triangular, and , , , and are all upper Hessenberg. Consequently, each of these four formulas involve two special symmetric rank 2k operations for upper Hessenberg-triangular pairs.
- 8.
- Compute , with H an upper Hessenberg matrix and E an upper triangular matrix. This operation is called by the module 7.
- 9.
- Compute either P or , where , with H an upper Hessenberg matrix, X a symmetric matrix, and E an upper triangular matrix. This module is needed for evaluating the Frobenius norm of P, used to obtain the relative residual for generalized continuous-time reduced Lyapunov equations. The matrix R in Equation (25) becomes . However, this formula should only be used when relative residual is needed. Note that P is a general matrix, with no structure. The computations can be performed as follows: using the module 6, compute , if , or , if ; then, compute , if , or , if , using a BLAS 3 trmm operation. Note that the Frobenius norms of P and coincide, and R can be obtained having either P or .
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| ARE | algebraic Riccati equation |
| CTLEX | continuous-time Lyapunov equation |
| DTLEX | discrete-time Lyapunov equation |
| TLEX | continuous or discrete-time Lyapunov equation |
References
- Green, M. Balanced Stochastic Realization. Linear Algebra Appl. 1988, 98, 211–247. [Google Scholar] [CrossRef]
- Peeters, R.; Hanzon, B.; Olivi, M. Balanced Realizations of Discrete-time Stable All-pass Systems and the Tangential Schur Algorithm. In Proceedings of the European Control Conference, Karlsruhe, Germany, 31 August–3 September 1999. [Google Scholar]
- Badía, J.M.; Benner, P.; Mayo, R.; Quintana-Ortí, E.S. Parallel Algorithms for Balanced Truncation Model Reduction of Sparse Systems. In Applied Parallel Computing: State of the Art in Scientific Computing, Proceedings of the 7th International Workshop, PARA 2004, Lyngby, Denmark, 20–23 June 2004; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3732, pp. 267–275. [Google Scholar]
- Lin, C.A.; Chiu, T.Y. Model Reduction via Frequency-weighted Balanced Realization. Control Theory Adv. Technol. 1992, 8, 341–351. [Google Scholar]
- Liu, Y.; Anderson, B.D.O. Singular Perturbation Approximation of Balanced Systems. Int. J. Control 1989, 50, 1379–1405. [Google Scholar] [CrossRef]
- Safonov, M.G.; Chiang, R.Y. A Schur Method for Balanced-truncation Model Reduction. IEEE Trans. Autom. Control 1989, AC–34, 729–733. [Google Scholar] [CrossRef]
- Tombs, M.S.; Postlethwaite, I. Truncated Balanced Realization of a Stable Non-minimal State-space System. Int. J. Control 1987, 46, 1319–1330. [Google Scholar] [CrossRef]
- Kleinman, D.L. On an Iterative Technique for Riccati Equation Computations. IEEE Trans. Autom. Control 1968, AC–13, 114–115. [Google Scholar] [CrossRef]
- Hewer, G.A. An Iterative Technique for the Computation of the Steady State Gains for the Discrete Optimal Regulator. IEEE Trans. Autom. Control 1971, AC–16, 382–384. [Google Scholar] [CrossRef]
- Mehrmann, V.L. The Autonomous Linear Quadratic Control Problem. Theory and Numerical Solution; Thoma, M., Wyner, A., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 1991; Volume 163. [Google Scholar]
- Lancaster, P.; Rodman, L. The Algebraic Riccati Equation; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sima, V. Algorithms for Linear-Quadratic Optimization; Taft, E.J., Nashed, Z., Eds.; Pure and Applied Mathematics: A Series of Monographs and Textbooks; Marcel Dekker, Inc.: New York, NY, USA, 1996; Volume 200. [Google Scholar]
- Benner, P. Accelerating Newton’s Method for Discrete-time Algebraic Riccati Equations. In Mathematical Theory of Networks and Systems, Proceedings of the MTNS-98 Symposium, Padova, Italy, 6–10 July 1998; Beghi, A., Finesso, L., Picci, G., Eds.; The Hong Kong University of Science and Technology: Hong Kong, China, 1998; pp. 569–572. [Google Scholar]
- Benner, P.; Byers, R. An Exact Line Search Method for Solving Generalized Continuous-time Algebraic Riccati Equations. IEEE Trans. Autom. Control 1998, 43, 101–107. [Google Scholar] [CrossRef]
- Kleinman, D.L. An Easy Way to Stabilize a Linear Constant System. IEEE Trans. Autom. Control 1970, AC-15, 692. [Google Scholar] [CrossRef]
- Armstrong, E.S.; Rublein, G.T. A Stabilization Algorithm for Linear Discrete Constant Systems. IEEE Trans. Autom. Control 1976, AC-21, 629–631. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Du Croz, J.; Duff, I.S.; Hammarling, S. Algorithm 679: A Set of Level 3 Basic Linear Algebra Subprograms. ACM Trans. Math. Softw. 1990, 16, 18–28. [Google Scholar] [CrossRef]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Software Environments Tools; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Hammarling, S.J. Numerical Solution of the Stable, Non-Negative Definite Lyapunov Equation. IMA J. Numer. Anal. 1982, 2, 303–323. [Google Scholar] [CrossRef]
- Van Huffel, S.; Sima, V.; Varga, A.; Hammarling, S.; Delebecque, F. High-Performance Numerical Software for Control. IEEE Control Syst. Mag. 2004, 24, 60–76. [Google Scholar]
- Penzl, T. Numerical Solution of Generalized Lyapunov Equations. Adv. Compup. Math. 1998, 8, 33–48. [Google Scholar] [CrossRef]
- Bartels, R.H.; Stewart, G.W. Algorithm 432: Solution of the matrix equation AX + XB = C. Comm Ass Comput. Mach. 1972, 15, 820–826. [Google Scholar]
- Golub, G.H.; Nash, S.; Van Loan, C.F. A Hessenberg-Schur Method for the Problem AX + XB = C. IEEE Trans. Autom. Control 1979, AC–24, 909–913. [Google Scholar] [CrossRef]
- Sorensen, D.C.; Zhou, Y. Direct Methods for Matrix Sylvester and Lyapunov Equations. J. Appl. Math. 2003, 2003, 277–303. [Google Scholar] [CrossRef]
- Jonsson, I.; Kågström, B. Recursive Blocked Algorithms for Solving Triangular Systems—Part I: One-Sided and Coupled Sylvester-Type Matrix Equations. ACM Trans. Math. Softw. 2002, 28, 392–415. [Google Scholar] [CrossRef]
- Jonsson, I.; Kågström, B. Recursive Blocked Algorithms for Solving Triangular Systems—Part II: Two-Sided and Generalized Sylvester and Lyapunov Matrix Equations. ACM Trans. Math. Softw. 2002, 28, 416–435. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MA, USA, 1996. [Google Scholar]
- Simoncini, V. Computational Methods for Linear Matrix Equations. SIAM Rev. 2016, 58, 377–441. [Google Scholar] [CrossRef]
- Kaabi, A. A Compact Algorithm for Solving Generalized Lyapunov Matrix Equations. Int. Math. Forum 2011, 6, 3293–3304. [Google Scholar]
- Kyncheva, V.K.; Yotov, V.V.; Ivanov, S.I. Convergence of Newton, Halley and Chebyshev Iterative Methods as Methods for Simultaneous Determination of Multiple Polynomial Zeros. Appl. Numer. Math. 2017, 112, 146–154. [Google Scholar] [CrossRef]
- Argyros, I.K.; Magreñán, Á.A.; Orcos, L.; Sarría, Í. Advances in the Semilocal Convergence of Newton’s Method with Real-World Applications. Mathematics 2019, 7, 299. [Google Scholar] [CrossRef]
- MathWorks®; Control System Toolbox™, R2015b; MathWorks: Natick, MA, USA, 2015.
- Benner, P.; Mehrmann, V.; Sima, V.; Van Huffel, S.; Varga, A. SLICOT—A Subroutine Library in Systems and Control Theory. In Applied and Computational Control, Signals, and Circuits; Datta, B.N., Ed.; Birkhäuser: Boston, MA, USA, 1999; Volume 1, pp. 499–539. [Google Scholar]
- Benner, P.; Kressner, D.; Sima, V.; Varga, A. Die SLICOT-Toolboxen für Matlab (The SLICOT Toolboxes for Matlab). Automatisierungstechnik 2010, 58, 15–25. [Google Scholar] [CrossRef]
- Sima, V. Performance of Lyapunov Solvers on Dedicated SLICOT Benchmarks Collections. In Proceedings of the 2018 22nd International Conference on System Theory, Control and Computing (ICSTCC 2018), Sinaia, Romania, 10–12 October 2018; pp. 158–163. [Google Scholar]
- Sima, V.; Benner, P. Numerical Investigation of Newton’s Method for Solving Continuous-time Algebraic Riccati Equations. In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), Vienna, Austria, 1–3 September 2014; Ferrier, J.L., Gusikhin, O., Madani, K., Sasiadek, J., Eds.; SciTePress: Setúbal, Portugal, 2014; pp. 404–409. [Google Scholar]
- Sima, V. Computational Experience with a Modified Newton Solver for Continuous-Time Algebraic Riccati Equations. In Informatics in Control, Automation and Robotics; Ferrier, J.L., Gusikhin, O., Madani, K., Sasiadek, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 55–71. [Google Scholar]
- Sima, V.; Benner, P. Numerical Investigation of Newton’s Method for Solving Discrete-time Algebraic Riccati Equations. In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2018), Porto, Portugal, 29–31 July 2018; Madani, K., Gusikhin, O.Y., Eds.; SciTePress: Setúbal, Portugal, 2018; pp. 66–75. [Google Scholar]
- Savov, S. Solution Bounds for Algebraic Equations in Control Theory; Professor Marin Drinov Academic Publishing House: Sofia, Bulgaria, 2014. [Google Scholar]
- Kressner, D.; Mehrmann, V.; Penzl, T. CTLEX—ACollection of Benchmark Examples for Continuous-Time Lyapunov Equations; SLICOT Working Note 1999-6; Katholieke Universiteit Leuven: Leuven, Belgium, 1999. [Google Scholar]
- Kressner, D.; Mehrmann, V.; Penzl, T. DTLEX—A Collection of Benchmark Examples for Discrete-Time Lyapunov Equations; SLICOT Working Note 1999-7; Katholieke Universiteit Leuven: Leuven, Belgium, 1999. [Google Scholar]
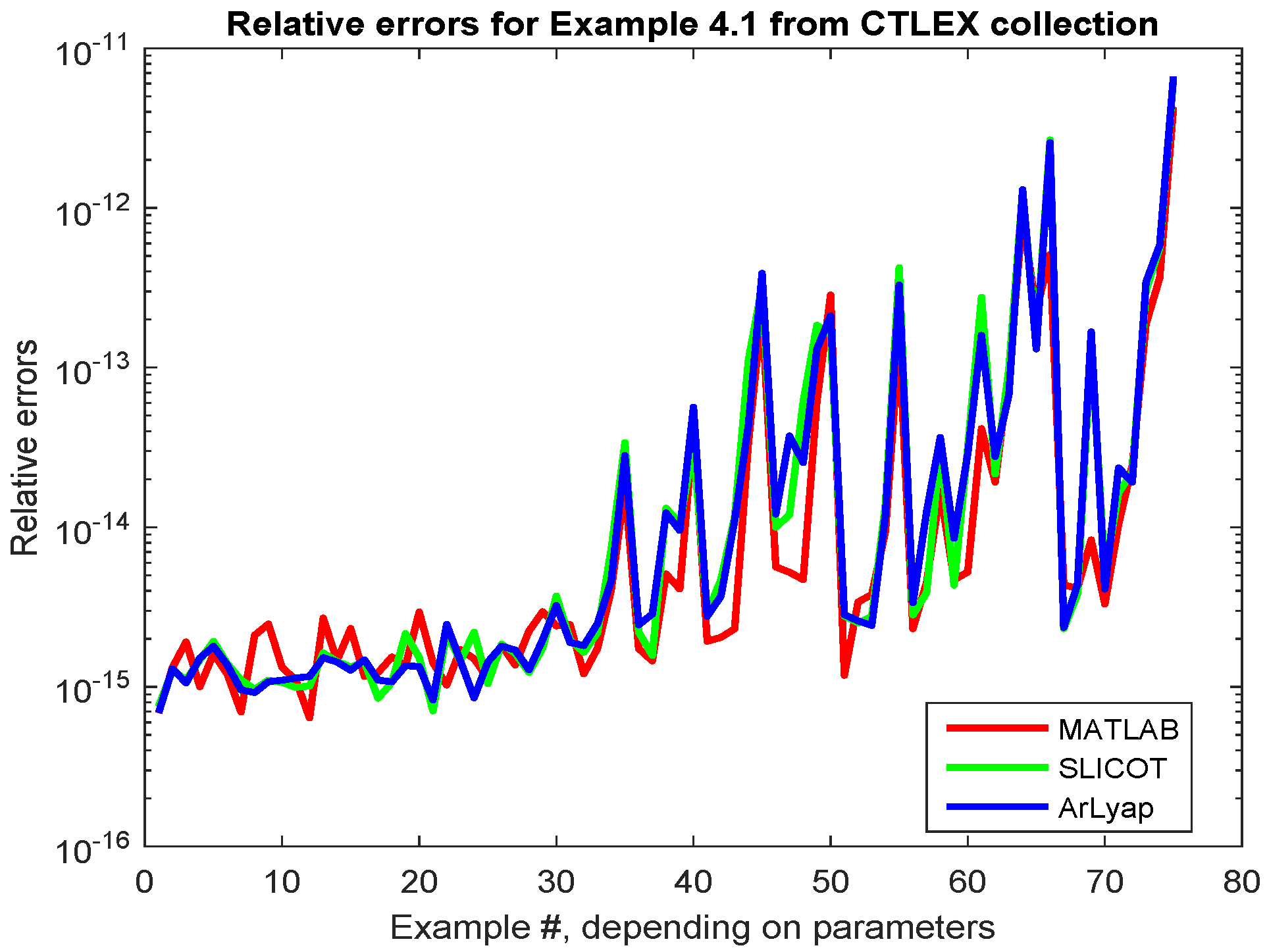
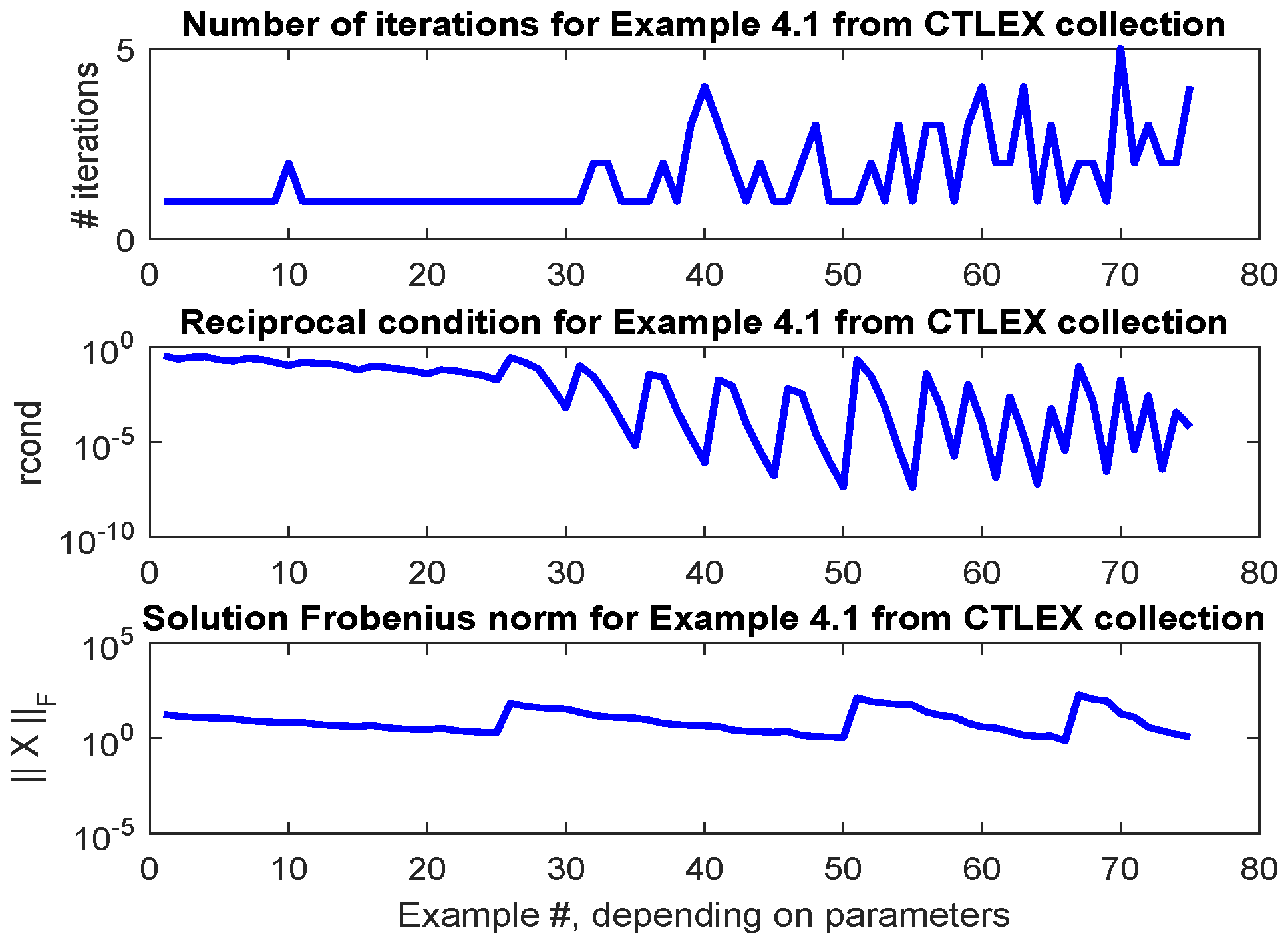
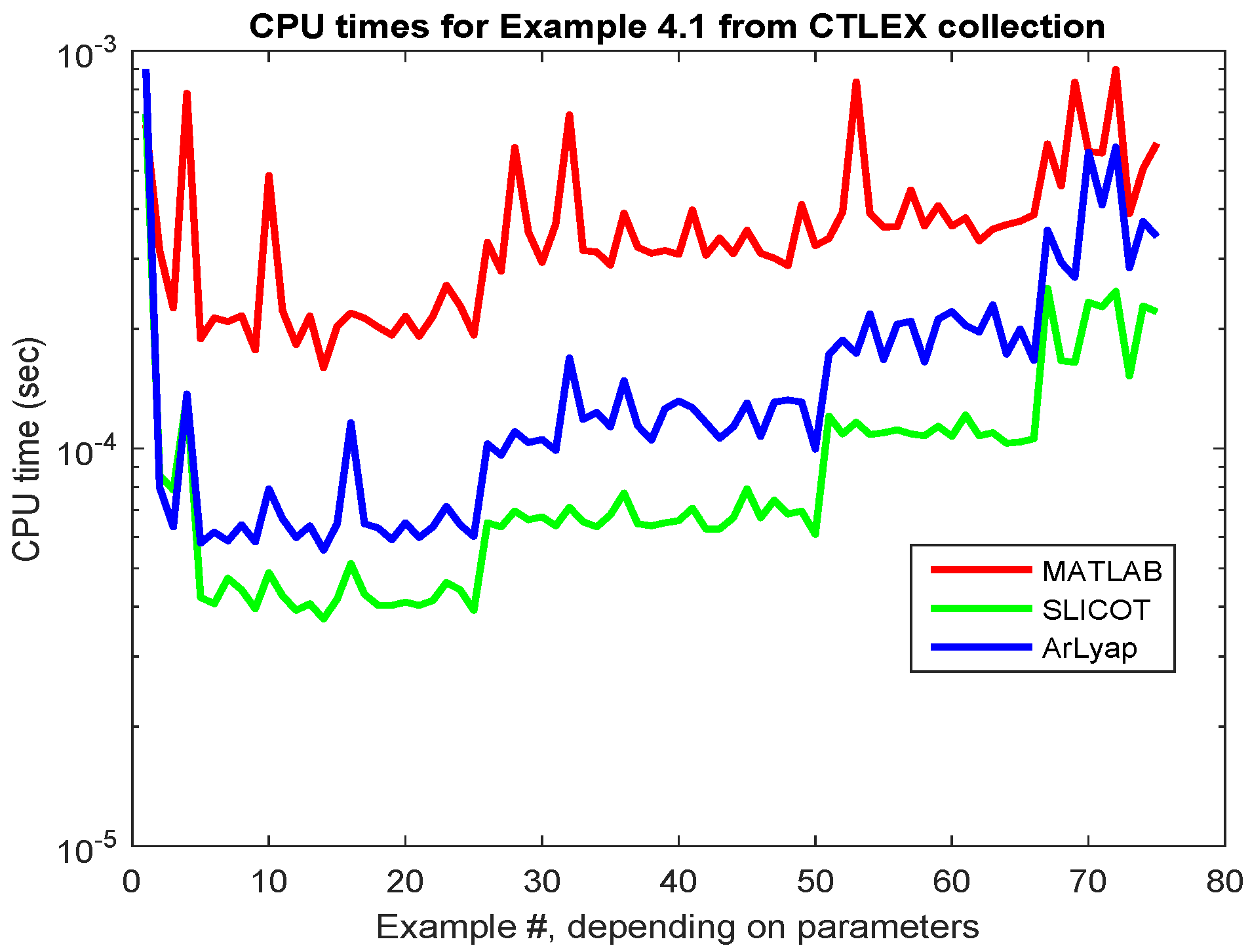
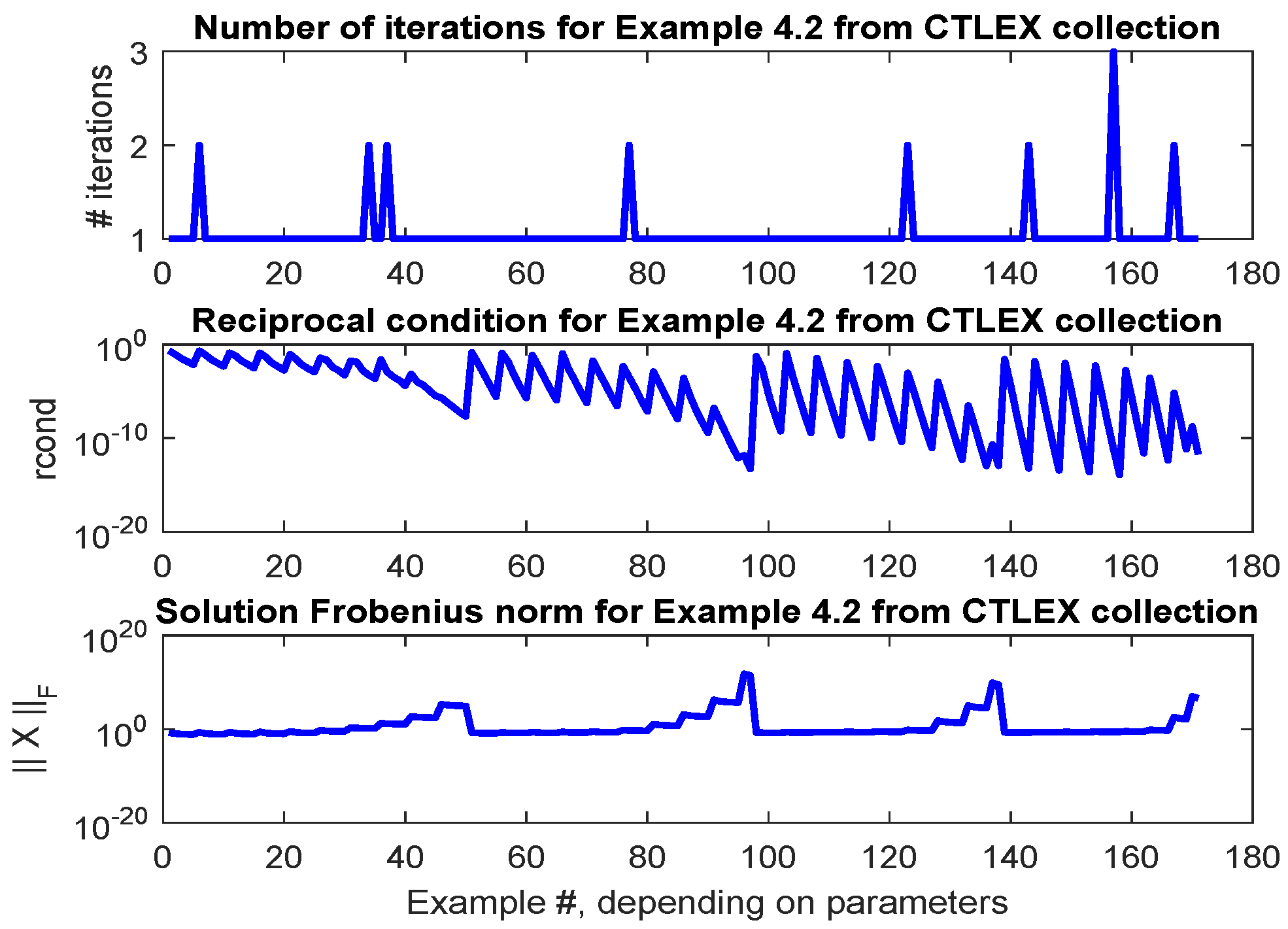



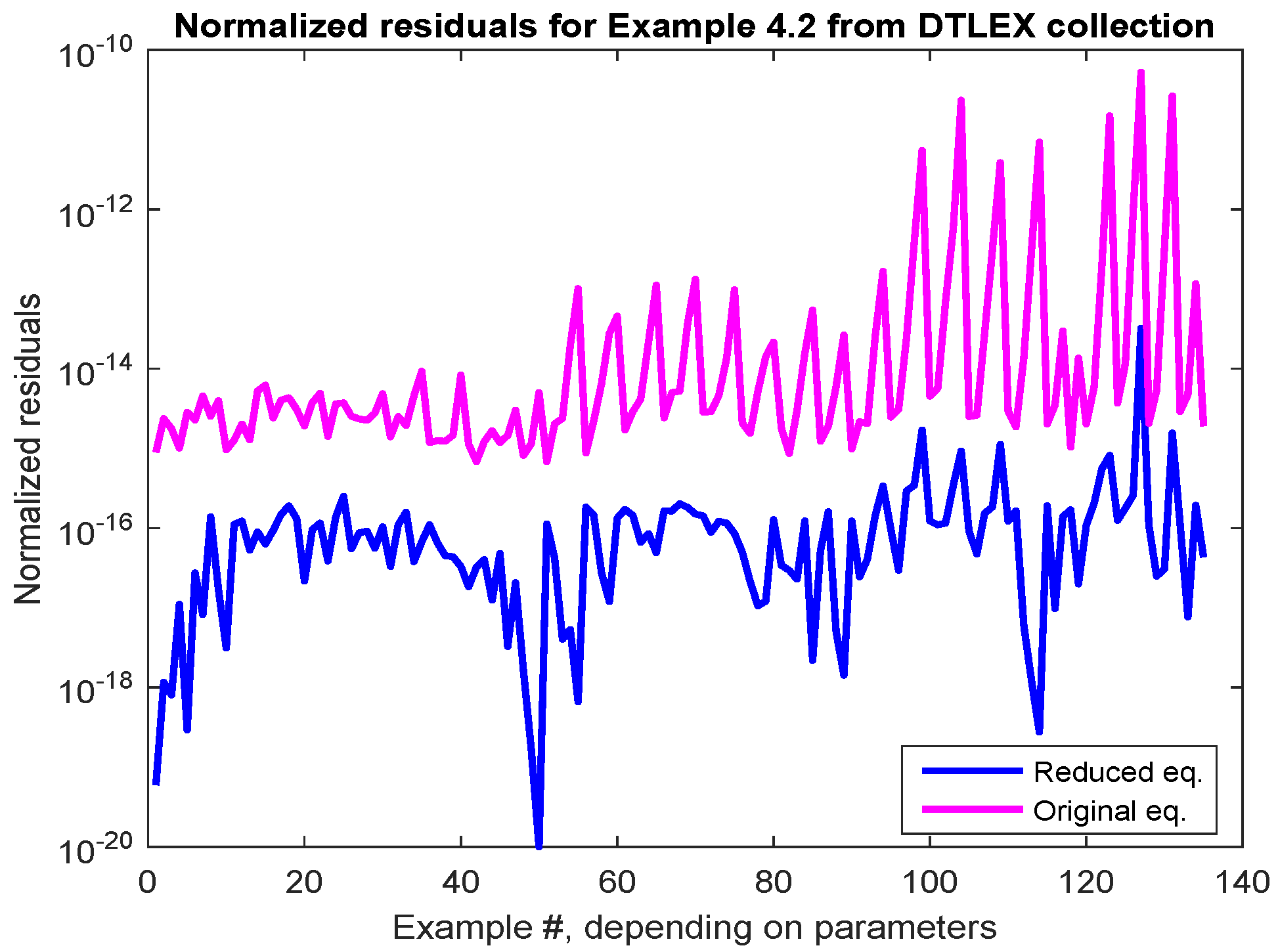
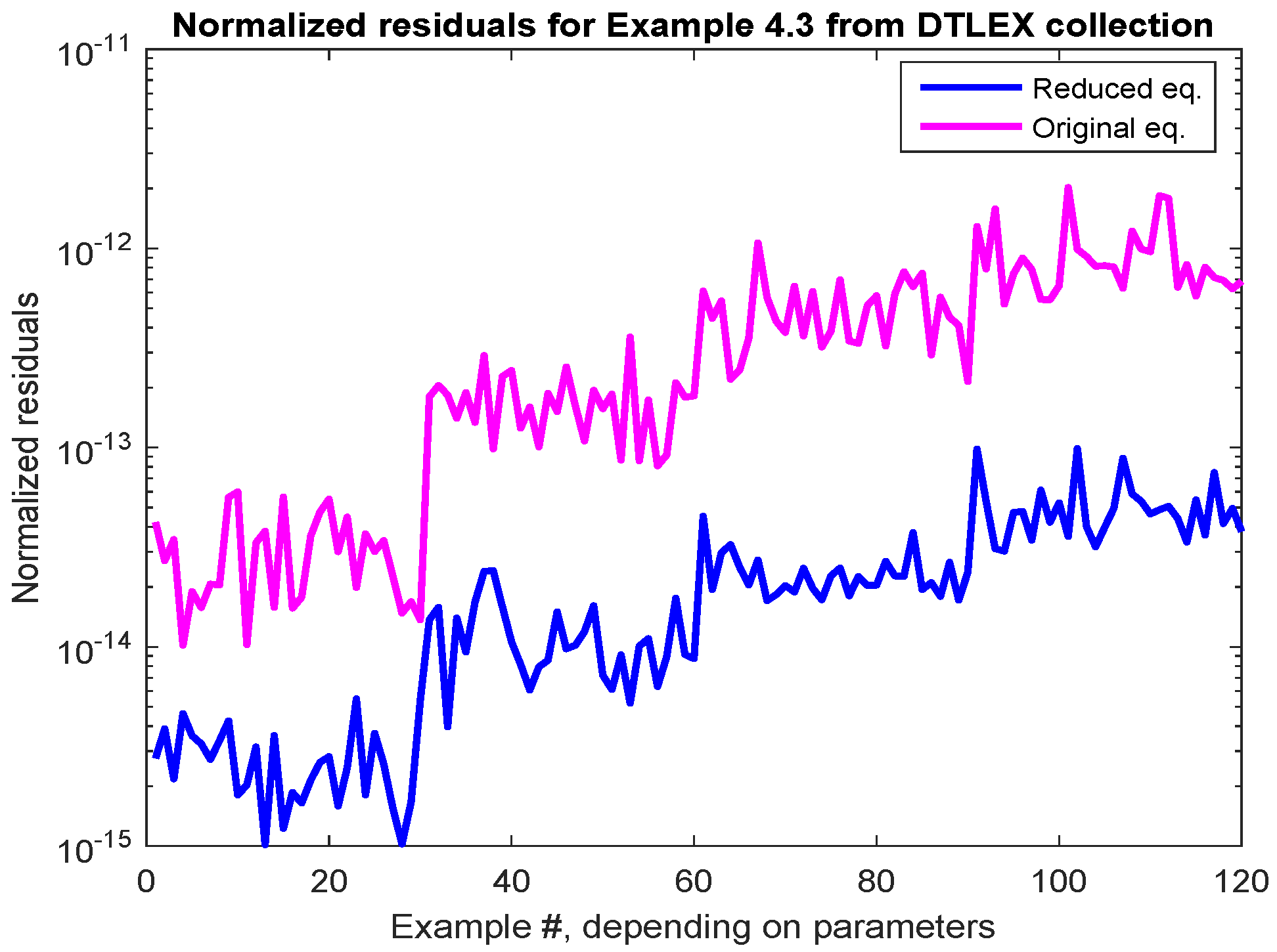
| Parameters | Algorithm | Normalized Residuals |
|---|---|---|
| , | ALyap | |
| ArLyap | ||
| , | ALyap | |
| ArLyap | ||
| , | ALyap | |
| ArLyap |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sima, V. Comparative Performance Evaluation of an Accuracy-Enhancing Lyapunov Solver. Information 2019, 10, 215. https://doi.org/10.3390/info10060215
Sima V. Comparative Performance Evaluation of an Accuracy-Enhancing Lyapunov Solver. Information. 2019; 10(6):215. https://doi.org/10.3390/info10060215
Chicago/Turabian StyleSima, Vasile. 2019. "Comparative Performance Evaluation of an Accuracy-Enhancing Lyapunov Solver" Information 10, no. 6: 215. https://doi.org/10.3390/info10060215
APA StyleSima, V. (2019). Comparative Performance Evaluation of an Accuracy-Enhancing Lyapunov Solver. Information, 10(6), 215. https://doi.org/10.3390/info10060215





