Optimal Control of Virus Spread under Different Conditions of Resources Limitations †
Abstract
1. Introduction
- -
- the class of susceptible subjects (S) that are the healthy individuals that may contract the virus;
- -
- the class of the infected individuals (I) not aware of their condition;
- -
- the class of the pre-AIDS patients (P);
- -
- the class of the AIDS patients (A).
2. The Mathematical Model, the Optimal Control Problem Formulation and Its Solution
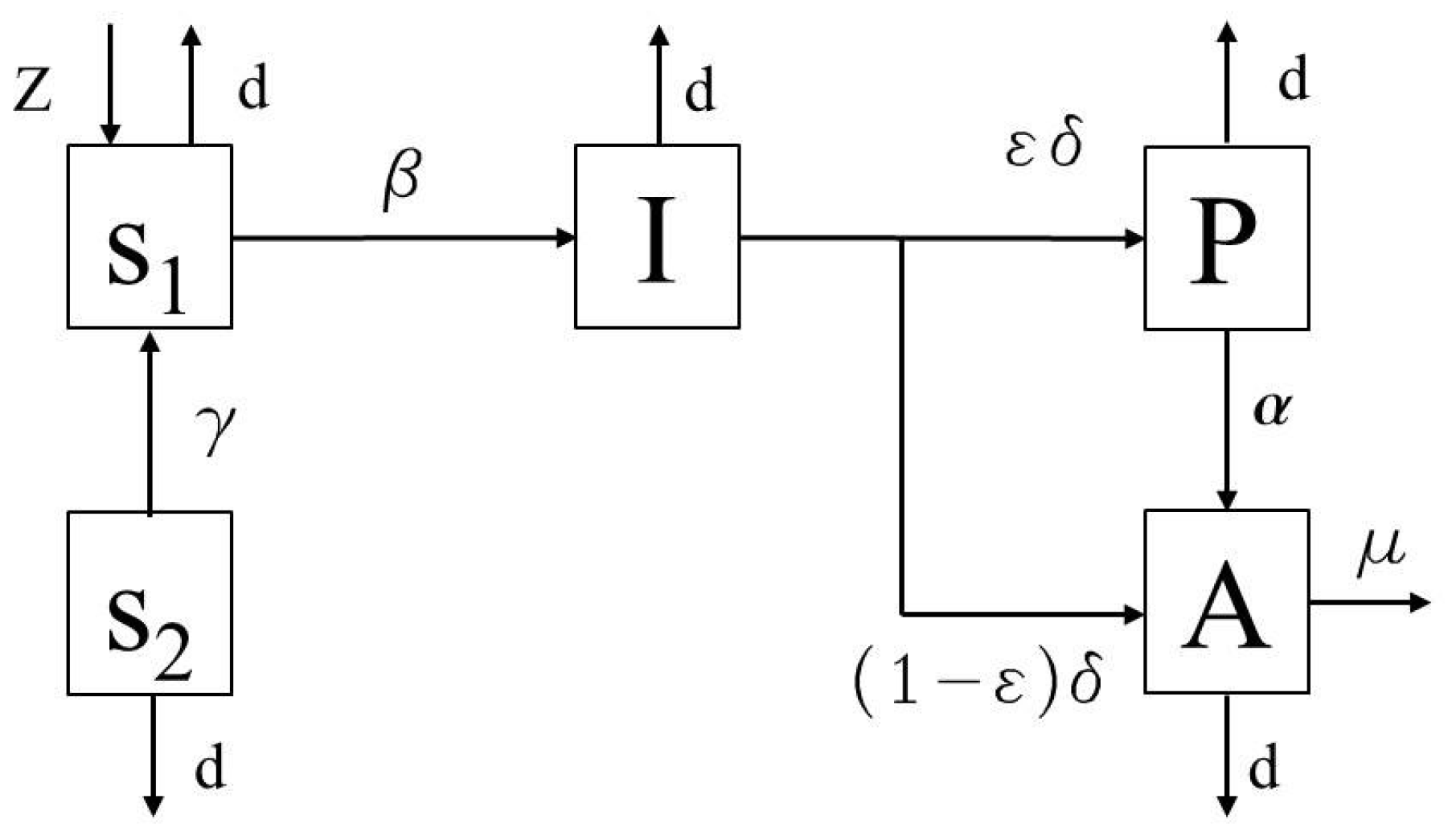
2.1. The HIV/AIDS Model
- -
- regulates the interaction responsible of the infectious propagation;
- -
- takes into account the fact that a wise individual in can, accidentally, assume a incautious behaviour as the persons;
- -
- weights the natural rate of subjects becoming aware of their status;
- -
- characterizes the natural rate of transition from to due to the evolution of the infectious disease;
- -
- determines the effect of the test campaign on the unaware individuals ;
- -
- is the fraction of individuals in which become, after test, classified as () or ((1 − ));
- -
- is the fraction of individuals which discover to be in the pre-AIDS condition or in the AIDS one;
- -
- d is responsible of the natural death rate, assumed the same for all the classes, while is the additional death factor for the individuals .
2.2. The Optimal Control
- i.
- each control is bounded, at each time instant, by an upper limit;
- ii.
- the instantaneous total control effort, given by the sum, at each time instant, of all the controls, is bounded by a total upper limit;
- iii.
- the total control effort of each input, measured by its integral over all the action time , is equal to a prefixed value;
- iv.
- the total control effort of all the inputs over the action time interval is equal to a global value.
2.3. Problem Formulation for Case i
2.4. Problem Formulation for Case ii
- A
- , , . In this case no solution is possible, since it requires the fulfilment of all the constraints at the same time, clearly impossible.
- B
- , , . This implies that and , that is, both the controls are not acting.
- C
- , , . Being that the first and the third constraint are satisfied on the boundary, one has and .
- D
- , , . This case is equivalent to C, with the controls exchanged: and .
- E
- , , . In this case the third constraint is verified on its boundary, giving for the solution .
- F
- , , . This situation corresponds to while can assume any value in .
- G
- , , . This is the dual case of F, so that one has while can assume any value in .
- H
- , , . These conditions correspond to both and in the interval .
- A
- not admissible, so no solutions can be obtained.
- B
- in this case one has and
- C
- D
- since this case is equivalent to C once and as well as and are exchanged, the controls are defined asand for the unknown multipliers one has
- E
- In this case the known functions are , and or, equivalently, . Equation (46) becomesand, after some easy manipulations, one can getfrom which the control can be computed. In fact,and, consequently,
- F
- making use of the values , andexpression (46) becomeswhich yields tofrom whichis explicitly obtained.
- G
- From this expression it is possible to compute
- H
2.5. Problem Formulation for Case iii
2.6. Problem Formulation for Case iv
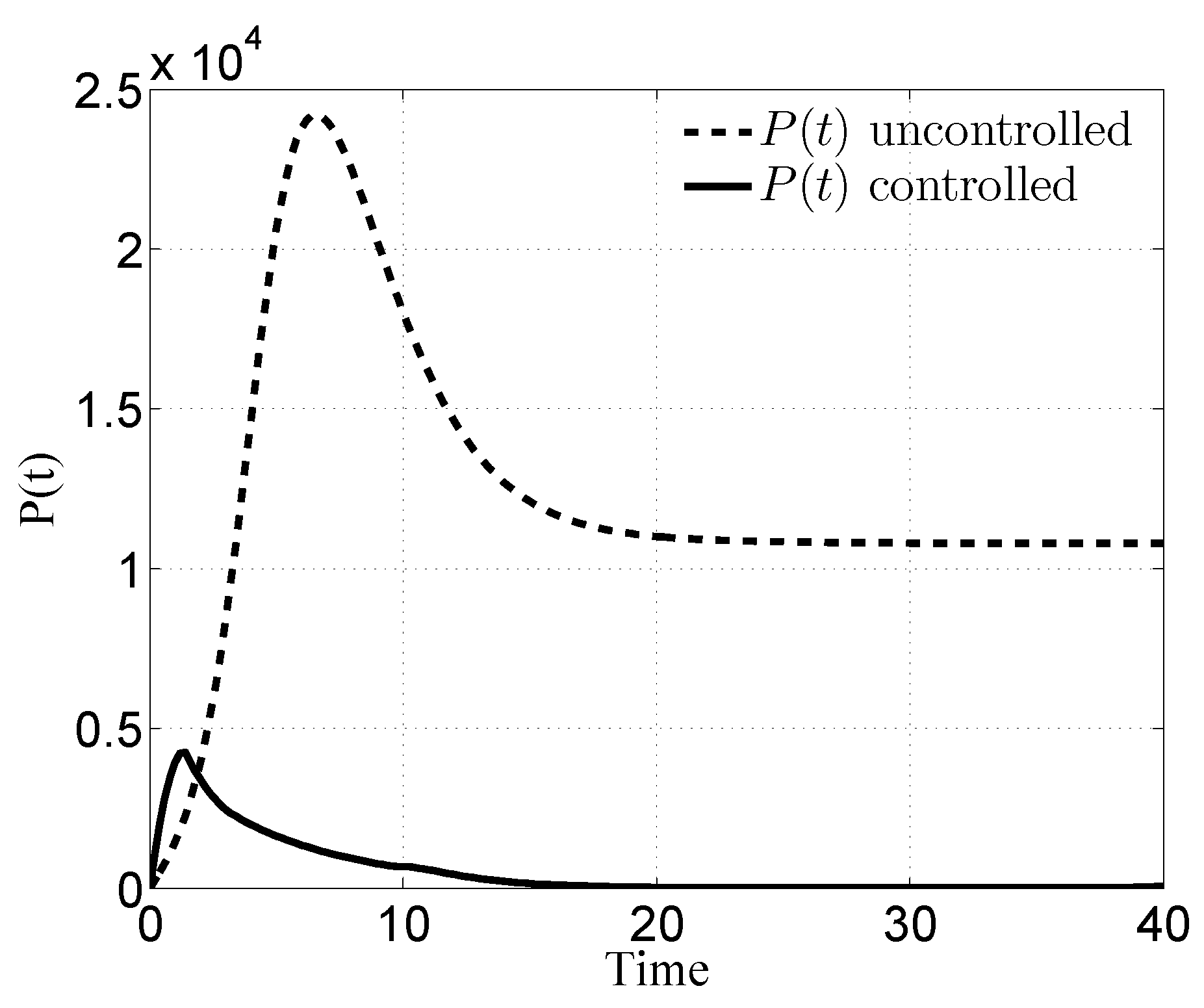
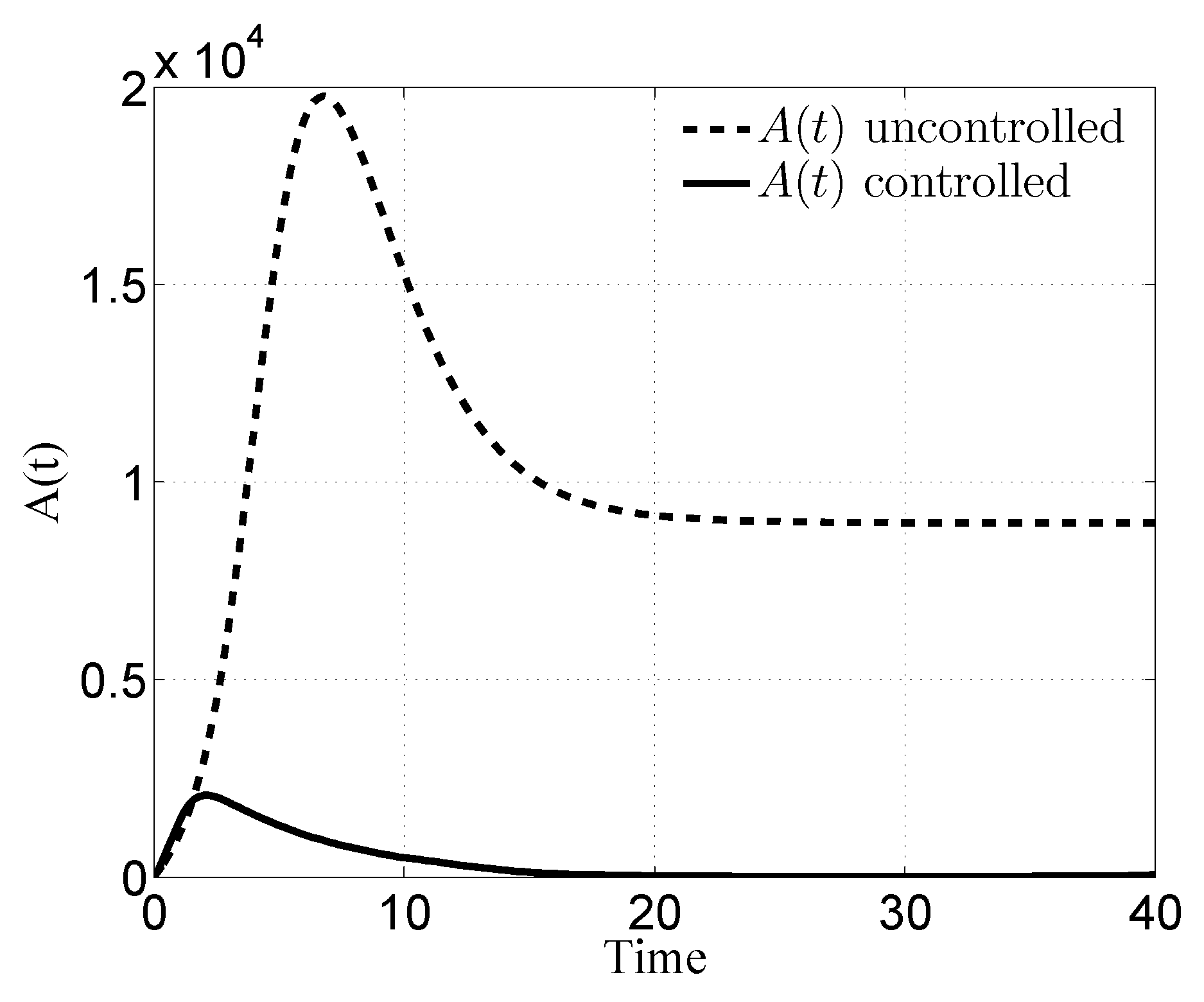
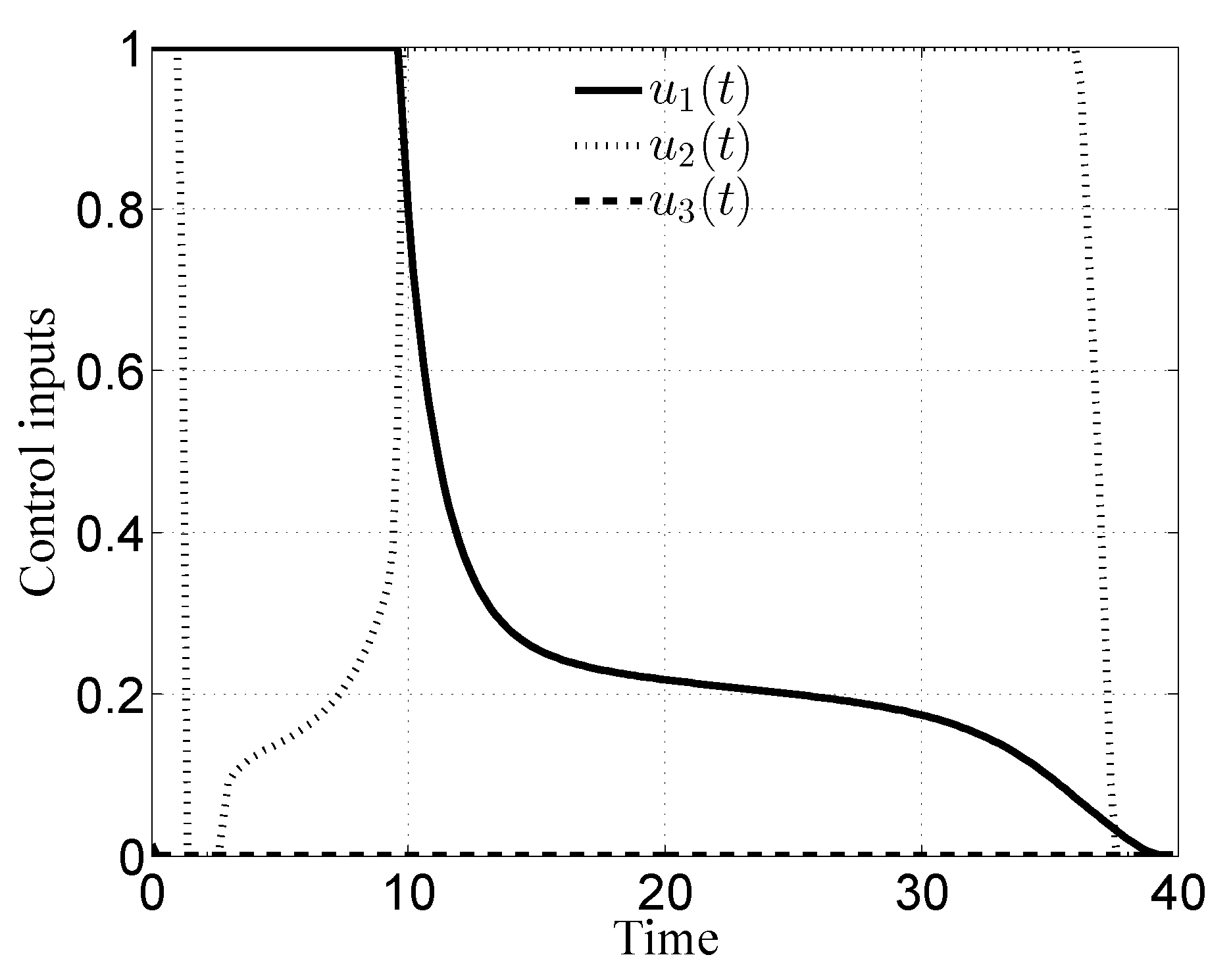
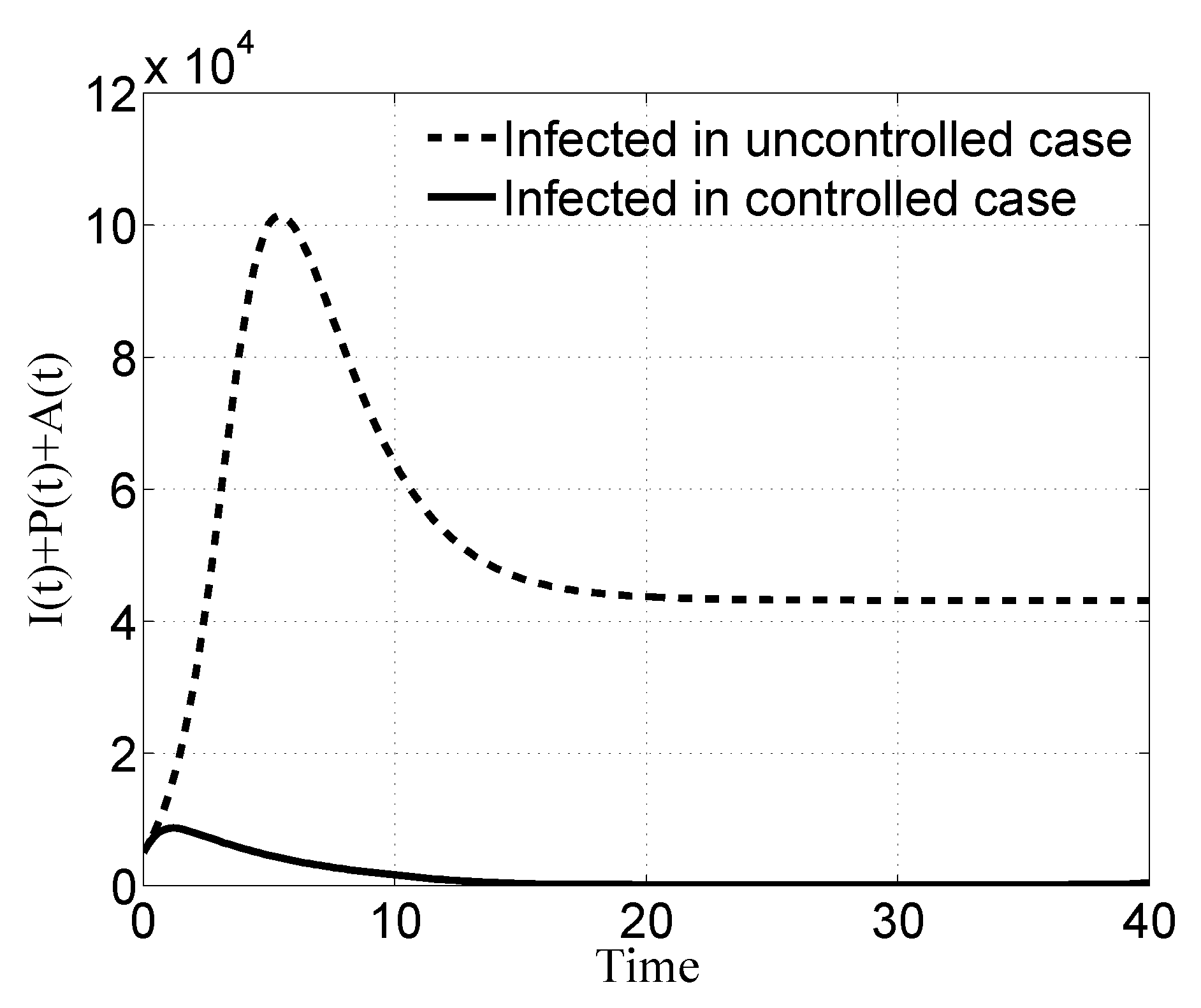
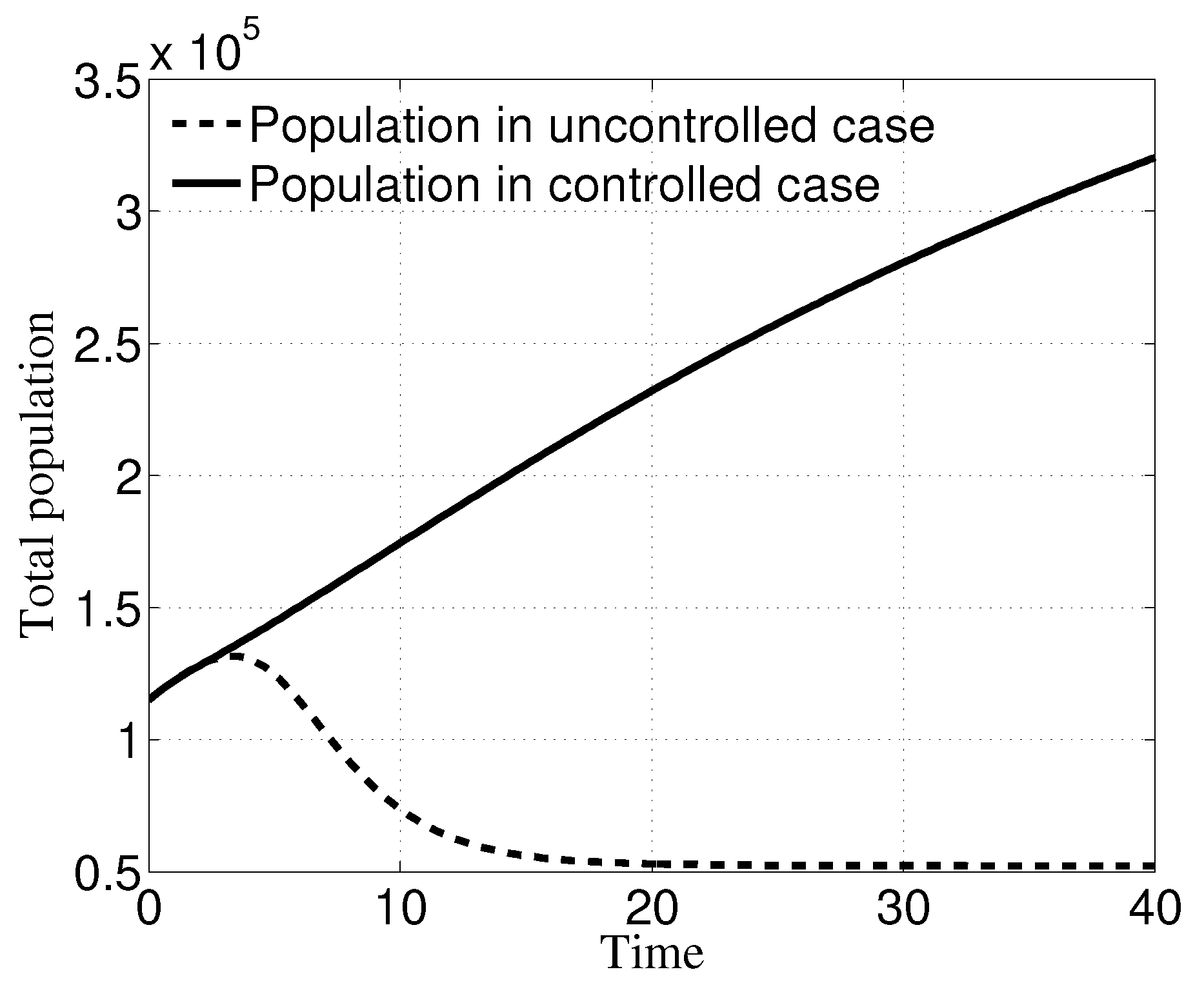
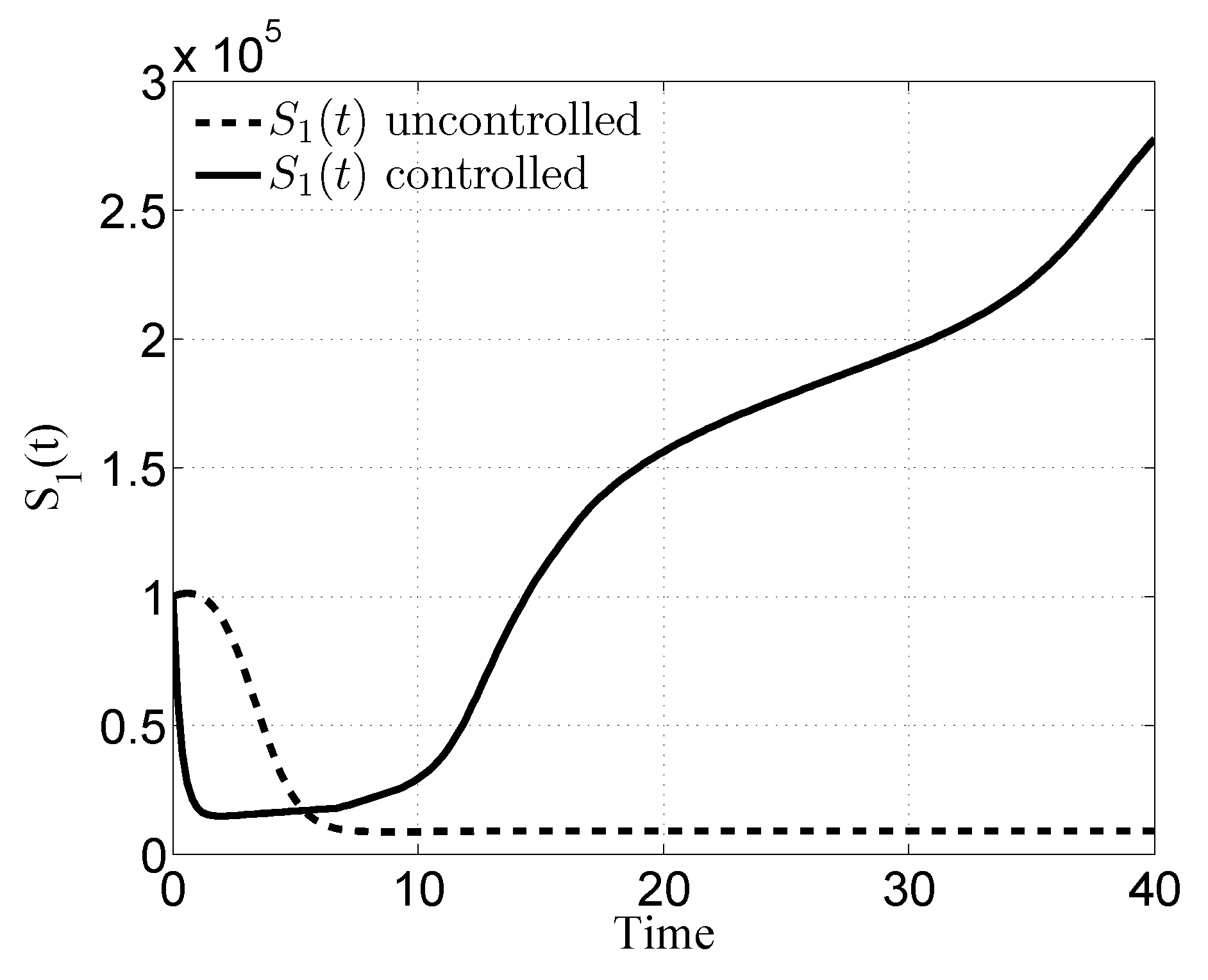
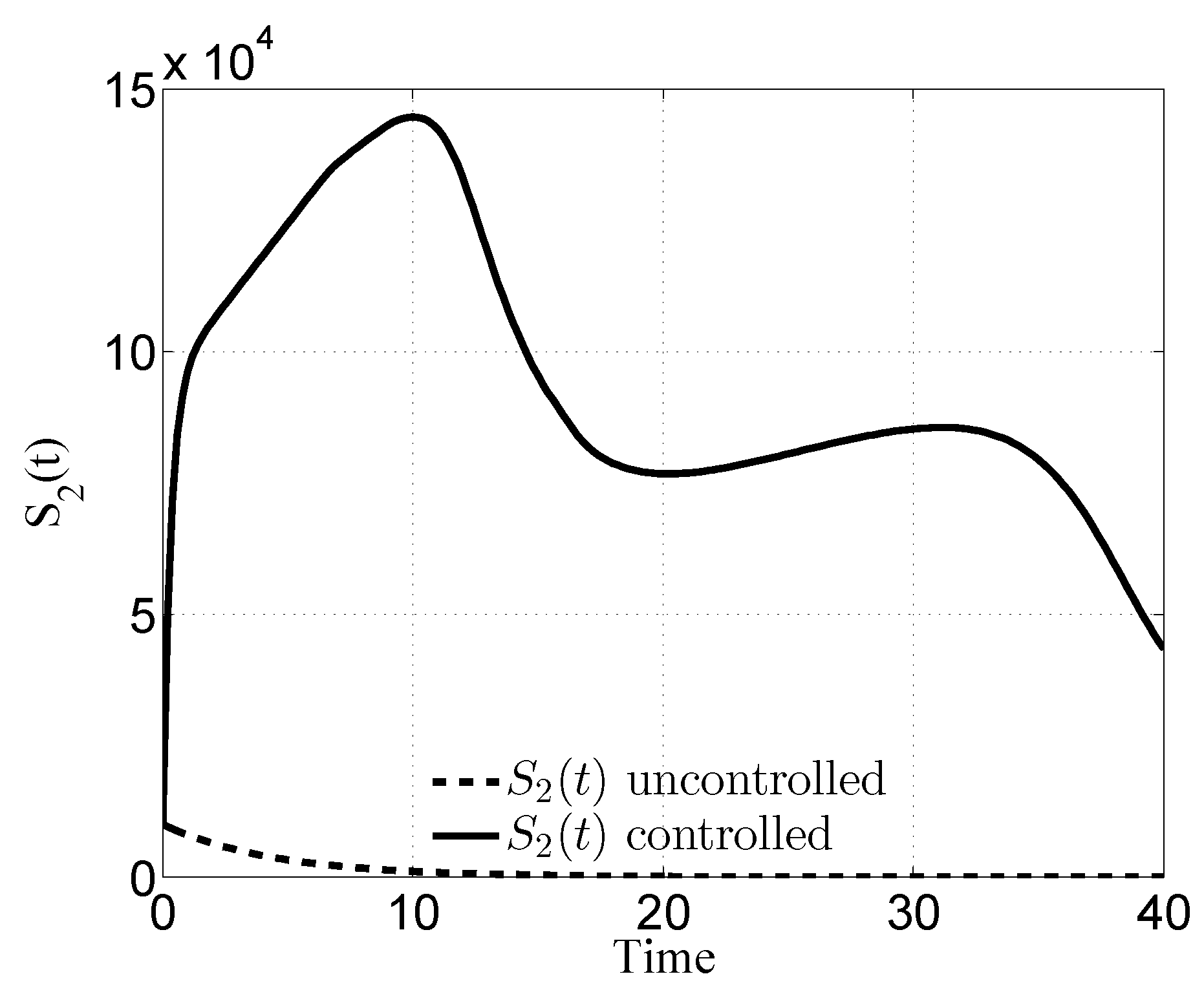
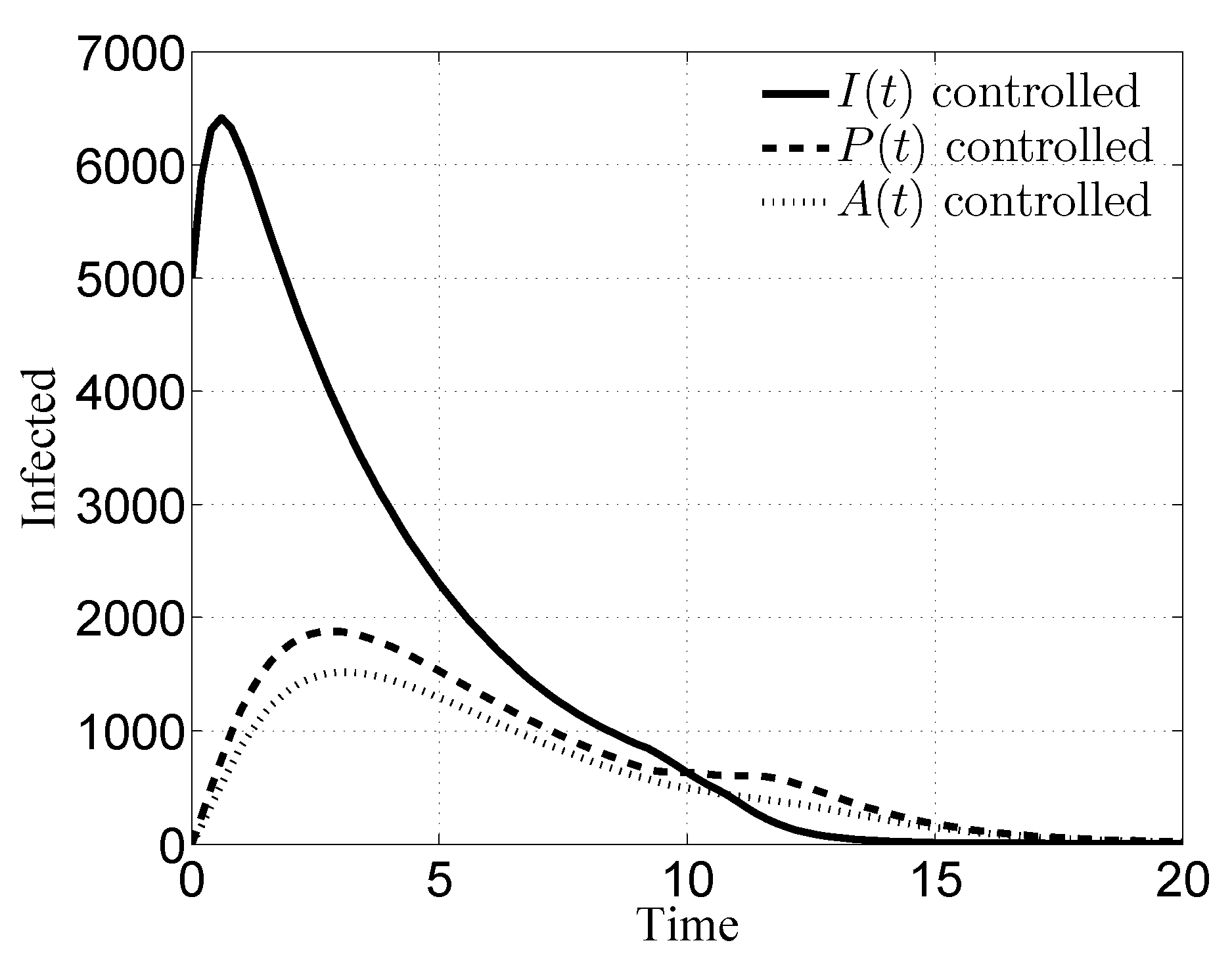
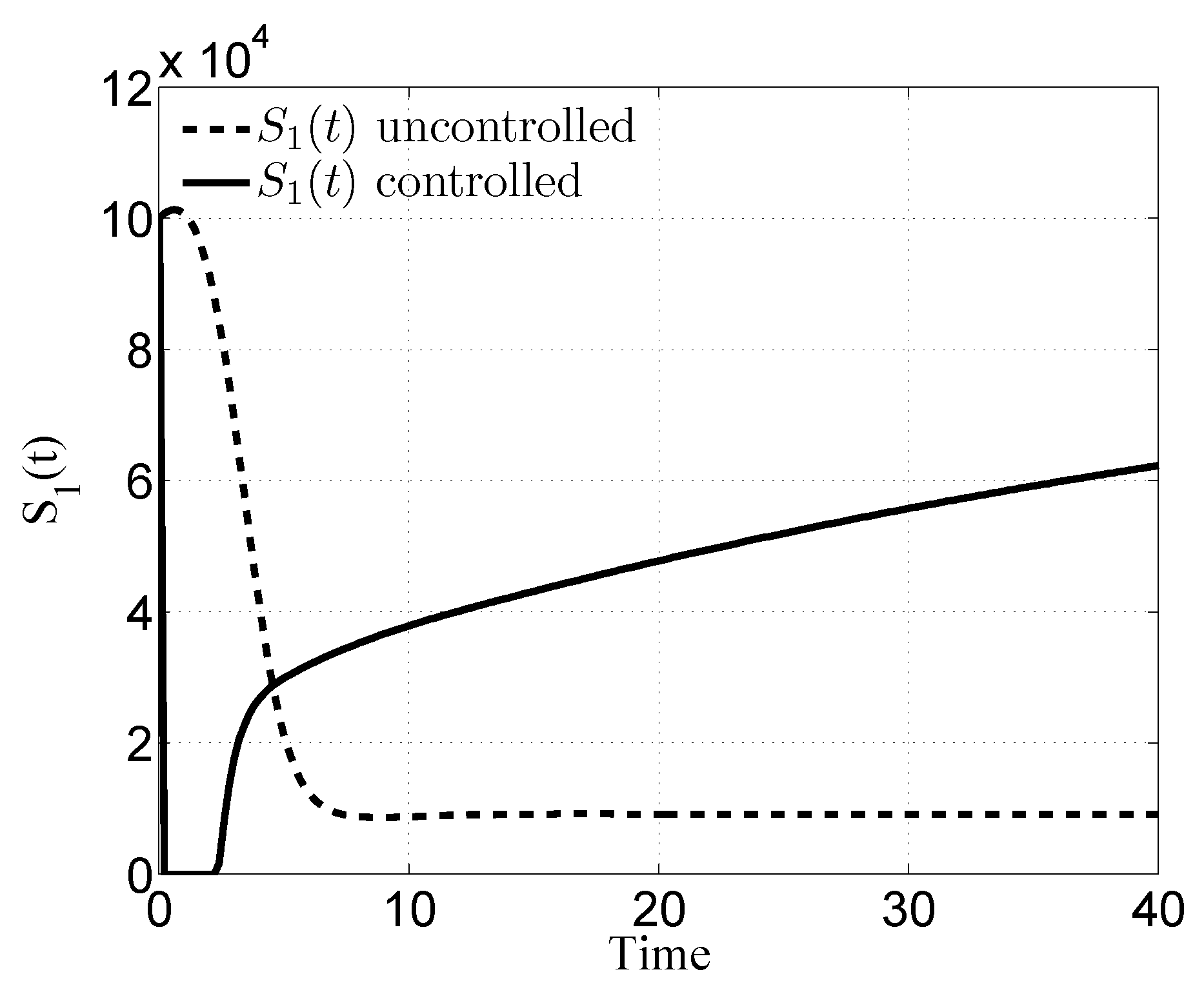
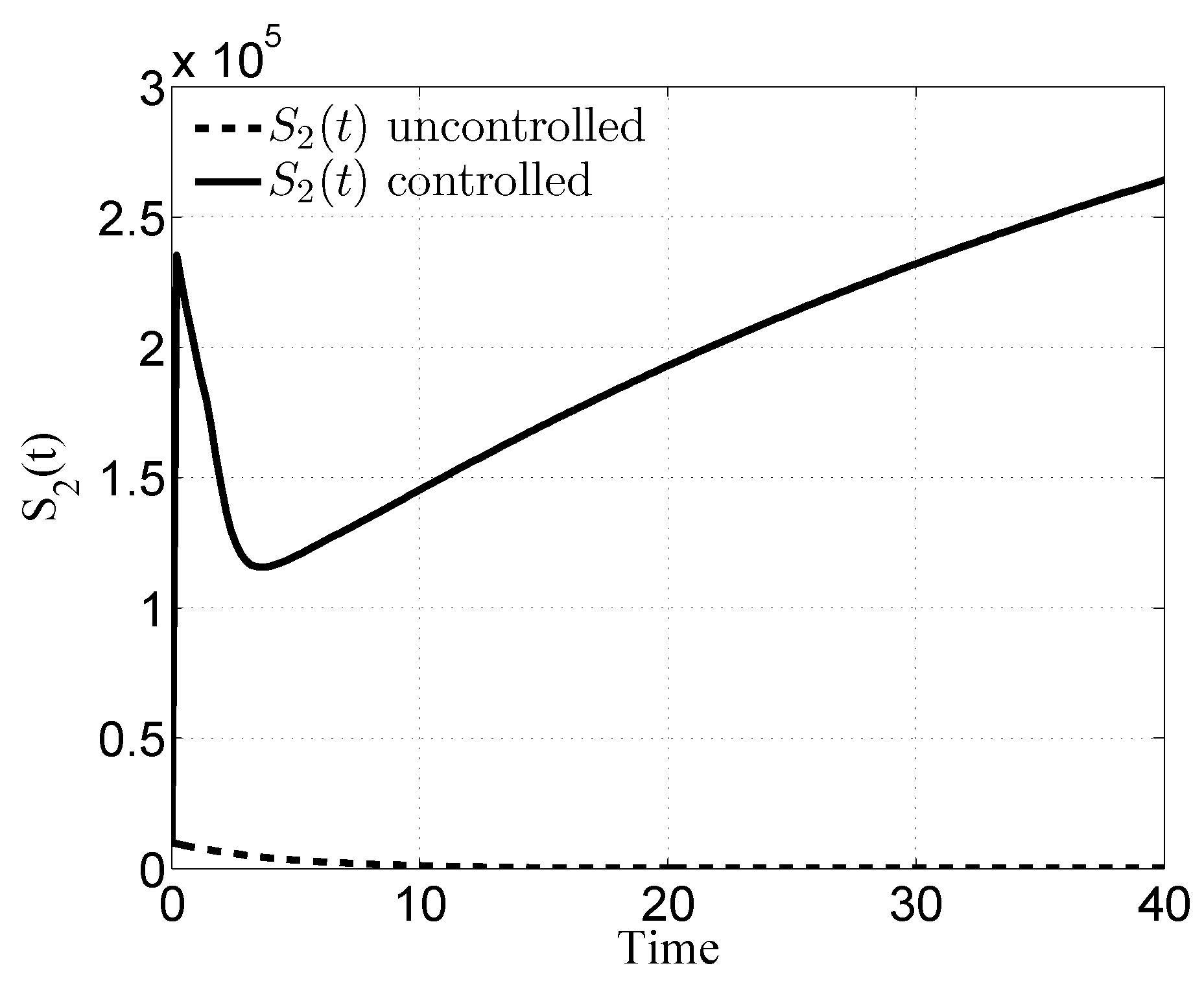
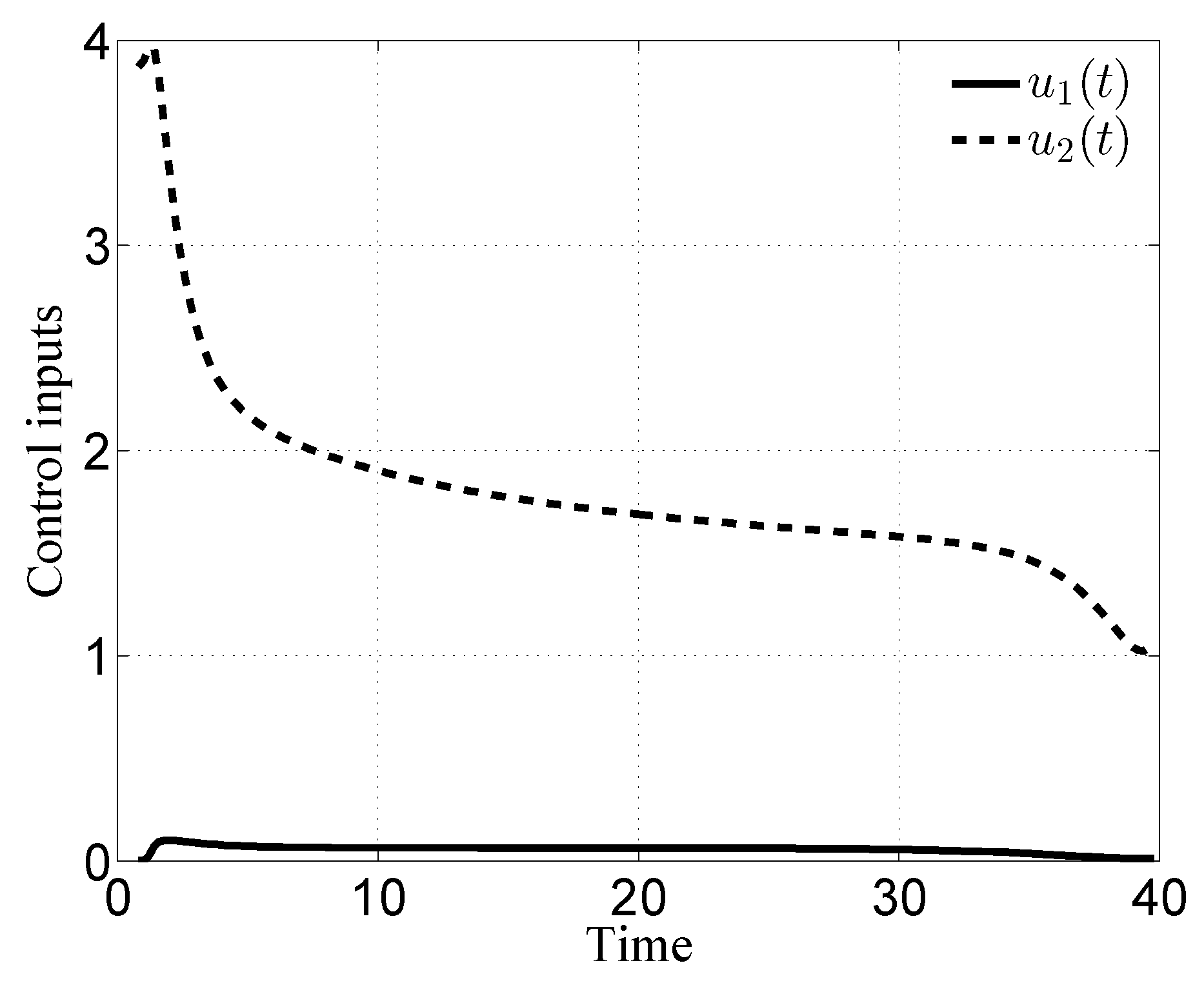
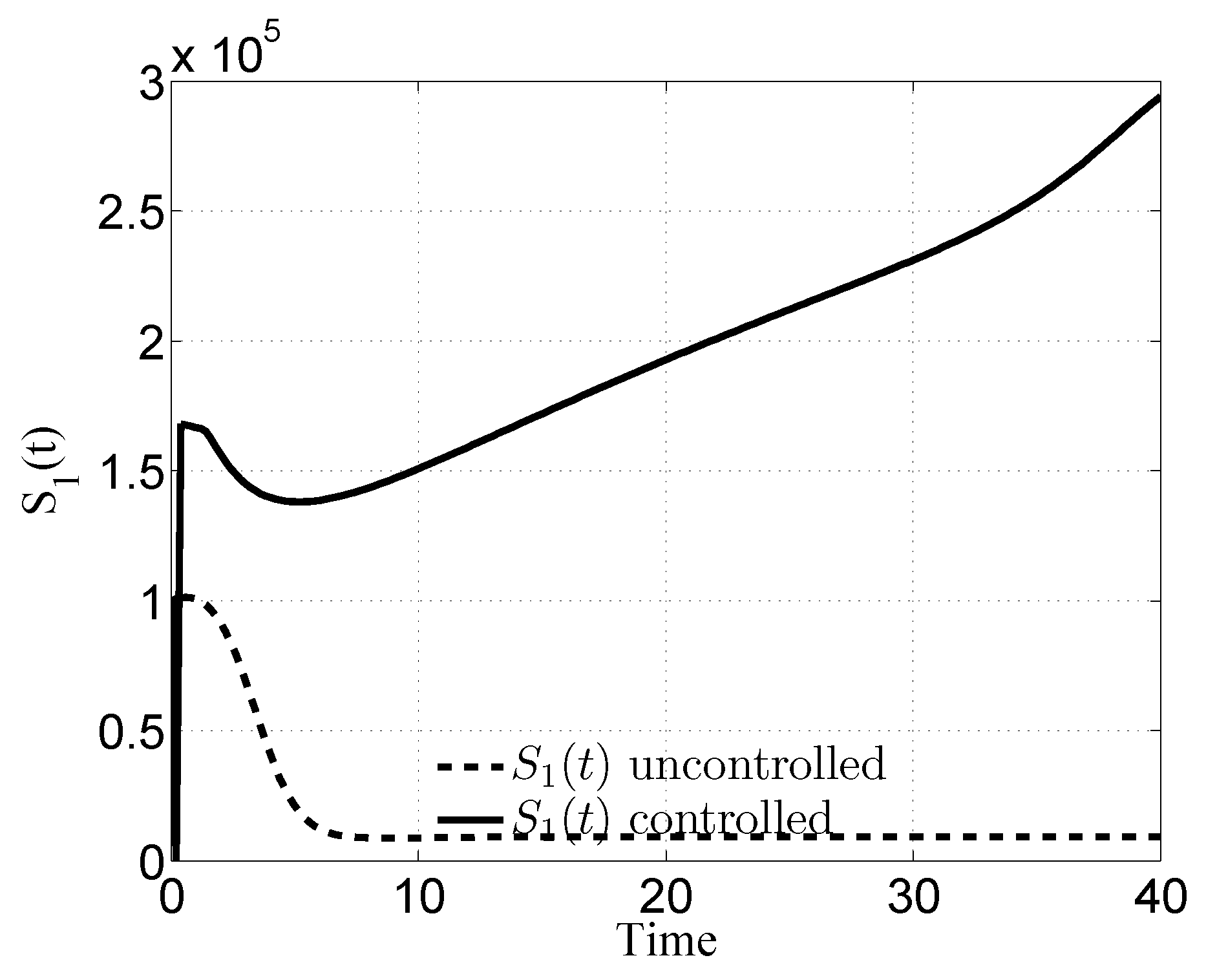
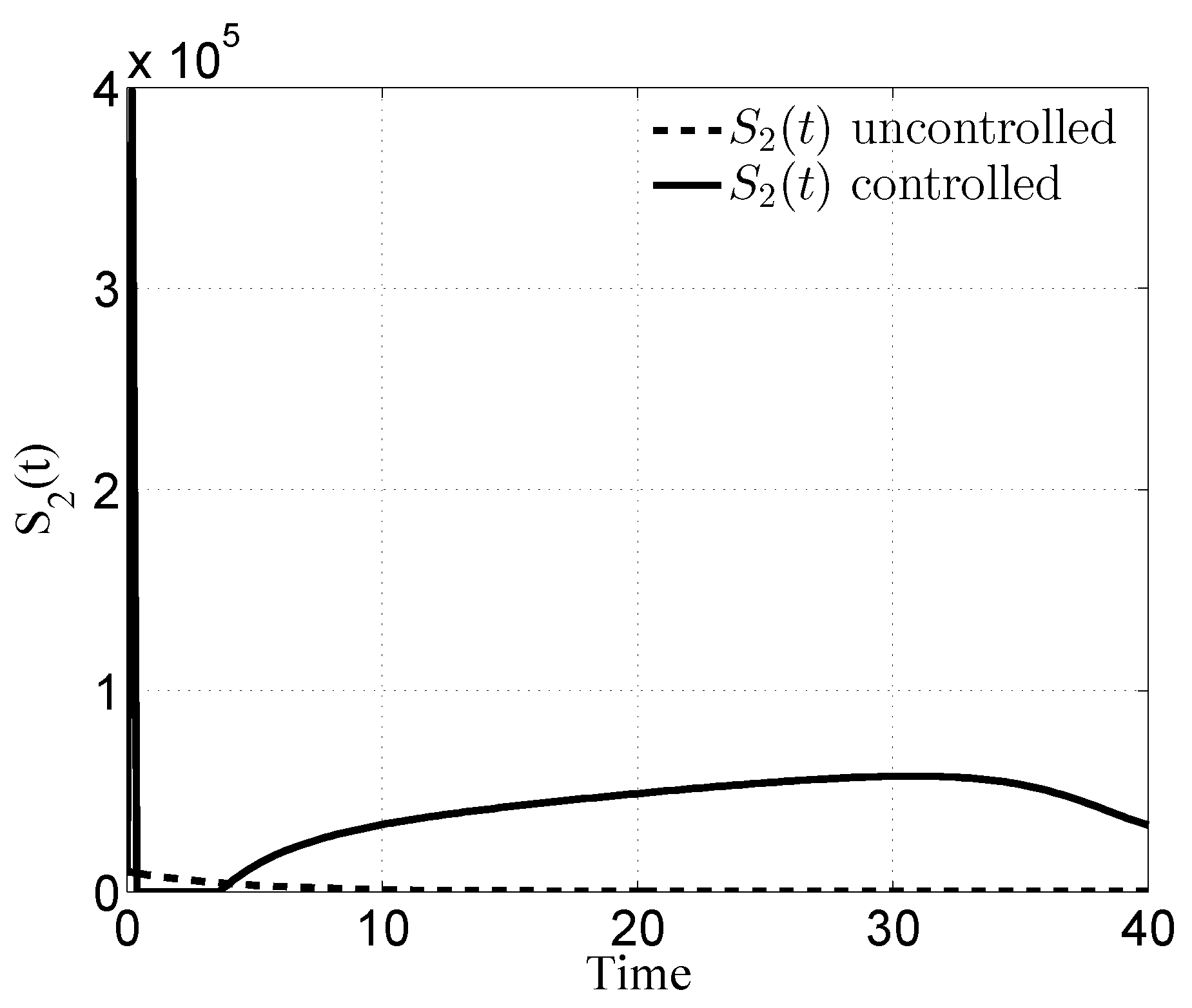
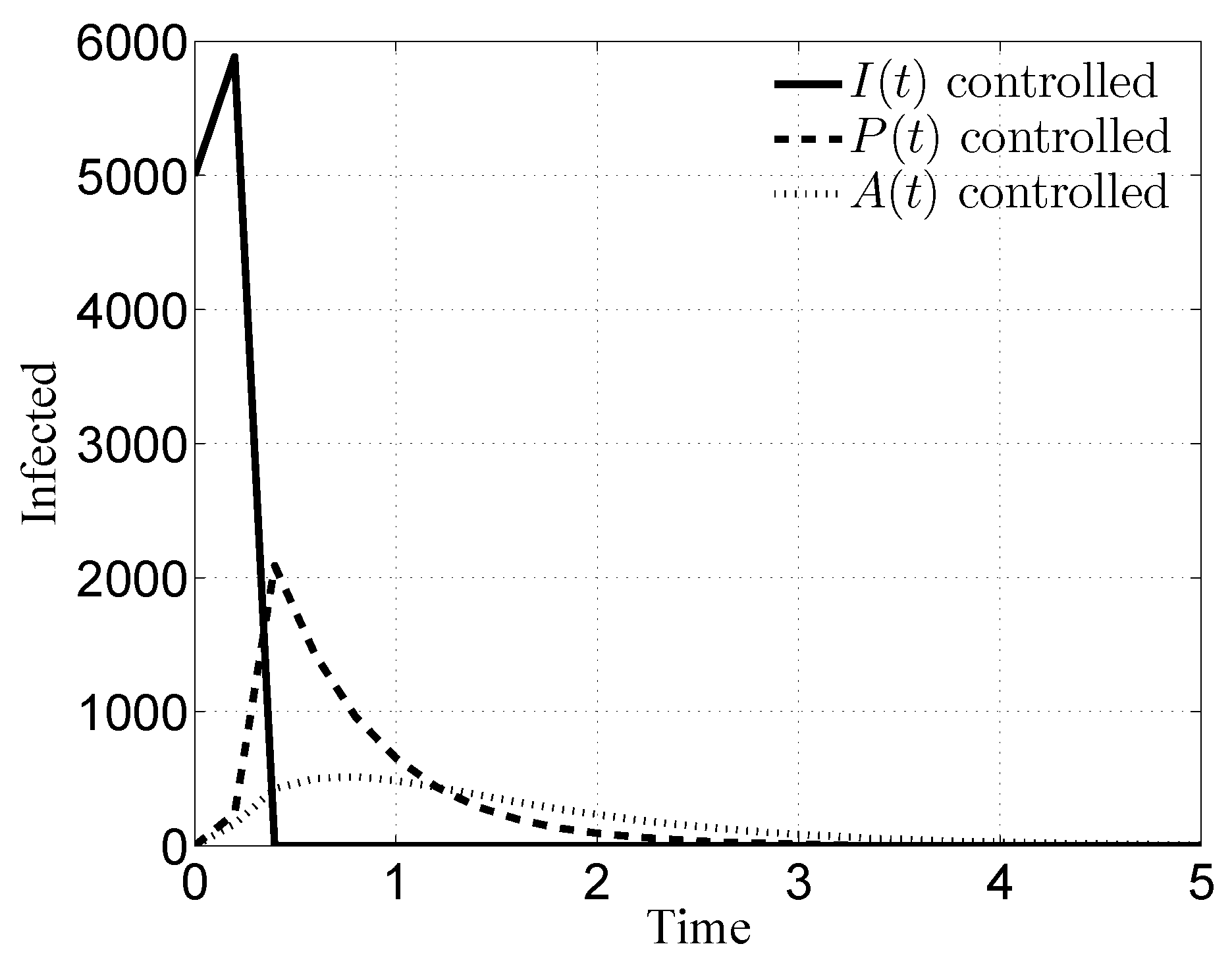
3. Numerical Results
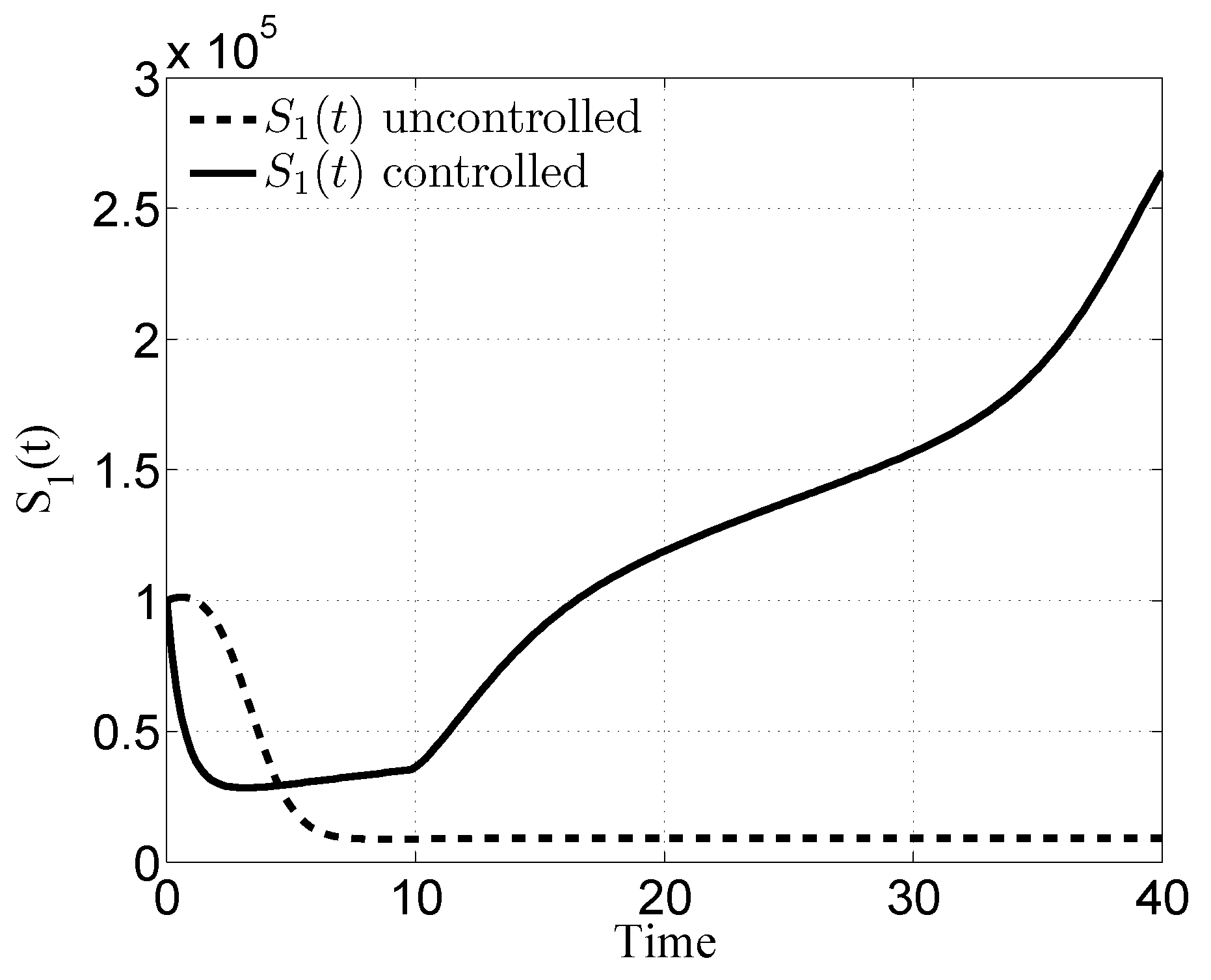
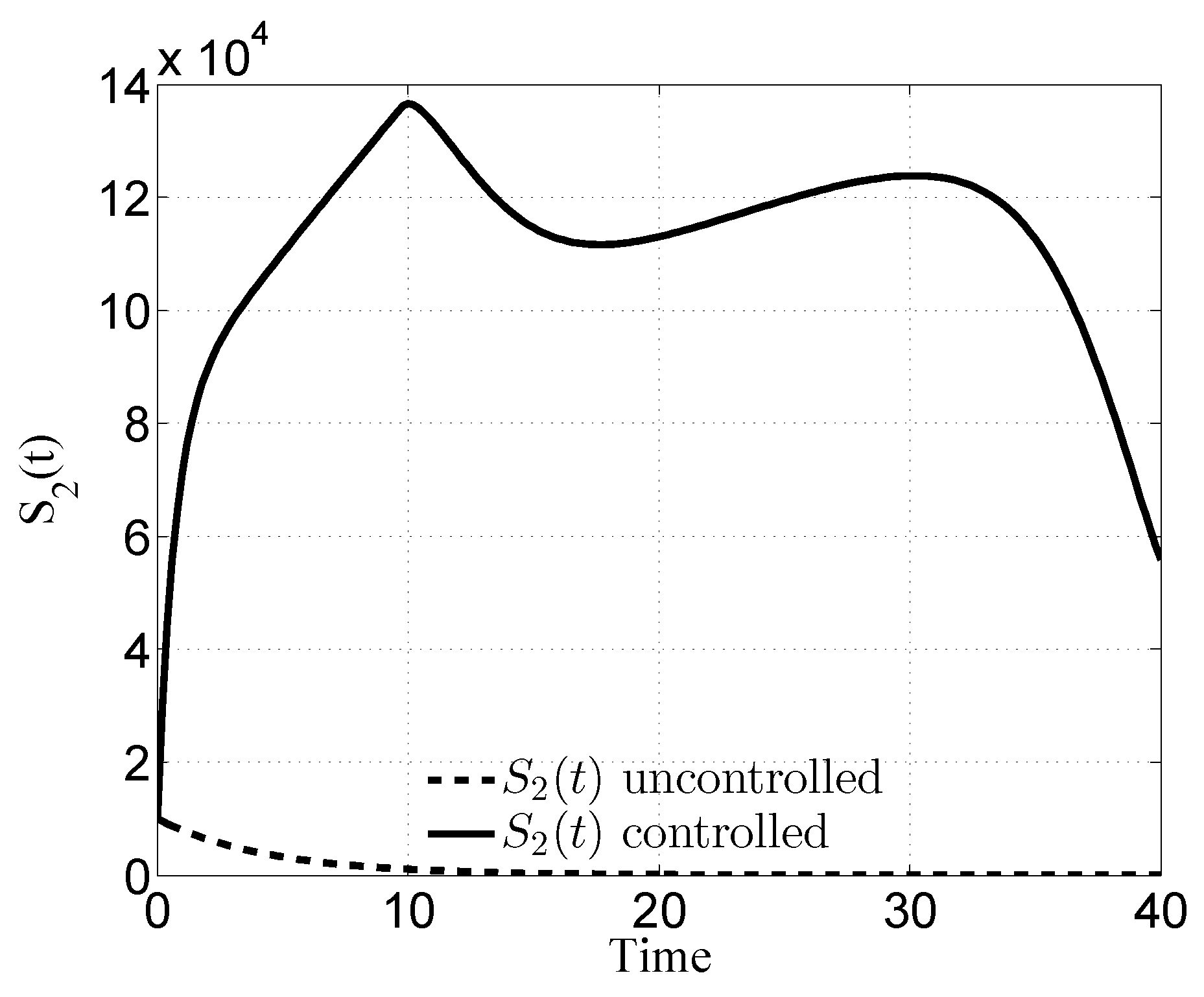
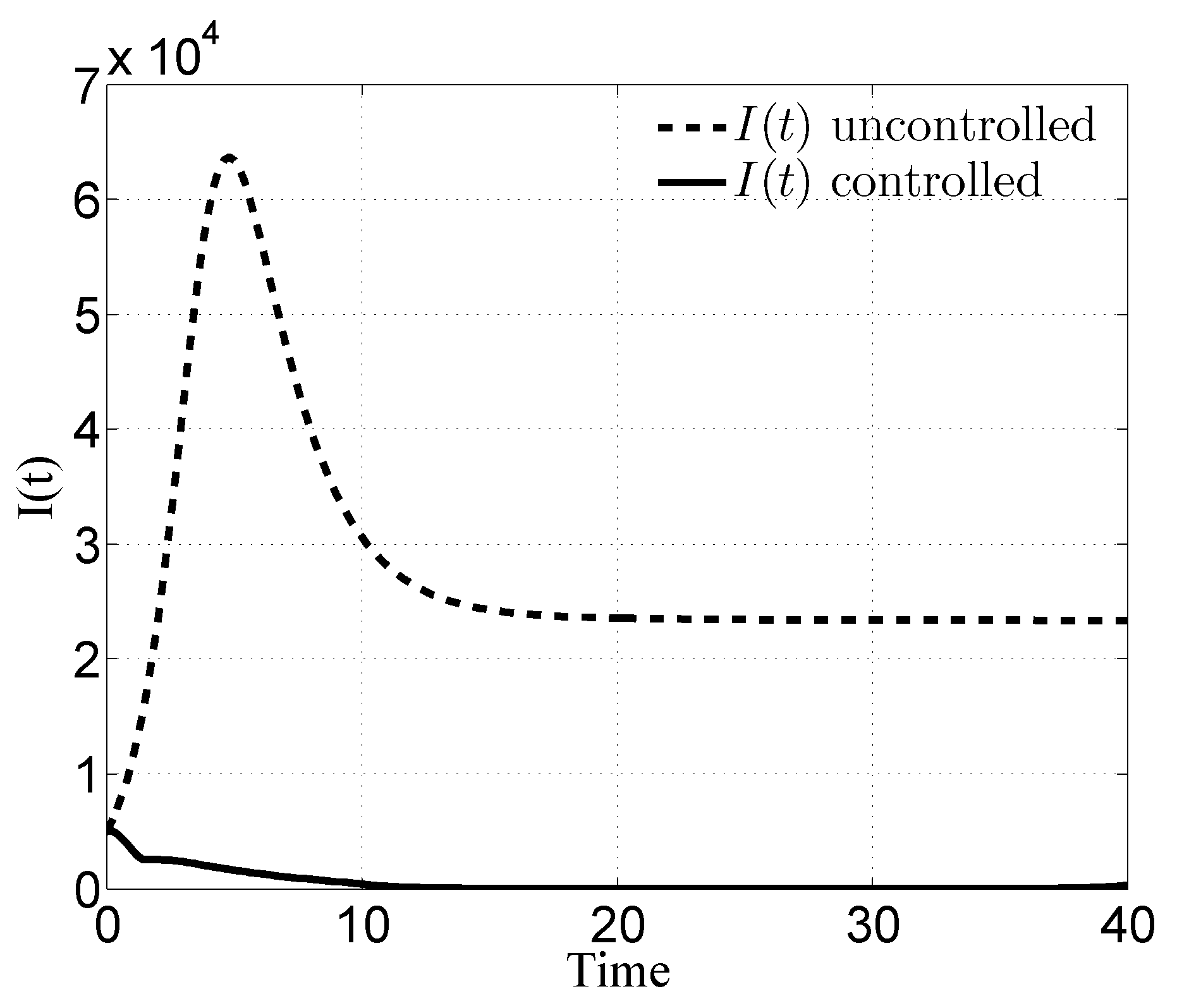
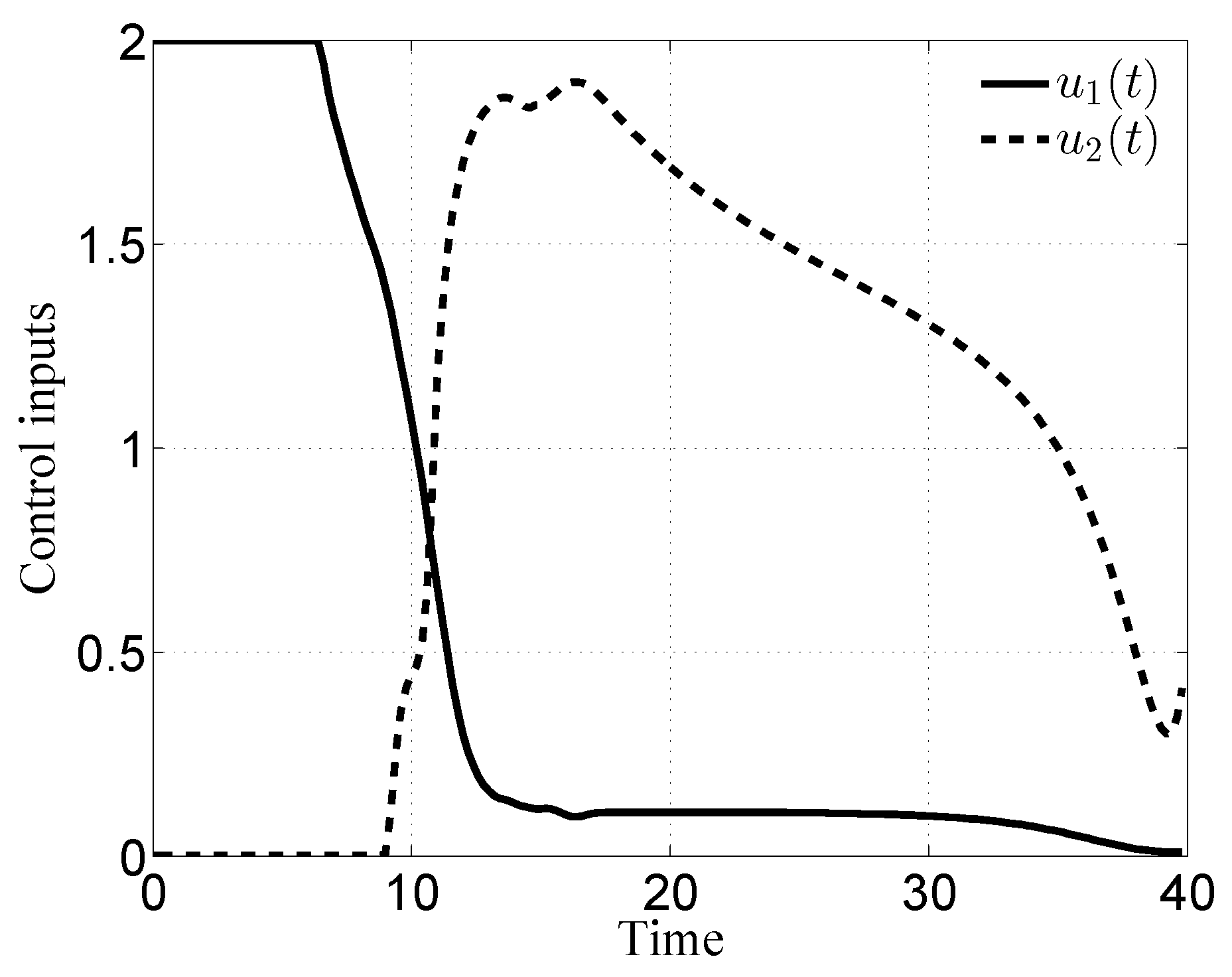
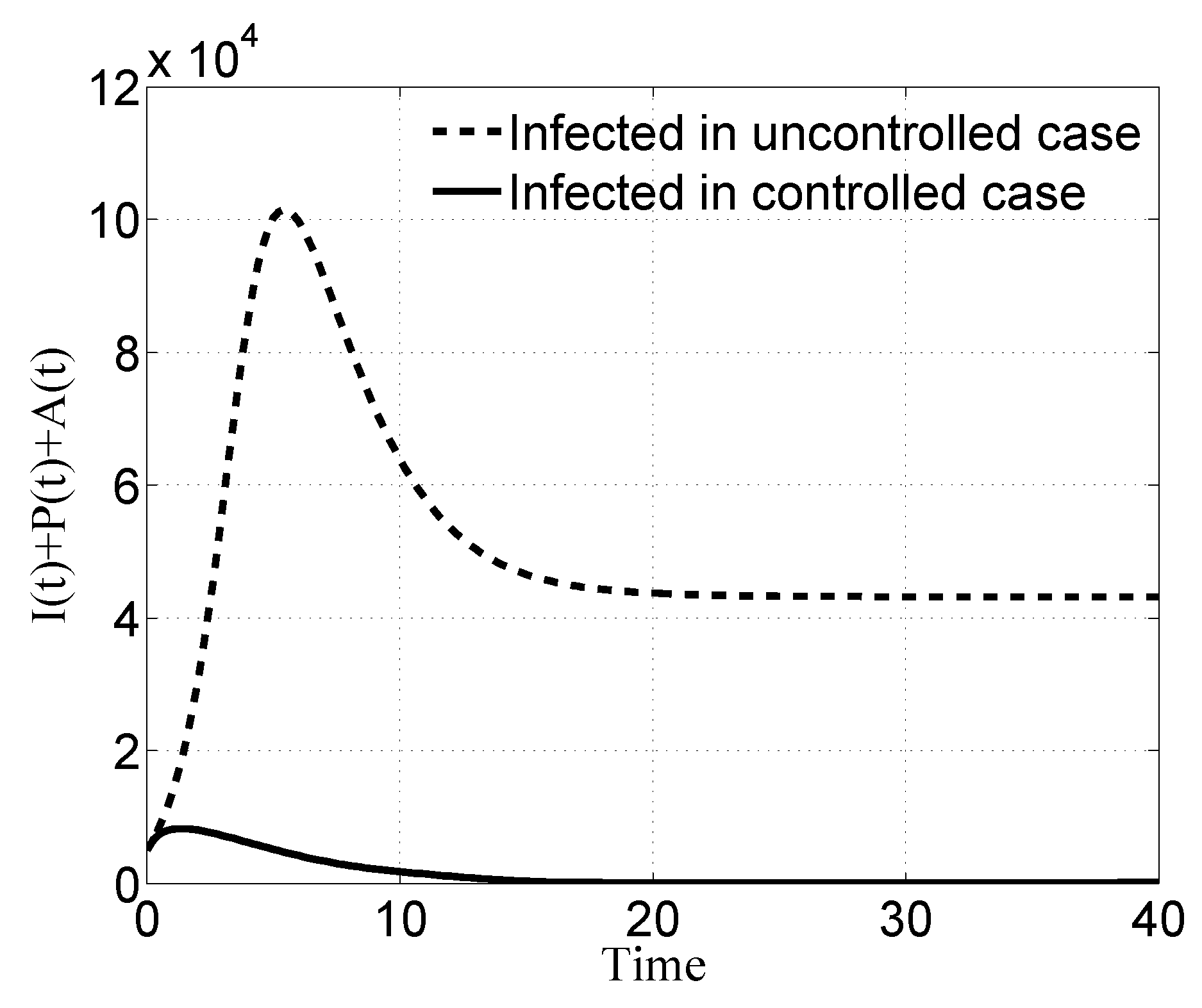
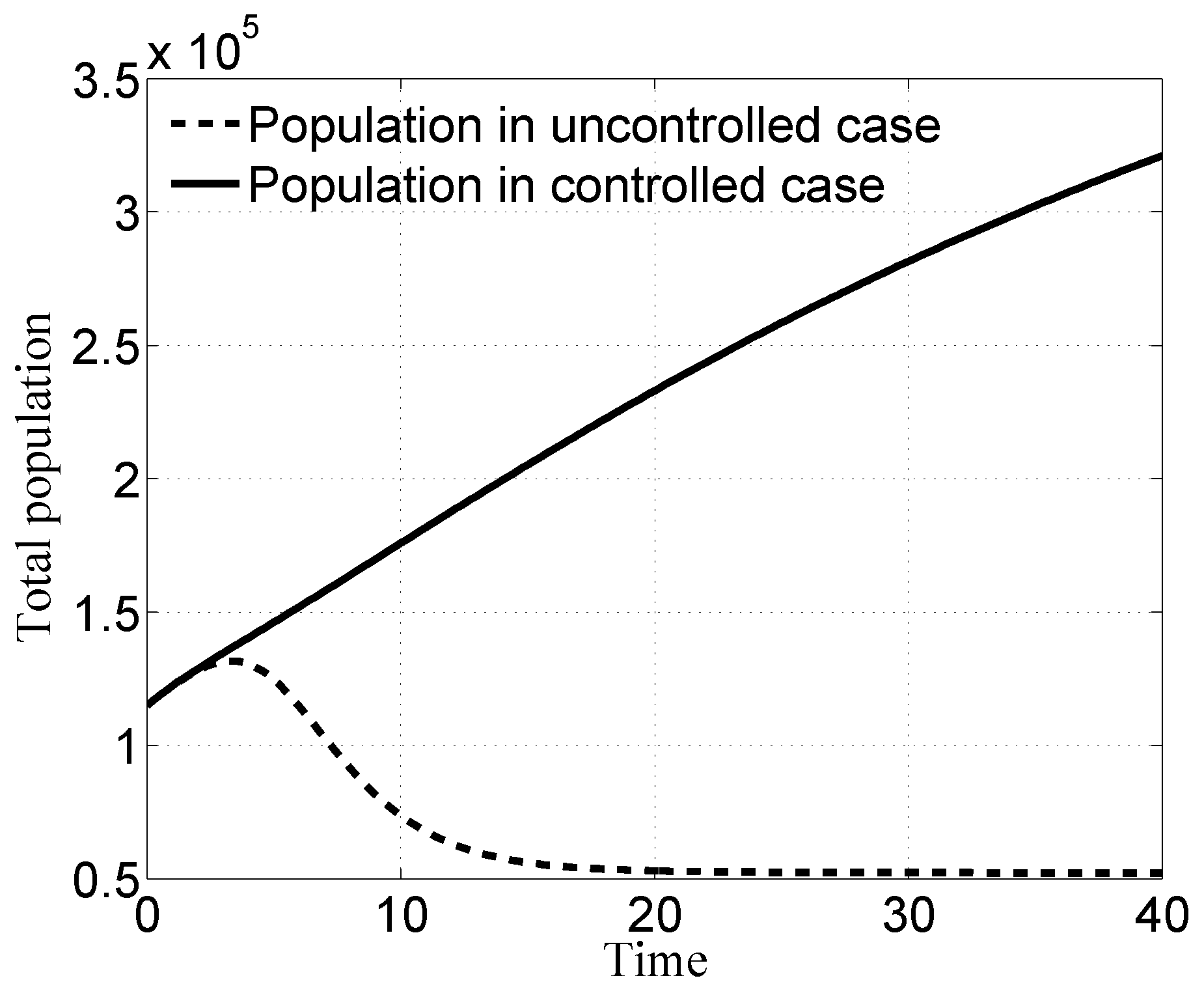
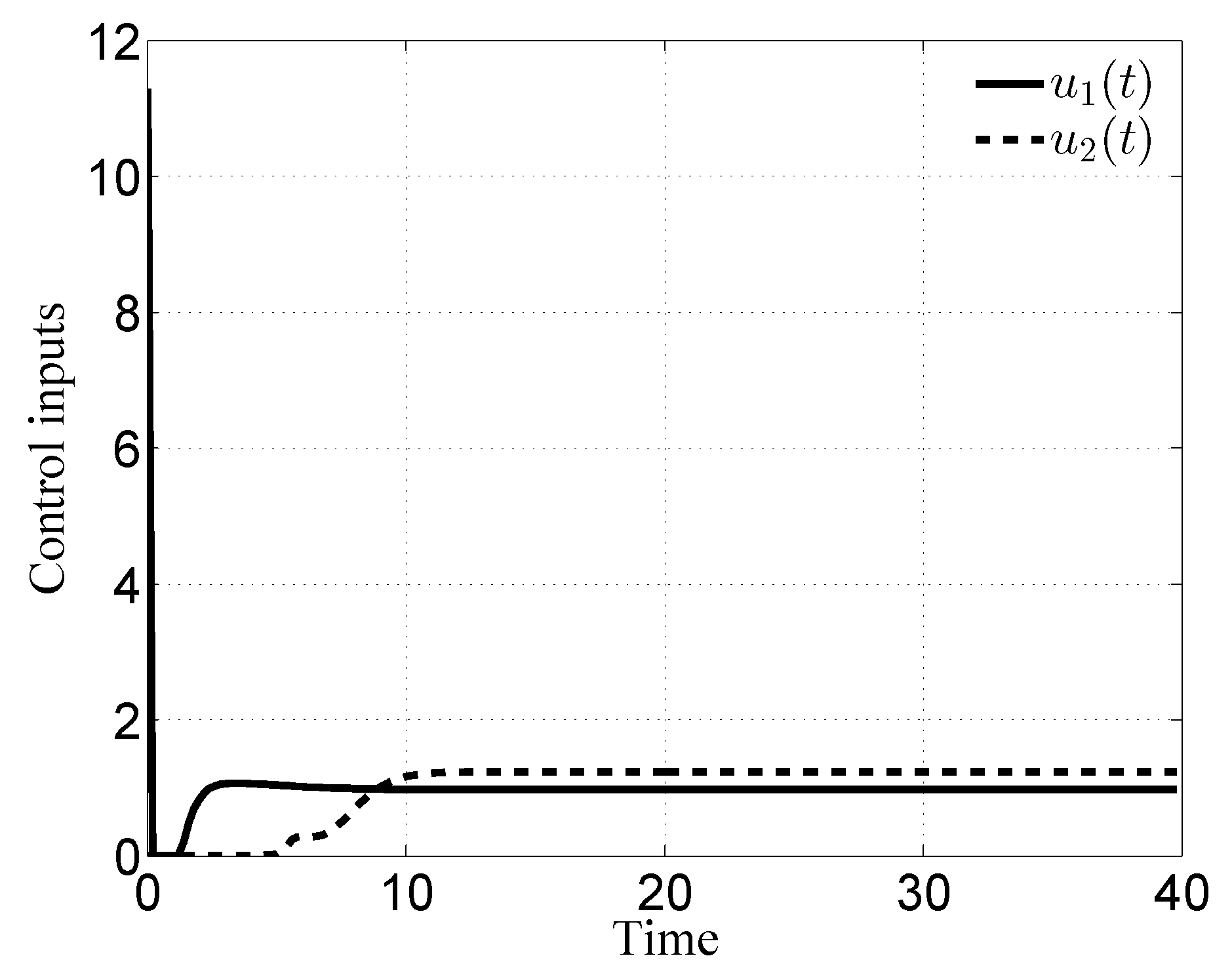
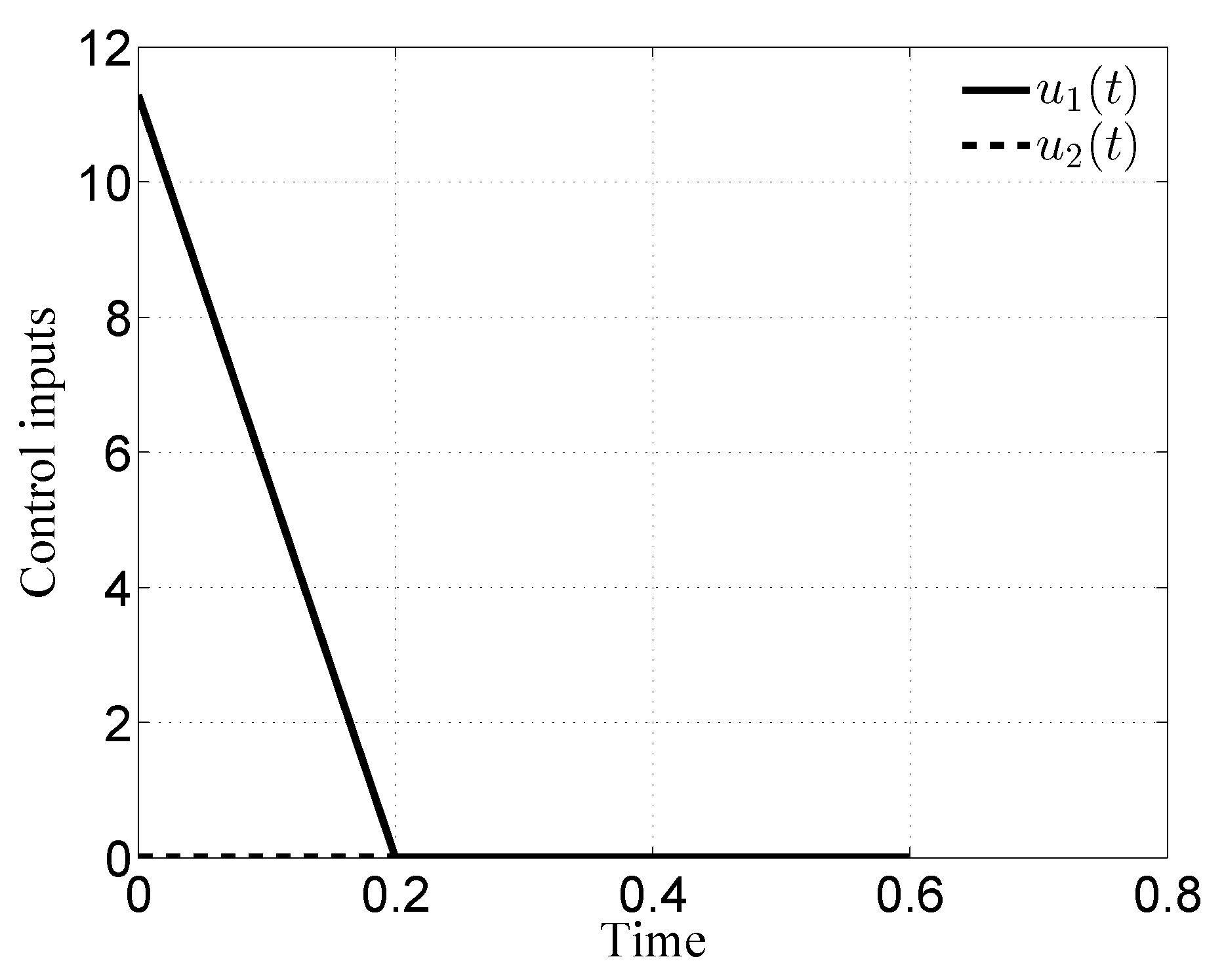
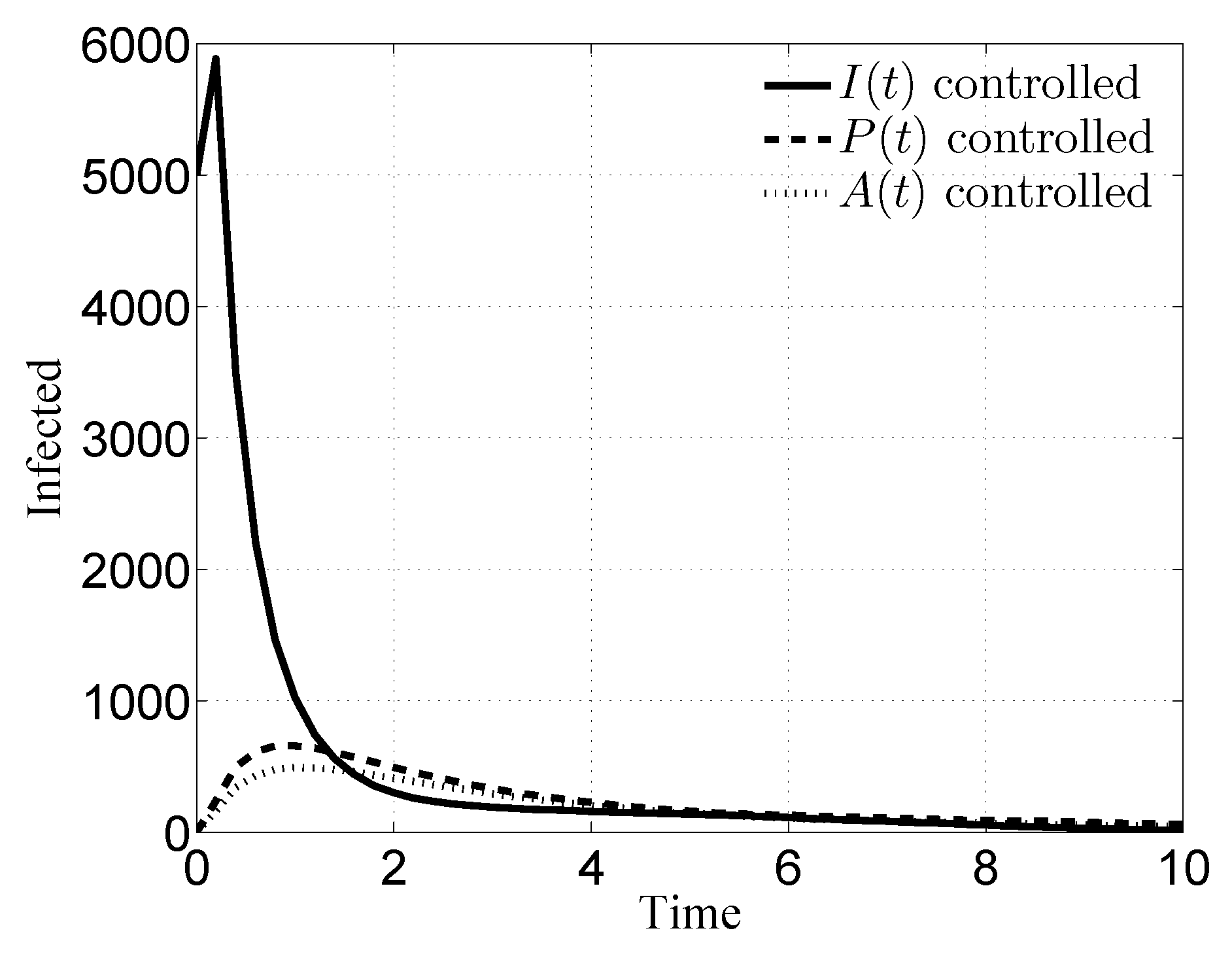
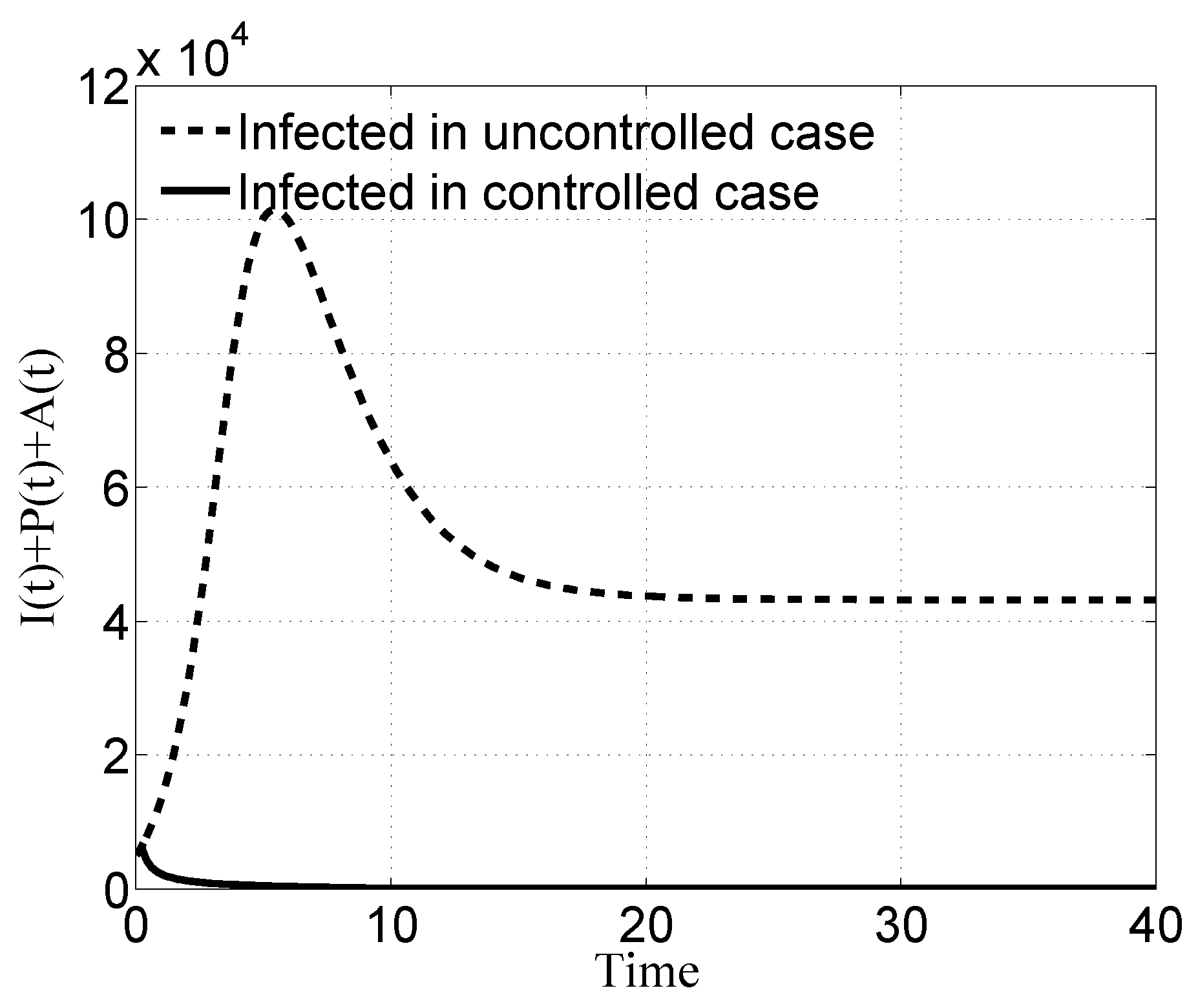
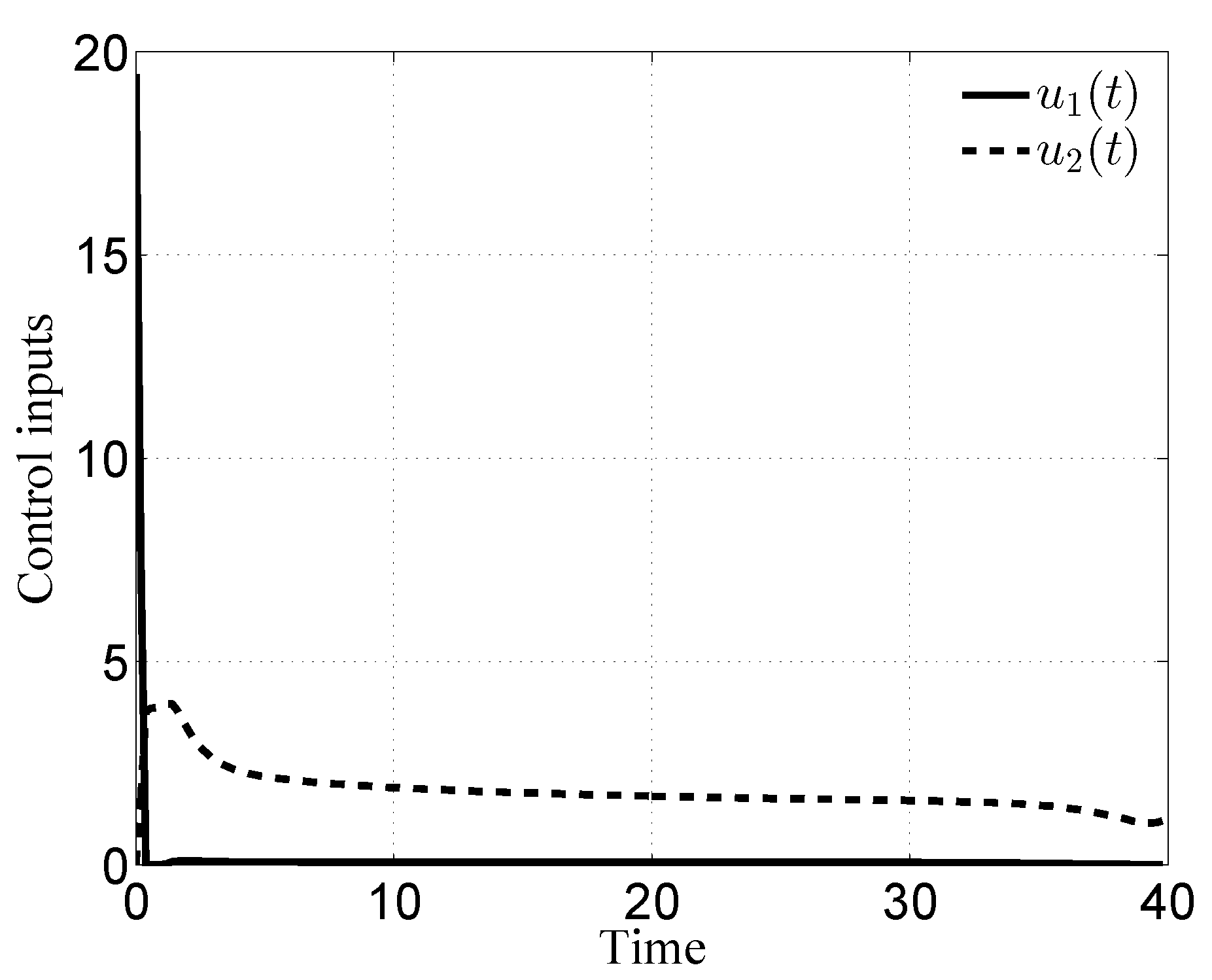
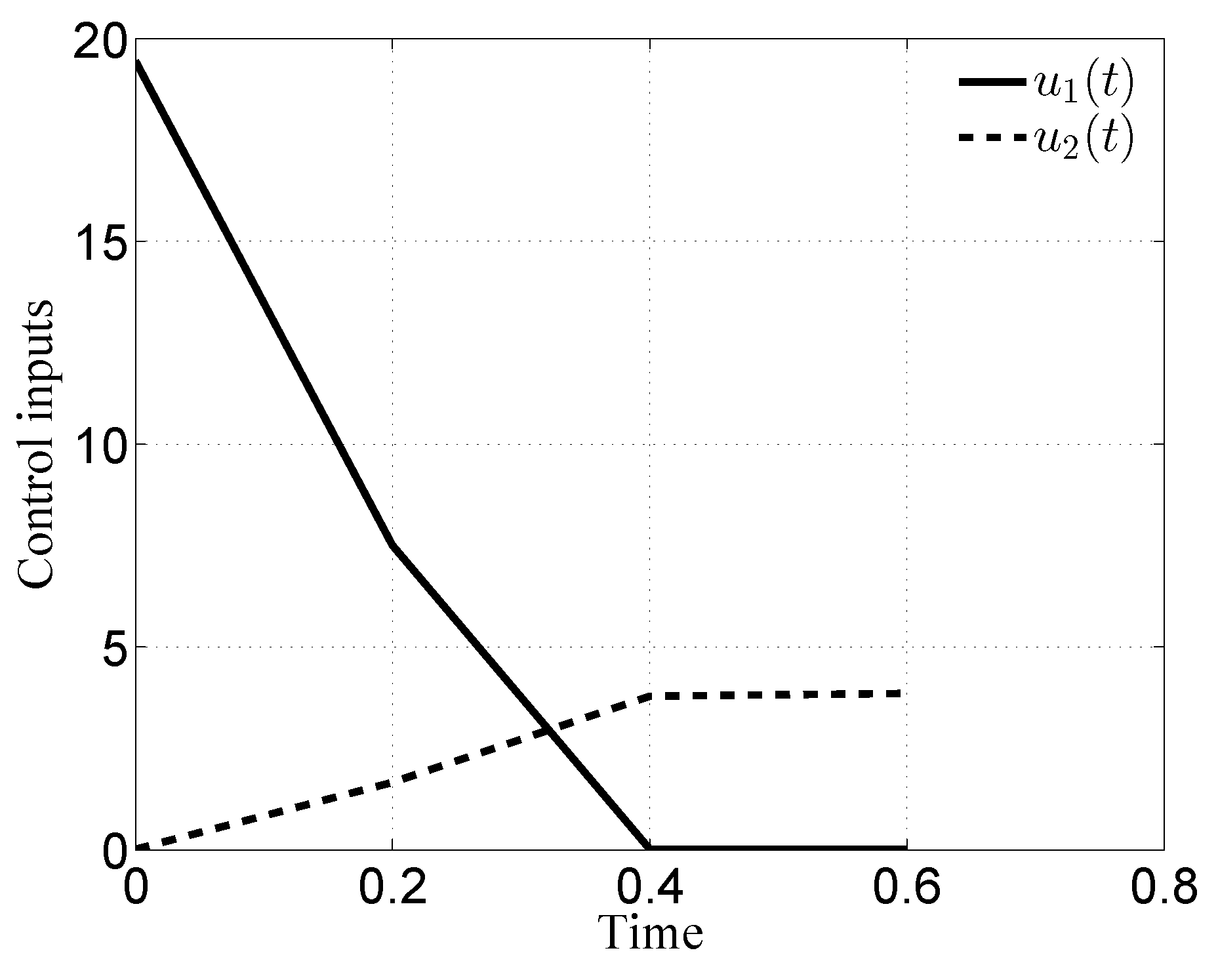
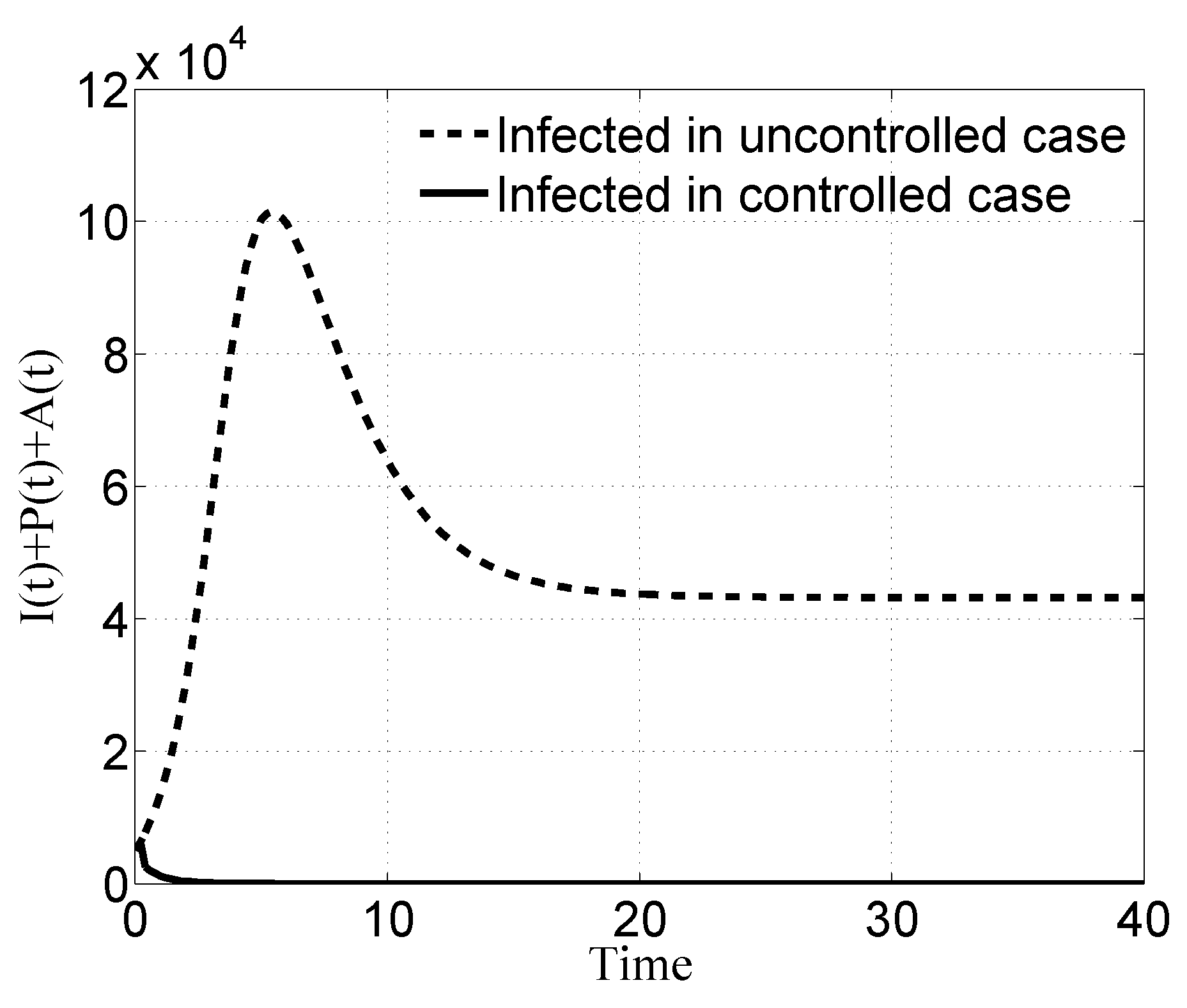
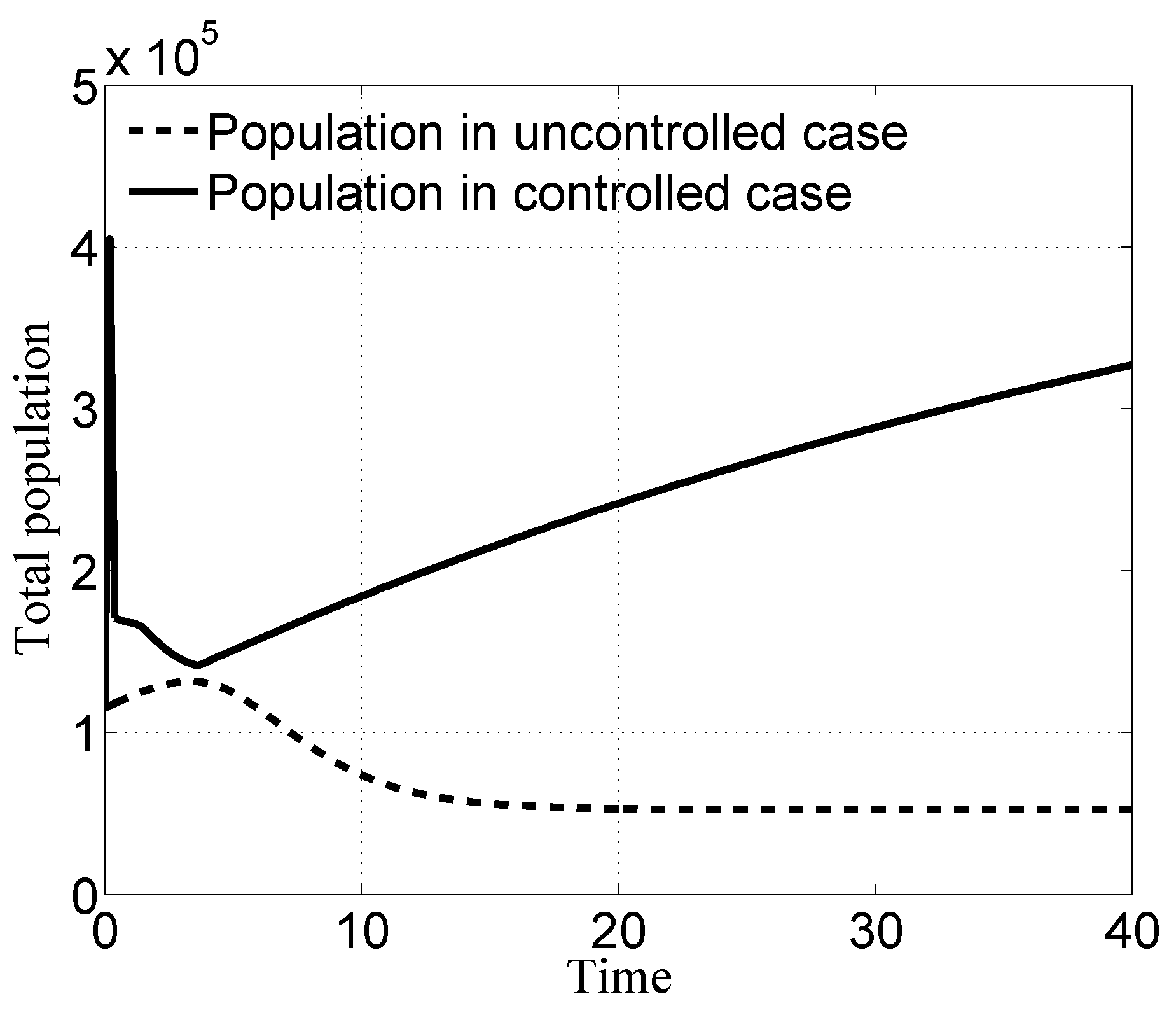
3.1. Case i
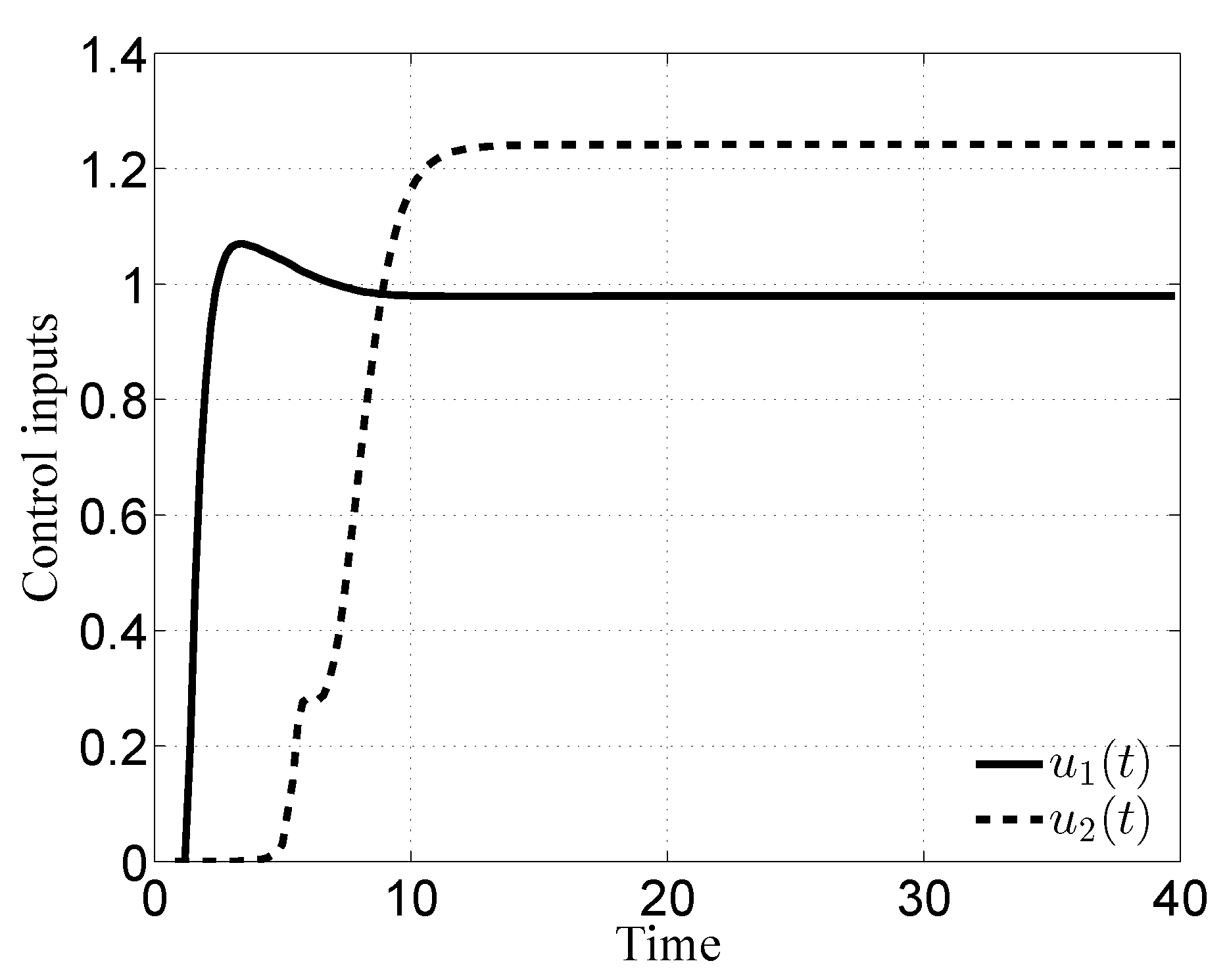
3.2. Case ii
3.3. Case iii
3.4. Case iv
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Guo, J.; Mu, B.; Wang, L.Y.; Yin, G.; Xu, L. Decision-Based System Identification and Adaptive Resource Allocation. IEEE Trans. Autom. Control 2017, 62, 2166–2179. [Google Scholar] [CrossRef]
- Li, J.; Han, Y. Optimal Resource Allocation for Packet Delay Minimization in Multi-Layer UAV Networks. IEEE Commun. Lett. 2017, 21, 580–583. [Google Scholar] [CrossRef]
- Xianglan, W.; Jun, Z. Optimal allocation of resources in the material production sector and human capital sector. In Proceedings of the 2011 IEEE 2nd International Conference on Computing, Control and Industrial Engineering, Wuhan, China, 20–21 August 2011. [Google Scholar]
- Winz, I.; Brierley, G.; Trowsdale, S. The Use of System Dynamics Simulation in Water Resources Management. Water Resour. Manag. 2009, 23, 1301–1323. [Google Scholar] [CrossRef]
- Viswanadham, N.; Balaji, K. Resource allocation for healthcare organizations. In Proceedings of the 2011 IEEE International Conference on Automation Science and Engineering, Trieste, Italy, 24–27 August 2011. [Google Scholar]
- He, Z.L.; Li, J.; Nie, L.; Zhao, Z. Nonlinear state-dependent feedback control strategy in the SIR epidemic model with resource limitation. Adv. Differ. Equ. 2017, 209, 1–18. [Google Scholar] [CrossRef]
- Denysiuk, R.; Torres, C.S.D. Multiobjective optimization to a TB-HIV/AIDS coinfection optimal control problem. Comput. Appl. Math. 2018, 37, 2112–2128. [Google Scholar] [CrossRef]
- Nareshn, R.; Tripathi, A.; Sharma, D. Modeling and analysis of the spread of AIDS epidemic with immigration of HIV infectives. Math. Comput. Modell. 2009, 48, 800–892. [Google Scholar]
- Wodarz, D.; Nowak, M. Specific therapy regimes could lead to long-term immunological control of HIV. Proc. Natl. Acad. Sci. USA 1999, 96, 14464–14469. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Astolfi, A. Control of HIV infection dynamics. IEEE Control Syst. 2008, 28, 28–39. [Google Scholar]
- Pinto, C.; Rocha, D. A new mathematical model for co-infection of malaria and HIV. In Proceedings of the 4th IEEE International Conference on Nonlinear Science and Complexity, Budapest, Hungary, 6–11 August 2012. [Google Scholar]
- Di Giamberardino, P.; Compagnucci, L.; Giorgi, C.D.; Iacoviello, D. A new model of the HIV/AIDS infection diffusion and analysis of the intervention effects. In Proceedings of the 25th Mediterranean Conference on Control and Automation, Valletta, Malta, 3–6 July 2017. [Google Scholar]
- Di Giamberardino, P.; Compagnucci, L.; Giorgi, C.D.; Iacoviello, D. Modeling the effects of prevention and early diagnosis on HIV/AIDS infection diffusion. IEEE Trans. Syst. Man Cybern. Syst. 2017, 99, 1–12. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Iacoviello, D. An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, Madrid, Spain, 26–28 July 2017. [Google Scholar]
- Di Giamberardino, P.; Iacoviello, D. Optimal Control of SIR Epidemic Model with State Dependent Switching Cost Index. Biomed. Signal Process. Control 2017, 31, 377–380. [Google Scholar] [CrossRef]
- Rutherford, A.R.; Ramadanovic, B.; Michelow, W.; Marshall, B.D.L.; Small, W.; Deering, K.; Vasarhelyi, K. Control of an HIV epidemic among injection drug users: simulations modeling on complex networks. In Proceedings of the 2016 Winter Simulations Conference, Washington, DC, USA, 11–14 December 2016. [Google Scholar]
- Di Giamberardino, P.; Iacoviello, D. Optimal Control to reduce the HIV/AIDS spread. In Proceedings of the 22nd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 10–12 October 2018. [Google Scholar]
- Bakare, E.A.; Nwagwo, A.; Danso-Addo, E. Optimal control analyis of an SIR epidemic model with constant recruitment. Int. J. Appl. Math. Res. 2014, 3, 273–285. [Google Scholar] [CrossRef]
- Lin, F.; Muthuraman, K.; Lawley, M. Optimal control theory approach to non-pharmaceutical interventions. Int. J. Appl. Math. Res. 2010, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Iacoviello, D.; Stasio, N. Optimal control for SIRC epidemic outbreak. Comput. Methods Programs Biomed. 2013, 110, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Owuor, O.N.; Johannes, M.; Kibet, M.S. Optimal vaccination strategies in an SIR epidemic model with time scales. Appl. Math. 2013, 4, 37454. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Control—Linear Quadratic Methods; Prcntice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Gill, P.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press: London, UK, 1981. [Google Scholar]
- Battiti, R. First and second order methods for learning: between steepest descent and Newton’s method. Neural Comput. 1992, 4, 141–166. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Giamberardino, P.; Iacoviello, D. Optimal Control of Virus Spread under Different Conditions of Resources Limitations. Information 2019, 10, 214. https://doi.org/10.3390/info10060214
Di Giamberardino P, Iacoviello D. Optimal Control of Virus Spread under Different Conditions of Resources Limitations. Information. 2019; 10(6):214. https://doi.org/10.3390/info10060214
Chicago/Turabian StyleDi Giamberardino, Paolo, and Daniela Iacoviello. 2019. "Optimal Control of Virus Spread under Different Conditions of Resources Limitations" Information 10, no. 6: 214. https://doi.org/10.3390/info10060214
APA StyleDi Giamberardino, P., & Iacoviello, D. (2019). Optimal Control of Virus Spread under Different Conditions of Resources Limitations. Information, 10(6), 214. https://doi.org/10.3390/info10060214





