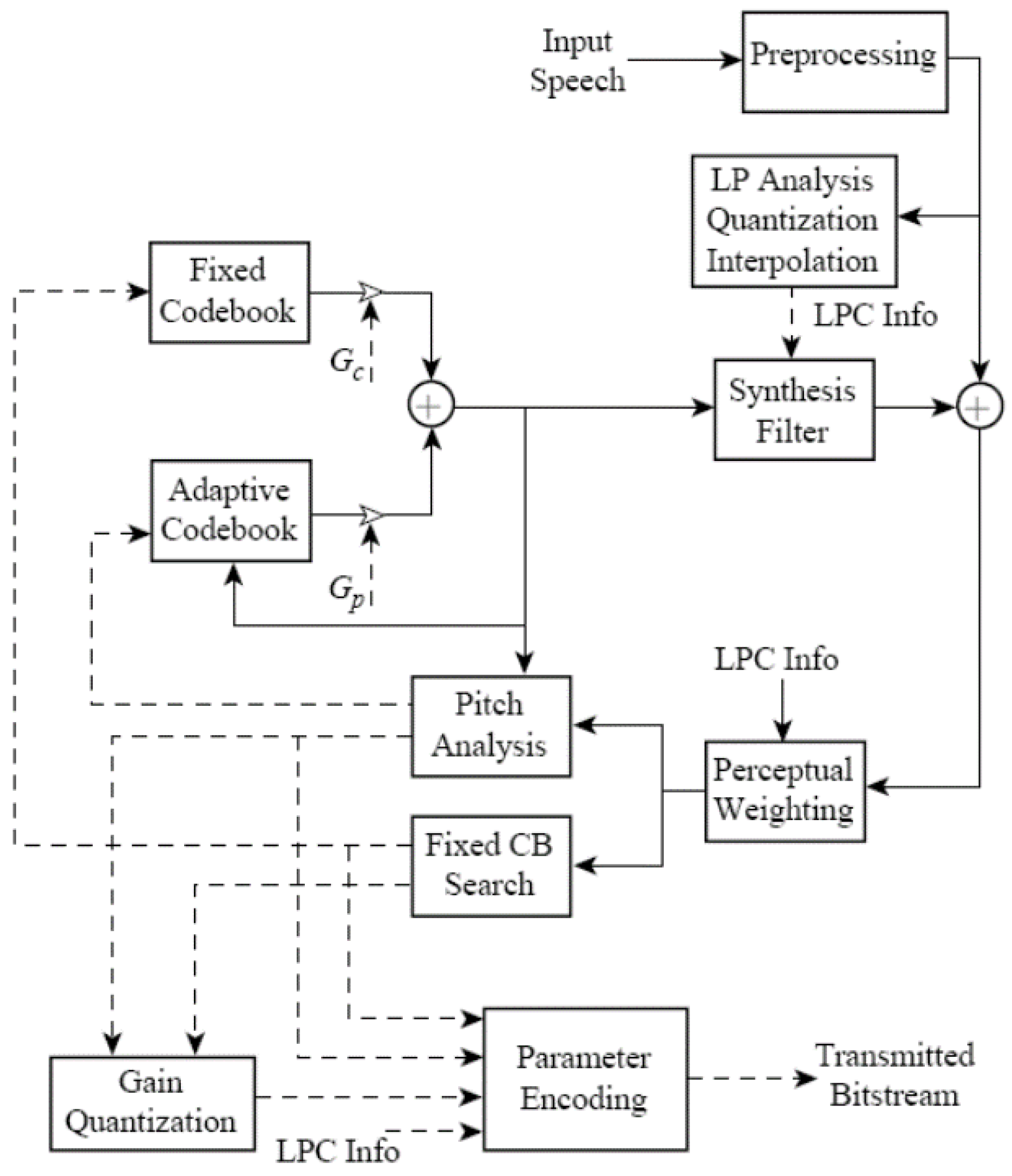
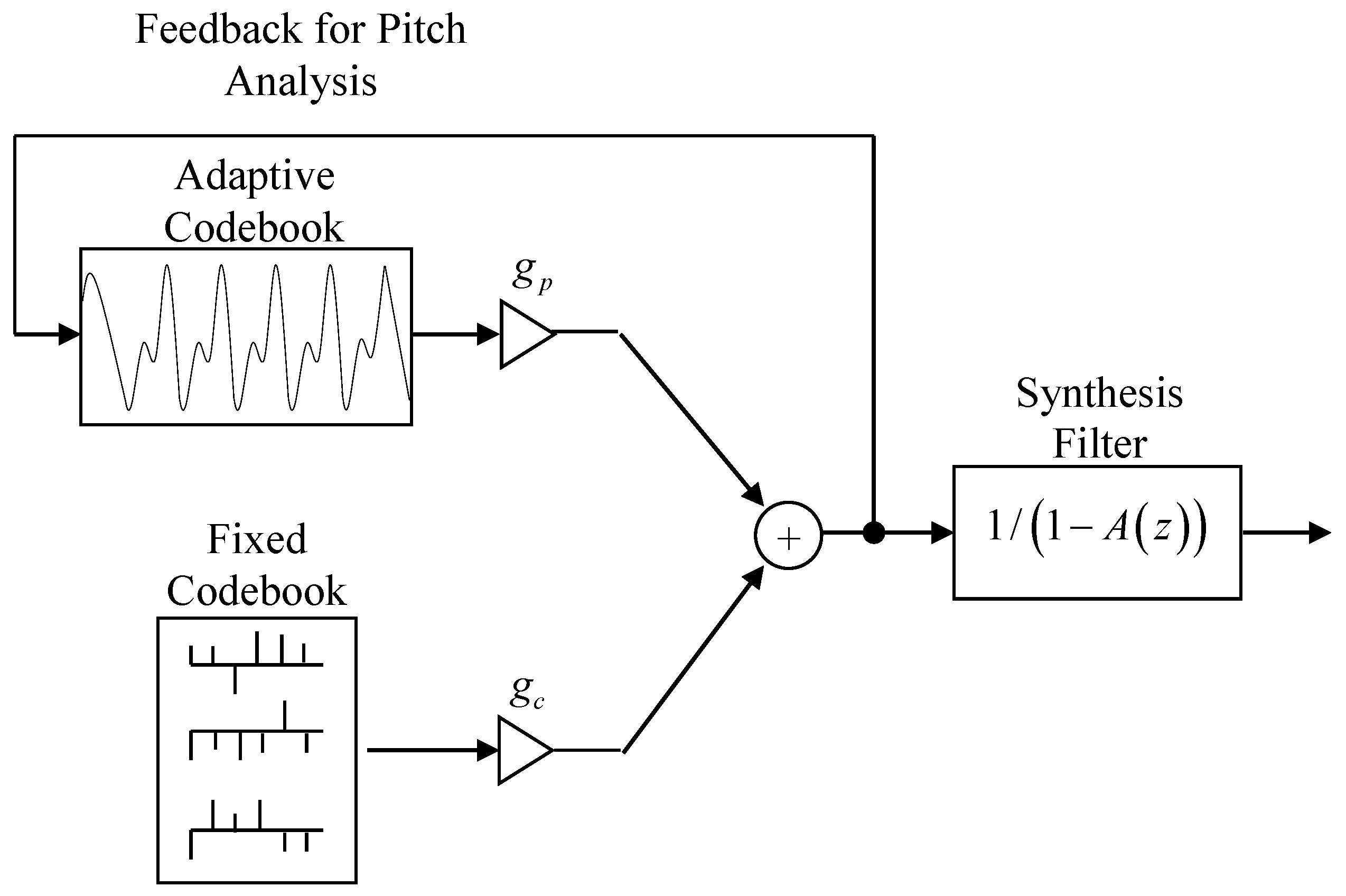
2. Code-Excited Linear Prediction (CELP)
Block diagrams of a code-excited linear prediction (CELP) encoder and decoder are shown in
Figure 1 and
Figure 2, respectively [
1,
2].
We provide a brief description of the various blocks in
Figure 1 and
Figure 2 to begin. The CELP encoder is an implementation of the Analysis-by-Synthesis (AbS) paradigm [
1]. CELP, like most speech codecs in the last 45 years, is based on the linear prediction model for speech, wherein the speech is modeled as
where we see that the current speech sample at time instant
k is represented as a weighted linear combination of
N prior speech samples plus an excitation term at the current time instant. The weights,
, are called the linear prediction coefficients. The synthesis filter in
Figure 1 has the form of this linear combination of past outputs and the fixed and adaptive codebooks model the excitation,
. The LP analysis block calculates the linear prediction coefficients, and we see that the block also quantizes the coefficients so that encoder and decoder use exactly the same coefficients.
The adaptive codebook is used to capture the long-term memory due to the speaker pitch and the fixed codebook is selected to be an algebraic codebook, which has mostly zero values and only a relatively few nonzero pulses. The pitch analysis block calculates the adaptive codebook long-term memory. The process is AbS in that for a block of (say)
M input speech samples, the linear prediction coefficients and long-term memory are calculated and a perceptual weighting filter is constructed using the linear prediction coefficients. Then, for every length
M sequence (codevector) in the fixed codebook, (say) there are
L code vectors in the fixed codebook, a synthesized sequence of speech samples are produced. This is the fixed codebook search block. The best codevector out of the
L in the fixed codebook in terms of the length
M synthesized sequence that best matches the input block of length
M based on minimizing the perceptually weighted squared error is chosen and transmitted to the CELP decoder along with the long-term memory, the predictor coefficients, and the codebook gains. These operations are represented by the parameter encoding block in
Figure 1 [
1,
10].
The CELP decoder uses these parameters to synthesize the block of
M reconstructed speech samples presented to the listener as shown in
Figure 2. There is also post-processing, which is not shown in the figure.
The quality and intelligibility of the synthesized speech is often determined by listening tests that produce mean opinion scores (MOS), which for narrowband speech vary from 1 up to 5 [
11,
12]. A well-known codec such as G.711 is usually included to provide an anchor score value with respect to which other narrowband codecs can be evaluated [
13,
14,
15].
It would be helpful to be able to associate a separate contribution to the overall performance by each of the main components in
Figure 2, namely the fixed codebook, the adaptive codebook, and the synthesis filter. Signal to quantization noise ratio (SNR) is often used for speech waveform codecs, but CELP does not attempt to follow the speech waveform, so SNR is not applicable. One characteristic of CELP codecs that is well known is that those speech attributes not captured by the short-term predictor must be accounted for, as best as possible, by the excitation codebooks, but an objectively meaningful measure of the individual component contributions is yet to be advanced.
In the next section, we propose a decomposition in terms of the mutual information and conditional mutual information with respect to the input speech provided by each component in the CELP structure, that appears particularly useful and interesting for capturing the performance and the trade-offs involved.
6. Log Ratio of Entropy Powers
We can use the definition of the entropy power in Equation (
6) to express the logarithm of the ratio of two entropy powers in terms of their respective differential entropies as [
8]
We can write a conditional version of Equation (
6) as
and from which we can express Equation (
11) in terms of the entropy powers at successive stages in the signal processing chain (
Figure 5), as
If we add and subtract
to the right-hand side of Equation (
13), we then obtain an expression in terms of the difference in mutual information between the two stages as
From the series of inequalities on the entropy power in Equation (
9), we know that both expressions in Equations (
13) and (
17) are greater than or equal to zero.
These results are from [
8] and extend the data processing inequality by providing a new characterization of the information loss between stages in terms of the entropy powers of the two stages. Since differential entropies are difficult to calculate, it would be particularly useful if we could obtain expressions for the entropy power at two stages and then use Equations (
13) and (
17) to find the difference in differential entropy and mutual information between these stages.
We are interested in studying the change in the differential entropy and mutual information brought on by different signal processing operations by investigating the log ratio of entropy powers.
In the following, we highlight several cases where Equation (
11) holds with equality when the entropy powers are replaced by the corresponding variances. The Gaussian and Laplacian distributions often appear in studies of speech processing and other signal processing applications [
10,
15,
20], so we show that substituting the variances for entropy powers in the log ratio of entropy powers for these distributions satisfies Equation (
11) exactly. For two i.i.d. Gaussian distributions with zero mean and variances
and
, we have directly that
and
, so
which satisfies Equation (
11) exactly. Of course, since the Gaussian distribution is the basis for the definition of entropy power, this result is not surprising.
For two i.i.d. Laplacian distributions with variances
and
[
21], their corresponding entropy powers
and
, respectively, so we form
Since
, the Laplacian distribution also satisfies Equation (
11) exactly [
5]. We thus conclude that we can substitute the variance, or for zero mean Laplacian distributions, the mean squared value for the entropy power, in Equation (
11), and the result is the difference in differential entropies.
Interestingly, using mean squared errors or variances in Equation (
11) is accurate for many other distributions as well. It is straightforward to show that Equation (
11) holds with equality when the entropy powers are replaced by mean squared error for the logistic, uniform, and triangular distributions as well. Furthermore, the entropy powers can be replaced by the ratio of the squared parameters for the Cauchy distribution.
Therefore, the satisfaction of Equation (
11) with equality occurs in more than one or two special cases. The key points are first that the entropy power is the smallest variance that can be associated with a given differential entropy, so the entropy power is some fraction of the mean squared error for a given differential entropy. Second, Equation (
11) utilizes the ratio of two entropy powers, and thus, if the distributions corresponding to the entropy powers in the ratio are the same, the scaling constant (fraction) multiplying the two variances will cancel out. Therefore, we are not saying that the mean squared errors equal the entropy powers in any case but for Gaussian distributions. It is the new quantity, the log ratio of entropy powers, that enables the use of the mean squared error to calculate the loss in mutual information at each stage.
9. Estimated versus Actual CELP Codec Performance
The analyses determining the mutual information in bits/sample between the input speech and the short-term linear prediction, the adaptive codebook, and the fixed codebook individually, are entirely new and provide new ways to analyze CELP codec performance by only analyzing the input source. In this section, we estimate the performance of a CELP codec by analyzing the input speech source to find the mutual information provided by each CELP component about the input speech and then subtract the three mutual informations from a reference codec rate in bits/sample for a chosen MOS value to get the final estimate of the rate required in bits/sample to achieve the target MOS.
For waveform speech coding, such as differential pulse code modulation (DPCM), for a particular utterance, we can study the rate in bits/sample versus the mean squared reconstruction error or SNR to obtain some idea of the codec performance for this input speech segment [
14,
15]. However, while SNR may order DPCM subjective codec performance correctly, it does not provide an indicator of the actual difference in subjective performance. Subjective performance is most accurately available by conducting subjective listening tests to obtain mean opinion scores (MOS). Alternatively, reasonable views of subjective performance can be obtained from software such as PESQ /MOS [
12]. We use the latter. In either case, however, MOS cannot be generated on a per-frame basis as listening tests and PESQ values are generated from longer utterances.
Therefore, we cannot use the per-frame estimates of mutual information from
Section 7 and need to calculate estimates of mutual information over longer sentences. To this end,
Table 4 contains autocorrelations for two narrowband (200 to 3400 Hz) utterances sampled at 8000 samples/s, “We were away a year ago,” spoken by a male and “A lathe is a big tool. Grab every dish of sugar,” spoken by a female, including the decomposition of the sentences into five modes, namely voiced, unvoiced, onset, hangover, and silence, and their corresponding relative frequencies. The two utterances are taken from the Open Speech Repository [
27]. These data are excerpted from tables in Gibson and Hu [
6] and are not calculated on a per-frame basis but averaged over all samples of the utterance falling in the specified subsource model.
From
Table 4, the voiced subsource models are set as
th order, with the 1 in the column vector representing the
term. The onset and hangover modes are modeled as
th order autoregressive (AR). We see from this table that the sentence “We were away … ,” is voiced, with a relative frequency of 0.98, and that the sentence “A lathe is a big … ,” has a breakdown of voiced (0.5265), silence (0.3685), unvoiced (0.0771), onset (0.0093), and hangover (0.0186). The
for each mode are also shown in the table.
We focus on G.726 as our reference codec. Generally, G.726 adaptive differential pulse code modulation (ADPCM) at 32 kbits/s or 4 bits/sample for narrowband speech is considered to be “toll quality”. G.726 is selected as the reference codec because ADPCM is a waveform-following codec and is the best-performing speech codec that does not rely on a more sophisticated speech model. In particular, G.726 utilizes only two poles and six zeros, and the parameter adaptation algorithms rely only on polarities. G.726 will track pure tones as well as other temporal waveforms in addition to speech. In G.726, no parameters are coded and transmitted, only the quantized and coded prediction error signal. Finally, both mean squared reconstruction error or SNR and MOS have meaning for G.726, which is useful since SPER plays a role in estimating the change in mutual information from the log ratio of entropy powers.
From
Table 5 and
Table 6, G.726 achieves a PESQ/MOS of about 4.0 for 4 bits/sample and for both sentences, “We were away a year ago,” spoken by a male speaker and “A lathe is a big tool. Grab every dish of sugar,” spoken by a female [
6]. Therefore, we use 4 bits/sample as our reference point for toll quality speech for these two sentences. We then subtract from the rate of 4 bits/sample the rates in bits/sample we associate with each of the CELP codec components as estimated from
Section 7 and
Section 8.
For “We were away … ,” we see from
Table 4 that the 10th order model of the voiced mode has a
, which corresponds to a mutual information reduction of 1.84 bits/sample. For this highly voiced sentence, we estimate the mutual information corresponding to the adaptive codebook as 0.5 bits/sample, and at a codec rate of 8000 bits/s, the fixed codebook mutual information would correspond to 0.5 bits/sample. Silence corresponds to about only 1 percent of the total utterance. If we sum these contributions up and subtract them from 4 bits/sample, we obtain
bits/sample. Inspecting
Table 5, the rates for the AMR and G.729 codecs at this MOS are 1.1 bits/sample, so there is surprisingly good agreement.
From
Table 4, we see that for the utterance, “A lathe is … ,” there is broader mix of speech modes, including significant silence and unvoiced components. Neither of these modes had to be dealt with for the sentence “We were away … ”. Since silence is almost never perfect silence and usually consists of low level background noise, we associate the bits/sample for silence with a silence detection/comfort noise generation (CNG) method [
25]. From
Table 6, we see that G.726 with CNG is about 1.2 bits/sample lower than G.726, even though it occurs for only a 0.3685 portion of the utterance. For the short-term prediction, the
= 0.0656, which corresponds to a mutual information of 1.96 bits/sample. The adaptive codebook contribution at 8 kbits/s can again be estimated as 0.5 bits/sample, and the fixed codebook component estimated at 0.5 bits/sample.
If we now combine all of these estimates with their associated relative frequencies of occurrence as indicated in
Table 4, we obtain a total mutual information of
bits/sample. Subtracting this from 4 bits/sample, we estimate that the CELP codec rate in bits/sample for an MOS = 4.0 would be 1.5 bits/sample. We see from
Table 6 that for AMR and G.729, their rate is 1.0 bits/sample. This gap can be narrowed if the adaptive codebook contribution is toward the upper end of the expected
of say 6 dB. In this case, the voiced component has the mutual information of
, so the total mutual information is 2.8, and then subtracting from 4 bits/sample, we obtain a CELP codec rate estimate of 1.2 bits/sample to achieve an MOS = 4.0. The actual CELP rate needed by G.729 and AMR for this MOS is about 1.0 bits/sample, which constitutes good agreement.