A Novel Fractional-Order Grey Prediction Model and Its Modeling Error Analysis
Abstract
:1. Introduction
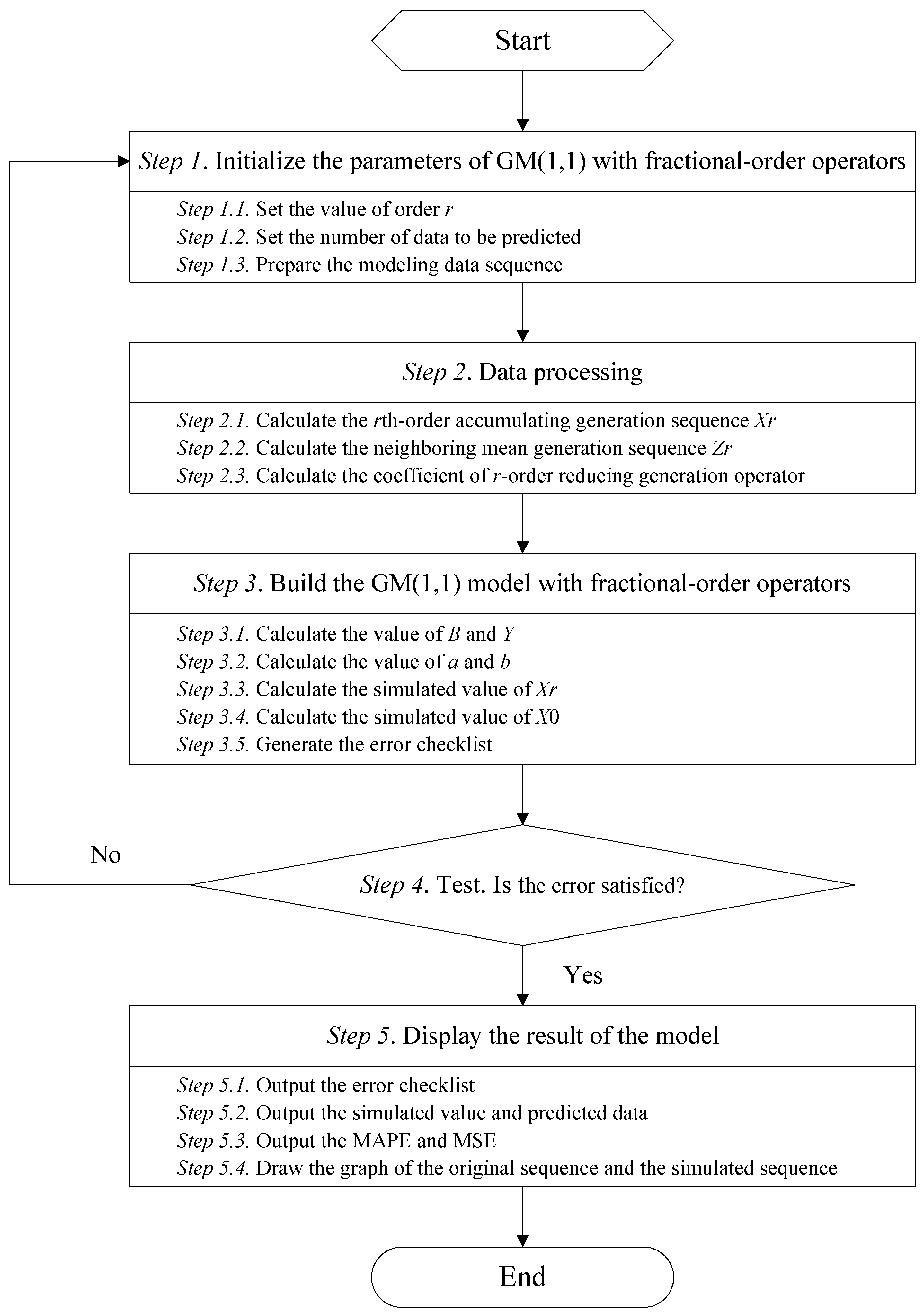
2. Fractional-Order Grey Prediction Model
3. Modeling Error Analysis
3.1. Data Preparation
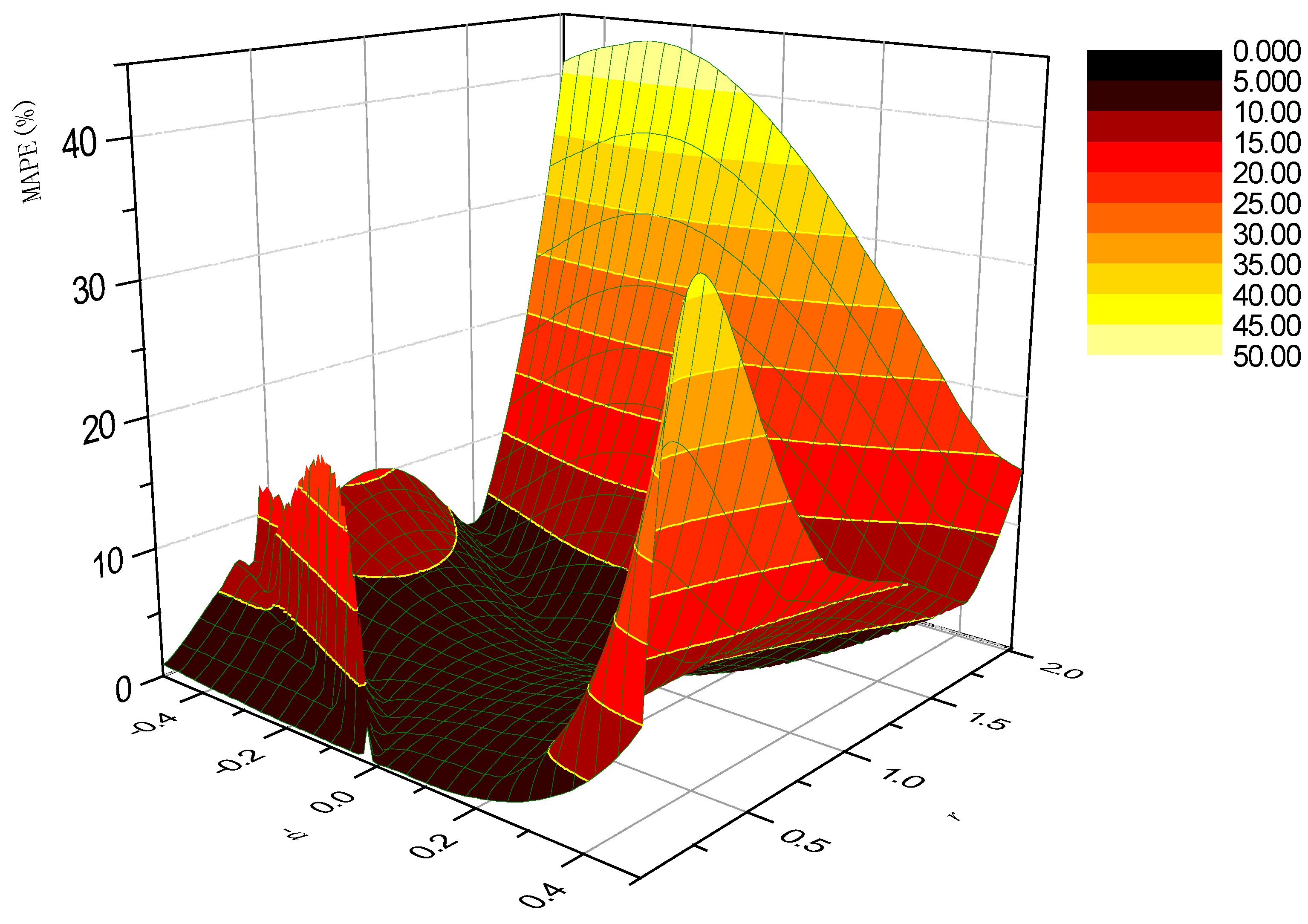
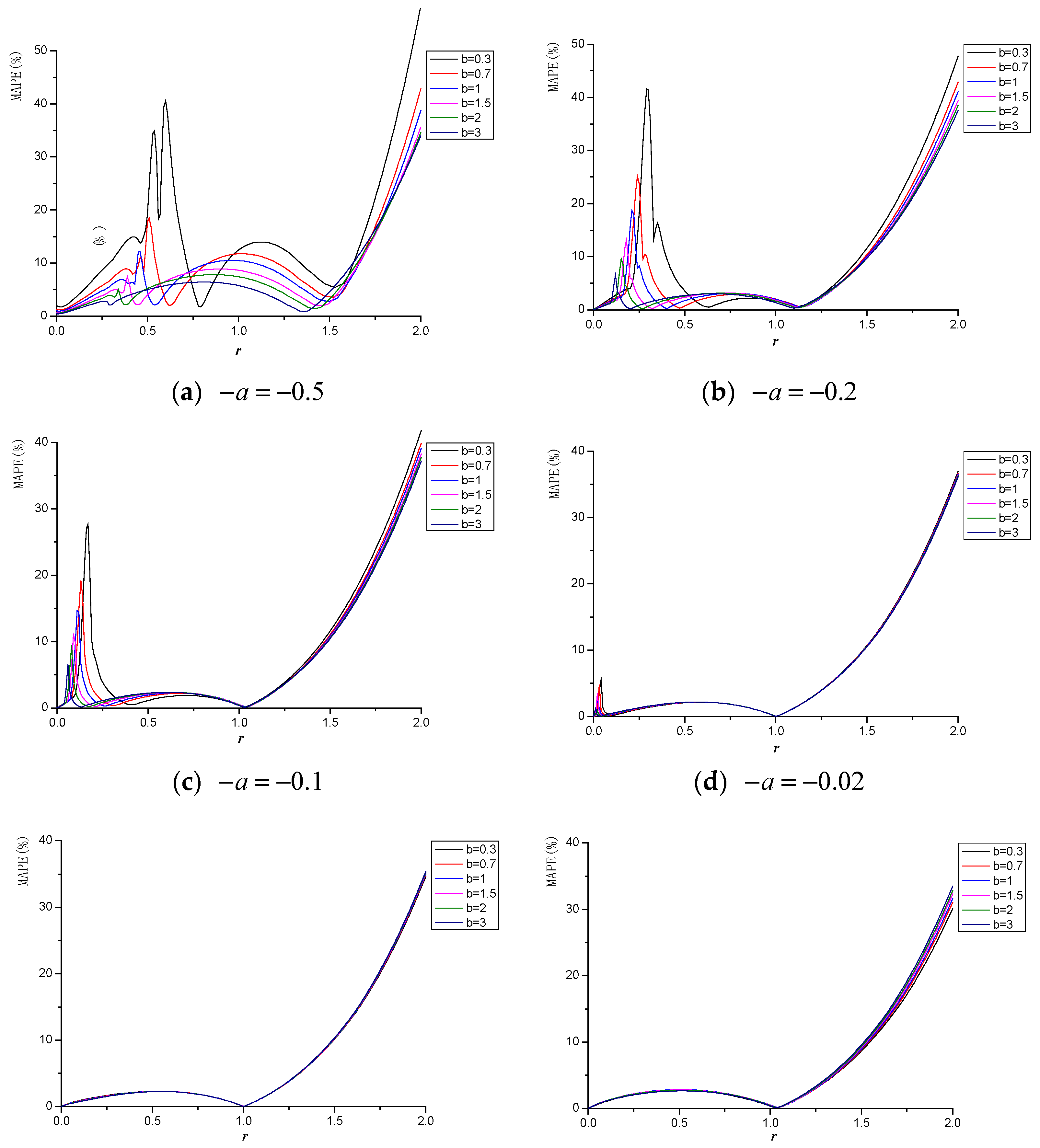
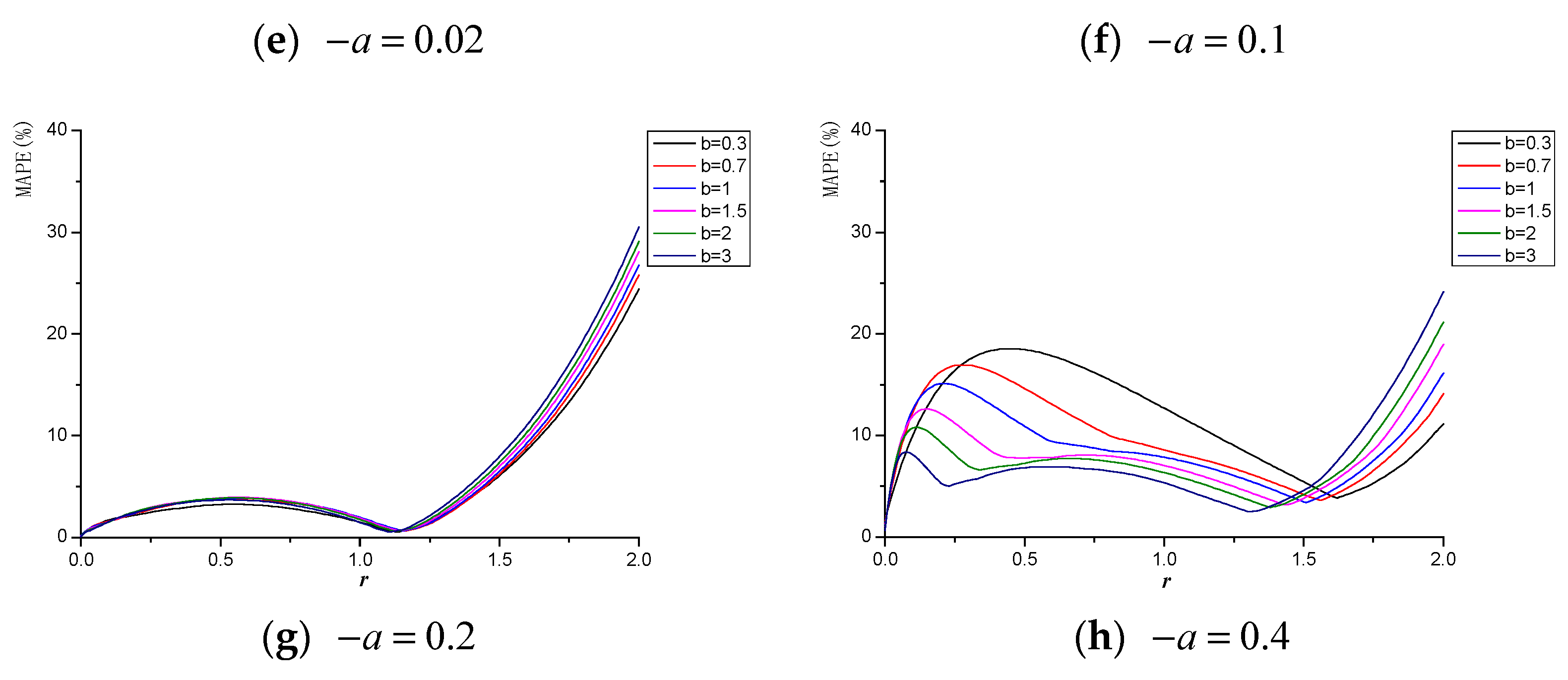
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| % This is the MATLAB program code for the fractional-order GM(1,1). clear all; % X0 is the original data sequence. X0 = [8.21 9.52 10.51 12.72 14.84 17.89 21.22 26.79]; % r is the order of fractional-order GM(1,1). If r = 1, the model is GM(1,1). r = 1; n = numel(X0); % Xr is the r-order accumulating generation sequence of the X0. If r = 0, the model is direct modeling GM(1,1). if r == 0 Xr = X0; else for k = 1:n tmp = 0; for i = 1:k cc2(k,i) = gamma(r + k − i)/(gamma(k – i + 1)*gamma(r)); tmp = tmp + cc2(k,i)*X0(i); end Xr(k) = tmp; end end % Zr is the neighboring mean production sequence of Xr. for I = 2:n; Zr(i − 1) = (Xr(i) + Xr(i − 1))/2; end; % Xr_1 is the first order reducing generation sequence of Xr. Xr_1(1) = X0(1); for k = 2:n; Xr_1(k) = Xr(k) − Xr(k − 1); end; % Calculate the coefficient of fractional-order reducing generation operator. for k = 1:n; for i = 0:k-1; if k – i ≥ 1 cc1(k,i + 1) = (−1)^i*gamma(r+1)/(gamma(i + 1)*gamma(r − i + 1)); else; cc1(k,i + 1) = 0; end; end; end; % Calculate the value of B and Y. B = ones(n − 1,2); Y = ones(n − 1,1); for i = 1:n − 1; Y(i,1) = Xr_1(i + 1); B(i,1) = −Zr(i); end; % Calculate the value of a and b. E = inv(B’*B)*B’*Y; a = E(1); b = E(2); % Calculate the simulated value of Xr. XrF(1) = X0(1); for k = 2:n XrF(k) = (X0(1)-b/a)*exp(-a*(k-1))+b/a; end % Calculate the simulated data of X0. if r == 0 X0F = XrF; else for k = 1:n tmp = 0; for i = 1:k tmp = tmp + XrF(k + 1 − i)*cc1(k,i); end X0F(k) = tmp; end end % Generate the MAPE checklist. A = zeros(n,5); A(1,1) = 1; A(1,2) = X0(1); for k = 2:n; A(k,1) = k; A(k,2) = X0(k); A(k,3) = X0F(k); A(k,4) = A(k,2)-A(k,3); A(k,5) = 100*abs(A(k,4))/A(k,2); A(k,6) = A(k,4)^2; end; % Calculate the Mean Absolute Percentage Error (MAPE) and Mean Squared Error of the Model. MAPE = mean(A(2:n,5)); MSE = mean(A(2:n,6)); clc; % Output the original data sequence X0. disp(‘The original sequence X0 is:’); disp(X0); % Output the error checklist. disp(‘The error checklist is:’); disp(‘ No. Original data Simulated data Simulation error APE ‘); disp(A(:,1:5)); disp([‘The MAPE(Mean Absolute Percentage Error) is: ‘,num2str(MAPE)]); disp([‘The MSE(Mean Squared Error) is: ‘,num2str(MSE)]); % Draw the graph of the original sequence X0 and the simulated sequence X0F. k = 1:1:n; plot(k,X0,’+-’,k,X0F,’*-’); legend(‘Original data’,’Simulated data’,0); |
References
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 5, 288–294. [Google Scholar]
- Liu, S.; Lin, Y. Grey Information: Theory and Practical Applications; Springer: London, UK, 2006. [Google Scholar]
- Liu, S.; Dang, Y.; Fang, Z. Grey System Theories and Its Applications; Science Press: Beijing, China, 2018. [Google Scholar]
- Ling, Y. GM(1,1) Zero setting modeling and its application. Syst. Eng. Theory Pract. 1996, 5, 108–112. [Google Scholar]
- Wang, Y.; Liu, G.; Liu, K. An extended step by step optimum direct modeling method of GM(1,1). Syst. Eng. Theory Pract. 2000, 9, 99–104. [Google Scholar]
- Wang, Y.; Li, Y.; Chen, M. The modeling method of GM(1,1) with a step by step optimum grey derivative’s background values. Syst. Eng. Electron. 2001, 7, 76–78. [Google Scholar]
- Yi, Z.; Yong, W.; Chang, X. An approach of GM(1,1) based on optimum grey derivative. J. Grey Syst. 2007, 4, 397–404. [Google Scholar]
- Wang, Y.; Chen, Z.; Gao, Z.; Chen, Y. A generalization of the GM(1,1) direct modeling method with a step by step optimizing grey derivative’s whiten values and its applications. Kybernetes 2004, 2, 382–389. [Google Scholar]
- Yuan, J.; Zhong, L.; Jiang, Q.; Tong, Q. Modeling and application of metabolic GM(1,1). J. WUT (Inf. Manag. Eng.) 2005, 2, 168–170. [Google Scholar]
- Xie, N.; Liu, S. Discrete GM(1,1) and mechanism of grey forecasting. Syst. Eng. Theory Pract. 2005, 1, 93–99. [Google Scholar]
- Xie, N.; Liu, S. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 2, 1173–1186. [Google Scholar]
- Cui, J.; Dang, Y.; Liu, S. Analysis on modeling accuracy of GM(1,1) based on new weakening operators. Syst. Eng. Theory Pract. 2009, 7, 132–138. [Google Scholar]
- Wang, Q.; Wei, Y. A kind of new strengthening buffer operator suitable for non-equigap GM(1,1). J. Grey Syst. 2009, 1, 105–112. [Google Scholar]
- Zeng, B.; Li, C. Improved multi-variable grey forecasting model with a dynamic background-value coefficient and its application. Comput. Ind. Eng. 2018, 118, 278–290. [Google Scholar] [CrossRef]
- Zeng, B.; Duan, H.; Bai, Y.; Meng, W. Forecasting the output of shale gas in China using an unbiased grey model and weakening buffer operator. Energy 2018, 151, 238–249. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C. Forecasting the natural gas demand in China using a self-adapting intelligent grey. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
- Zhang, B.; Xi, G. GM(1,1) model optimization based on the background value and boundary value correction. Syst. Eng. Theory Pract. 2013, 3, 682–688. [Google Scholar]
- Meng, W.; Liu, S.; Zeng, B. Standardization of interval grey number and research on its prediction modeling and application. Control Decis. 2012, 5, 773–776. [Google Scholar]
- Li, K.; Zhang, T. Forecasting electricity consumption using an improved grey prediction model. Information 2018, 9, 204. [Google Scholar] [CrossRef]
- Hu, Y.-C.; Jiang, P.; Chiu, Y.-J.; Tsai, J.-F. A novel grey prediction model combining markov chain with functional-link net and its application to foreign tourist forecasting. Information 2017, 8, 126. [Google Scholar] [CrossRef]
- Salmeron, J.L. An autonomous FGCM-based system for surveillance assets coordination. J. Grey Syst. 2016, 28, 27–35. [Google Scholar]
- Chang, C.J.; Dai, W.L.; Chen, C.C. A novel procedure for multimodel development using the grey silhouette coefficient for small-data-set forecasting. J. Oper. Res. Soc. 2014, 66, 1887–1894. [Google Scholar] [CrossRef]
- Aydemir, E.; Bedir, F.; Ozdemir, G. Degree of greyness approach for an EPQ model with imperfect items in copper wire industry. J. Grey Syst. 2015, 27, 13–26. [Google Scholar]
- Özdemir, A.; Özdagoglu, G. Predicting product demand from small-sized data: Grey models. Grey Syst. Theory Appl. 2017, 7, 80–96. [Google Scholar] [CrossRef]
- Ma, X. A brief introduction to the grey machine learning. J. Grey Syst. 2019, 31, 1–12. [Google Scholar]
- Liu, S.; Zeng, B.; Liu, J.; Xie, N. Several basic models of GM(1,1) and their applicable bound. Syst. Eng. Electron. 2014, 3, 501–508. [Google Scholar]
- Fang, S.; Wu, L.; Fang, Z.; Guo, X. Using fractional GM(1,1) model to predict the maintenance cost of weapon system. J. Grey Syst. 2013, 3, 9–15. [Google Scholar]
- Wu, L.; Liu, S.; Yao, L.; Xu, R.; Lei, X. Using fractional order accumulation to reduce errors from inverse accumulated generating operator of grey model. Soft Comput. 2014, 2, 483–488. [Google Scholar] [CrossRef]
- Xiao, X.; Guo, H.; Mao, S. The modeling mechanism, extension and optimization of grey GM(1,1). Appl. Math. Model. 2014, 5, 1896–1910. [Google Scholar] [CrossRef]
- Mao, S.; Gao, M.; Wen, J.; Nie, X. Generalized admissible region of class ratio for fractional accumulated GM(1,1) model. J. Grey Syst. 2014, 3, 55–68. [Google Scholar]
- Meng, W.; Liu, S.; Fang, Z.; Zeng, B. GM(1,1) with optimized order based on mutual fractional operators. Control Decis. 2016, 4, 661–666. [Google Scholar]
- Meng, W.; Zeng, B. Discrete grey model with inverse fractional operators and optimized order. Control Decis. 2016, 10, 1903–1907. [Google Scholar]
- Meng, W.; Yang, D.; Huang, H. Prediction of China’s sulfur dioxide emissions by discrete grey model with fractional order generation operators. Complexity 2018, 1, 1–14. [Google Scholar] [CrossRef]
| Seq. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −0.5 | 0.776 | 0.537 | 0.393 | 0.305 | 0.251 | 0.219 | 0.200 | 0.188 | 0.180 | |
| −0.4 | 0.890 | 0.669 | 0.521 | 0.422 | 0.355 | 0.310 | 0.281 | 0.261 | 0.247 | |
| −0.3 | 1.037 | 0.845 | 0.703 | 0.597 | 0.519 | 0.462 | 0.419 | 0.387 | 0.363 | |
| −0.2 | 1.238 | 1.089 | 0.968 | 0.868 | 0.787 | 0.720 | 0.665 | 0.621 | 0.584 | |
| −0.1 | 1.532 | 1.446 | 1.368 | 1.297 | 1.234 | 1.176 | 1.124 | 1.076 | 1.034 | |
| −0.05 | 1.737 | 1.690 | 1.646 | 1.604 | 1.564 | 1.526 | 1.490 | 1.456 | 1.423 | |
| −0.04 | 1.784 | 1.746 | 1.710 | 1.675 | 1.642 | 1.610 | 1.579 | 1.549 | 1.521 | |
| −0.03 | 1.834 | 1.805 | 1.777 | 1.750 | 1.724 | 1.699 | 1.674 | 1.650 | 1.627 | |
| −0.02 | 1.886 | 1.867 | 1.848 | 1.829 | 1.811 | 1.793 | 1.775 | 1.758 | 1.741 | |
| −0.01 | 1.942 | 1.932 | 1.922 | 1.912 | 1.903 | 1.893 | 1.884 | 1.875 | 1.866 | |
| 0.01 | 2.062 | 2.072 | 2.082 | 2.092 | 2.103 | 2.114 | 2.124 | 2.135 | 2.146 | |
| 0.02 | 2.127 | 2.148 | 2.169 | 2.190 | 2.212 | 2.234 | 2.257 | 2.280 | 2.304 | |
| 0.03 | 2.196 | 2.227 | 2.260 | 2.293 | 2.327 | 2.363 | 2.399 | 2.437 | 2.475 | |
| 0.04 | 2.269 | 2.311 | 2.355 | 2.401 | 2.449 | 2.499 | 2.551 | 2.605 | 2.661 | |
| 0.05 | 2.346 | 2.400 | 2.457 | 2.516 | 2.579 | 2.645 | 2.714 | 2.787 | 2.863 | |
| 0.1 | 2.809 | 2.926 | 3.054 | 3.196 | 3.353 | 3.526 | 3.718 | 3.930 | 4.164 | |
| 0.15 | 3.441 | 3.629 | 3.848 | 4.101 | 4.396 | 4.739 | 5.137 | 5.599 | 6.137 | |
| 0.2 | 4.317 | 4.587 | 4.917 | 5.321 | 5.814 | 6.415 | 7.150 | 8.048 | 9.145 | |
| 0.25 | 5.548 | 5.912 | 6.381 | 6.982 | 7.754 | 8.745 | 10.018 | 11.653 | 13.751 | |
| 0.3 | 7.300 | 7.772 | 8.410 | 9.270 | 10.432 | 12.000 | 14.116 | 16.973 | 20.830 | |
| 0.35 | 9.823 | 10.418 | 11.262 | 12.459 | 14.159 | 16.570 | 19.992 | 24.849 | 31.740 | |
| 0.4 | 13.489 | 14.223 | 15.318 | 16.951 | 19.387 | 23.021 | 28.442 | 36.530 | 48.596 | |
| 0.45 | 18.861 | 19.752 | 21.150 | 23.342 | 26.780 | 32.172 | 40.629 | 53.891 | 74.690 | |
| 0.5 | 26.786 | 27.856 | 29.619 | 32.526 | 37.320 | 45.223 | 58.253 | 79.736 | 115.15 | |
| 0.55 | 38.549 | 39.820 | 42.023 | 45.841 | 52.459 | 63.929 | 83.809 | 118.27 | 177.99 | |
| 0.6 | 56.100 | 57.598 | 60.328 | 65.301 | 74.364 | 90.876 | 120.96 | 175.79 | 275.68 | |
| 0.65 | 82.405 | 84.159 | 87.519 | 93.954 | 106.28 | 129.89 | 175.12 | 261.76 | 427.72 | |
| 0.7 | 121.99 | 124.03 | 128.14 | 136.42 | 153.09 | 186.66 | 254.26 | 390.40 | 664.55 | |
| 0.8 | 272.29 | 275.01 | 281.08 | 294.59 | 324.66 | 391.57 | 540.49 | 871.91 | 1609.5 | |
| 0.9 | 619.11 | 622.70 | 631.53 | 653.25 | 706.67 | 838.06 | 1161.2 | 1956.1 | 3911.1 | |
| 1 | 1426.9 | 1431.5 | 1444.2 | 1478.7 | 1572.6 | 1827.6 | 2520.8 | 4405.1 | 9527.2 |
| Seq. | Discrete GM | GM | Fractional-Order GM(1,1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.01 | 0.05 | 0.1 | 0.2 | 0.5 | 0.7 | 0.9 | 1.0 | 1.5 | 1.8 | ||||
| −0.5 | 10.6 | 10.5 | 1.0 | 1.0 | 1.2 | 2.0 | 3.8 | 4.6 | 7.8 | 10.4 | 10.5 | 2.8 | 19.5 | |
| −0.4 | 7.3 | 7.2 | 0.6 | 0.6 | 1.1 | 1.8 | 3.8 | 1.3 | 6.0 | 7.4 | 7.2 | 4.9 | 22.5 | |
| −0.3 | 4.3 | 4.3 | 0.3 | 0.4 | 0.9 | 1.8 | 3.7 | 1.1 | 4.3 | 4.8 | 4.3 | 7.9 | 24.9 | |
| −0.2 | 2.0 | 2.0 | 0.1 | 0.2 | 0.9 | 1.7 | 15.5 | 1.7 | 3.0 | 2.8 | 2.0 | 10.0 | 25.9 | |
| −0.1 | 0.5 | 0.5 | 0.0 | 0.2 | 0.8 | 9.8 | 1.2 | 2.0 | 2.3 | 1.4 | 0.5 | 10.8 | 25.3 | |
| −0.05 | 0.1 | 0.1 | 0.0 | 0.2 | 5.8 | 0.9 | 0.5 | 2.1 | 2.1 | 1.1 | 0.1 | 10.7 | 24.5 | |
| −0.04 | 0.1 | 0.1 | 0.0 | 0.2 | 7.7 | 0.4 | 0.7 | 2.1 | 2.0 | 1.0 | 0.1 | 10.7 | 24.3 | |
| −0.03 | 0.0 | 0.0 | 0.0 | 0.2 | 1.1 | 0.1 | 0.8 | 2.1 | 2.0 | 1.0 | 0.0 | 10.7 | 24.1 | |
| −0.02 | 0.0 | 0.0 | 0.0 | 0.2 | 0.2 | 0.3 | 1.0 | 2.1 | 2.0 | 1.0 | 0.0 | 10.6 | 23.8 | |
| −0.01 | 0.0 | 0.0 | 0.0 | 1.3 | 0.2 | 0.5 | 1.1 | 2.1 | 2.0 | 1.0 | 0.0 | 10.5 | 23.6 | |
| 0.01 | 0.0 | 0.0 | 0.0 | 0.1 | 0.4 | 0.7 | 1.3 | 2.2 | 2.0 | 1.0 | 0.0 | 10.4 | 23.1 | |
| 0.02 | 0.0 | 0.0 | 0.0 | 0.1 | 0.5 | 0.8 | 1.4 | 2.3 | 2.0 | 1.0 | 0.0 | 10.3 | 22.8 | |
| 0.03 | 0.0 | 0.0 | 0.0 | 0.1 | 0.6 | 0.9 | 1.5 | 2.3 | 2.1 | 1.0 | 0.0 | 10.1 | 22.6 | |
| 0.04 | 0.1 | 0.1 | 0.0 | 0.1 | 0.6 | 1.0 | 1.6 | 2.4 | 2.1 | 1.0 | 0.1 | 10.0 | 22.3 | |
| 0.05 | 0.1 | 0.1 | 0.0 | 0.1 | 0.6 | 1.0 | 1.6 | 2.4 | 2.2 | 1.0 | 0.1 | 9.9 | 22.0 | |
| 0.1 | 0.5 | 0.5 | 0.0 | 0.2 | 0.7 | 1.2 | 1.9 | 2.9 | 2.5 | 1.4 | 0.5 | 9.0 | 20.4 | |
| 0.15 | 1.1 | 1.1 | 0.1 | 0.2 | 0.7 | 1.3 | 2.2 | 3.3 | 3.0 | 2.0 | 1.1 | 7.9 | 18.6 | |
| 0.2 | 2.0 | 2.0 | 0.2 | 0.5 | 1.2 | 1.5 | 2.5 | 3.8 | 3.7 | 2.8 | 2.0 | 6.5 | 16.7 | |
| 0.25 | 3.1 | 3.0 | 0.3 | 0.8 | 2.1 | 2.8 | 3.0 | 4.6 | 4.5 | 3.7 | 3.0 | 5.0 | 14.6 | |
| 0.3 | 4.4 | 4.3 | 0.6 | 1.3 | 3.5 | 4.9 | 5.3 | 5.4 | 5.7 | 5.0 | 4.3 | 3.8 | 12.5 | |
| 0.35 | 6.0 | 6.0 | 0.9 | 2.1 | 5.6 | 8.0 | 9.2 | 7.0 | 6.9 | 6.5 | 6.0 | 3.4 | 10.3 | |
| 0.4 | 7.7 | 7.9 | 1.3 | 3.1 | 8.6 | 12.6 | 15.1 | 10.9 | 9.0 | 8.3 | 7.9 | 3.5 | 8.8 | |
| 0.45 | 9.7 | 10.0 | 1.8 | 4.5 | 12.9 | 19.2 | 23.7 | 17.5 | 12.6 | 10.6 | 10.0 | 5.7 | 8.2 | |
| 0.5 | 12.0 | 12.8 | 2.3 | 6.3 | 18.8 | 28.7 | 36.1 | 27.0 | 19.2 | 13.7 | 12.8 | 8.1 | 7.7 | |
| 0.55 | 15.1 | 16.2 | 3.0 | 8.7 | 27.1 | 41.9 | 53.7 | 40.3 | 28.1 | 19.4 | 16.2 | 10.6 | 7.8 | |
| 0.6 | 18.8 | 22.3 | 3.8 | 11.9 | 38.5 | 60.5 | 78.6 | 58.7 | 40.1 | 27.1 | 22.3 | 13.1 | 9.5 | |
| 0.65 | 25.1 | 30.0 | 4.6 | 16.2 | 54.2 | 86.2 | - | 83.6 | 55.9 | 36.8 | 30.0 | 15.6 | 11.9 | |
| 0.7 | 32.6 | 39.3 | 5.5 | 21.8 | 75.7 | - | - | - | 76.2 | 48.8 | 39.3 | 18.0 | 14.2 | |
| 0.8 | 51.5 | 63.4 | 7.5 | 38.8 | - | - | - | - | - | 81.2 | 63.4 | 23.4 | 18.6 | |
| 0.9 | 75.5 | 96.0 | 9.6 | 68.3 | - | - | - | - | - | - | 96.0 | 28.6 | 22.3 | |
| 1 | - | - | 11.6 | - | - | - | - | - | - | - | - | 33.7 | 25.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, W.; Zeng, B.; Li, S. A Novel Fractional-Order Grey Prediction Model and Its Modeling Error Analysis. Information 2019, 10, 167. https://doi.org/10.3390/info10050167
Meng W, Zeng B, Li S. A Novel Fractional-Order Grey Prediction Model and Its Modeling Error Analysis. Information. 2019; 10(5):167. https://doi.org/10.3390/info10050167
Chicago/Turabian StyleMeng, Wei, Bo Zeng, and Shuliang Li. 2019. "A Novel Fractional-Order Grey Prediction Model and Its Modeling Error Analysis" Information 10, no. 5: 167. https://doi.org/10.3390/info10050167
APA StyleMeng, W., Zeng, B., & Li, S. (2019). A Novel Fractional-Order Grey Prediction Model and Its Modeling Error Analysis. Information, 10(5), 167. https://doi.org/10.3390/info10050167




