Abstract
A new approach is presented to defining the amount of information, in which information is understood as the data about a finite set as a whole, whereas the average length of an integrative code of elements serves as a measure of information. In the framework of this approach, the formula for the syntropy of a reflection was obtained for the first time, that is, the information which two intersecting finite sets reflect (reproduce) about each other. Features of a reflection of discrete systems through a set of their parts are considered and it is shown that reproducible information about the system (the additive syntropy of reflection) and non-reproducible information (the entropy of reflection) are, respectively, measures of the structural order and the chaos. At that, the general classification of discrete systems is given by the ratio of the order and the chaos. Three information laws have been established: The law of conservation of the sum of chaos and order; the information law of reflection; and the law of conservation and transformation of information. An assessment of the structural organization and the level of development of discrete systems is presented. It is shown that various measures of information are structural characteristics of integrative codes of elements of discrete systems. A conclusion is made that, from the information-genetic positions, the synergetic approach to the definition of the quantity of information is primary in relation to the approaches of Hartley and Shannon.
1. Introduction
In the scientific and practical activity, we often deal with the discrete systems, the elements of which are described with the help of certain attributes. If the number of elements with a certain attribute is known, then we say that we have a finite set which is a part of the system. When two such sets A and B, distinguished by the attributes and intersect each other , we assert that these sets are interconnected and reflect (reproduce) certain information about each other. In this case, we take into account the philosophical conclusion about the inseparable connection of information with reflection [1,2,3,4], and by the term reflection we mean “the process and the result of the effect of one material system on another, which is the reproduction of one system features in features of another” [1] (p. 215). That is, when analyzing the interrelation of the sets A and B, the words “reflection” and “reproduction” may be considered as synonyms.
The term information does not currently have an unambiguous scientific definition. Therefore, speaking of what should be taken as information in the context of reflection of sets through each other, we proceed from the usual understanding of information as knowledge or data about something. Herewith, in this case, each of sets A and B we consider as a whole and, accordingly, we accept that in this case the information is data about a finite set as a single whole. This definition of information extends not only to the mutual reflection of two sets, but also to the reflection of individual sets, both through themselves and through arbitrary collections of other sets. Therefore, in order to distinguish information from other types of information, we consider it reasonable to give it a special name. This name, in our opinion, should take into account the fact that the interrelation of sets A and B is characterized by the fact that they interpenetrate each other and thereby form their joint image in the form of a connecting set K, the elements of which have the attributes of both sets. Considering the above, we will call information the syntropy of reflection, bearing in mind that the Greek word syntropy can be translated as the mutual convergence, affinity of objects. (The first occasion that the word syntropy was used in a similar sense was in 1921, by the German pediatricians Pfaundler and Seht [5], who called syntropy “the mutual inclination, attraction” of two diseases.) That is, syntropy of reflection is the information that two intersecting finite sets reproduce about each other as a single whole.
The quantitative assessment of the syntropy of reflection is relevant in solving various problems in many subject areas. For example, in the problems of pattern recognition, syntropy can be used as the informativeness of the attributes of the recognition objects, whereas in medical research it can be used to quantitatively characterize the interrelation of various diseases. At the same time, traditional approaches to determining the amount of information (Hartley’s combinatorial approach [6], Shannon’s probabilistic approach [7] and Kolmogorov’s algorithmic approach [8]) do not allow performing an adequate assessment of syntropy . This is due to the fact that in the traditional approaches other types of information are considered. In the approaches of Hartley and Shannon, information is the removed uncertainty of choosing one of many possibilities, or, as Weaver said (the first popularizer of Shannon’s theory), “information is a measure of one’s freedom of choice when one selects a message” [9] (p. 9). In this case, the greater the uncertainty of the situation, the more information a concrete choice gives. Accordingly, in the case when the sets A and B correspond to each other in a one-to-one manner and there is no difference in the elements, then there is simply no choice among the elements, and the Hartley and Shannon approaches will show that . At the same time, it is obvious that, with a one-to-one correspondence of the sets, the syntropy should have the maximum possible value, that is, . In Kolmogorov’s algorithmic approach, in turn, the length of the program for transforming one object into another is taken as information. Therefore, when , the algorithmic approach will also show that . In other words, the attempts to define the quantity using traditional approaches to quantifying information can lead to an apparent contradiction with common sense.
The indicated impossibility of assessing the syntropy of reflection using the traditional approaches to determining the amount of information has initiated special information-theoretical studies, the result of which was a synergetic theory of information (STI). The subject of cognition of this theory is the information-quantitative aspects of the reflection of interconnected finite sets, as well as the specificities of the reflection of discrete systems through the totality of their parts. In this case, information is understood as the data about a finite set as a single whole, whereas the measure of information is the average length of an integrative code of elements. Regarding the name of the theory, we can say the following.
In STI, finite sets are considered as holistic formations. Accordingly, it is considered that the elements of the sets take part in the information processes of reflection as an integral collection, without individually selecting any of them as a separate event, test result, etc. This is consistent with the philosophical conclusion about the argument that “any system of inanimate nature participates in the information process as if with “the whole body”, the whole structure” [1] (p. 113). Therefore, given that synergetic means joint action, this word was used in the name of the theory. It should also be noted that in STI such aspects of the structure of discrete systems as chaos and order are considered, which brings this theory closer to the traditional synergetics of Haken [10]. Moreover, while in traditional synergetics, chaos and order are dynamic characteristics of the systems (the nature of the trajectory of the systems in the phase space is considered), in STI they characterize the own structure of the system in the “here and now” mode. That is, it can be said that STI and Haken’s synergetic, with regard to the characteristics of discrete systems in terms of chaos and order, complement each other. Thus, we consider the name synergetic theory of information to be fully justified.
The present paper outlines the basics of STI. It is noted that some fragments of the theory were previously published by the author in the form of a series of papers in Russian [11,12,13,14,15], whereas the presented material is a generalization and revision of these articles and contains new theoretical results.
The main content of the paper consists of four Section 2, Section 3, Section 4 and Section 5. Section 2 presents a new (synergetic) approach to defining the amount of information within which the formula for the syntropy of reflection is obtained. Section 3 is devoted to the information analysis of the reflection of discrete systems through the totality of their parts, during which much attention is paid to such structural characteristics of systems as randomness and orderliness. In Section 4, the law of the conservation and transformation into each other of various types of information (information attributive to control and information that exists independently of control) is substantiated and meaningfully interpreted. In Section 5 we consider the integrative codes of the elements of discrete systems and show the integrative-code interrelation between various measures of information.
2. The Synergetic Approach to Determining the Amount of Information
2.1. The Problem of Estimating the Syntropy of Reflection of Finite Sets
The STI is based on the problem of quantitative estimation of the syntropy of reflection of finite sets. The formulation of this problem is as follows. Suppose that within a certain discrete system (Figure 1), two finite sets are distinguished by the attributes and : and , such that . The number of elements in the sets is, respectively, . It is required to define the syntropy of reflection , that is, the amount of information that the sets A and B reflect (reproduce) about each other as a single whole.
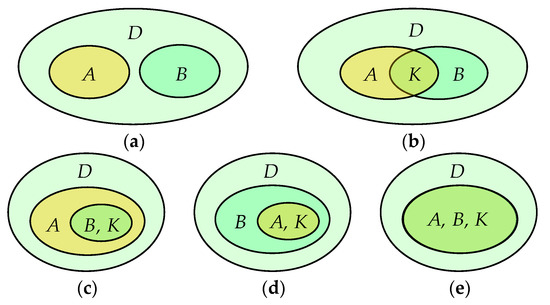
Figure 1.
Interconnection of sets A and B in the system D: (a) There is no relation (); (b) a partial relation (, , ); (c) a partial relation (); (d) a partial relation (); (e) a one-to-one relation ().
Obviously, . It is clear that if the values and are constant, the syntropy value increases with the increase of . It is also clear that if (Figure 1a), then ; whereas has its maximum value when (Figure 1e). Accordingly, in the latter case, the reflection of sets A and B through each other does not differ from their reflection through themselves, and the syntropy is equal to the information that each set reflects about itself as an integral formation. That is,
where is the information that the sets reflect about themselves.
It follows from the above that the value of syntropy must satisfy the inequalities: and . Therefore, we think that before solving the problem for the general case of the intersection of sets A and B (Figure 1b–d), it is necessary to define the amount of information that an arbitrary finite set A reflects about itself.
It seems natural to define the values and with the help of traditional information theory based on the work of Hartley [6] and Shannon [7]. At the same time, we have to admit that this cannot be done. The thing is that Hartley and Shannon considered information as the removed uncertainty of a random choice of one of the N possibilities (characters of the alphabet when sending messages). Moreover, Hartley considered the situation when all possibilities have the same probability and proposed an information measure that, when using the binary logarithm, looks like:
In turn, Shannon extended the views of Hartley to the general case, when , and, to measure information, he began to apply the entropy H of the set of probabilities:
In this case, the contribution of the i-th opportunity to the value of H is equal to its own information , which is called “surprises” by Tribus [16]:
If we try to use information measures (1–3) to determine and , then in the situation in Figure 1e we arrive at a contradiction with common sense. In this situation, the sets A and B consist of the same elements, which do not differ in any way and there is no choice . Accordingly, measures (1–3) will show that and , which cannot be. This suggests that, in the evaluation of syntropy and information , a new approach is required for the determination of the amount of information that should not be connected with the choice procedure. The development of this approach is presented below.
2.2. Attributive Information of a Finite Set
Any arbitrary finite set A has two attributive characteristics. This is the number of elements in the set and the attribute by which the set is distinguished. Therefore, assuming that , we will refer to information as attributive information. That is, attributive information is the information that the finite set A reflects about itself. We consider the set A as a single whole. This means that the elements of the set are not a mechanical collection of objects existing independently of each other, but an integral formation, uniting into which the elements acquire integrative properties that they do not have in their disjointed form. Taking this into account, in order to determine the value of attributive information , we consider it reasonable to adopt two axioms: The axiom of monotonicity and the axiom of integrativity.
The axiom of monotonicity: Attributive information of a finite set is a monotonically increasing function of the total number of its elements, that is, for any two finite sets A and B with the number of elementsandthere holds the inequality
The axiom of integrativity: An integrative code of the elements is a characteristic of a finite set A as a single whole. In this case, the integrative code is an individual for each element sequence of the symbols of an alphabet, the number of which(the code length) is a function of the total number of elementsin the set.
Let us now consider the process of increasing of the number of elements in the set A. We represent this process in the form of growth of an oriented tree, the set of suspended vertices of which is in one-to-one correspondence with the set A, while the maximum number of arcs emerging from one vertex is equal to the number of symbols (n) of the alphabet chosen for the compilation of integrative codes. In this case, each of the adjacent arcs is associated with its own symbol in alphabetical order, and the integrative code of an element is the sequence of symbols that are on the path of movement from the initial vertex of the tree to the suspended vertex corresponding to the given element. An example of such a code tree for when using an ordered pair of symbols as an alphabet is shown in Figure 2.
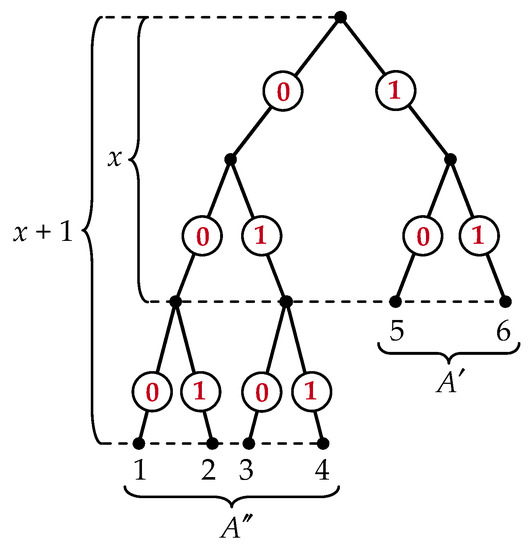
Figure 2.
Code tree for n = 2 and .
The analysis of Figure 2 shows that, in the general case, the set A is subdivided, with respect to the length of integrative codes , into two subsets and such that and , where is the integer part of . That is, is not a single-valued function of . Therefore, we will consider the average length of integrative codes
and start from an alphabet with a minimal number of symbols .
It is seen from Figure 2 that for an increase of by one results in a decrease by one of the numbers of elements with the code length x and an increase of the number of elements with the code length by two elements, that is:
Let us determine the value of and ; to this end, taking into account Equation (6), we write the system of equations:
Solving this system, we get:
Substituting the values of and from Equation (7) into Equation (5), we arrive at the expression for :
The quantity in Equation (8) satisfies the adopted axioms and can serve as a measure of attributive information .
Let us now consider the trees of codes for . Figure 3 presents such trees when and .
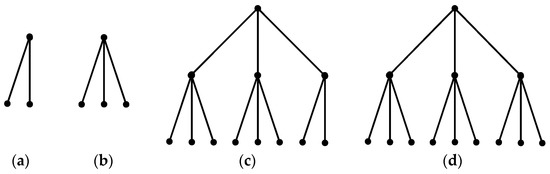
Figure 3.
Code trees for : (a) ; (b) ; (c) ; (d) .
It is seen from Figure 3 that when the initial vertex of the tree (Figure 3a,b) and the last of the suspended vertices (Figure 3c,d) are filled with the outgoing arcs, the average code length does not change, that is
Increasing n, we arrive at the general expression of the cases when retains its constant value for different values of :
Expression (9) indicates that for the values of contradict, in a number of cases, the monotonicity axiom (4). This allows us to draw an important conclusion: The average length of the integrative code of elements can act as a measure of the attribute information of the set only when the integrative codes are composed with the help of a binary alphabet.
Thus, we come to the conclusion that
and all our further reasoning will apply only to the case .
Analysis of Equation (8) shows that if the equality is observed, then ; whereas if the inequality holds, then . This suggests that, in the general case, exceeds by a certain quantity, and this can be clearly seen in Figure 4.
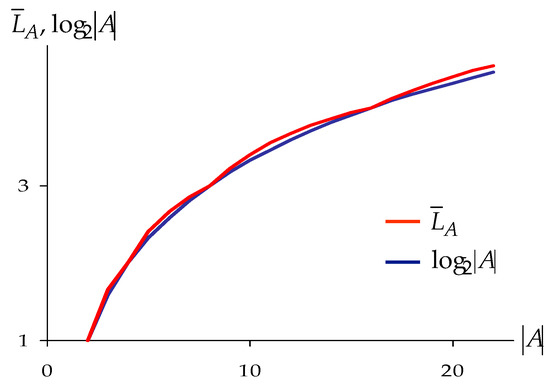
Figure 4.
Dependence of and on .
We will determine the maximum value of this quantity as the exact upper bound of the difference :
Applying the necessary condition for the extremum of function and setting , , we arrive, according to Equation (8), at the equation
which after differentiation acquires the form
and has a solution:
Substituting the value of from Equation (8) and the value of from Equation (12) into Equation (11), we get:
which is clearly illustrated in Figure 5.
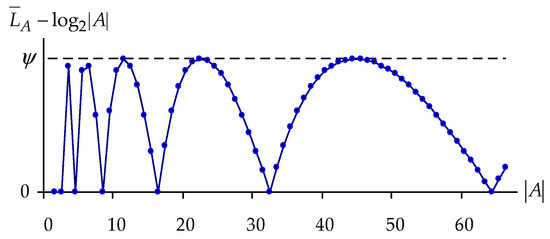
Figure 5.
Dependence of the difference on .
The value of the obtained constant (13) allows making the approximation
considering which, we can say the following.
The function , satisfies the axiom of monotonicity (4) and has a simpler form than in Equation (8). Therefore, in the sequel, for the convenience of theoretical constructions and practical calculations, instead of (10) we will use its approximation:
The obtained measure of attributive information (14) is similar in appearance to Hartley measure (1), but is fundamentally different from it in that in the measure the cardinality of the alphabet used is the number of the logarithm, whereas in the measure , the base of the logarithm. That is, the measures and are functions of different arguments. In the measure the argument is the cardinality of the entire set A, while in the measure the argument is the number N of characteristics, by which the elements of the set A differ from one another (for example, when transmitting the letter messages, is the total length of the message, whereas N is the cardinality of the alphabet, using which the message is written). Correspondingly, while analyzing one and the same sets with the help of Equations (1) and (14), in general case, we will obtain different results. Illustrative examples of such different results are given in Table 1 and Table 2, where the letter sequences and the corresponding values of and are given.

Table 1.
Information characteristics of letter sequences having the same length and a different variety of letters.

Table 2.
Information characteristics of letter sequences having different lengths and the same variety of letters.
It can be seen from Table 1 that does not depend on the variety of letters N, forming the sequence; and it follows from Table 2 that does not depend on the length of the sequence. In other words, Table 1 and Table 2 show that the attribute information of the set (14) and the Hartley information measure (1) are independent of each other and have different values in the same situation. Moreover, , whereas equality is observed only in the particular case when . All this suggests that, using Equations (1) and (14), different types of information are measured.
2.3. Syntropy of Reflection
We defined the value of the attributive information of a finite set as the average length of the integrative code of its elements (10), and we took the approximation (14) as the calculation formula. On this basis, the reflection syntropy can be represented as the reproduction of the average length of the integrative code of the elements of each of the intersecting sets A and B.
We now define the quantity and assume that the sets form an information communication system in which the sets A and B are alternatively the source and receiver of information, whereas the connecting set acts as a transmission medium or communication channel. The process of the information transference through such a communication system corresponds to the process of reflection of the sets A and B through each other. Let us consider this process, assuming that each set takes part in it simultaneously with the totality of its elements. We first consider the reflection of the set A through set B.
The integrative code of any element is a certain message about a finite set A as a holistic entity. The average length of such messages equals , and their total number is equal to . Accordingly, the amount of information sent by the reflected set A as a source of information to the connecting set K as a communication channel equals:
The carrying capacity of the set K, in turn, is bounded by the product ; and, accordingly, the amount of information that the set K can take from the set A is equal to this product. That is:
Since , then and, in the general case, the messages from the set A enter the set K in a truncated form. That is, the information when entering the set K is reduced to the value
Only messages can come to the reflecting set B from the connecting set K; each message contains the information . This means that the following amount of information comes from the set A to the set B as a receiver of information:
which is distributed over all elements . That is, the information is reproduced by set B in the form of information , which has the following form:
If we now consider the inverse process of reflecting the set B through the set A, then we obtain exactly the same result (15). It follows that
and the reflection syntropy , according to Equations (14) and (15), equals:
Equation (16) refers to the most general case of the intersection of sets A and B, when and (Figure 1b). In more particular cases, when (Figure 1c) and (Figure 1d), the syntropy can be represented in the following form:
Thus, having obtained Equations (16–18), we have solved the formulated problem of estimating the reflection syntropy , and actually developed a new approach to defining the amount of information based on the joint and simultaneous consideration of all elements of a finite set, without distinguishing any of them as a random event. At the same time, in our reasoning, the sets participated in information processes together with the totality of their elements. Therefore, we will call this new approach to a synergetic approach.
3. Information Aspects of the Reflection of Discrete Systems
3.1. Introductory Remarks
In the previous section, we carried out an information analysis of the reflection of two intersecting finite sets A and B through each other. Let us now consider the reflection of set A through the collection of sets distinguished in the system D by the values of the characteristic and assume that , , (Figure 6). In this case, for convenience, we will consider set A as a discrete system, and consider set as a part of this system.
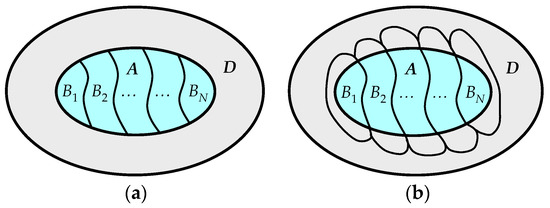
Figure 6.
Reflection of system A by a collection of sets : (a) System A is informationally closed; (b) system A is informationally open.
We also note that system A with respect to the environment (elements of the complementary set ) can be both closed and open in informational terms. That is, system A is informationally closed if (Figure 6a) and informationally open if (Figure 6b).
Taking into account the comments made, we proceed to the information analysis of the reflection of system A through the collection of sets and begin with the case when system A is informationally closed.
3.2. Reflection of Informationally Closed Systems
3.2.1. Additive Syntropy and Entropy of Reflection
The first thing we encounter when analyzing the informational aspects of the reflection of system A is its attributive information , which the system reflects about itself as a holistic entity. This information is reflected by the system through its N parts , which, in the case of the informational closeness of the system, coincide with the sets , that is, . At the same time, each part reflects a certain amount of information about the system, which is equal to syntropy , which according to Equation (17) has the form:
Accordingly, the total amount of information about system A, which is actually reproduced through N of its parts, is the additive syntropy of reflection, equal to the sum of partial syntropies (19):
Let us compare the information being reflected and the information that has been reflected . To this end, we multiply the right-hand sides of Equations (14) and (20) by and divide by . As a result of this operation, for we get the inequality
from which it follows that
Inequality (21) says that not all information about system A, as a single whole, is reflected through the totality of its parts, and there is always some part of information that remains unreflected. Denote this non-reflected information by the symbol S and define its value as the difference between the information being reflected and the information that has been reflected:
Let us represent (22) in expanded form and carry out simple transformations:
If we now multiply the right-hand side of Equation (23) by the total number of elements of the system and use natural logarithms, then we get a mathematical copy of statistical weight of a thermodynamic system, which is a measure of its entropy [17]. This circumstance gives us a reason to call the unreflected information S the entropy of reflection. That is, the entropy of reflection is the information about a discrete system that is not reflected (not reproduced) through a collection of its parts. In other words, entropy S characterizes inadequacy, the uncertainty of reflection of a discrete system through its parts, while the additive syntropy is a measure of adequacy, definitiveness of this reflection.
Until now, in our reasoning, we have never used such a concept as a probability. We just did not need to. At the same time, the quotient can be interpreted from the standpoint of the theory of probability as the probability of encountering the elements with the characteristic among all the elements of system A. With this interpretation of the indicated quotient, the entropy of reflection S is represented as follows:
Comparison of Equation (2) and Equation (24) shows that the reflection entropy S and the Shannon entropy H do not differ mathematically from each other, that is,
Equation (2) and Equation (23) are obtained in different ways, have different content-related interpretation and intended to measure different types of information. Therefore, to some extent, equality (25) is unexpected. In connection with this, it is appropriate to say that, regarding such similarities of different measures, such a well-known scientist as Kolmogorov said that “such mathematical analogies should always be emphasized, since the concentration of attention on them contributes to the progress of science” [18] (p. 39). In addition, we note that in Shannon’s theory [7], the derivation of the entropy H is based on three axioms (conditions), whereas only two axioms are in the foundation of STI.
Equality (25) indicates that STI and Shannon’s theory of information, though dealing with different types of information, is, at the same time, mathematically interrelated. The nature of this relationship, as will be shown in Section 5.2, has an integrative code character. Moreover, we note the following.
In Shannon’s theory, certain requirements are a priori imposed on the entropy H of the set of probabilities [7], and the entire theory, in fact, begins with the derivation of Formula (2). In STI, in turn, no preliminary conditions are set for the entropy of reflection S; it is obtained simply as the difference between the information being reflected and the information that has been reflected . That is, in the chronological sequence of obtaining information-synergetic functions , the entropy of reflection S is the closing member. This fact suggests that the synergetic information with which STI is dealing is genetically primary with respect to the probabilistic information, as measured in Shannon’s theory (we will come to the same conclusion, but from other standpoints, in Section 5.2). This is fully consistent with Kolmogorov’s conclusion that “information theory should precede probability theory, but not rely on it” [19] (p. 35). That is, STI can be viewed as a verification of this conclusion of recognized authority in the field of information theory.
3.2.2. Chaos and Order of Discrete Systems
The structure of any discrete system with a finite set of elements can be characterized with the help of such concepts as order and disorder or chaos. At the same time, these concepts are not unambiguously defined in modern science. Therefore, starting a conversation about the informational analysis of chaos and order in the structure of discrete systems, we first take a decision concerning the interpretation that will be used in the further presentation of our material.
So, we say that there is a complete order in the structure of the system in terms of the values of a certain attribute , if all elements have the same value of this attribute. That is, when all the elements in the composition of the system do not differ from each other in terms of this attribute, we say that the structure of the system is maximally ordered. In contrast, complete chaos in the structure of the system occurs when each element of the system has its own individual value of the attribute . That is, in this case, all the elements are different from each other, and we say that the structure of the system is maximally chaotic.
What has been said is formalized by the fact that, for complete order, , and for complete chaos, . In other cases, when , the system is in an intermediate state between complete chaos and complete order, and we say that the structure of the system is characterized by both chaos and orderliness. In this case, if the system changes its state in such a way that , then order develops into chaos, whereas if , then the chaos is transformed into order. Taking into account the comments made, we now turn to the information analysis of the structural features of discrete systems in terms of chaos and order.
An analysis of (20) and (23) shows that the value of the additive syntropy and the entropy of reflection S depends on the number of parts of the system and their mutual relations according to the number of elements. At the same time, the more chaotic the structure of the system is, that is, the more parts are identified in its composition and the less the parts differ from each other in terms of the number of elements, the larger is S and the smaller is . Conversely, the more order is in the structure of the system, that is, the smaller is the number of its parts and the more the parts differ from each other in terms of the number of elements, the larger is and the smaller is S. This indicates that and S depend on the degree of orderliness and randomness of the structures of discrete systems and can be considered as measures of order and chaos. Let us show this using a concrete example.
Figure 7 shows various states of a discrete system consisting of 16 elements, which are characterized by the “direction of motion” characteristic. According to the values of this characteristic, the system successively takes 5 states, which correspond to its division into 1, 2, 4, 8, 16 parts which have the same number of elements.
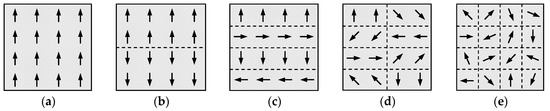
Figure 7.
Division of a system of 16 elements into equal parts according to the “direction of motion” attribute: (a) ; (b) ; (c) ; (d) ; (e) .
In the state of the system in Figure 7a, all elements move in the same direction and an ideal order is observed in the structure of the system. In Figure 7e we have the polar opposite, that is, each element of the system has an individual direction of movement, and the structure of the system is maximally chaotic. The states of the system in Figure 7b–d are intermediate to those in Figure 7a,e and are characterized by the fact that both chaos and orderliness are observed in the structure of the system. Calculating Equation (20) and Equation (23) for each state of the system the values of additive syntropy and entropy of reflection, we successively obtain: ; . That is, an increase in chaos and a decrease in order in the structure of the system in Figure 7 correspond to a decrease in the values of and an increase in the values of S.
Additive syntropy , as the reflected information, and the entropy of reflection S, as non-reflected information, are integral parts of the reflected information , that is:
At the same time, as was shown, the values of and S characterize the structure of a discrete system from the standpoints of order and chaos. Therefore, Equation (26) can be also interpreted as the following expression:
That is, it can be argued that Equation (26) and its interpretation (27) can be viewed as the law of conservation of the sum of chaos and order, which is valid for any structural transformation of the system without changing the total number of its elements. In other words, no matter what we do with the system without changing the total number of its elements, no matter into how many parts the system is divided by the values of any characteristic and whatever relations in terms of the number of elements are between the parts, the sum of chaos and order in the system structure will always remain constant. For example, for all the states of the system in Figure 7, there holds the equality: .
Let us now consider the specific features of the relationship between additive syntropy and entropy of reflection S with a constant number of elements of the system and a different number of its parts, correlated with each other in the number of elements in an arbitrary way. First, in accordance with Equations (14), (20), (23) and (26), we define the maximum and minimum values of and S for a fixed N.
When all parts of the system consist of only one element and, according to Equation (20), we have . Thus, it follows from Equation (26) that, in this case, . In other words, for syntropy assumes the minimal value, and entropy S, the maximum of all possible values for any N. Since in this case all parts of the system are equal with one another in terms of the number of elements , then in all other cases, when and , we should expect that syntropy is minimal, and entropy S, maximal. That is:
In turn, additive syntropy will assume its maximum value when the number of elements in one part is equal to , and each of the other parts includes only one element, that is:
Accordingly, the minimum entropy of reflection is equal to:
We construct the graphs of dependence of on the number N of parts of the system with and analyze the resulting diagram, which we will call the information field of reflection of discrete systems (Figure 8).
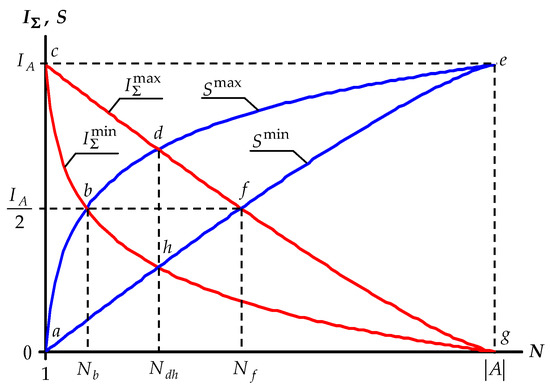
Figure 8.
Information field of reflection of discrete systems .
The graphs constructed in the figure initially form two contours—the entropic one abdefha and the syntropic one cdfghbc, which localize the ranges of all possible values of and S. The intersection of these contours at the points b and f, where equalities and are observed, allows, using the projection of these points on the horizontal axis, to identify three intervals of values of N: The left , the central , and the right ones. Let us consider the features of relationships between and S in these intervals and first let us determine the values of and .
At point b, according to Equations (28) and (29), we have the equation , the solution of which yields (hereinafter, the values of N are rounded to the nearest larger integer). A similar equation for the point f formed by the right-hand sides of (30) and (31) has no analytical solution. That is, the value of can only be determined numerically, which is as follows. For the members of the sequence are determined by and , and as the value of we take the value of N, after which . The values of calculated in this way lead to the regression equation .
Thus, for , we have three intervals of values of N:
- the left one: ;
- the central one: ;
- the right one: .
The systems that fall into the left interval according to the value of N are characterized by the fact that for any relations between their parts in terms of the number of elements, the inequality is preserved. That is, in the left interval of the values of N, the structural orderliness of the system is always greater than its randomness. In the right interval, the opposite situation is observed, when inequality holds for any structural transformation of the system, which corresponds to the predominance of chaos over the order in the structure of the system. In the central interval, there is an intersection of the regions of the possible values of and S, as a result of which there can be various relations between them , and there is a tendency towards structural harmony of chaos and order.
In other words, in the left interval of the values of N, we observe an irreversible predominance of order over chaos in the structure of the system, and in the right interval, on the contrary, irreversible predominance of chaos over order. In the central interval, in turn, the predominance of both order over chaos and chaos over order is reversible. Any discrete system with a finite set of elements, divided by the values of any characteristic into N parts, inevitably falls into one of the specified intervals, which allows all systems to be classified into three types according to the specific features of these intervals:
- ordered (left interval);
- harmonious (central interval);
- chaotic (right interval).
For example, the system in Figure 7, consisting of 16 elements, in its various states will be classified as follows: (a) Ordered (b) ordered (c) harmonious (d) chaotic ; (e) chaotic .
The division of the values of N into the left, center, and right intervals is not comprehensive. In addition to this division, the central interval is additionally subdivided into left and right parts according to the value , which corresponds to the combined projection of the points d and h. We note the features of these parts, and first we determine the value .
At the point d, the equality is observed, and at the point h, the equality . It follows that the value must satisfy the equation:
Equation (32) has no analytical solution, as a result, the values can only be obtained numerically (by analogy with the above determination of ). Such numerical solutions lead to the regression equation .
Thus, the left and right parts of the central interval have the form:
- the left part: ;
- the right part: .
The interrelationships of syntropy and entropy S in the left and right parts of the central interval are characterized by the fact that in the left part, , and in the right part, . That is, in the structure of systems from the left part there is a tendency for dominance of order over chaos, which weakens with increasing of N, and in the structure of systems from the right part, the opposite tendency for the prevalence of chaos over order is manifested, which increases together with the increase of N. These features of interrelations between and S in the left and right sides of the central interval, as well as the equality , observed in each of these parts along the bf line, provide a ground for further dividing harmonious systems into three kinds:
- ordered harmonious (the left part of the central interval);
- balanced harmonious (the entire central interval with );
- chaotic harmonious (the right part of the central interval).
Thus, all discrete systems with a finite set of elements are divided into three types according to the proportion of chaos and order in their structure; these types include five sorts of systems.
3.2.3. Structural Organization and Development of Discrete Systems
It is obvious that the structural organization of a discrete system depends on the randomness and orderliness of its structure. Moreover, the more order in the structure of the system, the more the system is organized, and vice versa, the more disorder, the less the level of organization is. Accordingly, to quantify the structural organization of systems, one or another function can be used, the arguments of which are measures of chaos and order. As such a function of the structural organization, we can use the ratio of additive syntropy to the entropy of reflection S, which will be called R-function (R is the first letter of the word reflection):
The greater the values of the R-function, the higher the structural organization of the system is. In this case, the values of R indicate what and to what extent predominates in the structure of the system: Chaos or order. For example, if , then order prevails in the structure of the system, otherwise, when , chaos. When , chaos and order balance each other, and the structural organization of the system are equilibrium. Accordingly, in the left interval of the values of N, systems always have , in the right interval, , whereas in the central interval, the structural organization of the systems may be diverse, that is, , or . In this case, when all elements of the system have one and the same characteristic, that is, when and , it is assumed that . For example, for the states of the system in Figure 7, whose syntropy and entropy S were determined above, we have the following values: (a) ; (b) ; (c) ; (d) ; (e) .
Apart from structural organization, discrete systems are also characterized by the level of their development, which is related to the ratio of chaos and order in the structure of the system and depends on the total number of system elements, the number of its parts and the distribution of the latter in terms of the number of elements. For a quantitative assessment of the structural development of systems, it seems natural to use the values of a certain function, the arguments of which are the additive syntropy and the entropy of reflection S. The behavior of such a function must be made consistent with the general laws of structural development, which can be represented as follows.
When , all elements of the system have the same distinguishing feature, the division of the system into parts is absent, and the structure of the system is not developed. In this case, , . In the interval , the formation takes place of various groups of elements with the same values of the attribute , as a result of which the system is divided into N parts and its structural development occurs, for which, , . In the state of the system, when , each element has an individual value of the attribute , and the system is split up into parts consisting of only one element. This corresponds to the complete destruction of any structure, that is, in this state of the system there is no structural development and , .
It follows from the above that when a system moves from the state to the state , the values of the function of structural development must first increase from zero to a certain maximum, and then decrease again to zero. As such a function, it is natural to take the product , which we will call the D-function of the structural development of discrete systems (D is the first letter of the word development):
The structural development function (34) assumes the minimum value when and , whereas this function has the maximum value when . The latter is explained by the fact that the product of two non-negative numbers with a constant sum is maximal when the numbers are equal. That is, the development function (34) is characterized by the fact that its values are the greater, the smaller the absolute value is, and, accordingly, we have:
In other words, the system reaches the maximum possible level of development when chaos and order in its structure are equal to each other.
In the general case, systems with different numbers of elements may have the same value of the development function D. In this case, if, for example, two systems and are given such that and , then it is clearly understood that the system is at a higher level of development than the system . Therefore, when comparing the structural development of various systems, it is expedient to use the relative value of development , which is convenient to express as a percentage:
In order to have a visual representation of the behavior of the structural development function, Table 3 shows its absolute and relative values, as well as the values , for different states of the discrete system in Figure 7.

Table 3.
Informational characteristics of the system states in Figure 7.
It is seen from the table that D and have the maximum value when and .
3.3. Reflection of Informationally Open Systems
When the system is informationally open (Figure 6b), it interacts with the environment. As a result of this interaction, part of the information being reflected passes into the environment and is distributed among the elements of the complementary sets , which, together with the parts of the system, form reflecting objects in the form of the sets . In this case, the reflection of the system as a whole becomes more uncertain and diffused. Accordingly, in relation to the informationally closed state, the additive syntropy of the reflection of the system decreases, while the entropy of reflection increases.
Obviously, in accordance with the general definition of syntropy (16), the additive syntropy of the informationally-open state of the system has the form
and, in the case , is reduced to the additive syntropy of the informationally closed state. The entropy S of reflection, in turn, is an invariant quantity with respect to any relations of the system with the environment (this follows from the fact that the ratio in Equation (23) does not depend on the degree of openness of the system). The latter circumstance suggests that, with the informational opening of the system, a new component appears in the entropy of its reflection, which characterizes the relationship of the system with the environment. In accordance with this, in order to meaningfully differentiate between S and , we will use the terms internal and external entropy of reflection.
We define the value of external entropy based on the balance between the information being reflected, the information that has been reflected and the non-reflected information . Since the information being reflected and the internal entropy S do not change during the informational opening of the system, the external entropy is defined as the difference between additive syntropies of the informationally closed and informationally open states:
The first factor under the sign of the last sum in Equation (38) is the ratio of the number of elements of the complementary set to the number of elements of the connecting set . That is, this factor characterizes the relationship of the system with the environment from the side of the set , that is why, we will call it the coefficient of informational openness of the system with respect to the characteristic :
The combination of the second and third factors, in this case, represents the syntropy of the reflection of an open system through the set . Therefore, taking into account Equation (39), the final expression of the external entropy of reflection has the form:
Let us return to the consideration of the information field of reflection of discrete systems in Figure 8. Obviously, the rectangular contour acega limits the total area of the information field, which includes all possible values of additive syntropy and entropy of reflection for both informationally open and closed systems. In Section 3.2.2 it was shown that if the system is informationally closed, then the areas of possible values of additive syntropy and reflection entropy are limited by the corresponding contours cdfghbc and abdefha. When the system informationally opens, its reflection becomes more uncertain and the areas of possible values of both additive syntropy and entropy increase. Moreover, the new values of additive syntropy are located below the graph of and, with an unlimited increase in the information openness of the system , they asymptotically approach the line ag, while the values of the total entropy of reflection are above the graph of and have as their the asymptote the line ce. Thus, the areas of possible values of the reflected and non-reflected information are limited, in the general case, by the following contours: The additive reflection syntropy, by acdfga, the reflection entropy, by acefha. Completing the description of the distribution of the information being reflected over the information field acega of the reflection, we also note that within it there is a vast area efge, into which the values of both additive syntropy and reflection entropy never fall.
3.4. Information Law of Reflection
Let us work out the information balance of reflection of discrete systems in the general case:
Equation (41) is a stable, single-valued relation between the information being reflected, the information that has been reflected and the non-reflected information, which makes it possible to give it the status of a law. Let us call this law the informational law of reflection and formulate it as follows: When reflecting a discrete system A through a collection of finite sets , such that , , there takes place a division of the reflected information into reflected and non-reflected parts, the first of which is equal to additive syntropy, and the second is the sum of the internal and external entropy of reflection. In the case, when the system is in the informationally closed state , Equation (41) reduces to Equation (26) and the non-reflected part of the information is equal only to the internal entropy S of reflection.
4. The Law of Conservation and Transformation of Information
The information law of reflection (41) is similar in its form to the known physical laws of conservation (of energy, electric charge, etc.). Already in the 50s and 60s of the last century, mathematicians and philosophers spoke about the need to establish such laws in the theory of information [4,20]. At that, special attention was paid to the fact that conservation laws in information theory should take into account the mutual transitions of different types of information into each other. Such information transitions can be seen in analyzing Equation (41) if, in accordance with Equation (25), we consider the internal entropy of reflection S as Shannon’s probabilistic information H, which is associated with a choice among many possibilities, whereas the additive syntropy and the outer entropy are considered as some kinds of synergetic information that exists independently of this choice. In this case, Equation (41) takes the form
and is interpreted as the law of conservation and transformation of information, which is formulated as follows: The total amount of synergistic and probabilistic information characterizing the structure of a discrete system and its relationship with the environment is always a constant value. Let us reveal the content of this law separately for informationally closed and informational open systems, for which we present them in graphical form, as shown in Figure 9.
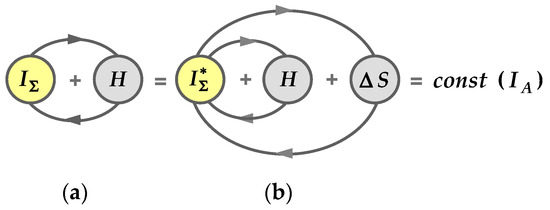
Figure 9.
Graphic expression of the law of conservation and transformation of information: (a) Informationally closed system; (b) informationally open system.
Informationally closed systems. When the system is informationally closed, the law of conservation and transformation of information (42) appears before us in its particular form
and the relations between different types of information, as well as their mutual transitions into each other, are determined by the direction in which the structural transformations of the system occur. So, if the number of parts of the system decreases, and even more so if at the same time some part of the system begins to dominate in terms of the number of elements, then the amount of synergetic information increases and the amount of probabilistic information H decreases.
In the limit, when the division of the system into parts ceases , its probabilistic information is completely transformed into synergetic information and, as such, ceases to exist in the system, that is, , . In this case, there is no variety of elements and possibilities of choice. In the case of inverse structural transformations, when the number of parts of the system increases, the opposite information process takes place and the synergetic information turns into the probabilistic information. This process exhausts itself and ends when the number of parts of the system becomes equal to the number of its elements and, correspondingly, , . The variety of elements and possibilities of choices are maximal in this situation.
Informationally open systems. When the system informationally opens, its interaction with the environment begins; as a result of that, some of the information reflected by the system goes into the environment in the form of the external entropy of reflection. If the system further begins to close again , then this information is returned to the system in the form of the corresponding increase in the values of . Since , then, irrespective of the degree of increase in the informational openness of the system , only a limited amount of information can go to the external environment. From this it follows that the system cannot give to the external environment, and also get back from the external environment an amount of information that exceeds the additive syntropy of reflection of its informationally closed state.
Also, as in the case of the informationally closed systems, we consider two opposite structural states of the system. In the first case, when the system is maximally ordered , only synergetic information is manifested in it and before the system is opened we have , . After the informational opening of the system and its unbounded growth , practically all the information reflected by the system is disseminated over the environment and, accordingly, , . In the second case, with the maximum randomness of the structure , all information of the system is represented only by a probabilistic form, which is invariant with respect to relations of the system with the external environment. Accordingly, both before the opening of the system and after its opening, equality is preserved, indicating that, if the structure of the system is maximally chaotic, then for any degree of openness of the system, there is no information exchange with the environment, and , . That is, reaching the highest possible level of structural chaos, the system becomes invisible to the external environment.
5. Information Measures in the Light of Integrative Codes
In Section 2 it was shown that the measure of attributive information of a finite set is the average length of the integrative code of its elements. Now we show what other information measures represent in terms of integrative codes both in the STI and in the Hartley-Shannon information theory.
5.1. Integrative Codes of the Elements of Discrete Systems
Let us consider two situations concerning finite sets that are identified in a universal set U by means of an attribute . In the first situation, the sets are isolated from each other and exist by themselves, whereas in the second situation, the sets are combined into a system and each of them is an independent part of this system.
When the set is isolated from other sets, its elements have the average length of an integrative code, and when the sets form a system A, then in the composition of this system the integrative codes of elements of any set have the average length . Since , then . This means that when combining sets into a system, the average length of the integrative code of their elements increases by the value of the difference . It follows that the integrative code of any element of system A is generally divided into two parts. In this case, the first part is formed due to the set of elements having the same value of the attribute , whereas the second part is a superstructure over the first, and is due to the combination of the collection of sets into a system. Since any set in the composition of the system A is a homogeneous group of elements with respect to , we give the indicated parts of integrative codes the following names: The first part is the group part of the code, the second part is the system part of the code. In addition, the length of these parts will be denoted by the following symbols: is the length of the group part, is the length of the system part.
Thus, the length L of the integrative code of any element of a discrete system, in the general case, can be represented as follows:
In order to have a visual representation of the division of integrative codes into the group and system parts, we refer to Figure 10, where the code trees of a discrete system A with the number of elements are shown. (Such a graphic illustration of the division of codes into parts is possible only when the logarithms and have integer values.) The figure shows three situations that reflect two polar (a), (c) and one common (b) cases of division of the system into N parts.
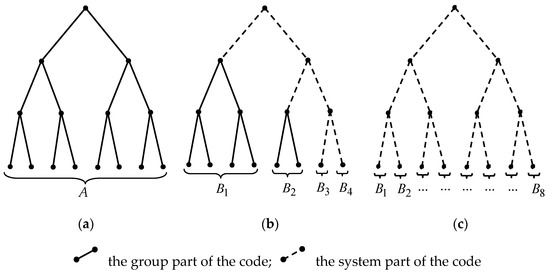
Figure 10.
The trees of integrative codes of a discrete system A with the number of elements : (a) There is no division of the system into parts ; (b) the general case of dividing the system into parts ; (c) the number of parts of the system is equal to the number of its elements .
In Figure 10a, there is no division of the system into parts , that is, all elements of the system have the same value of the attribute , and accordingly, all codes are represented only by the group part . The opposite situation is shown in Figure 10c, where the number of parts of the system is equal to the number of its elements , that is, in this case, each element of the system has an individual value of the attribute , and its integrative code consists only of the system part . Figure 10b shows the most general case of dividing a system into parts , when the number of elements in any part satisfies the inequality . In this case, if (parts and ), then the code is represented only by the system part , and if (parts and ), then in the structure of the code, both the group part and the system part are distinguished.
Let us now consider the quantitative aspects of integrative codes of elements in the composition of discrete systems, and let us begin with determining the size of the group part and the total length of the code. From Equations (10) and (14) it follows that the average length of the integrative code of the elements of system A and the average value of the group part of the code of the elements of any part are equal to:
The weighted average value of the length of the group part of the code for all parts of the system, in turn, has the form:
From Equations (44)–(46) it follows that the average length of the system part of the code of the elements of any part is equal to:
Accordingly, the weighted average value of the system part of the integrative code over all elements of system A has the form:
In the case when all parts of the system are equal, that is, when , we have:
Thus, we have established that the integrative codes of the elements of discrete systems are divided, in the general case, into the group and system parts, and also have determined the quantitative characteristics of these parts.
5.2. Integrative-Code Interpretation of the Information Measures
An analysis of the obtained characteristics of integrative codes, as they are compared with the information measures of combinatorial, probabilistic and synergetic approaches, allows us to give these measures the following interpretation.
Combinatorial and probabilistic approaches. The most widely known measure of information, the entropy of the Shannon probability set (2), is the weighted average of the system part of the integrative code of the elements of the discrete system (49):
When all parts of the system are equal, the combinatorial Hartley measure (1) is also expressed in terms of the weighted average of the system part of the code:
The self-information (3), appearing in the probabilistic approach, in turn, represents the average value of the system part of the code (48) of those elements of the system that have the same value of the attribute , that is:
Synergetic approach. The measure of attribute information (14), initially introduced in this approach, by definition (10), is the average length of the integrative code of all elements of both a single finite set and a discrete system as a whole. In this case, when , the integrative codes of the system are represented only by the group part and, accordingly,
The partial syntropy of the reflection of the system through any part of (17) is the corresponding term of the last sum in Equation (47) and, taking into account Equation (46), it is equal to
The additive syntropy of reflection (20), in turn, is equal to the weighted average value of the group part of the code of all elements in the system (47):
The entropy of reflection of the system through the collection of its parts (23), as well as the Shannon entropy (2), is equal to the weighted average value of the system part of the integrative code of the elements of the system (49), that is:
A summary of what has been said is Table 4, which presents the information measures of the combinatorial, probabilistic, and synergetic approaches, as well as their integrative-code interpretation.

Table 4.
Information measures and their integrative-code interpretation.
The above Table clearly shows that the information measures of the combinatorial and probabilistic approaches are functionally related only to the system part of the integrative code of the elements, while the synergetic approach includes both parts of the code together with its total length. In this case, the system part of the code is formed only when the individual sets are combined into a system, or when a homogeneous system begins to divide into parts. That is, prior to this union or division, the integrative codes are represented only by the group part, and there is only the attribute information of individual sets or a homogeneous system. It follows that the information considered in the synergetic approach is genetically primary with respect to the information measured in the combinatorial and probabilistic approaches. This is a confirmation of the conclusion made in Section 3.2.1 of the primacy of synergetic information, which was based on the sequence of obtaining information-synergetic functions , , , .
The general conclusion that can be made as a result of analysis of Table 4 is that the information measures of combinatorial, probabilistic and synergetic approaches are in their essence quantitative characteristics of the structural features of integrative codes of the elements of discrete systems. Figuratively speaking, one can say that these informational measures are masks behind which the characteristics of integrative codes are hidden. Moreover, the entropy S of reflection and the Shannon entropy H are two different masks of the weighted average value of the system part of the code. All this suggests that the synergetic information theory and information theory in the Hartley-Shannon version in their totality form a unified theory of the quantitative aspect of the phenomenon of information.
6. Conclusions
In the paper, we have passed the way from consideration of information aspects of reflection of arbitrary finite set to the estimation of structural organization and the level of development of discrete systems in terms of the proportion between chaos and order. In addition, a new (synergetic) approach is developed to defining the amount of information, where information is understood as the data about a finite set as an integral whole, whereas the measure of information is the average length of the integrative code of elements. It is shown that the synergetic approach has an integrative-code interrelation with the approaches of Hartley and Shannon and is primary to these approaches with respect to the information-genetic positions. In addition, three information laws have been established: The law of conservation of the sum of chaos and order; the information law of reflection; and the law of conservation and transformation of information. All this suggests that the synergetic theory of information is a new direction of information-theoretical research. In our opinion, further development of this theory, and also its introduction into the practice of scientific and applied research, can have a positive impact both on the general theory of information and on those subject areas in which objects of knowledge are discrete systems with a finite set of elements. This is supported by the fact that the equations and conclusions of STI, previously published in Russian [11,12,13,14,15], have already begun to be used in conducting research works in various thematic areas (for example, see References [21,22,23,24,25,26]).
Funding
This research received no external funding
Conflicts of Interest
The author declares no conflict of interest.
References
- Ursul, A.D. The Nature of Information. Philosophical Essay; Politizdat: Moscow, Russia, 1968; p. 288. [Google Scholar]
- Kolin, K.K. Philosophical Problems of Computer Science; Binom: Moscow, Russia, 2010; p. 264. ISBN 978-5-9963-0347-2. [Google Scholar]
- Ukraintsev, B.S. Information and reflection. Quest. Philos. 1963, 2, 26–38. (In Russian) [Google Scholar]
- Novik, I.B. Negentropy and the amount of information. Quest. Philos. 1962, 6, 118–128. (In Russian) [Google Scholar]
- Pfaundler, M.; von Seht, L. Über Syntropie von Krankheitszuständen. Z. Kinderheilkd. 1921, 30, 100–120. (In German) [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of Information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Shannon, E.C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the definition of the concept “quantity of information”. Probl. Peredachi Inf. 1965, 1, 3–11. [Google Scholar]
- Weaver, W. Recent contributions to the mathematical theory of communication. In The Mathematical Theory of Communication; Shannon, C.E., Weaver, W., Eds.; The University of Illinois Press: Urbana, IL, USA, 1964; pp. 1–28. [Google Scholar]
- Haken, H. Synergetics, an Introduction. Nonequilibrium Phase-Transitions and Self-Organization in Physics, Chemistry and Biology, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 1978. [Google Scholar]
- Vyatkin, V.B. Mathematical Models of Informational Assessment of the Characteristics of Ore Objects. Ph.D. Thesis for the Degree of Candidate of technical sciences, USTU-UPI, Ekaterinburg, Russia, 2004. [Google Scholar]
- Vyatkin, V.B. Synergetic approach to defining the amount of information. Inf. Technol. 2009, 12, 68–73. (In Russian) [Google Scholar]
- Vyatkin, V.B. Introduction to the synergetic theory of information. Inf. Technol. 2010, 12, 67–73. (In Russian) [Google Scholar]
- Vyatkin, V.B. Integrative-code interrelation between combinatorial, probabilistic and synergetic approaches to defining the amount of information. Inf. Technol. 2016, 22, 542–548. (In Russian) [Google Scholar]
- Vyatkin, V.B. Chaos and order of discrete systems in the light of the synergetic theory of information. Sci. J. Kuban State Agrarian Univ. 2009, 47, 96–129. (In Russian) [Google Scholar]
- Tribus, M. Thermostatics and Thermodynamics; an Introduction to Energy, Information and States of Matter, with Engineering Applications; University Series in Basic Engineering; D. Van Nostrand Company, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Planck, M. Einführung in Die Theoretische Physik. Band V: Einführung in Die Theorie der Wärme; Hirzel: Leipzig, Germany, 1930. (In German) [Google Scholar]
- Kolmogorov, A.N. Information Theory and Theory of Algorithms; Nauka: Moscow, Russia, 1987; p. 304. [Google Scholar]
- Kolmogorov, A.N. Combinatorial foundations of information theory and calculus of probabilities. Russ. Math. Surv. 1983, 38, 27–36. [Google Scholar] [CrossRef]
- Kharkevich, A.A. Essays on the General Theory of Communication; Gostekhizdat: Moscow, Russia, 1955; p. 268. [Google Scholar]
- Morozov, O.V.; Vasiliev, M.A. Stability of Federative Systems (the Questions of Methodology); Russian Academy of the National Economy and State Service: Moscow, Russia, 2015; p. 232. ISBN 978-5-7749-0958-2. [Google Scholar]
- Polikarpov, V.S.; Polikarpova, E.V. Wars of the Future. From the “Sarmat” Rocket to Virtual Confrontation; Algoritm: Moscow, Russia, 2015; p. 368. ISBN 978-5-906798-52-7. [Google Scholar]
- Berezhnoy, I.V.; Eremeev, Y.I.; Makovskiy, V.N. A method for assessing the level of organization in the problems of monitoring the military and technical systems. Proc. A.F. Mozhayskiy Mil. Space Acad. 2017, 659, 35–45. (In Russian) [Google Scholar]
- Simonian, G. Analysis of the state of geo-ecological systems in the view of synergetic theory of information. GISAP Phys. Math. Chem. 2014, 4, 18–21. [Google Scholar]
- Belinska, Y.V.; Bikhovchenko, V.P. Indicators of financial stability and innovative management of financial systems. Strateg. Prior. 2011, 3, 53–68. (In Ukrainian) [Google Scholar]
- Lisienko, V.G.; Sannikov, S.P. Synergetic bases of functioning the RFID systems on the example of natural areas. REDS Telecommun. Devices Syst. 2013, 3, 360–362. (In Russian) [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).