Abstract
Financial prediction is an important research field in financial data time series mining. There has always been a problem of clustering massive financial time series data. Conventional clustering algorithms are not practical for time series data because they are essentially designed for static data. This impracticality results in poor clustering accuracy in several financial forecasting models. In this paper, a new hybrid algorithm is proposed based on Optimization of Initial Points and Variable-Parameter Density-Based Spatial Clustering of Applications with Noise (OVDBCSAN) and support vector regression (SVR). At the initial point of optimization, ε and MinPts, which are global parameters in DBSCAN, mainly deal with datasets of different densities. According to different densities, appropriate parameters are selected for clustering through optimization. This algorithm can find a large number of similar classes and then establish regression prediction models. It was tested extensively using real-world time series datasets from Ping An Bank, the Shanghai Stock Exchange, and the Shenzhen Stock Exchange to evaluate accuracy. The evaluation showed that our approach has major potential in clustering massive financial time series data, therefore improving the accuracy of the prediction of stock prices and financial indexes.
1. Introduction
The analysis and forecast of financial time series are of primary importance in the economic world [1]. Compared to general data, financial data have their own particularity. There is a temporal correlation between data and data [2]. The financial time series are a dataset obtained from the selling price, limit up, and fluctuation of financial products in the financial field over time [3]. How to dig out valuable information in these massive data and find out rules to better guide scientific research has become a hot research topic. By studying the time series, the future trend of the index can be predicted [4]. In the capital market, where information is more and more open, it is an inevitable trend to disclose financial forecast information to a wider extent. Compared to historical financial information, financial forecasting has a strong correlation with decision-making services for investors, but as a kind of prior information, it is highly uncertain. If the reliability is low, it may mislead investors. In such a macro environment, many financial scholars are striving to explore financial forecasting methods [5].
Traditional data mining methods [6] have some limitations in data clustering and prediction. On one hand, the dimensions of time series are higher and higher, and the randomness is stronger and stronger [7]. On the other hand, traditional technology cannot achieve satisfactory results when dealing with noisy, random, and nonlinear financial time series. However, the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm can solve this problem better. The DBSCAN algorithm clusters different nodes from the perspective of a similarity measurement between nodes so that the different categories of nodes can be accurately evaluated [8]. In addition, support vector regression (SVR) is also combined to predict financial sequence research. The biggest feature of SVR is that it is proposed for the principle of structural risk minimization and has good generalization ability [9]. Therefore, this paper uses DBSCAN and SVR in the classification and regression of financial fields.
This paper combines existing clustering algorithms to mine, form a model of financial time series data, and predict relevant financial data. First, this article finds the limitations of the DBSCAN clustering algorithm in non-uniform density datasets and analyzes the feasibility of parameter adaptations of the DBSCAN algorithm. Second, the DBSCAN algorithm is improved by optimizing initial point and parameter adaption [10]. The article analyzes the influence of parameter dynamic change on the clustering effect and implements an improved algorithm combined with support vector regression [11]. Finally, the algorithm is applied to the prediction of financial time series data. The innovation points of this paper are as follows:
- The parameters of the DBSCAN algorithm are sensitive and global, so it cannot effectively cluster datasets of different densities. This paper proposes an Optimization Initial Points and Variable-Parameter DBSCAN (OVDBSCAN) algorithm based on parameter adaption;
- This paper combines the OVDBSCAN algorithm with SVR and proposes a new “hybridize OVDBSCAN with SVR” (HOS) algorithm. By establishing the regression prediction model, the regression prediction of the unsteady noise data is realized, and the prediction accuracy of stock price and the financial index is improved.
Section 1 mainly introduces the research background and structure of financial time series. Section 2 mainly introduces the current research status of the forecasting methods and models of financial time series at home and abroad. Section 3 proposes the parameter adaptive clustering algorithm based on financial time series data. In Section 4, the algorithm is used to conduct experiments and verify the improvement effect of the OVDBSCAN algorithm and predict the financial data. Section 5 is a summary of this paper.
2. Related Work
As early as the 1920s, the British mathematician Yule gave a regression model for predicting the law of market changes. Later, R. Agrawal [12] made a systematic elaboration on time series similarity. When the mathematician Robert F. Engel analyzed inflation in the financial market, he proposed the conditional variance model [13]. An American metrologist, G.E.P. Box, put forward the modeling theory, the analysis method of time series, and discussed the principle of the autoregressive integrated moving average model [14]. These methods are all classic methods of time series analysis. However, in the early days, most of these methods were used in a single variable and the same variance model. As financial markets have boomed and data have exploded, the barriers to early models have become more prominent and limited in dealing with large, complex, and noisy data. At the end of the last century, G. Das [15] proposed to intercept the data flow by sliding window, transforming the data obtained according to certain rules and then conducting clustering. Sheng-Hsun Hsu [16] proposed a self-organizing neural network and SVR to predict the stock price. Cheng-lung Huang [17] proposed a hybrid self-organizing feature map (SOFM)-SVR model for monetary expansion in financial markets. In the new century, artificial intelligence and mining technology have been improved and integrated with each other [18], which made data mining technology perfect. G. Peter compared the neural network model with the moving average (MA) model when predicting time series data and found that the neural network [19] had higher prediction accuracy when facing more complex nonlinear time series data.
The domestic research on the problem of financial time series not only expanded the application scope of relevant technologies and methods, but also improved and complemented relevant theories and put forward many solutions while introducing and learning the foreign models. For example, in 1980, Professor Jiahao Tang and other professors proposed a classical model known as the nonlinear domain, namely the threshold autoregressive model [20]. Qihui Yao proposed a method to approximate the nonlinear regression function of high dimension, which was a new metric and estimation algorithm. This new method provided the possibility of finding more reasonable measurements and making an accurate calculation. Zhengfeng Xiong [21] expounded the characteristics of financial time series. He proposed several important features and proposed a new estimation method through the wavelet transform method. Chao Huang et al. [22] proposed a time series dimensional reduction model for the trend volatility of financial time series data. The time complexity of this model is linear and is not sensitive to noise interference. Bin Li proposed a frequent structural model for the time correlation of time series data and realized the discovery of multiple financial time series [23]. These results provided a more accurate test method for the stationarity of regression models.
With the progress of internet technology and the accumulation of data in multiple fields, data analysis methods and mathematical models have been constantly improved. Due to the difference in financial background and characteristics at home and abroad, researchers have proposed a variety of predicted methods and models for financial time series data. As can be seen from the above, there are many methods for forecasting. Time series analysis [24] is the analysis of a set of discrete data. In the case of the same time interval, each point in time corresponds to one datum. This is a trend prediction analysis method, which mainly analyzes past data to predict the trend of future data. However, time series analysis is mainly applied to statistical methods for dynamic data processing of electric power and power systems. If there is a big change in the outside world, it predicts based on data that have occurred in the past, and there is often a large deviation. As a general function approximator, a neural network [25] can approximate the modeling of arbitrary nonlinear objects with arbitrary precision. Although neural network technology has made great progress, there are still some difficult problems to solve, such as the difficulty in determining the number of hidden layer nodes in a neural network, the existence of learning phenomena, local minimum problems in the training process, etc.
In order to solve these problems, this paper proposes a hybrid algorithm for the forecasting of financial time series data based on DBSCAN and SVR to better predict financial data. Based on the OVDBSCAN algorithm for data clustering, SVR changes the principle of empirical risk minimization in traditional neural networks and proposes the principle of structural risk minimization, so it has good generalization ability.
3. Hybridizing OVDBSCAN with a Support Vector Regression Algorithm
This paper chooses a density-based parameter adaptive clustering algorithm and proposes an algorithm for hybridizing OVDBCSAN with SVR, referred to as an HOS algorithm. The algorithm is mainly designed for large data volumes, high signal-to-noise ratios, and inconspicuous features. First of all, OVDBSCAN is an improvement over the DBSCAN algorithm. It is an unsupervised algorithm, and the data can be classified without manual laborious marking. Second, the cluster after OVDBSCAN clustering can make the cluster into a highly cohesive state through a parameter setting, which is not only conducive to the proposed consistency of the cluster but also improves the antinoise. Finally, the nonlinear regression prediction is made with SVR. Therefore, the HOS algorithm is proposed to deal with the characteristics of a high signal-to-noise ratio, instability, and nonlinearity in financial time series. The overall structure of the algorithm is shown in Figure 1.
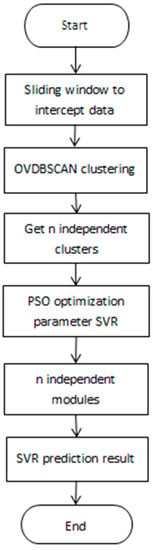
Figure 1.
“Hybridize Optimization Initial Points and Variable-Parameter Density-Based Spatial Clustering of Applications with Noise (OVDBSCAN) with support vector regression (SVR)” (HOS) structural process.
- The width of the sliding window is fixed. The data of n − 1 day are selected as the input data, and the data of the nth day as the output data, so that the data with a span of m years can be mined and studied. The format of the time series data intercepted by the sliding window is as follows, where I is the input sequence, O is the output sequence, x is the n − 1 input data on the nth day, and y is the output data on the nth day:
- There are two basic domain parameters in the OVDBSCAN algorithm: represents the distance threshold of a certain domain, and MinPts represents the number of sample points in the domain with radius First of all, select point p, find the distance of m points closest to point p, and calculate its average value. Then calculate the average distance of m nearest points from all points and store it in the distance_all of the structure. The average distance dataset of all points is clustered through DBSCAN to obtain cps clustering results, and the maximum value of the average distance point is obtained for each class i in cps. Then the distance between p and m closest to it is going to be of that kind of a point. The obtainedis clustered from small to large, and the smallest X is selected. MinPts remains unchanged, and DBSCAN clustering is performed on the dataset. Choose the second smallest until all are used. After clustering, n independent clusters A and their center points will be obtained.
- Model training of -SVR is carried out for n independent clusters A. Since the dataset is nonlinear, SVR introduces the kernel function to solve the nonlinear problem. The expression isThe radial basis function is used to select appropriate parameters, namely the penalty coefficient C, insensitive loss coefficient , and width coefficient , to train the cluster A model. The expression is as follows:
- Cluster , trained by model ε-SVR, is optimized for particle swarm optimization (PSO) parameters: can be set by past experience. Mean square error is obtained by k-fold cross validation:where is the predicted value of .
- After optimizing the parameters, the cluster that was optimized by the parameters is trained, and the model is obtained.
- The test data are matched with n cluster centers after clustering using the DBSCAN algorithm to find the most similar W cluster center and the model M corresponding to the W cluster.
- The predicted value of test data is calculated with the SVR of the corresponding model M. Complete dataset mining and regression analysis.
According to the subsequent experimental simulation and evaluation verification, compared to the traditional single methods (such as SVR’s and SOFM’s prediction of financial time series), HOS, the hybrid algorithm of OVDBSCAN and SVR proposed in this paper, can find a large number of similar classes and then establish a regression prediction model, which improves the accuracy of the prediction of stock prices and financial indexes.
3.1. DBSCAN Parameter Optimization
In the clustering algorithm, since k-means is sensitive to the initial point, it is often applied to the optimization of its initial point. Similarly, with DBSCAN [26,27], a clustering algorithm, people do not pay as much attention to the optimization of its initial point as k-means. However, through the research in this paper, it was found that the optimization of the initial point of the DBSCAN algorithm can improve the clustering effect to a certain extent. Inspired by some researchers’ initial point optimization of the k-means algorithm, this paper proposes an OVDBSCAN algorithm of initial point optimization and variable parameters to adapt to a density dataset of any shape and size changes.
The steps for initial point optimization are as follows:
- Find the distance of m points closest to P and average them. Find the average distance of m closest points from all points;
- The average distance dataset of m nearest points of all points is clustered through DBSCAN, and cps clustering results are obtained;
- Find the maximum value of the average distance point for each class i in cps;
- The distance between point P and the closest point m to it is the distance of this point.
The above method of finding ε at the initial point of optimization mainly deals with datasets of different densities. According to different densities, appropriate parameters are selected for clustering through optimization.
After the initial point optimization, DBSCAN clustering of variable parameters can be further carried out. The steps are as follows:
- The obtained in the above paper is sorted from small to large to start clustering;
- Select the smallest . MinPts remains unchanged. DBSCAN clustering is performed on the dataset;
- Select the second smallest. MinPts remains unchanged. Cluster the data marked as noise;
- Cycle through the above operations until all are used up and the clustering ends.
In the process of cyclic clustering, the value of is carried out from small to large. When is small, because the dataset is far away from and not clustered, the smaller value of can only cluster to the high-density point, but has no influence on the low-density data.
In the case of uneven data distribution, the DBSCAN algorithm may cluster high-density clusters into low-density clusters due to parameters, or may process elements in low-density clusters as noise. The parameter-adaptive OVDBSCAN algorithm can find clusters of any shape, and can effectively realize clustering of datasets with large density differences. The specific results are shown in the experiment in the fourth part of this paper.
3.2. PSO Optimization Parameters
A particle swarm optimization algorithm is an evolutionary computing technology whose idea is to find the optimal solution based on the collaboration between individuals in the group and the sharing of information [28].
3.2.1. Particle Swarm Optimization Principle
For each problem, the best solution is a bird in the search space, namely a “particle”, and the optimal solution is the “corn field” that the birds are looking for [29]. Each particle has a position vector and a velocity vector, and the adaptive value of the current position can be calculated according to the objective function, which can be understood as the distance from the “corn field”. The PSO is initialized as a group of random particles, and then the optimal solution is found by iteration. During the iteration, it completes self-renewal by tracking the “extreme value” (Pbest, Gbest). After tracing to the optimal value, the particle updates its speed and location based on the following two formulas:
where is the position of the current particle, is the velocity of the particle, and and are learning factors, usually with a value of 2. Rand () is a random number with a value between (0, 1).
3.2.2. PSO to Optimize
It can be seen from the above that has three parameters: ε can be set by previous experience. Therefore, the optimization of by PSO only needs to optimize c and γ. The fitness value is obtained by k-fold cross-validation to obtain the mean square error.
The optimization steps of the parameters are as follows: A set of (c, γ) is randomly generated as the initial value.
- Divide the training data into k parts: , , ..., ;
- Use the current (c,) for training, and obtain mean square error (MSE) by cross-validation;
- Initialize i, and let it equal 1;
- Use as the test dataset and the other as the training set;
- Calculate the MSE of the ith subset. Perform i = i + 1. Return to the fifth step until i = k + 1;
- Calculate the average value of k times of MSE;
- Select the average MSE value after k-fold cross-validation, and record the Pbest and Gbest of individuals and groups. Continue to find better (c, Repeat steps 2 through 8 until the set number of times is satisfied;
- End.
In summary, the main parameter of is (, c), where can be directly set to a certain constant, and and c can be obtained by PSO optimization parameters.
3.3. The Thought of the HOS Algorithm
The HOS algorithm not only has the clustering ability of OVDBSCAN, which can extract features, but also has the regression prediction ability of SVR. This allows data with similarities to be clustered, while noisy and nonstationary data are suppressed well. The idea of the HOS algorithm is that after the training data are clustered, they are divided into n clusters. Then each cluster is given to the SVR for training, and each cluster is trained to corresponding feature models to obtain n training. The model is then handed over to HOS for testing. The test data are calculated by OVDBSCAN to calculate the distance from the data point to the core point and then get the cluster with the shortest distance. The test data points are based on the model corresponding to the cluster for SVR regression prediction. The thought of HOS algorithm is shown in Figure 2.
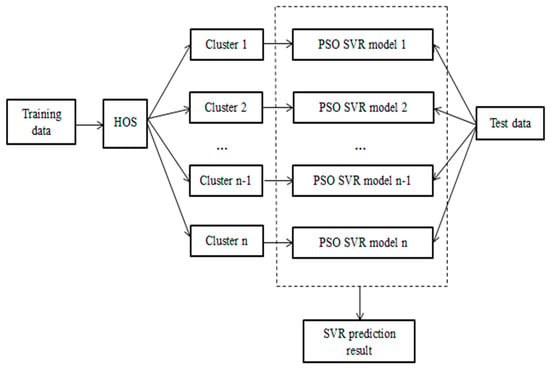
Figure 2.
The thought of HOS.
The hybrid algorithm proposed in this chapter clusters the data into multiple clusters, extracts the characteristics of each cluster, and makes the matching of these different features and test data to obtain the predicted result. According to the experimental needs, the system mainly has three functional modules:
- System interface module;
- Experimental introduction module. Explain the function of each module briefly;
- Experimental module for SVR model design. Implement various functions of SVR (dataset loading, parameter settings, regression demonstration).
The flow chart of the HOS algorithm is shown in Figure 3.
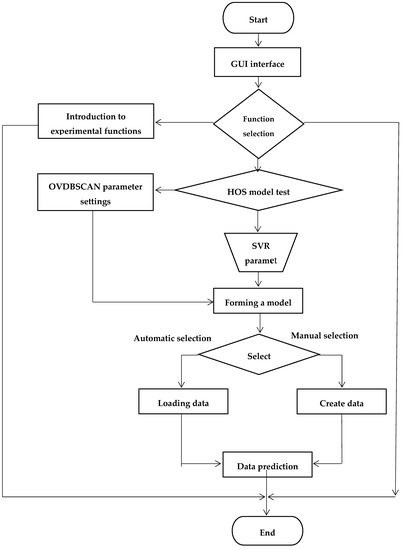
Figure 3.
HOS algorithm flow chart.
4. Research on Financial Time Series Predictions Based on HOS Algorithm
This experiment was conducted in Windows (CPU 2.10 GZ, memory 6 G). The operating system was Windows10. The test tool was MATLAB 2012. There were three experiments in this part. The first experiment was based on the algorithm optimization of the DBSCAN algorithm. It proved that the parameter adaptive algorithm OVDBSCAN had a better clustering effect on the data. The second experiment was based on the HOS algorithm for financial index prediction. It was found that the HOS algorithm was closer to the real value and had a stronger prediction ability. The third experiment was based on the HOS algorithm to predict the daily limit of a stock, which proved that the prediction result of the HOS algorithm was more accurate and can better guide people’s business behavior.
4.1. Optimization of Clustering Algorithm Based on DBSCAN Algorithm
This part proposed an OVDBSCAN algorithm for initial point optimization and variable parameters. It was verified through experiments that the OVDBSCAN algorithm could adapt to a density dataset of arbitrary shape and size.
4.1.1. Experimental Design
Three two-dimensional datasets were used for experiments. Dataset 1 was two different density clusters with noise data. Dataset 2 was three different clusters that all contained noise data. The first cluster had few data and had a higher density. The second cluster had a large amount of data and had a higher density. The third cluster had a small amount of data and had a low density. Dataset 3 had four clusters that contained noise but different densities.
Three dataset samples were clustered according to the OVDBSCAN algorithm. Inspired by [30], we found the average distance dis_means (7) of m = 7 points closest to point P. We found the average distance dis_allmeans () of all points. We performed DBSCAN clustering on dis_allmeans, where ε = 8, MinPts = 4. After the average distance through clustering, the maximum of 6 distances of the average distance point in each class was selected as the highest value of crane. The ε values of the three datasets were
- = 23.012816, = 78.175813;
- = 27.56658, = 80.039573, = 80.039673;
- = 40.1995502, = 83.743656;
In the above clustering process, MinPts was set to 4, and the effect of clustering on the three datasets is shown in Figure 4, Figure 5 and Figure 6.
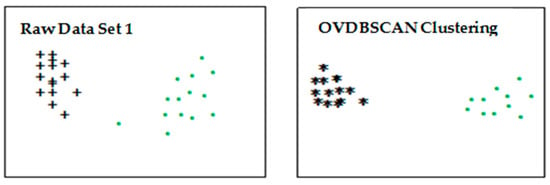
Figure 4.
Dataset 1 cluster process.
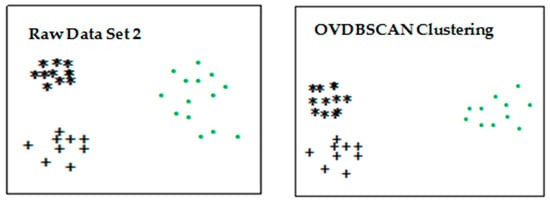
Figure 5.
Dataset 2 cluster process.
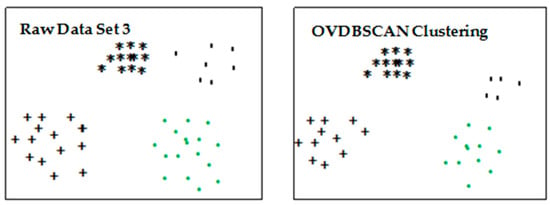
Figure 6.
Dataset 3 cluster process.
The clustering results in the figure above use different colors and shapes to distinguish different clusters. The results show that the improved DBSCAN algorithm implemented effective clustering for clusters with different densities.
In order to further illustrate the effect of the OVDBSCAN clustering algorithm, we used the data of dataset 1 to observe the influence on the clustering results by setting different ε values. See Figure 7.
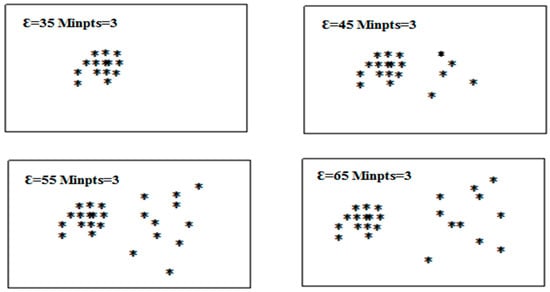
Figure 7.
The effect of change ε.
4.1.2. Experimental Results
It was known from the experimental results that the parameters had a great influence on the DBSCAN algorithm. When the parameters are not set properly, the clustering results have a certain deviation. In the case of uneven data distribution, the DBSCAN algorithm may cluster high-density clusters into low-density clusters due to parameters, or may process elements in low-density clusters as noise. The OVDBSCAN algorithm proposed in this paper can effectively achieve clustering of datasets with large density differences and can discover clusters of arbitrary shape. The idea is that different cluster densities are clustered using different ε based on the form of variable parameters. The experimental results showed that the OVDBSCAN algorithm was effective.
4.2. Financial Index Prediction Based on HOS Algorithm
4.2.1. Experimental Design
In order to verify the prediction effect of the HOS algorithm on a financial index, it was compared to the SVR algorithm and the SOFM-SVR algorithm prediction. The data obtained in this paper were data from Ping An Bank from 4 January 2013 to 31 December 2014, as experimental data. The experimental data are shown in Figure 8.
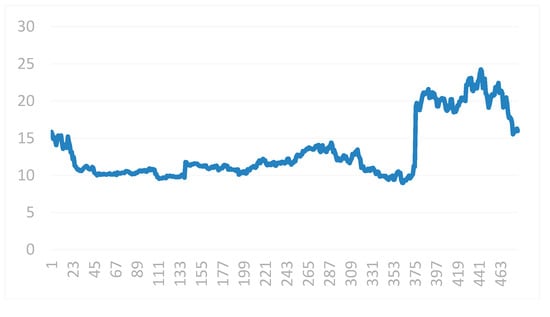
Figure 8.
Weighted index trend chart.
The data of these two years were divided into four groups to make the experimental results more concise and more convincing. The first 80% of each group of data were used as experimental data, and the last 20% were used as test data. The specific grouping situation is shown in Table 1.

Table 1.
Data grouping.
The financial data format downloaded from the above website is shown in Figure 9 below.
Figure 9.
Financial data format.
The (code, date, opening price, highest price, lowest price, closing price) will be described as In this paper, the data stream was processed by a sliding window with a window width of 4. The converted format was
As the predicted value, was the closing price of the next day. We represented the processed data as the volatility of the data. Since the range of fluctuations was the ratio of the previous day’s difference, the range of values was not large. Normalization of the original data was also unnecessary. This allowed for showing more internal connections between the data. Although the next day’s data trend was not directly linearly determined by the data of the day, it could be found through an analysis of the stock market in the past that there were still many higher repetition rates of the trend of the situation. Second, the trading situation of the day (such as the opening price and the highest price) is an important reference for investors, and directly affects investors’ investment behaviors (such as buying and selling). Therefore, it was very valuable to dig out the data of the day and analyze the market situation. The selection of financial index parameters by HOS is shown in Table 2 below.

Table 2.
The selection of parameters by HOS. PSO: Particle swarm optimization.
In order to test the predictive performance of the HOS algorithm, we used the mean absolute error (MAE), the mean square error (MSE), and the mean absolute percentage error (MAPE) [31,32].
The expression of MAE is
The expression of MSE is
The expression of MAPE is
represents the true value of each data. is the predicted value of the point, and n is the total number of data points. As with MSE and MAPE, if the value of MAE is smaller, the prediction accuracy is greater.
Using the above three indicators, the performance of the HOS algorithm on the four datasets of Ping An Bank through experiments is shown in Table 3 below.

Table 3.
Evaluation of algorithm index of HOS. MSE: Mean square error; MAE: Mean absolute error; MAPE: Mean absolute percentage error.
The performance of data evaluations using SVR and SOFM-SVR algorithms alone had given clear answers in the literature [33], and their performances are shown in Table 4 and Table 5.

Table 4.
Evaluation of algorithm index of SVR.

Table 5.
Evaluation of algorithm index of SOFM-SVR.
4.2.2. Experimental Results
Through a comparison of the above three methods, the performances of the HOS algorithm, SVR algorithm, and SOFM-SVR algorithm on MAPE, MAE, and MSE were found. The HOS algorithm performed best. The HOS algorithm predicted that the algorithm was closer to the real value than the latter two algorithms and had stronger prediction ability.
4.3. Prediction of the Next-Day Trading Limit of a Stock Based on the HOS Algorithm
4.3.1. Experimental Design
In the previous paper, through the experimental verification of the proposed hybrid algorithm, it was found that the HOS algorithm had a good prediction effect on the prediction of the financial index. In this section, the verified algorithm was used to analyze the trading price of a stock on that day and predict the next day’s closing price. This article did not output all the predicted results, only those that exceeded the rise and the code number of stocks that continued to rise.
The data obtained in this paper were 1000 data listed on the Shanghai Stock Exchange and 1000 data on the Shenzhen Stock Exchange. The total number of time series was 2000 × 485, which was 970,000. The time span was from 4 January 2013 to 31 December 2014. In order to make the experimental results have a clear contrast and to make the prediction more convincing, the experimental data were divided into two parts, as shown in Table 6.

Table 6.
Data grouping.
The original format of the data is shown in Figure 10.
Figure 10.
Original data format.
That is, , and the processing format is as follows:
The mean (n − 4, n) represents the average of the closing prices (close) for the five days from the n − 4 to the nth day. Thus, the original data format is transformed into code=(date, change(i − 5, i − 6), change(i − 4, i − 6), change(i − 3, i − 6), change(i − 2, i − 6), change(i − 1, i − 2) close(i − 1, i − 2), close(i, i − 1), close(i + 1, i), close(i + 1, i)) after processing the original data in the following manner. Change (i − 5, i − 6) is the comparison between the increase of the i − 5 daily average and the increase of the i − 6 daily average, and close(i − 1, i − 2) is the comparison between the increase of the closing price on the i − 1 day and the increase of the closing price on the i − 2 day.
The purpose of doing this with raw data was to better reflect trends in share prices and recent days of trading in huge numbers of stocks. Investors tend to be concerned about a stock’s trading in the last few days and make a judgment of the day’s investing behavior based on recent trading trends. From the final experimental results, it could be found that such data processing was effective and meaningful.
The parameter settings for stock forecasting are shown in Table 2 above. All next-day gains are shown in Figure 11, Figure 12 and Figure 13 (regardless of whether the day was up or down): All the first days of the days, the daily increase of the daily limit (the daily limit of the day when the daily limit was not updated would record the data of the next day’s gain), and the next day’s increase in the HOS forecast (that is, after the intervention of the HOS algorithm, all the output prompts were recorded as the next day’s increase data).
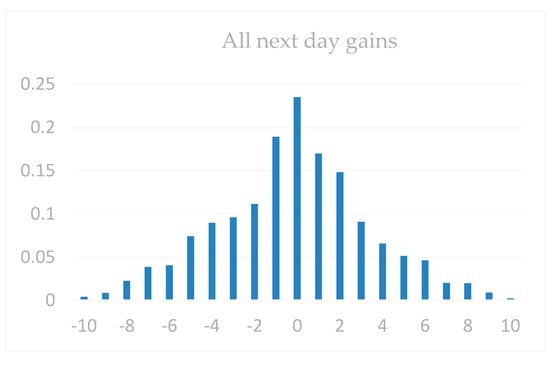
Figure 11.
Comparison of the next day’s rise in the days of dataset 1.
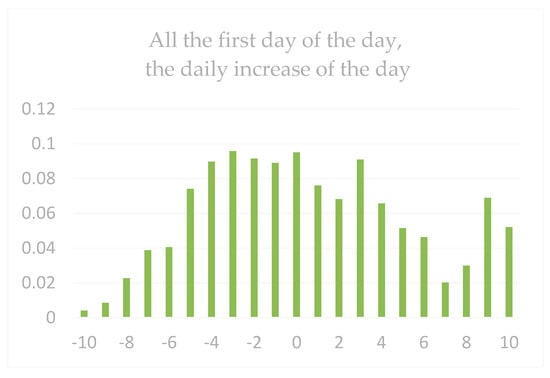
Figure 12.
Comparison of the day’s first rise in the days of dataset 1.
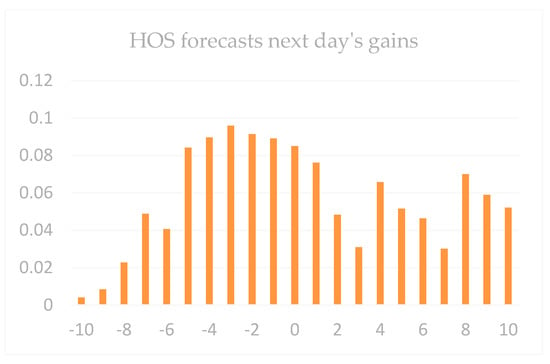
Figure 13.
Comparison of the day’s rise in the days of dataset 1.
It can be seen from the figure that in all the next day’s gains, the gain density around 0 was higher. Therefore, it was really difficult for average investors to observe the massive financial data and draw corresponding forecasts. Because of the whole process of the increase, the market showed a relatively stable state. Therefore, only by scientifically and effectively researching these data could we discover the laws. It could be found from the increase in the first daily limit of the first day of the day that it was still the highest concentration of the increase in 0 and spread to both ends, especially for the next day. Because the daily limit of the day is an important reference for investors, this directly affects the investor’s investment trend the next day.
In order to have a digital comparison of the chart, the next day’s increases in the three cases of dataset 1 are shown in Table 7 below.

Table 7.
The contrast of the next day.
From the above table, we can see that the increase was higher than 3 and had a higher ratio than the first daily limit. On one hand, dataset 1 was caused by low market volume. On the other hand, this algorithm needs to be improved in data applications.
As shown in Figure 14, Figure 15 and Figure 16, it can be found from the morphological comparison chart of dataset 2 that the HOS algorithm proposed in this paper had its advantages in predicting the next-day trading limit of stocks. From its distribution graph, it could be found that it was not concentrated near a certain point, and the proportion of increases below −5 was negligible. The overall distribution moved up significantly. For a better data comparison, see Table 8.
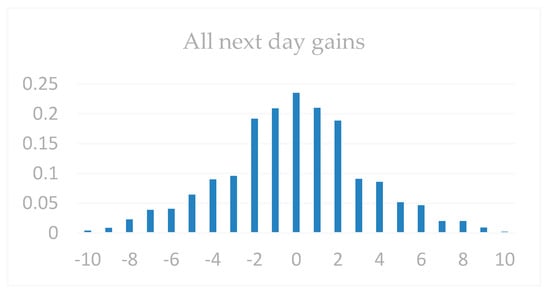
Figure 14.
Comparison of the next day’s rise in the days of dataset 2.
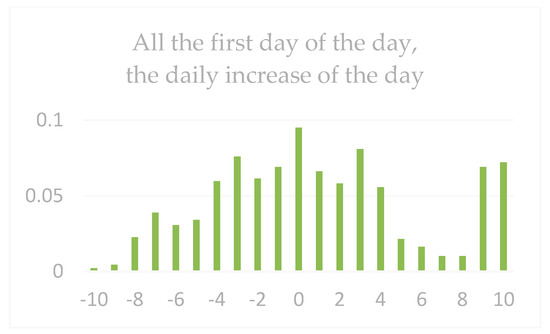
Figure 15.
Comparison of the day’s “the first rise in the day” of dataset 2.
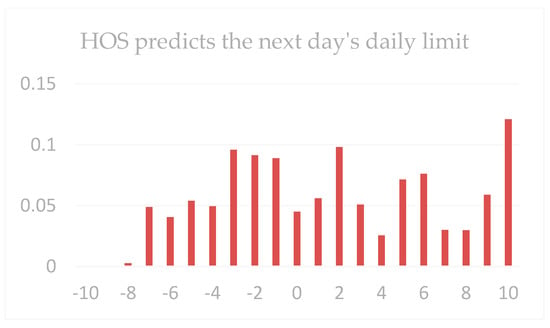
Figure 16.
Comparison of the day’s rise in the days of dataset 2.

Table 8.
The contrast of the next day.
4.3.2. Experimental Results
The analysis of the two datasets through the above experiments showed that the HOS algorithm had obvious advantages over other prediction methods in the prediction results of the next day’s increase in a stock’s daily limit.
4.4. Stock Price Predicting Based on HOS Algorithm
4.4.1. Experimental Design
For stock price predicting, the data used in this paper came from the listed stock data of Minsheng Bank (stock code sh600016) and China Unicom (stock code sh600050) of the Shanghai Stock Exchange. The interception period was from 4 January 2013 to 31 December 2014. The first 80% of the data were used as the training set, and the rest were used as the test set. The data were divided as shown in Table 9.

Table 9.
Data time division.
The format of the stock data downloaded from the website was (stock code, trading time, opening price, maximum amount, minimum amount, closing price, price change), and its format is as shown in Figure 17.
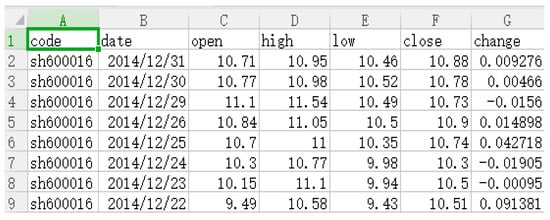
Figure 17.
Stock data format.
The table can be described as follows. We normalized the data to be transformed between [0, 1]. Here we used the linear normalization method, and the conversion method is as follows:
X is the raw data.represents the maximum value in the dataset. is the minimum value. The parameter settings are the same as in Table 2. In order to test the predictive performance of the HOS algorithm, we used MSE and MAPE to evaluate the evaluation index. Through the regression analysis and prediction of the stock prices of the two companies, it could be found that the HOS algorithm had a small prediction error in the data. In order to see the effect more intuitively, the actual value and predicted value of the test set data are shown here in Figure 18 and Figure 19.
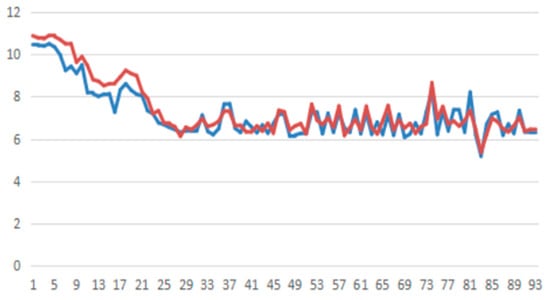
Figure 18.
Forecasting value of the test set of Minsheng Bank ( actual value
actual value  predicted value).
predicted value).
 actual value
actual value  predicted value).
predicted value).
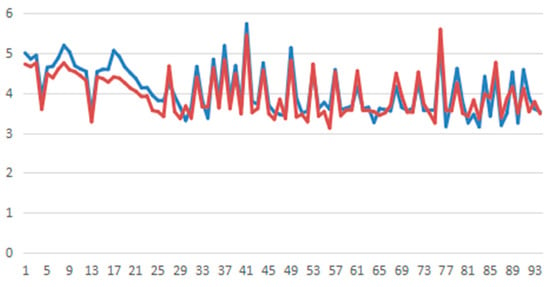
Figure 19.
Forecasting value of the test set of Chine Unicom ( actual value
actual value  predicted value).
predicted value).
 actual value
actual value  predicted value).
predicted value).
4.4.2. Experimental Results
It could be found that the HOS algorithm forecasted the stock price more accurately. This has a great reference value for investors, and the HOS algorithm can better guide people’s economic behavior.
5. Conclusions
In this paper, we proposed a new hybrid algorithm for the forecasting of financial time series based on DBSCAN and SVR. OVDBSCAN optimizes the global invariability of parameters and realizes parameter adaptation. This provides direction for good clustering of datasets of different densities. HOS is able to establish regression prediction models by finding a large number of similar classes, which improves the accuracy of the financial index and stock next-day trading limit predictions. The experimental results confirmed the effectiveness and robustness of the proposed algorithm. However, the running time of the HOS algorithm compared to traditional SVR and SOFM algorithms is much larger than the latter two algorithms. Therefore, our future direction is to improve the ability of processing the data. We will consider not loading all data into the model, but rather selecting the data in the form of random sampling. Judging from the evaluation indexes, the accuracy of the HOS algorithm prediction still has a lot of room for improvement.
Author Contributions
M.H. and Q.B. conceived and designed the algorithm. W.F. analyzed the dataset. Q.B. and Y.Z. designed, performed, and analyzed the experiments. All authors read and approved the final manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant #: 61462022 and Grant #61662019), the Major Science and Technology Project of Hainan province (Grant #: ZDKJ2016015), the Natural Science Foundation of Hainan province (Grant #:617062), and the Higher Education Reform Key Project of Hainan province (Hnjg2017ZD-1).
Acknowledgments
The authors would like to express their great gratitude to the anonymous reviews that helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dablemont, S.; Verleysen, M.; Van Bellegem, S. Modelling and Forecasting financial time series of “tick data”. Forecast. Financ. Mark. 2007, 5, 64–105. [Google Scholar]
- Washio, T.; Shinnou, Y.; Yada, K.; Motoda, H.; Okada, T. Analysis on a Relation Between Enterprise Profit and Financial State by Using Data Mining Techniques. In New Frontiers in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yan, L.J. The present situation and future development trend of financial supervision in China. Cina Mark. 2010, 35, 44. [Google Scholar]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recogn. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Rubin, G.D.; Patel, B.N. Financial Forecasting and Stochastic Modeling: Predicting the Impact of Business Decisions. Radiology 2017, 283, 342. [Google Scholar] [CrossRef] [PubMed]
- Qadri, M.; Ahmad, Z.; Ibrahim, J. Potential Use of Data Mining Techniques in Information Technology Consulting Operations. Int. J. Sci. Res. Publ. 2015, 5, 1–4. [Google Scholar]
- Xu, Y.; Ji, G.; Zhang, S. Research and application of chaotic time series prediction based on Empirical Mode Decomposition. In Proceedings of the IEEE Fifth International Conference on Advanced Computational Intelligence, Nanjing, China, 18–20 October 2012. [Google Scholar]
- Ertöz, L.; Steinbach, M.; Kumar, V. Fiding Clusters of Different Sizes, Shapes, and Densities in Noise, High Dimensional Data; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Li, L.H.; Tian, X.; Yang, H.D. Financial time series prediction based on SVR. Comput. Eng. Appl. 2005, 41, 221–224. [Google Scholar]
- Fu, Z.Q.; Wang, X.F. The DBSCAN algorithm based on variable parameters. Netw. Secur. Technol. Appl. 2018, 8, 34–36. [Google Scholar]
- Li, L.; Xu, S.; An, X.; Zhang, L.D. A Novel Approach to NIR Spectral Quantitative Analysis: Semi-Supervised Least-Squares Support Vector Regression Machine. Spectrosc. Spectr. Anal. 2011, 31, 2702–2705. [Google Scholar]
- Agrawal, R.; Faloutsos, C.; Swami, A. Efficient similarity search in sequence database. In Proceedings of the 4th International Conference on Foundations of Data Organization and Algorithms, Chicago, IL, USA, 13–15 October 1993; Springer: London, UK, 1993; pp. 69–848. [Google Scholar]
- Park, J.; Sriram, T.N. Robust estimation of conditional variance of time series using density power divergences. J. Forecast. 2017, 36, 703–717. [Google Scholar] [CrossRef]
- Rojas, I.; Pomares, H. Time Series Analysis and Forecasting; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Das, G.; Lin, k.; Mannila, H.; Renganathan, G.; Smyth, P. Rule discovery from time series. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998. [Google Scholar]
- Hsu, S.H.; Hsieh, P.A.; Chih, T.C.; Hsu, K.C. A two-stage architecture for stock price forecasting by integrating self-organizing map and support vector regression. Expert Syst. Appl. 2009, 36, 7947–7951. [Google Scholar] [CrossRef]
- Huang, C.L.; Tsai, C.Y. A hybrid SOFM-SVR with a filter-based feature selection for stock market forecasting. Expert Syst. Appl. 2009, 36, 1529–1539. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Folkes, S.R.; Lahav, O.; Maddox, S.J. An artificial neural network approach to the classification of galaxy spectra. Mon. Not. R. Astron. Soc. 2018, 283, 651–665. [Google Scholar] [CrossRef]
- Tang, J.H. A review on the nonlinear time series model of regularly sampled data. Math. Progress 1989, 18, 22–43. [Google Scholar]
- Xiong, Z.F. Wavelet Method for Fractal Dimension Estimation of Financial Time Series. Syst. Eng. Theory Pract. 2002, 22, 48–53. [Google Scholar]
- Xu, M.; Huang, C. Financial Benefit Analysis and Forecast Based on Symbolic Time Series Method. CMS 2011, 19, 1–9. [Google Scholar]
- Li, B.; Zhang, J.P.; Liu, X.J. Time-series Detection of Uncertain Anomalies Based on Hadoop. Chin. J. Sens. Actuators 2015, 7, 1066–1072. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control. J. Time 2010, 31, 303. [Google Scholar]
- Xi, L.; Muzhou, H.; Lee, M.H.; Li, J.; Wei, D.; Hai, H.; Wu, Y. A new constructive neural network method for noise processing and its application on stock market prediction. Appl. Soft Comput. 2014, 15, 57–66. [Google Scholar] [CrossRef]
- Kumar, K.M.; Reddy, A.R.M. A fast DBSCAN clustering algorithm by accelerating neighbor searching using Groups method. Pattern Recognit. 2016, 58, 39–48. [Google Scholar] [CrossRef]
- Limwattanapibool, O.; Arch-Int, S. Determination of the appropriate parameters for K-means clustering using selection of region clusters based on density DBSCAN (SRCD-DBSCAN). Expert Syst. 2017, 34, e12204. [Google Scholar] [CrossRef]
- Wang, F.S.; Chen, L.H. Particle Swarm Optimization (PSO); Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Gou, J.; Lei, Y.X.; Guo, W.P.; Wang, C.; Cai, Y.Q.; Luo, W. A novel improved particle swarm optimization algorithm based on individual difference evolution. Appl. Soft Comput. 2017, 57, 468–481. [Google Scholar] [CrossRef]
- Shah, G.H. An improved DBSCAN, a density based clustering algorithm with parameter selection for high dimensional data sets. In Proceedings of the Nirma University International Conference on Engineering, Ahmedabad, India, 28–30 November 2013. [Google Scholar]
- Wei, W.; Jiang, J.; Liang, H.; Gao, L.; Liang, B.; Huang, J.; Zang, N.; Liao, Y.; Yu, J.; Lai, J.; et al. Application of a Combined Model with Autoregressive Integrated Moving Average (ARIMA) and Generalized Regression Neural Network (GRNN) in Forecasting Hepatitis Incidence in Heng County, China. PLoS ONE 2016, 11, e0156768. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Cai, Y.; Wu, Y.; Zhong, R.; Li, Q.; Zheng, J.; Lin, D.; Li, Y. Time series analysis of weekly influenza-like illness rate using a one-year period of factors in random forest regression. BioSci. Trends 2017, 11, 292–296. [Google Scholar] [CrossRef] [PubMed]
- Lodwick, W.A.; Jamison, K.D. A computational method for fuzzy optimization. In Uncertainty Analysis in Engineering and Sciences: Fuzzy Logic, Statistics and Neural Network Approach; Avvub, B.M., Guota, M.M., Eds.; Kluwer Academic Publisher: Boston, MA, USA, 1998. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).