Novel Parameterized Utility Function on Dual Hesitant Fuzzy Rough Sets and Its Application in Pattern Recognition
Abstract
:1. Introduction
2. Preliminaries
2.1. The Notion of DHFS
2.2. The Notion of DHFRS
3. Main Results
3.1. Analysis on DHFRSs
3.2. A Kind of Novel Utility Function on DHFRSs
- (i)
- (ii)
- ;
- (iii)
- ;
- (iv)
- ;
- (v)
- ,
3.3. Novel Dual Hesitant Fuzzy Rough Pattern Recognition Method
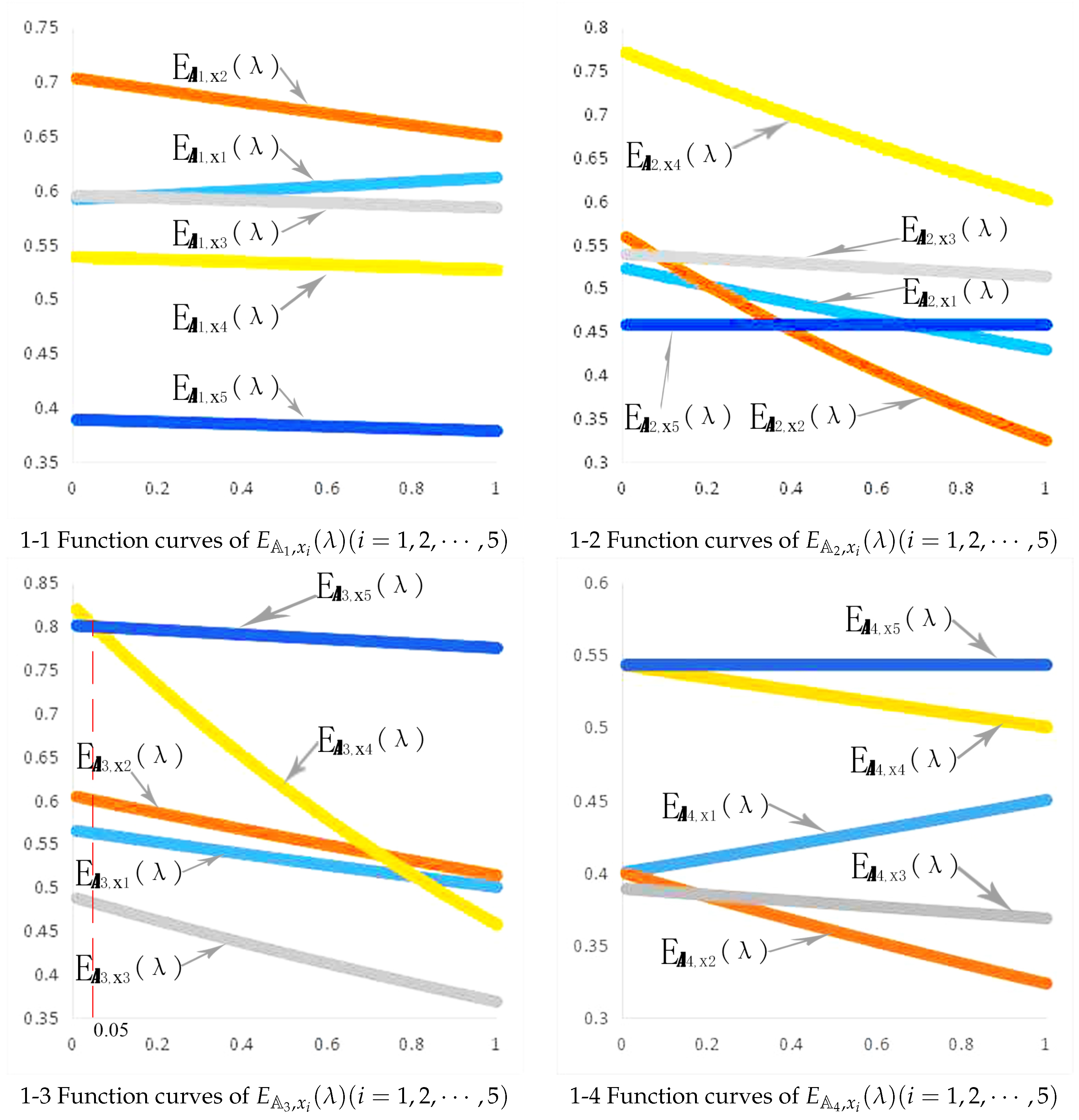
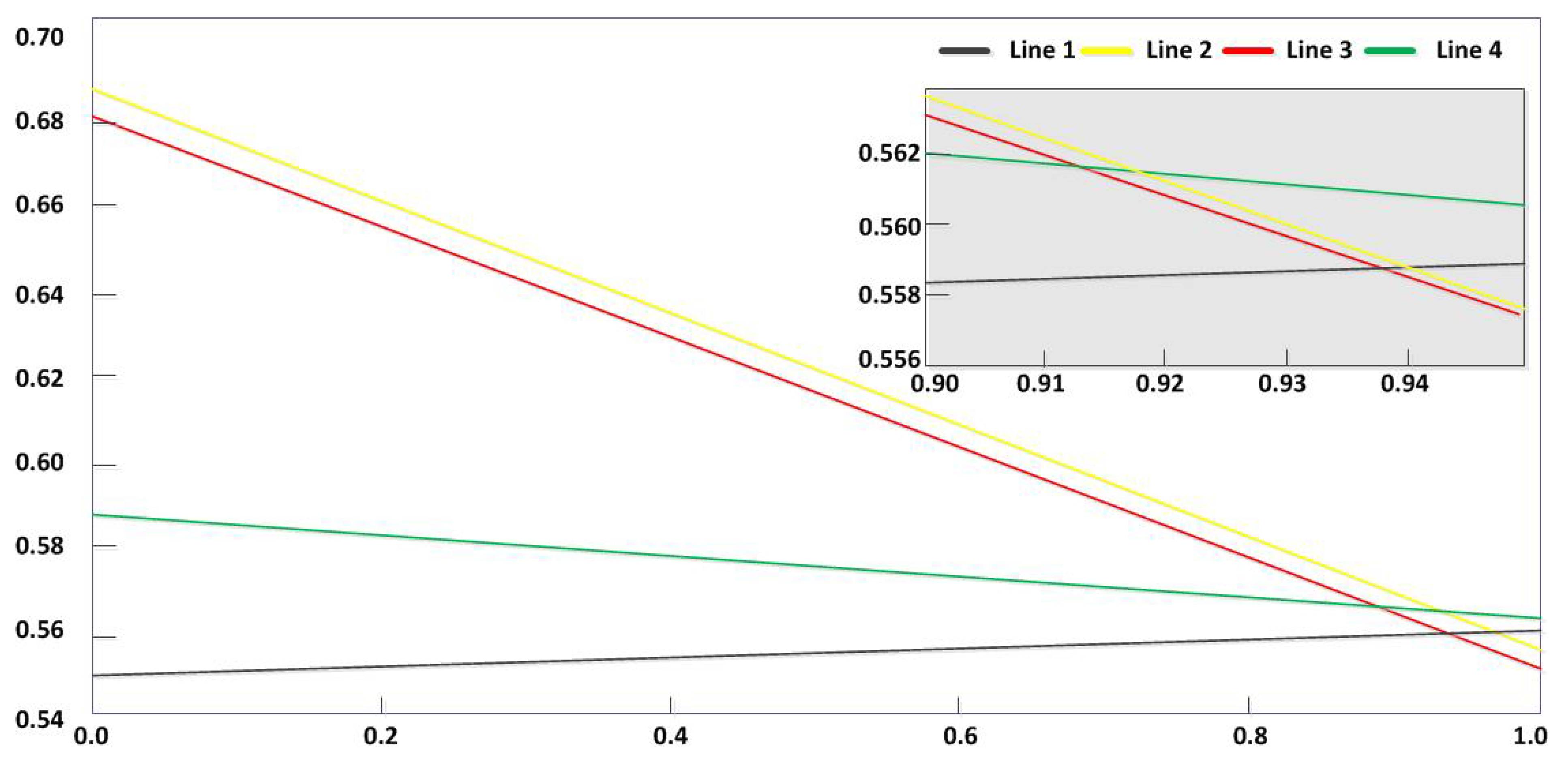
4. Illustrative Examples
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 18th IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S.; Xia, M.M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 1–13. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Miyamoto, S. Multisets and Fuzzy Multisets. Soft Computing and Human-Centered Machines; Springer: Tokyo, Japan, 2000; pp. 9–33. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way decisions with probabilistic rough sets. Inf. Sci. 2010, 180, 341–353. [Google Scholar] [CrossRef]
- Ma, W.M.; Sun, B.Z. Probabilistic rough set over two universes and rough entropy. Int. J. Approx. Reason. 2012, 53, 608–619. [Google Scholar] [CrossRef]
- Sun, B.Z.; Ma, W.M.; Liu, Q. An approach to decision making based on intuitionistic fuzzy rough sets over two universes. J. Oper. Res. Soc. 2013, 64, 1079–1089. [Google Scholar] [CrossRef]
- Yan, R.X.; Zheng, J.G.; Liu, J.L.; Zhai, Y.M. Research on the model of rough set over dual-universes. Knowl. Based Syst. 2010, 23, 817–822. [Google Scholar] [CrossRef]
- Yang, H.L.; Li, S.G.; Wang, S.Y.; Wang, J. Bipolar fuzzy rough set model on two different universes and its application. Knowl. Based Syst. 2012, 35, 94–101. [Google Scholar] [CrossRef]
- Yang, H.L.; Li, S.G.; Guo, Z.L.; Ma, C.H. Transformation of bipolar fuzzy rough set models. Knowl. Based Syst. 2012, 27, 60–68. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 1990, 17, 191–209. [Google Scholar] [CrossRef]
- Radzikowska, A.M.; Kerre, E.E. A comparative study of fuzzy rough sets. Fuzzy Sets Syst. 2002, 126, 137–155. [Google Scholar] [CrossRef]
- Dai, J.H.; Tian, H.W. Fuzzy rough set model for set-valued data. Fuzzy Sets Syst. 2013, 229, 54–68. [Google Scholar] [CrossRef]
- Tiwari, S.P.; Srivastava, A.K. Fuzzy rough sets, fuzzy preorders and fuzzy topologies. Fuzzy Sets Syst. 2013, 210, 63–68. [Google Scholar] [CrossRef]
- Yang, X.B.; Song, X.N.; Qi, Y.S.; Yang, J.Y. Constructive and axiomatic approaches to hesitant fuzzy rough set. Soft Comput. 2014, 18, 1067–1077. [Google Scholar] [CrossRef]
- Zhang, H.; Shu, L.; Liao, S.; Xiawu, C. Dual hesitant fuzzy rough set and its application. Soft Comput. 2015, 21, 3287–3305. [Google Scholar] [CrossRef]
- Zhang, H.D.; Shu, L. Generalized interval-valued fuzzy rough set and its application in decision making. Int. J. Fuzzy Syst. 2015, 17, 279–291. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamucar, D. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Vasiljevic, M.; Fazlollahtabar, H.; Stevic, Z.; Veskovic, S. A rough multicriteria approach for evaluation of supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar] [CrossRef]
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar] [CrossRef]
- Pamucar, D.; Bozanic, D.; Lukovac, V.; Komazec, N. Normalized weighted geometric bonferroni mean operator of interval rough numbers—application in interval rough DEMATEL-COPRAS. Mech. Eng. 2018, 16, 171–191. [Google Scholar] [CrossRef]
- Pamucar, D.; Stevic, Z.; Zavadskas, E.K. Integration of interval rough AHP and interval rough MABAC methods for evaluating university web pages. Appl. Soft Comput. 2018, 67, 141–163. [Google Scholar] [CrossRef]
- Pamucar, D.; Petrovic, I.; Cirovic, G. Modification of the Best–Worst and MABAC methods: A novel approach based on interval-valued fuzzy-rough numbers. Expert Syst. Appl. 2018, 91, 89–106. [Google Scholar] [CrossRef]
- Zhang, F.W. Several Kinds of Uncertain Multi-Attribute Decision-Making Methods and Their Application in Transportation Management; People’s Communication Press: Beijing, China, 2016. [Google Scholar]
- Mukhametzyanov, I.; Pamucar, D. A sensitivity analysis in MCDM problems: A statistical approach. Decis. Mak. Appl. Manag. Eng. 2018, 1, 51–80. [Google Scholar] [CrossRef]
- Zhang, F.W.; Xu, S.H. Multiple attribute group decision making method based on utility theory under interval-valued intuitionistic fuzzy environment. Group Decis. Negotiat. 2016, 25, 1261–1275. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. An intuitionistic fuzzy set based approach to intelligent data analysis: An application to medical diagnosis. In Recent Advances in Intelligent Paradigms and and Applications; Springer: New Tork, NY, USA, 2002; pp. 57–70. [Google Scholar]
- Tian, H.; Li, J.R.; Zhang, F.W.; Xu, Y.J.; Cui, C.H.; Deng, Y.J.; Xiao, S.J. Entropy analysis on intuitionistic fuzzy sets and interval-valued intuitionistic fuzzy sets and its applications in mode assessment on open communities. J. Adv. Comput. Intell. Intell. Inform. 2018, 22, 147–155. [Google Scholar] [CrossRef]
- Cao, Z.; Jiang, S.; Zhang, J.; Guo, H. A unified framework for vehicle rerouting and traffic light control to reduce traffic congestion. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1958–1973. [Google Scholar] [CrossRef]
- Cao, Z.; Guo, H.; Zhang, J.; Niyato, D.; Fastenrath, U. Finding the shortest path in stochastic vehicle routing: A cardinality minimization approach. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1688–1702. [Google Scholar] [CrossRef]
- Cao, Z.; Guo, H.; Zhang, J. A multiagent-based approach for vehicle routing by considering both arriving on time and total travel time. ACM Trans. Intell. Syst. Technol. 2018, 18, 25. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Y.; Rao, A.; Klanner, F.; Erschen, S.; Chen, W.; Zhang, L.; Guo, H. An accurate solution to the cardinality-based punctuality problem. IEEE Intell. Transp. Syst. Mag. 2018. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Dual hesitant Pythagorean fuzzy Hamacher aggregation operators in multiple attribute decision making. Arch. Control Sci. 2017, 27, 365–395. [Google Scholar] [CrossRef]
| (0.4,0.0) | (0.7,0.0) | (0.3,0.3) | (0.1,0.7) | (0.1,0.8) | |
| (0.3,0.5) | (0.2,0.6) | (0.6,0.1) | (0.2,0.4) | (0.0,0.8) | |
| (0.1,0.7) | (0.0,0.9) | (0.2,0.7) | (0.8,0.0) | (0.2,0.8) | |
| (0.4,0.3) | (0.7,0.0) | (0.2,0.6) | (0.2,0.7) | (0.2,0.8) | |
| (0.1,0.7) | (0.1,0.8) | (0.1,0.9) | (0.2,0.7) | (0.8,0.1) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, F.; Sun, J.; Wang, W.; Tang, X. Novel Parameterized Utility Function on Dual Hesitant Fuzzy Rough Sets and Its Application in Pattern Recognition. Information 2019, 10, 71. https://doi.org/10.3390/info10020071
Wu Z, Zhang F, Sun J, Wang W, Tang X. Novel Parameterized Utility Function on Dual Hesitant Fuzzy Rough Sets and Its Application in Pattern Recognition. Information. 2019; 10(2):71. https://doi.org/10.3390/info10020071
Chicago/Turabian StyleWu, Zhongjun, Fangwei Zhang, Jing Sun, Wenjing Wang, and Xufeng Tang. 2019. "Novel Parameterized Utility Function on Dual Hesitant Fuzzy Rough Sets and Its Application in Pattern Recognition" Information 10, no. 2: 71. https://doi.org/10.3390/info10020071
APA StyleWu, Z., Zhang, F., Sun, J., Wang, W., & Tang, X. (2019). Novel Parameterized Utility Function on Dual Hesitant Fuzzy Rough Sets and Its Application in Pattern Recognition. Information, 10(2), 71. https://doi.org/10.3390/info10020071





