Performance Analysis of Hybrid Protocol Based AF EH Relaying over Asymmetric Fading Channels
Abstract
:1. Introduction
- Different from the existing works [21,22,23] with a focus on the outage performance of a hybrid protocol over symmetric fading channels, we consider a more practical asymmetric fading channels, where the source-relay and relay-destination links experience Rician fading and Rayleigh fading, respectively. In particular, we derive the expressions for the bound of outage probability and outage capacity based on the high SNR approximation and the Gaussian-Chebyshev quadrature.
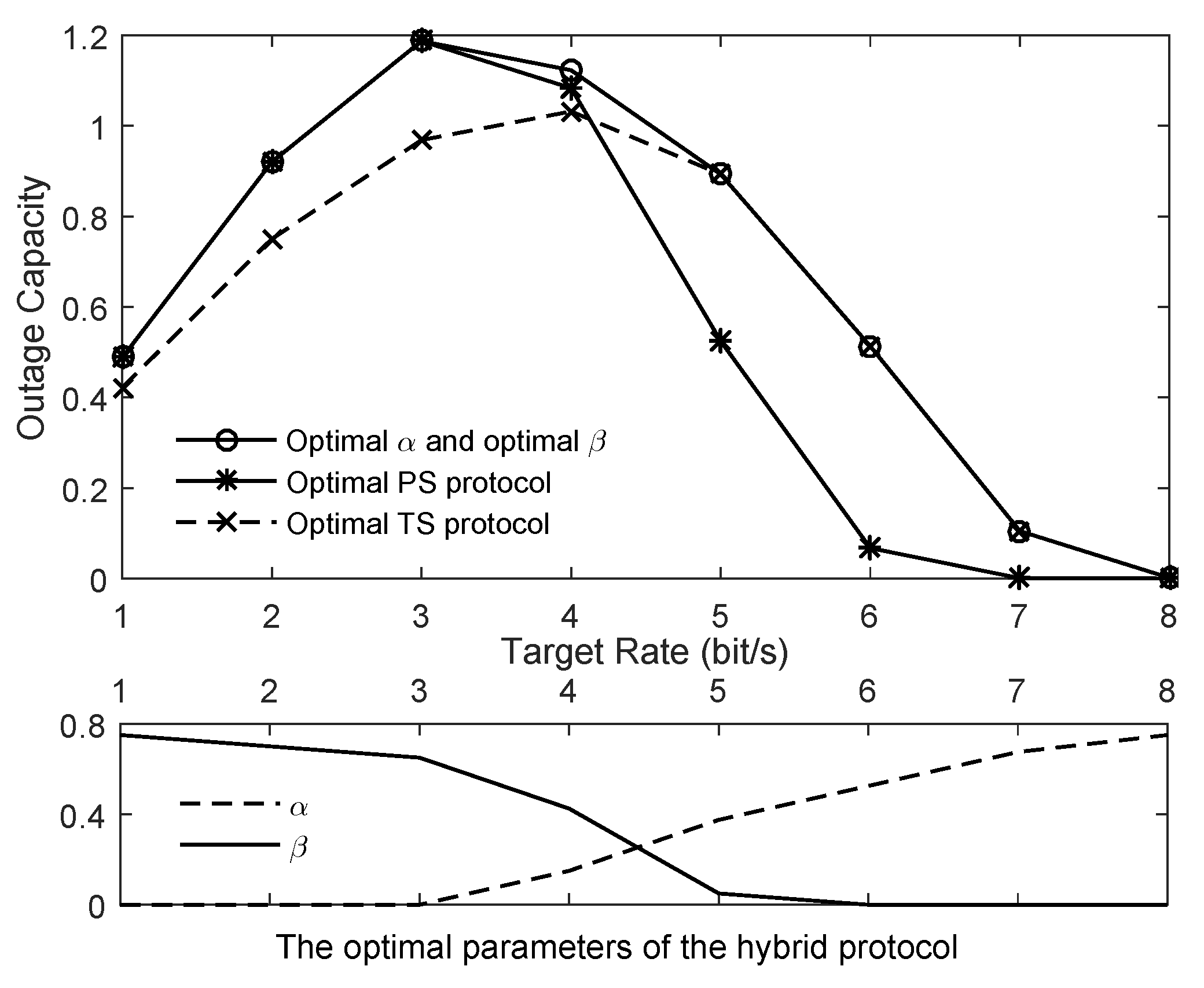
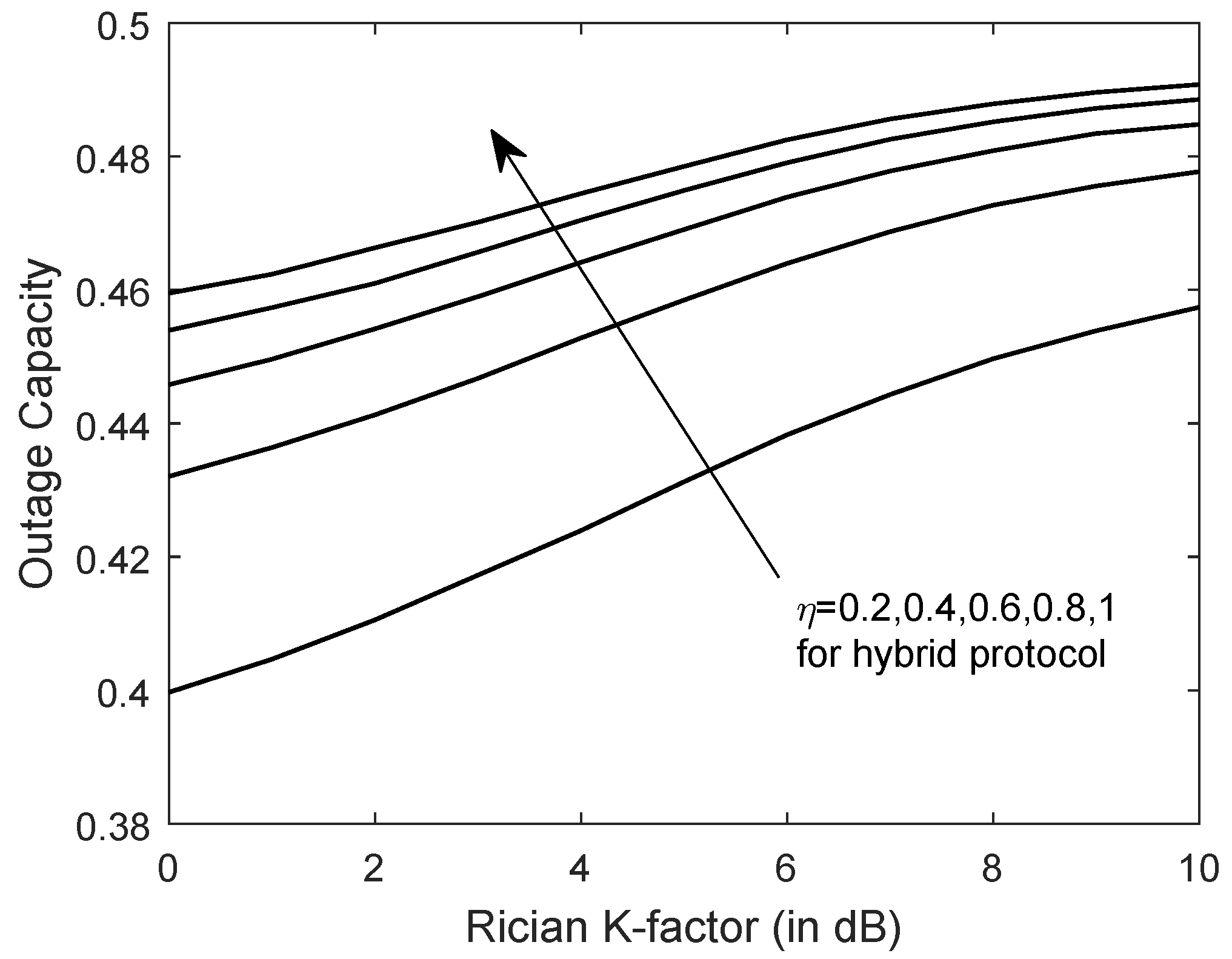
- Numerical results are presented to verify the derived expression, and study the impacts of various network parameters on the outage capacity of hybrid protocol based relay networks. This provides some insights in selecting the parameters of hybrid protocol, i.e., TS and PS ratios, under different relay network settings. It can also be revealed that the parameters of hybrid protocol have a significant impact on the outage capacity, and that a larger Rician factor achieves a higher outage capacity. Besides, we compare the outage capacity achieved by the hybrid protocol, PS protocol and TS protocol. It is shown that the hybrid protocol can be reduced to the PS or TS mode at some system settings so as to reduce the cost of complexity while maintaining the required outage capacity.
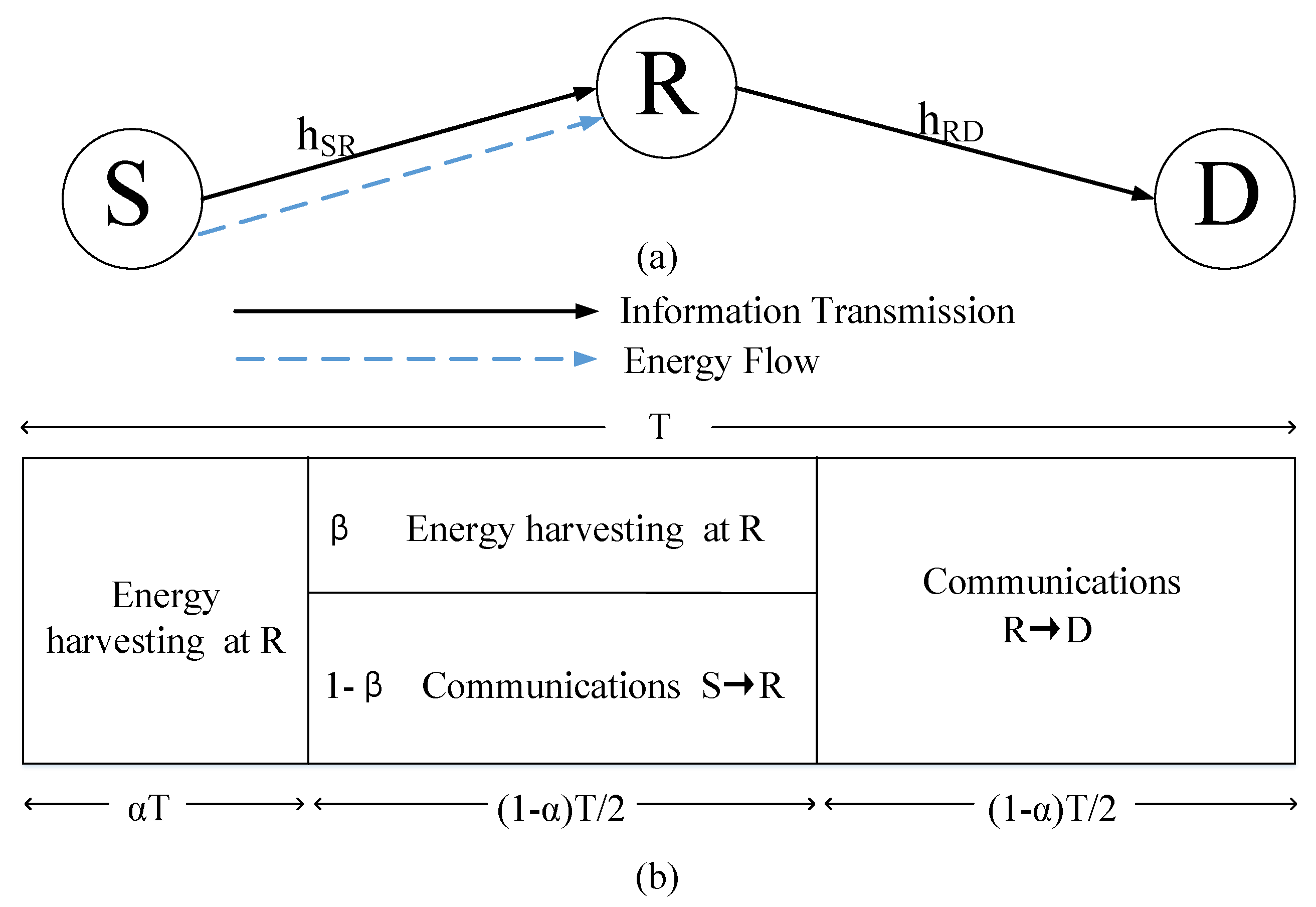
2. System Model and Working Flow
2.1. System Model
2.2. Analytical Model
2.2.1. Source-Relay Transmission
2.2.2. Relay-Destination Transmission
3. Outage Performance
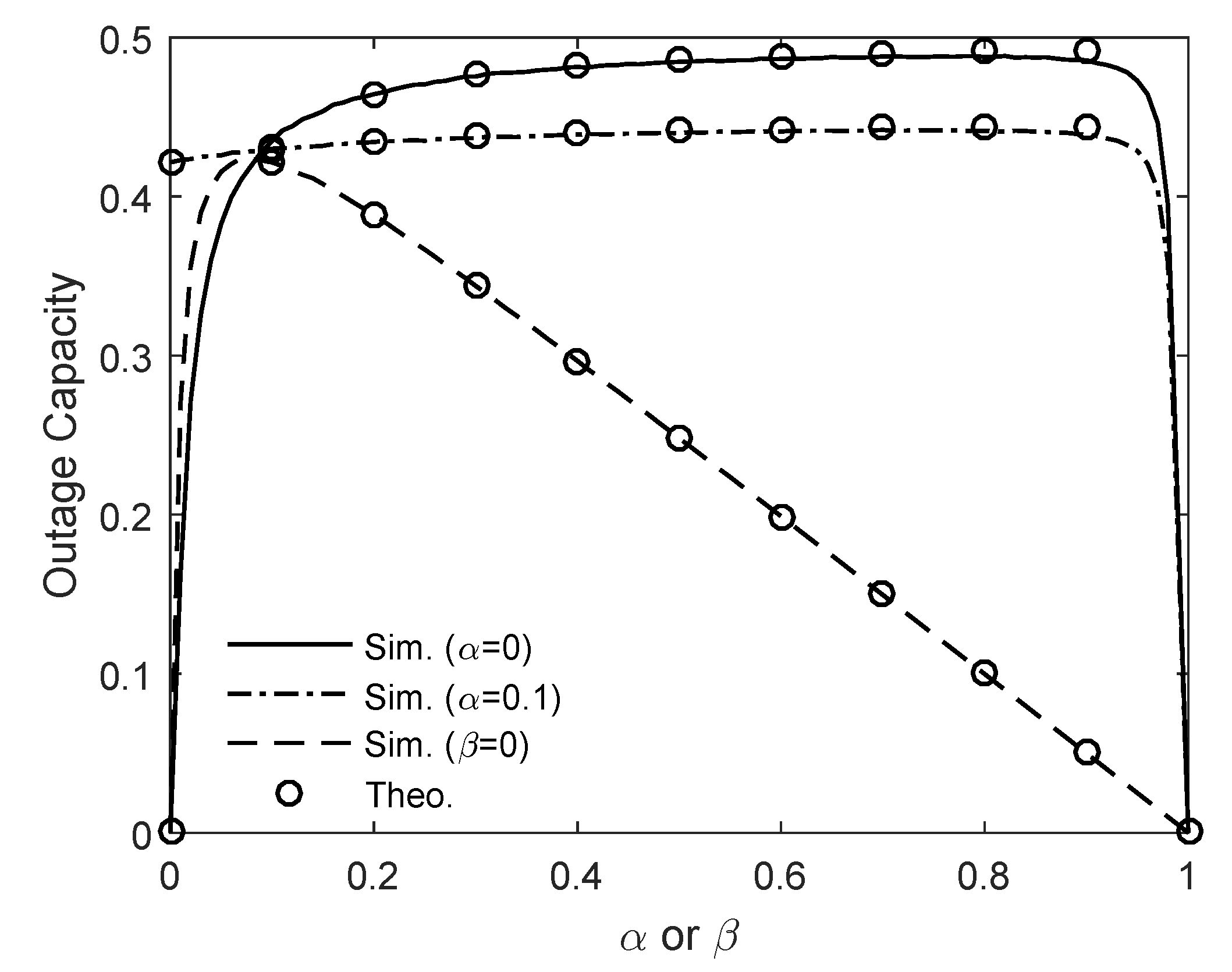
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, W.; Zhou, S.; Chen, Y.; Wang, S.; Chu, X.; Niu, Z. Simultaneous information and energy flow for IoT relay systems with crowd harvesting. IEEE Commun. Mag. 2016, 54, 143–149. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S.; Dey, S. Massive MIMO channel-aware decision fusion. IEEE Trans. Signal Process. 2015, 63, 604–619. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Romano, G.; Rossi, P.S. Channel-aware decision fusion in distributed MIMO wireless sensor networks: Decode-and-Fuse vs. Decode-then-Fuse. IEEE Trans. Wirel. Commun. 2012, 11, 2976–2985. [Google Scholar] [CrossRef]
- Shirazinia, A.; Dey, S.; Ciuonzo, D.; Rossi, P.S. Massive MIMO for decentralized estimation of a correlated source. IEEE Tran. Signal Process. 2016, 64, 2499–2512. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, J.; Swindlehurst, A.L.; López-Salcedo, J.A. Massive MIMO for wireless sensing with a coherent multiple access channel. IEEE Trans. Signal Process. 2015, 63, 3005–3017. [Google Scholar] [CrossRef]
- Ding, G.; Gao, X.; Xue, Z.; Wu, Y.; Shi, Q. Massive MIMO for distributed detection with transceiver impairments. IEEE Trans. Veh. Technol. 2018, 67, 604–617. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Mitsis, G.; Papavassiliou, S. Interest-aware energy collection & resource management in machine to machine communications. Ad Hoc Netw. 2018, 68, 48–57. [Google Scholar]
- Perera, T.D.P.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous wireless information and power transfer (SWIPT): Recent advances and future challenges. IEEE Commun. Surv. Tutor. 2018, 20, 264–302. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, M.; Liu, Y. Energy-efficient SWIPT in IoT distributed antenna systems. IEEE Internet Things J. 2018, 5, 2646–2656. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Zhou, F.; Al-Dhahir, N.; Zhang, H. Power splitting-based swipt with dual-hop DF relaying in the presence of a direct link. IEEE Syst. J. 2018, 1–5. [Google Scholar] [CrossRef]
- Lee, H.; Song, C.; Choi, S.H.; Lee, I. Outage probability analysis and power splitter designs for SWIPT relaying systems with direct link. IEEE Commun. Lett. 2017, 21, 648–651. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Wang, D.; Zhou, F.; Hu, R.Q.; Zhang, H. Optimal transmission schemes for DF relaying networks using SWIPT. IEEE Trans. Veh. Technol. 2018, 67, 7062–7072. [Google Scholar] [CrossRef]
- Atapattu, S.; Jiang, H.; Evans, J.; Tellambura, C. Time-switching energy harvesting in relay networks. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 5416–5421. [Google Scholar]
- Rabie, K.M.; Salem, A.; Alsusa, E.; Alouini, M.S. Energy-harvesting in cooperative AF relaying networks over log-normal fading channels. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–7. [Google Scholar]
- Ding, H.; da Costa, D.B.; Wang, X.; Dias, U.S.; de Sousa, R.T.; Ge, J. On the effects of LOS path and opportunistic scheduling in energy harvesting relay systems. IEEE Trans. Wirel. Commun. 2016, 15, 8506–8524. [Google Scholar] [CrossRef]
- Rabie, K.M.; Adebisi, B.; Alouini, M.S. Wireless power transfer in cooperative DF relaying networks with log-normal fading. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Ye, J.; Lei, H.; Liu, Y.; Pan, G.; da Costa, D.B.; Ni, Q.; Ding, Z. Cooperative communications with wireless energy harvesting over Nakagami-m fading channels. IEEE Trans. Commun. 2017, 65, 5149–5164. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Wang, D.; Lu, G. Power splitting protocol design for the cooperative NOMA with SWIPT. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–5. [Google Scholar]
- Yan, J.; Liu, Y. A dynamic SWIPT approach for cooperative cognitive radio networks. IEEE Trans. Veh. Technol. 2017, 66, 11122–11136. [Google Scholar] [CrossRef]
- Atapattu, S.; Evans, J. Optimal energy harvesting protocols for wireless relay networks. IEEE Trans. Wirel. Commun. 2016, 15, 5789–5803. [Google Scholar] [CrossRef]
- Pilanawithana, B.; Atapattu, S.; Evans, J. Energy allocation and energy harvesting in wireless relay networks with hybrid protocol. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Tao, R.; Salem, A.; Hamdi, K.A. Adaptive relaying protocol for wireless power transfer and information processing. IEEE Commun. Lett. 2016, 20, 2027–2030. [Google Scholar] [CrossRef]
- Zhao, F.; Lin, H.; Zhong, C.; Hadzi-Velkov, Z.; Karagiannidis, G.K.; Zhang, Z. On the capacity of wireless powered communication systems over rician fading channels. IEEE Trans. Commun. 2018, 66, 404–417. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Shi, L.; Hu, R.Q.; Zhang, H. Improved hybrid relaying protocol for DF relaying in the presence of a direct link. IEEE Wireless Commun. Lett. 2018. [Google Scholar] [CrossRef]
- Suraweera, H.A.; Karagiannidis, G.K.; Smith, P.J. Performance analysis of the dual-hop asymmetric fading channel. IEEE Trans. Wirel. Commun. 2009, 8, 2783–2788. [Google Scholar] [CrossRef]
- Ding, H.; Ge, J.; da Costa, D.B.; Guo, Y. Outage analysis for multiuser two-way relaying in mixed rayleigh and rician fading. IEEE Commun. Lett. 2011, 15, 410–412. [Google Scholar] [CrossRef]
- Nuttall, A.H. Some integrals involving the q-function. IEEE Trans. Inform. Theory 1972, 21, 95–96. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. In table of integrals, series, and products. Math. Comput. 1981, 20, C1157–C1160. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Romain, J.E. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
| Notations | Meaning |
|---|---|
| The zeroth order modified Bessel function of the first kind | |
| Probability of a random event | |
| The minimal function | |
| The first-order Marcum Q function | |
| Euler’s constant and its value is 0.5772156649 | |
| The exponential integral function | |
| Incomplete gamma function |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Lu, G.; Shi, L.; Ye, Y. Performance Analysis of Hybrid Protocol Based AF EH Relaying over Asymmetric Fading Channels. Information 2019, 10, 50. https://doi.org/10.3390/info10020050
Sheng X, Lu G, Shi L, Ye Y. Performance Analysis of Hybrid Protocol Based AF EH Relaying over Asymmetric Fading Channels. Information. 2019; 10(2):50. https://doi.org/10.3390/info10020050
Chicago/Turabian StyleSheng, Xutao, Guangyue Lu, Liqin Shi, and Yinghui Ye. 2019. "Performance Analysis of Hybrid Protocol Based AF EH Relaying over Asymmetric Fading Channels" Information 10, no. 2: 50. https://doi.org/10.3390/info10020050
APA StyleSheng, X., Lu, G., Shi, L., & Ye, Y. (2019). Performance Analysis of Hybrid Protocol Based AF EH Relaying over Asymmetric Fading Channels. Information, 10(2), 50. https://doi.org/10.3390/info10020050





