Grey Wolf Algorithm and Multi-Objective Model for the Manycast RSA Problem in EONs

Abstract

Manycast routing and spectrum assignment (RSA) in elastic optical networks (EONs) has become a hot research field. In this paper, the mathematical model and high efficient algorithm to solve this challenging problem in EONs is investigated. First, a multi-objective optimization model, which minimizes network power consumption, the total occupied spectrum, and the maximum index of used frequency spectrum, is established. To handle this multi-objective optimization model, we integrate these three objectives into one by using a weighted sum strategy. To make the population distributed on the search domain uniformly, a uniform design method was developed. Based on this, an improved grey wolf optimization method (IGWO), which was inspired by PSO (Particle Swarm Optimization, PSO) and DE (Differential Evolution, DE), is proposed to solve the maximum model efficiently. To demonstrate high performance of the designed algorithm, a series of experiments are conducted using several different experimental scenes. Experimental results indicate that the proposed algorithm can obtain better results than the compared algorithm.

1. Introduction

The rapid growth of numerous high-rate various applications, such as internet protocol television, video on demand, and cloud computing, requires an efficient networking infrastructure; the future optical network tends to be dynamic, heterogeneous, and unpredictable [1,2]. To tackle this issue, elastic optical networks (EONs) [3] are proposed to realize flexible and efficient spectrum allocation with much finer spectrum granularity. In particular, EONs provide just-right bandwidth for the arriving request connection dynamically, which brings better spectrum assignment flexibility [4,5]. Orthogonal frequency division multiplexing is a multi-carrier modulation technology. It can distribute the high-speed data stream into several orthogonal low-speed subcarriers [6]. The adjacent subcarriers have the spectrum overlapping of a subcarrier bandwidth. This subcarrier is referred to the frequency slot (FS). The elastic optical network can allocate several consecutive frequency slots to each connection request according to the required bandwidth by using orthogonal frequency division multiplexing as a spectrum-efficient modulation technology. Adjacent spectrum bandwidths assigned to two connection requests in the same link should be separated by the guaranteed frequency slots (GFs). Similar to the routing and wavelength assignment problem in wavelength division multiplexing networks [7], a routing and spectrum assignment (RSA) problem exists in the elastic optical network [8]. In order to establish a light-path for the connection request in the elastic optical network, three constraints should be satisfied as follows: (1) Spectrum consistency means that the start frequency slot index on different links of a path must be identical; (2) Spectrum continuity means that we must assign consecutive frequency slots to a specific connection request. That is to say, a large connection request can not be divided into several smaller connection requests; (3) A frequency slot on a link should be assigned to one connection request at most. Generally speaking, the objective of static routing and spectrum assignment is to minimize the the maximum index of the used frequency slots with unlimited resources, and to minimize the ratio of blocking with limited resources. Certainly, there are some other optimization objectives, such as energy consumption, cost, etc.

In this paper, we focus on the manycast routing and spectrum assignment problem in EONs. The main contributions of this paper are as follows. First, to minimize network power consumption, the total occupied spectrum and maximum index of the used frequency spectrum, we established a multi-objectives optimization model. Second, we first integrate these three objectives into one by using a weighted sum strategy to handle this multi-objective optimization model. Then, an improved grey wolf optimization method (IGWO), which was inspired by PSO (Particle Swarm Optimization, PSO) and DE (Differential Evolution, DE) is proposed to solve the maximum model efficiently. Finally, a series of experiments are conducted in several different experimental scenes.

The rest of this paper is organized as follows. Some related works are introduced in Section 2. Section 3 gives the network architecture and the optimization model. To solve the optimization model effectively, we propose an improved grey wolf optimization algorithm in Section 4. To evaluate the algorithm proposed, simulation experiments are conducted, and the experimental results are analyzed in Section 5. The paper is concluded with a summary in Section 6.

2. Related Works

To detect potential access conflicts and prevent both processes from updating data simultaneously in distributed database systems, the concept of manycast has been proposed first [9,10]. The problem of manycasting over optical burst-switched networks has been investigated [11,12,13]. The main challenge is providing reliability despite random contentions optical burst-switched networks for the problem of manycasting. This research focuses on distributed routing or unicast routing algorithms to provide reliable manycast for dynamic traffic. Some literature is focusing on the problem of manycast routing and wavelength assignment in wavelength division multiplexing networks (WDM) [14,15,16]. However, this research is focusing on the manycast routing and wavelength assignment in wavelength division multiplexing networks. Thus, these algorithms can not work on the elastic optical networks well. There are some different network properties among optical burst-switched networks, wavelength division multiplexing networks, and elastic optical networks; the manycast routing and spectrum assignment problem in elastic optical networks mainly considers efficient network resource utilization and request blocking probability reduction. The literature [16] investigated the manycast routing and spectrum assignment (MRSA) problem in WDM networks. The proposed heuristics observably improved network performance in required wavelengths reduction over realistic networks. However, some factors have not been considered in EONs, such as modulation level and spectrum assignment constraints. Because of unique spectrum flexibility in EONs, it has an essential difference compared to supporting manycast with WDM networks and optical burst-switched networks. Thus far, there have only been a few studies about the MA-RMLSA problem in EONs. The energy-efficiency MA-RMLSA strategy was proposed by green-energy aware destination nodes selection [17]. The proposed algorithm has a high performance on decreasing the energy consumption of the network. While the authors focus on the network energy consumption, it may not have advantages over some other objectives, such as spectrum resource utilization, maximum index of used frequency slots, etc. Impairment-aware manycast routing, modulation level, and spectrum assignment problem in EONs are investigated. Two decomposed MILPs (Mixed Integer Linear Programming) and corresponding heuristic algorithms are proposed to find a light-tree and assign modulation level and spectrum to the given requests, sequentially [18]. The authors in [19] studied an integrated approach to optimally place content replicas across DCs (Data Centers) by concurrently solving the routing and wavelength assignment (RWA) problem for both inter-DC content replication and synchronization traffic following the manycast routing paradigm, and end-user-driven user-to-DC communication following the anycast routing paradigm, with the objective to reduce the overall network capacity usage.

3. Problem Description and Mathematical Modeling

In this section, problem description and mathematical modeling of the manycast routing and spectrum assignment (RSA) problem in elastic optical networks (EONs) will be given.

3.1. Problem Description

We use an undirected graph $V=(V,E)$ to denote a network, where $V=\{V_1,V_2,\cdots ,V_{N_V}\}$ and $N_V$ denote the nodes set and the number of the nodes in the network, respectively. $E=\left\{l_{ij}\right|V_i,V_j\in V\}$ denotes the link set, and $N_E$ denotes the number of links in the network. If $l_{ij}=l_{ji}=1$, there is a link between $V_i$ and $V_j$; otherwise, $l_{ij}=l_{ji}=0$. Let $f=\{f_1,f_2,\cdots ,f_u,\cdots ,f_{N_F}\}$ denote the set of available frequency slots (FSs) in each link, and $N_F$ be the number of frequency slots.

$R=\{R_1,R_2,\cdots ,R_k,\cdots ,R_{N_R}\}$ denotes a set of connection requests, where $N_R$ is the number of connection requests, and $R_k$ is the k-th connection request. $R_k$ can be represented as $R_k=(s_k,D_k,B_k)$, where $s_k$ and $B_k$ represent the source node and the numbers of frequency slots of $R_k$ required. $D_k=\{D_k^1,D_k^2,\cdots ,D_k^{N_D^k}\}$ is the set of destination node, where $N_D^k$ is the number of destination node; when $N_D^k=1$, it will be a unicast routing request. In this paper, we assume that all nodes in the network are able to split their incoming connection request to any number of other nodes. This architecture is the same as the scheme introduced in [16].

The manycast routing and spectrum assignment (RSA) problem in elastic optical networks (EONs) can be summarized as: to achieve some objectives, the proper path should be selected for each connection request. Then, the optimal scheme of spectrum assignment should be determined for all of the connection requests.

3.2. Mathematical Modeling

In this section, we present a mathematical model for manycast routing and spectrum assignment in EONs. The first objective is minimize the total power consumption, and the total power consumption is calculated by [17]

$$P=\sum _{V_i\in V}\sum _{V_j\in V}{Q}_{ij}{A}_{ij}{P}_{OA}+\sum _{V_j\in V}{P}_j{P}_{OXC}\left(V_j\right),$$

(1)

where $Q_{ij}$ is a boolean variable; $Q_{ij}=1$ if and only if link $l_{ij}$ is used in the network to provision all manycast requests. $A_{ij}$ and $P_{OA}$ denote the number of optical amplifiers in the link $l_{ij}$ and the power consumption of each optical amplifier, respectively. $P_j$ is a boolean variable; $P_j=1$ if and only if node $V_j$ is used in the network to provision all manycast requests. $P_{OXC}\left(V_j\right)$ is the power consumption of optical cross connect in node $V_j$. Since Equations (2) and (3) satisfy

$$\sum _{V_i\in V}\sum _{V_j\in V}{Q}_{ij}{A}_{ij}{P}_{OA}\le \sum _{V_i\in V}\sum _{V_j\in V}{A}_{ij}{P}_{OA},$$

(2)

$$\sum _{V_j\in V}{P}_j{P}_{OXC}\left(V_j\right)\le \sum _{V_j\in V}{P}_{OXC}\left(V_j\right),$$

(3)

the total power consumption can be normalized as

$$F_1=\frac{{\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{V_j\in V}}{Q}_{ij}{A}_{ij}{P}_{OA}+{\displaystyle \sum _{V_j\in V}}{P}_j{P}_{OXC}\left(V_j\right)}{{\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{V_j\in V}}{A}_{ij}{P}_{OA}+{\displaystyle \sum _{V_j\in V}}{P}_{OXC}\left(V_j\right)}.$$

(4)

Thus, we have $0\le F_1\le 1$, and the first objective function can be expressed as

$$min{F}_1=min\left\{\frac{{\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{V_j\in V}}{Q}_{ij}{A}_{ij}{P}_{OA}+{\displaystyle \sum _{V_j\in V}}{P}_j{P}_{OXC}\left(V_j\right)}{{\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{V_j\in V}}{A}_{ij}{P}_{OA}+{\displaystyle \sum _{V_j\in V}}{P}_{OXC}\left(V_j\right)}\right\}.$$

(5)

The second objective is minimize the total occupied frequency slots, and the total occupied spectrum is

$$F_S=\sum _{R_k\in R}\sum _{V_i\in V}\sum _{V_j\in V}\sum _{f_u\in f}{y}_{ij}^{ku},$$

(6)

where $y_{ij}^{ku}$ represents a binary valuable; $y_{ij}^{ku}=1$ if and only if the frequency slot $f_u$ on link $l_{ij}$ is allocated to connection request $R_k$. We have $F_S\le N_E\times N_F$, and the total occupied frequency slots can be normalized as

$$F_2=\frac{1}{N_E\times N_F}\sum _{R_k\in R}\sum _{V_i\in V}\sum _{V_j\in V}\sum _{f_u\in f}{y}_{ij}^{ku}.$$

(7)

Thus, $0\le F_2\le 1$, and the second objective function can be represented by

$$min{F}_2=min\left\{\frac{1}{N_E\times N_F}\sum _{R_k\in R}\sum _{V_i\in V}\sum _{V_j\in V}\sum _{f_u\in f}{y}_{ij}^{ku}\right\}.$$

(8)

The third objective is minimize the maximum index of used frequency slots (MIUFS) in the network; we can express this objective function as

$$min{F}_3=min\left\{\frac{1}{N_F}\underset{l_{ij}\in E}{max}n\left(F_{ij}\right)\right\},$$

(9)

where $n\left(F_{ij}\right)$ denotes the maximum index of used frequency slots on link $l_{ij}$. Since we have $n\left(F_{ij}\right)\le N_F(\forall l_{ij}\in E)$, $0\le F_3\le 1$.

To simplify the model, we integrate the three objectives into one to be minimized by the sum weighted strategy as follows:

$$minF=min\left\{{\alpha }_1{F}_1+{\alpha }_2{F}_2+{\alpha }_3{F}_3\right\},$$

(10)

where ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are three weights to adjust the importance of the three objectives, and we have $0\le {\alpha }_1,{\alpha }_2,{\alpha }_3\le 1$, ${\alpha }_1+{\alpha }_2+{\alpha }_3=1$. Since $0\le F_1,F_2,F_3\le 1$, $0\le f\le 1$. The objective should be made under some conditions. These conditions constitute the constraints of the problem as follows:

Constraint (a): the same spectrum slots are not assigned to two requests. That is,

$$\sum _{R_k\in R}{y}_{ij}^{ku}\le 1,\forall V_i,V_j\in V,f_u\in f.$$

(11)

Constraint (b): contiguous frequency slots should be allocated to the connection request,

$$\sum _{u^{\prime }=u}^{u+B_k-1}{y}_{ij}^{k{u}^{\prime }}\ge B_k\times x_{ij}^{ku},\forall R_k\in R,V_i,V_j\in V,f_u\in f,$$

(12)

where $x_{ij}^{ku}$ represents a binary valuable, $x_{ij}^{ku}=1$ if and only if $f_u$ is the first frequency slot on link $l_{ij}$ allocated to connection request $R_k$.

Constraint (c): all the destinations must be reached, we can express this constraint as

$$\sum _{V_i\in V}\sum _{V_j\in D_k}\sum _{f_u\in f}{x}_{ij}^{ku}=N_D,\forall R_k\in R.$$

(13)

Constraint (d): at least one outgoing traffic should leave the source node.

$$\sum _{V_j\in V}\sum _{f_u\in f}{x}_{s_{k}j}^{ku}\ge 1,\forall R_k\in R.$$

(14)

Constraint (e): it ensures that the source node could not have incoming traffic:

$$\sum _{V_i\in V}\sum _{f_u\in f}{x}_{i{s}_k}^{ku}=0,\forall R_k\in R.$$

(15)

Constraint (f): each node, except the source node, can have at most one piece of incoming traffic.

$$\sum _{V_i\in V\backslash \left\{s_k\right\}}\sum _{f_u\in f}{x}_{ij}^{ku}\ge 1,\forall R_k\in R,V_j\in V.$$

(16)

Constraint (g): one node, except the source node, could not have outgoing traffic unless it has incoming traffic,

$$\sum _{V_j\in V}{x}_{ij}^{ku}\le N_V\sum _{V_j\in V}{x}_{ji}^{ku},\forall R_k\in R,f_u\in f,V_i\ne s_k.$$

(17)

Constraint (h): if a node is not one of the target destinations and has incoming traffic, it should have one or more pieces of outgoing traffic,

$$\sum _{V_j\in V}{x}_{ij}^{ku}\le \sum _{V_j\in V}{x}_{ji}^{ku},\forall R_k\in R,f_u\in f,V_i\notin D_k.$$

(18)

Based on the objectives and constraints above, we can set up a global constrained optimization model as follows:

$$\left\{\begin{array}{c}minF=min\left\{{\alpha }_1{F}_1+{\alpha }_2{F}_2+{\alpha }_3{F}_3\right\}\hfill \\ s.t.\hfill \\ \left(a\right){\displaystyle \sum _{R_k\in R}}{y}_{ij}^{ku}\le 1,\forall V_i,V_j\in V,f_u\in f;\hfill \\ \left(b\right){\displaystyle \sum _{u^{\prime }=u}^{u+B_k-1}}{y}_{ij}^{k{u}^{\prime }}\ge B_k\times x_{ij}^{ku},\forall R_k\in R,V_i,V_j\in V,f_u\in f;\hfill \\ \left(c\right){\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{V_j\in D_k}}{\displaystyle \sum _{f_u\in f}}{x}_{ij}^{ku}=N_D,\forall R_k\in R;\hfill \\ \left(d\right){\displaystyle \sum _{V_j\in V}}{\displaystyle \sum _{f_u\in f}}{x}_{s_{k}j}^{ku}\ge 1,\forall R_k\in R;\hfill \\ \left(e\right){\displaystyle \sum _{V_i\in V}}{\displaystyle \sum _{f_u\in f}}{x}_{i{s}_k}^{ku}=0,\forall R_k\in R;\hfill \\ \left(f\right){\displaystyle \sum _{V_i\in V\backslash \left\{s_k\right\}}}{\displaystyle \sum _{f_u\in f}}{x}_{ij}^{ku}\ge 1,\forall R_k\in R,V_j\in V;\hfill \\ \left(g\right){\displaystyle \sum _{V_j\in V}}{x}_{ij}^{ku}\le N_V{\displaystyle \sum _{V_j\in V}}{x}_{ji}^{ku},\forall R_k\in R,f_u\in f,V_i\ne s_k;\hfill \\ \left(h\right){\displaystyle \sum _{V_j\in V}}{x}_{ij}^{ku}\le {\displaystyle \sum _{V_j\in V}}{x}_{ji}^{ku},\forall R_k\in R,f_u\in f,V_i\notin D_k.\hfill \end{array}\right.$$

(19)

The problem of manycast routing and spectrum assignment in EONs is the hardest combinatorial optimization problems. The existing algorithms cannot be applied directly, and are necessary to make some improvements or revisions. To solve the global constrained optimization model established, we propose an improved grey wolf optimization method and denote it as IGWO.

4. Grey Wolf Optimization (GWO)

The Grey Wolf Optimization (GWO) algorithm simulates the leadership hierarchy and hunting mechanism of grey wolves [20] and has been proven to be an effective technique for many hard problems [21,22,23]. However, it is not suitable to directly apply the algorithms mentioned above to the problems of manycast routing and spectrum assignment in EONs, and it is necessary to make some improvements or revisions on them. In this section, we will describe the proposed IWGO detailed.

4.1. Encoding Scheme

In the manycast routing and spectrum assignment problem, we should determine the optimal scheme of routing and spectrum assignment. For the spectrum assignment, it is much easier to assign spectra using first fit strategy [6] than using the method with encoding. Thus, it only needs to encode for routing scheme.

Each individual in routing population represents a routing scheme for all the connection requests. $Q_k=\{Q_k^1,Q_k^2,\cdots ,Q_k^q,\cdots ,Q_k^{N_k^Q}\}$ denotes the candidate paths set of connection request $R_k$ that is calculated by the K-Shortest path algorithm in advance, where $N_k^Q$ is the number of the candidate paths and $Q_k^q$ is the q-th path. We assume that $y=(y_1,y_2,\cdots ,y_{N_R})$ is an individual in path selection population. $y_k=q$ if and only if $R_k$ occupies the path $Q_k^q$.

4.2. Population Initialization

In the proposed improved Grey Wolf Optimization (IWGO) algorithm, we use uniform design method to generate the population. To generate points to be uniformly distributed on the experimental domain, a uniform design method was developed. It generates a small number of the uniformly distributed representative points in a domain by using a uniform array $U(S,H)={\left[U_{i,j}\right]}_{H\times S}$, where $U_{i,j}$ denotes the level of the j-th factor in the i-th combination with the j-th factor representing the j-th variable and its level being its value [24,25].

To construct uniform design array, many methods are presented—not only simple but also efficient methods are proposed. Firstly, we construct a hypercube over an S-dimensional space:

$$C^S=\left\{(c_1,c_2,\cdots ,c_S)|a_i\le c_i\le b_i,i=1,2,\cdots ,S\right\},$$

where $a_i$ and $b_i$ are the lower and upper bounds of the i-th factor (i.e., i-th variable), respectively. Then, a hyper-rectangle is formed between $a_i$ and $d_i$ as follows:

$$C\left(d\right)=\left\{(c_1,c_2,\cdots ,c_S)|a_i\le c_i\le d_i,i=1,2,\cdots ,S\right\}\subset C^S.$$

Finally, H uniformly distributed points are selected randomly from $C^S$. Assume that $H\left(d\right)$ is the number of points fallen into the hyper-rectangle $C\left(d\right)$, and the fraction of points in $C\left(d\right)$ is $H\left(d\right)/H$. As the volume of hypercube $C^S$ is ${\prod }_{i=1}^S(b_i-a_i)$, the volume of $C\left(d\right)$ is ${\prod }_{i=1}^S(d_i-a_i)$. The H uniform distributed points in $C^S$ should minimize

$$\underset{x\in C^S}{sup}\left\{\frac{H\left(d\right)}{H}-\frac{{\displaystyle \prod _{i=1}^S}(d_i-a_i)}{{\displaystyle \prod _{i=1}^S}(b_i-a_i)}\right\}.$$

(20)

Hence, we can map these H points in $C^S$ to the problem domain with S factors and $\chi$ levels uniformly, where H is an odd and $H>S$. It has been proved that $U_{i,j}$ can be given by [26]:

$$U_{i,j}=(i{\sigma }^{j-1}mod\chi )+1,$$

(21)

where $\sigma$ is a constant related to the number of factors S and level $\chi$. The H sample points scattered uniformly in the hypercube can be selected.

4.3. Improved Grey Wolf Optimization (IGWO) for Manycast RSA

In the Grey Wolf Optimization method, each grey wolf denotes an individual. Four types of grey wolves $\beta$, $\gamma$, $\delta$, and $\omega$ denote the optimal individual, suboptimum individual, third-optimum individual, and other individuals. Assume that there are $N_I$ grey wolves, and the position of $i(i=1,2,\cdots ,N_I)$-th wolf can be denoted as $x_i=(x_i^1,x_i^2,\cdots ,x_i^d,\cdots ,x_i^D)$. We can update the position of i-th wolf by

$$x_i^d(t+1)=z_p^d\left(t\right)-A·|C·z_p^d\left(t\right)-x_i^d\left(t\right)|,$$

(22)

where $z_p=(z_i^1,z_i^2,\cdots ,z_i^d,\cdots ,z_i^D)$ and t denote the position vector of the prey and the current iteration, respectively. A and C denote coefficient vectors, and are calculated as follows:

$$A=2·a·r_1-a,$$

(23)

$$C=2·a·r_2,$$

(24)

where $r_1$, $r_2$ are two random vectors in $[0,1]$; a linearly decreases from 2 to 0 during the course of iterations. The position of other wolves can be updated according to the position of individual $\beta$, $\gamma$, $\delta$ (denoted as $x_{\beta }$, $x_{\gamma }$ and $x_{\delta }$)

$$\left\{\begin{array}{c}{x}_{i,\beta }^d(t+1)=x_{\beta }^d\left(t\right)-A·|C·x_{\beta }^d\left(t\right)-x_i^d\left(t\right)|,\hfill \\ x_{i,\gamma }^d(t+1)=x_{\gamma }^d\left(t\right)-A·|C·x_{\gamma }^d\left(t\right)-x_i^d\left(t\right)|,\hfill \\ x_{i,\delta }^d(t+1)=x_{\delta }^d\left(t\right)-A·|C·x_{\delta }^d\left(t\right)-x_i^d\left(t\right)|.\hfill \end{array}\right.$$

(25)

To enhance the search ability and increase the convergent speed, an efficient position update method of individual is proposed as follows:

$$\begin{array}{cc}\hfill x_i^d(t+1)=& \frac{x_{i,\beta }^d\left(t\right)+x_{i,\beta }^d\left(t\right)+x_{i,\beta }^d\left(t\right)}{3}+r_3·(x_{i,best}^d\left(t\right)-x_i^d\left(t\right))\hfill \\ \hfill & +r_4·(x_j^d\left(t\right)-x_i^d\left(t\right))+r_5·(X_i^d\left(t\right)-x_i^d\left(t\right)),\hfill \end{array}$$

(26)

where $r_3,r_4$ and $r_5$ are three random vectors in $[0,1]$; $x_{i,best}$ denotes the best position of i-th individual in the past. $x_j(j\ne i)$ represents a random individual in current iteration. $X_i^d\left(t\right)$ can be calculated by

$$X_i^d\left(t\right)=\frac{1}{\mu }\sum _{t^{\prime }=t-\mu }^t{x}_i^d\left(t^{\prime }\right),$$

(27)

where $\mu (1\le \mu \le t-1)$ is a constant. In this position update method of an individual, the position of the other individual and its past position information are used like PSO and DE. Thus, it can enhance the search ability and increase the convergent speed.

In the encoding scheme, each gene in all individuals is a positive integer. However, some real numbers can be obtained with Equation (26). For this situation, we only use the integer portion as the gene of the individual. In addition, some gene value, which is greater than the upper bound, can be obtained. For this situation, we only use the integer portion as the gene of the individual. The gene value is modulus the upper bound to make the individual update to a feasible solution. Through these two methods, an infeasible solution can be modified as a feasible solution.

4.4. Framework of the IGWO

To make the proposed improved grey wolf optimization algorithm understood clearly, we give the framework of the proposed algorithm in Algorithm 1. In the algorithm, step 1 is to initialize the population according to the uniform design method. It can improve the search ability of the algorithm. In step 2, fitness is calculated for all the wolves in the population by using the fitness function (objective function is defined as fitness function in this work). Step 4 to step 9 is update the position of all the wolves by using Equation (23), Equation (24), and Equation (26). All the infeasible solutions are converted to feasible solutions in Step 10. Step 11 is calculate the fitness for all the wolves after the position updated. The position of optimal individual, suboptimum individual, third-optimum individual ($x_{\beta }$, $x_{\gamma }$, and $x_{\delta }$) are updated in step 12.

Algorithm 1: Framework of the IGWO

5. Experiments and Analysis

To demonstrate the effectiveness and efficiency of the proposed algorithm, several experiments are conducted, and the results are presented in this section. In Section 5.1, the parameters used in the algorithms are given. Experimental results are presented in Section 5.2. Finally, the experimental analysis is given in Section 5.3.

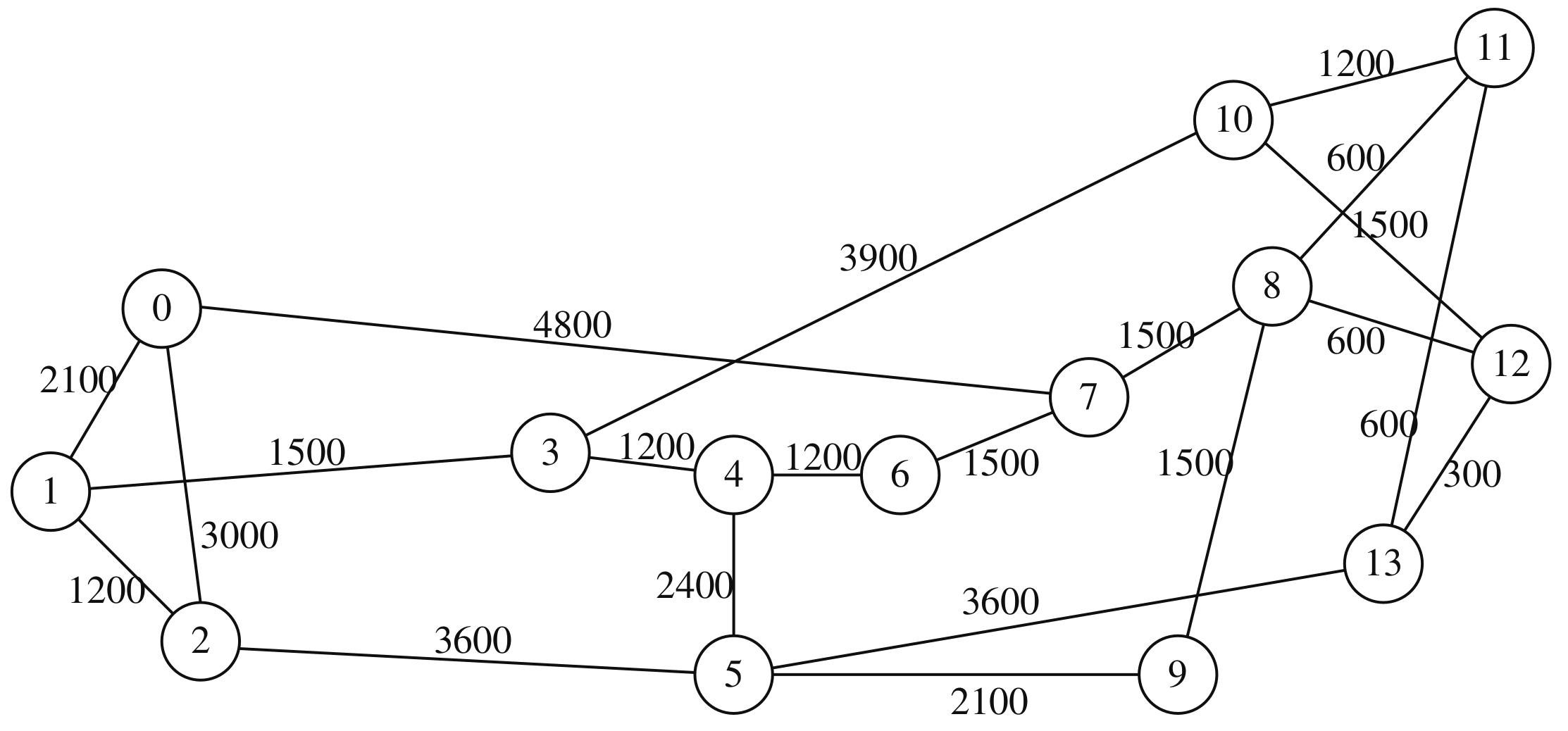
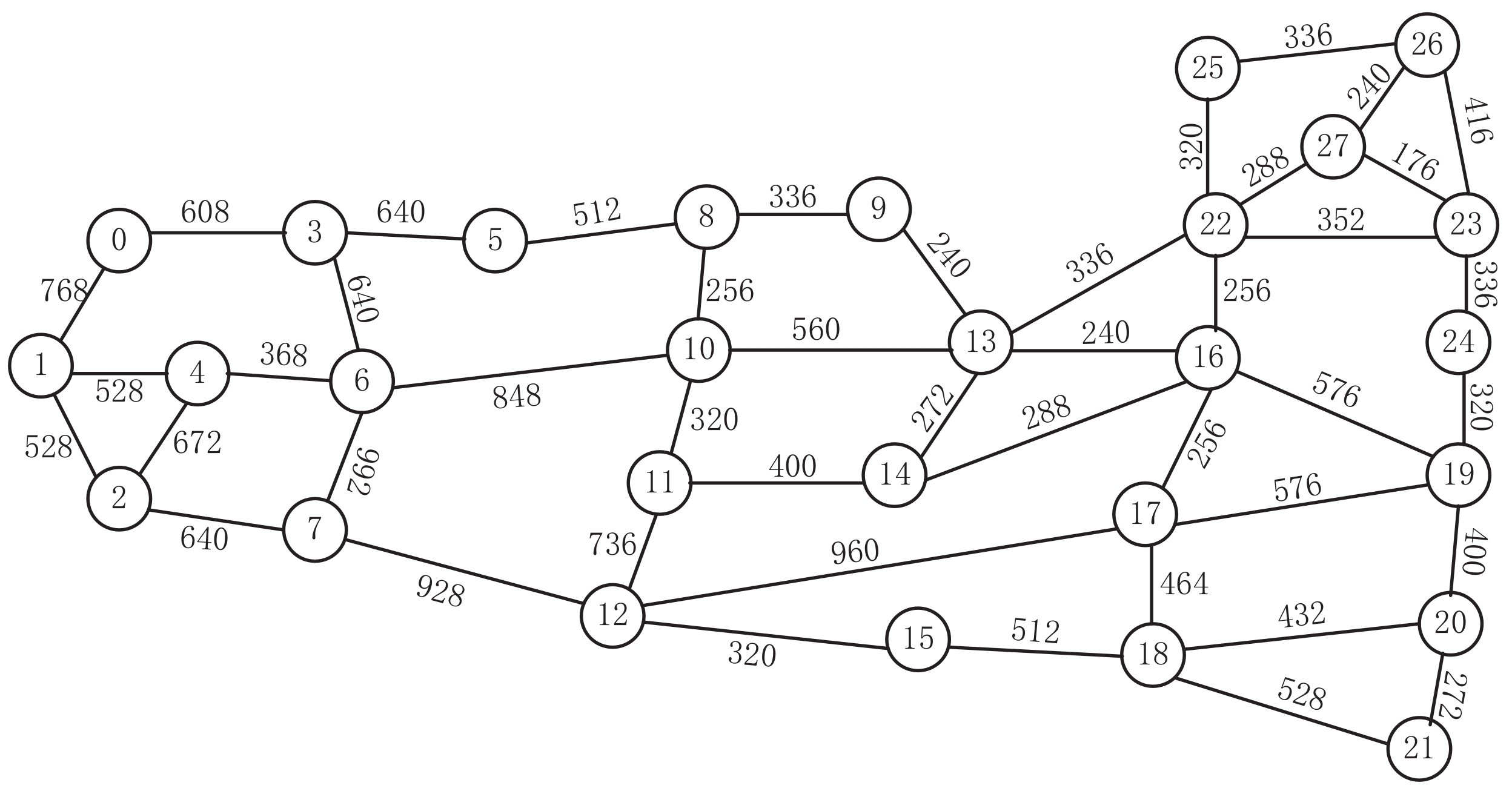
5.1. Parameters Setting

In the experiments, two widely used networks are used as shown in Figure 1 and Figure 2, i.e., NSFNET (National Science Foundation Network) with 14 nodes and 21 links and US Backbone (United States Backbone) with 27 nodes and 44 links, respectively [27,28], respectively, in Figure 1 and Figure 2; each number on the link denotes the distance between adjacent nodes, and the unit of the link distance is Km. We assume that FSs is 12.5 GHz, and transmission distance of BPSK (Binary Phase Shift Keying), QPSK (Quadrature Phase Shift Keying), 8QAM (8 Quadrature Amplitude Modulation), 16QAM (16 Quadrature Amplitude Modulation) are 9600, 4800, 2400 and 1200 km, respectively. Four groups’ connection requests are generated, and their numbers are 250, 500, 750 and 1000, respectively. All connection requests in every group satisfy uniform distribution among all nodes in two topologies. In our work, a large number of experiments are conducted for each case. To make the algorithm converge to an optimal solutions, $t_{max}=2000$ and $\mathsf{\mu }=3$ are adopted. Generally speaking, when the population size is large, it will require a long computation time. In addition, when the population size is small, it will result in a bad diversity of population. Thus, $N_I=100$ is selected in many research works. Like existing works, we use $N_I=100$ in the algorithm. Each connection request requires frequency slots that satisfy uniform distribution in [1, 10], and each link has 1000 frequency slots, i.e., $N_F$ = 1000.

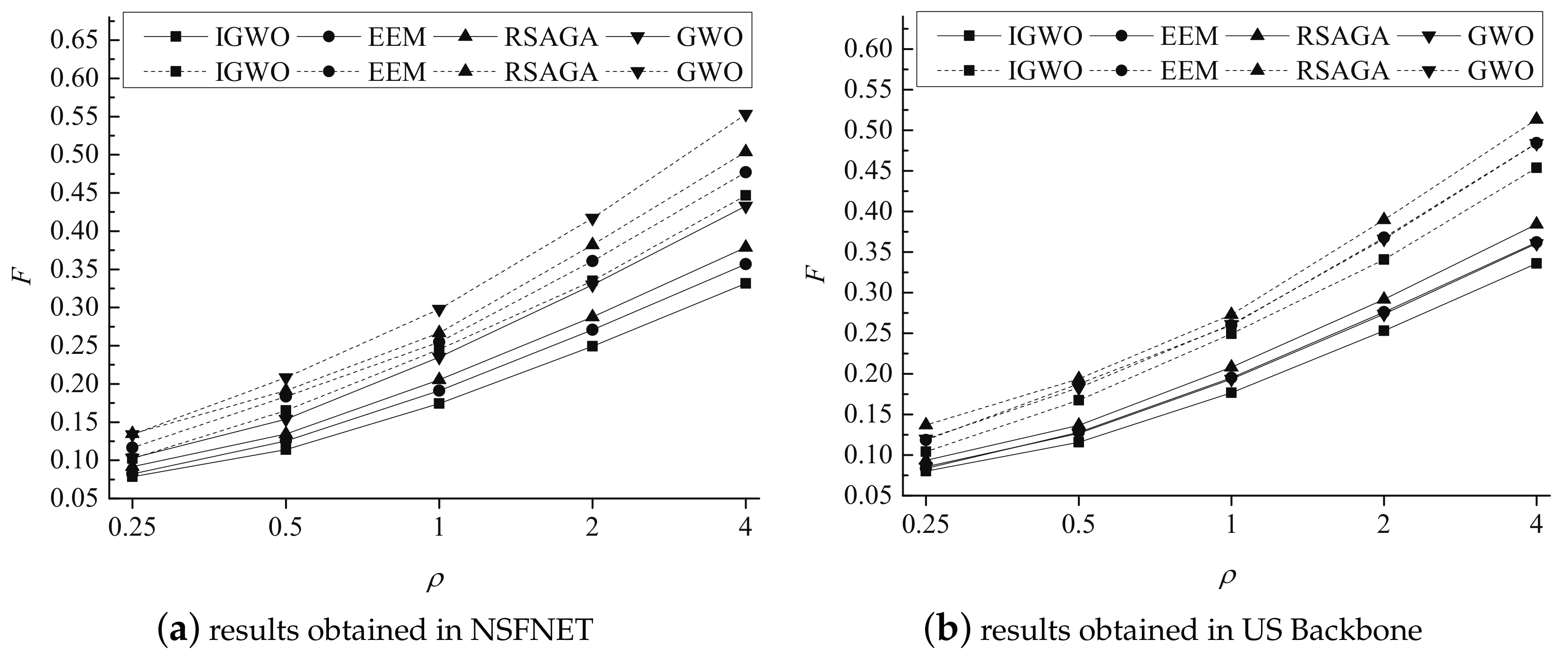
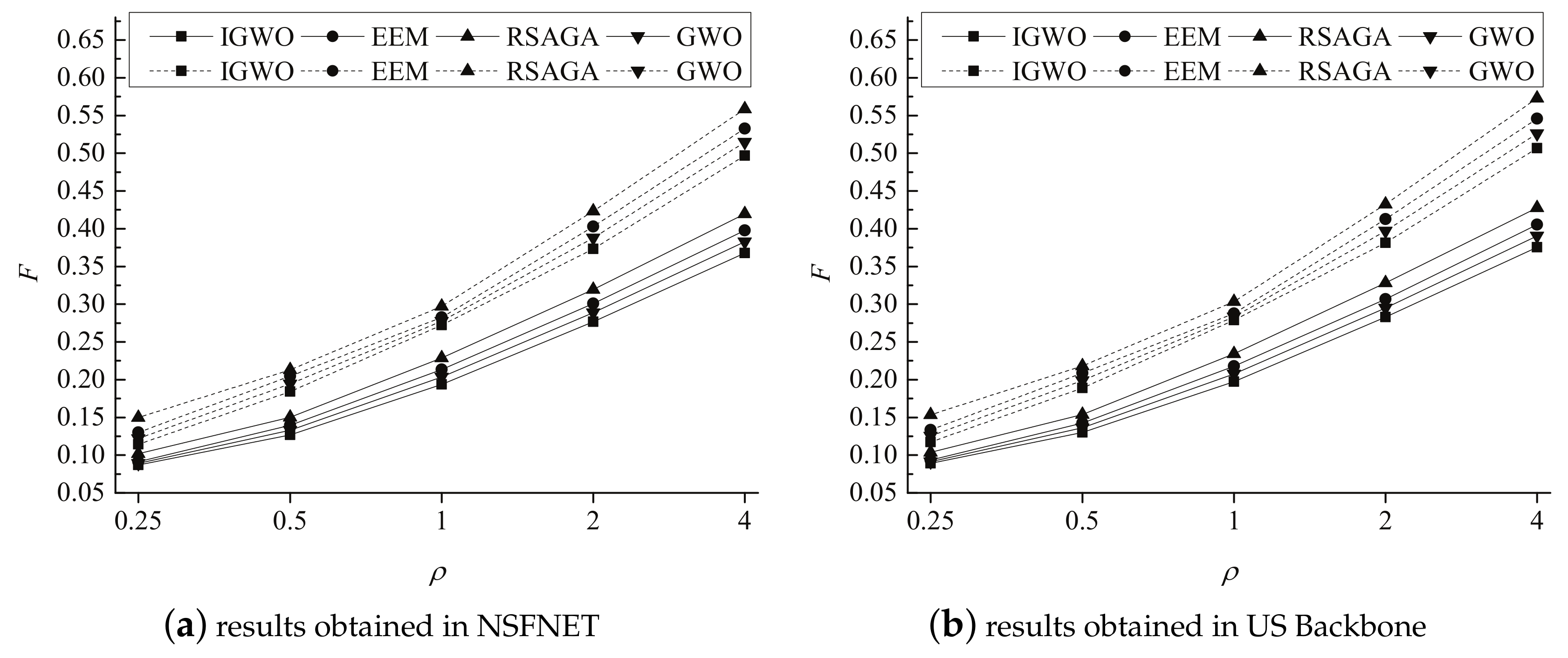
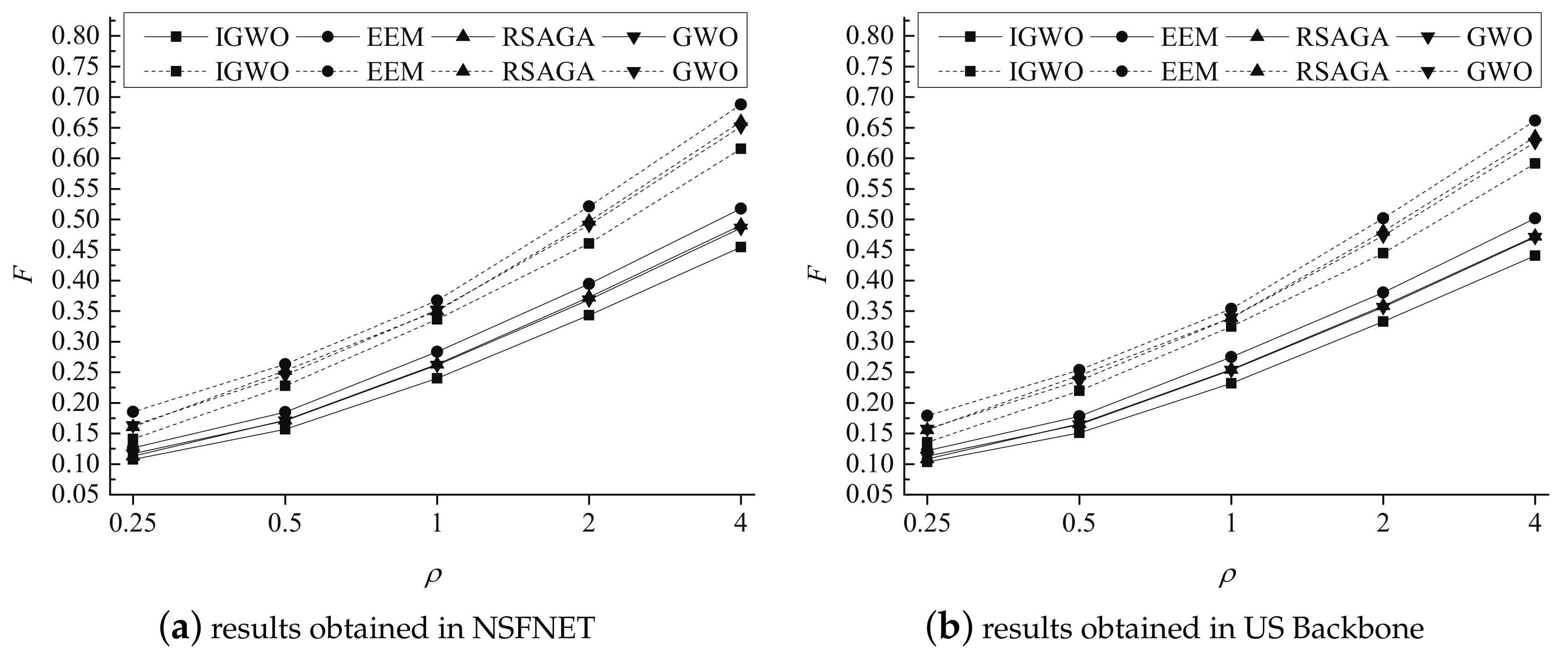
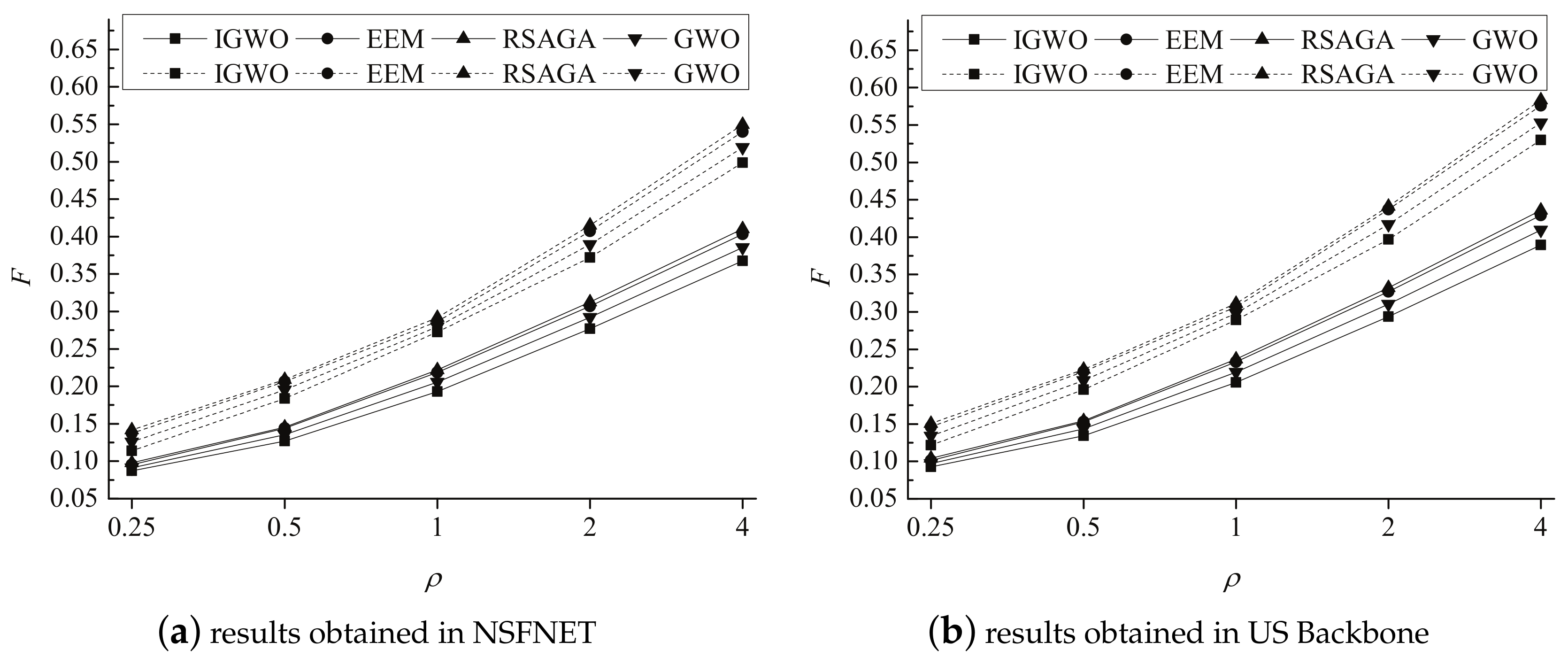
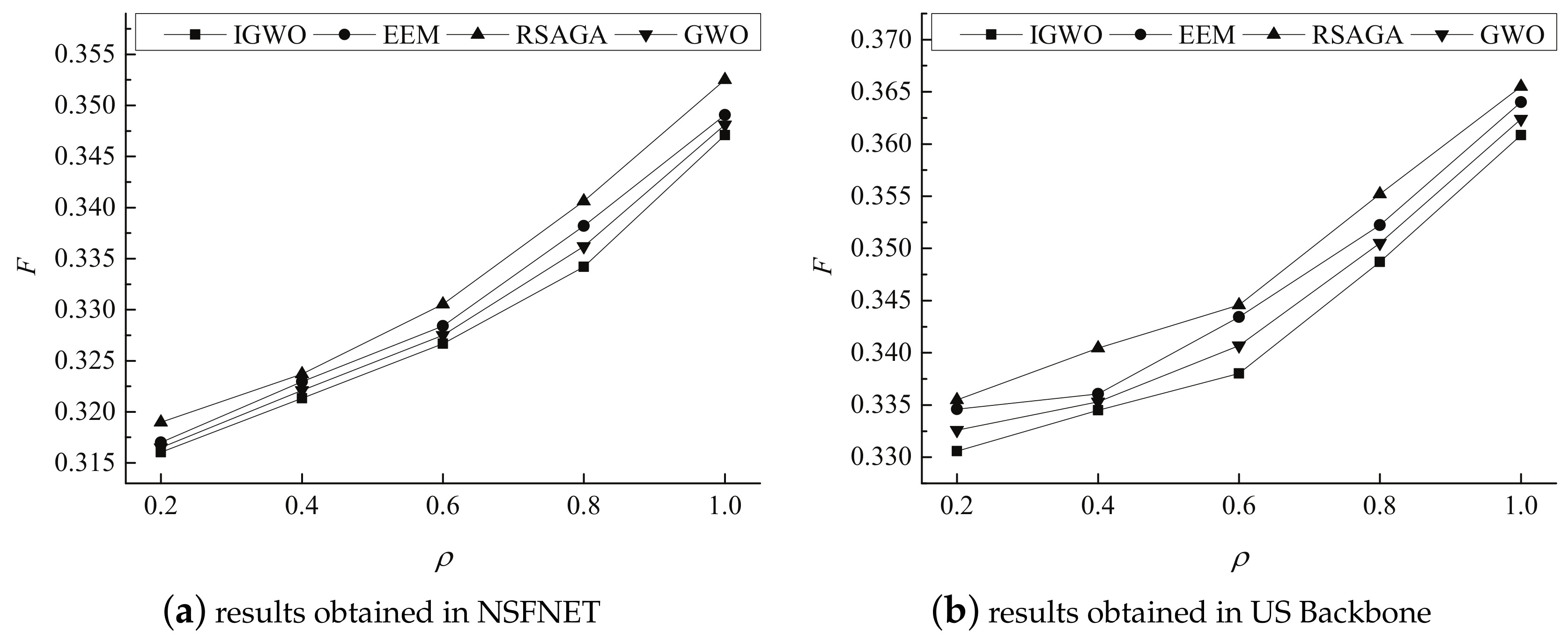
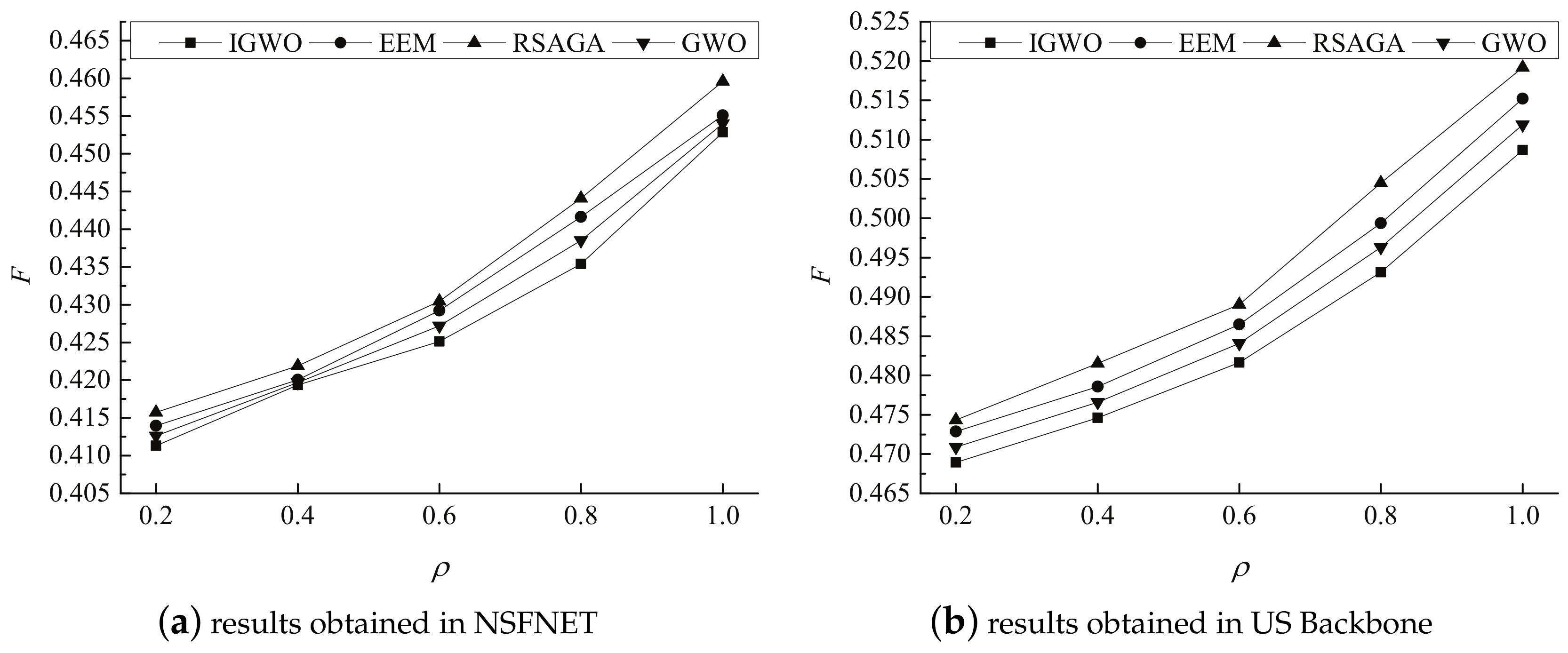
5.2. Experimental Results

To demonstrate the performance of the proposed algorithm, we compare the proposed algorithm IGWO with other three algorithms. The first is EEM, which was proposed in [17]. Another one was proposed in [29], and denoted as RSAGA. RSAGA optimizes the MA-RMLSA problem in routing constitution, modulation level allocation, and spectrum assignment jointly, to enhance the performance of the network. In addition, we also compared IGWO with GWO (Grey Wolf Optimization), which was proposed in [20].

To demonstrate the performance of proposed model and algorithm, we design two experimental scenes. In the first scene, we fixed the number of destination nodes as $N_D=N_V/3$ and $N_D=2N_V/3$, i.e., $N_d=N_D/N_V=1/3$ and $N_d=N_D/N_V=2/3$. That is to say, the number of destination nodes is generated in $[N_V/6,N_V/3]$ and $[N_V/3,2N_V/3]$ randomly. Figure 3 shows the results obtained in NSFNST topology and US Backbone topology when ${\alpha }_1=1,{\alpha }_2=0,{\alpha }_3=0$. Figure 4 shows the results obtained in NSFNST topology and US Backbone topology when ${\alpha }_1=0,{\alpha }_2=1,{\alpha }_3=0$. Figure 5 shows the results obtained in NSFNST topology and US Backbone topology when ${\alpha }_1=0,{\alpha }_2=0,{\alpha }_3=1$. Figure 6 shows the results obtained in NSFNST topology and US Backbone topology when ${\alpha }_1={\alpha }_2={\alpha }_3=1/3$. In each experiment, the number of connection requests are set as $N_R=\rho N_V(N_V-1)$, and $\rho =$ 0.25, 0.5, 1, 2 and 4, respectively. In each figure, the experimental results of $N_D=N_V/3$ are given with a full line, and experimental results of $N_D=2N_V/3$ are given with a dashed line.

In the second scene, we fixed the three weights ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ as ${\alpha }_1=1/3,{\alpha }_{2}1/3$ and ${\alpha }_3=1/3$, i.e., the objective function is $minF=min\{{\alpha }_1{F}_1+{\alpha }_2{F}_2+{\alpha }_3{F}_3\}$. Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the results obtained in NSFNST topology and US Backbone topology when $\rho =0.25$, $\rho =0.5$, $\rho =1$, $\rho =2$ and $\rho =4$, respectively. In each experiment, the number of connection requests are set as $N_D=\theta N_V$, and $\theta =$ 0.2, 0.4, 0.6, 0.8 and 1, respectively.

5.3. Experimental Analysis

In the first experimental scene, the experimental results are obtained by the proposed algorithm (IGWO) and three compared algorithms (EEM, RSAGA, and GWO) are shown in Figure 3, Figure 4, Figure 5 and Figure 6. In Figure 5, the experimental results are obtained in NSFNET and US BackBone when ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ are selected as 1, 0, and 0, respectively. Thus, the objective function is to minimize total power consumption. From the experimental results, we can see that the IGWO can obtain better results than the three compared algorithms. The total power consumption obtained by the IGWO is 2.8%–4.9% less than those obtained by EEM, RSAGA, and GWO when the number of connection requests is 0.25 $N_V(N_V-1)$. When the number of connection requests is 4 $N_V(N_V-1)$, the total power consumption obtained by IGWO is 6.9%–11.6% less than those obtained by EEM, RSAGA, and GWO, respectively. That is to say, the IGWO can obtain a smaller total power consumption and save more power used than EEM, RSAGA, and GWO with the increase of the number of connection requests. The RSAGA algorithm is to minimize the maximum index of used frequency slots, and the EEM algorithm can decrease the energy consumption. Thus, the total power consumption obtained by EEM is less than that obtained by RSAGA. The proposed algorithm IGWO uses uniform design to generate initial population; it can enhance the search ability of the algorithm. Thus, it can obtain the best scheme among the three algorithms. From the experimental results, we can see that the total power consumption obtained when the number of destination node is $N_{DC}=2N_V/3$ is larger than that obtained when the number of destination node is $N_{DC}=N_V/3$ for the same number of connection requests. With the increase of destination node, it will increase the number of connection requests. Thus, the total power consumption is increased.

When ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ are selected as 0, 1, and 0, the objective function is to minimize the total occupied frequency slots. The experimental results obtained in two networks are shown in Figure 4 with the different number of connection requests. From the experimental results, we can see that the IGWO can obtain better results than the three compared algorithms. The total occupied frequency slots obtained by the IGWO is 4.2%–6.2% less than those obtained by EEM, RSAGA, and GWO when the number of connection requests is 0.25 $N_V(N_V-1)$. When the number of connection requests is 4 $N_V(N_V-1)$, the total power consumption obtained by IGWO is 8.6%–10.7% less than those obtained by EEM, RSAGA, and GWO, respectively. That is to say, the IGWO can obtain a smaller total occupied frequency slots and save more frequency slots used than EEM, RSAGA, and GWO with the increase in the number of connection requests. The proposed algorithm IGWO uses uniform design to generate initial population; it can enhance the search ability of the algorithm. Thus, it can obtain the best scheme among the three algorithms. From the experimental results, we can see that the total occupied frequency slots obtained when the number of destination node is $N_{DC}=2N_V/3$ is larger than that obtained when the number of destination node is $N_{DC}=N_V/3$ for the same number of connection requests. With the increase of destination node, it will increase the number of connection requests. Thus, the total occupied frequency slots is increased.

In Figure 5, the experimental results are obtained in NSFNET and US BackBone when ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ are selected as 0, 0, and 1, respectively. Thus, the objective function minimizes the maximum index of used frequency slots. From the experimental results, we can see that the IGWO can obtain better results than the three compared algorithms. The total occupied frequency slots obtained by the IGWO are 3.8%–5.9% less than those obtained by EEM, RSAGA, and GWO when the number of connection requests is 0.25 $N_V(N_V-1)$. When the number of connection requests is 4 $N_V(N_V-1)$, the maximum index of used frequency slots obtained by IGWO is 8.1%–11.2% less than those obtained by EEM, RSAGA, and GWO, respectively. That is to say, the IGWO can obtain a smaller maximum index of used frequency slots than EEM, RSAGA, and GWO with the increase of the number of connection requests. The proposed algorithm IGWO uses uniform design to generate initial population and well-designed strategy of position update; it can enhance the search ability of the algorithm. Thus, it can obtain the best scheme among the three algorithms. From the experimental results, we can see that the maximum index of used frequency slots obtained when the number of destination node is $N_{DC}=2N_V/3$ is larger than that obtained when the number of destination node is $N_{DC}=N_V/3$ for the same number of connection requests. With the increase of destination node, it will increase the number of connection requests. Thus, the maximum index of used frequency slots is increased.

Figure 6 shows that the experimental results obtained in NSFNET and US BackBone when ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ are selected as 1, 1, and 1, respectively. Similarly, we also can see that the IGWO can obtain better results than EEM, RSAGA, and GWO. The objective function obtained by the IGWO is 3.7%–5.8% less than those obtained by EEM, RSAGA, and GWO when the number of connection requests is 0.25 $N_V(N_V-1)$. When the number of connection requests is 4 $N_V(N_V-1)$, the objective function obtained by IGWO is 8.2%–11.6% less than those obtained by EEM, RSAGA, and GWO, respectively. The IGWO can obtain a smaller objective function than EEM, RSAGA, and GWO with the increase of the number of connection requests. The proposed algorithm IGWO uses uniform design to generate initial population and a well-designed strategy of position update; it can enhance the search ability of the algorithm. Thus, it can obtain the best scheme among the three algorithms. From the experimental results, we can see the objective function obtained when the number of destination nodes is $N_{DC}=2N_V/3$, which is larger than that obtained when the number of destination node is $N_{DC}=N_V/3$ for the same number of connection requests. With the increase of destination node, it will increase the number of connection requests. Thus, the objective function is increased.

In the second experimental scene, the experimental results obtained by the proposed algorithm (IGWO) and three compared algorithms (EEM, RSAGA, and GWO) are shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. In this experimental scene, we set ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ as 1, 1 and 1, respectively. From the experimental results, we can see that IGWO can obtain better results than EEM, RSAGA, and GWO for different connection requests in two networks. In each figure, the objective function is increased with the increase in the number of destination nodes. When the number of destination nodes is $N_D=0.2N_V$, the objective function obtained by IGWO is 3.5%–5.8% less than those obtained by EEM, RSAGA, and GWO, respectively. The objective function obtained by the IGWO is 8.6%–11.7% less than those obtained by EEM, RSAGA, and GWO when the number of connection requests is $N_D=N_V$. With the increase of destination node, it will increase the number of connection requests. Thus, the objective function is increased. In addition, EEM minimizes the total power consumption, and RSAGA minimizes maximum index of used frequency slots, so EEM, RSAGA, and GWO cannot be distinguished when ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ as 1, 1, and 1.

As shown in the experimental results, we can see that IWGO can obtain better results than that obtained by GWO. In the IGWO, we improved the strategy of the position update method for the individual. The position of another individual and its past position information are used like PSO and DE. Thus, it can enhance the search ability and increase the convergent speed. In addition, the parameter $\mathsf{\mu }$ is used. It can help to take advantage of the trajectory information of the individuals. When $\mathsf{\mu }=1$, the proposed IGWO degraded to the standard GWO algorithm. Position update method can use the past $\mathsf{\mu }$ position information when $\mathsf{\mu }\ge 1$. Thus, IGWO is better than GWO for this optimization problem. That is to say, IGWO can obtain a better solution than GWO.

6. Conclusions

In this paper, we investigate the manycast RSA problem in EONs. A multi-objective optimization model, which minimizes network power consumption, the total occupied spectrum, and maximum index of used frequency spectrum, is established. To solve this multi-objective optimization model, we integrate these three objectives into one by using a weighted sum strategy. Then, an improved grey wolf optimization method (IGWO) is proposed. To demonstrate high performance of the designed algorithm, a series of experiments are conducted in several different experimental scenes. Experimental results indicate that the proposed algorithm can obtain better results than the compared algorithm. According to the experimental results, we can find that the objective function obtained by the proposed algorithm is 3%–12% less than those obtained by compared algorithms in different networks. However, integrating these objectives into one by using the weighted sum method also has some disadvantages. Thus, we will investigate the efficient algorithm based on the multi-objective optimization algorithm, such as MOEA/D, or other swarm intelligent algorithm. In addition, there are other objectives for the manycast RSA Problem in EONs. The multi-objective optimization algorithm will be investigated to obtain the Pareto front. Thus, it can give more decision-making plans to decision-makers.