Abstract
The test oracle problem exists widely in modern complex software testing, and metamorphic testing (MT) has become a promising testing technique to alleviate this problem. The inference of efficient metamorphic relations (MRs) is the core problem of metamorphic testing. Studies have proven that the combination of simple metamorphic relations can construct more efficient metamorphic relations. In most previous studies, metamorphic relations have been mainly manually inferred by experts with professional knowledge, which is an inefficient technique and hinders the application. In this paper, a genetic algorithm-based approach is proposed to construct composite metamorphic relations automatically for the program to be tested. We use a set of relation sequences to represent a particular class of MRs and turn the problem of inferring composite MRs into a problem of searching for suitable sequences. We then dynamically implement multiple executions of the program and use a genetic algorithm to search for the optimal set of relation sequences. We conducted empirical studies to evaluate our approach using scientific functions in the GNU scientific library (abbreviated as GSL). From the empirical results, our approach can automatically infer high-quality composite MRs, on average, five times more than basic MRs. More importantly, the inferred composite MRs can increase the fault detection capabilities by at least more than the original metamorphic relations.
1. Introduction
With the emergence of modern large-scale software systems, software testing has become an essential and expensive part of verifying the correctness of the program. Software testing is typically accomplished by selecting some program inputs as test cases, executing the selected test cases, and verifying the test results [1]. Most of these test cases have implicitly assumed that there exists a systematic mechanism (known as oracle) that helps testers verify the test result given any possible program input. However, when faced with more complex test scenarios, such as complex scientific functions, the output values corresponding to the test inputs can not be obtained well. Such a problem, termed as an oracle problem, is a fundamental challenge to be solved in software testing.
In order to alleviate the oracle problem, metamorphic testing (MT) is a software testing method proposed by Chen [2,3], which does not need the test oracle. This test technique first generates a set of metamorphic relations (MRs) according to the nature of the test program and then tests the software by judging whether the test case satisfies the metamorphic relations. Since MT is proposed, it has been widely applied on the test of various programs in many fields for its simple and efficient characteristics, such as image processing [4,5], network diagnosis [6,7], machine learning [8,9], bioengineering [10], and scientific software [11]. However, the metamorphic relations are generally constructed manually by the testers or developers who understand the principle of the test program, or are determined according to prior knowledge, which is an obstacle to software test automation. For example, for the program of the trigonometric function , some MRs like “” are easy to understand and infer, but some MRs like “” are not. Therefore, how to construct metamorphic relations efficiently and automatically is the core problem in metamorphic testing.
To alleviate this labor-intensive work, several works have been proposed to improve the inference of metamorphic relations. Some studies try to classify the classification of MRs based on machine learning methods [12,13], or attempt to construct more MRs based on information of the existence of the initial MRs [14,15]. Other recent research has yield MR identification based on the concepts of category and choice [16,17]. Liu [14] verified that the composition of metamorphic relations can improve the failure-detection capabilities rather than any particular metamorphic relations. However, the composition of metamorphic relations still needs to be constructed manually by the tester in an ad hoc way. As software becomes more and more complex and the increment number of composite layers increases, manual construction of composite metamorphic relations has become extremely difficult. With the cognitive bias in human experience, it is also easy to ignore critical metamorphic relations with manual operation. Therefore, how to construct complex composite metamorphic relations automatically and improve failure-detection capabilities by making full use of the information in predefined simple metamorphic relations is a significant research issue. Simultaneously, it is also interesting to study the influence of different layers on the composition of metamorphic relations.
In this paper, we focus on the automatic generation of multi-layer composite metamorphic relations. Then we propose a search-based automatic construction method of composite metamorphic relations by analyzing multiple executions of the program to be tested. In particular, we transform the construction of efficient composite metamorphic relations as the search for optimal composite sequences. We then use a genetic algorithm (GA) [18] to optimize the problem owing to the high efficiency of the discrete optimization problem, which alleviates the need for artificial construction of metamorphic relations. Furthermore, we analyze the influence of the number of composite layers on the failure-detection capabilities of composite metamorphic relations. We conduct three empirical studies on the scientific functions of the GNU scientific library (GSL) (http://www.gnu.org/software/gsl/) to evaluate our approach. In the first study, we verify the feasibility of our approach. In the second study, we investigate the quality of the composite metamorphic relations inferred by our approach. The third study investigates the impact of the number of composite layers on the fault detection capability of composite metamorphic relations. Our empirical results demonstrate that our approach can infer several high-quality composite metamorphic relations in an acceptable time frame.
The remainder of the paper is structured as follows: Section 2 introduces a brief review of the relevant works on the metamorphic relation inference, genetic algorithm, and search-based software testing. Section 3 presents the details of the proposed method. Section 4 reports the experimental results on the GSL scientific functions and the discussion. Section 5 presents the conclusions of the paper.
2. Related Works
2.1. Metamorphic Relation Inference
To improve the inference of metamorphic relations, several works have been proposed. Zhang [19] proposed a search-based approach to the automatic inference of polynomial MRs for a scientific program under test. More specifically, the particle swarm optimization algorithm is used to search for metamorphic relations in the form of linear or polynomial equations. Kanewala [12] proposed a predictive model using machine learning techniques to determine the classification of metamorphic relations. By giving three specific types of metamorphic relations, this method works by extracting a function’s control flow graph and predicting the category of the predefined metamorphic relations. In a later work [13], Kanewala extended the method using graph kernels, which provide various ways of measuring similarity among graphs. The intuition behind this approach was that functions that have similar control flow and data dependency graphs might have similar metamorphic relations. Chen [16] proposed a specification-based methodology and associated tool called METRIC for the identification of metamorphic relations based on the category-choice framework. Su [15] presented an approach named KABU for the dynamic inference of likely metamorphic relations inspired by previous work on the inference of program invariants. The inference process is constrained by searching for a set of predefined metamorphic relations. Javier [17] proposed an approach to infer likely metamorphic relations automatically for Atlas Transformation Language (ATL) model transformations. Liu [14] proposed a method named composition of metamorphic relations (CMR) to construct new metamorphic relations by combining several existing relations.
Our work is most related to the research proposed by Liu [14], which proved the combination of several existing MRs could construct effective composite metamorphic relations. Different from our approach, in that method, the composite metamorphic relations still need to be constructed manually by the testers from scratch. Our approach focuses on the automatic construction of multi-layer composite metamorphic relations, which can construct composite metamorphic relations more efficiently and accurately.
2.2. Genetic Algorithm
The genetic algorithm [18] is an adaptive heuristic optimization algorithm based on natural selection and genetic evolution. It is the basis of a large class of evolutionary algorithms, which generates new solutions through a series of evolutionary operations, such as selection, crossover, mutation, and so on. In recent years, several enhanced GA variants have been proposed to improve the search performance [20,21,22]. The general algorithm framework of the genetic algorithm is shown in Figure 1.
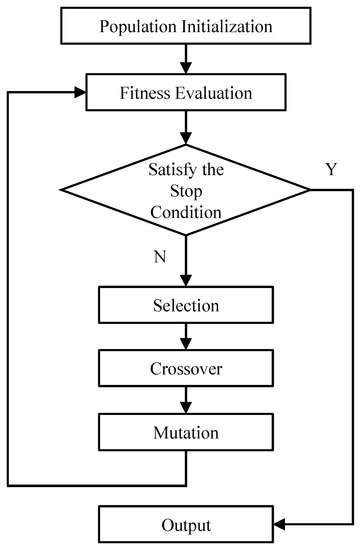
Figure 1.
Flowchart of the genetic algorithm.
Many problems in software engineering can be transformed into the combinatorial optimization problem. Thus, the genetic algorithm, which is simple and suitable for discrete problems, has been widely applied in software engineering [23,24,25,26,27,28]. Particularly, Mu [25] proposed a hybrid genetic algorithm-based strategy for software architecture re-modularization. Dai [28] proposed a genetic algorithm-based approach for testing-resource allocation problems that can be used for software systems with complex structures. In software testing, genetic algorithms are also efficiently applied to improve test efficiency, such as test planning [29], test case generation [23], and regression testing [30].
2.3. Search-Based Software Testing
Many problems in software engineering with a large complex search space can be transformed into discrete optimization problems. Thus it is very suitable to introduce search based methods, such as genetic algorithms [24], simulated annealing algorithms [31], and multi-objective optimization [32], to optimize problems in software engineering. Since the concept of search-based software engineering [33] (SBSE) was put forward, search-based methods have been widely used in the field of software engineering, such as test suit generation [24], fault localization [34], program analysis [35], software refactoring [36], and project scheduling [37].
Search-based software testing [38] (SBST) is the sub-area of the search-based software engineering concerned with software testing. We observe that approximately half of all SBSE papers are SBST papers [39]. MT is one of the software testing approaches. Although SBST is promising and essential, few works have been made to utilize the search-based methods to promote the efficiency of MT. Zhang [19] proposed a particle swarm optimization algorithm-based approach to the automatic inference of polynomial MRs for the scientific programs under test.
3. Our Approach
Before presenting our approach in Section 3.1, we first give a brief introduction to metamorphic testing. The concept of multi-layer composite metamorphic relations is revealed in Section 3.2. After that, our GA-based search algorithm for determining the composite metamorphic relation sequences is exhibited in Section 3.3.
3.1. Metamorphic Testing
Metamorphic testing is a technique conceived to alleviate the oracle problem. Rather than checking the output of an individual test, metamorphic testing checks whether multiple test executions fulfill certain metamorphic relations. A metamorphic relation of the program under test is an intrinsic property that relates two or more input data and their expected outputs. For example, consider the scientific functions under test , one of its metamorphic relations can be expressed as . Suppose the source test case is x, then the follow-up test case can be , if the source test case and its follow-up test case violate the metamorphic relation , then program under test must contain a bug.
Metamorphic relations are the core position of the metamorphic testing. Metamorphic relation is an intrinsic property of the program under test, which describes how a change to the input would result in a change to the output. Then we can define an MR as
where and denote the original input and changed input, respectively, and denote the outputs corresponding to and , is the relation between input and , and is the relation between output and .
According to Chen [3], an MR is supposed to hold among multiple executions. Suppose that f is the function under test, and denote a set of M test inputs and the corresponding outputs, respectively. Then a more general form of a metamorphic relation can be given as
where R is the relation between inputs , is the relation between outputs , and the MR can be marked as .
Although a program under test may have multiple MRs, the failure-detection capabilities of different MRs may be varied. Therefore, it is important to construct a better MR with a better failure-detection capability.
3.2. Multi-Layer Composite Metamorphic Relations
It is clear that metamorphic relations are the core part of metamorphic testing, and Liu [14] verified the superiority of the composition of metamorphic relations (CMR). Let be k metamorphic relations of the test function f under test, all k MRs satisfy the Formula (2). Suppose and are two metamorphic relations, composite metamorphic relation means that is composite to if and only if for any source test case T for , its corresponding follow-up test case satisfies [14]. Similarly, for all k metamorphic relations, if is composite to (), the k-layer composite metamorphic relation is said to be the composition of if and only if for any source test case T for , its corresponding follow-up test case satisfies . It should be noticed that the composition is sensitive to the order of metamorphic relations. For example, that exists does not imply that exists as well, and even if both and exist, they are not necessarily equivalent to each other.
New composite metamorphic relations will embed all properties associated with the original fundamental metamorphic relations, and reduce the number of test cases generated and executed in metamorphic testing. However, the construction of composite metamorphic relations is conditional, and not all metamorphic relations can be compounded. As mentioned above, composite rules need to be satisfied between the test case and follow-up test case of metamorphic relations. Furthermore, just like the construction of basic MRs, the inference of composite metamorphic relations is still involved with much human intelligence for analyzing specification, finding the necessary characteristics of the program under test. Therefore, the automatic inference of multi-layer composite metamorphic relations has become urgent.
3.3. GA-Based Approach for Searching Composite MRs
As mentioned above, the main difficulty of CMR inference is the construction of CMRs that needs to satisfy the composite rules. To solve the problem of the automatic construction of multi-layer composite metamorphic relations, we turn the problem of CMRs construction into a search problem that searches for optimal composite sequences. Then a genetic algorithm-based approach is applied. The framework of the proposed algorithm is described in Algorithm 1.
| Algorithm 1 Genetic algorithm applied to CMR construction. |
|
First, an initial population is set (see lines 1–2). Each individual in the population represents a possible solution to the problem, i.e., a sequence of composite metamorphic relation. The maximum size of an individual is a parameter of the composite layer that can be defined by the user. An individual of the initial population is constructed randomly. More details about the representation of individuals can be found in the next Section 3.3.1.
In the remaining steps of code in the Algorithm 1, the search space is explored. In each iteration, the fitness value for each individual in the population is determined. This value counts the number of inputs that satisfy the Formula (1). A new population is constructed by evolutionary operators, i.e., selection, crossover, and mutation based on the fitness value (see Section 3.3.2 for more details). The execution of the algorithm continues for a certain number, and individual with the best fitness value overall iterations will be returned.
As one execution of our GA algorithm generates only one possible CMR, we need to execute our GA algorithm several times to obtain several CMRs. Due to the random initialization of the individuals and the random factors (crossover rate and mutation rate), different executions of our GA algorithm may not always produce a good enough solution (whose fitness value is lower than a threshold denoted as F). In such cases, we drop all not good enough solutions. All related parameter-setting of our GA algorithm is presented in Section 4.1.
3.3.1. Representation of Individuals
Suppose denotes the set of basic metamorphic relations, and m represents the number of basic metamorphic relations. K denotes the composite layer (namely individual size). As already mentioned, an individual in the population represents a sequence of CMR. Each position in the individual is constructed randomly from 1 to m, and then a random individual is plotted in Figure 2.
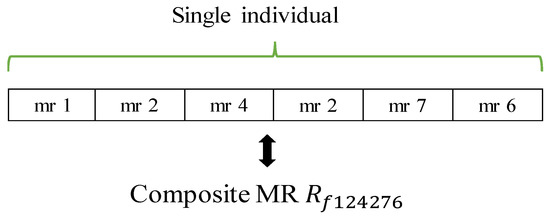
Figure 2.
Individual representation. Metamorphic relation (MR).
3.3.2. Genetic Operators
In order to retain the chromosome with the higher fitness value, the individuals with high fitness value are selected to crossover after the evaluation of the CMR sequence. We use roulette wheel selection [40] to choose the individuals on which crossover and mutation will be applied.
To apply the crossover operation, the single-point selection is used. This operation is performed according to the random crossover point from 1 to K. In the crossover operation, two offsprings are generated from the parent individuals. Figure 3 illustrates an example of a crossover operation with a single point. All genes after the crossover point in the parents are swapped to produce the offspring.
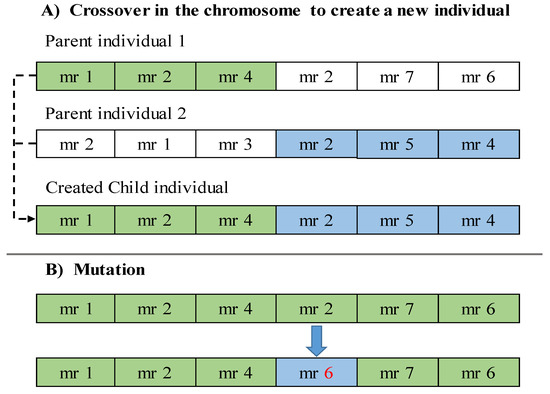
Figure 3.
Crossover and mutation operation.
In the mutation operation, one gene of an individual is chosen randomly and replaced by other genes from the set of basic metamorphic relations. As shown in Figure 3, is replaced by , and is selected from the basic MRs set randomly.
3.3.3. Fitness Function
Formally, given a program under test (denoted as P) and M test inputs (denoted as ), the fitness function can be transformed into a search problem of finding several CMR sequences such that for almost every input (), the CMR sequence and satisfy Formula (1).
Thus, we can define the fitness functions as follows. Given the CMR sequence , if and input () satisfy Formula (1), we define ; otherwise we define . Therefore, the fitness of the CMR sequence can be defined as
Actually, the fitness of a CMR sequence counts the number of inputs that satisfy Formula (1) by multiple executions of the program P.
4. Experimental Results
In order to verify the effectiveness of our proposed approach, we select some scientific functions in the open-source software GNU scientific library (abbreviated as GSL) for experimental verification and carry out three groups of experiments. First of all, we verify the feasibility of the proposed method, that is, the proposed approach can infer effective composite metamorphic relations. Secondly, we analyze the quality of the derived composite metamorphic relations. We used the mutation testing [41] to analyze the mutation score of each composite metamorphic relations. Finally, we analyze the effect of the number of composite layers on composite metamorphic relations.
4.1. Experimental Settings
The MT used in this paper is a black box test method, that is, we do not focus on the inside of the source code as we only need to care about the results of multiple program runs. Therefore, our experiment is not sensitive to the language of the test functions. The test functions selected in this paper are from the open-source software library GNU scientific library (abbreviated as GSL). The GNU scientific library is a numerical calculation function library written in C++. The experiments used in this paper are all written in C++.
There are many scientific calculation functions in GSL. In this paper, the trigonometric functions and in the “specfunc” directory are selected. Due to the nature of trigonometric functions, it is difficult for us to deduce the MRs intuitively. They can only be analyzed through verification, which is suitable for MT. The scientific functions are also suitable for the experimental analysis of CMR. In the GSL, the valid code of the two test functions and is about 100 lines, and the core code is about 40 lines. Since the composite MRs need to be compounded based on the given simple MRs, eight simple MRs are respectively given for the two test trigonometric functions, that is, the number of initial MRs for both function is . Details of the initial MRs of two test functions are shown in Table 1.

Table 1.
Eight basic MRs of and and the corresponding mutation scores.
We use the genetic algorithm to construct the CMRs of different composite layers, and set different initial population sizes for different composite MRs. In this section, we construct 2-layer (2-CMR), 3-layer (3-CMR), and 4-layer (4-CMR) composite MRs, respectively. The setting of population size is important to GA; Chen [42] investigated that the population size for the population-based search methods can be set up four to six times as large as the dimension of the individual for problems in low dimensions. Thus, in this paper, we set the initial population size of the algorithm as 12, 20, and 30 individuals, respectively. In the experiments, the empirical parameters of the genetic algorithm are set as, according to the study of Eiben [43], the probability of crossover can be set as . And for the discrete optimization, the mutation rate should be larger than that in the continuous optimization [44], and then we set the mutation rate as . The crossover and mutation rate remain unchanged during the iteration of genetic algorithm. And the stop generation is 100. Considering the randomness of the genetic algorithm, we implement the algorithm 100 times for each population and record several complex CMR sets with strong failure-detection capabilities corresponding to the number of layers.
As the functions under test selected in the experiments are all trigonometric functions, the test input of the algorithm is the real number generated randomly within a certain range (here we set the interval as ). In the genetic algorithm, the number of test inputs for the evaluation fitness of the CMRs is 100 (). We set the threshold to select good enough solutions F as .
4.2. CMR Inference
In this section, we demonstrate the quantity statistics of the inferred CMRs and the average time required for executing the program. Table 2 and Table 3 show the statistics of the CMRs derived based on the proposed approach in this paper. As can be seen from Table 2, for two classical trigonometric functions, the number of 2-CMRs ranges from 3 to 59, the number of 3-CMRs is from 5 to 102, and the number of 4-CMRs is from 7 to 143. This indicates that our approach infers plenty of compositional MR for the test trigonometric functions. As shown in Table 3, the execution time of our approach to inferring the compositional MRs for each trigonometric function is from 29.25 s to 789.15 s, which is acceptable. With the increase of composite layers, the time required is also increased. Therefore, our approach is able to infer at least five times more MRs than the initial set of MRs. The statistical data in Table 2 and Table 3 indicates that our approach is feasible and efficient.

Table 2.
The statistics on number of composition of metamorphic relations (CMRs).

Table 3.
The statistics on running time for CMRs.
We also compare our GA-based approach with the basic simulated annealing algorithm (SAA) [45], which displayed impressive performance in discrete optimization problems such as Traveling Salesman Problem (TSP) [46]. The initial and end temperature of SAA are set as 200 and 0.005, respectively. The cool coefficient is set as 0.95. And we also run the SAA 100 times. The comparison of the average number of inferred CMRS by the GA-based and SAA-based approach is plotted in Figure 4. As shown in Figure 4, the proposed GA-based approach can construct more CMRs than the SAA-based approach in all situations, which indicates the high efficiency of our approach.
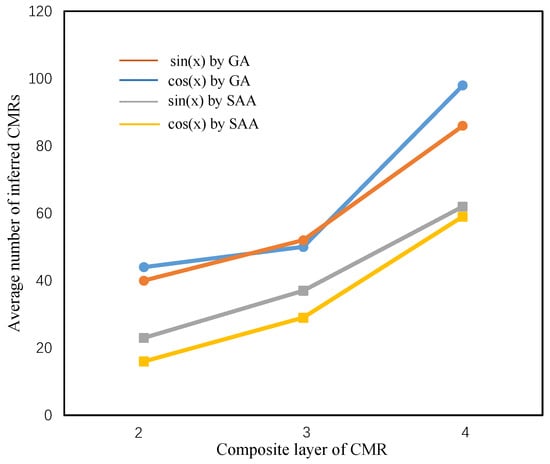
Figure 4.
Comparison of a genetic algorithm (GA)-based approach and a simulated annealing algorithm (SAA)-based approach.
4.3. Quality of Inferred CMRs
As shown in Section 4.2, our approach can infer several CMRs, and we then want to test the quality of these CMRs. First, we need to investigate the correctness of the derived CMRs. As the test functions selected in this paper are typical scientific calculation functions, we can verify the correctness of the derived CMRs through WolframAlpha [47]. We verified that the derived composite metamorphic relations are correct and valid.
Table 4 presents typical CMRs of the trigonometric functions and . From the table, these typical CMRs include complex MRs of the trigonometric functions than the basic MRs in Table 1. For example, these 2-CMRs, represented by , can reflect the periodical and trigonometric transformation characteristics of the function. The inferred 3-CMRs, represented by , show the quadratic relation between and besides the symmetric and periodical characteristics of the function.

Table 4.
Typical CMRs of and and the corresponding mutation score.
We note that the number of CMRs listed in Table 4 is less than the number of inferred MRs shown in Table 2, and this is because some of the CMRs inferred by the algorithm are equal. In fact, some of the CMRs we derive are equivalent, as Chen [3] demonstrated that more MRs could perform more complete testing processes, so these equivalent composite MRs derived from other basic MRs are not redundant. For example, in order to the reveal the faults that can be detected only by , it may be more costly to check the two basic MRs (i.e., and ) rather than one MR. To check the , testers may run the function twice, whereas checking the latter two MRs and , testers may run the function four times. Therefore, the CMR reduces the number of times the program needs to run and thus improves efficiency.
In order to test the fault detection capabilities of the derived CMRs, we use mutation testing [41] to conduct experiments. We generate 168 mutants for both and of GSL through Mujava [48]. The detailed types of mutants are listed in Table 5, including Arithmetic Operator Deletion (AODU), Arithmetic Operator Insertion (AOIS), Arithmetic Operator Replacement (AORB), Assignment Operator Replacement (ASRS), Constant Deletion (CDL), Conditional Operator Insertion (COI), Logical Operator Insertion (LOI), Logical Operator Replacement (LOR), Operator Deletion (ODL), Relational Operator Replacement (ROR) and Variable Deletion (VDL). The mutants of the subject program are listed in Table 6. In this paper, the mutation score (MS) [41] is used as the evaluation to measure the quality of the composite MRs. Let T denotes the source test case of the program under test, and denotes the follow-up test case, which derived from metamorphic relations . denotes the mutants produced by Mujava. One can judge whether the kills the mutant by verifying the results of T and . The mutation score can be obtained by counting the proportion of the number of killed mutants to the total number of mutants. The mutation score of metamorphic relation can be defined as
where , , and denote the number of killed mutants by , total number of mutants, and equivalent mutants in the mutants set, respectively.

Table 5.
Mutant types generated by Mujava.

Table 6.
Mutants of the subject program.
In Table 1, we construct eight basic MRs of and , respectively, and the mutation scores of the corresponding basic MRs are listed on the right side of the table according to the mutation testing. It can be seen from the table that for the eight basic MRs of , with a few exceptions such as , the fault detection capabilities of basic MRs is relatively poor. The average mutation score of the basic MRs set of is 0.23. The mutation scores corresponding to the basic MRs of are similar.
As shown in the right side of Table 4, the mutation scores of some typical CMRs of and are given. It can be seen from the table that the mutation scores of these CMRs are higher than that of the basic MRs. All mutation scores of CMRs are higher than 0.5. The results show that the method of inferring the CMRs based on the genetic algorithm can construct several composite MRs with strong fault detection capabilities, and the mutation scores are much higher than the initial MRs, which verifies the feasibility of the proposed approach.
It is worth noting that few initial MRs with high fault detection capabilities, such as of (mutation score is 0.4), can construct CMRs with higher faults detection capability, such as , . However, more initial MRs with lower mutation score, such as and of , can construct CMRs with high faults detection capability, such as . This indicates that the construction of the CMRs is not sensitive to the faults detection capability of the initial MRs. Therefore, one only needs to construct some simple MRs for the program under test, which also makes the method proposed in this paper more applicable.
4.4. Influence of Composite Layers
As shown in Table 4 of Section 4.3, with the increase of the number of composite layers, the corresponding mutation scores also show an upward trend, and there are simple statistics shown in Table 7. We see from Table 7 that the average mutation scores of the two trigonometric functions increase with the increase of the number of composite layers, and the average mutation scores of 3-CMR and 4-CMR are relatively close. Thus, in order to verify the influence of composite layers on inferred CMRs, we increase the number of composite layers of the CMRs. The obtained relationship between the number of composite layers and the average mutation scores of the CMRs is shown in Figure 5.

Table 7.
The average mutation scores of multi-layer CMRs.
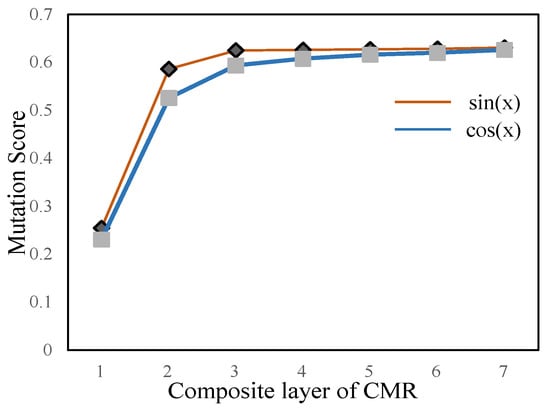
Figure 5.
Illustration of the mutation score changes with the increase of composite layers.
From Figure 5, it can be seen that the CMRs can indeed enhance the fault detection capabilities, but as the number of layers increases to a certain number, the fault detection capabilities of CMRs will tend to be stable. In particular, the improved range of the mutation scores of the two-layer and three-layer composite MRs is relatively apparent. When the number of composite layers is greater than three-layer, the enhanced range of fault detection capabilities will not be noticeable. With more layers of CMRs, more work is needed to construct the corresponding follow-up test cases. Therefore, we can conclude that two-layer and three-layer composite MRs can be better to practical metamorphic testing.
5. Conclusions
We have proven that the composition of basic metamorphic relations can construct more effective composite metamorphic relations (CMRs) [14]. However, the construction of CMRs still needed to be inferred manually by testers, which was a bottleneck of the application. One of the main difficulties is the condition of constructing CMRs, and this has to satisfy the composite rules. In this paper, a GA-based approach for automatic construction of composite metamorphic relations was proposed by analyzing multiple executions of the same program under test. We viewed the problem of composite MRs inference as a searching problem, then used the GA algorithm to search for the optimal composite sequences that satisfied the composite rules. Then we conducted three empirical studies to validate the correctness and efficiency of our approach. It turns out that our proposed method can infer several CMRs with high quality in an acceptable time (from 29 s to 789 s), and are effective in detecting faults by mutant testing. On average, at least five times more composite MRs, in terms of quantity, can be constructed compared to the initial MRs. We also analyzed the effect of the composite layer on CMR’s fault detection capabilities. The results show that with the increase in the number of composite layers, the fault detection capabilities will increase by , at least. However, the improvement of fault detection capability is limited. Additionally, the experiments illustrate that setting composite layers at three is the best choice.
There are some limitations to the proposed method in this paper. For example, the input of the program only supports numerical values, and it is not suitable for arrays or pointers. Therefore, we may improve the existing GA approach by transforming these non-numerical values into numerical values. Our approach can only infer the composite metamorphic relations in the form of equality so far, and further, some metamorphic relations will be represented by the inequality. Then, our future research should be carried out from the following two perspectives. First, we will extend the genetic algorithm-based method to non-scientific functions and the form of inequalities. Second, we will extend our work to find a set of CMRs with the least number and highest fault detection capabilities, and the multi-objective optimization method will be useful for this extended work.
Author Contributions
Z.X. performed the experiments and wrote the papaer; H.W. and F.Y. proposed the idea and designed the model.
Funding
This research was funded by the National Natural Science Foundation of China [Grant No. 61672391 and 61702239], the Foundation of Fujian Province Great Teaching Reform, China [No. FBJG 20180015], and the Science Foundation of Jiangxi Provincial Department of Education [GJJ170765, GJJ170798].
Acknowledgments
We are grateful for the discussion and data collection by Xiongtao Xia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barr, E.T.; Harman, M.; McMinn, P.; Shahbaz, M.; Yoo, S. The oracle problem in software testing: A survey. IEEE Trans. Softw. Eng. 2014, 41, 507–525. [Google Scholar] [CrossRef]
- Chen, T.Y.; Kuo, F.; Tse, T.H.; Zhou, Z. Metamorphic Testing and Beyond. In Proceedings of the 11th International Workshop on Software Technology and Engineering Practice, Amsterdam, The Netherlands, 19–21 September 2003; pp. 94–100. [Google Scholar]
- Chen, T.Y.; Kuo, F.; Liu, H.; Poon, P.; Towey, D.; Tse, T.H.; Zhou, Z.Q. Metamorphic Testing: A Review of Challenges and Opportunities. ACM Comput. Surv. 2018, 51, 4. [Google Scholar] [CrossRef]
- Guderlei, R.; Mayer, J. Towards Automatic Testing of Imaging Software by Means of Random and Metamorphic Testing. Int. J. Softw. Eng. Knowl. Eng. 2007, 17, 757–781. [Google Scholar] [CrossRef]
- Chan, W.K.; Ho, J.C.F.; Tse, T.H. Finding failures from passed test cases: Improving the pattern classification approach to the testing of mesh simplification programs. Softw. Test. Verif. Reliab. 2010, 20, 89–120. [Google Scholar] [CrossRef]
- Sun, C.; Wang, G.; Mu, B.; Liu, H.; Wang, Z.; Chen, T.Y. A Metamorphic Relation-Based Approach to Testing Web Services Without Oracles. Int. J. Web Serv. Res. 2012, 9, 51–73. [Google Scholar] [CrossRef][Green Version]
- Segura, S.; Parejo, J.A.; Troya, J.; Cortés, A.R. Metamorphic Testing of RESTful Web APIs. IEEE Trans. Softw. Eng. 2018, 44, 1083–1099. [Google Scholar] [CrossRef]
- Xie, X.; Ho, J.W.K.; Murphy, C.; Kaiser, G.E.; Xu, B.; Chen, T.Y. Testing and validating machine learning classifiers by metamorphic testing. J. Syst. Softw. 2011, 84, 544–558. [Google Scholar] [CrossRef]
- Nakajima, S.; Chen, T.Y. Generating Biased Dataset for Metamorphic Testing of Machine Learning Programs. In Proceedings of the International Conference Testing Software and Systems, Paris, France, 15–17 October 2019; pp. 56–64. [Google Scholar]
- Shahri, M.P.; Srinivasan, M.; Reynolds, G.; Bimczok, D.; Kahanda, I.; Kanewala, U. Metamorphic Testing for Quality Assurance of Protein Function Prediction Tools. In Proceedings of the 2019 IEEE International Conference On Artificial Intelligence Testing, Newark, CA, USA, 4–9 April 2019. [Google Scholar] [CrossRef]
- Lin, X.; Simon, M.; Niu, N. Hierarchical metamorphic relations for testing scientific software. In Proceedings of the International Workshop on Software Engineering for Science, Gothenburg, Sweden, 2 June 2018; pp. 1–8. [Google Scholar]
- Kanewala, U.; Bieman, J.M. Using machine learning techniques to detect metamorphic relations for programs without test oracles. In Proceedings of the 24th International Symposium on Software Reliability Engineering, Pasadena, CA, USA, 4–7 November 2013; pp. 1–10. [Google Scholar]
- Kanewala, U.; Bieman, J.M.; Ben-Hur, A. Predicting metamorphic relations for testing scientific software: A machine learning approach using graph kernels. Softw. Test. Verif. Reliab. 2016, 26, 245–269. [Google Scholar] [CrossRef]
- Liu, H.; Liu, X.; Chen, T.Y. A New Method for Constructing Metamorphic Relations. In Proceedings of the 12th International Conference on Quality Software, Xi’an, China, 27–29 August 2012; pp. 59–68. [Google Scholar]
- Su, F.; Bell, J.; Murphy, C.; Kaiser, G.E. Dynamic Inference of Likely Metamorphic Properties to Support Differential Testing. In Proceedings of the 10th International Workshop on Automation of Software Test, Florence, Italy, 23–24 May 2015; pp. 55–59. [Google Scholar]
- Chen, T.Y.; Poon, P.; Xie, X. METRIC: METamorphic Relation Identification based on the Category-choice framework. J. Syst. Softw. 2016, 116, 177–190. [Google Scholar] [CrossRef]
- Troya, J.; Segura, S.; Cortés, A.R. Automated inference of likely metamorphic relations for model transformations. J. Syst. Softw. 2018, 136, 188–208. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms and the Optimal Allocation of Trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Hao, D.; Xiong, Y.; Xie, B.; Zhang, L.; Mei, H. Search-based inference of polynomial metamorphic relations. In Proceedings of the International Conference on Automated Software Engineering, Vasteras, Sweden, 15–19 September 2014; pp. 701–712. [Google Scholar]
- Deng, Y.; Liu, Y.; Zhou, D. An improved genetic algorithm with initial population strategy for symmetric TSP. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Kora, P.; Yadlapalli, P. Crossover operators in genetic algorithms: A review. Int. J. Comput. Appl. 2017, 162. [Google Scholar] [CrossRef]
- Li, X.; Wong, W.E.; Gao, R.; Hu, L.; Hosono, S. Genetic algorithm-based test generation for software product line with the integration of fault localization techniques. Empir. Softw. Eng. 2018, 23, 1–51. [Google Scholar] [CrossRef]
- Sharma, C.; Sabharwal, S.; Sibal, R. A Survey on Software Testing Techniques using Genetic Algorithm. arXiv 2014, arXiv:1411.1154. [Google Scholar]
- Mu, L.; Sugumaran, V.; Wang, F. A Hybrid Genetic Algorithm for Software Architecture Re-Modularization. Inf. Syst. Front. 2019, 1–29. [Google Scholar] [CrossRef]
- Boopathi, M.; Sujatha, R.; Kumar, C.S.; Narasimman, S.; Rajan, A. Markov approach for quantifying the software code coverage using genetic algorithm in software testing. Int. J. Bio-Inspired Comput. 2019, 14, 27–45. [Google Scholar] [CrossRef]
- Goyal, S.; Mishra, P.; Lamichhane, A.; Gandhi, P. Software test case optimization using genetic algorithm. Int. J. Sci. Eng. Sci. 2018, 1, 69–73. [Google Scholar]
- Dai, Y.S.; Xie, M.; Poh, K.L.; Yang, B. Optimal testing-resource allocation with genetic algorithm for modular software systems. J. Syst. Softw. 2003, 66, 47–55. [Google Scholar] [CrossRef]
- Ray, M.; Mohapatra, D.P. Multi-objective test prioritization via a genetic algorithm. Innov. Syst. Softw. Eng. 2014, 10, 261–270. [Google Scholar] [CrossRef]
- Raju, S.; Uma, G. Factors oriented test case prioritization technique in regression testing using genetic algorithm. Eur. J. Sci. Res. 2012, 74, 389–402. [Google Scholar]
- Bank, M.; Ghomi, S.M.T.F.; Jolai, F.; Behnamian, J. Application of particle swarm optimization and simulated annealing algorithms in flow shop scheduling problem under linear deterioration. Adv. Eng. Softw. 2012, 47, 1–6. [Google Scholar] [CrossRef]
- Ramírez, A.; Romero, J.R.; Ventura, S. A survey of many-objective optimisation in search-based software engineering. J. Syst. Softw. 2019, 149, 382–395. [Google Scholar] [CrossRef]
- Jiang, H.; Tang, K.; Petke, J.; Harman, M. Search Based Software Engineering [Guest Editorial]. IEEE Comput. Int. Mag. 2017, 12, 23–71. [Google Scholar] [CrossRef]
- Sun, S.; Guo, J.; Zhao, R.; Li, Z. Search-Based Efficient Automated Program Repair Using Mutation and Fault Localization. In Proceedings of the 42th Annual Computer Software and Applications Conference, Tokyo, Japan, 23–27 July 2018; pp. 174–183. [Google Scholar]
- Zeller, A. Search-Based Program Analysis. In Proceedings of the Search Based Software Engineering—Third International Symposium, Szeged, Hungary, 10–12 September 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Mohan, M.; Greer, D. A survey of search-based refactoring for software maintenance. J. Softw. Eng. R D 2018, 6, 3. [Google Scholar]
- Rezende, A.V.; Silva, L.; Britto, A.; Amaral, R. Software project scheduling problem in the context of search-based software engineering: A systematic review. J. Syst. Softw. 2019, 155, 43–56. [Google Scholar] [CrossRef]
- Harman, M.; Jia, Y.; Zhang, Y. Achievements, Open Problems and Challenges for Search Based Software Testing. In Proceedings of the 8th International Conference on Software Testing, Verification and Validation, Graz, Austria, 13–17 April 2015; pp. 1–12. [Google Scholar] [CrossRef]
- Segura, S.; Fraser, G.; Sánchez, A.B.; Cortés, A.R. A Survey on Metamorphic Testing. IEEE Trans. Softw. Eng. 2016, 42, 805–824. [Google Scholar] [CrossRef]
- Bajaj, A.; Sangwan, O.P. A Systematic Literature Review of Test Case Prioritization Using Genetic Algorithms. IEEE Access 2019, 7, 126355–126375. [Google Scholar] [CrossRef]
- Papadakis, M.; Kintis, M.; Zhang, J.; Jia, Y.; Traon, Y.L.; Harman, M. Chapter Six - Mutation Testing Advances: An Analysis and Survey. Adv. Comput. 2019, 112, 275–378. [Google Scholar]
- Chen, S.; Montgomery, J.; Röhler, A.B. Measuring the curse of dimensionality and its effects on particle swarm optimization and differential evolution. Appl. Intell. 2015, 42, 514–526. [Google Scholar] [CrossRef]
- Eiben, Á.E.; Hinterding, R.; Michalewicz, Z. Parameter control in evolutionary algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
- Doerr, B.; Doerr, C.; Ebel, F. From black-box complexity to designing new genetic algorithms. Theor. Comput. Sci. 2015, 567, 87–104. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Chen, Z.; Yang, W.; Shi, D.; Zhao, K. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Appl. Soft Comput. 2011, 11, 3680–3689. [Google Scholar] [CrossRef]
- Delgado, F. Meaningful Learning of Math and Sciences Using Wolfram Alpha Widgets. In Proceedings of the EdMedia+ Innovate Learning, Victoria, BC, Canada, 24 June 2013; pp. 1794–1799. [Google Scholar]
- Ma, Y.; Offutt, J.; Kwon, Y.R. MuJava: An automated class mutation system. Softw. Test. Verif. Reliab. 2005, 15, 97–133. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).