A Global Extraction Method of High Repeatability on Discretized Scale-Space Representations
Abstract
:1. Introduction
2. Sketch of GPE
- Compute the point of maximal response in through Equation (3).
- Update the set .
3. Discretization and Transformation of Scale-Space Representations
3.1. Choice of an Appropriate Kernel
3.2. Size of Convolution Templates
3.3. Algorithm for Discretizing and Transforming Scale-Space Representations
| Algorithm 1: Sampling a scale-space representation |
| Input: (i) an image to be processed, ; (ii) the maximal pixel scale, N. |
| Calculate the maximal gray level in the image. |
for
|
| end for |
| Build a 3-dimensional array by ; |
| Output: the array , and the maximal gray level . |
4. Extracting Features from Discretized Scale-Space Representations
| Algorithm 2: Extracting extrema in discretized scale-space representations |
| Input: (i) the sample (an array) and the maximal gray leve obtained by Algorithm 1; (ii) the relative error threshold ; (iii) a positive real number ; (iv) the resolution of interpolation . |
| Calculate the threshold for the error tolerance by Equation (7) |
for
|
| end for |
| Build a matrix by all records (column vectors) from step (d); |
| Output: the matrix consisting of extracted local features. |
5. Simulations
5.1. Comparison with Affine Detectors
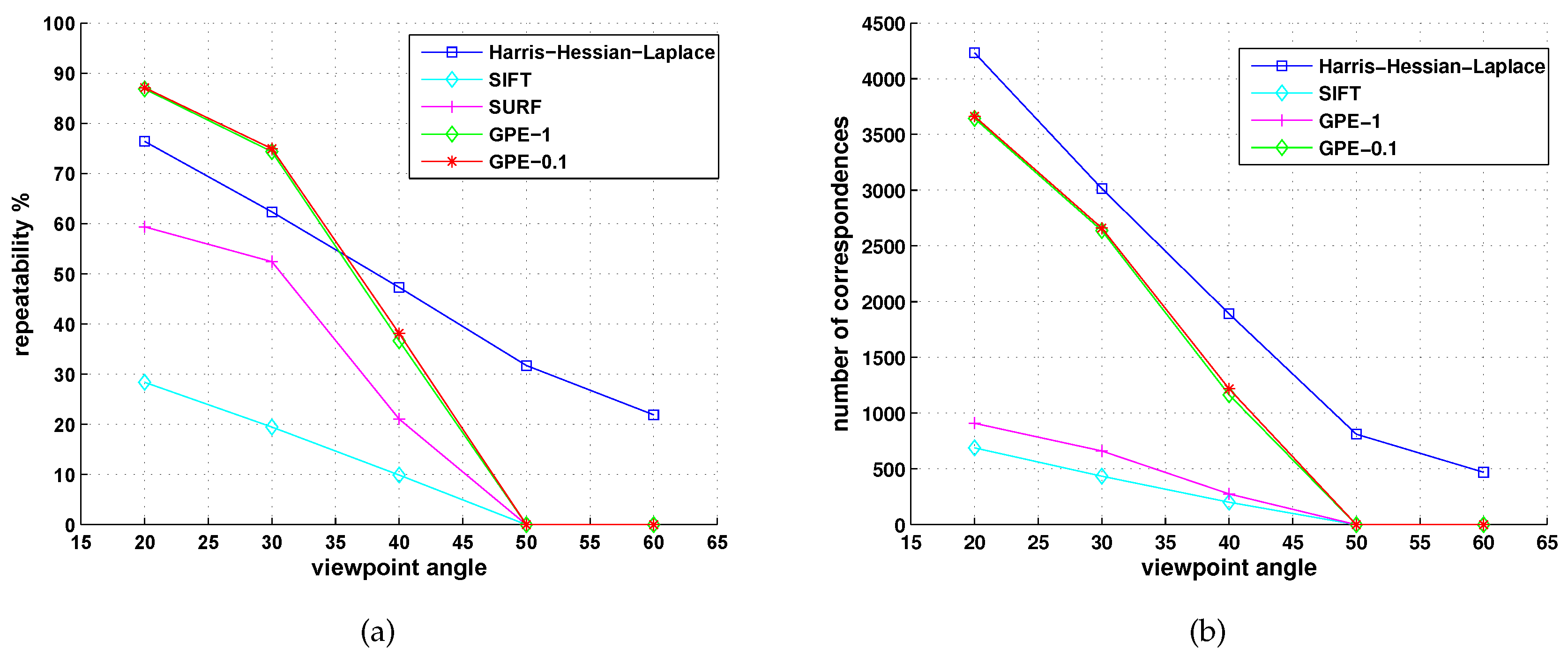
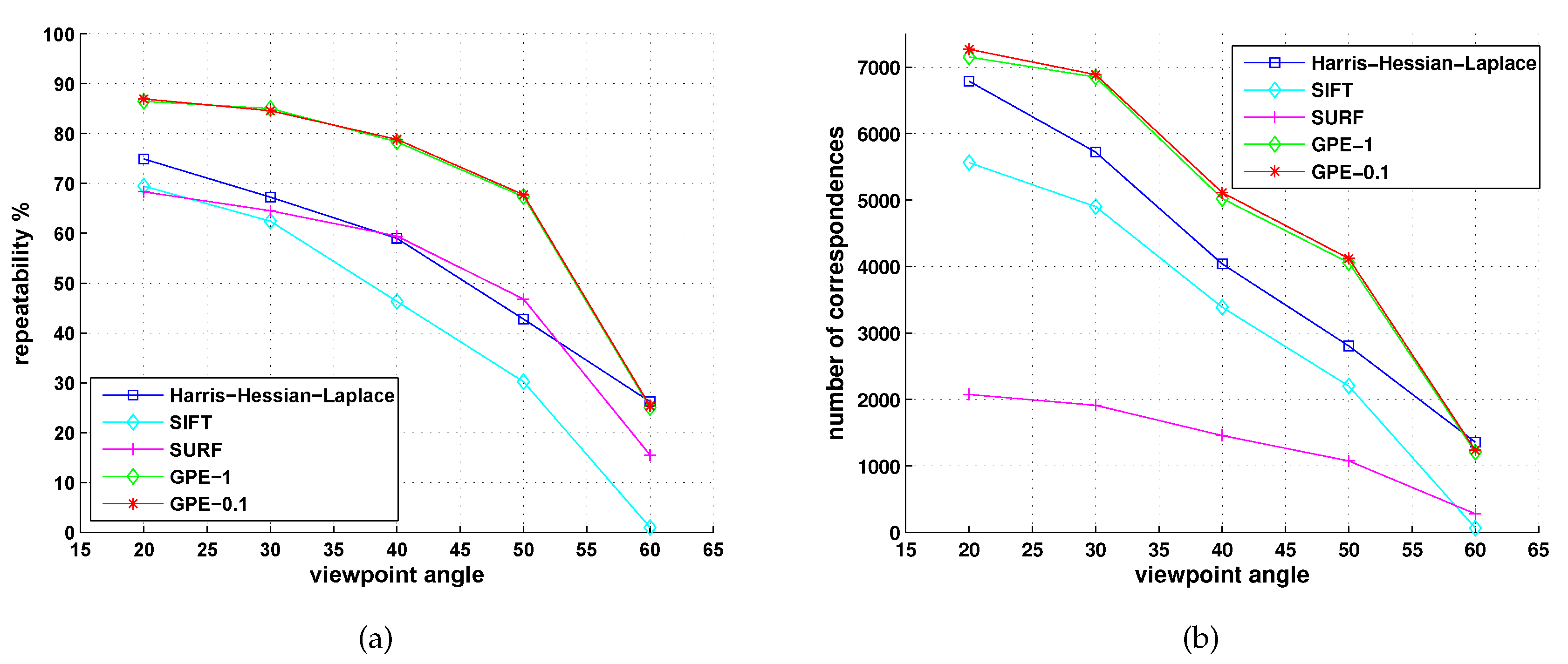
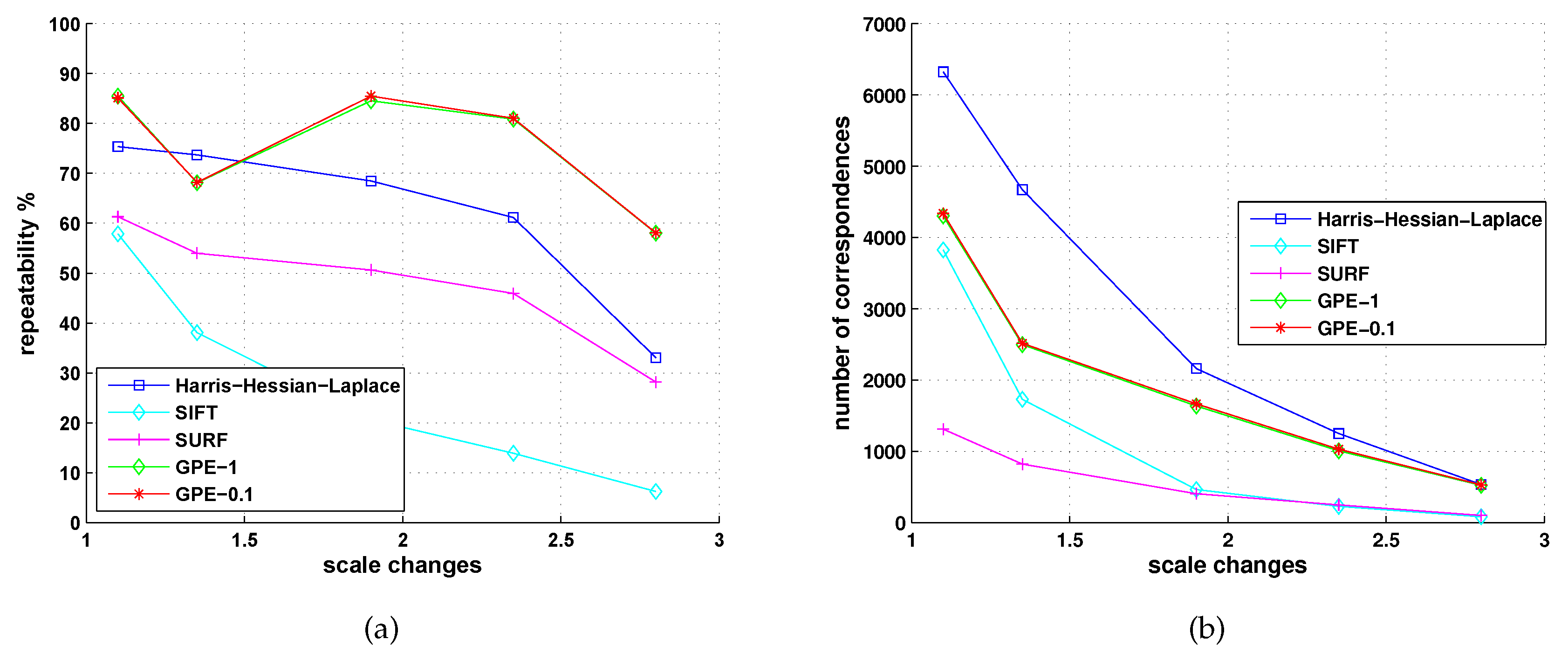
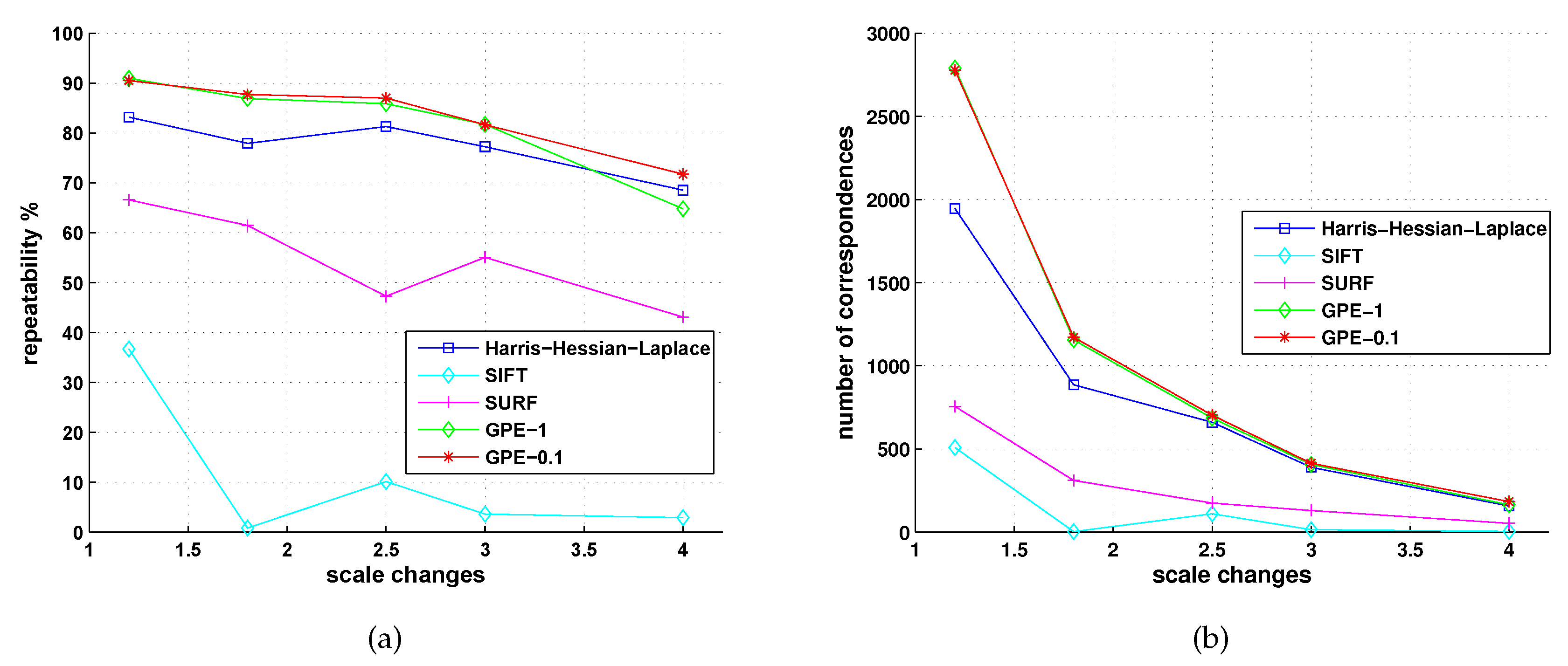
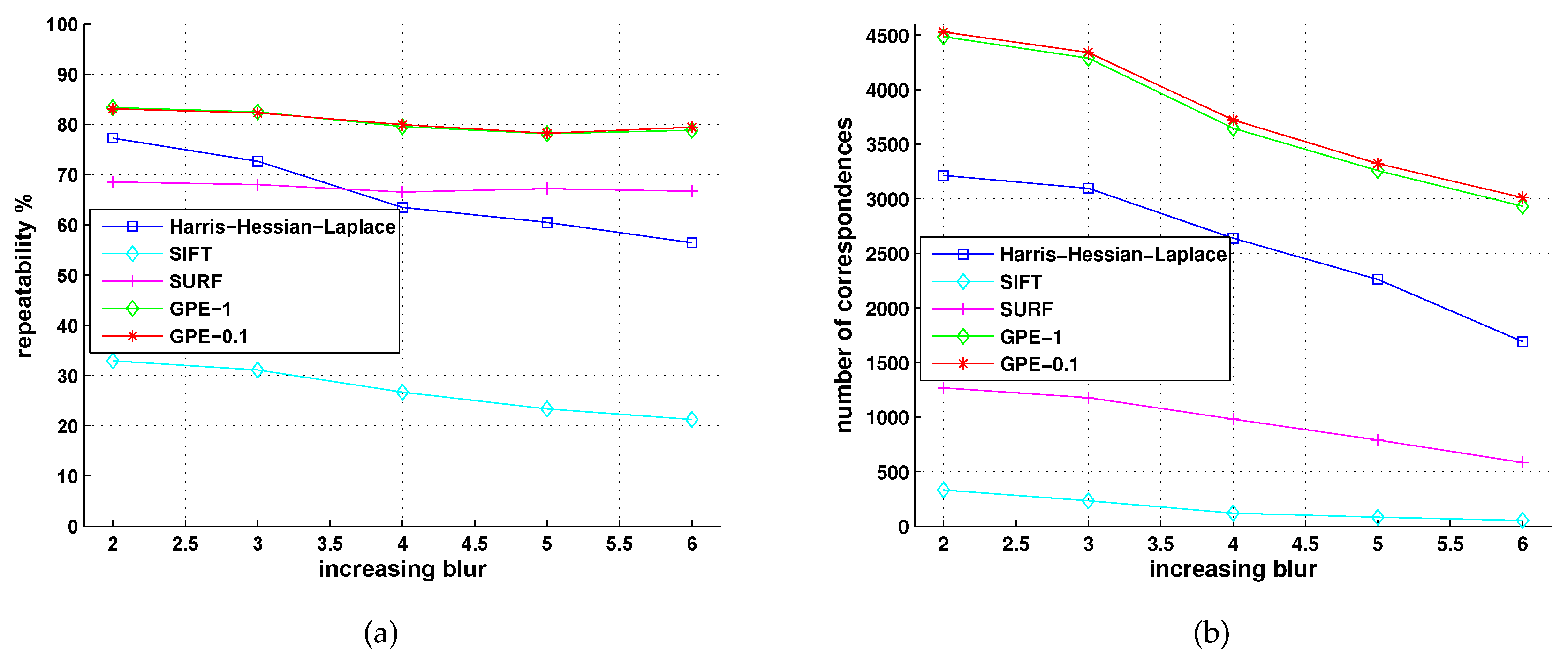
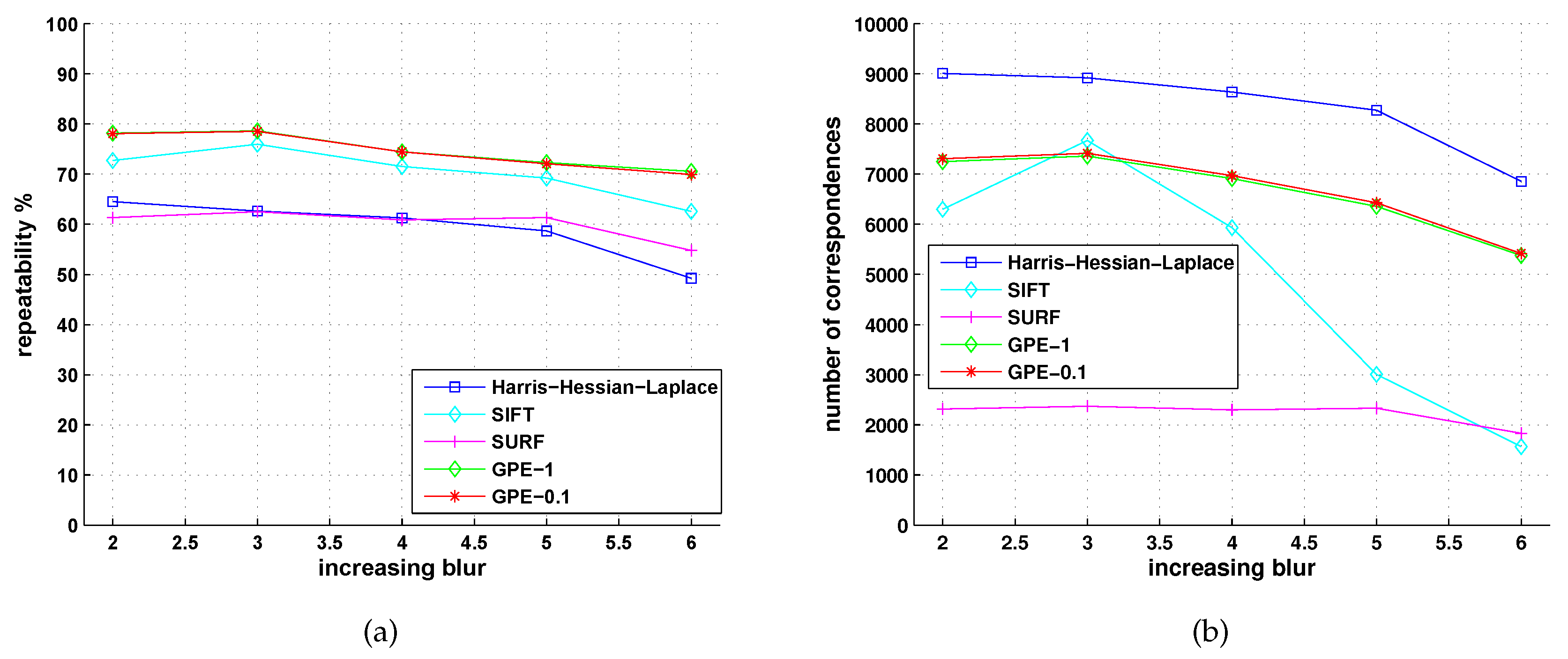
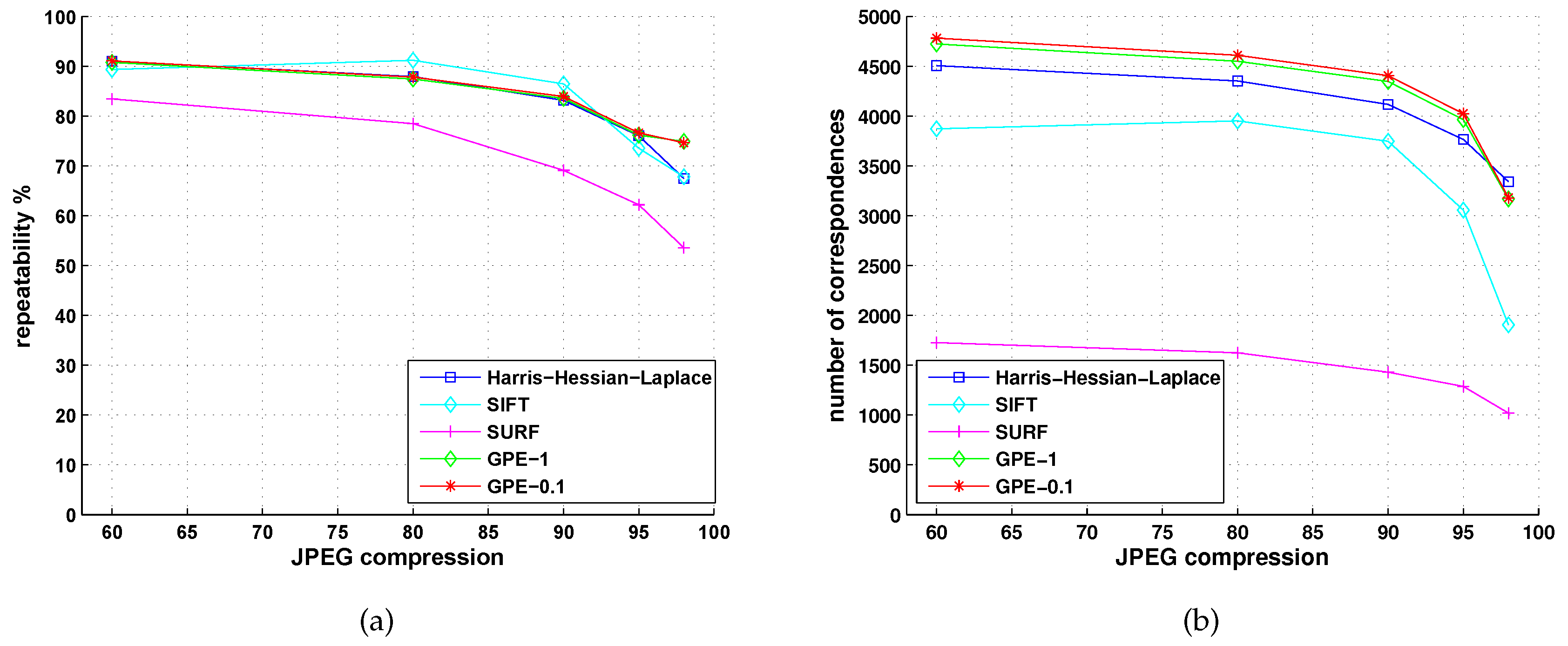
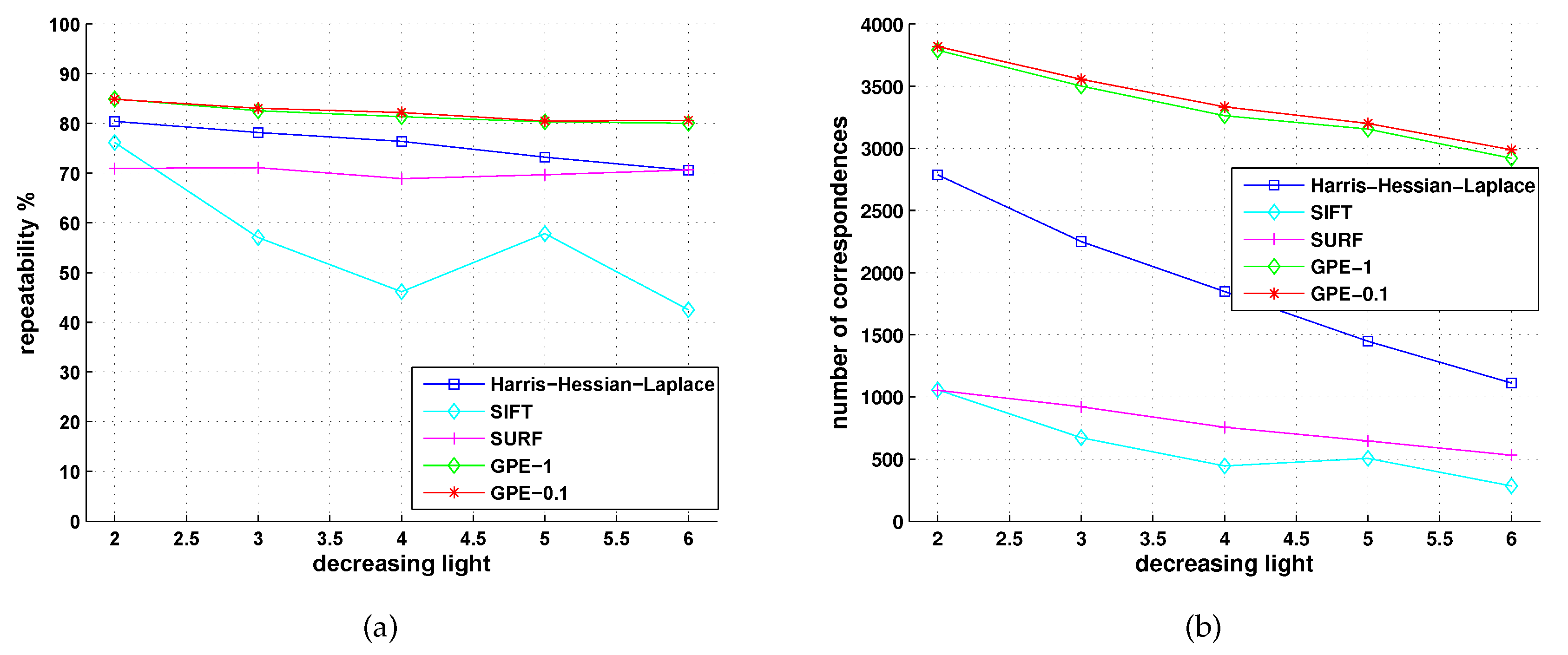
5.2. Comparison with Detectors of Fast-Hessian, DoG, Harris-Laplace and Hessian-Laplace
5.3. Comparison with Locally Contrasting Keypoints Detector
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harris, C.; Stephens, M. A combined corner and edge detector. Proc. Alvey Vision Conf. 1988, 1988, 147–151. [Google Scholar]
- Dufournaud, Y.; Schmid, C.; Horaud, R. Matching images with different resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 15 June 2000; Volume 1, pp. 612–618. [Google Scholar] [CrossRef]
- Lindeberg, T. Feature Detection with Automatic Scale Selection. Int. J. Comput. Vis. 1998, 30, 79–116. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale-space theory: A basic tool for analyzing structures at different scales. J. Appl. Stat. 1994, 21, 225–270. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. iccv 1999, 2, 1150–1157. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Indexing based on scale invariant interest points. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, July 7–14 2001; Volume 1, pp. 525–531. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. An Affine Invariant Interest Point Detector. In Computer Vision—ECCV 2002: 7th European Conference on Computer Vision Copenhagen, Denmark, May 28–31, 2002 Proceedings, Part I; Heyden, A., Sparr, G., Nielsen, M., Johansen, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 128–142. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Computer Vision—ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, May 7–13, 2006. Proceedings, Part I; Leonardis, A., Bischof, H., Pinz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Lomeli-R, J.; Nixon, M.S. The Brightness Clustering Transform and Locally Contrasting Keypoints. In Computer Analysis of Images and Patterns; Azzopardi, G., Petkov, N., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 362–373. [Google Scholar]
- Lomeli-R, J.; Nixon, M.S. An extension to the brightness clustering transform and locally contrasting keypoints. Mach. Vis. Appl. 2016, 27, 1187–1196. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Gool, L.V. A Comparison of Affine Region Detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Scale & Affine Invariant Interest Point Detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar] [CrossRef]
- Schaffalitzky, F.; Zisserman, A. Multi-view Matching for Unordered Image Sets, or “How Do I Organize My Holiday Snaps?”. In Computer Vision—ECCV 2002: 7th European Conference on Computer Vision Copenhagen, Denmark, May 28–31, 2002 Proceedings, Part I; Heyden, A., Sparr, G., Nielsen, M., Johansen, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 414–431. [Google Scholar] [CrossRef]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust Wide Baseline Stereo from Maximally Stable Extremal Regions. Br. Mach. Vis. Conf. 2002, 22, 384–393. [Google Scholar]
- Tuytelaars, T.; Gool, L.V. Wide baseline stereo matching based on local, affinely invariant regions. In Proceedings of the British Machine Vision Conference 2000 (BMVC 2000), Bristol, UK, 11–14 September 2000; pp. 412–425. [Google Scholar]
- Tuytelaars, T.; Van Gool, L. Matching Widely Separated Views Based on Affine Invariant Regions. Int. J. Comput. Vis. 2004, 59, 61–85. [Google Scholar] [CrossRef]
- Kadir, T.; Zisserman, A.; Brady, M. An Affine Invariant Salient Region Detector. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2004; pp. 228–241. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shi, B. A Global Extraction Method of High Repeatability on Discretized Scale-Space Representations. Information 2019, 10, 376. https://doi.org/10.3390/info10120376
Zhang Q, Shi B. A Global Extraction Method of High Repeatability on Discretized Scale-Space Representations. Information. 2019; 10(12):376. https://doi.org/10.3390/info10120376
Chicago/Turabian StyleZhang, Qingming, and Buhai Shi. 2019. "A Global Extraction Method of High Repeatability on Discretized Scale-Space Representations" Information 10, no. 12: 376. https://doi.org/10.3390/info10120376
APA StyleZhang, Q., & Shi, B. (2019). A Global Extraction Method of High Repeatability on Discretized Scale-Space Representations. Information, 10(12), 376. https://doi.org/10.3390/info10120376




