Adaptive Inverse Controller Design Based on the Fuzzy C-Regression Model (FCRM) and Back Propagation (BP) Algorithm
Abstract
:1. Introduction
2. T-S Fuzzy Model
3. T-S Fuzzy Model Identification Using FCRM
4. Proposed Algorithm
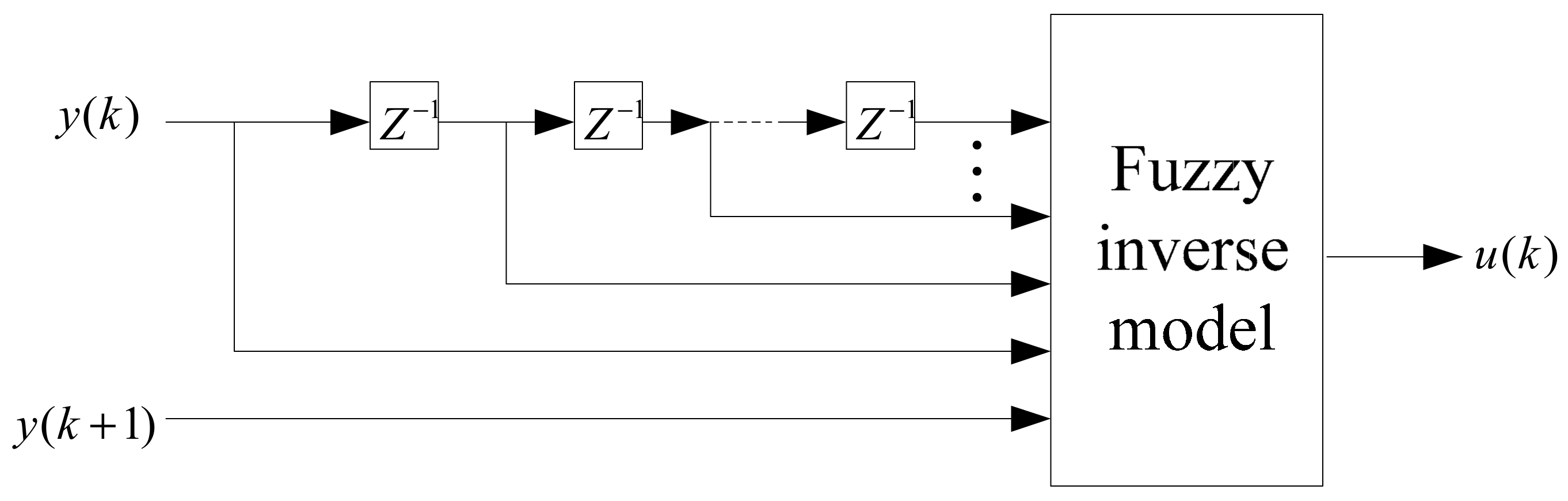
4.1. Inverse Modeling Using FCRM
- Step 1. Initialize matrix U0(c×N) to satisfy the Constrains (3), the clustering number c, parameter m (usually m = 2), termination threshold ε > 0, and maximum number of iterations Cyc, set r = 1;
- Step 2. Calculate the r-th iteration by Equation (11);
- Step 3. Calculate the r-th iteration by Equation (8), if matrix norms ||Ur− Ur-1|| < ε, or the iteration variation r equal to Cyc, go to Step 4, else r = r + 1 and go to Step 2;
- Step 4. Calculate the premise parameter by Equation (13);
- Step 5. The consequent parameters of T-S fuzzy model are the θ values obtained by FCRM clustering algorithm.
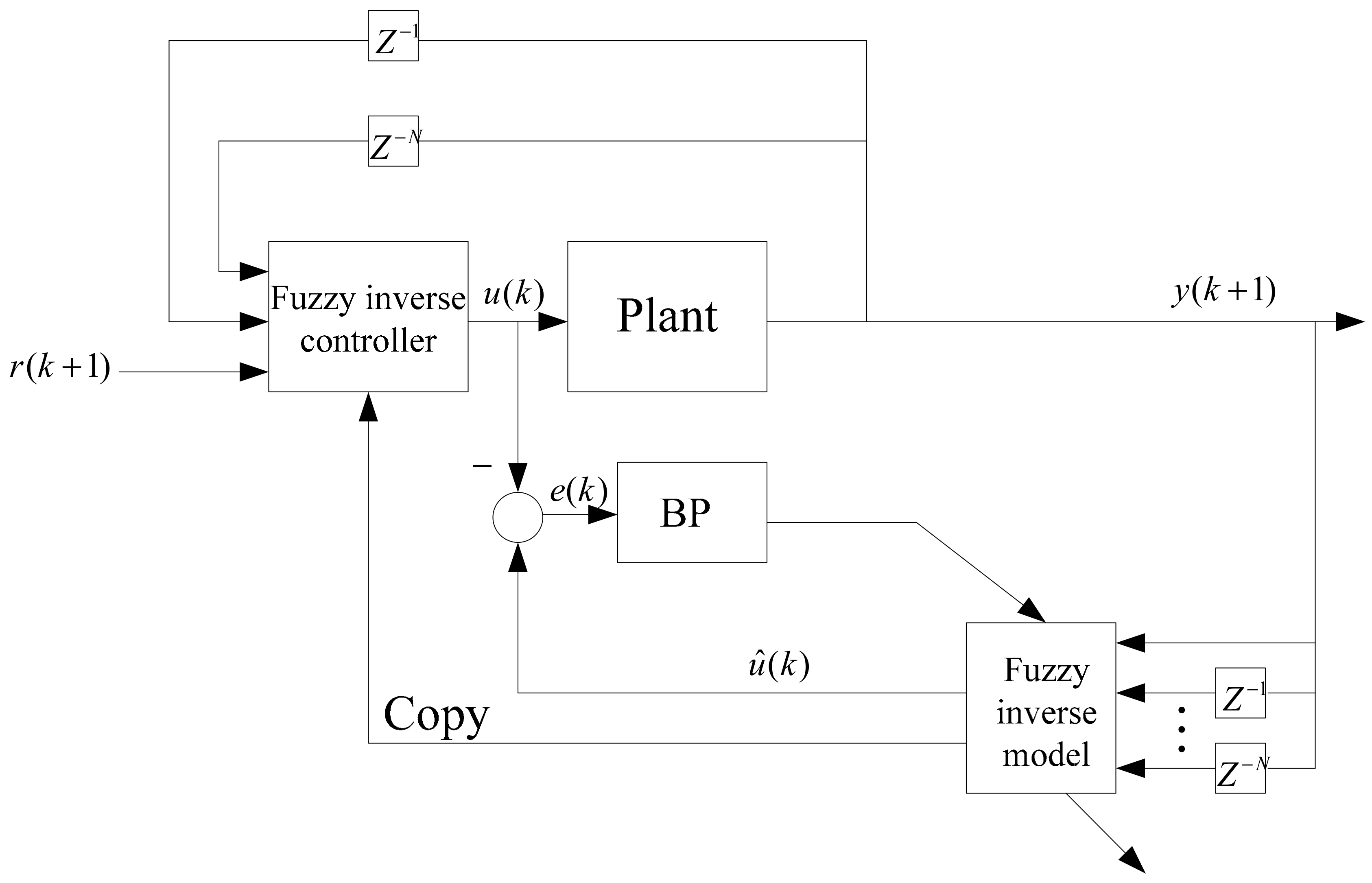
4.2. Online Adaptive Inverse Controller Structure
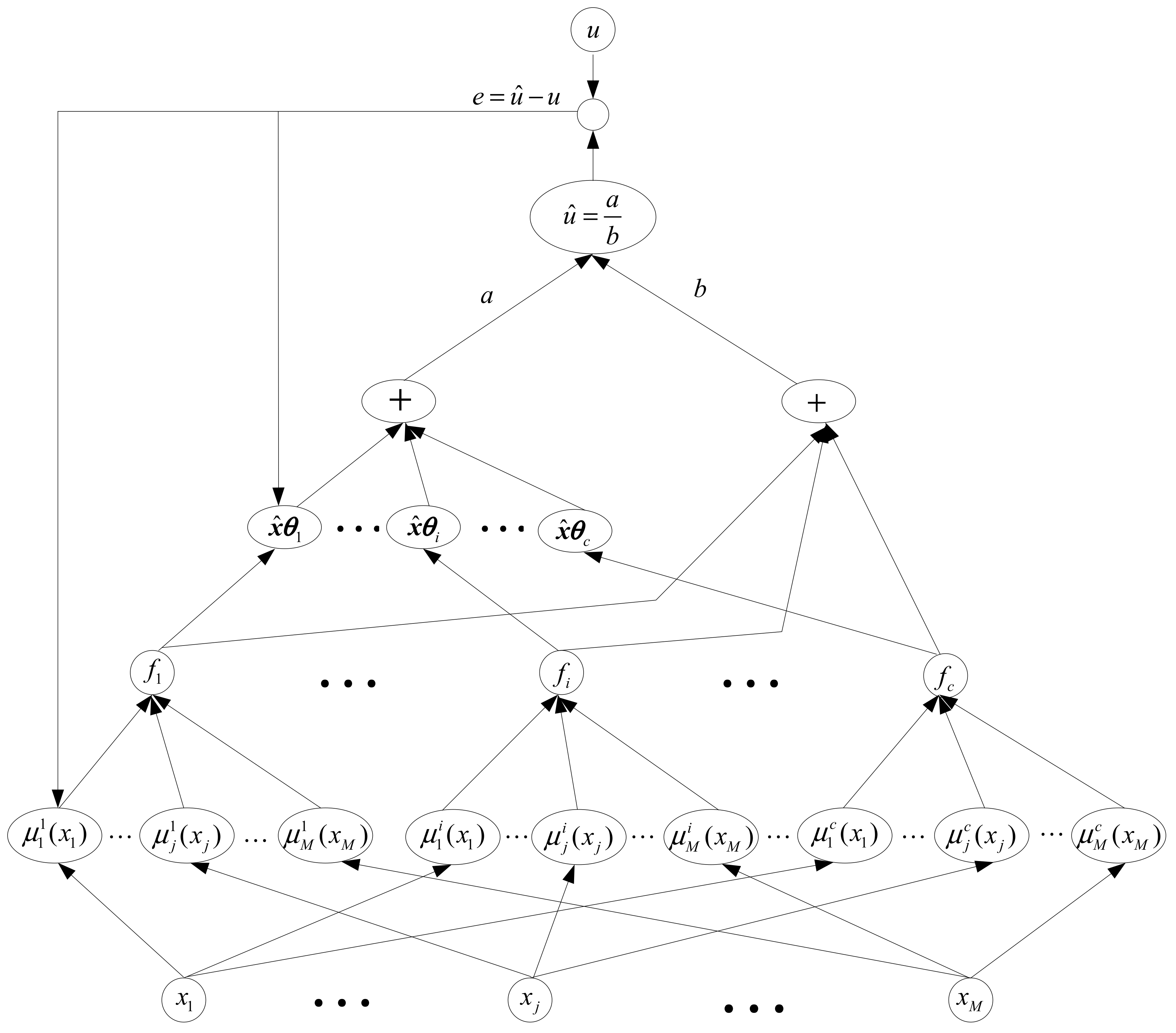
4.3. Online Parameter Adjustment
- (1)
- (2)
- Updating :where and yi is shown as Equation (1).
- (3)
- Updating :where .
- (4)
- Updating θ:where and .
5. Simulation Examples
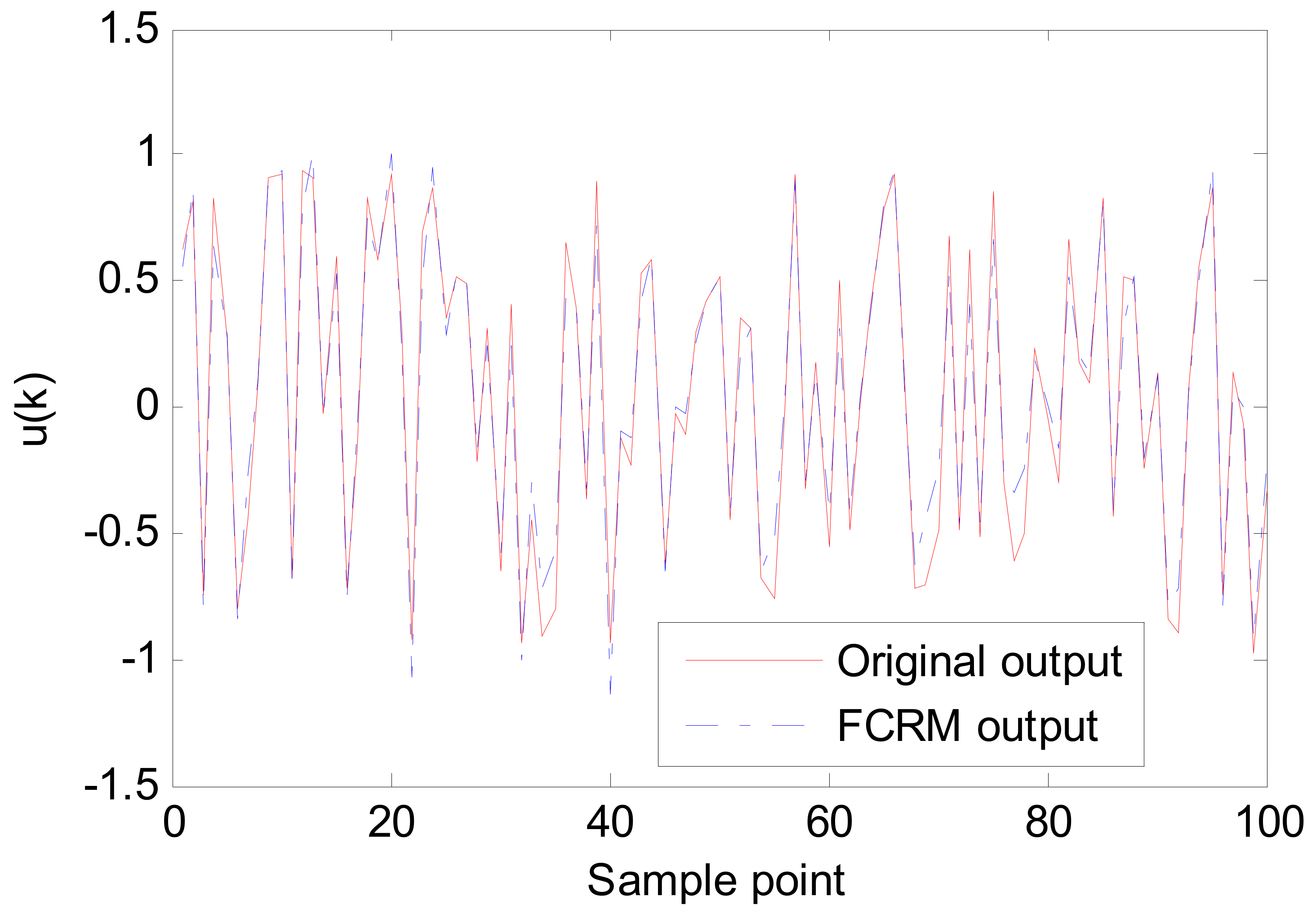
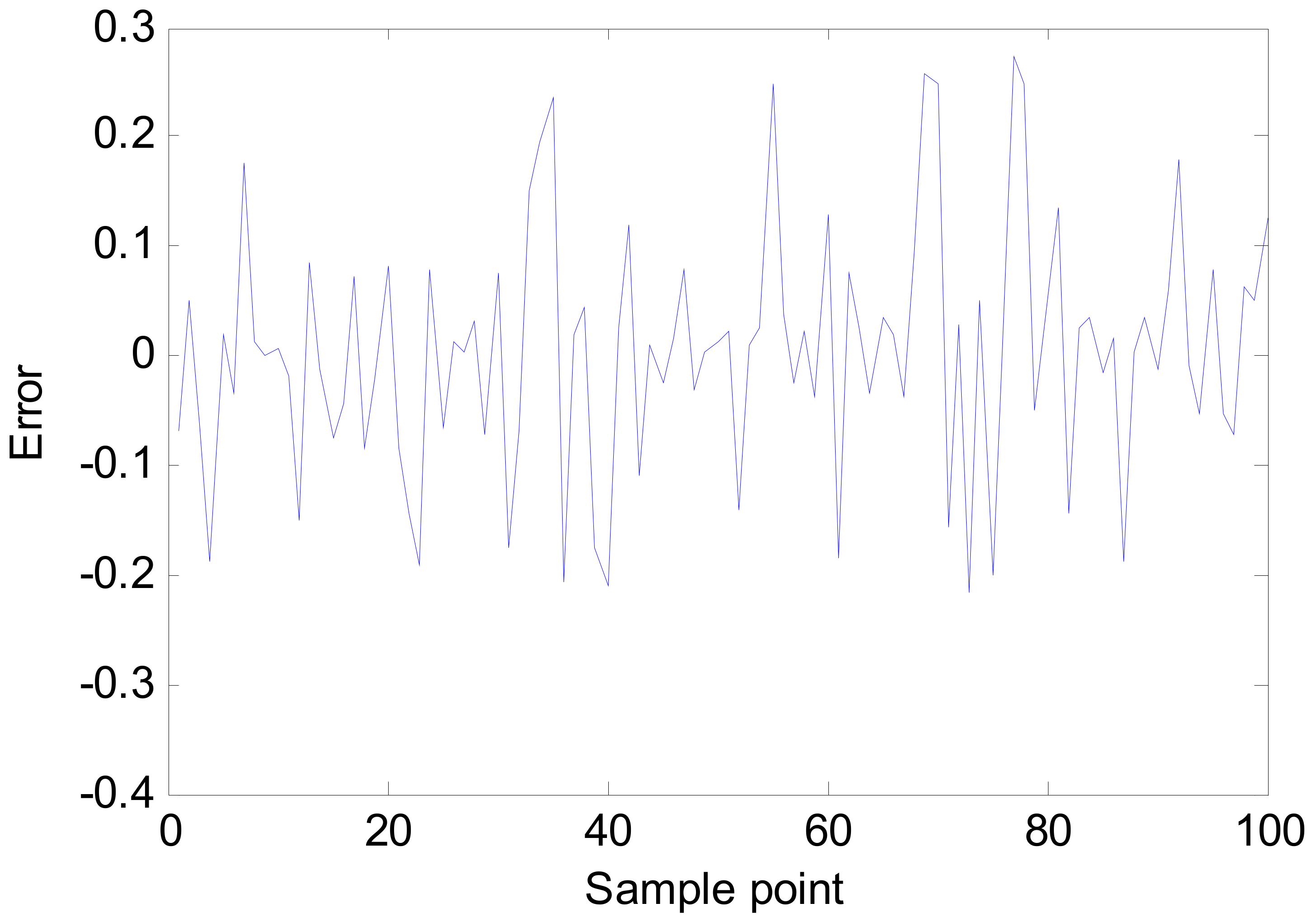
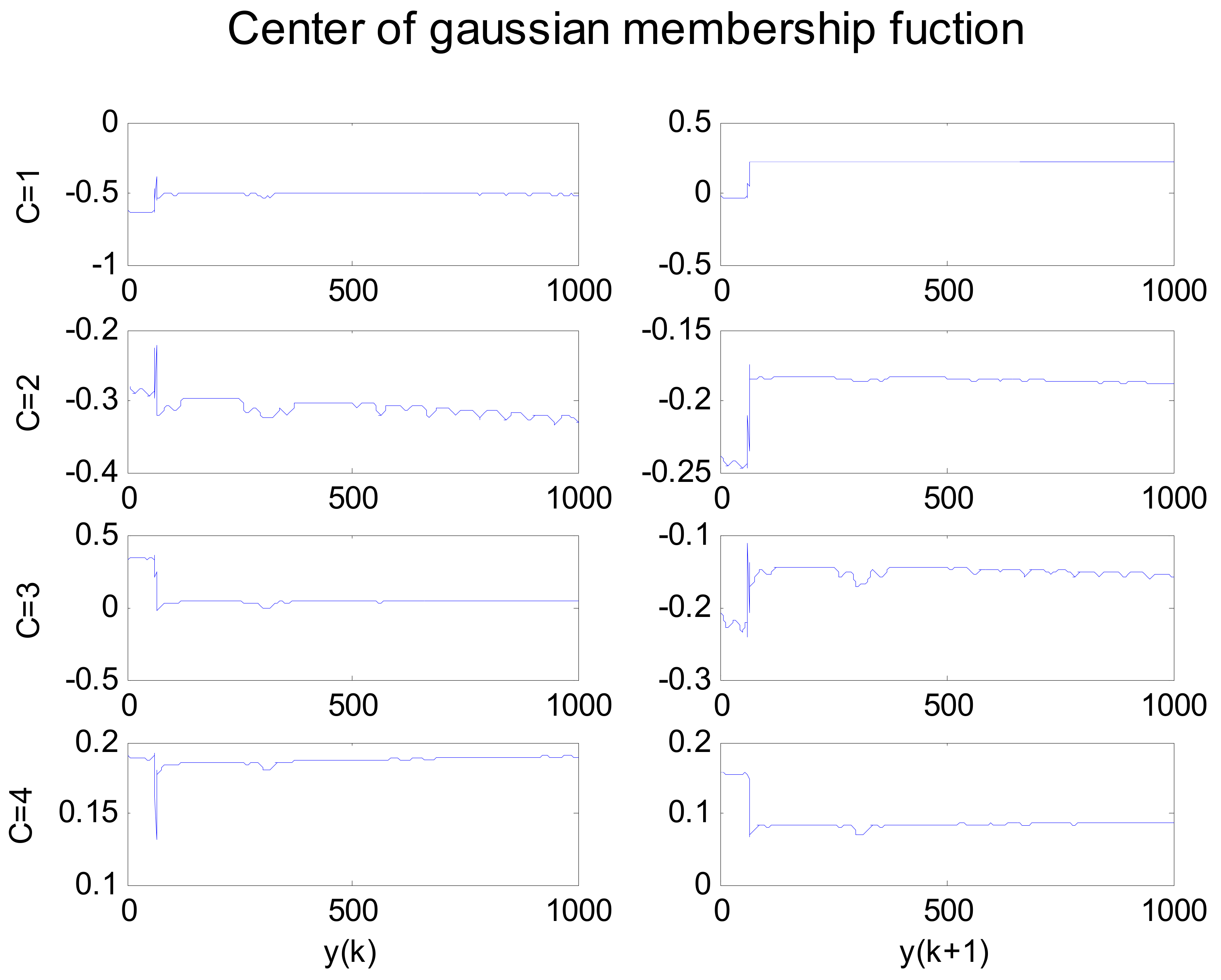
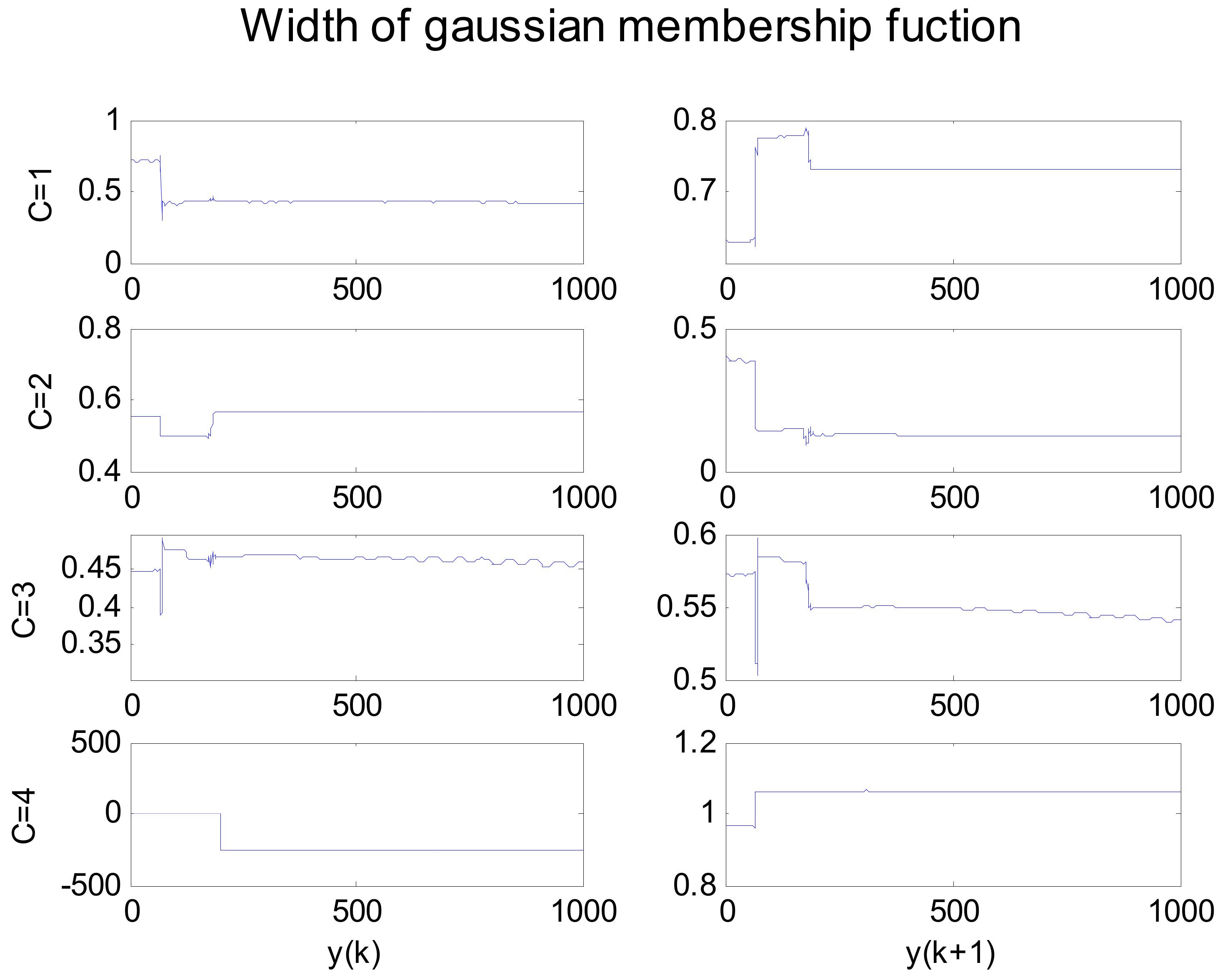
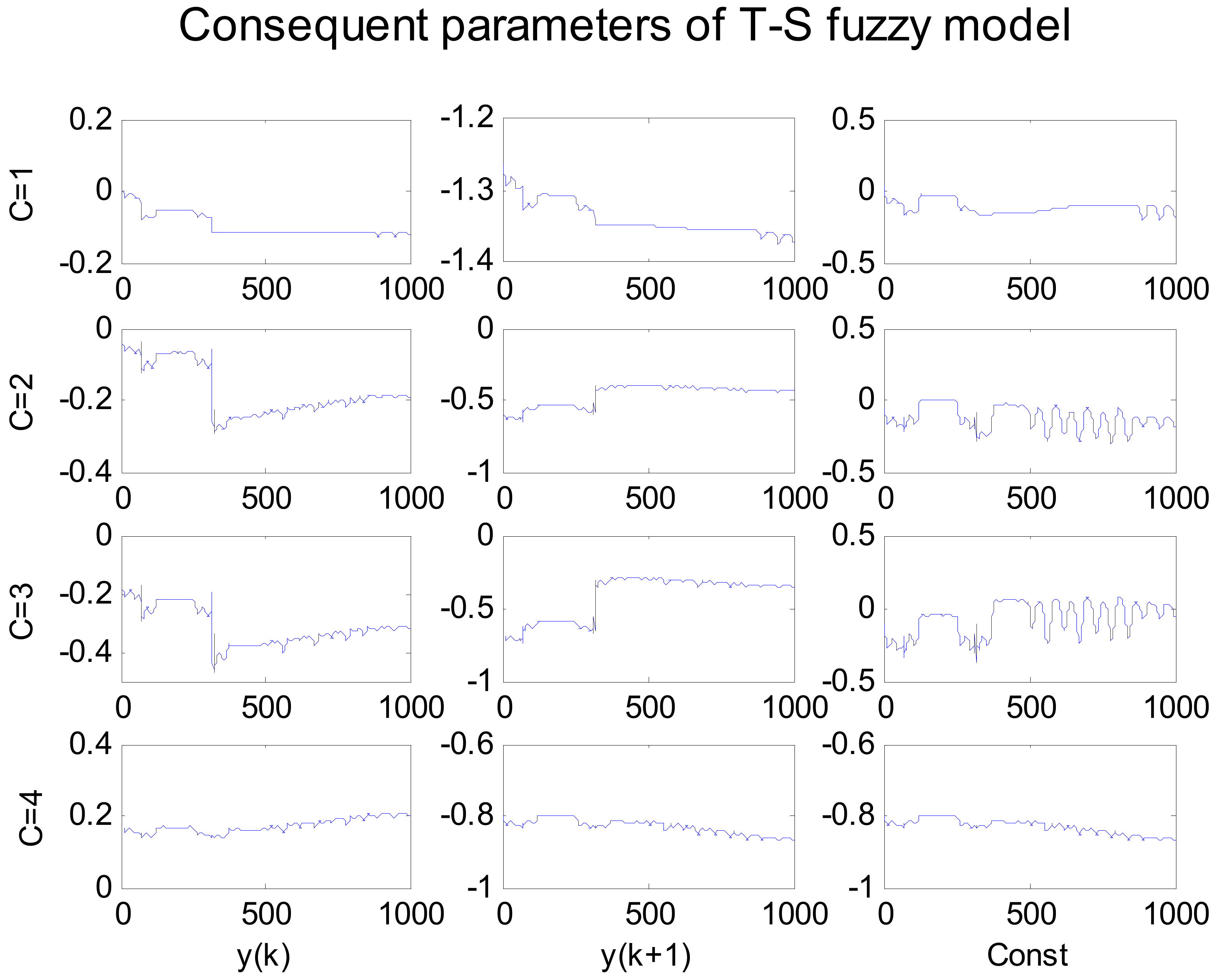
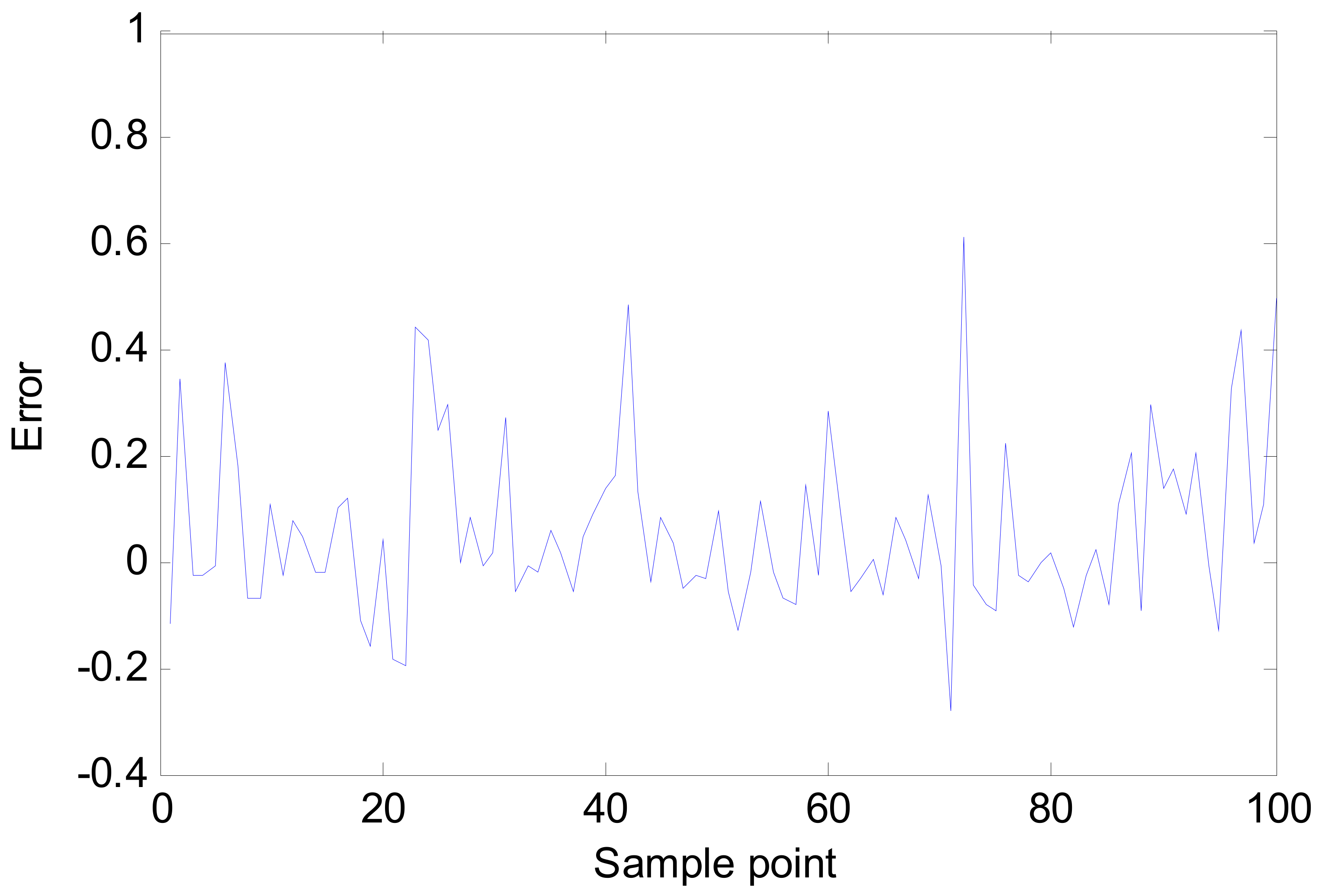
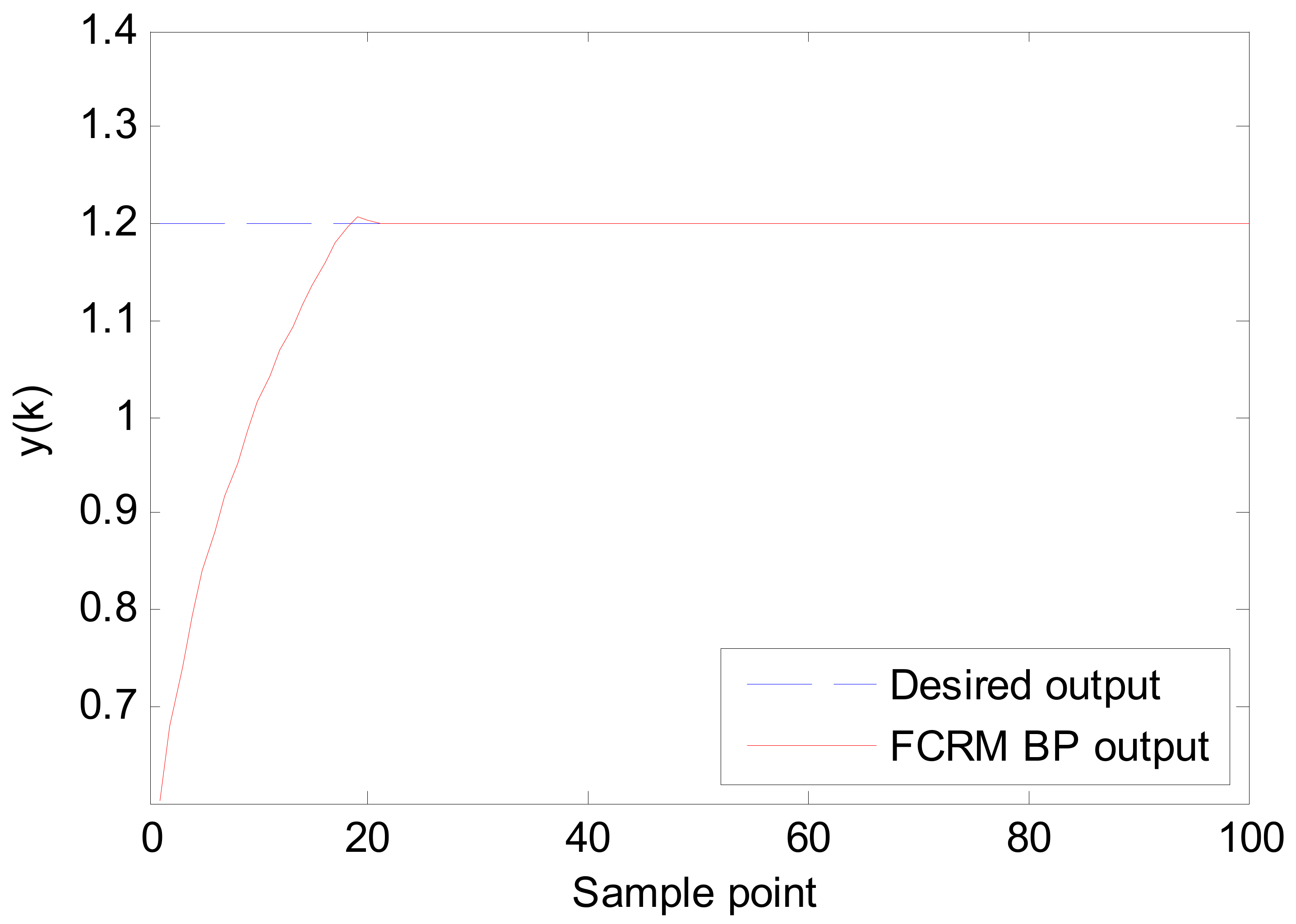
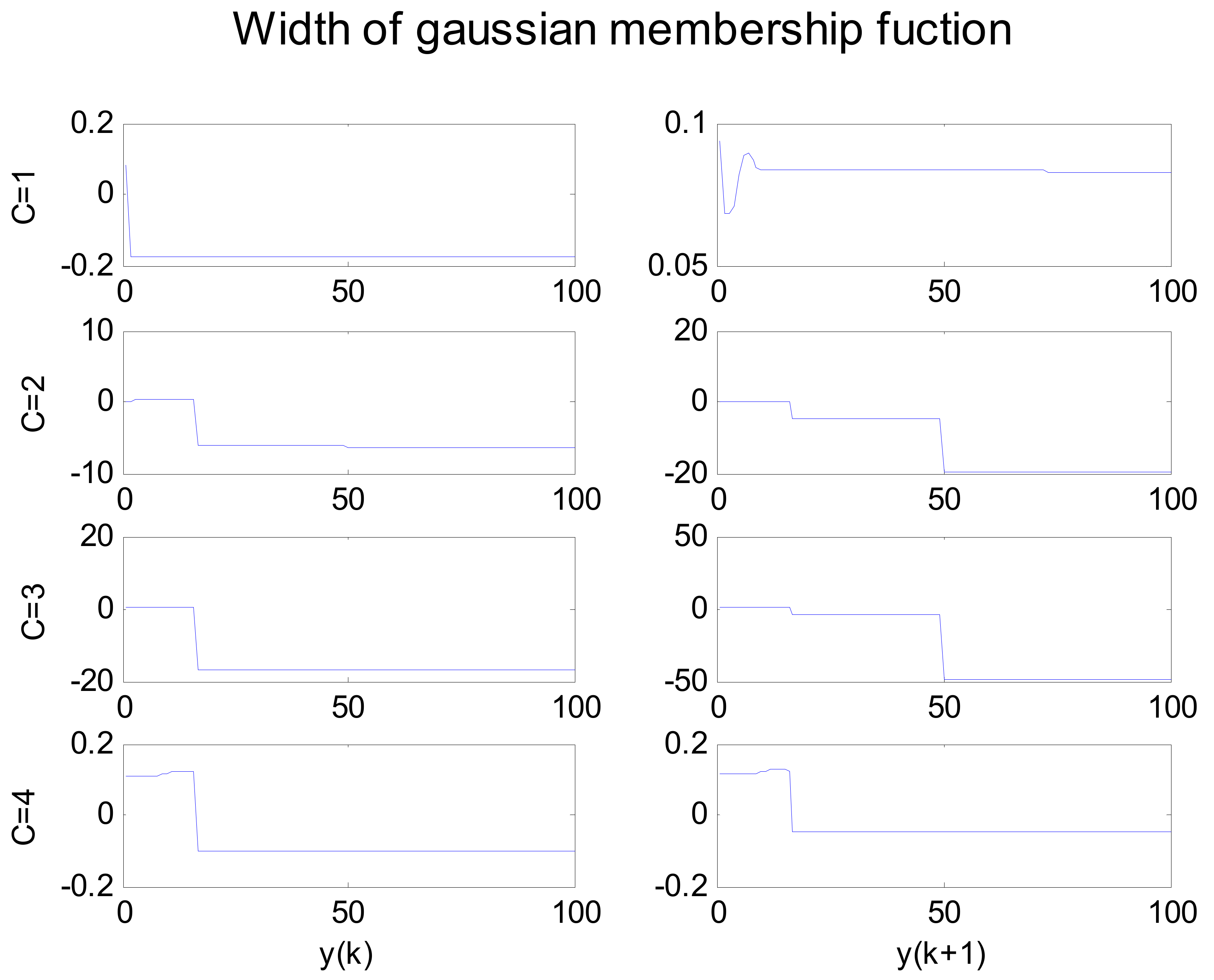
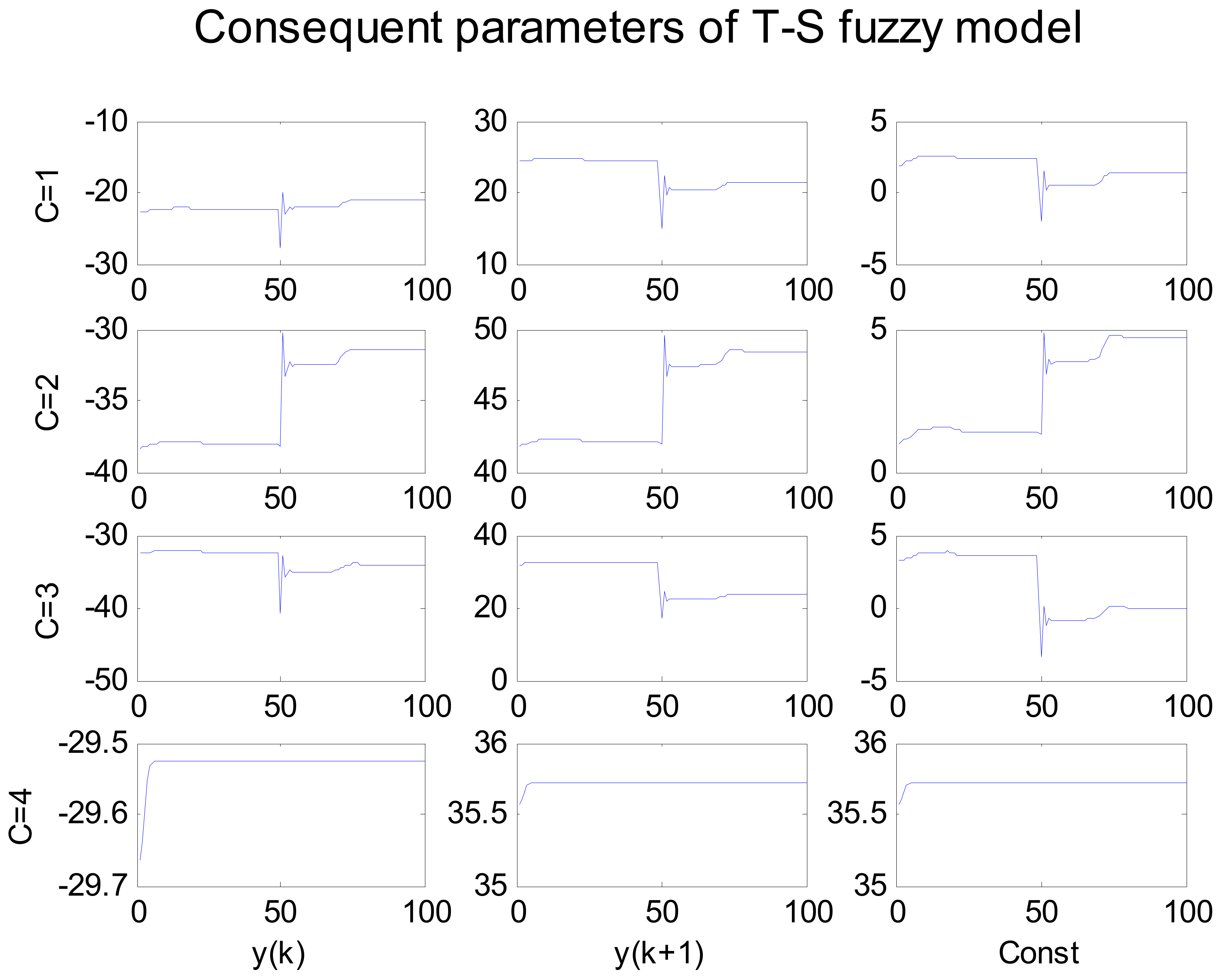
5.1. Simulation 1
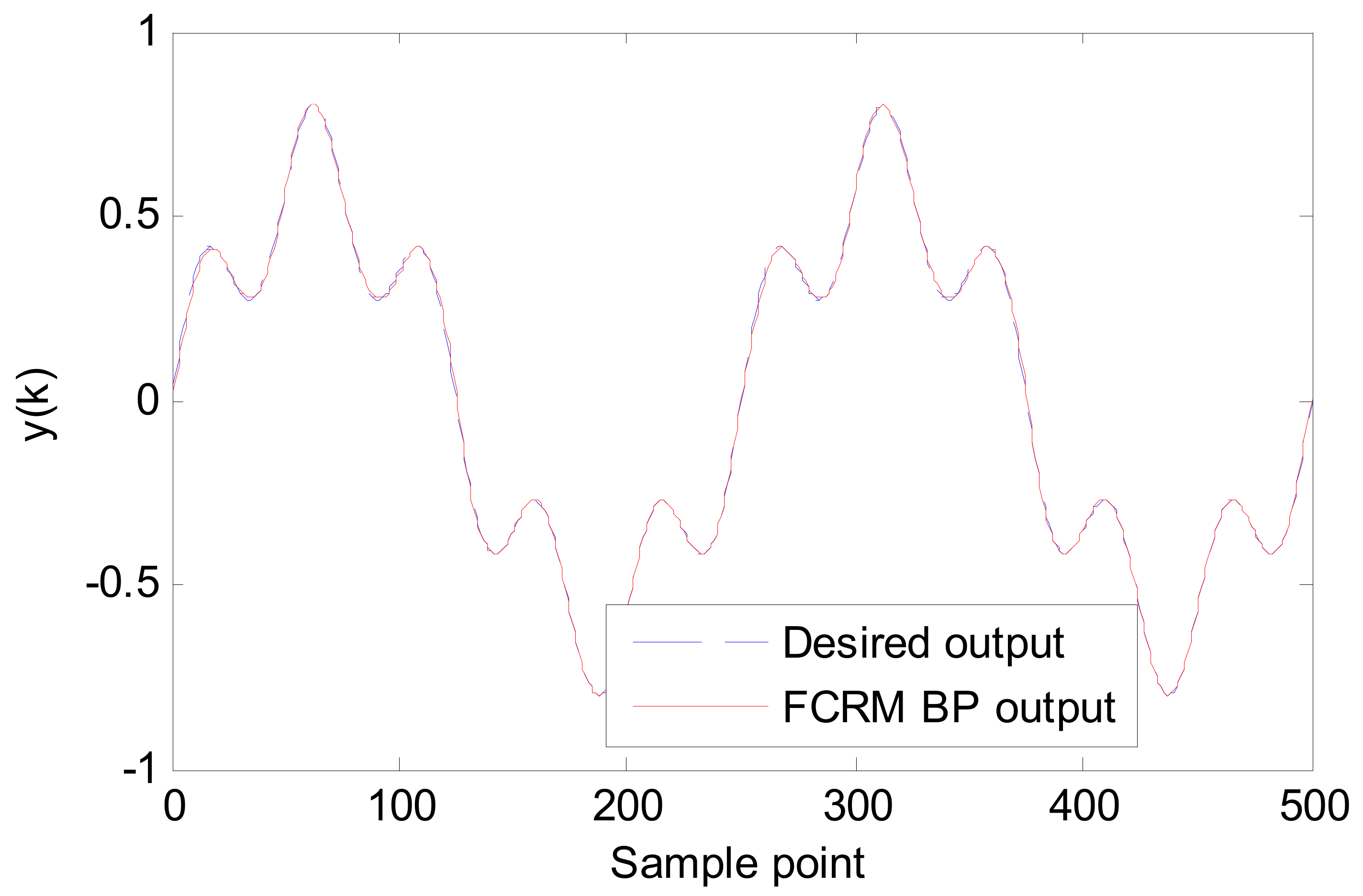
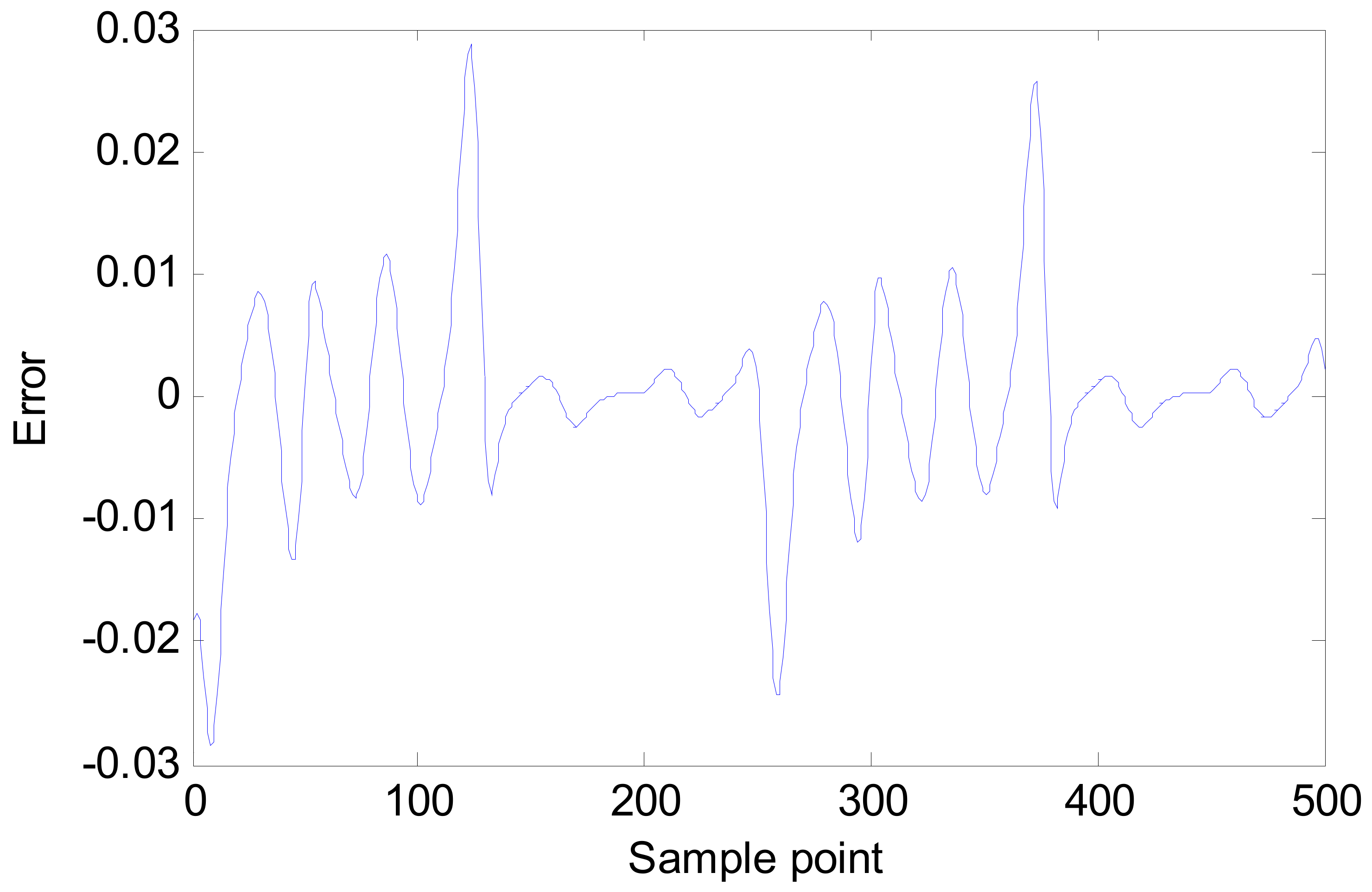
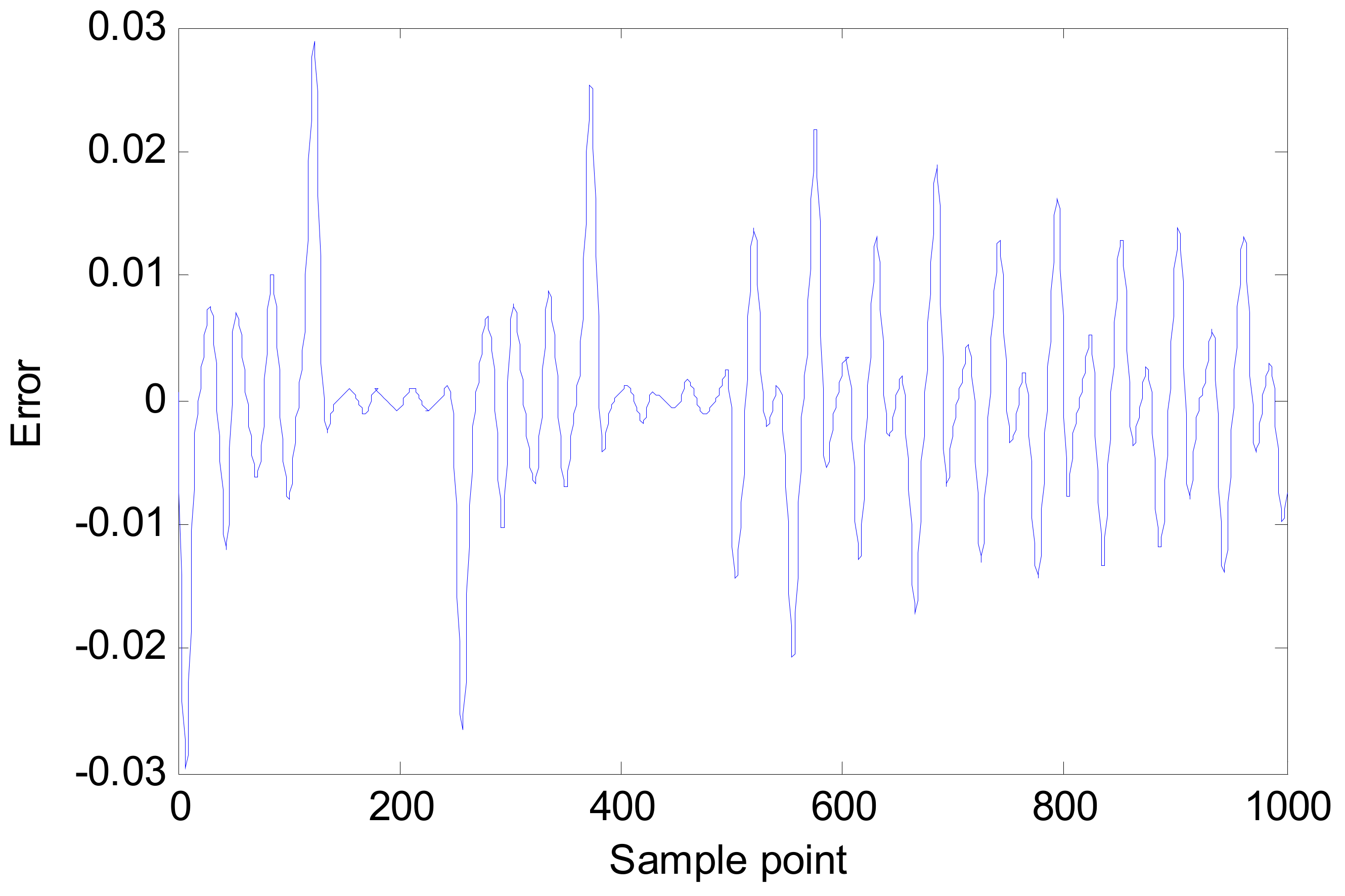
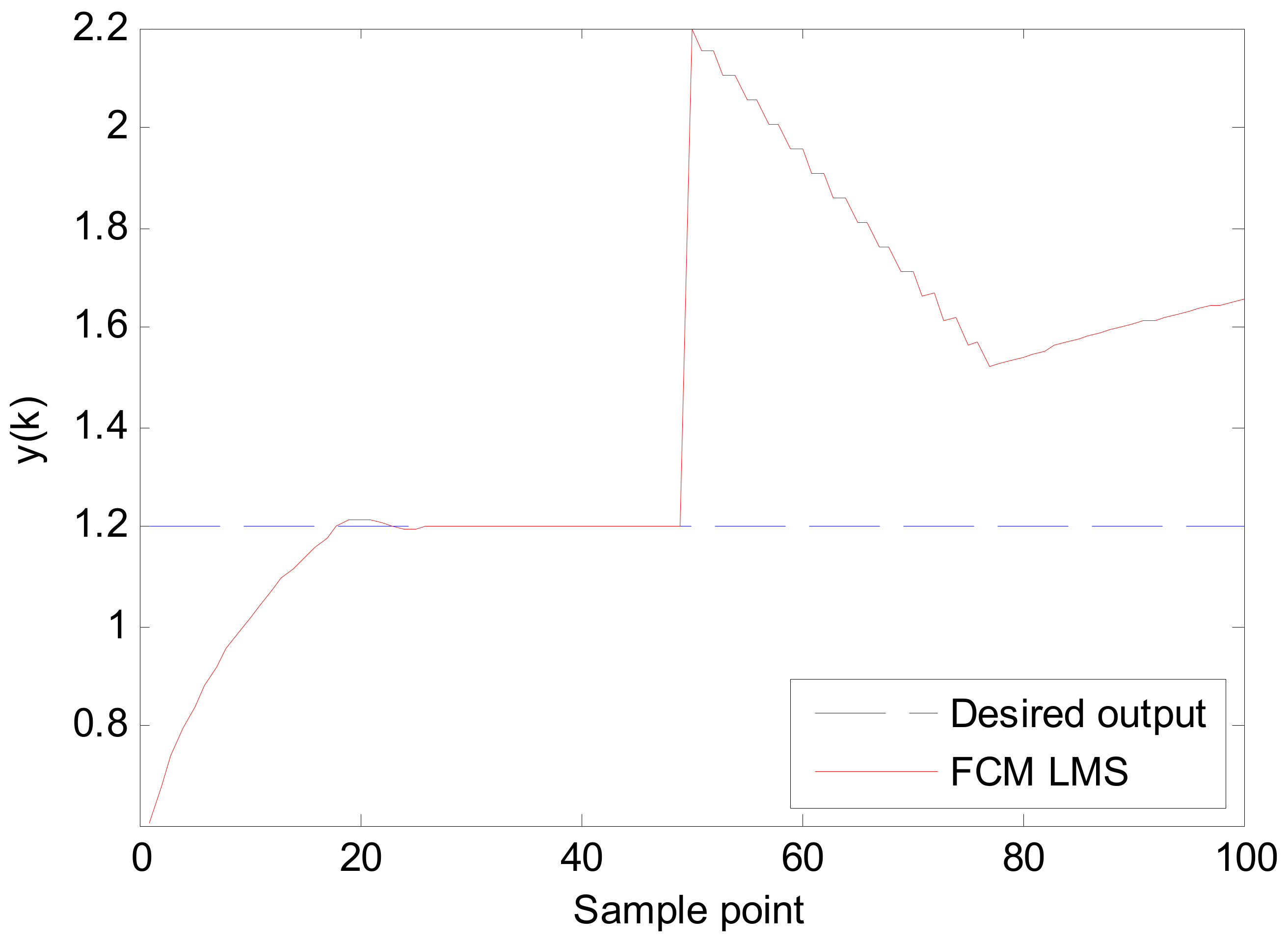
5.2. Simulation 2
6. Conclusions
Funding
Conflicts of Interest
References
- Yi, J.H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.G. An improved NSGA-III algorithm with adaptive mutation operator for big data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Gandomi, A.H.; Hao, G.S.; Wang, H. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2014, 24, 853–871. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Ardila, C.; Capacho, R. Local search methods for the solution of implicit inverse problems. Soft Comput. 2018, 22, 4819–4832. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Yang, X.S. Improved Tabu Search and Simulated Annealing methods for nonlinear data assimilation. Appl. Soft Comput. 2019. [Google Scholar] [CrossRef]
- De La Sen, M. On the robust adaptive stabilization of a class of nominally first-order hybrid systems. IEEE Trans. Autom. Control 1999, 44, 597–602. [Google Scholar] [CrossRef]
- Bilbao-Guillerna, A.; De la Sen, M.; Ibeas, A.; Alonso-Quesada, S. Robustly stable multiestimation scheme for adaptive control and identification with model reduction issues. Discret. Dyn. Nat. Soc. 2005, 2005, 31–67. [Google Scholar] [CrossRef]
- Yoo, S.J. Adaptive control of non-linearly parameterised pure-feedback systems. IET Control Theory Appl. 2012, 6, 467–473. [Google Scholar] [CrossRef]
- Widrow, B.; Walach, F. Adaptive Inverse Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Yingnong, D.; Chongzhao, H. Adaptive inverse control based on volterra polynomial basis function neural networks. J. Xi’an Jiao Tong Univ. 2000, 34, 8–12. [Google Scholar]
- Dang, Y.N.; Han, C.Z. Direct adaptive inverse control strategy based on modified VPBF neural networks. Control Decis. 2001, 16, 633–636. [Google Scholar]
- Hu, T.T.; Kang, B.; Shan, Y.N. Study on identification of adaptive inverse control system based on dynamic function linked neural network. Comput. Sci. 2017, 44, 203–208. [Google Scholar]
- Salman, R. Neural networks of adaptive inverse control systems. Applied Math. Comp. 2005, 163, 931–939. [Google Scholar] [CrossRef]
- Liu, F.C.; Liu, Y.; Dou, J.M.; Zhang, Y.-X. Model reference adaptive inverse control based on T-S fuzzy model. Syst. Eng. Electron. 2013, 35, 1940–1947. [Google Scholar]
- Liu, F.C.; Zhang, Y.X.; Wang, Y.J.; Dou, C. Adaptive inverse control method based on fuzzy inverse mode. Chin. J. Sci. Instrum. 2010, 31, 961–967. [Google Scholar]
- Ding, H.S.; Mao, J.Q.; Lin, Y. Adaptive direct inverse control based on fuzzy tree models. Acta Autom. Sin. 2008, 34, 574–580. [Google Scholar] [CrossRef]
- Gao, J.J.; Li, X.M.; Liu, Y.; Liu, F. Adaptive inverse control based on interval type 2 T-S fuzzy model. Fuzzy Syst. Math. 2016, 30, 59–73. [Google Scholar]
- Deng, L.C. Adaptive Inverse Control on Object of Superheated Steam Temperature for Boiler. Ph.D. Thesis, Chong Qing University, Chongqing, China, 2007. [Google Scholar]
- Chen, H.; Wang, G.J.; Wang, Z.J. Adaptive inverse control for feed water and superheated steam temperature of supercritical pressure boiler. J. Chongqing Univ. 2013, 36, 32–36. [Google Scholar]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. An inverse controller design method for interval type-2 fuzzy models. Soft Comput. 2015, 21, 1–22. [Google Scholar] [CrossRef]
- Wang, T.C.; Tong, S.C. Direct inverse control of cable-driven parallel system based on type-2 fuzzy systems. Inf. Sci. 2015, 310, 1–15. [Google Scholar] [CrossRef]
- Ulu, C. Exact Analytical Inversion of Interval Type-2 TSK Fuzzy Logic Systems with Closed Form Inference Methods. Appl. Soft Comput. 2015, 37, 60–70. [Google Scholar] [CrossRef]
- Liu, F.C.; Liu, Y.; Xu, W.L.; Liu, J. Fuzzy adaptive inverse control for pneumatic loading system. J. Mech. Eng. 2014, 50, 185–190. [Google Scholar] [CrossRef]
- Wang, T.; Tong, S.; Yi, J.; Li, H. Adaptive Inverse Control of Cable-Driven Parallel System Based on Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2015, 23, 1803–1816. [Google Scholar] [CrossRef]
- Cheng-Dong, L.; Jian-Qiang, Y.; Yi, Y.; Dong-Bin, Z. Inverse Control of Cable-driven Parallel Mechanism Using Type-2 Fuzzy Neural Network. Acta Autom. Sin. 2010, 36, 459–464. [Google Scholar]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Interval type-2 fuzzy inverse controller design in nonlinear IMC structure. Eng. Appl. Artif. Intell. 2011, 24, 996–1005. [Google Scholar] [CrossRef]
- Fallah, M.; Moetakef-Imani, B. Adaptive inverse control of chatter vibrations in internal turning operations. Mech. Syst. Signal Process. 2019, 129, 91–111. [Google Scholar] [CrossRef]
- Liu, F.C.; Gao, X.; Wu, S.C. Research on adaptive inverse control and its future developments. Chin. J. Sci. Instrum. 2008, 29, 2683–2688. [Google Scholar]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Adaptive fuzzy model based inverse controller design using BB-BC optimization algorithm. Expert Syst. Appl. 2011, 38, 12356–12364. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M.; Sugeno, M. Fuzzy Identification of Systems and its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Chen, J.Q.; Xi, Y.G.; Zhang, Z.J. A clustering algorithm for fuzzy model identification. Fuzzy Sets Syst. 1998, 98, 319–332. [Google Scholar] [CrossRef]
- Kung, C.C.; Su, J.Y. Affine Takagi-Sugeno fuzzy modelling algorithm by fuzzy c-regression models clustering with a novel cluster validity criterion. IET Control Theory Appl. 2007, 1, 1255–1265. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Xiang, X.; Li, Q.; An, X. T–S fuzzy model identification based on a novel fuzzy c-regression model clustering algorithm. Eng. Appl. Artif. Intell. 2009, 22, 646–653. [Google Scholar] [CrossRef]




© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian Zhong, S. Adaptive Inverse Controller Design Based on the Fuzzy C-Regression Model (FCRM) and Back Propagation (BP) Algorithm. Information 2019, 10, 377. https://doi.org/10.3390/info10120377
Jian Zhong S. Adaptive Inverse Controller Design Based on the Fuzzy C-Regression Model (FCRM) and Back Propagation (BP) Algorithm. Information. 2019; 10(12):377. https://doi.org/10.3390/info10120377
Chicago/Turabian StyleJian Zhong, Shi. 2019. "Adaptive Inverse Controller Design Based on the Fuzzy C-Regression Model (FCRM) and Back Propagation (BP) Algorithm" Information 10, no. 12: 377. https://doi.org/10.3390/info10120377
APA StyleJian Zhong, S. (2019). Adaptive Inverse Controller Design Based on the Fuzzy C-Regression Model (FCRM) and Back Propagation (BP) Algorithm. Information, 10(12), 377. https://doi.org/10.3390/info10120377





